Mulyana
KALKULUS
UNTUK
STATISTIKA
BUKU AJAR
UNIVERSITAS PADJADJARAN
FAKULTAS MIPA
JURUSAN STATISTIKA
BANDUNG
2005
10 5 0 5 10 11.81 5.91 5.91 11.81 f x( ) g x( ) x10 5
0
5
10
8.05
4.03
4.03
8.05
gx
( )
hx
( )
x
i
Kata Pengantar
Diktat ini disusun dalam upaya pengadaan bahan ajar Kalkulus I di Fakultas Teknik Universitas Pasundan, mengingat mata kuliah ini merupakan mata kuliah dasar keakhlian, sehingga materi kuliah yang diberikan diharapkan dapat mendukung para mahasiswa Fakultas Teknik Universitas Pasundan dalam mempelajari materi kuliah ilmu-ilmu teknik yang banyak memerlukan pemahaman ilmu kalkulus. Selain itu, karena mata kuliah Kalkulus ini merupakan salah satu mata kuliah yang diberikan pada kelas-kelas paralel, yang diajarkan oleh beberapa dosen, sehingga keragaman materi dan pencapaian materi kemungkinannya cukup besar. Oleh karena itu, dengan adanya diktat ini diharapkan keragaman tersebut dapat diperkecil.
Penulis merasa materi pada diktat ini masih belum sempurna, sehingga kritik dan saran untuk perbaikan dan penyempurnaannya sangat diharapkan, karena editing akan selalu dilakukan setiap waktu, agar diktat ini dapat dijadikan acuan sebagai bahan ajar mata kuliah Kalkulus untuk mahasiswa fakultas teknik. Kritik, saran, dan bantuan pemikiran dari semua pihak sehingga terwujudnya diktat ini, dan harapan untuk menjadikan diktat ini sebagai acuan materi perkuliahan, sekali lagi sangat diharapkan, dan diucapkan banyak terima kasih atas semua kerja-samanya.
Bandung , Oktober 2004 Penulis
ii DAFTAR ISI Halaman Kata Pengantar i Daftar Isi ii BAB I PENDAHULUAN 1
I.1. Struktur Bilangan 1
I.2. Sistem Bilangan Riil 2
I.3. Kalimat Matematis 4
I.4. Persamaan Linier 5
I.5. Persamaan Kuadrat 5
I.6. Bentuk-Bentuk Pertidaksamaan 8
I.6.1. Pertidaksamaan Linier 8
I.6.2. Pertidaksamaan Irasional 9
I.6.3. Pertidaksamaan Pangkat Dua atau Lebih 11
I.6.4. Pertidaksamaan Pecahan 13
I.6.5. Pertidaksamaan Yang Mengandung Nilai Mutlak 15
BAB II FUNGSI DAN GRAFIK 19
II.1. Deskripsi Fungsi 19
II.2. Gambar Fungsi 21
II.3. Fungsi Komposisi 23
II.4. Beberapa Bentuk Fungsi 24
II.4.1. Fungsi Linier 24
II.4.2. Fungsi Kuadrat 29
II.4.3. Fungsi Pangkat 33
II.4.4. Fungsi Logaritma 33
II.4.4. Fungsi Siklometri (fungsi goniometri , fungsi trigonometri) 34
II.5. Fungsi Irisan Kerucut 39
II.5.1. Lingkaran 39
II.5.2. Ellips 42
iii
BAB III LIMIT DAN KEKONTINUAN FUNGSI 46
III.1. Cara menghitung nilai limit 46
III.2. Dalil-Dalil Limit Fungsi 48
III.3. Limit Kiri , Limit Kanan 50
III.4. Kekontinuan Fungsi 52
BAB IV TURUNAN (DIFERENSIASI) 54
IV.1. Arti Turunan Fungsi 55
IV.2. Dalil Dasar Untuk Turunan 55
IV.3. Turunan Fungsi Implisit 58
IV.4. Turunan dan Kekontinuan Fungsi 59
IV.5. Turunan Orde Tinggi 60
IV.6. Nilai Ekstrim Fungsi 61
1
BAB I
SISTEM BILANGAN
Bilangan adalah sebuah aksioma, sehingga tidak perlu didefinisikan. Untuk
menyatakan sebuah bilangan digunakan lambang bilangan, yang berupa himpunan benda
sejenis yang ada di sekitar kita. Misalnya bilangan lima, dapat dilambangkan oleh lima jari
atau lima buah benda sejenis. Untuk keperluan perhitungan, digunakan gambar lambang
bilangan yang dinamakan dengan angka. Angka inilah yang digunakan sebagai “wakil
bilangan”. Misal pernyataan 5 + 2 = 7. Dalam hal ini, 5, 2 dan 7, bukan sebagai angka, tetapi sebagai wakil dari bilangan “lima”, “dua” dan “tujuh”.
I.1. Struktur Bilangan
Bilangan dapat dikelompokan atas himpunan, 1. Bilangan asli : {1 , 2 , 3 , . . . }
2. Bilangan cacah : {0 , 1 , 2 , 3 , . . . }
Pada himpunan bilangan ini didefinisikan bilangan prima, yaitu bilangan yang hanya
habis dibagi oleh dirinya sendiri. Misal : 2, 3, 5, 7, 11, 13, 17, . . . 3. Bilangan bulat : { . . . , −3 , –2 , −1 , 0 , 1 , 2 , 3 , . . . }
Bilangan yang berada di “sebelah kiri” 0 atau bilangan yang lebih kecil dari 0, dinamakan bilangan negatif. Yang di “kanannya” atau bilangan yang lebih besar dari
0, dinamakan bilangan positif.
4. Bilangan real yang terdiri atas bilangan rasional dan bilangan irasional
Bilangan rasional adalah bilangan yang dapat disajikan dalam bentuk b
a , b tidak sama dengan 0 (ditulis b ≠ 0), dengan a dan b bilangan bulat. Bilangan rasional jika disajikan dalam bilangan desimal, yaitu bilangan yang disajikan dengan menggunakan tanda koma (,) jika nilainnya antara 0 dengan 1. Maka pada desimalnya (bilangan disebelah kanan tanda koma) terjadi pengulangan bilangan atau “terhenti”pada 0. Misalnya,
... 14 2857142857 , 0 7 2 = , 1,333... 3 4 = , 0,2500... 4 1 = , 3 = 0,000…
2 Dalam bilangan rasional, pernyataan
b a
, b ≠ 0, jika a lebih kecil dari b (ditulis a < b), dinamakan pecahan murni, sedangkan jika a lebih besar dari b (ditulis a > b),
dinamakan pecahan campuran, sebab bentuknya dapat disajikan atas bilangan bulat
dan pecahan murni, misalnya :
3 1 1 3
4 = . Bilangan yang tidak memiliki ciri seperti bilangan rasional dinamakan bilangan irasional.
Bilangan irasional merupakan kawan (komplemen) dari bilangan rasional. Bilangan irasional jika disajikan dalam bilangan desimal, maka pada desimalnya tidak akan terjadi pengulangan. Yang termasuk bilangan irasional diantaranya,
1. π = 3,141592654…, yang biasa diidentikan dengan 7 22,
2. bilangan eksponensial e = 2,7182818…, yang biasa diidentikan dengan 3,
3. bilangan akar yang tidak dapat dirasionalkan, misalnya 2, 5 , dan sejenisnya 5. Bilangan kompleks, yaitu bilangan yang disajikan oleh :
a + ib
dengan a dan b bilangan real, i = −1 yang dinamakan bilangan imaginer.
Pada sajian ini a dinamakan bagian real dan b bagian imaginer.
3
Gambar I.1 Struktur Bilangan
Jika dinotasikan, N = himpunan bilangan asli, C = himpunan bilangan cacah, Z = himpunan bilangan bulat, Q = himpunan bilangan rasional, I = himpunan bilangan
irasional, R = himpunan bilangan real, dan K = himpunan bilangan kompleks, maka berlaku hubungan,
1. C = N ∪ {0} 2. Q ∩ I = φ 3. R = Q ∪ I
4. N ⊂ C ⊂ Z ⊂ R ⊂ K
I.2. Sistem Bilangan Real
Dalam matematika, yang disebut dengan sistem, adalah himpunan tidak kosong yang di dalamnya dilibatkan operasi terhadap anggota himpunannya. Pada himpunan bilangan real, operasi antar anggotanya adalah, perkalian (notasinya, x atau . ), yang memiliki kawan, pembagian (notasinya, : atau ÷ ), dan perjumlahan (notasinya, + ) yang memiliki kawan, pengurangan (notasinya, −−−− ). Pada proses perhitungan, operasi perkalian harus
bilangan kompleks bilangan
imaginer bilangan real
bilangan
irasional bilangan rasional bilangan
pecahan bilangan bulat
bilangan bulat
negatif bilangan cacah
bilangan nol
4
didahulukan dari operasi perjumlahan, kecuali jika operasi perjumlahan itu ada didalam tanda kurung, sedangkan operasi perkalian dengan pembagian, dan perjumlahan dengan pengurangan, sifatnya setara, artinya mana yang lebih dulu disajikannya. Jadi yang
dimaksud dengan sistem bilangan real adalah himpunan bilangan real yang di
dalammya dilibatkan operasi-operasi x dan +.
Sistem bilangan real merupakan sitem bilangan yang banyak digunakan dalam perhitungan sehari-hari dan persoalan terapan. Operasi dalam sistem bilangan real memiliki sifat :
1. Tertutup.
Jika a dan b bilangan real, maka a x b (ditulis ab) dan a + b juga bilangan real.
2. Komutatif.
Jika a dan b bilangan real, maka ab = ba , dan a + b = b + a . 3. Asosiatif.
Jika a , b , dan c bilangan real, maka a(bc) = (ab)c , dan a + (b + c) = (a + b) 4. Distributif.
Jika a , b , dan c bilngan real, maka a(b + c) = ab + ac
Sifat asosiatif dan distributif menyatakan bahwa operasi dalam tanda kurung harus selalu didahulukan.
5. Trikhotomi.
Jika a dan b bilangan real, maka hanya satu dari tiga hubungan di bawah ini yang berlaku.
1) a = b,
2) a > b yang berarti : a – b positif ( a – b > 0), 3) a < b yang berarti : a – b negatif ( a – b < 0),
Sifat trikhotomi ini menyimpulkan, jika a dan b bilangan real, maka kemungkinannya a = b atau a b. Dan jika a b, maka kemungkinannya a < b atau a > b.
Dalam sistem bilalangan real, disajikan pula pernyataan a ≥ b, atau a ≤ b. Perbedaan arti dari sajian a ≥ b dengan a > b, (a ≤ b dengan a ≤ b) adalah : jika a < b (a > b) artinya a dengan b murni tidak sama. Tetapi untuk a ≤ b (a ≥ b) tidak murni tidak sama,
5
Sebagai implikasi dari sifat trikhotomi, maka berlaku hubungan 1) a + b > 0, jika a > 0, b > 0,
a + b < 0, jika a < 0, b < 0,
ab > 0, jika a > 0, b > 0, atau a < 0, b< 0 ab < 0, jika a > 0, b < 0, atau a < 0, b > 0. 2) untuk setiap bilangan real c,
(1) a + c > b + c, jika a > b, (2) a + c < b + c, jika a < b,
(3) jika a > b, maka ac > bc, jika c > 0. Dan ac < bc, jika c < 0, sebaliknya,
jika a < b, maka ac < bc, jika c > 0. Dan ac > bc, jika c < 0.
6. Adanya unsur satuan
Definisi
s dinamakan unsur satuan dari x terhadap operasi *, jika s*x = x atau x*s = x.
Dalam sistem bilangan real, unsur satuan terhadap perkalian (x) adalah 1, dan terhadap
perjumlahan (+) adalah 0.
7. Adanya unsur kawan
Definisi
k dinamakan unsur kawan dari x terhadap operasi *, jika k*x = s atau x*k = s, s unsur satuan.
Dalam sistem bilangan real, unsur kawan dari x terhadap perkalian adalah : x 1
(x-1), dan terhadap perjumlahan : –x.
Berdasarkan unsur kawan ini, berlaku pernyataan x : y = x y 1 = y x dan x – y = x + (−y).
6
I.3. Kalimat Matematis
Kalimat matematis adalah kalimat yang memiliki nilai salah atau benar. Jika nilainya
dapat ditentukan secara langsung tanpa sebuah proses perhitungan, maka kalimat matematis dinamakan kalimat tertutup. Sedangkan jika tidak langsung (nilainya harus dicari melalui
sebuah proses perhitungan) dinamakan kalimat terbuka.
Contoh
Kalimat tertutup : 2 + 3 = 5
3 x 6 < 20
Kalimat terbuka : x + 3 = 5
3x < 20
Dalam sistem bilangan real, yang termasuk kalimat tertutup adalah kesamaan dan ketidaksamaan, sedangkan kalimat terbuka persamaan dan pertidaksamaan.
Gambar I.2
Struktur Kalimat Matematis
Sifat trikhotomi merupakan perwujudan (implemantion) dari kalimat tertutup dalam sistem bilangan real. Sebab jika ada dua bilangan real a dan b, maka kemungkinannya, a sama dengan b (a = b), atau a tidak sama dengan b a ≠ b (a ≠ b). Dalam hal a ≠ b, kemungkinannya, a > b atau a < b.
Bentuk ketidaksamaan, a > b (a < b), dinamakan ketidaksamaan murni, sedangkan a≥ , b (a ≤ b) dinamakan ketidaksamaan tidak murni.
Karena nilai dari kalimat tertutup dapat ditentukan secara langsung, sehingga untuk menentukan jawabnya tidak diperlukan perhitungan atau analisis tertentu, maka tidak ada
KALIMAT MATEMATIS KALIMAT
TERBUKA TERTUTUP KALIMAT
KESAMAAN
7
pembahasan lanjut tentang kalimat tertutup. Pembahasan lanjut dilakukan hanya untuk kalimat terbuka, yaitu persamaan dan pertidaksamaan, sebab untuk menentukan jawabnya diperlukan perhitungan tertentu.
Sudah dikemukakan, dalam sistem bilangan riil, yang termasuk dalam kalimat terbuka
adalah persamaan, yaitu kalimat terbuka yang melibatkan tanda sama dengan (=), dan
pertidaksamaan yaitu kalimat terbuka yang melibatkan tanda tidak sama dengan
(> , ≥ , < , ≤).
Dalam persamaan atau pertidaksamaan,
1. Bagian di sebelah kiri tanda = , > , ≥ , < atau ≤ , dinamakan ruas kiri, dan disebelah kanannya, ruas kanan,
2. Lambang yang memiliki nilai, dengan nilainya ditentukan atau diperoleh melalui sebuah
proses perhitungan, sehingga persamaan menjadi kesamaan atau pertidaksamaan
menjadi ketidaksamaan, dinamakan variabel,
3. Nilai variabel yang menyebabkan persamaan atau pertidaksamaan bernilai benar,
dinamakan jawab, akar, solusi atau penyelesaian.
Dalam buku ajar ini, akan digunakan kata jawab, sebagai hasil perhitungan dari persamaan
atau pertidaksamaan yang bernilai benar.
I.4. Beberapa Bentuk Persamaan
Sudah dikemukakan, persamaan adalah kalimat matematis terbuka yang melibatkan tanda =. Untuk mencari jawab sebuah persamaan, lakukan langkah-langkah sebagai berikut, 1. Ruas kanan disama dengankan 0,
2. Jika dimungkinkan, maka faktorkan ruas kiri atas faktor-faktor linear. Jika tidak, maka lakukan analisis ciri.
8
I.4.1. Persamaan Linear
Persamaan linear merupakan persamaan yang bentuknya paling sederhana. Bentuk umum persamaannya adalah
ax + b = 0
dengan a ≠ 0 dan b, bilangan real. x variabel. Jawab dari persamaan ini adalah, x = −
a b
Contoh 1.
Tentukan jawab persamaan 2x – 3x2 + 1 = 5x – 3x2 – 7
Jawab :
Ruas kanan disama dengankan 0 2x – 3x2 + 1 − 5x + 3x2 + 7 = 0 −3x + 8 = 0 Sehingga jawab persamaannya : x = −
3 8 − = 3 8 = 3 2 2
I.4.2. Persamaan Kuadrat
Bentuk umum dari persamaan kuadrat adalah 0 c bx
ax2 + + =
dengan a ≠ 0 , b dan c bilangan real. x variabel.
Jawab dari persamaan kuadrat dapat diperoleh dengan cara 1. Metode faktorisasi.
Konsepsinya,
(1) faktorkan hasil kali a dengan c, dengan jumlah kedua faktornya sama dengan b. a x c = d = d1 x d2 , d1 + d2 = b,
(2) ubah persamaan kuadrat menjadi ax2 + d1x + d2x + c = 0 (3) lakukan perhitungan sebagai kerikut.
ax2 + d1x + d2x + c = (ax2 +d1x) + (d2x + c) = ax(x + a d1 ) + d2(x + 2 d c ) = 0 Karena a x c = d1 x d2 yang identik dengan
a d1 = 2 d c = e , maka (ax + d2)(x + e) = 0
9 Sehingga jawabnya, ax + d2 = 0 x1 = a d2 − x + e = 0 x2 = −e = a d1 − 2. Dengan menggunakan rumus.
Konsepsinya, jika x1 dan x2 jawab persamaan kuadrat, maka dipenuhi hubungan : a 2 ac 4 b b x1 2 2 − ± − = ., .
dalam formulasi tersebut, b2 – 4ac = D , dinamakan diskriminan.
Nilai diskriminan dapat digunakan untuk menentukan ciri dari jawab persamaan. Jika 1) D > 0, maka persamaan kuadrat memiliki dua jawab bilangan real,
2) D = 0 maka persamaan memiliki satu jawab bilangan real,
3) D < 0 maka persamaan memiliki jawab bilangan kompleks.
Contoh 2.
Tentukan jawab dari persamaan 2x2 – 3x – 2 = 0 !
Jawab :
Dengan cara faktorisasi:
(2) x (−2) = −4 = (−4) x (1) , sebab (−4) + (1) = −3 .
Jika dihubungkan dengan teorinya : a = 2 , d1 = −4 , d2 = 1 , maka jawabnya
x1 = a d2 − = 2 1 − x2 = a d1 − = 2 4 − − = 2
Dengan menggunakan rumus :
D = (-3)2 – 4(2)(-2) = 25 > 0, jadi persamaan kuadrat memiliki jawab dua bilangan real, yaitu
10
( )
( )
4 5 3 2 2 25 3 x1.,2 = − − ± = ± 2 4 5 3 x1 = + = 2 1 4 5 3 x2 =− − =Jadi jawab persamaan 2x2 – 3x – 2 = 0 adalah, x = 2 dan x = 2 1 − . Jika disajikan dalam sebuah bentuk himpunan, maka himpunan jawabnya,
H = { 2 1 − . 2}.
Dari rumus untuk mencari jawab persamaan kuadrat ax2 +bx+c=0, yaitu
a 2 ac 4 b b x1.2 2 − ± − = , yang berarti a 2 ac 4 b b x1 2 − + − = dan a 2 ac 4 b b x2 2 − − − = .
Maka diperoleh hubungan 1) a b a 2 b 2 a 2 ac 4 b b a 2 ac 4 b b x x1 2 2 2 =− − = − − − + − + − = + 2)
( )
(
)
( )
− − − = − − − − + − = 2 2 2 2 2 2 2 1 a 2 ac 4 b b a 2 ac 4 b b a 2 ac 4 b b x . x(
)
a c a 4 ac 4 a 4 ac 4 b b = 2 − 22− = 2 =Yang menyimpulkan bahwa, jika x1 dan x2 jawab persamaan kuadrat ax2 + bx + c = 0, maka berlaku hubungan 1) a b x x1 + 2 =− 2) a c x . x1 2 = .
11
Contoh 3.
Jika x1 dan x2 jawab persamaan 3x2 + 2x – 1 = 0 , maka dengan tidak menghitung nilai-nilainya, hitunglah a) x12 + X22 ! b) x12 – x22 ! Jawab : a)
(
)
9 10 3 2 9 4 3 1 2 3 2 x x 2 x x x x 2 2 1 2 2 1 2 2 2 1 = + = − − − = − + = + b) − =(
−)(
+)
=(
−)
− 3 2 x x x x x x x x 1 2 1 2 1 2 2 2 2 2 1 2 2 2 1 2 1 2x x x x 3 2 − + − =(
)
32 9 10 3 2 3 1 2 9 10 3 2 x x 2 x x 3 2 2 1 2 2 2 1 =− + − − − = − + − = 9 8 9 16 3 2 =− =− Contoh 4.Bangun persamaan kuadrat yang jumlah nilai jawabnya sama dengan 3, dan hasil kalinya sama dengan –2 !
Jawab :
Jika dimisalkan bentuk persamaannya ax2 + bx + c = 0 dan x1 , x2 , maka x1 + x2 = − a b = 3 b = −3a x1x2 = a c = −2 c = −2a sehingga persamaan yang dicari
ax2 – 3x –2a = 0.
Karena a ≠ 0 maka kedua ruas dari persamaan dapat dibagi oleh a , sehingga bentuk persamaan kuadratnya,
12
Contoh 5.
Bangun persamaan kuadrat yang jawab-jawabnya lebih besar 2 dari persamaan −3x2 + 4x –2 = 0
Jawab :
Jika dimisalkan x1 , x2 jawab persamaan
−3x2 + 4x –2 = 0 ,
dan y1 , y2 jawab persamaan kuadrat yang akan dibangun dengan persamaan ay2 + by + c = 0 , maka y1 + y2 = − a b = (x 1 + 2)(x2 + 2) = (x1 + x2) + 4 = − 3 4 − + 4 = 3 16 b = − 3 16a y1y2 = a c = (x 1 + 2)(x2 +2) = x1x2 + 2(x1 + x2) + 4 = − 3 2 − − + 2 − − 3 4 + 4 = 3 22 c = 3 22a
Sehingga bentuk persamaan yang dicari adalah
0 a 3 22 ay 3 16 ay2 − + = .
Karena a 0, jika persamaan dibagi a dan dikalikan 3 , maka persamaan kuadrat yang dicari, 0 22 y 16 y 3 2 − + = , atau 0 22 x 16 x 3 2 − + =
jika variabelnya disajikan oleh x
Definisi
Bentuk kuadrat ax2 + bx + c, dinamakan
1) definit positif, jika ax2 + bx + c > 0, untuk sembarang nilai x. Hal ini akan terjadi jika D = b2 – 4ac < 0 dan a > 0.
2) definit semi positif, jika ax2 + bx + c 0, untuk sembarang nilai x. Hal ini terjadi jika D = b2 – 4ac 0 dan a > 0.
3) definit negatif, jika ax2 + bx +c < 0, untuk sembarang nilai x. Hal ini terjadi jika D = b2 – 4ac < 0 dan a< 0
13
4) definit semi positif, jika ax2 + bx +c 0, untuk sembarang nilai x. Hal ini terjadi jika D = b2 – 4ac 0 dan a< 0
I.4.3. Persamaan Polinom
Persamaan anxn + an-1xn-1 + . . . + a1x + a0 = 0, dengan n 3 dan an 0, dinamakan
persamaan polinom berderajat n. Menyelesaikan persamaan ini, tidak sesederhana dan
semudah seperti menyelesaikan persamaan kuadrat atau persamaan linear, karena untuk memfaktorkan ruas kiri tidak ada acuan khusus. Salah satu acuan yang dapat digunakan (walaupun belum tentu mudah prosesnya), adalah faktor dari konstanta persamaan (a0).
Contoh 6
Tentukan jawab persamaan 6x3 – 13x2 + 4x + 3 = 0
Jawab :
a0 = 3 = 3 x 1 = −3 x − 1
Jika disubtitusikan x = 1 ke ruas kiri 6(1)3 – 13(1)2 + 4(1) + 3 = 6 – 13 + 4 + 3 = 0 maka x - 1 salah satu faktor dari 6x3 – 13x2 + 4x + 3.
Untuk mencari faktor yang lainnya,
1) bagi 6x3 – 13x2 + 4x + 3 oleh (x – 1) (6x3–13x2+4x+3) : (x–1) = 6x2–13x–3 2) faktorkan 6x2 – 13x – 3 6x2 – 13x – 3 = (2x – 3)(3x + 1).
Sehingga faktorisasi persamaan : 6x3 – 13x2 + 4x + 3 = (x – 1)(2x – 3)(3x + 1) = 0 dan jawabnya x – 1 = 0 x1 = 1 2x – 3 = 0 x2 = 2 3 = 1 2 1 3x + 1 = 0 x3 = 3 1 − Contoh 7
Tentukan jawab persamaan 2x3 − 7x2 + 7x − 5 = 0
Jawab :
a0 = −5 = 5 x −1 = −5 x 1. Jika disubtitusikan ke ruas kiri :
14
x = −1 2(−1)3 – 7(−1)2 + 7(−1) – 5 = −2 – 7 – 7 – 5 = −21 0 x = 5 2(5)3 – 7(5)2 + 7(5) – 5 = 250 – 175 + 35 – 5 = 105 0
x = −5 2(−5)3 – 7(−5)2 + 7(−5) – 5 = −250 – 175 – 35 – 5 = −465 0
Jadi tidak ada jawab persamaan yang merupakan bilangan bulat.
Jika menelaah hasil perhitungan, nilai persamaan untuk x = −5 dengan x = 5 berbeda tanda. Artinya, dalam selang −5 < x < 5, ada nilai x yang menyebabkan persamaan sama dengan 0. Jika disubtitusikan x =
2
5 ke ruas kiri, maka diperoleh hasil 2( 2 5)3 – 7( 2 5)2 + 7( 2 5) – 5 = 4 125 − 4 175 + 2 35 − 5 = 0 Yang berarti, (x − 2 5
) adalah salah satu faktor persamaan. Sehingga faktorisasinya, 2x3 − 7x2 + 7x − 5 = (x −
2
5)(x2 – x + 1).
Jika dihitung, determinan dari bentuk kuadrat x2 – x + 1, D = (−1)2 − 4(1)(1) = −3 < 0, dan koefisien kuadratnya, a = 1 > 0. Sehingga bentuk kuadrat (x2 – x + 1) definit positif, atau x2 – x + 1 > 0, untuk setiap nilai x.
Sehingga jawab persamaan 2x3 − 7x2 + 7x − 5 = 0 adalah : x = 2 5.
Untuk menyelesaikan persamaan polinom berderajat n, n 3, jika sulit dilakukan secara “manual”, dapat digunakan perangkat lunak komputer (software), diantaranya Mathcad.
Mathcad adalah perangkat lunak komputer untuk membantu perhitungan dalam persoalan Matematika dan terapannya. Program ini sangat berguna bagi para profesional, pendidik, dan mahasiswa, yang sering menggunakan kalkulus untuk menyelesaikan persoalan terapan. Karena program ini memiliki kemampuan yang tinggi, dalam proses penyelesaiannya. Sebagai sebuah spreadsheet, cukup sederhana dalam penggunaannya.
Misalnya untuk mencari jawab persamaan
2x4 - x3 + 3x2 - x -2 = 0.
Jika dilakukan secara “manual”, prosesnya tidak sederhana dan memerlukan waktu yang cukup lama. Sedangkan jika diselesaikan dengan menggunakan Mathcad 2000, maka prosesnya cukup sederhana, sebagai berikut.
15
1. “Jalankan” program Mathcad 2000, sehingga diperoleh tampilan seperti di bawah ini.
2) “Tutup” tampilan Resource Centre, sehingga tampilan menjadi seperti di bawah ini.
3) Pada “ruang editor” (bidang putih yang ada “ponter” +) secara berurut tulis f(x) 2x4 - x3 + 3x2 - x -2
x (tulis sembarang nilai)
soln root(f(x),x), selanjutnya klik pada fungsi Evaluati…
soln = Catatan
tanda , dapat diperoleh dengan mengkliknya pada fungsi Calculator atau
16
Dari tampilan spreadsheet, diperoleh himpunan jawabnya
H = {0,885 , -0,578 , 0,097 + 1,349i , 0,097 - 1,349i}
I.5. Bentuk-bentuk Pertidaksamaan
Sudah dikemukakan, pertidaksamaan adalah kalimat matematis yang melibatkan tanda >, , <, atau . Menentukan jawab sebuah pertidaksamaan identik dengan penyelesaian sebuah persamaan, yaitu
1) ruas kanan disama dengankan 0,
2) jika memungkinkan, lakukan faktorisasi ruas kiri. Jika tidak, lakukan telaah ciri,
3) gunakan garis bilangan, yaitu garis yang titik-titiknya merupakan wakil dari bilangan
real,
4) tentukan daerah tanda pada garis bilangan,
5) tentukan daerah tanda yang sesuai dengan pertidaksamaannya.
Di bawah ini disajikan beberapa bentuk pertidaksamaan yang sering muncul dalam persoalan sehari-hari atau terapan.
I.5.1. Pertidaksamaan Linear
Pertidaksamaan linear adalah pertidaksamaan yang variabel-variabel pada setiap ruasnya berderajat satu, dan pertidaksamaan ini merupakan pertidaksamaan yang paling sederhana bentuk dan penyelesaiannya.
17
Contoh 8.
Tentukan harga x yang memenuhi pertidaksamaan 5x – 3 < 2x + 9 !
Jawab :
5x – 3 < 2x + 9 5x – 2x < 9 + 3 3x < 12 x <4
Jawab pertidaksamaan,
x < 4 . Jika disajikan pada garis bilangan
) 4
Contoh 9.
Tentukan himpunan jawab dari pertidaksamaan 3x + 2 ≤ 7x + 10 !
Jawab :
3x + 2 ≤ 7x + 10 3x – 7x ≤ 10 – 2 −4x ≤ 8 x ≥ 2
Jadi himpunan jawabnya,
H = { x | x ≥ 2 } . Jika disajikan pada garis bilangan
[ 2
Contoh 10.
Tentukan harga x yang memenuhi pertidaksamaan 3x – 2 ≤ 4x + 1 ≤ 6x - 3 !
Jawab :
Karena semua ruas memuat variabel, sebaiknya dilakukan pemecahan jawaban yang selanjutnya dilakukan penggabungan, sebagai berikut
18 [ 3 (
2
Jawab pertidaksamaan adalah irisan kedua garis bilangan, yaitu : x ≥ 3 .
I.5.2. Pertidaksamaan Irasional
Pertidaksamaan irasional adalah pertidaksamaan yang satu atau beberapa suku variabelnya berada di bawah tanda akar, sehingga untuk mencari jawabnya harus diperhatikan syarat dari suku di bawah tanda akarnya, agar diperoleh nilai dalam bilangan
real. Prinsip mencari jawab dari pertidaksamaan ini, adalah dengan mengubah suku
irasional menjadi rasional, yang salah satu diantaranya melalui proses pengkuadratan.
Contoh 11.
Selesaikan pertidaksamaan 3x−2 <5 !
Jawab :
Agar nilai dari 3x− real, maka harus dipenuhi syarat : 3x – 2 ≥ 0 x ≥ 2 2 x ≥ 3 2 Untuk penyelesaian pertidaksamaannya, kuadratkan kedua ruasnya. Karena suku pada masing-masing ruas positif, maka tanda pertidaksamaan tidak berubah.
3x – 2 4x + 1 < 6x – 3 3x – 2 4x + 1 3x – 4x 1 + 2 −x 3 x 3 4x + 1 < 6x – 3 4x – 6x < −3 – 1 −2x < −4 x > 2
19 2
x
3 − < 5
(
3x−2)
2 < 52 3x – 2 < 25 3x < 25 + 2 x < 9 Jika kedua jawab digabungkan dengan menggunakan garis bilangan,[ 3 2 ) 9
maka himpunan jawabnya
< ≤ = x 9 3 2 x H Contoh 12.
Untuk harga-harga x manakah yang memenuhi pertidaksamaan 2x−3< 3x−4 ?
Jawab :
Syarat untuk suku di bawah tanda akar agar diperoleh bilangan real
2x – 3 ≥ 0 x ≥ 2 3 (1) 3x – 4 ≥ 0 x ≥ 3 4 (2)
Untuk penyelesaian pertidaksamaannya. Karena ruas kiri dan ruas kanan merupakan bilangan positif, maka jika keduanya dikuatdratkan, tidak akan mengubah tanda pertidaksamaan.
(
) (
2)
2 4 x 3 3 -2x 4 x 3 3 x 2 0< − < − < − 2x – 3 < 3x – 4 2x – 3x < -4 + 3 −x < −1 x > 1 (3)20
Jika ketiga jawab, (1), (2), dan (3), digabungkan dengan menggunakan garis bilangan
[ 2 3 [ 3 4 ( 1
maka himpunan jawabnya : = ≥
2 3 x x H . Contoh 13.
Tentukan harga x yang memenuhi pertidaksamaan x+6− x−1<1 !
Jawab :
Syarat untuk unsur di bawah tanda akar
x + 6 ≥ 0 x ≥ -6 (1) x – 1 ≥ 0 x ≥ 1 (2) Penyelesaian pertidaksamaannya
(
) (
)
(
x 1)
( )
3 x 1 9 x 10 (3) 3 1 x 6 1 x 2 x 1 x 2 6 x 1 x 1 x 2 1 6 x 1 x 1 6 x 1 x 1 6 x 1 1 x 6 x 2 2 2 2 > > − > − > − > − + − < + − + − + < + − + < + − + < + < − − + [ −6 [ 1 ( 1021
I.5.3 Pertidaksamaan Polinom
Untuk menyelesaikan pertidaksamaan polinom, dapat dilakukan dengan proses sebagai berikut
1. Jadikanlah ruas kanan sama dengan 0 , dan pangkat variabel yang paling tinggi koefisiennya positif.
2. Unsur di ruas kiri, jika mungkin uraikan atas faktor-faktor linier, dan hitung nilai-nilai yang menyebabkan faktor-faktor sama dengan 0 (nilai ini dinamakan nilai nol).
3. Sajikan nilai-nilai nol pada garis bilangan, dan lakukan uji tanda untuk menentukan daerah himpunan jawab, dengan cara sebagai berikut :
3.1. ambil sebuah nilai yang bukan nilai nol dan subtitusikan ke ruas kiri. 3.2 perhatikan tanda dari nilai yang diperoleh, positif (+) atau negatif (-).
3.3 tandai daerah di mana nilai yang diambil tersebut berada dengan tanda yang diperoleh, dan tanda berubah jika melewati nilai nol yang berasal dari faktor berpangkat ganjil, sedangkan jika berasal dari faktor berpangkat genap tanda tetap.
Contoh 14.
Tentukan himpunan jawab dari pertidaksamaan 5x2 – 4x + 11 < 2x2 + 6x + 8 !
Jawab : 5x2 – 4x + 11 < 2x2 + 6x + 8 5x2 – 4x + 11 – 2x2 – 6x – 8 < 0 3x2 – 10x + 3 < 0 (3x – 1)(x – 3) < 0 Nilai-nilai nolnya : 3x – 1 = 0 x = 3 1 x – 3 = 0 x = 3
Ambil sembarang nilai x yang tidak sama dengan 3
1 dan 3. Misalnya x = 0. Subtitusikan x = 0 ke ruas kiri :
(3x – 1)(x – 3) = (3.0 – 1)(0) – 3) = 3 > 0 yang berarti daerah di sebelah kiri
3
1 bertanda + , antara 3
1 dan 3 bertanda −, dan di sebelah kanan 3 bertanda + , sehingga gambar daerah tandanya :
22 + + + − − − + + + 3 1 3
Karena tanda pertidaksamaannya < 0 , jadi himpunan jawabnya < < = x 3 3 1 x H . Contoh 15.
Tentukan harga x yang memenuhi pertidaksamaan (x2 – 4x + 3)(x2 – 3x – 10) > 0
Jawab : (x2 – 4x + 3)(x2 – 3x – 10) > 0 (x –2 )2(x –5)(x + 2) > 0 Nilai-nilai nolnya : x – 2 = 0 x = 2 x – 5 = 0 x = 5 x + 2 = 0 x = -2
Gambar daerah tandanya :
+ + + - - - - - - + + +
−2 2 5
Karena tanda pertidaksamaan > 0 , jadi himpunan jawabnya H = { x x <−2 } ∪ { x x > 5 }
Contoh 16.
Tentukan batas-batas harga x yang memenuhi pertidaksamaan 3x2 – x + 10 > x2 + 2x - 2
Jawab :
3x2 – x + 10 > x2 + 2x – 2 3x2 – x +10 – x – 2x + 2 > 0 2x2 – 3x + 12 > 0 Karena bentuk kuadrat 2x2 – 3x + 12, memiliki ciri diskriminannya :
23 koefisien kuadratnya :
a = 2 > 0,
maka bentuk kuadrat 2x2 – 3x + 12 definit positif, 2x2 – 3x + 12 > 0 untuk setiap nilai x. Sehingga himpunan jawabnya,
H = { x x bilangan real }.
I.5.4. Pertidaksamaan Pecahan
Pertidaksamaan pecahan adalah pertidaksamaan yang merupakan sebuah pecahan atas suku-suku. Untuk menyelesaikan pertidaksamaan ini prosesnya sebagai berikut,
1. Ruas kanan disama dengankan 0
2. Lakukan perhitungan di ruas kiri sehingga diperoleh sebuah bentuk pecahan atas suku-suku, yang selanjutnya ubah menjadi bangun perkalian.
3. Faktorkan bangun perkalian tersebut (jika bisa), dan tentukan nilai-nilai nolnya. 4. Sajikan nilai-nilai nol pada garis bilangan dan lakukan penentuan daerah tanda.
Contoh 17.
Tentukan harga x yang memenuhi pertidaksamaan 6
4 x 5 3 x 2 ≤ + − ! Jawab :
(
)
0 4 5x 27 28x 0 4 5x 4 5x 6 3 2x 0 6 4 5x 3 2x 6 4 x 5 3 x 2 ≤ + − − ≤ + + − − ≤ − + − ≤ + − ⇔ (−28x – 27)(5x + 4) ≤ 0 Nilai nolnya : −28x – 27 = 0 x = − 28 27 = − 140 135 5x + 4 = 0 x = − 5 4 = − 140 11224 Gambar daerah tanda
− − − + + + − − − 28 27 − 5 4 −
sehingga himpunan jawabnya, = ≤− ≥−
5 4 x x 28 27 x x H Contoh 18. Selesaikan pertidaksamaan 6 x 5 x 3 x 2 3 x 2 − + ≤ − + ! Jawab :
(
)(
) (
)(
)
(
2x 3)(
x 6)
0 3 x 2 5 x 6 x 3 2x 0 6 x 5 x 3 x 2 3 x 2 6 x 5 x 3 x 2 3 x 2 ≤ − − − + − − + ≤ − + − − + − + ≤ − +(
)
(
)(
)
(
)(
)
(
16x 3)(
2x 3)(
x 6)
0 0 6 x 3 x 2 3 x 16 0 6 x 3 x 2 15 x 7 x 2 18 x 9 x 2 2 2 ≤ − − − − ⇔ ≤ − − − − ≤ − − − + − − − Nilai-nilai nolnya : −16x – 3 = 0 x = 16 3 − 2x – 3 = 0 x = 2 3 x – 6 = 0 x = 6Gambar daerah tandanya
+ + + − − − + + + − − − 16 3 − 2 3 6
sehingga himpunan jawabnya,
{
xx 6}
2 3 x 16 3 x H= − ≤ ≤ ≥
25
Contoh 19.
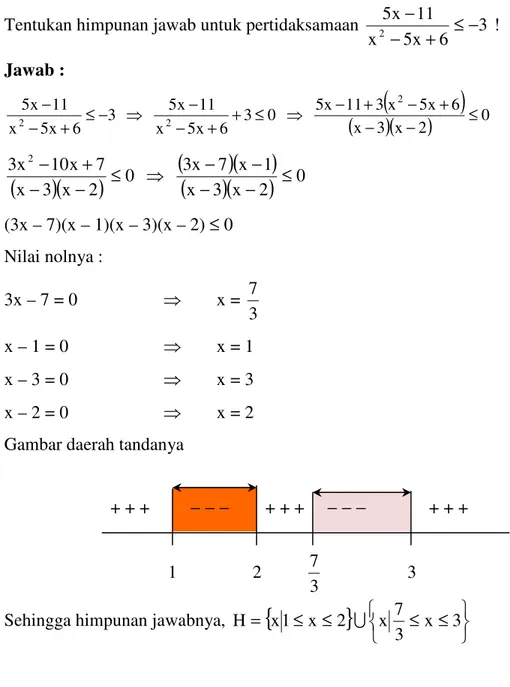
Tentukan himpunan jawab untuk pertidaksamaan 3
6 x 5 x 11 x 5 2 − + ≤− − ! Jawab :
(
)
(
x 3)(
x 2)
0 6 x 5 x 3 11 5x 0 3 6 x 5 x 11 x 5 3 6 x 5 x 11 x 5 2 2 2 − − ≤ + − + − ≤ + + − − − ≤ + − −(
)(
)
(
(
x 3)(
)(
x 2)
)
0 1 x 7 x 3 0 2 x 3 x 7 x 10 x 3 2 ≤ − − − − ≤ − − + − (3x – 7)(x – 1)(x – 3)(x – 2) ≤ 0 Nilai nolnya : 3x – 7 = 0 x = 3 7 x – 1 = 0 x = 1 x – 3 = 0 x = 3 x – 2 = 0 x = 2Gambar daerah tandanya
+ + + − − − + + + − − − + + + 1 2
3
7 3
Sehingga himpunan jawabnya, =
{
≤ ≤}
≤x≤33 7 x 2 x 1 x H
I.5.5. Pertidaksamaan Yang Mengandung Nilai Mutlak
Nilai mutlak dari x , ditulis x , didefinisikan sebagai berikut
< = > = 0 x jika , x -0 x jika , 0 0 x jika , x x
Berdasarkan definisi tersebut berarti nilai mutlak dari suatu bilangan riil adalah bilangan positif atau 0. Sebagai contoh, 3 = 3 , −3 = −(−3) = 3.
26
Secara ilmu ukur x adalah jarak dari x ke 0 pada garis bilangan real.
x x
-x 0 x
Gambar I.3
Sajian ilmu ukur dari x
Sifat-sifat dari nilai mutlak
1. Untuk setiap bilangan real x , berlaku hubungan : 1) x ≥ 0
2) x = −x
3) x2 = x2 = x2
2. Untuk setiap bilangan real x dan y , berlaku hubungan : 1) x = y ⇔ x = ±y ⇔ x2 = y2
1) x − y = y − x
3) x + y ≤ y + x dan x − y ≤ x + y
4) x −y ≤ x − y dan x − y = x − y
5) xy = xy dan
y x y x =
3. Untuk setiap bilangan real x dan a ≥ 0 , berlaku hubungan : 1) x ≤ a , a > 0 ⇔ −a ≤ x ≤ a ⇔ x2 ≤ a2
2) x ≥ a , a > 0 ⇔ x ≥ a atau x ≤ -a ⇔ x2 ≥ a2
Berdasarkan telaahan dari nilai mutlak tersebut, proses penyelesaian pertidaksamaan yang mengandung nilai mutlak, adalah dengan mengubah pertidaksamaan menjadi pertidaksamaan yang tidak mengandung nilai mutlak. Selanjutnya penyelesaian pertidaksamaan dilakukan berdasarkan bentuk kasusnya. Menghilangkan nilai mutlak dalam pertidaksamaan dilakukan dengan memperhatikan sifat-sifat dari nilai mutlak seperti yang telah dikemukakan.
27
Contoh 20.
Tentukan himpunan jawab pertidaksamaan a. x2 − x ≤ 2 b. x2 – x −1 ≥ 1 Jawab : a. x2 − x ≤ 2 ⇔ −2 ≤ x2 – x ≤ 2 −2 ≤ x2 – x ≤ 2 −2 ≤ x2 – x x2 – x ≤ 2 −2 – x2 + x ≤ 0 x2 – x + 2 ≥ 0 x2 – x –2 ≤ 0 (x – 2)(x + 1) ≤ 0
Karena bentuk kuadrat x2 – x + 2 Nilai nol : x – 2 = 0 x = 2
diskriminannya : D=(−1)2– 4(1)(2) = −7<0 x + 1 = 1 x = −1
koefisien kuadratnya : a = 1 > 0 Gambar daerah tandanya
yang berarti pertidaksamaan
x2 – x + 2 ≥ 0, selalu benar, + + + − − − + + +
atau himpunan jawabnya, −1 2
H1 = { xx bilangan riil }. sehingga himpunan jawabnya,
H2 = { x−1 ≤ x ≤ 2 }.
Karena H1 ∩ H2 = H2 , jadi himpunan jawab pertidaksamaan x2 −x ≤ 2 adalah H2 = { x−1 ≤ x ≤ 2 }
28 b. x2 – x − 1 ≥ 1 ⇔ x2 – x – 1 ≥ 1 atau x2 – x – 1 ≤ −1 x2 – x − 1 ≥ 1 x2 – x – 1 ≥ 1 x2 – x – 1 ≤ −1 x2 – x – 1 – 1 ≥ 0 x2 – x – 2 ≥ 0 x2 – x – 1 + 1≤ 0 x2 – x ≤ 0 (x –2)(x + 1) ≥ 0 x(x – 1) ≤ 0
Nilai nol : x – 2 = 0 x = 2 Nilai nolnya : x = 0
x + 1 = 0 x = −1 x – 1 = 0 x = 1
Gambar daerah tandanya Gambar daerah tandanya
+ + + - - - + + + + + + - - - + + +
−1 2 0 1
himpunan jawabnya, himpunan jawabnya,
H1 = { xx ≤ −1 } ∪ { xx ≥ 2 } H2 = { x0 ≤ x ≤ 1 }
Jika kedua himpunan jawab diiriskan dengan menggambarkan daerah tandanya
+ + + - - - + + +
−1 2
+ + + - - - + + +
0 1
maka himpunan jawab pertidaksamaan x2 – x − 1 ≥ 1 adalah himpunan kosong, H = φ.
Sehingga tidak ada nilai x memenuhi pertidaksamaan x2 – x − 1 ≥ 1
Contoh 21. Selesaikanlah pertidaksamaan 1 x 2 x 1 x x + − ≤ −
29 Jawab :
(
)
(
(
)
)
(
)
(
(
x 1)
)
0 2 x 1 x x 1 x 2 x 1 x x 1 x 2 x 1 x x 1 x 2 x 1 x x 1 x 2 x 1 x x 2 2 2 2 2 2 2 2 2 2 2 2 ≤ + − − − + − ≤ − + − ≤ − + − ≤ − + − ≤ −(
) (
) (
)
(
) (
)
{
(
(
)
} (
) (
{
)(
)
)
}
(
)
{
} (
{
)(
)
}
[
] (
[
{
)
} (
{
)(
)
}
]
(
) (
)
(
)
{
}
{
(
)
}
(
) (
)
(
)
(
)
(
x 1) (
x 1)
0 1 x 2 x 2 1 x 4 0 1 x 1 x 1 x 2 x x x x 1 x 2 x x x x 0 1 x 1 x 1 x 2 x 1 x x 1 x 2 x 1 x x 0 1 x 1 x 1 x 2 x 1 x x 0 1 x 1 x 1 x 2 x 1 x x 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 ≤ + − + − − ≤ + − + − − + + + − − − + ≤ + − − − + + − − − + ≤ + − − − − + ≤ + − − − − + Nilai-nilai nolnya : 1) 4x –1 = 0 x = 4 1 (1) x – 1 = 0 x = 1 (2) (x + 1)2 = 0 x + 1 = 0 x = −1 (3) 2) 2x2 – 2x + 1 = 0.Karena bentuk kuadrat 2x2 – 2x + 1 memiliki nilai diskriminan D=(−2)2 – 4(2)(1) = −4 <0 dan nilai koefisien kuadrat
a > 0, maka 2x2–2x+1 > 0, untuk setiap nilai x. Sehingga gambar daerah tandanya
− − − − − − + + + + + +
-1
4
1 1
dan himpunan jawabnya, = ≤
4 1 x x H
30
Jika kita menelaah proses penyelesaian sebuah pertidaksamaan, yang pada dasarnya adalah, bagaimana menentukan nilai nol dari ruas kiri, setelah ruas kanan disama dengankan nol ? Maka jika diinginkan menyelesaikan sebuah pertidaksamaan dengan menggunakan program Mathcad, identik dengan menyelesaikan sebuah persamaan dari bentuk ruas kirinya, yang dilanjutkan dengan menentukan daerah tandanya.
SOAL-SOAL UNTUK LATIHAN
1. Bentuk pembagian b
a , dengan a 0, terdefinisikan, jika b 0. Bukti : Jika
0
a = b, maka a = 0.b = 0.
Hal ini kontradiktif dengan ketentuan bahwa a 0 Selanjutnya tunjukan bahwa bentuk pembagian,
0
0 juga tidak terdefinisikan.
2. Dalil fundamental dalam ilmu hitung (aritmetika) : Setiap bilangan asli merupakan hasil perkalian dari bilangan prima.
Makna dari dalil tersebut, untuk menunjukan apakah bilangan asli merupakan bilangan prima, adalah dengan memfaktorkannya atas bilangan-bilangan prima. Jika memiliki lebih dari satu faktor bilangan prima, maka bilangan asli itu bukan bilangan prima. Misal : 4 = 2.2 , 24 = 2.2.2.3 , 95 = 5.19 , dan sejenisnya, bukan bilangan prima.
Untuk bilangan-bilangan di bawah ini, mana yang merupakan bilangan prima
a) 240 b) 119 c) 1723 d) 5433 e) 12771 f) 155711 g) 57655
3. Menunjukan bahwa 2 bilangan irasional dengan pembuktian kontradiktif. Misalkan 2 adalah bilangan rasional, sehingga dapat disajikan 2 =
b
a , a dan b bilangan asli yang tidak sama dengan 1, b 0. Jika kedua ruas dikuadratkan, maka 2 = 22
b
a 2b2 = a2 a2 = 2.b.b
Berdasarkan dalil fundamental, kuadrat bilangan asli dapat disajikan dalam perkalian atas bilangan prima yang bersifat tunggal, dengan banyaknya bilangan prima masing-masing genap.
31 Dari sajian, a2 = 2.b.b
1) jika b bilangan asli ganjil, maka banyaknya bilangan prima 2 dalam perkalian hanya satu, ganjil
2) jika b bilangan asli genap, b = 2.b1 a2 = 2.2.b1.2.b1 = 2.2.2.b1.b1 , maka bilangan prima 2 dalam perkalian ada tiga, ganjil
Karena a2 kuadrat bilangan asli, jadi kontradiksi dengan dalil fundamental, atau 2
bukan bilangan rasional.
Untuk bilangan-bilangan di bawah ini, tunjukan bahwa merupakan bilangan irasional, dengan mengunakan kontradiktif dalil fundamental
a) 3 b) 5 c) 12 d) 18 e) 15 f) 10 g) 30
4. Tunjukan bahwa
a) Jika a dan b bilangan rasional, maka c = a.b , bilangan rasional.
Apakah hal ini berlaku untuk bilangan irasional ? Lakukan analisisnya !
b) Jika a bilangan rasional dan b bilangan irasional, maka c = a.b , bilangan irasional. c) Jika a bilangan rasional, a 0, dan b bilangan irasional, maka c = a.b , bilangan
irasional.
5. Tunjukan bahwa jika a > 0, b > 0, maka a) a < b jika dan hanya jika a2 < b2 b) a < b jika dan hanya jika
a 1 >
b 1 6. Tunjukan bahwa jika a < b , maka a <
2 b a+
< b ! 7. Tentukan jawab persamaan-persamaan di bawah ini
a) 2x3 – 3x2 = 5 + 7x – 3x2 + 2x3
b) 4x3 + 2x2 – 3x + 5 = 3x2 + 7x + 4x2 – 3 c) 2x3 – 3x2 – 6x + 1 = −2 + 2x + 2x2 – 4x3 d) 3 – 3x + 2x2 – 2x3 + 2x4 = x3 + 9x2 – 15x + 7 e) 5x2 – x3 + x + 3 = x3 – 2x2 – 3x + 3
32
8. Jika x1 dan x2 jawab persamaan 2x2 + 3x + 4 = 0, maka dengan tidak menghitung nilai-nilai x1 dan x2 , hitunglah
a) x13 − x23 b) x13 + x23 c) x14 − x24 d) x14 + x24
e) x12 – 2x1x2 + x22
9. Jika ditetapkan persamaan kuadrat 3x2 – 2x + 3 = 0, maka bangun persamaan kuadrat
yang jawab-jawabnya a) dua kali lebih besar b) lebih besar dua
c) dua kali lebih besar dan lebih besar dua
10. Tentukan jawab pertidaksamaan-pertidaksamaan di bawah ini a) x3 – 2x2 – 3x + 2 −4 + 2x + 3x – x3 b) 2x5 – 3x4 + 2x3 < 6x4 – 9x3 -2x2 + 12x – 8 c) 2 x 1 x − − − 2 x x 6 + − ≤ − 2 x 15 − d) 2x + 5 ≤ − 2 x 3 3 x x 2 2 − − − e) 1 x 3 11 x 5 x 6 2 + + + > 1 x 2 3 x + − f) 2 x 2 x 9 x 5 2 − − + + 2 x 1 x + − 4 x 1 x 2 − − g) 2 x 1 x − − + 2x2 −3x+1 2 x 15 − h) 2x + 5 − 2 x x 6 + − > 3 – 2x
33 11. Tunjukan bahwa
a) x < y jika dan hanya jika x2 < y2 b) Jika a > b > 0 maka a > b c) a + b + c ≤ a + b + c d) Jika x ≤ 2 maka 1 x 7 x 2 x 2 2 + + + ≤ 15 e) Jika x 0 maka x2 + 2 x 1 2 f) Jika a 0 dan b 0 maka ab ≤
2 b a+ g) 2 x 1 3 x 1 2 + + + ≤ x 3 1 2 + + x 2 1 + ≤ 3 1 + 2 1 h) 9 x 2 x 2 + − ≤ 9 2 x +
i) x < x2 jika x < 0 atau x >1, dan x > x2 jika 0 < x < 1
j) Jika a 0 bilangan rasional dan b bilangan irasional, maka a + b dan ab adalah bilangan irasional.
34
BAB II
FUNGSI REAL DAN GRAFIKNYA
Fungsi adalah bentuk khusus dari relasi (perkawanan) antara dua buah himpunan tidak kosong. Jika kedua himpunan yang direlasikan, dengan relasinya membangun sebuah fungsi, adalah himpunan bilangan real, maka fungsi dinamakan fungsi real. Pada bab ini
akan disajikan deskripsi dan konsepsi pada fungsi real.
II.1. Deskripsi Fungsi
Fungsi dari himpunan X ke himpunan Y, adalah sebuah relasi (perkawanan) dengan cara, setiap anggota himpunan X hanya dikawankan (dipasangkan) dengan satu dan hanya satu kali dengan anggota himpunan Y.
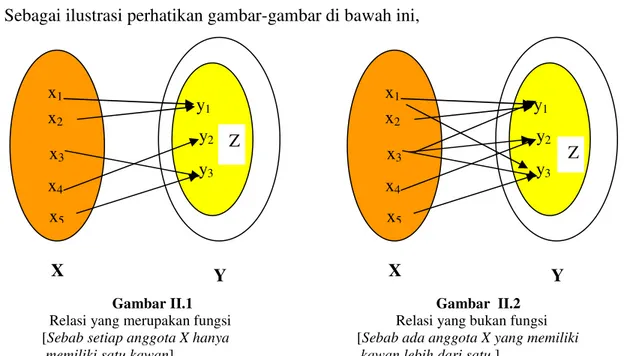
Sebagai ilustrasi perhatikan gambar-gambar di bawah ini,
Gambar II.1 Gambar II.2
Relasi yang merupakan fungsi Relasi yang bukan fungsi [Sebab setiap anggota X hanya [Sebab ada anggota X yang memiliki memiliki satu kawan] kawan lebih dari satu ]
Untuk menyatakan sebuah fungsi dari himpunan X ke himpunan Y, dapat digunakan salah satu dari bentuk notasi di bawah ini,
Tabel II.1
Bentuk-bentuk Notasi Fungsi
Notasi Panah Persamaan Ekplisit Persamaan Implisit
f : X → Y x → y Y = f(X) f (X , Y) = 0 x1 x2 x3 x4 x5 X Y y1 y2 y3 x1 x2 x3 x4 x5 X Y y1 y2 y3 Z Z
35
Dalam deskripsi fungsi tersebut, X disebut Domain (daerah asal) dan Y Kodomain (daerah
kawan). Sedangkan himpunan Z yang merupakan himpunan bagian dari Y, dengan setiap anggotanya adalah kawan dari X, disebut Range (daerah harga, daerah peta).
Misalnya fungsi seperti pada Gambar 1, rangenya : Z = {y1 , y2 , y3}.
Berdasarkan kondisi dari range dan cara perkawanannya, fungsi dibedakan atas
1. Fungsi ke dalam (into), yaitu fungsi dengan rangenya merupakan himpunan bagian
murni dari kodomain.
2. Fungsi pada (onto), yaitu fungsi dengan rangenya sama dengan kodomain.
3. Fungsi satu-Satu (one to one), yaitu fungsi dengan setiap anggota X dan Y hanya
memiliki satu dan hanya satu pasangan.
Fungsi satu-satu ini dibedakan atas fungsi satu-satu pada dan fungsi satu-satu ke dalam.
Untuk ilustrasi perhatikan gambar-gambar di bawah ini
Gambar II.3 Gambar II.4
f : X → Y , fungsi kedalam f : X → Y , fungsi pada
[sebab ada anggota Y yang tidak memiliki kawan] [sebab setiap anggota Y memiliki kawan]
X Y Z X Y Z
36
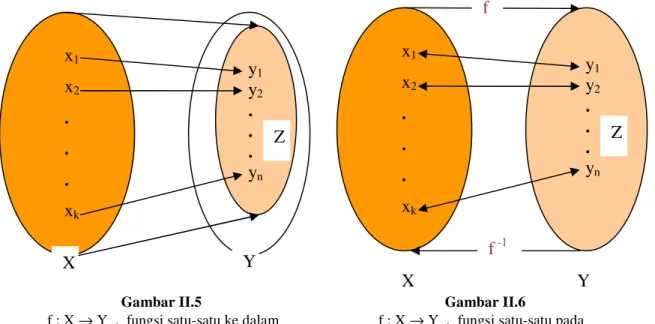
Gambar II.5 Gambar II.6
f : X → Y , fungsi satu-satu ke dalam f : X → Y , fungsi satu-satu pada
Setiap fungsi yang merupakan fungsi satu-satu pada, akan memiliki fungsi invers.
Definisi
Jika
f : X → Y
xi → yi
fungsi satu-satu pada, maka fungsi g : Y → X,
yi → xi
dinamakan fungsi invers dari f, ditulis : f −1
Misal, jika
X = { x | x bilangan real , x ≥ 0 } dan Y = { y | y bilangan real , y ≥ 0 },
maka fungsi
f : X → Y
x → y = x2
adalah fungsi satu-satu pada, dan fungsi inversnya f -1 : Y → X y → x = y x1 x2 . . . xk y1 y2 . . . yn Z X Y x1 x2 . . . xk y1 y2 . . . yn Z X Y f f -1
37
II.2. Sistem Salib Sumbu
Setiap bentuk fungsi dapat digambarkan sajian hubungan elemen domain dengan kodomainnya. Untuk menggambarkannya diperlukan sebuah media, yang dinamakan
sistem salib sumbu, yaitu dua garis berpotongan tegak lurus, yang masing-masing titiknya
menyajikan bilangan riil. Sumbu datar, dinamakan sumbu absis, dinotasikan dengan X, dan
“berperan” sebagai domain. Sedangkan sumbu tegak, dinamakan sumbu ordinat,
dinotasikan dengan Y, dan “berperan” sebagai kodomain. Titik potong sumbu absis dengan ordinat dinamakan titik pusat, dan dinotasikan dengan O.
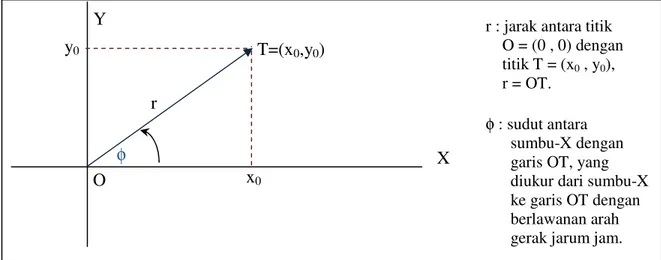
Pasangan nilai berurut (x0 , y0), dengan x0 nilai pada sumbu absis, dan y0 pada sumbu
ordinat, dinamakan koordinat. x0 dinamakan absis, dan y0 ordinat. Koordinat seperti ini
dinamakan koordinat kartesius.
Gambar II.7 Sistem Koordinat Kartesius
O=(0,0) x0 sumbu absis
y0 T=(x0,y0) Y X su m bu o rd in at
38
X Selanjutnya perhatikan gambar di bawah ini.
r : jarak antara titik O = (0 , 0) dengan titik T = (x0 , y0), r = OT. φ : sudut antara sumbu-X dengan garis OT, yang diukur dari sumbu-X ke garis OT dengan berlawanan arah gerak jarum jam.
Gambar II.9 Sistem Koordinat Polar
Koordinat titik T yang disajikan dalam pasangan r dengan φ,
T = (r , φ),
dinamakan Koordinat Polar.
Dengan menggunakan goneometri, dapat diformulasikan hubungan antara koordinat polar dengan koordinat kartesius. Jika (r,φ) koordinat polar dari koordinat kartesius (x0,y0),
maka r = 2 0 2 0 y x + dan tg φ = 0 0 x y .
Koordinat polar dapat digunakan sebagai koordinat alternatif, jika analisis dengan menggunakan koordinat kartesius sulit diselesaikan.
II.3. Diagram dan Grafik
Gambar dari fungsi dinamakan Grafik, jika bentuknya sebuah garis atau lengkungan.
Sedangkan jika sebuah pencaran titik, disebut Diagram.
Misalnya, fungsi dari himpunan X = {-2 , -1 , 0 , 1 , 2} ke himpunan Y = {0 , 1 , 2 , 3 , 4} dengan bentuk f : X → Y x → y = x2 φ r y0 Y x0 O T=(x0,y0)
39 maka diagramnya Y • 4 - • 3 - 2 - • 1 - • • X -2 -1 0 1 2 Gambar II.7 Diagram fungsi f : x → y = x2
Sedangkan jika X = {x x bilangan riel}, Y = {y y bilangan riel}, dan bentuk fungsinya
2 x y x Y X : f = → → maka grafiknya Y 4 - 3 - 2 - 1 - X -2 -1 0 1 2 Gambar 8 Grafik fungsi f : x → y = x2
Menggambarkan grafik fungsi, jika dilakukan secara “manual”, maka prosesnya sebagai berikut.
40 1. Menentukan titik-titik yang dilalui oleh grafik.
a. Titik-titik tertentu, misalnya titik potong dengan sumbu koordinat, titik ekstrim, titik simetris dan sejenisnya.
b. Titik-titik sembarang, yang dapat dilakukan dengan menentukan sembarang nilai x, dan mensubtitusikannya ke persamaan fungsi. Prosesnya dapat dilakukan melalui sebuah tabel perhitungan
Misal untuk fungsi y = x2.
x y = x2 Koordinat Titik -2 (-2)2 = 4 (-2 , 4) -1 (-1)2 = 1 (-1 , 1) 1,5 (1,5)2 = 2,25 (1,5 , 2,25) dst
2. Menggambarkan koordinat titik-titik yang dilalui grafik.
3. Menghubungkan titik-titik yang digambarkan pada langkah pertama,
Tingkat “akurasi” dan “estetika” grafik yang digambarkan secara “manual”, sangat bergantung pada pengalaman dan keahlian menggambar dari si-pembuat-nya. Untuk mendapatkan gambar grafik fungsi yang bagus, tanpa diperlukan pengalaman dan daya estetika, dengan proses cukup sederhana adalah dengan menggunakan program komputer
Mathcad. Langkah-langkah menggambarkan grafik fungsi dengan Mathcad 2000 :
41
2) “Tutup” tampilan Resource Centre, sehingga diperoleh tampilan
3) Pada “pointer” + tulis persamaan fungsi yang akan digambarkan dengan formulasi f(x) “persamaan fungsi”
Tanda , dapat diperoleh dengan mengkliknya pada fungsi Calculator atau Evaluati…
Misal fungsi yang akan digambarkan, Y = 2x2 – 3x + 1. Formulasi penulisan pada “bidang editor” seperti di bawah ini.
42
4) “Klik” gambar grafik yang ada pada sudut kiri atas “kotak Graph” (lihat tanda panah), sehingga diperoleh tampilan
5) Pada “kotak hitam kecil” di bawah “kotak putih besar”, tulis : x, dan f(x) yang ada di sebelah kirinya.
6) “Klik” persamaan fungsi, sehingga diperoleh tampilan tulis : x tulis : f(x)
klik persamaan fungsi setelah menulis x dan f(x) di kotak hitam kecil
pada kotak putih klik dua kali untuk formating grafik
43
7) “Klik” dua kali pada kotak putih yang ada gambar grafik f(x), untuk formating grafik,
8) Lakukan formating grafik sehingga diperoleh gambar yang bagus, menurut si pembuat.
44
II.4. Fungsi Komposisi
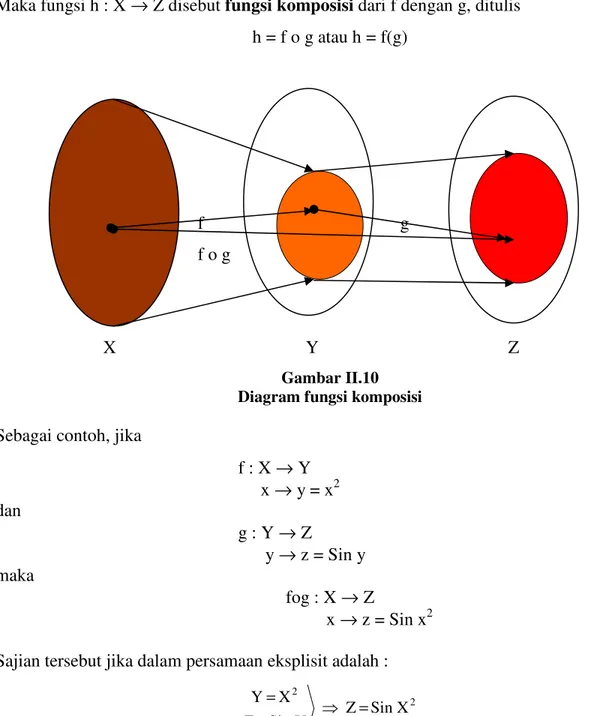
Jika f : X → Y , fungsi dari himpunan X ke Y, dan g : Y → Z , fungsi dari himpunan Y
ke Z, yang merelasikan elemen-elemen dari range fungsi f, dengan elemen himpunan Z. Maka fungsi h : X → Z disebut fungsi komposisi dari f dengan g, ditulis
h = f o g atau h = f(g)
f ff f g f o g
X Y Z
Gambar II.10 Diagram fungsi komposisi
Sebagai contoh, jika
f : X → Y x → y = x2 dan g : Y → Z y → z = Sin y maka fog : X → Z x → z = Sin x2
Sajian tersebut jika dalam persamaan eksplisit adalah :
2 2 X Sin Z Y Sin Z X Y = = =
45
II.4. Operasi Pada Fungsi
Karena nilai dari fungsi real adalah bilangan real, maka himpunan dari fungsi real yang tidak kosong, yang di dalamnya dilibatkan operator perkalian dan perjumlahan, merupakan sebuah sistem bilangan real. Sehingga jika dimiliki dua buah fungsi atau lebih, dengan domain dan kodomain yang sama, maka dapat dilakukan proses perkalian, perjumlahan, atau kombinasi keduanya, beserta operasi kawannya. Domain dan kodomain fungsi hasil operasi adalah irisan dari domain dan range fungsi komponennya.
Perhatikan ilustrasi di bawah ini.
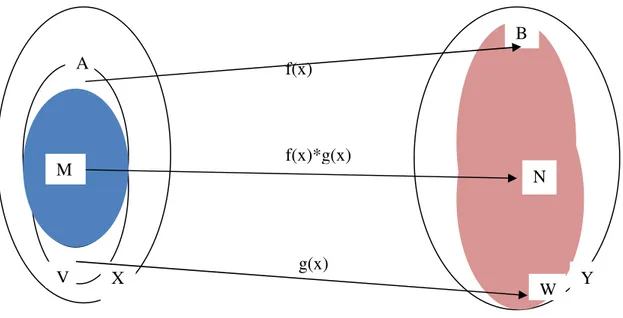
Gambar II.11 Konsepsi Operasi Fungsi
Jika f(x), fungsi dari himpunan A ke himpunan B ; dan g(x), fungsi dari himpunan V ke himpunan W ; maka operasi f(x) dengan g(x) yang disajikan oleh f(x)*g(x), adalah fungsi dari himpunan M = A∩V ke himpunan N = B∪W.
Sebagai contoh, jika
f(x) = x2 , domain = {−∞ < x < ∞} , kodomain = {x 0}
g(x) = Sin x , domain = {−π x π} , kodomain = {−1 x 1}
dan dilakukan operasi fungsi, H(x) = f(x) + g(x) dan I(x) = f(x).g(x), yang jika digambarkan grafiknya dengan Mathcad, hasilnya seperti di bawah ini
f(x) g(x) f(x)*g(x) X A B V W M N Y
46 3.14 0 3.14 4 4 f x( ) g x( ) H x( ) I x( ) x II.5. Beberapa Bentuk Fungsi II.5.1. Fungsi Linear
Fungsi linear (atau fungsi pangkat satu) jika disajikan dalam persamaan eksplisit bentuknya :
Y = aX + b dan dalam persamaan implisit bentuknya :
aX + bY + c = 0
Domain, kodomain, dan range dari fungsi linear adalah himpunan bilangan real, dan fungsi ini merupakan fungsi satu-satu pada, dengan fungsi inversnya
a b X a 1 Y = −
Fungsi linear biasa juga disebut persamaan garis, karena grafiknya merupakan garis
lurus.
f(x) = x2
g(x) = Sin x H(x) = f(x) + g(x) I(x) = f(x).g(x)
Pada gambar tersurat, untuk fungsi H(x) dengan I(x),
domain = {−π x π}
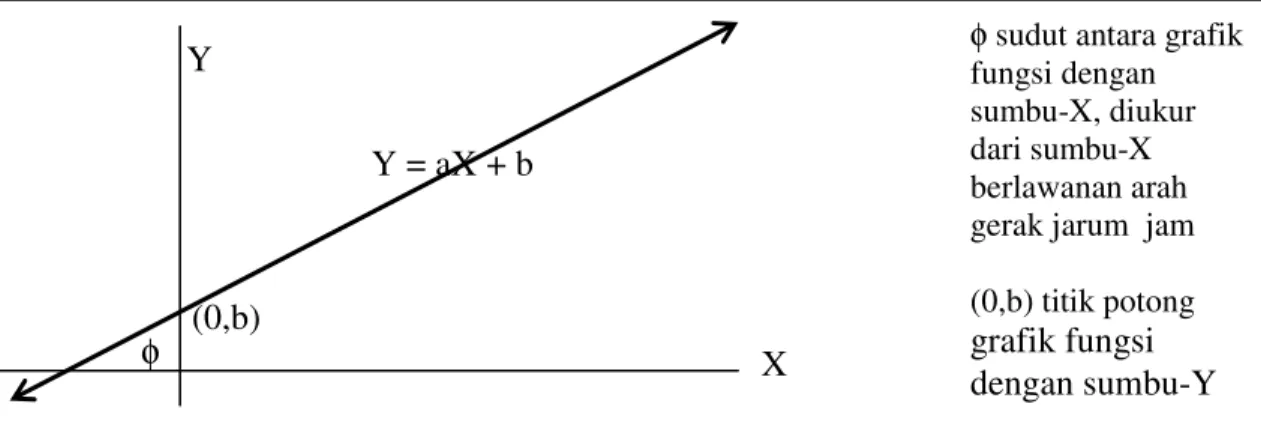
47 Y = aX + b Gambar II.12 Grafik fungsi linear
Pada persamaan eksplisit, Y = aX + b, jika φ sudut antara sumbu-X dengan grafik fungsi,
maka
a = Tg φ
dinamakan Koefisien Arah atau Gradient. Sedangkan φ disebut Sudut Arah.
Dalam persamaan implisit,
aX + bY + c = 0 koefisien arah grafik fungsi sama dengan
b a
− , dan koordinat titik potong grafik dengan
sumbu-Y : −
b c , 0 .
Cara menggambarkan grafik fungsi linear ada dua cara, yaitu berdasarkan 1) dua titik yang dilalui grafik
2) nilai koefisien arah dan sebuah titik yang dilalui grafik.
Contoh soal 1.
Gambarkan grafik fungsi Y = 2X − 3 !
Jawab :
1. Jika berdasarkan dua titik yang dilalui grafik, maka ambil dua nilai sembarang dari X dan hitung nilai Y sesuai dengan persamaan fungsinya, misalnya :
X −2 1
Y 2(−2) – 3 = −7 2(1) – 3 = −1
φ X
Y
(0,b)
φ sudut antara grafik
fungsi dengan sumbu-X, diukur dari sumbu-X berlawanan arah gerak jarum jam (0,b) titik potong
grafik fungsi dengan sumbu-Y
48 garis arah Y -2 1 X -1 (1 , -1) -7
2. Jika berdasarkan nilai koefisien arah dan sebuah titik yang dilalui grafik, maka
1) gambarkan garis arah dengan sudut arah φ, yang nilai koefisien arahnya 2,
Tg φ = 2.
2) tentukan sebuah titik yang dilalui grafik, dan untuk kemudahan ambil titik potong grafik dengan sumbu-Y, (0 , -3),
3) gambarkan garis yang sejajar garis arah dan melalui titik potong tersebut
Y 2 φ 1 X (0 , -3) (2 , -7)
49
Berdasarkan cara menggambarkan grafiknya, membangun persamaan fungsi linear, dapat dilakukan berdasarkan
1. dua titik yang dilalui grafik
2. nilai koefisien arah dan sebuah titik yang dilalui grafik.
Persamaan fungsi linear jika melalui titik (x0 , y0) dan (x1 , y1) adalah
0 1 0 0 1 0 x x x X y y y Y − − = − −
Jika disajikan dalam persamaan eksplisit, bentuknya menjadi
0 1 1 0 0 1 0 1 0 1 0 1 0 0 1 0 0 1 0 0 0 1 0 1 0 1 0 0 0 1 0 1 0 1 0 1 x x x y x y X x x y y x x x y x y x x x y x y X x x y y y x x x y y X x x y y Y − − − − − = − − + − − − − − = + − − − − − =
Sedangkan persamaannya jika nilai koefisien arah, a dan melalui titik (x0 , y0) adalah,
Y – y0 = a(X – x0)
Yang jika disajikan dalam persamaan eksplisit, bentuknya
Y = aX – ax0 +y0 = aX – (ax0 – y0) Contoh soal 2.
Tentukan persamaan fungsi linear, jika grafiknya a. melalui titik-titik (-1 , 2) dan (2 , -3)
b. memiliki koefisien arah –2 dan melalui titik (2 , 3)
Jawab : a. 3 1 X 5 2 Y ) 1 ( ) 2 ( ) 1 ( X ) 2 ( ) 3 ( ) 2 ( Y = + − − − − − − = − − − (3)(Y – 2) = (−5)(X + 1) Y – 6 = −5X – 5 5X + 3Y – 6 + 5 = 0 5X + 3Y – 1 = 0 (persamaan eksplisit) 3 1 X 3 5 Y=− − (persamaan implisit) b. Y – (3) = (2)(X - 2) Y = 2X – 4 + 3 Y = 2X – 1 (persamaam implisit) 2X − Y − 1 = 0 (persamaan eksplisit)
50
ϕ
ϕ1 ϕ2
l : Y= mX + n
II.5.1.1. Sudut antara dua grafik
Salah satu segi yang dapat diturunkan dari koefisien arah grafik fungsi linear, adalah sudut antara dua grafik seperti di bawah ini.
Y
X
Gambar II.13
ϕ sudut antara g dan l (0≤ ϕ ≤ ½π)
Pada Gambar II.13.
ϕ1 sudut arah l Tg ϕ1 = m ϕ2 sudut arah g Tg ϕ2 = a ϕ = ϕ2− ϕ1 Tg ϕ = Tg (ϕ2− ϕ1) = ) ( Cos ) ( Sin 1 2 1 2 ϕ − ϕ ϕ − ϕ = 1 2 1 2 1 2 1 2 Sin Sin Cos Cos Sin Cos Cos Sin ϕ ϕ + ϕ ϕ ϕ ϕ − ϕ ϕ = 1 2 1 2 1 2 1 2 1 2 1 2 1 2 1 2 Cos Cos Sin Sin Cos Cos Cos Cos Cos Cos Sin Cos Cos Cos Cos Sin ϕ ϕ ϕ ϕ + ϕ ϕ ϕ ϕ ϕ ϕ ϕ ϕ − ϕ ϕ ϕ ϕ = 1 2 1 2 1 1 2 2 Cos Cos Sin Sin 1 Cos Sin Cos Sin ϕ ϕ ϕ ϕ + ϕ ϕ − ϕ ϕ = 1 2 1 2 Tg Tg 1 Tg Tg ϕ ϕ + ϕ − ϕ = am 1 m a + −
Karena sudut antara dua grafik yang digunakan adalah sudut lancip, 0 ≤ ϕ ≤ ½π, yang
berarti Tg ϕ 0. Sedangkan dari formulasi kesamaan dimungkinkan Tg ϕ ≤ 0, maka pada
51
formulasi kesamaan, ruas kanan harus disajikan dalam harga mutlak. Sehingga jika ϕ sudut
antara dua grafik fungsi linear, g : Y=aX + b dengan l : Y= mX + n, maka am 1 m -a Tg + = ϕ
II.5.1.2. Dua grafik fungsi linear
Dari konsepsi sudut antara dua grafik fungsi linear, maka dapat disimpulkan bahwa antara dua grafik fungsi linear hanya satu dari dua hal di bawah ini yang berlaku, yaitu 1) Sejajar.
Dua grafik fungsi linear akan sejajar jika koefisien arah keduanya sama, a = m. 2) Berpotongan, yang dibedakan atas
a) berpotongan tegak lurus.
Dua grafik fungsi linear akan berpotongan tegak lurus jika hasil kali koefisien arahnya sama dengan –1, a.m = −1.
b) berpotongan biasa.
Untuk menentukan titik potong dua grafik dapat dilakukan dengan mempersamakan kedua persamaan fungsinya.
Jika diketahui dua grafik fungsi linear, Y = aX + b dan Y = nX + m , maka koordinat titik potongnya dapat dihitung dengan cara sebagai berikut :
m nX Y b aX Y + = + = aX + b = mX + n aX – mX = n – b (a – m)X = n – b X = m a b n − − dari persamaan Y = aX + b Y = − − m a b n a + b m a bm an m a ) m a ( b m a ) b n ( a Y − − = − − + − − =
sehingga koordinat titik potongnya.
− − − − m a bm an , m a b n
52
Y Y Y
X X X
sejajar berpotongan berpotongan tegak lurus
Gambar II.14
Kemungkinan dua grafik fungsi linear
Contoh soal 3.
Tentukan persamaan fungsi linear yang grafiknya berpotongan tegak lurus dengan grafik fungsi
3 X 2 Y=− +
dan melalui titik potong grafik fungsi 3 X 2
Y= + dengan Y=−3X−2!
Jawab :
Jika a koefisien arah grafik yang tegak lurus grafik Y = −2X + 3 , maka (a)(−2) = −1 a =
2 1
Koordinat titik potong grafik Y = 2X + 3 dengan Y = −3X – 2 :
2 X 3 Y 3 X 2 Y − − = + = 2X + 3 = −3X – 2 2X + 3X = −2 – 3 5X = −5 X = −1 3 X 2 Y 1 X + = =
Y = 2(−1) + 3 = 1 koordinat titik potongnya : (−1 , 1),
Sehingga persamaan fungsi linear yang dicari, adalah fungsi yang grafiknya melalui titik (−1 , 1) dengan koefisien arah
2 1 , yaitu : Y – (1) = 2 1 (X – (−1) Y = 2 1 X + 2 1 + 1 Y = 2 1 X + 1 2 1 .
53 Persamaan fungsi jika disajikan dalam
persamaan implisit, maka diperoeh hasil Y = 2 1 X + 1 2 1 2Y = X + 3 X – 2Y + 3 = 0
Jika grafik fungsi-fungsi tersebut digambarkan dengan menggunakan program Mathcad pada domain {−10 ≤ x ≤ 10}, maka hasilnya seperti di
samping ini.
Dengan fungsi-fungsi yang ditetapkan : f(x) : Y = −2X + 3 , g(x) : Y = 2X + 3 ,
h(x) : Y = −3x – 2 ,
dan fungsi yang dicari : i(x) : Y = 2 1 X + 1
2 1 .
II.5.2. Fungsi Kuadrat
Persamaan fungsi kuadrat, atau biasa juga disebut persamaan parabola tegak, adalah :
Y = aX2 + bX + c , a ≠ . 0 Selanjutnya perhatikan proses aljabar di bawah ini :
a 2 b b ac 4 aY 4 a 2 1 X a 4 b ) c Y )( a 4 ( a 2 b X a 4 b a c Y 2a b X a c Y a 2 b a 2 b X a b X a c Y X a b X c Y bX aX c bX aX Y 2 2 2 2 2 2 2 2 2 2 2 2 − + − ± = + − ± = + + − = + − = − + + − = + − = + + + =
Karena 4aY−4ac+b2 akan bernilai real jika 4aY−4ac+b2 ≥0, atau
0 a jika , a 4 ac 4 b Y≥− 2− > , dan , jika a 0 a 4 ac 4 b Y ≤− 2− < . Maka range fungsi kuadrat adalah,
Y = { a 4 ac 4 b y≥− 2 − } , jika a < 0 atau Y = { a 4 ac 4 b y≤− 2 − } , jika a > 0. i(x) h(x) g(x) f(x) 10 0 10 10.78 10.78 f x( ) g x( ) h x( ) i x( ) x
Gambar posisi grafik fungsi linier yang ditetapkan dengan yang dicari
54 Dari hubungan a 4 b ) c Y )( a 4 ( a 2 b X+ = ± −2 + 2 , karena 0 a 4 b ) c Y )( a 4 ( 2 2 ≥ + − , maka a 4 b ) c Y )( a 4 ( a 2 b X+ = −2 + 2 , jika 0 a 2 b X+ ≥ atau a 2 b X ≥− a 4 b ) c Y )( a 4 ( a 2 b X+ =− −2 + 2 , jika 0 a 2 b X+ ≤ atau a 2 b X≤ −
Hal ini menyimpulkan bahwa, fungsi kuadrat merupakan fungsi satu-satu pada, jika domainnya X = { a 2 b x≥− } atau X = { a 2 b x≤− }. Dalam domain tersebut, fungsi inversnya
a 2 b X jika , a 2 b ) ac 4 b ( aX 4 a 2 1 Y= − 2 − − >− a 2 b X jika , a 2 b ) ac 4 b ( aX 4 a 2 1 Y=− − 2 − − <−
Sehingga jika domainnya −∞< X<∞ maka fungsi kuadrat bukan fungsi satu-satu pada, tetapi hanya merupakan fungsi ke dalam.
Dari uraian tersebut, garis dengan persamaan
a 2
b
X=− , dinamakan Sumbu Simetris,
dan nilai a 4 ac 4 b
Y =− 2− , adalah nilai ekstrim fungsi. Nilai ekstrim ini, merupakan nilai
minimum jika a > 0, dan nilai maksimum jika a < 0.
Untuk menggambarkan fungsi kuadrat secara “manual” diperlukan komponen-komponen :
1. Sumbu simetris, yaitu garis dengan persamaan
a 2
b X=− .
2. Titik ekstrim, yaitu titik dengan koordinat − − −
a 4 ac 4 b , a 2 b 2
3. Titik potong dengan sumbu-sumbu koordinat,
1) dengan sumbu-Y : X = 0 Y = c koordinat titik potongnya (0 , c) 2) dengan sumbu-X : Y = 0 aX2 + bX + c = 0