ANALISIS NUMERIK MODEL EPIDEMIK SIR (SUSCEPTIBLE, INFECTIOUS, RECOVERED) PADA PENYEBARAN PENYAKIT TUBERCULOSIS DI YOGYAKARTA.

i ANALISIS NUMERIK MODEL EPIDEMIK SIR (SUSCEPTIBLE, INFECTIOUS, RECOVERED) PADA PENYEBARAN PENYAKIT

TUBERCULOSIS DI YOGYAKARTA

SKRIPSI

Diajukan Kepada Fakultas Matematika Dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta

Sebagai Salah Satu Persyaratan Guna Memperoleh Gelar Sarjana Sains

Halaman judul

Oleh Okky Rositarini NIM. 13304131028

PROGRAM STUDI MATEMATIKA

FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA

v MOTTO

Dan Tuhanmu berfirman, “Berdo’alah kepada-Ku, niscaya akan Kuperkenankan bagimu”.

(QS. Al Mu’min:60)

Barang siapa keluar untuk mencari ilmu maka dia berada di jalan Allah

(HR. Turmudzi)

Bila kau tak tahan lelahnya belajar, maka kau harus tahan perihnya menanggung kebodohan.

(Imam Ayafi’i)

Banyak kegagalan dalam hidup ini dikarenakan orang-orang tidak menyadari betapa dekatnya mereka dengan keberhasilan saat mereka menyerah.

(Thomas Alva Edison)

vi

PERSEMBAHAN

Karya sederhana ini saya persembahkan untuk :

Kedua orang tua saya, Bapak Rosadi dan Ibu Darini yang senantiasa memberikan

doa dan kasih sayang serta dukungannya yang tiada henti.

Adikku Phiesca Verdian Rizki yang tersayang yang menambah kebahagiaan

dalam keluarga.

Semua guru, dosen, dan pendidik, terimakasih sudah memberikan ilmunya

kepada saya .

Sahabat-sahabat terbaikku terkhusus Noni Cahayani Azazmi yang selalu

menemaniku dalam susah maupun senang.

Teman-teman Matematika B 2013 dan teman-teman yang lain yang tidak bisa

vii

ANALISIS NUMERIK MODEL EPIDEMIK SIR (SUSCEPTIBLE, INFECTIOUS, RECOVERED) PADA PENYEBARAN PENYAKIT

TUBERCULOSIS DI YOGYAKARTA Oleh:

Okky Rositarini NIM. 13305141028

ABSTRAK

Penyakit Tuberculosis adalah salah satu penyakit menular yang disebabkan oleh bakteri Mycobacterium Tuberculosis. Penelitian ini bertujuan untuk mengetahui model matematika penyebaran penyakit Tuberculosis, mengetahui titik ekuilibrium, bilangan reproduksi, kestabilan titik ekuilibrium, dan hasil simulasi numerik penyebaran penyakit Tuberculosis khususnya di Kota Yogyakarta pada tahun 2014.

Tahapan yang dilakukan untuk menganalisis model penyebaran penyakit Tuberculosis adalah dengan membentuk model matematika SIR (Susceptible, Infectious, Recovered), kemudian menentukan titik ekuilibrium, menentukan bilangan reproduksi dasar, dan menganalisa kestabilan disekitar titik ekuilibrium, serta menganalisis numerik dengan melakukan simulasi menggunakan Software Maple 15.

Model SIR pada penyebaran penyakit Tuberclosis merupakan model yang berbentuk sistem persamaan diferensial nonlinear. Hasil analisis dari model SIR tersebut diperoleh dua titik ekuilibrium, yaitu titik ekuilibrium bebas penyakit dan endemik. Titik ekuilibrium bebas penyakit stabil asimtotik loka jika bilangan reproduksi dasar kurang dari satu dan sebaliknya titik ekilibrium bebas penyakit tidak stabil jika bilangan reproduksi dasar lebih dari satu. Selanjutnya, berdasarkan simulasi yang dibentuk dari model SIR dengan nilai awal dan parameter yang diberikan diperoleh penyakit Tuberculosis semakin besar laju kontak atau laju penularan maka penyakit akan semakin menyebar dan semakin kecil laju kesembuhan maka penyakit juga akan semakin menyebar.

viii

KATA PENGANTAR Asslamu’alaikum wr wb,

Alhamdulillah, puji syukur penulis panjatkan kepada Allah SWT yang telah memberikan rahmat, hidayah, serta nikmat karunia, dan ridha-Nya sehingga penulis dapat menyelesaikan penulisa Skripsi yang berjudul“Analisis Numerik Model Epidemik SIR (Susceptible, Infectious, Recovered) pada Penyebaran Penyakit Tuberculosis di Yogyakarta”.

Tugas akhir ini dibuat sebagai salah satu syarat untuk memperoleh gelar Sarjana Sains (S.Si). Penulis menyadari bahwa tanpa bantuan dari berbagai pihak penulisan tugas akhir ini tidak dapat terselesaikan dengan baik. Pada kesempatan ini, penulis mengucapkan terima kasih kepada semua pihak yang telah membantu dan memberikan dukungan kepada penulis, yaitu:

1. Bapak Dr. Hartono selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta

2. Bapak Dr. Ali Mahmudi, M.Pd selaku Ketua Jurusan Pendidikan Matematika FMIPA Universitas Negeri Yogyakarta yang telah memberikan kelancaran dalam akademik.

3. Bapak Dr. Agus Maman Abadi, M.Si selaku Ketua Program Studi Matematika FMIPA Universitas Negeri Yogyakarta

ix

bimbingan, dan masukkan sehingga penulis dapat menyelesaikan tugas akhir ini.

5. Ibu Nikenasih Binatari, M.Si selaku dosen pembimbing akademik yang telah memberikan bimbingan selama perkuliahan.

6. Bapak dan ibu dosen Jurusan Pendidikan Matematika yang telah memberikan ilmu kepada penulis secara langsung maupun tidak langsung. 7. Bapak, ibu, dan keluarga yang tidak pernah lelah memberikan dukungan,

nasihat, bimbingan, serta doa kepada penulis.

8. Teman-teman, sahabat-sahabat, serta semua pihak yang tidak dapat saya sebutkan satu per satu yang telah memberikan dukungan dan membantu secara langsung maupun tidak langsung dalam kelancaran penulisan tugas akhir ini.

Penulis menyadari bahwa penyusunan tugas akhir ini masih jauh dari sempurna sehingga masih banyak kekurangan. Oleh karena itu, kritik dan saran sangat diharapkan untuk membangun tugas akhir ini supaya menjadi lebih baik.

Akhir kata, semoga tugas akhir ini dapat bermanfaat tidak hanya bagi penulis tetapi juga bagi pembaca.

Wassalamu’alaikum wr wb.

Yogyakarta, 8 April 2017 Penulis

x DAFTAR ISI

HALAMAN JUDUL ... i

LEMBAR PERSETUJUAN... ii

PERNYATAAN ... ii

PENGESAHAN ... iv

MOTTO ... v

PERSEMBAHAN ... vi

ABSTRAK ... vii

KATA PENGANTAR ... viii

DAFTAR ISI ... x

DAFTAR TABEL ... xii

DAFTAR GAMBAR ... xiii

DAFTAR LAMPIRAN ... xiv

DAFTAR SIMBOL ... xv

BAB I PENDAHULUAN ... 1

A.Latar Belakang ... 1

B.Identifikasi Masalah ... 4

C.Pembatasan Masalah ... 4

D.Rumusan Masalah ... 4

E.Tujuan Penelitian ... 5

F.Manfaat Penelitian ... 6

BAB II LANDASAN TEORI ... 7

A.Model Matematika ... 7

B.Persamaan Diferensial ... 9

C.Sistem Persaman Diferensial ... 12

1.Sistem Persamaan Diferensian Linear ... 13

2.Sistem Persamaan Diferensial Nonlinear ... 14

D.Titik Ekuilibrium ... 17

E.Linearisasi ... 19

F.Bilangan Reproduksi Dasar

 

R0 ... 23

G.Nilai Eigen ... 26

H.Kestabilan Titik Ekuilibrium ... 28

xi

BAB IIIHASIL DAN PEMBAHASAN... 39

A.Permasalahan Nyata Penyebaran Penyakit Tuberculosis ... 39

B.Model Matematika Penyebaran Penyakit Tuberculosis... 40

C.Analisis Model Penyebaran Penyakit Tuberculosis ... 44

1.Titik Ekuilibrium ... 44

2.Bilangan Reproduksi Dasar

 

R₀ ... 48

3.Analisis Kestabilan ... 50

D.Analisis Numerik Model SIR pada Penyebaran Penyakit Tuberculosis ... 57

1.Simulai R₀ 1 ... 58

2.Simulasi R₀ 1 ... 59

BAB IVPENUTUP ... 64

A.Kesimpulan ... 64

B. Saran ... 65

DAFTAR PUSTAKA ... 67

xii

DAFTAR TABEL

xiii

DAFTAR GAMBAR

Gambar 2.1. Proses Pemodelan Matematika ... 8

Gambar 2.2. Simulasi Kestabilan Titik Ekuilibrium ... 29

Gambar 3.1. Diagram Alir Model Matematika Tuberculosis... 42

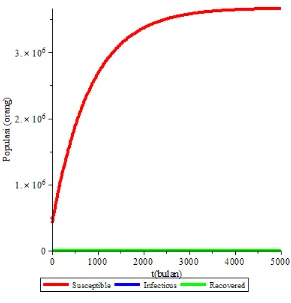
Gambar 3.2. Grafik Simulasi untuk R₀ 0,005018788208... 59

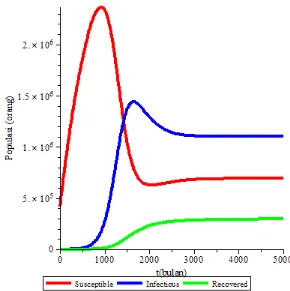
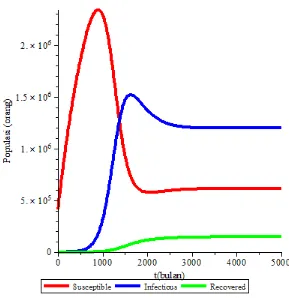
Gambar 3.3. Grafik Simulasi untukR₀ 3,023980394 ... 60

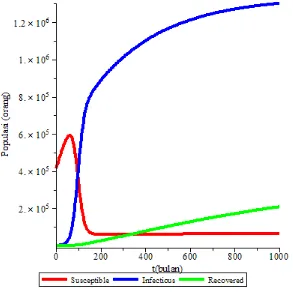
Gambar 3.4. Grafik Simulasi untuk R₀ 24.94004448 ... 61

xiv

DAFTAR LAMPIRAN

Lampiran 1. Program maple untuk gambar proyeksi potret fase solusi-solusi S,I,R terhadap t dengan R₀ 0, 005018788208 ... 68

Lampiran 2. Program maple untuk gambar proyeksi potret fase solusi-solusi S,I,R terhadap t dengan R₀ 3, 023980394 ... 68

Lampiran 3. Program maple untuk gambar proyeksi potret fase solusi-solusi S,I,R terhadap t dengan R₀ 24.94004448 ... 70

xv

DAFTAR SIMBOL

Simbol Definisi

 

N t Jumlah populasi pada suatu daerah pada saat t.

( )

S t Banyaknya individu yang sehat dan rentan tehadap penyakit Tuberculosis pada saat t. (Susceptible)

( )

I t Banyaknya individu yang terinfeksi dan dapat menularkan Tuberculosis kepada individu lain. (Infectious)

( )

R t Banyaknya individu yang sembuh setelah terinfeksi Tuberculosis. (Recovered)

 Laju kelahiran populasi.  _{Laju kematian alami.}

t

 Laju kematian yang disebabkan oleh penyakit Tuberculosis.

b Laju penularan penyakit Tuberculosis.

c Laju individu sembuh setelah terinfeksi Tuberculosis.  Nilai eigen

I Matriks identitas x Turunan x terhadap t

0

R Bilangan reproduksi dasar ˆ

x Titik ekuilibrium n

Himpunan bilangan real dimensi n ( )_i

e 

 Bagian real nilai eigen ke-i

xvi 0

x Kondisi awal

 

0

Df x Turunan f di x₀

 

0

Jf x Matriks jacobian di x₀

 Himpunan bagian atau sama dengan  Elemen/anggota

0

E Titik ekuilibrium bebas penyakit

1

1 BAB I PENDAHULUAN

A.Latar Belakang

Kesehatan adalah suatu hal yang sangat penting dalam kehidupan karena jika seseorang mengalami masalah kesehatan maka aktivitas seseorang tersebut akan terganggu. Masalah kesehatan yang sering menjadi perhatian masyarakat adalah penyakit menular karena masyarakat harus waspada terhadap penyakit tersebut.

Penyakit yang menular secara terus menerus melalui individu yang terinfeksi ke individu yang sehat merupakan suatu masalah yang sangat diperhatikan oleh negara maupun dunia. Penularan penyakit bisa terjadi melalui interaksi di dalam rantai infeksi baik secara langsung maupun tidak langsung. Salah satu contoh penyakit menular adalah penyakit Tuberculosis.

Penyakit Tuberculosis (TB) adalah salah satu penyakit menular yang disebabkan oleh bakteri Mycobacterium Tuberculosis. Sebagian besar bakteri tersebut menyerang paru-paru, akan tetapi dapat juga menyerang organ tubuh lainnya. Penyakit ini tergolong sebagai salah satu penyakit yang menyebabkan kematian. Menurut Kementrian Kesehatan Republik Indonesia tahun 2011, sepertiga dari populasi dunia sudah tertular dengan TB dimana sebagian besar penderita TB adalah usia produktif (15-55 tahun).

2

bintik-bintik kecil pada dinding alveolus. Adapun gelaja penderita Tuberculosis diantaranya batuk-batuk, sakit dada, nafas pendek, hilang nafsu makan, demam, kedinginan, berat badan turun, dan kelelahan. (Slamet Suyono, 2001).

Salah satu pendekatan untuk menjelaskan solusi pada penyebaran penyakit Tuberculosis yaitu dengan cara pembuatan model matematika. Langkah pertama yang digunakan dalam pembuatan model matematika adalah dengan menyatakan masalah dunia nyata ke dalam pengertian matematika. Model matematika yang dibuat kemudian akan disimulasika yang nantinya diharapkan dapat membantu untuk mencari solusi bagaimana mengatasi penyebaran penyakit Tuberculosis. (Widowati dan Sutimin, 2007).

Model matematika yang digunakan untuk memodelkan penyebaran penyakit Tuberculosis terdapat beberapa model, salah satunya adalah model SIR (Susceptible, Infectious, Recovered). Pada model ini, populasi dibagi menjadi 3 bagian, yaitu individu yang sehat tetapi rentan terhadap penyakit Tuberculosis yang disebut Susceptible, individu yang terinfeksi dan dapat menularkan penyakit Tuberculosis disebut Infectious, individu yang telah sembuh terhadap penyakit Tuberculosis. Secara garis besar, model epidemik SIR menggambarkan alur penyebaran penyakit dari kelompok individu Susceptible menjadi Infectious melalui kontak langsung ataupun melalui perantara. Kemudian kelompok individu Infectious yang mampu bertahan terhadap penyakit akan sembuh dan menjadi individu Recovered. (Ilmiyati dan Hengki, 2014).

3

Penyebaran Penyakit Tuberculosis” yang mengalisis model matematika meliputi titik kestabilan, nilai eigen, dan bilangan reproduksi dasar

 

R₀ yang kemudian dilakukan simulasi analisis numeriknya untuk menguji parameter-parameter yang telah dibuat yang bertujuan untuk mengetahui kapan penyakit akan menjadi endemik. Sedangkan M. Rifki Taufik, dkk (2015) membahas menggunakan model VEIT (Vaccinated, Exposed, Infected, Threated). Penelitian tersebut membahas penyakit Tuberculosis.

Pada penulisan skripsi ini akan membahas tentang model matematika SIR untuk penyebaran penyakit Tuberculosis. Pada penulisan Fredlina, K. Queena Fredlina, dkk (2012) data yang dipakai hanya diasumsikan saja dan metode Runge-Kutta orde 4. Dalam penulisan ini model SIR untuk penyebaran penyakit Tuberculosis akan digunakan untuk simulasi analisis numerik pada penderita Tuberculosis di wilayah Yogyakarta dan menganalisis kestabilan menggunakan kriteria Routh-Hurwitz serta mensimulasikan dengan menggunakan Software Maple 15.

4

kemudian akan ditunjukkan grafik simulasinya dengan menggunakan Software Maple. Menggunakan hasil analisis numerik tersebut diharapkan dapat diketahui cara mengatasi penyakit Tuberculosis. .

B.Identifikasi Masalah

1. Penyakit Tuberculosis masih banyak ditemukan terutama di wilayah Yogyakarta.

2. Upaya keberhasilan pengobatan penyakit Tuberculosis di Kota Yogyakarta masih dibawah target nasional.

3. Masih terdapat kematian akibat penyakit Tuberculosis. 4. Penyakit Tuberculosis bersifat endemik pada populasi.

5. Belum maksimalnya peran matematika dalam membantu penyelesaian penyebaran penyakit Tuberculosis di Yogyakarta.

C.Pembatasan Masalah

Skripsi ini membahas tentang penyebaran penyakit Tuberculosis menggunakan model SIR (Susceptible, Infectious, Recovered). Selanjutnya, model tersebut akan disimulasikan analisis numeriknya berdasarkan data jumlah penderita Tuberculosis di wilayah Daerah Istimewa Yogyakarta (DIY) dengan menggunakan Software Maple 15 .

D.Rumusan Masalah

Berdasarkan latar belakang tersebut maka permasalahan dalam penelitian ini dirumuskan sebagai berikut :

5

2. Bagaimana analisis titik ekuilibrium model SIR pada penyebaran penyakit Tuberculosis?

3. Bagaimana analisis bilangan reproduksi dasar

 

R₀ model SIR pada penyebaran penyakit Tuberculosis?

4. Bagaimana analisis kestabilan model SIR pada penyebaran penyakit Tuberculosis?

5. Bagaimana simulasi numerik pada penyebaran penyakit Tuberculosis di wilayah Daerah Istimewa Yogyakarta (DIY)?

E.Tujuan Penelitian

Berdasarkan permasalahan tersebut, maka tujuan dari penulisan ini adalah sebagai berikut :

1. Mengetahui model matematika untuk penyebaran penyakit Tuberculosis dengan model SIR (Susceptible, Infectious, Recovered).

2. Mengetahui analisis titik ekuilibrium model SIR pada penyebaran penyakit Tuberculosis.

3. Mengetahui analisis bilangan reproduksi dasar

 

R₀ model SIR pada penyebaran penyakit Tuberculosis.

4. Mengetahui analisis kestabilan model SIR pada penyebaran penyakit Tuberculosis.

6 F. Manfaat Penelitian

Manfaat yang dapat diperoleh dari penulisan ini adalah :

1. Menambah pengetahuan tentang model matematika penyebaran penyakit Tuberculosis dengan model SIR (Susceptible, Infectious, Recovered).

2. Dapat menjadi referensi baru dalam pengembangan ilmu matematika di bidang pemodelan penyakit menular.

7 BAB II

LANDASAN TEORI

Pada bab ini akan diuraikan beberapa teori-teori yang digunakan sebagai landasan teori dalam pembahasan tugas akhir skripsi ini. Teori-teori yang digunakan berupa definisi-definisi serta teorema-teorema yaitu sebagai berikut:

A.Model Matematika

Model matematika adalah representasi dan penjelasan mengenai permasalahan dalam dunia nyata ke dalam pernyataan matematik supaya didapatkan suatu solusi. Beberapa jenis-jenis model matematika adalah sebagai berikut : (Widowati & Sutimin, 2007)

a. Model Empiris

Model empiris diperoleh dari hasil pengamatan. Gagasan utama pada pendekatan model empiris adalah menjelaskan persamaan matematika yang dapat menghasilkan grafik untuk mencocokkan data.

b. Model Simulasi

Pada pendekatan model simulasi, program komputer dapat digunakan dalam simulasi suatu model matematika seperti menggunakan Software Maple, Matlab, dll.

c. Model Deterministik dan Stokastik

8

kepastian yang tidak stabil (nilainya tidak pasti). Pada model stokastik mengandung distribusi peluang.

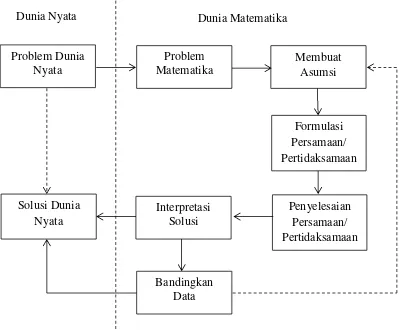
Proses pemodelan matematika dapat dinyatakan dalam diagram alur Gambar 2.1. berikut : (Widowati & Sutimin, 2007)

Gambar 2.1. Proses Pemodelan Matematika

Pemodelan matematika dimulai dari adanya permasalahan pada dunia nyata. Permasalahan pada dunia nyata diharapkan langsung mendapatkan solusi pada dunia nyata itu sendiri, namun jika masih kesulitan maka permasalahan tersebut dibawa ke permasalahan matematika untuk kemudian dibuat beberapa asumsi meliputi identifikasi variabel-variabel yang selanjutnya digunakan dalam

Dunia Nyata _{Dunia Matematika}

Problem Dunia Nyata

Solusi Dunia Nyata

Membuat Asumsi Problem

Matematika

Interpretasi Solusi

Bandingkan Data

Formulasi Persamaan/ Pertidaksamaan

9

memformulasikan persamaan/pertidakasamaan. Asumsi yang digunakan dalam pembatasan masalah ini digunakan untuk mempelajari masalah tersebut secara sederhana. (Cahyono, Edi, 2013).

Ketika model diformulasikan maka langkah berikutnya adalah menyelesaikan persamaan/pertidaksamaan. Selanjutnya interpretasi solusi, yaitu tahap setelah menyelesaiakan persamaan/pertidaksamaan yang bisa dilihat hasilnya menggunakan tabel, grafik, dan lain-lain. Hasil interpretasi solusi kemudian bisa langsung dibawa ke solusi permasalahan nyata, selain itu juga masih bisa dengan membandingkan data. Misalnya, pada waktu membandingkan, mungkin terdapat perbedaan hasil dan model dapat diperbaiki lagi dengan membangun model dari awal.

B.Persamaan Diferensial Definisi 2.1. (Ross, 1984)

Persamaan diferensial adalah persamaan yang melibatkan turunan dari

variabel-variabel tak bebas dan terhadap variabel-variabel-variabel-variabel bebas.

Berdasarkan banyaknya variabel bebas yang dilibatkan, persamaan diferensial terbagi menjadi dua, yaitu persamaan diferensial biasa dan persamaan diferensial parsial.

Definisi 2.2. (Ross, 1984)

Persamaan diferensial biasa adalah suatu persamaan diferensial yang melibatkan

10 Definisi 2.3. (Ross, 1984)

Persamaan diferensial parsial adalah suatu persamaan diferensial yang

melibatkan turunan dari satu atau lebih variabel tak bebas terhadap dua atau

lebih variabel bebas

Contoh 2.1

Contoh persamaan diferensial biasa

2 2

2 0

d y dy

xy

dx dx

   _{ } 

  (persamaan diferensial orde 2)

4 2

4 5 2 3 sin d y d y

x t

dt  dt   (persamaan diferensial orde 4).

Contoh 2.2

Contoh persamaan diferensial parsial

r r

r

s t

 _ _

 

2 2 2

2 2 2 0.

u u u

x y z

 _ _ _

  

Contoh 2.3

Contoh persamaan diferensial dan solusinya

2 dy

x dx 

maka solusinya adalah

11 2 dy x dx





2 . yx c

Berdasarkan contoh dari persamaan diferensial, maka dapat diketahui bahwa solusi persamaan diferensial adalah berupa fungsi yang memenuhi persamaan diferensial, yaitu jika fungsi tersebut disubstitusikan pada persamaan diferensial maka akan menghasilkan suatu pernyataan yang benar atau terpenuhi.

Persamaan Diferensial Linear Orde n Definisi 2.4. (Ross, 1984)

Persamaan diferensial linear orde n dengan variabel tak bebas y dan variabel

bebas x dapat dituliskan dalam bentuk sebagai berikut:

 

 

1

 

 

 

0 1 1 ... 1

n n

n n

n n

d y d y dy

a x a x a x a x y b x

dx dx dx



 

    

dengan a₀ 0 dan a x_i( ) merupakan fungsi atas x untuk setiap i0,1, 2,..., .n Contoh 2.4

Persamaan diferensial orde n

1. 2dx 2x 3

dt   (orde 1)

2. 3

3 5 9

d x dx x

dt  dt   (orde 3)

3.

4 2

4 2

5d x 3d x 13x 1

12 C.Sistem Persaman Diferensial

Sistem persamaan diferensial merupakan gabungan dari dua atau lebih persamaan diferensial. Diketahui vektor x n, dengan x



x x x₁, ₂, ₃,...,x_n



T

dan x x x₁, ₂, ₃,...,x_n . Jika notasi x dx dt

 untuk menyatakan turunan x terhadap

t, maka:

3 1 2

x , , ,..., .

T n

dx dx

dx dx

dt dt dt dt

       sehingga

















1

1 1 2 3

2

2 1 2 3

3 1 2 3

3

1 2 3

, , ,..., , , ,..., , , ,..., , , ,..., n n n n n n dx dt

f x x x x

dx

f x x x x

dt

f x x x x

dx dt

f x x x x

dx dt      _{  }  _{  }  _{  }  _{  }  _{  }  _{  }  _{  }           (2.1)

Pada Persamaan (2.1) jika secara eksplisit memuat variabel t maka sistem tersebut disebut sebagai sistem non autonomous dan sebaliknya jika tidak secara eksplisit memuat variabel t maka disebut sebagai sistem autonomous. Sistem autonomous dapat dinyatakan dalam bentuk:

13

Sistem persamaan diferensial dibagi menjadi 2, yaitu: 1. Sistem Persamaan Diferensial Linear

Sistem persamaan diferensial linear orde satu dengan variabel tak bebas

1, 2, 3,..., n

x x x x dan variabel bebas t dinyatakan sebagai berikut:

 

 

 

 

1

11 1 12 2 13 3 1 1 2

21 1 22 2 23 3 2 2 3

31 1 32 2 33 3 3 3

1 1 2 2 3 3

. n n

n n

n n

n

n n n nn n n

dx

a x a x a x a x H t

dt dx

a x a x a x a x H t

dt dx

a x a x a x a x H t

dt

dx

a x a x a x a x H t

dt

     

     

     

     

(2.2)

Jika H ti

 

dengan i1, 2,3,...,n bernilai nol, maka Sistem (2.2) disebut

sistem persamaan diferensial linear homogen, sedangkan jika ada H t_i

 

benilai taknol, maka Sistem (2.2) disebut sistem persamaan diferensial nonhomogen.

Sistem Persamaan (2.2) dapat dinyatakan dalam suatu bentuk persamaan sebagai berikut:

 

xAxH t (2.3)

14

 

H t adalah matriks ukuran n x 1 yang merupakan fungsi dari t. Berikut Persamaan (2.2) yang dituliskan dalam bentuk matriks:

 

 

 

11 12 1 1 1

21 22 2 2 2

1 2 3

. n

n

n n n nn n n

a a a x H t

a a a x H t

dy dt

a a a a x H t

                                        (2.4) Contoh 2.5

Diberikan sistem persamaan diferensial linear sebagai berikut:

2 3 6 dx x y dt dy x y dt  _{ }    _{ }  (2.5)

Sistem Persamaan (2.5) merupakan persamaan diferensial linear homogen. 2. Sistem Persamaan Diferensial Nonlinear

Definisi 2.5. (Ross, 1984)

Persamaan diferensial nonlinear adalah persamaan diferensial biasa yang tidak

linear.

15 Contoh 2.6

Diberikan sistem persamaan diferensial nonlinear sebagai berikut:





1 1 2 2 2 1 dx x x dt dx x dt  _{ }    _  (2.6) Penyelesaian:  2 2 dx x dt  2 2 1 dx dt x 

Integralkan kedua ruas, diperoleh

2

2 1

d x dt

x 





2 1 2

ln x   c t c

2

ln x  t c

2

t c x e

2 .

t x ke

 1

1(1 2) dx

x x

dt  

1 2

1 1

(1 )

dx x dt

16 1 1 1

(1 t)

dx ke dt

x  

Integralkan kedua ruas, diperoleh

1 1 1

(1 t)

dx ke dt

x  





1 3 4

ln x   c t ketc

1 5

ln x  t ketc

5

1

t t ke c

x e 

1 1

t t ke

x k e e

misalkan k₁k k₂ maka

1 2

t t ke

x k ke e

2

1 2 2 .

x

x k x e

Sehingga diperoleh penyelesaiannya adalah

2

t x ke

2

1 2 2

x x k x e

17 Contoh 2.7

Persamaan diferensial yang memuat variabel tak bebas dan turunan-turunannya berpangkat selain satu:

3 3 4. dy

x dt  

Contoh 2.8

Persamaan diferensial yang memuat perkalian dari variabel tak bebas dan/atau turunan-turunannya:

1

1 2 3 .1 dx

x x x

dt  

Contoh 2.9

Persamaan diferensial yang memuat fungsi transedental daari variabel tak bebas dan turunan-turunannya:

2 3 x 4. dy

e

dt  

D.Titik Ekuilibrium Definisi 2.6. (Perko, 2001)

18 Contoh 2.10

Akan ditentukan titik ekuilibrium dari Sistem Persamaan (2.6). Misalkan Sistem

(2.6) dapat dituliskan dalam bentuk x f x

 

dengan

 

1 2 ₂2 1 2

. x x x f x

x x 

 

  _ 

  Titik

ekuilibrium xˆ



x xˆ ˆ1, 2



dari Sistem (2.6) dapat diperoleh jika f

 

xˆ 0, sehingga sistem tersebut menjadi

1 2 2 ˆ ˆ ˆ 0 x x x 





2 1

ˆ ˆ 1 0 x x  

2 1

ˆ 0 dan ˆ 1.

x  x 

Untuk xˆ₂ 0, maka

2 1 2

ˆ ˆ 0

x x 

1 ˆ 0 x 

sehingga diperoleh titik ekuilibrium

 

0, 0 T.

Untuk xˆ₁1, maka

2 1 2 ˆ ˆ 0 x x 

2 2

ˆ

1x 0

2 2 ˆ 1 x 

2 ˆ 1 x 

19

Jadi Sistem (2.6) mempunyai titik ekuilibrium

 

0, 0 T dan

 

1,1T.

E.Linearisasi

Linearisasi merupakan suatu proses untuk mengubah sistem persamaan nonlinear menjadi sistem persamaan linear. Linearisasi dilakukan pada sistem persamaan nolinear yang bertujuan untuk mengetahui perilaku sistem disekitar titik ekuilibriumnya. Adapun syarat linearisari adalah bagian real akar karakteristiknya tidak nol.

Diberikan sistem persamaan nonlinear sebagai berikut:

 

x=f x (2.7)

dengan x L n, :f L n, fungsi nonlinear dan kontinu.

Lineariasi dapat menggunakan matriks Jacobian. Berikut adalah penjelasan mengenai matriks Jacobian:

Teorema 2.1. (Perko, 2001)

Jika f : n  n terdiferensial di x maka diferensial parsial₀ i , , 1, 2,..., , j

f

i j n

x

 _



di x ada untuk semua ₀ n

x dan

 

₀

 

₀ 1

.

n

j j j

f

Df x x x x

x



 



20 Bukti:

 

 

 

 

 

 

 

 

 

 

1 1 1 0

0 1 0 2

1 2

2

2 2

0

0 1 0 2

1 2

0 1

0 1 0 2 0

1 2 n n n n n j j j

n n n

n n

f

f f

x x

x x x x

x

x x

f

f f

x x

x x x x

f

x

x x

x x x

f f f

x x x x x x

x x x

            _  _  _                 __  _{ }  _                   _  _  _                   



 

 

 

 

 

 

 

 

 

1 1 1

0 0 0

1 2

1

2 2 2

0 0 0 2

1 2

0 0 0

1 2

n

n

n

n n n

n

f f f

x x x

x x x

x

f f f

x x x x

x x x

x

f f f

x x x

x x x

     _{  }   _{  }     _{  } _{     }   _{  }  _{  } _{  }           

 

0 . Df x x



dengan Df x

 

₀ disebut sebagai matriks Jacobian dari fungsi f : n  nyang terdiferensial pada n

x dan Df x

 

₀ dapat dinotasikan Jf x

 

₀ .

Kemudian akan ditunjukkan proses linearisasi dari suatu sistem persamaan diferensial. Misalkan xˆ



x xˆ ˆ₁, ₂,...,xˆ_n



T adalah titik ekuilibrium Sistem (2.7) maka pendekatan linear untuk Sistem (2.7) diperoleh dengan menggunakan ekspansi Taylor disekitar titik ekuilibrium tersebut, sebagai berikut

            1

1 1

1 1 2 1 1 2 1 2 1 1 1 2

1

ˆ ˆ, ,...,ˆn T ˆ ˆ, ,...,ˆn T ˆ ˆ, ,...,ˆn T ˆ ˆ ˆ, ,...,ˆn T n ˆn f n

f f

f x x x f x x x x x x x x x x x x x R

x x

 

      

 

            2

2 2

2 1 2 2 1 2 1 2 1 1 1 2

1

ˆ ˆ, ,...,ˆn T ˆ ˆ, ,...,ˆn T ˆ ˆ, ,...,ˆn T ˆ ˆ ˆ, ,...,ˆn T n ˆn f n

f f

f x x x f x x x x x x x x x x x x x R

x x

 

      

21

(2.8)

 1 2   1 2   1 2   1 1  1 2   

1

ˆ ˆ, ,...,ˆ T ˆ ˆ, ,...,ˆ T n ˆ ˆ, ,...,ˆ T ˆ n ˆ ˆ, ,...,ˆ T ˆ _n

n n n n n n n n f

n

f f

f x x x f x x x x x x x x x x x x x R

x x

 

      

 

selanjutnya dengan pendekatan linear untuk Sistem (2.8) adalah

            1

1 1 1

1 1 2 1 1 1 2 2 2 1 2

1 2

ˆ ˆ, ,...,ˆn T ˆ ˆ ˆ, ,...,ˆn T ˆ ˆ ˆ, ,...,ˆn T n ˆn f n

f f f

x x x x x x x x x x x x x x x x R

x x x

  

       

  

            ₂

2 2 2

2 1 2 1 1 1 2 2 2 1 2

1 2

ˆ ˆ, ,...,ˆ_n T ˆ ˆ ˆ, ,...,ˆ_n T ˆ ˆ ˆ, ,...,ˆ_n T _n ˆ_{n f}

n

f f f

x x x x x x x x x x x x x x x x R

x x x

  

       

  

(2.9)

 1 2   1 1  1 2   2 2  1 2   

1 2

ˆ ˆ, ,...,ˆ ˆ ˆ ˆ, ,...,ˆ ˆ ˆ ˆ, ,...,ˆ ˆ

n

T T T

n n n

n n n n n n f

n

f f f

x x x x x x x x x x x x x x x x R

x x x

  

       

  

dengan

1, 2,..., n

f f f

R R R disebut sebagai bagian nonlinear yang selanjutnya dapat diabaikan karena nilainya mendekati nol, sehingga Sistem (2.9) dapat ditulis dalam bentuk matriks berikut





























1 1 1

1 2 1 2 1 2

1 2

1

2 1 2

1 2 1 2 1 2

2

1 2

1 2 1 2

1 2

ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ

ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ

T T

n n n

n

T T

n n n

n

n

T

n n

n

f f f

x x x x x x x x x

x x x

x

f f f

x x x x x x x x x

x

x x x

x

f f

x x x x x

x x               _{   }       _{ }  





















1 1 2 2 1 2 ˆ ˆ . ˆ ˆ ˆ, ,...,ˆ n n T n n n n x x x x x x f

x x x x

x      _{  }  _{  }   _{  }  _{ }   _{  }   _  _ _        (2.10)

22





























1 1 1

1 2 1 2 1 2

1 2

1

2 1 2

1 2 1 2 1 2

2

1 2

1 2 1 2

1 2

ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ

ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ

ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ

T T

n n n

n

T T

n n n

n

n

T

n n

n

f f f

x x x x x x x x x

x x x

x

f f f

x x x x x x x x x

x

x x x

x

f f

x x x x x

x x               _{   }       _{ }  









1 2 1 2 . ˆ ˆ, ,...,ˆ n T n n n n y y y f

x x x x

x      _{  }  _{  }  _{  }  _{  }  _{  }  _           (2.11)

Sistem (2.11) merupakan linearisasi Sistem (2.18), sehingga diperoleh matriks Jacobian dari Sistem (2.7), yaitu:

 

































1 1 1

1 2 1 2 1 2

1 2

2 1 2

1 2 1 2 1 2

1 2

1 2 1 2 1 2

1 2 ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,...,ˆ ˆ ˆ, ,. T T

n n n

n

T T

n n n

n

T

n n n

n n

n

f f f

x x x x x x x x x

x x x

f f f

x x x x x x x x x

x x x

Jf x

f f f

x x x x x x x x

x x x

                  





. ˆ ..,x_n T

                      Contoh 2.11

Diberikan

 

1 2 ₂2 1 2 x x x f x

x x 

 

  _ 

  pada titik 0

 

1,1

T

x  . Akan dicari matriks Jacobian

dari fungsi f x

 

sebagai berikut:

1 1

1 2 2 2

2 2 2 1 2 1 1 2 f f

x x x x

23

 

1,1 1 0 .

1 2

T

Df   _   

Jadi, matrik Jacobian dari sistem tersebut adalah

 

1,1 1 0 .

1 2

T

Df   _ 

 

F. Bilangan Reproduksi Dasar

 

R₀

Adapun definisi mengenai bilangan reproduksi dasar adalah sebagai berikut:

Definisi 2.7. (Diekmann & Heesterbeek, 2000)

Bilangan reproduksi dasar

 

R₀ merupakan jumlah rata-rata kasus individu terinfeksi yang disebabkan oleh satu individu terinfeksi selama masa terinfeksinya

dalam keseluruhan populasi rentan.

Jika R₀ 1 maka penyakit hanya menginfeksi kurang dari satu individu rentan sehingga kemungkinan penyakit akan hilang dari populasi. Jika R₀ 1 maka individu yang terinfeksi akan menginfeksi lebih dari satu individu yang rentan, sehingga individu yang terinfeksi dalam suatu populasi akan menularkan penyakit tersebut dan penyakit akan menyebar dalam populasi dan jika R₀ 1 maka individu yang terinfeksi akan menularkan tepat kepada satu individu.

Misalkan ada n kelas terinfeksi dan m kelas yang tidak terinfeksi (rentan) serta x n dan y m adalah subpopulasi dari masing-masing kelas dan untuk

,

n m , sehingga:

 

 

24

 

y_j x y, , dengan j1, 2,...,m

dengan _i adalah laju individu baru yang terinfeksi yang menambah pada kelas

terinfeksi, sedangkan_i adalah laju perkembangan penyakit kematian, dan atau kesembuhan yang mengurangi populasi dari suatu kelas.

Perhitungan bilangan reproduksi dasar

 

R₀ berdasarkan linierisasi dari sistem persamaan diferensial yang didekati pada titik ekuilibrium bebas penyakit. Persamaan kompartemen terinfeksi yang telah dilinearisasi dapat dituliskan sebagai berikut:





x F V x

dengan F dan V adalah matriks berukuran n x n, dan i



0, ₀



j

F y

u   

 dan



0, 0



i

j

V y

u   

 .

Selanjutnya didefinisikan matriks K sebagai berikut:

1

K FV

dengan K disebut sebagai next generation matrix. Nilai harapan dari infeksi sekunder pada populasi rentan adalah eigen terbesar dari matriks K (Driessche & Watmough, 2002) sehingga

 



1



0 .

25 Contoh 2.12

Diberikan sistem persamaan diferensial berikut:

dS

SI S dt

dI

SI I I

dt dR

I R

dt

  

  

 

  

  

 

(2.12)

dengan S menyatakan populasi individu sehat dan rentan pasa saat t, I menyatakan populasi terinfeksi pada saat t, dan R menyatakan yang sembuh pada saat t. Sistem (2.12) mempunyai titik ekuilibrium bebas penyakit E0 



1, 0, 0



.

Pada Sistem (2.12) kelas terinfeksi adalah I , sehingga diperoleh Next generation matrix dapat diperoleh dari kelas I, maka dapat dituliskan sebagai berikut:







, ,







,



,



I  S R I  S R I

dengan  



SI



dan  



II



, maka hasil linearisasi dari dan 

masing-masing adalah F 

 

S dan V 



 



. Sehingga diperoleh Next generation matrix berikut:

 

1 1

. S

K FV S 

   

  

  _{ }

 

26

Kemudian substitusikan nilai titik ekuilibrium bebas penyakit E₀ 



1, 0, 0



ke Persamaan (2.13) diperoleh:

K 

  



maka diperoleh nilai R₀ dari sistem (2.12) adalah

0 .

R 

  



G.Nilai Eigen

Nilai eigen dalam suatu matriks akan digunakan dalam menentukan kestabilan dari suatu titik kritis. Nilai eigen suatu matriks dapat didefinisikan dalam Definisi 2.9.

Definisi 2.8. (Anton, 1987)

Jika A adalah matriks n x n, maka vektor taknol x di dalam n dinamakan vektor

eigen (eigenvector)dari A jika Ax adalah kelipatan skalar dari x, yaitu:

Axx (2.14)

untuk suatu skalar . Skalar  dinamakan nilai eigen (eigenvalue) dari A dan x

dikatakan vektor eigen yang bersesuaian dengan . Dari Persamaan (2.14) diperoleh:

Axx

AxIx

27

dengan I adalah matriks identitas. Supaya  menjadi nilai eigen, maka harus ada pemecahan taknol dari Persamaan (2.15). Persamaan (2.15) akan memiliki pemecahan taknol jika dan hanya jika:

det(IA)0. (2.16)

Persamaan (2.16) dinamakan persamaan karakteristik A dan skalar yang memenuhi Persamaan (2.16) adalah nilai eigen dari A.

Jika A adalah matriks n x n, maka polinomial karakteristik A mempunyai bentuk:

1 1

det(IA)n cn  ... c_n

Contoh 2.13

Diketahui matriks 3 2 . 1 0 B  _



 

Tentukan nilai-nilai eigen dari matriks B!

Jawab:

Persamaan karakteristik dari B adalah





det IB 0

3 2

0 1



  



2

3 2 0

28



2



 1



0

sehingga diperoleh nilai eigen 2 dan  1.

H.Kestabilan Titik Ekuilibrium

Kestabilan titik ekuilibrium dari suatu sistem persamaan diferensial baik linear maupun nonlinear diberikan dalam definisi berikut.

Definisi 2.9. (Olsder & Woude, 2004)

Diberikan sistem persamaan diferensial orde satu x f x

 

dengan n x dan



, 0



x t x adalah solusi persamaan tersebut pada saat t dengan kondisi awal

 

0 0 x x .

(i) Vektor x yang memenuhi ˆ f x

 

ˆ 0 dikatakan sebagai titik ekuilibrium.

(ii) Titik ekuilibrium x dikatakan stabil jika diberikan untuk setiapˆ  0 ada 0

  sedemikian sehingga jika x₀ xˆ  dan x t x



, ₀



 xˆ  untuk

setiap t0.

(iii) Titik ekuilbrium x dikatakan stabil asimtotik jika titik ekuilibriumnya stabil ˆ

dan terdapat ₁0 sedemikian sehingga lim



, ₀



ˆ 0

t x t x  x , bila

0 ˆ 1 x  x  .

(iv) Titik ekuilibrium x dikatakan tidak stabil jika tidak memenuhi (ii). ˆ

29

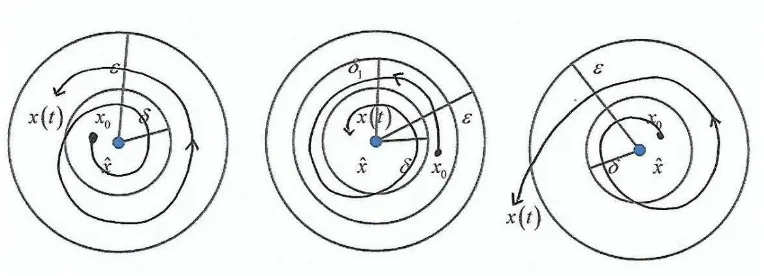
Stabil Stabil asimtotik Tidak stabil

Gambar 2.2. Simulasi Kestabilan Titik Ekuilibrium

Matriks jacobian dapat dapat digunakan dalam mengidentifikasi sifat kestabilan sistem nonlinear disekitar titik ekuilbrium apabila sistem tersebut memiliki titik ekuilibrium hiperbolik. Selanjutnya diberikan teorema mengenai sifat kestabilan suatu sistem nonlinear yang ditinjau dari nilai eigen matriks jacobian Jf x

 

ˆ .

Definisi 2.10. (Wiggins, 1990)

Sebuah titik ekuilibrium dikatakan hiperbolik jika bagian real nilai eigen dari

matriks jacobian adalah tidak nol. Jika bagian manapun nilai eigen dari matriks

jacobian adalah nol, maka titik ekuilibrium disebut nonhiperbolik.

Teorema 2.2. (Olsder & Woude, 2004)

Diberikan sistem persamaan diferensial xAx, dengan A adalah matriks

[image:45.595.114.496.88.226.2]

30

(i) Titik ekuilibrium xˆ0 dikatakan stabil asimtotik jika dan hanya jika 0 1, 2,...,

i

e i k

    .

(ii) Titik ekuilibrium xˆ0 dikatakan stabil jika dan hanya jika 0 1, 2,...,

i

e i k

    dan jika setiap nilai eigen , imajiner dengan

0 i

e

  , maka multiplisitas aljabar dan geometri untuk nilai eigen harus

sama.

(iii) Titik ekuilibrium xˆ0 dikatakan tidak stabil jika dan hanya jika terdapat paling sedikit satu e₁0 untuk i1, 2,...,k.

Bukti:

(i) Bukti dari kiri ke kanan

Akan ditunjukkan jika titik ekuilibrium xˆ0 stabil asimtotik maka 0 1, 2,...,

i

e i k

    .

Berdasarkan Definisi 2.9. titik ekuilibrium xˆ0 dikatakan stabil asimtotik jika lim



, ₀



ˆ 0

t x t x  x . Hal ini berarti bahwa untuk



0



, ,

t  x t x akan

menuju xˆ0. Karena x t x



, ₀



merupakan penyelesaian dari sistem

persamaan diferensial, sehingga x t x



, ₀



memuat _ee i t_{. Oleh karena itu,}

supaya _ee i t

menuju xˆ0, maka  harus bernilai negatif. Bukti dari kanan ke kiri

31



, 0



x t x merupakan penyelesaian dari sistem persamaan diferensial,

sehingga x t x



, ₀



selalu memuat e i t

e  . Jika e_i 0, maka untuk



0



, ,

t  x t x akan menuju xˆ0. Sehingga berdasarkan Definisi 2.9. titik

ekuilibrium xˆ0 stabil asimtotik. (ii) Bukti dari kiri ke kanan

Akan ditunjukkan bahwa jika titik ekuilibrium xˆ0 stabil, maka 0 1, 2,...,

i

e i k

    .

Andaikan e_i 0, maka penyelesaian persamaan diferensial



, 0



x t x yang selalu memuat _ee i t

akan menuju  atau menjauhi titik ekuilibrium xˆ0untuk t, sehingga sistem tidak stabil. Hal tersebut bertentangan dengan yang diketahui. Jadi terbukti bahwa jika titik ekuilibrium xˆ0 stabil, makae_i   0 i 1, 2,...,k. Bukti lain, jika

0 i

e

  maka saat t, berakibat x t x



, ₀



0sehingga titik

ekuilibrium xˆ0 stabil. Bukti dari kanan ke kiri

Akan ditunjukkan bahwa jika e_i   0 i 1, 2,...,kmaka titik ekuilibrium xˆ0 dikatakan stabil dan jika setiap nilai eigen , imajiner dengan e_i 0, maka multiplisitas aljabar dan geometri untuk nilai eigen harus sama.

Penyelesaian x t x



, 0



merupakan penyelesaian dari sistem

persamaan diferensial, maka x t x



, 0



selau memuat

 i e t

32

maka titik ekuilibrium xˆ0 stabil asimtotik (pasti stabil). Jika e_i 0 maka berupa nilai eigen berupa bilangan kompleks murni. Multiplisitas aljabar berhubungan dengan nilai eigen sedangkan geometri berhubungan dengan vektor eigen. Oleh karena itu, akan dibuktikan bahwa banyak nilai eigen dan vektor eigen adalah sama.

Tanpa mengurangi pembuktian secara umum, diambil sembarang sistem pada 2 yang mempunyai nilai eigen bilangan kompleks murni.

1 1

2 2

0

, 0, 0. 0

x p x

p q

x q x



 _   _{ }

    

 

    (2.17)

Nilai eigen dari Sistem (2.17) ditentukan dengan mensubstitusikan matriks 0

0 p A

q 

 

  

  ke dalam persamaan det(AI)0 sehingga diperoleh:

0 p q

 

 

  .

Persamaan karakteristik dari matriks A adalah

2

0 pq   

2 pq   

i pq  

1 i pq

33

Berdasarkan definisi, x



x x₁, ₂



T adalah vektor eigen dari A yang bersesuaian dengan  jika dan hanya jika x adalah penyelesaian nontrivial dari



AI x



0, yaitu dari

1 2 0. x p x q             _ 

    (2.18)

Jika ₁i pq, maka Persamaan (2.18) menjadi

1 2

0.

i pq p x

x

q i pq

      _{  }       

Matriks augmentasi dari sistem di atas, yaitu

0 . 0 p

i pq

q _{i pq}

         

Baris pertama matriks dikalikan i pq

pq sehingga diperoleh

1 0

. 0 i pq

q

q _{i pq}

 _ 

 

 

 _ 

 

Kemudian baris kedua matriks 1

q sehingga diperoleh

34

Selanjutnya baris kedua dikurangi dengan baris pertama sehingga diperoleh matriks dalam bentuk eselon baris tereduksi

1 0

.

0 0 0

i pq q           

Berdasarkan matriks eselon baris tereduksi tersebut diperoleh penyelesaian

1 2 0

i pq x x q   1 2 i pq x x q 

misalkan x₂ t, maka x₁ i pq t q

 , dapat ditulis sebagai berikut:

1 2 . 1 i pq x t q x     _        _ _

Jadi, vektor yang bersesuaian dengan ₁ i pq yaitu 1 2

. 1

x _{i pq}

x             

Jika ₁ i pq, maka Persamaan (2.18) menjadi

1 2

0.

i pq p x

x

q i pq

 _ _{ }



 _{  }

   

 

Matriks augmentasi dari sistem di atas, yaitu

0 . 0 p i pq

q _{i pq}

35 Baris pertama matriks dikalikan i pq

pq

 sehingga diperoleh

1 0

. 0 i pq

q

q _{i pq}

 

 

 

 

 

Kemudian baris kedua matriks 1

q sehingga diperoleh

1 0 . 1 0 i pq q i pq q              

Selanjutnya baris kedua dikurangi dengan baris pertama sehingga diperoleh matriks dalam bentuk eselon baris tereduksi

1 0

.

0 0 0

i pq q          

Berdasarkan matriks eselon baris tereduksi tersebut diperoleh penyelesaian

1 2 0

i pq x x q   1 2 i pq x x q  

misalkan x₂ t, maka 1

i pq

x t

q

  , dapat ditulis sebagai berikut:

36

Jadi, vektor yang bersesuaian dengan ₁ i pq yaitu 1 2

. 1

x i pq

x

 

  

  

 

   

Sehingga terbukti bahwa banyaknya nilai eigen sama dengan vektor eigen. (iii) Bukti dari kiri ke kanan

Akan dibuktikan jika titik ekuilibrium xˆ0 tidak stabil, maka 0

i

e_

 

untuk setiap i1, 2,..., k.

Titik ekuilibrium xˆ0 dikatakan tidak stabil jika t, maka



, 0



x t x akan menuju . Karena x t x



, ₀



merpakan penyelesaian dari

sistem persamaan diferensial, maka x t x



, 0



memuat

 

.

i e t

e  Hal ini dapat

dipenuhi bahwa e_i 0. Bukti dari kanan ke kiri

Akan dibuktikan jika e_i 0 untuk setiap i1, 2,..., k, maka titik ekuilibrium xˆ0 tidak stabil.

Jika e_i 0, maka saat nilai t, berakibat x t x



, 0



  sehingga titik ekilibrium tidak stabil.

Contoh 2.14

Diberikan matriks

1 3

1 2

A  _   

37

1 3 1 0 1 2

det( ) det 0

1 2 0 1 2 2

A I  



    

  _{ } _{ } 

  

   

 



1



 2 



 4 0

2

6 0

   



2



 3



0

1 2

  dan ₂  3.

Jadi nilai eigen dari matriks A adalah ₁ 2 dan

2 3

   .

I. Kriteria Routh-Hurwitz

Menentukan kestabilan diperlukan perhitungan untuk menentukan nilai eigen dari matriks jacobian, adapun salah satu cara untuk menentukan nilai eigen tersebut yaitu menggunakan kriteria Routh-Hurwitz .

Definisi 2.12. (Olsder & Woude, 2004)

Kriteria Routh-Hurwitz:

Semua akar-akar dari polinomial (2.30) memiliki bagian real negatif jika dan

hanya jika tabel Routh-Hurwitz terdiri dari n+1 baris dan semua elemen kolom

pertama pada tabel memiliki tanda yang sama (semua elemen bertanda positif

atau negatif).

Diberikan suatu persamaan karakteristik dari akar-akar persamaan matiks

nxn

A sebagai berikut:

1 2

0 1 2 ... 1

n n n

n n

38

dengan a i_i, 0,1, 2,...,n dan a₀ 0 merupakan koefisien dari persamaan karakteristik matrik A. Akar-akar dari Persamaan (2.30) dapat diketahui dengan menyusun tabel Routh sebagai berikut:

0 2 4 1 3 5 1 2 3 1 2 3

a a a

a a a

b b b

c c c

dengan , ,i 1, 2,..., nb c_{i i}  didefinisikan sebagai berikut:

1 2 0 3 1 4 0 5 1 2 0 2 1

1 2

1 1 1

1 3 1 2 1 5 1 3 1 2 1 1 1

1 2

1 1 1

, , ,

, , , .

n n

n

n n

n

a a a a a a a a a a a a

b b b

a a a

b a a b b a a b b a a b

c c c

b b b



 

  

  

  

  

(2.20)

39 BAB III

HASIL DAN PEMBAHASAN A. Permasalahan Nyata Penyebaran Penyakit Tuberculosis

Tuberculosis merupakan salah satu penyakit menular yang disebabkan oleh bakteri Mycobacterium Tuberculosis. Penularan penyakit Tuberculosis paling banyak dan paling mudah melalui udara, oleh karena itu organ yang pertama kali diserang adalah organ pernapasan. Selain menular penyakit tersebut juga bisa menyebabkan kematian.

Individu baru dapat masuk ke dalam populasi karena adanya kelahiran dan individu dapat dikatakan keluar dari populasi karena kematian. Jumlah populasi adalah semua individu yang sehat atau rentan terhadap penyakit Tuberculosis, individu yang terinfeksi Tuberculosis, dan individu yang telah sembuh setelah terinfeksi Tuberculosis. Individu yang rentan akan mengalami 2 kemungkinan, yaitu akan meninggal ataupun akan terinfeksi Tuberculosis. Kemudian individu yang terinfeksi juga mengalami 2 kemungkinan, yaitu individu akan sembuh atau individu akan meninggal.

40

subpopulasi Recovered ialah semua individu yang benar-benar sudah sembuh dari penyakit Tuberculosis.

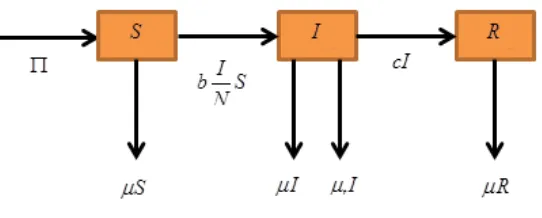
B.Model Matematika Penyebaran Penyakit Tuberculosis

Dalam menyederhanakan model matematika penyebaran penyakit Tuberculosis, diberikan asumsi-asumsi sebagai berikut :

1. Populasi penduduk bersifat tertutup yang artinya pertambahan atau pengurangan penduduk hanya dikarenakan oleh kelahiran dan kematian, sedangkan pertambahan dan pengurangan yang disebabkan oleh faktor lain diabaikan.

2. Populasi bersifat homogen yang artinya setiap individu mempunyai kemungkinan yang sama untuk dapat terjangkit penyakit Tuberculosis.

3. Kematian yang disebabkan oleh faktor lain selain terinfeksi Tuberculosis dianggap sebagai kematian alami.

4. Individu yang belum terserang penyakit termasuk ke dalam kelas susceptible. 5. Individu pada kelas recovered tidak akan kembali lagi menjadi individu pada

kelas infectious.

[image:56.595.142.517.602.723.2]

6. Terjadi kematian akibat terinfeksi Tuberculosis.

Tabel 3.1. Variabel dan parameter yang digunakan dalam model

Simbol Definisi Syarat

 

N t Jumlah populasi pada suatu daerah pada saat t. N0

( )

S t Banyaknya individu yang sehat dan rentan tehadap penyakit Tuberculosis pada saat t.

( ) 0