MODEL SUSCEPTIBLE INFECTED RECOVERED (SIR) DENGAN IMIGRASI DAN SANITASI
oleh
EVY DWI ASTUTI M0108087
SKRIPSI
ditulis dan diajukan untuk memenuhi sebagian persyaratan memperoleh gelar Sarjana Sains Matematika
JURUSAN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SEBELAS MARET
SURAKARTA 2012
ABSTRAK
Evy Dwi Astuti. 2012. MODEL SUSCEPTIBLE INFECTED RECOVE-RED (SIR) DENGAN IMIGRASI DAN SANITASI. Fakultas Matematika dan Ilmu Pengetahuan Alam. Universitas Sebelas Maret.
Salah satu model matematika yang dapat digunakan untuk menggambarkan fe-nomena penyebaran penyakit yaitu model SIR. Penyakit yang berkarakteristik SIR yaitu, apabila individu telah terinfeksi penyakit kemudian sembuh, individu tersebut tidak terinfeksi lagi. Penyebaran penyakit infeksi dapat dipengaruhi oleh faktor imigrasi. Upaya pencegahan penyebaran penyakit infeksi dapat dilakukan dengan cara perbaikan sanitasi. Sanitasi merupakan program kebersihan ling-kungan yang diharapkan dapat menurunkan kontak antara individu yang rentan penyakit dengan individu yang terinfeksi penyakit. Dengan demikian, penyebar-an penyakit dapat dikurpenyebar-angi dengpenyebar-an program spenyebar-anitasi.
Tujuan dari penelitian adalah mengkonstruksi model SIR dengan imigrasi dan sanitasi, menganalisis model dan menginterpretasi model. Model SIR de-ngan imigrasi dan sanitasi memiliki dua jenis titik kesetimbade-ngan yaitu, titik kesetimbangan bebas penyakit dan titik kesetimbangan endemik. Simulasi dila-kukan untuk mengetahui pengaruh sanitasi terhadap jumlah individu terinfeksi. Semakin tinggi tingkat sanitasi, jumlah individu terinfeksi semakin berkurang.
Evy Dwi Astuti. 2012. SUSCEPTIBLE INFECTED RECOVERED (SIR) MODEL WITH IMMIGRATION AND SANITATION. Faculty of Mathematics and Natural Sciences, Sebelas Maret University.
One of the mathematical models that can be used to describe the phenomenon disease spread is SIR model. The characterized SIR’s diseases is if an individual has been infected and then recovered, the individual will not be infected again. The infectious diseases’s spread can be affected by immigration factor. The efforts prevent infectious diseases’s spread can be done by improved sanitation. The sanitation is a environmental hygiene can be expected to reduce the contact between susceptible individuals with the infected individuals. Thus, the spread of disease can be reduced by sanitation program.
The purposes of the research are to construct theSIR model with immigra-tion and sanitaimmigra-tion, to analize the model and to interpret the model. The SIR model with immigration and sanitation have two kinds equilibrium point. They are disease free equilibrium point and endemic equilibrium point. The sanitation was done to know the affect of sanitation toward a number of infected individuals. When the sanitation increase, the number of infected individuals decreases.
KATA PENGANTAR
Segala puji dan syukur penulis panjatkan kepada Allah SWT yang telah melimpahkan rahmat dan hidayah-Nya sehingga penulis berhasil menyelesaikan skripsi ini. Ucapan terima kasih penulis sampaikan kepada
1. Ibu Sri Kuntari, M.Si. sebagai pembimbing I dan Bapak Bowo Winarno, S.Si, M.Kom. sebagai pembimbing II yang telah memberi bimbingan dan arahan dalam penulisan skripsi.
2. Ibu Dra.Purnami Widyaningsih, M.App.Sc, Ibu Dra. Respatiwulan M.Si. yang telah memberikan saran dan masukan dalam penulisan skripsi ini.
3. Seluruh pihak yang telah memberikan semangat, motivasi dan kerja sama-nya.
Penulis berharap semoga laporan ini bermanfaat.
Surakarta, Juli 2012
Penulis
PERSEMBAHAN
Sebuah karya sederhana ini kupersembahkan untuk
Bapak, Ibu, kakak serta adik sebagai wujud atas doa, semangat, dan pengorbanan yang diberikan kepada saya.
Daftar Isi
HALAMAN JUDUL . . . i
HALAMAN PENGESAHAN . . . ii
ABSTRAK . . . iii
ABSTRACT . . . iv
KATA PENGANTAR . . . v
PERSEMBAHAN . . . vi
DAFTAR ISI . . . vii
DAFTAR GAMBAR . . . ix
I PENDAHULUAN 1 1.1 Latar Belakang Masalah . . . 1
1.2 Perumusan Masalah . . . 2
1.3 Tujuan . . . 3
1.4 Manfaat . . . 3
II LANDASAN TEORI 4 2.1 Tinjauan Pustaka . . . 4
2.1.1 Pemodelan Matematika . . . 4
2.1.2 Sistem Autonomous. . . 5
2.1.3 Model SIR Klasik . . . 5
2.1.4 Kesetimbangan dan Kestabilan . . . 7
2.2 Kerangka Berpikir . . . 10
III METODE PENELITIAN 12 IV PEMBAHASAN 14 4.1 Konstruksi Model . . . 14
4.2 Kesetimbangan Model . . . 17
4.2.1 Titik Kesetimbangan Tanpa Sanitasi . . . 17
4.2.2 Titik Kesetimbangan Sanitasi Maksimal . . . 18
4.3 Kestabilan Titik Kesetimbangan . . . 19
4.3.1 Kestabilan Titik Kesetimbangan E00 dan Ee0 . . . 19
4.3.2 Kestabilan Titik Kesetimbangan E01 dan Ee1 . . . 20
4.4 Penerapan . . . 22
V PENUTUP 26 5.1 Kesimpulan . . . 26
5.2 Saran . . . 27
DAFTAR PUSTAKA 28
Daftar Gambar
2.1 Perubahan jumlah individu pada model epidemi SIR . . . 6
2.2 Perubahan jumlah individu pada model endemik SIR . . . 6
2.3 Trayektori pada bidang fase . . . 10
4.1 Perubahan jumlah individu model SIR dengan imigrasi . . . 16
4.2 Perubahan jumlah individu model SIR dengan imigrasi dan sanitasi 17 4.3 (a) Jumlah individu susceptible (b) Jumlah individu infected (garis putus-putus), dan jumlah individu recovered (garis putus-putus renggang) . . . 23
4.4 (a) Trayektori di titik kesetimbangan (1500,0) ketika H = 0 (b) Trayektori di titik kesetimbangan (1500,0) ketikaH = 1 . . . 24
4.5 Penurunan jumlah individu kelompok I ketika H = 0 (garis tebal putus-putus), H = 0.25 (garis tipis), H = 0.5 (garis tipis putus-putus),H = 0.75 (garis tebal) dan H = 1 (garis tebal putus-putus renggang) . . . 25
Bab I
PENDAHULUAN
1.1
Latar Belakang Masalah
Menurut CDC [3], penyakit kolera pertama kali muncul di Peru pada bulan Januari 1991 kemudian menyebar ke Ecuador, Colombia, Chile, Brazil, Mexico, dan Guatemala. Penyakit kolera dapat menjadi parah, dan mengancam jiwa te-tapi dapat dicegah dan diobati. Penyakit kolera disebabkan oleh bakteri vibrio cholerae yang berkembang biak dan menyebar melalui kotoran manusia. Apabila kotoran yang mengandung bakteri ini mengkontaminasi air mengalir seperti air sungai, mengakibatkan individu lain yang melakukan kontak dengan air tersebut beresiko terinfeksi. Misalnya cuci tangan yang tidak bersih lalu makan, mencuci sayuran atau makanan dengan air yang telah terkontaminasi. Bahkan penyakit tersebut dapat bersifat endemik, yaitu penyakit menyerang suatu wilayah terten-tu dalam kurun wakterten-tu lebih dari saterten-tu tahun.
Kolera merupakan penyakit yang telah lama menyerang manusia, dan terus menjadi masalah bagi kesehatan masyarakat dunia (Johnson [9]). Lebih dari 100.000 orang di dunia meninggal akibat penyakit kolera setiap tahunnya.
Perpindahan individu dari satu wilayah ke wilayah lain sangat mempenga-ruhi penyebaran penyakit. Seseorang yang telah terinfeksi membawa penyakit ketika masuk ke wilayah tertentu, orang tersebut berpotensi menularkan penya-kit ke orang lain. Imigrasi dapat berpengaruh terhadap penyebaran penyapenya-kit infeksi. Menurut Picollo dan Billings [13], faktor imigrasi sangat mempengaruhi laju penyebaran penyakit infeksi.
Menurut Cl´audia [4], penyakit kolera berkembang di daerah dengan ling-kungan yang kotor atau kebersihan lingling-kungan yang rendah. Untuk mengurangi penyebaran penyakit infeksi dibutuhkan upaya pencegahan. Upaya yang
pat dilakukan yaitu dengan perbaikan sanitasi. Hetchcote [7], Guimaraens dan Code¸co [6] menyebutkan bahwa adanya keefektifan sanitasi dapat mengurangi penyebaran penyakit infeksi. Faktor-faktor yang termasuk dalam sanitasi da-pat berupa kebersihan saluran air, pengelolaan air bersih, kebersihan air minum, kebersihan makanan.
Perkembangan ilmu pengetahuan dan teknologi di segala bidang mempu-nyai peranan yang penting dalam kehidupan manusia khususnya dalam masalah penyebaran penyakit infeksi. Fenomena penyebaran penyakit dapat digambar-kan melalui pemodelan matematika. Menurut Hetchcote [7], model SIR dapat digunakan untuk menggambarkan fenomena penyebaran penyakit infeksi. Un-tuk mengkonstruksi model dibutuhkan asumsi, batasan dan parameter-parameter yang berpengaruh. Kemudian dari model tersebut dapat diketahui perilaku pe-nyebaran penyakit infeksi pada suatu populasi.
Model SIR dibagi menjadi tiga kelompok yaitu kelompok individu rentan terinfeksi penyakitSusceptible (S), kelompok individu terinfeksi penyakitInfected (I) dan kelompok telah sembuh dari penyakit Recovered (R). Pada model SIR, individu yang telah sembuh dari penyakit tidak terinfeksi lagi dikarenakan telah memiliki kekebalan tubuh.
Pada tahun 2005, Picollo dan Billings [13] telah meneliti tentang model SIR dengan memperhatikan faktor imigrasi. Pada tahun yang sama Guimaraens dan Code¸co [6] telah meneliti tentang model SIR dengan memperhatikan faktor sanitasi. Selanjutnya, penulis meneliti tentang model SIR dengan imigrasi dan sanitasi. Penelitian meliputi konstruksi model, menganalisis model dan mengin-tepretasi model.
1.2
Perumusan Masalah
Berdasarkan latar belakang masalah dapat diambil tiga perumusan masalah yaitu
1. bagaimana mengkonstruksi model SIR dengan imigrasi dan sanitasi?
2. bagaimana menentukan titik kesetimbangan dan kestabilan titik kesetim-bangan tersebut?
3. bagaimana mengintepretasikan model SIR dengan imigrasi dan sanitasi?
1.3
Tujuan
Tujuan dari penelitian ini adalah
1. dapat mengkonstruksi model SIR dengan imigrasi dan sanitasi,
2. dapat menentukan titik kesetimbangan dan kestabilan titik kesetimbangan tersebut, dan
3. dapat mengintepretasikan model SIR dengan imigrasi dan sanitasi.
1.4
Manfaat
Penelitian ini diharapkan dapat menambah pengetahuan tentang penga-ruh imigrasi serta sanitasi terhadap penyebaran penyakit infeksi sehingga dapat menurunkan jumlah individu terinfeksi.
Bab II
LANDASAN TEORI
2.1
Tinjauan Pustaka
Kermak dan McKendrick [10] pada tahun 1929 menyatakan bahwa feno-mena penyebaran penyakit dapat dijelaskan melalui model epidemi SIR. Tetapi model tersebut hanya dapat digunakan untuk mempelajari penyebaran penya-kit infeksi yang terjadi dalam kurun waktu kurang dari satu tahun. Menurut Hetchcote [7], penyebaran penyakit infeksi yang terjadi dalam kurun waktu le-bih dari satu tahun digunakan model endemik SIR. Pada penelitian sebelumnya, Picollo dan Billings [13] telah meneliti tentang fenomena penyebaran penyakit infeksi yang mempertimbangkan faktor imigrasi.
Faktor imigrasi memiliki pengaruh cukup tinggi dalam penyebaran penya-kit, untuk mengurangi penyebarannya dibutuhkan upaya pencegahan yaitu sa-nitasi pada wilayah tertentu. Pada artikel Guimaraens dan Code¸co [6] meneliti tentang model SIR dengan pengaruh sanitasi, untuk mengetahui seberapa besar pengaruh sanitasi terhadap penurunan individu infected. Dalam penelitian ini ingin mengetahui pengaruh dari sanitasi terhadap model SIR dengan imigrasi.
Berikut ini, diberikan landasan teori untuk mendukung tujuan penelitian. Landasan teori tersebut meliputi pemodelan matematika, sistem autonomous, model SIR, kesetimbangan dan kestabilan.
2.1.1
Pemodelan Matematika
Menurut Meyer [11], pemodelan matematika merupakan suatu alat yang digunakan untuk mendeskripsikan permasalahan yang terjadi dalam kehidupan sehari-hari ke dalam bentuk matematis. Sehingga permasalahan tersebut dapat lebih mudah untuk diselesaikan.
2.1.2
Sistem
Autonomous
Sistem persamaan diferensial nonlinear orde satu yang terdiri dari tiga persamaan, mempunyai bentuk umum
dS
dt =f1(S, I, R), dI
dt =f2(S, I, R), dR
dt =f3(S, I, R),
(2.1)
dengan f1, f2, f3 adalah persamaan nonlinier. Menurut Ross [14], sistem (2.1)
akan memiliki penyelesaian jika fungsi f1, f2, f3 merupakan fungsi kontinu.
Me-nurut Boyce [2], jika variabelttidak muncul secara eksplisit untuk setiapf1, f2, f3
maka sistem (2.1) disebut sistem autonomous.
Nilai (S, I, R) yang memenuhi sistem (2.1) secara simultan disebut penye-lesaian dari sistem. Jika penyepenye-lesaian sistem persamaan (2.1) disajikan dalam bidang fase, maka akan terbentuk kurva penyelesaian di bidang fase yang disebut dengan trajektori.
2.1.3
Model
SIR
Klasik
Menurut Hetchcote [7], dalam model SIR populasi terbagi menjadi 3 ke-lompok yaitu keke-lompok individu susceptible (S), kelompok individu infected (I) dan kelompok individu recovered (R). Dalam model ini diasumsikan populasi konstan dengan populasi bercampur secara homogen. Hanya terdapat satu ma-cam penyebaran penyakit infeksi sehingga hanya terdapat satu mama-cam kontak penularan penyakit infeksi, yaitu kontak dengan penderita penyakit infeksi yang sama dengan masa inkubasi diabaikan. Individu yang telah sembuh dari penyakit infeksi tidak akan tertular lagi.
Pada penyebaran penyakit infeksi terdapat dua macam model SIR klasik yang dapat dipelajari yaitu model epidemi SIR dan model endemik SIR. Model epidemiSIRdigunakan untuk mempelajari fenomena penyebaran penyakit infeksi dalam kurun waktu kurang dari satu tahun. Perubahan jumlah individu pada model epidemi SIR dapat dilihat pada Gambar 2.1.
S
NI
R
SIb
g
I
Gambar 2.1. Perubahan jumlah individu pada model epidemi SIR
Sehingga model epidemi SIR dapat disajikan pada sistem (2.2)
dS
denganβ merupakan laju kontak danγ merupakan laju kesembuhan. Sedangkan
S, I, dan R berturut-turut merupakan banyaknya individu susceptible, infected, dan recovered. Jumlah populasi sistem (2.2) adalah konstan sehingga mengaki-batkan S(t) +I(t) +R(t) =N.
Sedangkan model endemikSIR digunakan untuk mempelajari fenomena pe-nyebaran penyakit yang terjadi dalam kurun waktu lebih dari satu tahun. Dalam model endemik SIR terdapat faktor yang harus dipertimbangkan yaitu laju kela-hiran dan laju kematian. Perubahan jumlah individu pada model endemik SIR dapat dilihat pada Gambar 2.2.
S
NI
R
Gambar 2.2. Perubahan jumlah individu pada model endemik SIR
Sehingga model endemik SIR dapat disajikan pada sistem (2.3)
denganµmerupakan laju kelahiran, laju kematian pada sistem (2.3) sama dengan laju kelahiran. Sehingga mengakibatkan jumlah populasi konstan, S(t) +I(t) +
R(t) =N.
2.1.4
Kesetimbangan dan Kestabilan
Menurut Panfilov [12], jika penyelesaian dari sistem merupakan titik se-timbang maka sistem tidak berubah sepanjang waktu. Menurut Bellomo dan Preziosi [1], definisi titik kesetimbangan dapat diartikan secara matematis, yang disajikan pada Definisi 2.1.1.
Definisi 2.1.1. Titik (S∗, I∗, R∗) yang berada pada bidang fase merupakan titik
kesetimbangan apabila
f1(S∗, I∗, R∗) = 0, f2(S∗, I∗, R∗) = 0, f3(S∗, I∗, R∗) = 0.
Menurut Bellomo dan Preziosi [1], untuk mengetahui perilaku sistem di sekitar titik kesetimbangan digunakan kestabilan titik kesetimbangan. Titik ke-setimbangan yang stabil berarti jika terdapat perubahan kecil pada sistem maka akan berpengaruh kecil terhadap penyelesaiannya. Sedangkan, titik kesetimbang-an ykesetimbang-ang stabil asimtotis memiliki arti jika terdapat perubahkesetimbang-an pada sistem, maka perubahan tersebut cenderung menghilang. Sedangkan titik kesetimbangan yang tidak stabil berarti bahwa jika terdapat perubahan kecil pada sistem maka akan terjadi perubahan yang besar pada penyelesaiannya (Finizio dan Ladas [5]).
Titik (S∗, I∗, R∗) merupakan titik kesetimbangan dari (2.1). Dengan
demi-kian untuk titik (S, I, R) di sekitar titik kesetimbangan, fungsi f dapat didekati
dengan deret Taylor.
Karena titik (S∗, I∗, R∗) merupakan titik kesetimbangan, sehingga
f1(S∗, I∗, R∗) = 0, f2(S∗, I∗, R∗) = 0, f3(S∗, I∗, R∗) = 0.
Suku yang memuat (S −S∗),(I −I∗),(R −R∗) bernilai kecil, karena (S, I, R)
terlalu dekat dengan titik kesetimbangan (S∗, I∗, R∗). Dengan demikian, sistem
(2.1) dapat didekati dengan,
dapat disajikan dalam bentuk matriks
Jacobian. Masih menurut Bellomo dan Preziosi [1], Haberman [8], kestabilan
dari sistem linear (2.4) dapat ditentukan dengan mencari nilai eigen dari J(x). Hal tersebut akan disajikan dalam Teorema 2.1.1
Teorema 2.1.1. Misalλi merupakan nilai eigen dari matriks JacobianJ(x)yang
dievaluasi pada titik kesetimbangan(S∗, I∗, R∗)danR
e(λi)adalah bagian real dari
λi maka
1. untuk setiap i berlaku Re(λi)<0, maka (S∗, I∗, R∗) stabil asimtotis,
2. untuk setiap i berlaku Re(λi)>0, maka (S∗, I∗, R∗) tidak stabil.
Selanjutnya, tipe kestabilan dari sistem berdasarkan nilai eigen matriks Ja-cobian disajikan pada Tabel 2.1 dan trajektori pada bidang fase disajikan pada Gambar 2.3.
Tabel 2.1. Kriteria kestabilan berdasarkan nilai eigen Nilai eigen Titik Kestabilan
real, tidak sama, simpul stabil asimtotis : semuanya negatif bertanda sama tidak stabil : semuanya positif real, tidak sama, sadel tidak stabil
berlawanan tanda
real, sama simpul stabil asimtotis : semuanya negatif tidak stabil : jika semuanya positif kompleks konjugate spiral stabil asimtotis : bagian real negatif bukan imajiner murni tidak stabil : bagian real positif imajiner murni pusat stabil
Gambar 2.3. Trajektori pada bidang fase
2.2
Kerangka Berpikir
Berdasarkan landasan teori yang telah diuraikan dapat disusun kerangka pemikiran sebagai berikut. Penyakit kolera dapat menjadi parah, dan meng-ancam jiwa tetapi dapat dicegah dan diobati. Penyakit kolera disebabkan oleh bakterivibrio cholerae yang berkembang biak dan menyebar melalui kotoran ma-nusia. Penyakit tersebut dapat bersifat endemik, yaitu penyakit menyerang suatu wilayah tertentu dalam kurun waktu lebih dari satu tahun.
Perpindahan individu dari satu wilayah ke wilayah lain sangat mempenga-ruhi penyebaran penyakit. Seseorang yang telah terinfeksi membawa penyakit
ketika masuk ke wilayah tertentu, orang tersebut berpotensi menularkan penya-kit ke orang lain. Imigrasi dapat berpengaruh terhadap penyebaran penyapenya-kit infeksi. Menurut Picollo dan Billings [13], faktor imigrasi sangat mempengaruhi laju penyebaran penyakit infeksi.
Upaya pencegahan penyebaran penyakit infeksi dapat dilakukan dengan ca-ra perbaikan sanitasi. Faktor-faktor yang termasuk dalam sanitasi dapat berupa kebersihan saluran air, pengelolaan air bersih, kebersihan air minum, kebersihan makanan.
ModelSIR dengan imigrasi dan sanitasi dapat digunakan untuk memodel-kan fenomena penyebaran penyakit infeksi. Model SIR merupakan sistem persa-maan differensial nonlinier orde satu. Pada model ini, variabel t tidak muncul secara eksplisit sehingga model dapat disebut sebagai sistem autonomous.
Perilaku sistem dari model endemik SIR dapat dilihat dari kestabilan titik kesetimbangannya. Tipe kestabilan dapat ditentukan melalui nilai eigen dari matriks Jacobian atau melihat perilaku sistem dari trayektori pada bidang fase.
Bab III
METODE PENELITIAN
Metode yang diterapkan dalam penelitian ini adalah studi literatur. Langkah-langkah yang dilakukan untuk mencapai tujuan dalam penelitian.
1. Mengidentifikasi keadaan, perilaku, interaksi, dan kejadian dalam populasi tetap dengan adanya imigrasi dan perlakuan sanitasi.
2. Menentukan batasan, asumsi, dan parameter yang dibutuhkan untuk mem-bentuk model.
3. Membentuk model SIR dengan imigrasi dan sanitasi berdasarkan langkah 1 dan 2.
Langkah 1-3 dilakukan untuk membentuk model SIR dengan imigrasi dan sanitasi.
4. Menentukan titik kesetimbangan dari model SIR dengan imigrasi dan sa-nitasi menggunakan Definisi 2.1.1.
5. Menentukan tipe kestabilan dari titik kesetimbangan menggunakan Teore-ma 2.1.1 dan Tabel 2.1.
Langkah 4-5 dilakukan untuk menentukan tipe kestabilan dari titik kese-timbangan.
6. Menerapkan model yang didapat pada suatu kasus.
7. Menggambarkan grafik penyelesaian fungsi S dan I untuk membantu men-deskripsikan perilaku model SIR.
8. Melakukan simulasi numerik menggunakan parameter yang bervariasi untuk mengetahui perubahan puncak endemik.
9. Membandingkan hasil-hasil yang diperoleh pada langkah (8).
10. Menginterpretasikan hasil yang diperoleh.
Langkah 6-10 dilakukan untuk mengintepretasikan model SIR dengan imi-grasi dan sanitasi.
Bab IV
PEMBAHASAN
4.1
Konstruksi Model
Pada bagian ini, dibahas tentang penurunan model SIR dengan imigrasi dan sanitasi. Penurunan model ini mengacu pada Hetchcote [7] dan Guimaraens dan Code¸co [6].
Menurut Hetchcote [7], penyebaran penyakit infeksi dapat dimodelkan de-ngan mengelompokkan jumlah individu pada populasinya menjadi 3 kelompok, yaitu susceptible, infected, dan recovered. Pada kelompok susceptible yaitu S(t) merupakan kelompok yang sehat tetapi rawan terinfeksi penyakit dalam waktut. Kelompokinfected yaituI(t) merupakan kelompok yang telah terinfeksi penyakit dalam waktu t, sedangkan kelompok recovered yaitu R(t) merupakan kelompok yang telah memiliki kekebalan tubuh dalam waktu t.
Untuk penurunan modelSIRdiperlukan asumsi. Berikut ini asumsi-asumsi menurut Hetchcote [7],
1. populasi konstan,
2. individu lahir dan imigrasi merupakan individu sehat tetapi rentan terin-feksi penyakit,
3. jumlah individu dalam populasi bercampur secara homogen, sehingga bisa terjadi kontak langsung dengan individu terinfeksi atau melalui perantara lainnya dalam penularan penyakit. Laju kontak atau penularannya adalah konstan,
4. masa inkubasi penyakit diabaikan,
5. hanya terdapat satu macam penyebaran penyakit infeksi, dan
6. individu yang sembuh dari penyakit infeksi tidak akan terinfeksi lagi.
Seperti yang telah diasumsikan bahwa hanya terdapat satu macam jenis pe-nyakit sehingga setiap individu pada kelompok S dan R memiliki kemungkinan yang sama dapat melakukan kontak dengan kelompok I. Terdapat sebanyak I
individu yang terinfeksi yang mengakibatkan kelompok S mempunyai kemung-kinan terinfeksi sebesar proporsi kelompokI yaitu I
N dengan laju kontakβ, yang
mengakibatkan berkurangnya jumlah individu pada kelompok S sebesarβSIN pa-da waktut. Adanya kelahiran yang merupakan individu yang sehat tetapi rentan terserang penyakit mengakibatkan bertambahnya jumlah individu pada kelom-pok S. Dimisalkan µ1 dan µ2 merupakan laju kelahiran dan laju imigrasi, oleh
karena itu individu pada kelompok S bertambah sebesar (µ1 +µ2)N. Adanya
kematian alami karena kerentanan individu pada kelompok S terhadap penya-kit mengakibatkan berkurangnya individu pada kelompok S sebesar (µ1+µ2)S.
Sehingga didapat laju perubahan individu pada kelompokSpada waktutadalah
dS
dt = (µ1+µ2)N −β SI
N −(µ1 +µ2)S. (4.1)
Berkurangnya individu pada kelompok S karena terinfeksi penyakit meng-akibatkan bertambahnya individu pada kelompok I sebesar individu pada ke-lompokS yang terinfeksi yaituβSIN. Pada kelompok individu I terjadi kematian alami mengakibatkan berkurangnya individu pada kelompokI sebesar (µ1+µ2)I.
Individu pada kelompok I yang sembuh dari penyakit tidak akan terinfeksi lagi mengakibatkan berkurangnya jumlah individu infected dengan laju kesembuhan
γ sebanyakγI. Sehingga didapat laju perubahan individu pada kelompokI pada waktu t adalah
dI dt =β
SI
N −γI−(µ1+µ2)I. (4.2)
Individu infected yang telah sembuh dan memiliki kekebalan permanen mengakibatkan bertambahnya jumlah individu pada kelompok R sebesar γI. Individu pada kelompok R yang tidak dapat bertahan karena daya tahan tu-buh individu yang cenderung lemah sehingga menyebabkan terjadinya kematian sehingga mengakibatkan berkurangnya individurecovered sebesar (µ1+µ2)R.
hingga didapat laju perubahan individu pada kelompok R pada waktu t adalah
dR
dt =γI−(µ1+µ2)R. (4.3)
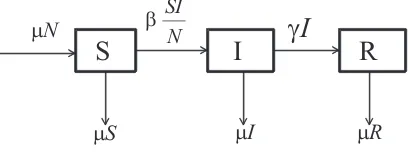
Perubahan jumlah individu pada modelSIR dengan imigrasi dapat dilihat pada Gambar 4.1.
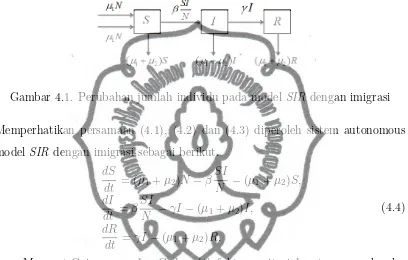
Gambar 4.1. Perubahan jumlah individu pada modelSIR dengan imigrasi Memperhatikan persamaan (4.1), (4.2) dan (4.3) diperoleh sistem autonomous model SIR dengan imigrasi sebagai berikut.
dS
Menurut Guimaraens dan Code¸co [6], faktor sanitasi dapat menurunkan la-ju kontak. Faktor sanitasi merupakan fungsi c(H) yang berpengaruh terhadap laju kontak individu pada kelompokS dengan individu pada kelompokI. Fungsi
c(H) = (β−αH) merupakan sebuah fungsi kontinu yang mendeskripsikan efek sanitasi pada laju kontak, dengan α merupakan sebuah konstanta dan H me-rupakan tingkat sanitasi yang bernilai 0 sampai 1. Penambahan faktor sanitasi pada laju kontak penyebaran pada sistem persamaan (4.20) dapat dilihat pada Gambar 4.2.
Mempertimbangkan faktor sanitasi pada model SIR dengan imigrasi dan sanitasi maka model dapat dimodifikasi menjadi
Gambar 4.2. Perubahan jumlah individu pada model SIR dengan imigrasi dan sanitasi
dengan S(0), I(0), µ1, µ2, β, γ >0 dan R(0) ≥ 0. Sistem (4.5) bukan merupakan
sistem yangautonomous, selanjutnya diselidiki ketika sistem (4.5) tanpa sanitasi (H = 0) dan ketika sistem (4.5) dengan sanitasi maksimal (H= 1).
4.2
Kesetimbangan Model
Kesetimbangan model dilihat ketika tanpa sanitasi dan sanitasi maksimal. Hal ini dikarenakan akan dilihat perbedaan titik kesetimbangan ketika model tanpa sanitasi dengan sanitasi maksimal.
4.2.1
Titik Kesetimbangan Tanpa Sanitasi
Individu yang telah sembuh memiliki kekebalan tubuh, sehingga tidak men-jadi pertimbangan yang serius. Oleh karena itu, individu yang menmen-jadi pertim-bangan adalah individu susceptible dan individu infected. Pada sistem persa-maan (4.5) baris pertama dan kedua tidak mengandung R, sehingga baris keti-ga dapat ditentukan melalui baris pertama dan kedua yang telah dihitung, dan
S+I+R =N. Oleh karena itu, sistem persamaan (4.5) dapat dituliskan sebagai sistem
dS
dt = (µ1+µ2)N −β SI
N −(µ1+µ2)S, dI
dt =β SI
N −γI −(µ1+µ2)I.
(4.6)
Menurut Bellomo dan Preziosi [1], sistem persamaan (4.6) dalam keadaan
setimbang jika
Dari sistem persamaan (4.7), diperoleh dua jenis titik kesetimbangan sebagai berikut.
1. Titik kesetimbangan E00= (S00, I00, R00).
Titik kesetimbangan E00 merupakan titik kesetimbangan yang bebas
pe-nyakit dengan S00 = N, I00 = 0 dan R00 = 0. Nilai I00 = 0 berarti tidak
terdapat individu infected yang menyebarkan penyakit. 2. Titik kesetimbangan Ee0 = (Se0, Ie0, Re0).
Titik kesetimbangan Ee0 merupakan titik kesetimbangan endemik dengan
Se0 = N(µ1+βµ2+γ), nya dilihat kesetimbangan model ketika sanitasi mencapai maksimal.
4.2.2
Titik Kesetimbangan Sanitasi Maksimal
Sistem persamaan (4.5) dapat dituliskan sebagai sistem
dS
Menurut Bellomo dan Preziosi [1], sistem persamaan (4.8) dalam keadaan setim-bang jika
Dari sistem persamaan (4.9), diperoleh dua jenis titik kesetimbangan sebagai berikut.
1. Titik kesetimbangan E01= (S01, I01, R01).
denganS01 =N, I01 = 0 danR01= 0. Nilai I01= 0 berarti tidak terdapat
individu infected yang menyebarkan penyakit. 2. Titik kesetimbangan Ee1 = (Se1, Ie1, Re1).
Titik kesetimbangan Ee1 merupakan titik kesetimbangan endemik dengan
Se1 =−N(µ(1α+−µβ2)+γ),
Ie1 = N µ1(α−β+γ+µ(α1−)+βN µ)(γ2+(αµ−1+βµ+2γ)+µ2)+2N µ1µ2 dan Re1 =N−Se1−Ie1. Dilihat
dariEe0 dan Ee1, individu terinfeksi mengalami penurunan ketika
memper-hatikan faktor sanitasi.
4.3
Kestabilan Titik Kesetimbangan
Menurut Bellomo dan Presziosi [1], kriteria kestabilan sistem persamaan diferensial dapat ditentukan dari nilai eigen matriks Jacobian.
4.3.1
Kestabilan Titik Kesetimbangan
E00
dan
E
e01. Kestabilan Titik Kesetimbangan E00.
Berdasarkan (4.6) didapat matriks Jacobian sebagai berikut.
J =
Dengan mengevaluasi matriks Jacobian (4.10) di titik kesetimbangan E00,
diperoleh
Persamaan karakteristik dari (4.11) sebagai berikut
P(λ) =λ2+λ(2µ1+ 2µ2−β+γ) + ((−µ1−µ2)(β−γ−µ1−µ2)) (4.12)
Nilai eigen matriks Jacobian (4.11) merupakan akar persamaan karakteris-tik (4.12). Nilai eigen (4.12) yaituλ1 =−µ1−µ2 danλ2 =β−γ−µ1−µ2.
2. Kestabilan Titik Kesetimbangan Ee0.
Mengevaluasi matriks Jacobian (4.10) di titik kesetimbanganEe0, diperoleh
J(Ee0) =
Persamaan karakteristik dari (4.13) adalah
P(λ) = λ2+Aλ+B (4.14)
Nilai eigen matriks Jacobian (4.13) merupakan akar persamaan karakteris-tik (4.14). Nilai eigen (4.14) yaitu
λ1 =
4.3.2
Kestabilan Titik Kesetimbangan
E01
dan
E
e11. Kestabilan Titik Kesetimbangan E01.
Berdasarkan (4.6) didapat matriks Jacobian sebagai berikut.
Dengan mengevaluasi matriks Jacobian (4.15) di titik kesetimbangan E01,
Persamaan karakteristik dari (4.16) sebagai berikut.
P(λ) =λ2+λ(2µ1+ 2µ2−β+α+γ) + ((−µ1−µ2)
(β−α−γ−µ1−µ2))
(4.17)
Nilai eigen matriks Jacobian (4.16) merupakan akar persamaan karakteris-tik (4.17). Nilai eigen (4.17) yaituλ1 =−µ1−µ2danλ2 =β−α−γ−µ1−µ2.
Sistem (4.8) stabil asimtotis ketikaβ <0. 2. Kestabilan Titik Kesetimbangan Ee1.
Mengevaluasi matriks Jacobian (4.15) di titik kesetimbanganEe1, diperoleh
J(Ee1) =
Persamaan karakteristik dari (4.18) adalah
P(λ) =λ2+λ((γ+2µ1+2µ2)+(β−α)
β . Nilai eigen matriks Jacobian
dengan
B =−αγ2+ (µ1+µ2)(αβ−3αγ) +β2µ1−2α(µ21+µ22)−4αµ1µ2,
C =(µ1+µ2)(−αβγ+β2γ+ 2αγ2−βγ2) +β2µ21−(µ21+µ22)
(αβ−4αγ+ 2βγ)−µ1µ2(2αβ−2β2−8αγ+ 4βγ)+
(µ21µ2+µ1µ22)(6α−3β) + 2α(µ31+µ32)−βµ32.
Sistem (4.8) stabil asimtotis ketika padaλ1 nilai dari
√
Diberikan data penyebaran penyakit kolera menurut Cl´audia [4] dan Leah [9]. Diberikan nilai parameter yaitu laju kontak β = 0.8, laju kesembuhan γ = 0.4, laju kelahiran µ1 = 0.15875, laju imigrasi µ2 = 0.15. Jumlah populasi
yaitu N = 1500 individu, dengan banyaknya individu awal terinfeksi I(0) = 100 individu, sedangkan banyaknya individu awal yang sehat tetapi rawan terinfeksi
S(0) = 1400 individu. Berdasarkan sistem (4.1) dan data yang telah diberikan diperoleh,
Sistem (4.20) bukan merupakan sistem autonomous. Terlebih dahulu sistem (4.20) dilihat tanpa sanitasi dengan nilaiα= 0.75. Menggunakan metode Runge-Kutta orde empat dan bantuan software Mathematicha 8.0, penyelesaian sistem (4.20) dalam waktu 50 hari dapat dilihat pada Gambar 4.3.
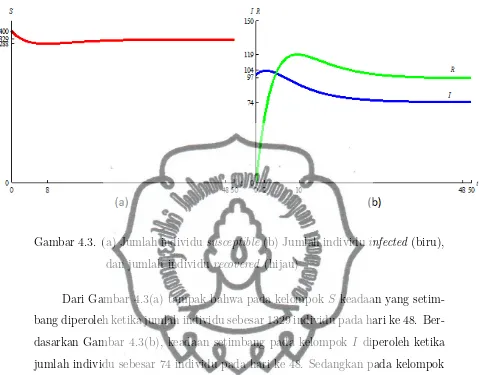
Gambar 4.3. (a) Jumlah individususceptible (b) Jumlah individuinfected (biru), dan jumlah individu recovered (hijau)
Dari Gambar 4.3(a) tampak bahwa pada kelompok S keadaan yang setim-bang diperoleh ketika jumlah individu sebesar 1329 individu pada hari ke 48. Ber-dasarkan Gambar 4.3(b), keadaan setimbang pada kelompok I diperoleh ketika jumlah individu sebesar 74 individu pada hari ke 48. Sedangkan pada kelompok
R, keadaan setimbang diperoleh ketika jumlah individu sebesar 97 individu pada hari ke 48.
Untuk mengetahui perilaku penyebaran penyakit kolera akan ditentukan kestabilan disekitar titik kesetimbangan. Untuk mengetahui tipe kestabilan ter-sebut dapat digunakan nilai eigen dari matriks Jacobian atau trayektori di se-kitar titik kesetimbangannya. Berdasarkan nilai eigen matriks Jacobian, ketika
Gambar 4.4. (a) Trajektori di titik kesetimbangan (1500,0) ketika H = 0 (b) Trayektori di titik kesetimbangan (1500,0) ketika H = 1 Berdasarkan Gambar 4.4(a), tampak bahwa arah trajektori tidak menuju titik kesetimbangan bebas penyakit (1500,0). Melainkan arahnya berhenti di titik kesetimbangan endemik (1329,74). Artinya tipe kestabilan titik kesetim-bangan bebas penyakit adalah tidak stabil. Berdasarkan Gambar 4.4(b), tampak bahwa arah trajektori menuju titik kesetimbangan (1500,0). Dengan demikian tipe kestabilan di titik kesetimbangan bebas penyakit ketika H = 1 adalah stabil asimtotis.
Ketika dilakukan simulasi terhadap faktor imigrasi, didapat hasil bahwa semakin tinggi laju imigrasi maka jumlah individu terinfeksi juga semakin ber-tambah. Hal ini dikarenakan pada perubahan jumlah individu infected (dI
dt =
c(H)SI
N −γI −(µ1 +µ2))I. Hal ini mengakibatkan jumlah individu terinfeksi
semakin berkurang.
Puncak endemik pada kelompok I dapat berubah sewaktu-waktu dengan nilai parameter yang berubah-ubah pula. Untuk menurunkan puncak endemik
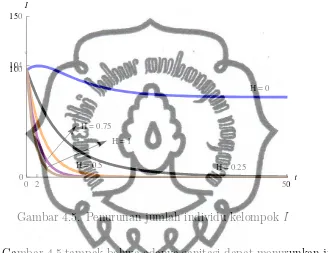
dibutuhkan suatu upaya pencegahan. Upaya pencegahan dapat dilakukan de-ngan cara memperbaiki sanitasi untuk menurunkan jumlah individu terinfeksi. Menurut Guimaraens dan Code¸co [6], tingkat sanitasi bernilai dari 0 sampai 1. Simulasi dilakukan pada nilai H = 0, H = 0.25, H = 0.5, H = 0.75 dan H = 1. Penurunan jumlah individu pada kelompok I dapat dilihat dari Gambar 4.5.
H = 0
H = 0.25 H = 0.5
H = 0.75
H = 1
0 2 50t
0 100 104 150
I
Gambar 4.5. Penurunan jumlah individu kelompok I
Dari Gambar 4.5 tampak bahwa adanya sanitasi dapat menurunkan jumlah individu terinfeksi.
Bab V
PENUTUP
5.1
Kesimpulan
Berdasarkan pembahasan dapat disimpulkan bahwa
1. Model SIR dengan imigrasi dan sanitasi dapat di tuliskan sebagai
dS
merupakan konstanta, dan 0≤H ≤1.
2. Ada dua jenis titik kesetimbangan pada model SIR dengan imigrasi dan sanitasi yaitu titik kesetimbangan bebas penyakit dan endemik.
(a) Titik Kesetimbangan ketika H = 0, yaitu titik kesetimbangan bebas penyakit E00 = (S00, I00, R00) = (N,0,0) dan titik kesetimbangan en-(b) Titik Kesetimbangan ketika H = 1, yaitu titik kesetimbangan bebas
penyakit E01 = (S01, I01, R01) = (N,0,0) dan titik kesetimbangan
en-demik Ee1 = (Se1, Ie1, Re1) dengan Se1 =−N(µ(1α+−µβ2)+γ),
Ie1 = N µ1(α−β+γ+µ(α1)+−βN µ)(γ2+(αµ1−+βµ+2γ)+µ2)+2N µ1µ2 dan Re1 =N −Se1−Ie1.
3. Adanya faktor sanitasi dapat mempengaruhi jumlah individu terinfeksi. Se-makin tinggi tingkat sanitasi mampu menurunkan jumlah individu terinfek-si menuju konditerinfek-si bebas penyakit.
5.2
Saran
Dalam penulisan skripsi ini, untuk mengetahui perubahan jumlah individu terinfeksi melalui grafik penyelesaian. Bagi pembaca yang tertarik, dapat menen-tukan besarnya rasio reproduksi untuk mengetahui terjadinya perubahan jumlah individu terinfeksi.
DAFTAR PUSTAKA
[1] Bellomo, N., and L. Preziosi,Modelling Mathematical Methods and Scientific Computation, CRC Press, Florida, 1995.
[2] Boyce, W. E., and R. C. DiPrima, Elementary Differential Equation and Boundary Value Problem, John Wiley and Son,Inc, New York, 1986.
[3] CDC, Cholera–western hemisphere, and recommendations for treatment of cholera, 1991.
[4] Code¸co, C. T., Endemic and Epidemic Dynamics of Cholera: The Role of The Aquatic Reservoir, Rio de Janeiro, 2001.
[5] Finizio, N., and G. Ladas, Persamaan Diferensial Biasa dengan Penerapan Modern, Proceedings of the Royal Society of London Series A 2ed (1988). [6] Guimaraens, M. A. and C. T. Code¸co, Experiments with Mathematical
Mo-dels to Simulate Hepatitis A Population Dynamics Under Different Levels of Endemicity, Cad. Sa´ude P´ublica, Rio de Janeiro, 2005.
[7] Hetchcote, H. W., The Mathematics of Infectious Diseases, SIAM Review 42 (2000), no. 4, 599–653.
[8] Haberman, R., Mathematical Models (Mechanical Vibrations, Population Dynamic, and Traffic Flow), Prentice-Hall, Inc, New Jersey, 1971.
[9] Johnson, L.,Modeling Cholera, University of California Santa Cruz, 2004.
[10] Kermack W. O., and A. G. McKendrick, . A Contribution to The Mathe-matical Theory of Epidemics, Proceedings of the Royal Society of London Series A 115 (1927), 700–721.
[11] Meyer, W. J., Concepts of mathematical modeling, McGraw-Hill, Inc, New York, 1984.
[12] Panvilov, A., Qualitive Analysis of Differential Equations, Utrecht Universi-ty, Utrecht, 2004.
[13] Picollo, C. III, and L. Billings, The Effect of Vaccinations in an Immigrant Model, Mathematical and Computer Modelling 42 (2005), 291–299.
[14] Ross, S. L., Differential Equations, John Wiley and Sons, Inc, New York, 1984.