ANALISIS KINERJA METODE ASM DALAM MENYELESAIKAN MASALAH TRANSPORTASI FUZZY DAN LINIER

(1)

ANALISIS KINERJA METODE ASM DALAM

MENYELESAIKAN MASALAH TRANSPORTASI

FUZZY DAN LINIER

Dian Arvianto1, Sapti Wahyuningsih2

Universitas Negeri Malang E – mail : dian_arvianto@yahoo.co.id

ABSTRAK: Masalah transportasi fuzzy dan linier merupakan salah satu masalah

dalam Riset Operasi. Masalah transportasi fuzzy dan linier ini adalah suatu masalah bagaimana untuk mengangkut barang produksi dari berbagai sumber ke berbagai tujuan dengan biaya angkut seminimal mungkin. Metode terkecil – MODI merupakan salah satu metode untuk menyelesaikan masalah transportasi fuzzy dan linier. Metode ini melalui dua tahap pengerjaan, tahap pertama dikerjakan dengan metode terkecil sebagai metode pencari solusi awal. Tahap kedua dikerjakan dengan menggunakan metode MODI untuk mengecek keoptimuman dari solusi awal, sehingga dapat diperoleh hasil yang optimum. Selain dua metode tersebut terdapat metode untuk menyelesaikan masalah transportasi fuzzy dan linier yaitu metode ASM.

Metode ASM adalah salah satu metode optimalisasi masalah transportasi yang langsung menguji keoptimuman dari tablo transportasi. Metode ASM diawali dengan mengurangi biaya pada baris atau kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada baris ada kolom yang belum nol maka mengurangi biaya pada kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada kolom ada baris yang belum nol maka mengurangi biaya pada baris dengan biaya terkecil. Setelah mengurangkan biaya pada baris atau kolom akan ada biaya nol pada baris dan kolom. Setelah itu dihitung jumlah nol pada tiap-tiap baris dan kolom (tidak termasuk nol yang dipilih). Pilih jumlah nol yang minimum lalu alokasikan persediaan dan permintaan pada sel yang biayanya nol. Pencarian ini tetap berlanjut sampai semua permintaan terpenuhi dan semua persediaan habis.

Dalam menyelesaikan masalah transportasi fuzzy dan linier selain menggunakan metode terkecil – MODI bisa menggunakan metode ASM untuk menyelesaikannya. Pada masalah transportasi fuzzy dan linier, baik dikerjakan dengan metode ASM dan metode terkecil – MODI diperoleh hasil yang sama.

Kata kunci : Masalah Transportasi Fuzzy dan Linier, Metode ASM, Jumlah Total

Nol

Matematika adalah bidang ilmu yang dapat diaplikasikan untuk menyelesaikan masalah dalam kehidupan sehari-hari. Masalah di luar bidang matematika biasanya akan dibawa ke dalam penyelesaian matematika, yaitu dengan mencari model matematikanya. Riset operasi adalah salah satu cabang matematika. Salah satu masalah dalam riset operasi adalah masalah transportasi. Masalah transportasi biasanya dimodelkan ke dalam suatu tablo, yang berisi kapasitas permintaan, kapasitas persediaan, biaya pengiriman barang dari sumber ke tujuan, banyaknya tujuan dan banyaknya sumber. Masalah transportasi menjelaskan masalah pendistribusian suatu komoditas atau produk dari sejumlah sumber (supply) ke sejumlah tujuan (demand) dengan tujuan meminimumkan biaya pengangkutan. Masalah transportasi dibedakan menjadi dua macam yaitu masalah transportasi linier dan masalah transportasi fuzzy. Salah satu metode dalam riset operasi yang dapat

1. Dian Arvianto adalah mahasiswa jurusan Matematika FMIPA Universitas Negeri Malang 2. Sapti Wahyuningsih adalah dosen jurusan Matematika FMIPA Universitas Negeri Malang

(2)

digunakan untuk menyelesaikan masalah transportasi adalah metode terkecil – MODI.

Dalam menyelesaikan masalah transportasi fuzzy dan linier selain menggunakan metode terkecil – MODI bisa menggunakan metode ASM untuk menyelesaikannya. Metode ASM merupakan metode alternatif untuk menyelesaikan masalah transportasi fuzzy dan linier.

Metode ASM diawali dengan mengurangi biaya pada baris atau kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada baris ada kolom yang belum nol maka mengurangi biaya pada kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada kolom ada baris yang belum nol maka mengurangi biaya pada baris dengan biaya terkecil. Setelah mengurangkan biaya pada baris atau kolom akan ada biaya nol pada baris dan kolom. Setelah itu dihitung jumlah nol pada tiap-tiap baris dan kolom (tidak termasuk nol yang dipilih). Pilih jumlah nol yang minimum lalu alokasikan persediaan dan permintaan pada sel yang biayanya nol. Pencarian ini tetap berlanjut sampai semua permintaan terpenuhi dan semua persediaan habis.

HASIL YANG DIPERLUKAN :

1. Mendeskripsikan kinerja metode ASM dalam menyelesaikan masalah transportasi linier dan fuzzy

2. Penerapan metode Robust Ranking untuk mengubah masalah transportasi fuzzy ke masalah transportasi linier

PEMBAHASAN

Secara umum masalah transportasi linier dapat dimodelkan sebagai berikut. Fungsi tujuan dari masalah transportasi linier adalah sebagai berikut,

∑ ∑ (B.Susanta, 1993 : 200) dengan,

: Biaya transportasi barang dari sumber ke tujuan ,

: Banyak barang yang diangkut dari sumber ke tujuan ,

Pemodelan masalah transportasi linier dapat dilihat sebagai berikut,

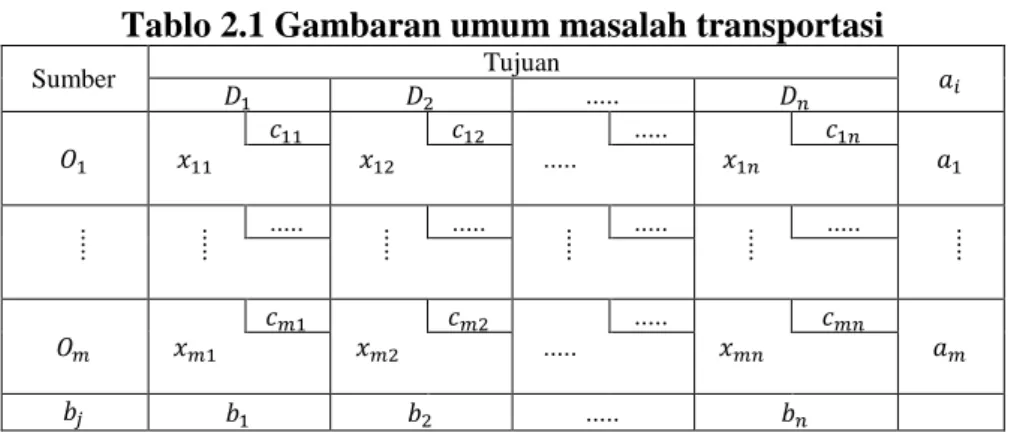
Tablo 2.1 Gambaran umum masalah transportasi

Sumber Tujuan ... ... ... ... ... ... ... ... ... ... ... ... ... ... ... ...

(3)

Keterangan :

: Sumber ke : Tujuan ke : Persediaan ke : Permintaan ke

: Biaya transportasi barang dari sumber ke tujuan ,

: Banyak barang yang diangkut dari sumber ke tujuan ,

Masalah Transportasi Seimbang

Masalah transportasi seimbang adalah jumlah persediaan dari beberapa sumber sama dengan jumlah permintaan beberapa tempat tujuan, yaitu

(B. Susanta, 1993 : 202) m n i j i j b  a

 

Masalah Transportasi Tidak Seimbang

Masalah transportasi tidak seimbang adalah jumlah persediaan dari beberapa sumber tidak sama dengan jumlah permintaan beberapa tempat tujuan. Dalam kasus masalah transportasi tak seimbang, dimana persediaan lebih besar dari permintaan atau sebaliknya yaitu sebagai berikut.

(B. Susanta, 1993 : 202) m n i j i j m n i j i j b a b a  

 

Bilangan Fuzzy

Bilangan fuzzy adalah suatu bilangan yang memiliki bobot nilai

keanggotaan 1 jika bilangannya termasuk dalam anggota penuh dan bobot nilai 0 jika bilangannya tidak termasuk pada anggota. Bobot ini disebut dengan sebagai fungsi keanggotaan, dinotasikan dengan  dan tertutup pada Rdengan interval tertutup

 

0,1 (S. Narayanamoorty, 2013 : 72).

Operasi Bilangan Fuzzy Definisi 1

Misalkan A



a b c, ,



dan B



d e f, ,



adalah dua bilangan fuzzy triangular atau bilangan fuzzy segitiga Maka,

Dengan, ∑ ̃ ̃ ∑ ̃ ̃ ∑ ̃ ∑ ̃ Definisi 3

Suatu himpunan dari alokasi x_ijyang memenuhi baris dan kolom ekuivalen merupakan solusi feasible fuzzy. (Mohanaselvi, 2012 : 371)

Definisi 4

Suatu solusi feasible fuzzy untuk masalah transportasi fuzzy dengan m sebagai sumber dan n sebagai tujuan dikatakan solusi feasible dasar fuzzy jika jumlah alokasinya (m n  1). Jika jumlah alokasi pada solusi dasar fuzzy kurang dari

(m n  1), ini disebut sebagai solusi feasible dasar fuzzy yang merosot. (Mohanaselvi, 2012 : 371)

Definisi 5

Suatu solusi feasible fuzzy dikatakan solusi fuzzy yang optimal jika total biaya transportasi fuzzy minimum. (Mohanaselvi, 2012 : 371)

(5)

Teorema 1 (Eksistensi dari solusi feasible fuzzy)

Kondisi syarat perlu dan syarat cukup untuk eksistensi dari solusi feasible fuzzy, untuk masalah transportasi fuzzy adalah

1 m n i j i j i a b   

 

Bukti :

(Kondisi syarat perlu)

Misalkan terdapat solusi feasible fuzzy untuk masalah transportasi fuzzy yang diberikan seperti pada penjelasan sebelumnya,

Maka 1 1 1 1 dan m n n m ij i ij j i j j i x a x b      



, sehingga diperoleh 1 1 m n i j i j a b   

 

(Kondisi syarat cukup) Misal diasumsikan bahwa

1 1 m n i j i j a b   

 

. Lalu distribusikan persediaan pada sumber ke dengan proporsinya ke permintaan dari semua tujuan.

Misalkan x_ij _ib_j, dimana _i adalah faktor proporsional dari sumber ke . Karena persediaan harus didistribusikan secara keseluruhan.

1 1 Diperoleh , m n ij i j i j x  b   



Oleh karena itu

Dalam menyelesaikan permasalahan transportasi fuzzy, tablo fuzzy harus diubah terlebih dahulu ke bentuk linier agar lebih mudah dalam pengerjaannya.

(6)

Adapun metode untuk mengubah tablo masalah transportasi fuzzy ke tablo permasalahan transportasi linier, adalah sebagai berikut.

Metode Robust Ranking

Jika _{Q adalah bilangan fuzzy, maka Robust Ranking dapat didefinisikan} sebagai berikut, 1 0 ( ) (0,5)( , ) R Q 



L U d Keterangan :

 

R Q : Robust Ranking untuk himpunan fuzzy triangular Q .

Q dapat berupa himpunan permintaan fuzzy, himpunan persediaan fuzzy, atau himpunan biaya fuzzy

1

0



: integral dengan batas 0 sampai 1

(0,5) : nilai tengah dari interval

 

0,1

( , )L U : Perhitungan batas atas dan batas bawah dari himpunan fuzzy Q Misalkan terdapat himpunan permintaan fuzzy, himpunan persediaan fuzzy atau himpunan biaya fuzzy triangular dengan Q( , , )a b c triangular, maka













( , )L U  ba a c,  c b  .

Metode ASM

Metode ASM adalah salah satu metode optimalisasi masalah transportasi yang langsung menguji keoptimuman dari tablo transportasi. Jadi untuk mendapatkan solusi yang optimum, metode ASM tidak perlu menggunakan metode lain lagi seperti MODI.

Langkah – langkah metode ASM :

1. Menyusun tablo transportasi untuk masalah transportasi yang diberikan. 2. Kurangi entri biaya setiap baris pada tablo transportasi dengan masing –

masing baris yang paling minimum dan setelah dihasilkan tablo yang baru atau tereduksi, lanjutkan dengan mengurangi entri biaya setiap kolom dari tablo transportasi yang dihasilkan setelah pengurangan entri biaya setiap baris.

3. Dalam matriks biaya yang telah dikurangi akan ada setidaknya satu nol di setiap baris atau kolom. Pilih nol pertama, perhatikan nol yang dipilih, hitung jumlah total nol (tidak termasuk nol yang dipilih) di baris dan kolom . Kemudian pilih nol selanjutnya dan hitung jumlah total nol-nol pada baris dan kolom dengan cara yang sama.

4. Pilih jumlah nol yang telah terhitung pada langkah 3 yang minimum dan alokasikan persedian dan permintaan pada sel. Jika terdapat lebih dari satu jumlah nol yang terhitung pada langkah 3 yang bernilai sama maka pilih salah satu.

5. Setelah langkah 4, hapus baris atau kolom yang sudah jenuh untuk perhitungan lebih lanjut dimana pasokan dari sumber tertentu habis atau permintaan untuk tujuan tertentu terpenuhi. Periksa apakah matriks yang

(7)

dihasilkan memiliki setidaknya satu nol dalam setiap baris dan setiap kolom. Jika tidak, ulangi langkah 2, jika sebaliknya ke langkah 6.

6. Ulangi langkah 4 sampai semua permintaan terpenuhi dan semua persediaan habis sehingga diperoleh biaya yang optimum.

(Abdul Quddoos, dkk : 2012 : 1272)

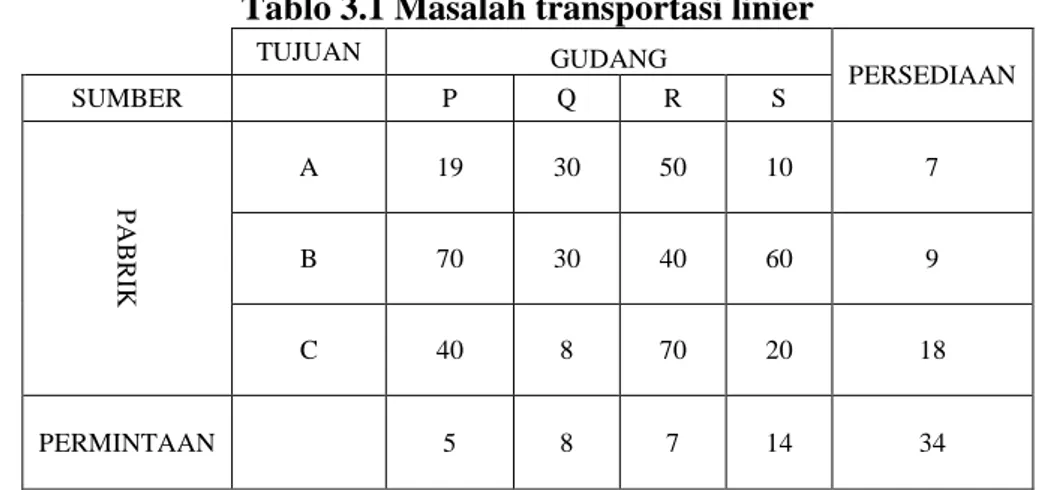
Contoh masalah transportasi linier

Diberikan permasalahan transportasi linier sebagai berikut:

Pabrik A, B, dan C adalah pabrik pembuatan kursi yang produknya

kemudian akan dikirim dengan menggunakan truk ke empat gudang distribusi P, Q, R, S. Keterangan tentang permintaan, persediaan, serta biaya pengiriman barang adalah sebagai berikut

Tablo 3.1 Masalah transportasi linier

TUJUAN _GUDANG PERSEDIAAN SUMBER P Q R S P ABRIK A 19 30 50 10 7 B 70 30 40 60 9 C 40 8 70 20 18 PERMINTAAN 5 8 7 14 34

Dengan dikerjakan menggunakan metode ASM diperoleh hasil sebagai berikut.

P Q R S a_i A 5 19 30 50 2 10 7 B 70 2 30 7 40 60 9 C 40 6 8 70 12 20 18 j b 5 8 7 14 34

Jadi total biaya pengiriman barang dari sumber ke tujuan yang dikerjakan dengan menggunakan metode ASM sebesar 743

Contoh Masalah transportasi fuzzy

Pabrik A, B dan C adalah perusahaan pembuatan gelas. Produk tersebut di kirim ke empat agen K, L, M, N. Perusahaan tersebut membutuhkan data – data baik data permintaan, data biaya, ataupun data persediaan dari bulan – bulan sebelumnya, akan diambil data 3 bulan terakhir yang akan meramalkan biaya transportasi yang dikeluarkan untuk bulan selanjutnya. Sehingga masalah tersebut dapat dimodelkan menjadi masalah transportasi fuzzy sebagai berikut.

(8)

Tabel 3.2 Permasalahan transportasi fuzzy yang disederhanakan K L M N a_i A (1,2,3) (3,5,7) (5,7,9) (0,4,8) (20,50,80) B (0,2,4) (5,6,7) (0,3,6) (0,4,8) (25,50,75) C (1,2,4) (4,5,6) (0,1,2) (5,6,7) (30,50,70) j b (10,30,50) (20,40,60) (35,55,75) (10,25,40) (75,150,225)

Setelah dikerjakan dengan metode pendekatan Robust Ranking dan metode ASM didapatkan hasil sebagai berikut

K L M N a_i A 10 2 40 5 7 4 50 B 20 2 6 5 3 25 4 50 C 2,25 5 50 1 6 50 j b 30 40 55 25 150

Jadi total biaya pengiriman barang dari sumber ke tujuan yang dikerjakan dengan menggunakan metode ASM sebesar 425

Dari permasalahan di atas diperoleh tablo transportasi linier. Untuk tablo transportasi fuzzynya sebagai berikut,

K L M N a_i A (0,10,20) (1,2,3) (20,40,60) (3,5,7) (5,7,9) (0,4,8) (20,50,80) B (10,20,30) (0,2,4) (5,6,7) (5,5,5) (0,3,6) (10,25,40) (0,4,8) (25,50,75) C (1,2,4) (4,5,6) (30,50,70) (0,1,2) (5,6,7) (30,50,70) j b (10,30,50) (20,40,60) (35,55,75) (10,25,40) (75,150,225)

Jadi untuk menyelesaikan masalah transportasi linier diperlukan metode Robust Ranking untuk mengubah masalah transportasi fuzzy ke masalah transportasi linier sehingga lebih mudah untuk menelesaikannya.

PENUTUP Kesimpulan

Berdasarkan pembahasan diperoleh kesimpulan bahwa

1. Metode ASM merupakan salah satu metode optimalisasi untuk mencari pengalokasian barang yang tepat sehingga total biaya pengiriman menjadi minimum. Metode ASM diawali dengan mengurangi biaya pada baris atau

(9)

kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada baris ada kolom yang belum nol maka mengurangi biaya pada kolom dengan biaya terkecil. Jika pada waktu pengurangan biaya pada kolom ada baris yang belum nol maka mengurangi biaya pada baris dengan biaya terkecil. Setelah mengurangkan biaya pada baris atau kolom akan ada biaya nol pada baris dan kolom. Setelah itu dihitung jumlah nol pada tiap-tiap baris dan kolom (tidak termasuk nol yang dipilih). Pilih jumlah nol yang minimum lalu alokasikan persediaan dan permintaan pada baris atau kolom yang memiliki biaya nol. Pada masalah transportasi fuzzy yaitu suatu masalah transportasi dimana biaya, permintaan, persediaan nominalnya terletak antara selang tertentu sehingga mengakibatkan ketidakpastian dalam menentukan nominal yang pasti. Sedangkan untuk masalah transportasi linier, permintaan, persediaan, biaya nominalnya jelas.

2. Pada penerapan metode ASM untuk masalah transportasi fuzzy, tablo transportasi fuzzy diubah terlebih dahulu ke dalam transportasi linier dengan menggunakan metode Robust Ranking, sehingga lebih mudah menyelesaikan masalah transportasi fuzzy.

Saran

Setelah dijelaskan mengenai metode ASM, baik langkah – langkah maupun contoh penerapannya, apabila pada saat menyelesaikan masalah transportasi fuzzy menggunakan metode Robust Ranking untuk mengubah masalah transportasi fuzzy ke masalah transportasi linier sehingga lebih mudah untuk

menyelesaikannya

DAFTAR PUSTAKA

Bazirzadeh, Hadi.’ An Approach for Solving Fuzzy Transportation Problem’, Applied Mathematical Sciences, (2011), Vol 5, No 32, Page 1549 – 1566.

Fegade, M.R, Jadhav, V.A, Muley A.A. ‘Solving Fuzzy Transportation

Problemusing Zero Suffix and Robust Ranking Methodology’,IOSR

Journal of Engineering, (2012), Vol 2, Page 36 – 39.

Mohanaselvi, S. ‘Fuzzy Optimal Solution to Fuzzy Transportation Problem: A

New Approach’, International Journal on Computer Science and Engineering, (2012), Vol 4, No 03, Page 367 – 375.

Narayanamoorthy,S., Saranya,S. and Maheswari,S. ‘A Method for Solving Fuzzy

Transportation Problem (FTP) using Fuzzy Russell’s Method’,

International Journal of Intelegent System and Applications, (2013), Vol 02, Page 71 – 75.

P, Pandian and Natarajan, G. ‘A New Method for Finding an Optimal Solution of

Fully Intervel Integer Transportation Problems’, Applied Mathematical Sciences, (2010), Vol 04, No 37, Page 1819 – 1830.

Quddoos, Abdul, dkk. A New Method for Finding an Optimal Solution for Transportation Problems. International Journal on Computer and Engineering, (2012), Vol 4, No. 07, Page 1271 – 1274.

(10)

Susanta, B. 1993.Program Linier. Jakarta. Departeman Pendidikan dan Kebudayaan Direktorat Jenderal Pendidikan Tinggi.

(11)

Artilcl oleh Dian Arvimto ini

Telafu

&ndfuetnSui:' .t [&10ry, 25 JuIi 2013 '

Pc[nHffing

i I\e*48& 25 JuliEs'I3

!

{se?a Dim

Affauto

Nftil,4093124t'?ffi Dra.''$rytt

Msi.

NIP.'196:212lI