PERBANDINGAN WAKTU KESTABILAN
MODEL VIROTHERAPY DAN RADIOVIROTHERAPY
UNTUK PENYAKIT TUMOR
SKRIPSI
Disusun untuk Memenuhi Syarat Memperoleh Gelar Sarjana Sains di Jurusan Matematika
Oleh:
Mila Kurnia Ruswandi
208700544
JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI SUNAN GUNUNG DJATI
BANDUNG
PERBANDINGAN WAKTU KESTABILAN
MODEL VIROTHERAPY DAN RADIOVIROTHERAPY
UNTUK PENYAKIT TUMOR
SKRIPSI
Disusun untuk Memenuhi Syarat Memperoleh Gelar Sarjana Sains di Jurusan Matematika
Oleh:
Mila Kurnia Ruswandi
208700544
JURUSAN MATEMATIKA
FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS ISLAM NEGERI SUNAN GUNUNG DJATI
BANDUNG
HALAMAN PENGESAHAN
PERBANDINGAN WAKTU KESTABILAN
MODEL VIROTHERAPY DAN RADIOVIROTHERAPY
UNTUK PENYAKIT TUMOR
Oleh:
Mila Kurnia Ruswandi
208700544
Menyetujui:
Lulus diuji tanggal 30 Agustus 2012.
Mengetahui: Pembimbing I,
Diny Zulkarnaen, M.Si NIP.198212132011011008
Pembimbing II,
Rini Cahyandari, M.Si NIP.198201152009122003
Penguji I,
Dr. Elis Ratna Wulan, S.Si., M.T NIP. 197301122000032001
Penguji II,
Arief Fatchul Huda, S.Si., M.Kom NIP. 197206091999031003
Ketua Jurusan Matematika,
Dr. Elis Ratna Wulan, S.Si., M.T NIP. 197301122000032001
Dekan Fakultas Sains dan Teknologi,
Dr. H. M. Subandi, Drs., Ir., MP NIP. 195404241985031004
HALAMAN PERNYATAAN KEASLIAN TULISAN
Saya yang bertanda tangan di bawah ini:
Nama : Mila Kurnia Ruswandi
NIM : 208700544
Fakultas/Jurusan : Sains dan Teknologi / Matematika
Judul Penelitian : Perbandingan Waktu Kestabilan Model Virotherapy dan
Radiovirotherapy untuk Penyakit Tumor
Menyatakan dengan sebenar-benarnya bahwa hasil penelitian saya ini tidak terdapat unsur-unsur penjiplakan atau karya ilmiah yang pernah dilakukan atau dibuat oleh orang lain, kecuali yang secara tertulis dikutip dalam naskah ini dan disebutkan dalam sumber kutipan dan daftar pustaka. Apabila ternyata hasil penelitian ini terbukti terdapat unsur-unsur jiplakan, maka saya bersedia untuk mempertanggung jawabkan, serta diproses sesuai peraturan yang berlaku.
Bandung, 30 Agustus 2012 Yang membuat pernyataan
Mila Kurnia Ruswandi Nim. 208700544
PERSEMBAHAN
Alhamdulillah segala puji syukur kehadirat Mu ya Rohim, Engkau anugerahkan
segala kenikmatan kepada hambaMu ini.
Karya ini kupersembahkan untuk kedua orang tuaku tercinta dan terkasih.
Yang telah memberikan segala dukungan berupa materi maupun moril, yang
selalu mendoakan, yang selalu berjuang untuk membuatku menjadi orang yang
berarti. Tak ada yang bisa menggantikan setiap pengorbanan yang telah mereka
MOTTO
“Setiap Bertambah Ilmuku Bertambah Tahu Pula Aku Akan Kebodohanku”
Berangkat dengan penuh keyakinan Berjalan dengan penuh keikhlasan IstIqomah dalam menghadapI cobaan “ YAKIN, IKHLAS DAN ISTIQOMAH”
ABSTRAK
Perbandingan Waktu Kestabilan Model Virotherapy dan Radiovirotherapy untuk Penyakit Tumor
Mila Kurnia Ruswandi (208700544)
Tumor merupakan penyakit yang diakibatkan oleh pertumbuhan sel atau jaringan tubuh yang tidak normal. Penyakit tumor menjadi ancaman serius terhadap kesehatan manusia, banyak orang yang meninggal akibat penyakit tersebut. Adapun alternatif untuk mengatasi permasalahan penyakit tumor yaitu dengan melakukan teknik pengobatan virotherapy dan radiovirotherapy. Pertumbuhan tumor dengan metode pengobatan virotherapy dipengaruhi oleh laju kematian sel dan laju reproduksi virus, dan pertumbuhan tumor dengan metode pengobatan radiovirotherapy dipengaruhi oleh dosis radiasi dan dosis virus. Berdasarkan kedua teknik pengobatan di atas terdapat hubungan dengan suatu pemodelan matematika, dimana di dalamnya dapat ditentukan titik tetap, jenis kestabilan titik tetap, dan perbandingan waktu kestabilan dari model virotherapy dan radiovirotherapy untuk penyakit tumor. Hasil analisis perbandingan dari kedua teknik pengobatan tersebut dilihat dari waktu kestabilannya. Waktu kestabilan yang diperoleh untuk model virotherapy yaitu dimulai pada saat = 571 hari dan waktu kestabilan yang diperoleh untuk model radiovirotherapy yaitu dimulai pada saat = 599 hari. Sehingga dari kedua model tersebut waktu kestabilan yang diperoleh lebih cepat adalah pada model virotherapy.
Kata Kunci: Virotherapy, Radiovirotherapy, Titik Tetap, Kestabilan, Penyakit
ABSTRACT
Comparison of Time Stability Model virotherapy and Radiovirotherapy for Tumor Diseases
Mila Kurnia Ruswandi (208700544)
The tumor is a disease caused by the growth of cells or tissue that is not normal. Tumor disease is a serious threat to human health, many people died from the disease. As an alternative to overcome the problems of tumor diseases with virotherapy treatment techniques and radiovirotherapy. The growth of tumor virotherapy treatment method is influenced by the rate of cell death and viral reproductive rate, and tumor growth by radiovirotherapy treatment methods are influenced by the dose of radiation and the dose of virus . Based on the above two techniques of treatment there is a relationship with a mathematical model, where it can be determined a fixed point, the stability of a fixed point type, and the comparison of the time stability of model virotherapy and radiovirotherapy for tumor diseases. The results of a comparative analysis of the two treatment techniques are seen from time stability. Time stability for model virotherapy starts at t = 571 days and time stability for model radiovirotherapy starts at t = 599 days. So that from the models obtained stability time is faster on the model virotherapy.
Keywords: Virotherapy, Radiovirotherapy, Equilibrium points, Stability, Tumor
i
KATA PENGANTAR
Segala puji syukur bagi Allah SWT atas limpahan rahmat, taufiq dan hidayah-Nya, sehingga penulis dapat menyelesaikan penulisan skripsi yang berjudul “Perbandingan Waktu Kestabilan Model Virotherapy dan
Radiovirotherapy untuk Penyakit Tumor”. Skripsi ini ditulis untuk melengkapi
tugas akhir dari perkuliahan yang telah dijalankan oleh penulis selama masa studinya di Jurusan Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri (UIN) Sunan Gunung Djati Bandung.
Shalawat serta salam semoga senantiasa tercurah kepada Rosulullah Muhammad SAW beserta keluarga, sahabat dan pengikutnya hingga akhir zaman.
Penulis menyadari bahwa banyak pihak yang telah berpartisipasi dan membantu dalam menyelesaikan penulisan ini. Oleh sebab itu, iringan do’a dan ucapan terima kasih yang sebesar - besarnya penulis sampaikan, terutama kepada:
1. Ruswandi (bapak), Siti Lasmanah (ibu), dan adik-adikku tercinta: Agus Nihayatuzain, Anjailasmawanti dan Ziddan Hayatulasmawan, yang dengan sepenuh hati memberikan dukungan moril maupun spirituil serta ketulusan do’anya sehingga penulisan skripsi ini dapat terselesaikan.
2. Bapak Dr. H. M. Subandi, Drs., Ir., MP, selaku Dekan Fakultas Sains dan Teknologi.
3. Ibu Dr. Elis Ratna Wulan, S.Si., MT selaku Ketua Jurusan Matematika Fakultas Sains dan Teknologi Universitas Islam Negeri Sunan Gunung Djati Bandung.
4. Ibu Siti Julaeha, M.Si selaku pembimbing akademik yang telah memberikan bimbingan dan motivasi kepada penulis.
5. Bapak Diny Zulkarnaen, M.Si., selaku dosen pembimbing I dan Ibu Rini Cahyandari, M.Si., selaku dosen pembingbing II yang telah bersedia meluangkan waktu, memberikan ilmu dan kesabaran dalam membimbing penulis. Semua ilmu yang bapak dan ibu berikan sangat bermanfaat bagi penulis.
ii 6. Segenap dosen pengajar di Fakultas Sains dan Teknologi khususnya di Jurusan
Matematika, terimakasih atas ilmu yang telah diberikan kepada penulis.
7. Teman-teman Matematika, terutama angkatan 2008 yang telah membantu menyelesaikan tulisan ini.
8. Pihak-pihak lain yang telah membantu penulis dalam menyelesaikan tulisan ini.
Tiada gading yang tak retak, begitu pun dengan esensi penulisan skripsi ini, penulis menyadari dalam penulisan ini masih banyak kekurangan. Oleh karena itu, penulis mengharapkan kritik dan saran yang sifatnya membangun guna untuk memperbaiki penulisan selanjutnya. Harapan semoga tulisan ini dapat memberikan manfaat bagi kita semua. Amien.
Bandung, 2012
iii
DAFTAR ISI
Halaman HALAMAN JUDUL HALAMAN PENGESAHAN HALAMAN PERNYATAAN HALAMAN PERSEMBAHAN MOTTO ABSTRAK ABSTRACT KATA PENGANTAR ... iDAFTAR ISI ... iii
DAFTAR GAMBAR ... v
DAFTAR LAMPIRAN ... vii
BAB I PENDAHULUAN 1.1 Latar Belakang ... 1 1.2 Rumusan Masalah ... 3 1.3 Batasan Masalah ... 3 1.4 Tujuan Penelitian ... 3 1.5 Metode Penelitian ... 4 1.6 Sistematika Penulisan ... 4
BAB II LANDASAN TEORI 2.1 Sistem Persamaan Diferensial ... 6
2.2 Sistem Persamaan Diferensial Autonomous ... 6
2.3 Persamaan Diferensial ... 6
2.4 Titik Tetap ... 8
2.5 Pelinearan ... 9
2.6 Nilai Eigen dan Vektor Eigen ... 10
2.7 Sifat Stabilitas Titik Tetap... 11
iv
BAB III KESTABILAN TITIK TETAP MODEL VIROTHERAPY,
RADIOVIROTHERAPY DAN CHEMOTHERAPY
3.1 Model Virotherapy ... 15
3.2 Model Radiovirotherapy ... 17
3.4 Analisis Model Virotherapy ... 21
3.4.1 Menentukan Titik Tetap Model Virotherapy ... 21
3.4.2 Analisis Kestabilan Titik Tetap Model Virotherapy ... 24
3.5 Analisis Model Radiovirotherapy ... 29
3.5.1 Menentukan Titik Tetap Model Radiovirotherapy ... 29
3.5.2 Analisis Kestabilan Titik Tetap Model Radiovirotherapy .. 33
BAB IV SIMULASI DAN PERBANDINGAN WAKTU KESTABILAN MODEL VIROTHERAPY DAN RADIOVIROTHERAPY UNTUK PENYAKIT TUMOR 4.1 Dinamika Populasi Pertumbuhan Tumor dengan Virotherapy ... 39
4.1.1 Dinamika Populasi Untuk > ... 39
4.1.2 Dinamika Populasi Untuk < ... 42
4.1.3 Dinamika Populasi Untuk = ... 47
4.1.4 Dinamika Populasi Keberhasilan Terapi ... 50
4.2 Dinamika Populasi Pertumbuhan Tumor dengan Radiovirotherapy ... 54
4.3 Perbandingan Waktu Kestabilan Model Virotherapy Dan Radiovirotherapy ... 64
BAB V KESIMPULAN DAN SARAN 5.1 Kesimpulan ... 66
5.2 Saran ... 67
DAFTAR PUSTAKA RIWAYAT HIDUP LAMPIRAN
v
DAFTAR GAMBAR
Halaman
2.1 Rumus Euler ... 12
3.1 Skema Diagram Model Virotherapy ... 16
3.2 Skema Diagram Model Radiovirotherapy ... 19
4.1 Populasi Sel Tumor Yang Tidak Terinfeksi Ketika > ... 40
4.2 Populasi Sel Tumor Yang Terinfeksi Virus Ketika > ... 41
4.3 Populasi Partikel Virus Ketika > ... 42
4.4 Populasi Sel Tumor Yang Tidak Terinfeksi Ketika < ... 43
4.5 Populasi Sel Tumor Yang Terinfeksi Virus Ketika < ... 44
4.6 Populasi Partikel Virus Ketika < ... 45
4.7 Dinamika Populasi , , terhadap waktu ketika < ... 46
4.8 Populasi Sel Tumor Yang Tidak Terinfeksi Ketika = ... 47
4.9 Populasi Sel Tumor Yang Terinfeksi Virus Ketika = ... 48
4.10 Populasi Partikel Virus Ketika = ... 49
4.11 Populasi Sel Tumor Yang Tidak Terinfeksi Untuk Keberhasilan Terapi ... 50
4.12 Populasi Sel Tumor Yang Terinfeksi Virus Untuk Keberhasilan Terapi ... 51
4.13 Populasi Partikel Virus Untuk Keberhasilan Terapi ... 51
vi 4.15 Dinamika Populasi , , , Terhadap Waktu
Untuk Keberhasilan Terapi ... 53 4.16 Populasi Sel Tumor Yang Tidak Terinfeksi
Dan Tidak Rusak Oleh Radiasi ... 54 4.17 Populasi Sel Tumor Terinfeksi Juga Tidak Rusak Oleh Radiasi ... 55 4.18 Populasi Sel Yang Rusak Akibat Radiasi ... 56 4.19 Populasi Partikel Virus ... 56 4.20 Dinamika Populasi , , , Terhadap Waktu ... 57 4.21 Populasi Sel Tumor Yang Tidak Terinfeksi Dan Tidak Rusak
Oleh Radiasi Ketika dan Ditingkatkan ... 59 4.22 Populasi Sel Tumor Terinfeksi Juga Tidak Rusak Oleh Radiasi
Ketika dan Ditingkatkan ... 60 4.23 Populasi Sel Yang Rusak Akibat Radiasi
Ketika dan Ditingkatkan ... 61 4.24 Populasi Partikel Virus Ketika dan Ditingkatkan ... 62 4.25 Dinamika Populasi , , , Terhadap Waktu
vii
DAFTAR LAMPIRAN
Lampiran A-1. Pengecekan Titik Tetap Model Virotherapy dan Radiovirotherapy Lampiran B-1. Data Hasil Numerik Model Virotherapy Ketika > .
Lampiran B-2. Data Hasil Numerik Model Virotherapy Ketika < . Lampiran B-3. Data Hasil Numerik Model Virotherapy Ketika = . Lampiran B-4. Data Hasil Numerik Model Virotherapy Untuk Keberhasilan
Terapi.
Lampiran B-5. Data Hasil Numerik Model Radiovirotherapy
Lampiran B-6. Data Hasil Numerik Model Radiovirotherapy Ketika = 1.5 dan = 0.01.
Lampiran B-7. Data Hasil Numerik Model Radiovirotherapy Ketika = 1.5 dan = 0.07.
Lampiran B-8. Data Hasil Numerik Model Radiovirotherapy Ketika = 1.5 dan = 7.
Lampiran C-1. Sintaks Plot Untuk Gambar 4.1 sampai Gambar 4.3 dengan software Matlab.
Lampiran C-2. Sintaks Plot Untuk Gambar 4.4 sampai Gambar 4.7 dengan software Matlab.
Lampiran C-3. Sintaks Plot Untuk Gambar 4.8 sampai Gambar 4.10 dengan software Matlab.
Lampiran C-4. Sintaks Plot Untuk Gambar 4.11 sampai Gambar 4.15 dengan software Matlab.
viii Lampiran C-5. Sintaks Plot Untuk Gambar 4.16 sampai Gambar 4.25 dengan
1
BAB I
PENDAHULUAN
1.1 Latar Belakang Masalah
Perkembangan teknologi saat ini memberikan perubahan nyata terhadap kehidupan, pesatnya kemajuan ilmu pengetahuan menjadi salah satu faktor utama dan memberikan pengaruh positif terhadap perubahan kemajuan zaman, ditandai dengan banyaknya lahir ilmu-ilmu modern yang dapat mengatasi berbagai macam permasalahan dengan memanfaatkan teknologi-teknologi modern, salah satu contohnya di dalam ilmu kedokteran atau ilmu kesehatan. Ilmu kedokteran dengan memanfaatkan teknologi di dalamnya memberikan pengaruh positif terhadap perkembangan dalam menyikapi permasalahan, dengan pemanfaatan teknologi tersebut dapat menjawab permasalahan yang sebelumnya belum terpecahkan.
Penyakit tumor, sebelumnya merupakan penyakit yang sulit untuk ditangani, mungkin pada masanya menjadi penyakit nomor satu yang paling mematikan. Tumor merupakan masalah kesehatan yang sangat serius sebagai penyebab kematian utama di dunia sekaligus secara ilmiah memiliki tantangan yang besar dan kompleks. Tumor adalah penyakit yang disebabkan oleh pertumbuhan sel-sel jaringan tubuh yang tidak normal. Sel-sel tumor berkembang dengan cepat tidak terkendali dan akan terus membelah diri. Sel tumor akan membelah terus meskipun tubuh tidak memerlukannya, sehingga akan terjadi penumpukan sel baru yang disebut tumor ganas. [7].
Perkembangan teknologi, memberikan manfaat khususnya bagi masyarakat dunia, yakni dengan pemanfaatan teknologi dalam bidang kedokteran bisa menjawab permasalahan berbagai macam penyakit dengan dirancanganya berbagai macam peralatan modern yang dikhususkan untuk berbagai macam penyakit.
Ada beberapa pilihan untuk pengobatan tumor yang dapat ditawarkan bila sudah terdiagnosis secara pasti dintaranya: bedah, virotherapy, radiovirotherapy,
2
targeted therapy, radiotherapy, chemotherapy, terapi hormon, immunoterhapy
dan kombinasinya [14].
Dalam dunia kedokteran, para ahli mengkombinasikan efek positif dan negatif dari serangan virus menjadi suatu terapi pengobatan tumor yang disebut
virotherapy. Terapi pengobatan tumor tersebut menggunakan virus jenis Measles Virus (MV) yang dapat diatur secara khusus untuk menginfeksi sel tumor, karena
ekspresi virus MV sangat tinggi terhadap receptor CD46 yang digunakan oleh virus sebagai alat untuk masuk ke sel tumor target. MV sangat selektif dan mempunyai potensi aktivitas kerusakan sel atau oncolytic.[11]
Kemudian, radiovirotherapy yang merupakan bentuk eksperimen pengobatan tumor menggunakan penggabungan antara virus dan penyinaran radiasi. Virus diatur ke ekspresi bentuk human sodium iodide symporter (NIS) yang menyediakan sel tumor terinfeksi ke konsentrasi isotop iodide. Virus MV-NIS ini menahan aktivitas oncolytic alami dari virus induk, tetapi mempunyai keuntungan dapat melenyapkan hambatan tumor ke virus ketika dikombinasikan dengan radioidide.[11]
Bajzer dkk (2007) memodelkan secara matematis pertumbuhan tumor
virotherapy berdasarkan populasi partikel virus. Dan Dingli (Munasir, 2010)
memodelkan secara matematis pertumbuhan tumor radiovirotherapy berdasarkan penyinaran radiasi dan partikel virus.
Berdasarkan kajian pemodelan tersebut maka dalam penulisan ini akan membahas tentang analisis kestabilan dan perbandingan waktu kestabilan model
virotherapy dan radiovirotherapy untuk pengobatan penyakit tumor. Pertama,
menentukan titik tetap untuk setiap model tersebut. Selanjutnya matriks Jacobi dengan melakukan pelinearan terhadap setiap variabel. Kemudian menentukan nilai eigen dengan menyelesaikan persamaan karakteristik, nilai eigen digunakan untuk menganalisis kestabilan titik tetapnya.
Berdasarkan uraian di atas maka penulis tertarik untuk melakukan kajian riset dengan judul. “PERBANDINGAN WAKTU KESTABILAN MODEL
3
1.2 Rumusan Masalah
Berdasarkan latar belakang di atas beberapa masalah yang akan dibahas dalam penulisan ini meliputi:
1. Bagaimana penerapan model matematika untuk virotherapy dan
radioviroherapy untuk penyakit tumor?
2. Bagaimana kestabilan titik tetap pada model virotherapy dan
radiovirotherapy untuk penyakit tumor?
3. Bagaimana perbandingan waktu kestabilan model virotherapy dan
radiovirotherapy untuk penyakit tumor dengan menentukan nilai
parameter melalui simulasi?
1.3 Batasan Masalah
Penulisan ini difokuskan pada pembahasan dengan beberapa batasan masalah sebagai berikut:
1. Model matematika yang dikaji hanya model dalam bentuk persamaan diferensial biasa.
2. Tidak semua titik tetap dari model virotherapy dan radiovirotherapy di analisis kestabilannya. Pada model virotherapy di analisis dua titik tetap dan pada model radiovirotherapy di analisis satu titik tetap.
1.4 Tujuan Penelitian
Tujuan dari penulisan ini adalah:
1. Mengetahui penerapan model matematika untuk virotherapy dan
radiovirotherapy untuk penyakit tumor.
2. Mengetahui jenis kestabilan titik tetap pada model virotherapy dan
radiovirotherapy untuk penyakit tumor.
3. Mengetahui hasil perbandingan waktu kestabilan dari model
virotherapy dan radiovirotherapy dengan menentukan nilai parameter
4
1.5 Metodologi Penelitian
Tahap-tahap yang digunakan dalam penulisan ini agar mencapai tujuan adalah:
1. Studi literatur, meliputi pemahaman teoritis tentang model pengobatan
virotherapy dan radiovirotherapy untuk penyakit tumor dan
kestabilannya melalui jurnal, buku, artikel dan internet. 2. Data yang digunakan merupakan data acak
3. Simulasi data dan grafiknya menggunakan program Matlab.
1.6 Sistematika Penulisan
Skripsi ini menggunakan sistematika penulisan sebagai berikut:
BAB I PENDAHULUAN
Dalam bab ini berisi tentang latar belakang masalah, rumusan masalah, batasan masalah, tujuan penelitian, metodologi penelitian dan sistematika penulisan.
BAB II LANDASAN TEORI
Dalam bab ini berisi tentang sistem persamaan diferensial, sistem persamaan diferensial autonomous, persamaan diferensial, titik tetap, pelinearan, nilai eigen dan vektor eigen, sifat stabilitas titik tetap dan metode Euler.
BAB III KESTABILAN TITIK TETAP MODEL VIROTHERAPY DAN
RADIOVIROTHERAPY.
Dalam bab ini berisi tentang pembahasan berupa model
virotherapy, model radiovirotherapy, analisis model virotherapy,
menentukan titik tetap model virotherapy, analisis kestabilan model
virotherapy, analisis model radiovirotherapy, menentukan ttik tetap
model radiovirotherapy, dan analisis kestabilan model
5 BAB IV SIMULASI DAN PERBANDINGAN WAKTU KESTABILAN MODEL VIROTHERAPY DAN RADIOVIROTHERAPY UNTUK PENYAKIT TUMOR.
Dalam bab ini berisi tentang simulasi dinamika populasi model pertumbuhan virotherapy dan radiovirotherapy untuk penyakit tumor serta perbandingan waktu kestabilan model virotherapy dan
radiovirotherapy berdasarkan kajian teori.
BAB V PENUTUP
Dalam bab ini berisi kesimpulan sebagai jawaban dari rumusan permasalahan serta saran untuk pihak yang terkait.
6
BAB II
LANDASAN TEORI
2.1 Sistem Persamaan Diferensial
Sistem persamaan diferensial adalah suatu persamaan diferensial berorde dan telah dinyatakan sebagai suatu sistem dari persamaan berorde satu. Persamaan itu dapat ditulis dalam bentuk:
= ( , ( ), ( ), … , ( )( ))
Sistem persamaan diferensial merupakan persamaan diferensial yang mempunyai lebih dari satu persamaan yang harus konsisten serta trivial. Sistem persamaan diferensial adalah gabungan dari buah persamaan diferensial dengan
buah fungsi tak diketahui, dimana merupakan bilangan bulat positif lebih
besar sama dengan dua.[8]
2.2 Sistem Persamaan Diferensial Autonomous
Misalkan suatu sistem persamaan diferensial biasa dinyatakan sebagai berikut:
̇ = ( ), ∈ (2.1)
dengan merupakan fungsi kontinu bernilai real dari dan mempunyai turunan parsial kontinu. Sistem persamaan (2.1) disebut sistem persamaan diferensial biasa autonomous karena tidak memuat secara eksplisit di dalamnya.[15]
2.3 Persamaan Diferensial
Secara umum, persamaan diferensial adalah suatu persamaan yang memuat turunan dari satu atau beberapa fungsi yang tidak diketahui dengan turunannya. Persamaan diferensial muncul dalam banyak penerapan teknik (rekayasa) dan penerapan-pennerapan lainnya, seperti model matematis dari berbagai sistem fisis dan sistem-sistem lainnya. Menurut peubah bebas persamaan diferensial dapat
7 dibedakan menjadi dua macam yaitu persamaan diferensial biasa dan persamaan diferensial parsial.[9]
Persamaan diferensial biasa diartikan sebagai suatu persamaan yang melibatkan turunan pertama atau lebih dari fungsi sebarang terhadap peubah , persamaan ini dapat pula melibatkan itu sendiri, fungsi yang diberikan dan konstanta, Berdasarkan turunan tertinggi yang dimiliki, persamaan diferensial biasa dikategorikan menjadi persamaan diferensial biasa orde 1 yaitu yang turunan tertingginya adalah turunan pertama, persamaan diferensial biasa orde 2 yaitu turunan kedua merupakan turunan tertingginya, persamaan diferensial biasa orde 3 yaitu turunan ketiga merupakan turunan tertingginya dan seterusnya.[9] Sebagai contoh:
1. = + (2.2)
2. 2 + − = 0 (2.3)
3. + cos( ) − 3 = sin (2 ) (2.4)
4. 2 − 2 = 1 − (2.5)
Persamaan (2.2) dan (2.3) merupakan persamaan diferensial biasa orde 1. Persamaan (2.4) merupakan persamaan diferensial biasa orde 2 dan persamaan (2.5) merupakan persamaan diferensial biasa orde 3.
Persamaan diferensial parsial diartikan sebagai suatu persamaan yang melibatkan turunan parsial dari fungsi sebarang dengan dua peubah bebas atau lebih.[9]
Sebagai contoh:
1. + = 6
2. = 3 sin( + ) + + (1 + )
Persamaan diferensial dilihat dari bentuk fungsi atau pangkatnya dapat dikelompokkan ke dalam dua kelas besar adalah yang dinamakan persamaan linear dan tak linear. Sebuah persamaan diferensial termasuk persamaan diferensial linier jika memenuhi dua hal berikut:[13]
8 1. Variabel-variabel terikat dan turunannya paling tinggi berpangkat
satu.
2. Tidak mengandung bentuk perkalian antara sebuah variabel terikat dengan variabel terikat lainnya, atau turunan yang satu dengan turunan lainnya, atau variabel terikat dengan sebuah turunan.
Jadi istilah linier berkaitan dengan kenyataan bahwa tiap suku dalam persamaan diferensial itu, peubah-peubah , , … , ( ) berderajat satu atau nol. Bentuk umum persamaan diferensial linier orde-n adalah:[13]
( ) + ( ) + ⋯ + ( ) = ( ).
Sebagai contoh:
1. − 4 =
2. + 2 + 4 =
Selanjutnya persamaan diferensial yang bukan persamaan linear disebut persamaan diferensial tak linear. Dengan demikian persamaan diferensial , , , … , ( ) = 0 merupakan persamaan diferensial tak linear, jika salah satu dari berikut dipenuhi oleh .[13]
1. tidak berbentuk polinom dalam , , … , ( ).
2. berbentuk polinom berpangkat 2 atau lebih dalam , , … , ( ) . Sebagai contoh :
1. + ′′ = 0 merupakan persamaan diferensial tak linear karena ( , , , ′′) = + ′′ polinom berpangkat dua dalam , , ′′. 2. cos + = 0 merupakan persamaan tak linear karena
tidak berbentuk polinom dalam , , .
2.4 Titik Tetap
Misalkan diberikan sistem persamaan diferensial biasa sebagai berikut:
= ̇ = ( ) (2.6)
Titik ̇ disebut titik tetap, titik tetap persamaan (2.6) didapat jika ( ̇ ) = 0. Titik tetap disebut juga titik kritis atau titik kesetimbangan.[15]
9 Untuk lebih jelasnya dapat dilihat contoh di bawah ini.
Misal ( )= + 8 + 15. Maka untuk mencari titik tetapnya adalah dengan cara ( )= 0, maka diperoleh
( ) = + 8 + 15 = 0 ( + 3)( + 5) = 0
= −3 = −5
Jadi didapatkan titik tetapnya adalah = −3 dan = −5.
2.5 Pelinearan
Analisis kestabilan sistem persamaan diferensial tak linear dapat dilakukan melalui pelinearan. Misalkan diberikan sistem persamaan diferensial biasa tak linear
̇ = ( ), ∈ (2.7)
dengan ( ) ∈ adalah suatu fungsi bernilai vektor dalam t (waktu) dan : → adalah suatu fungsi mulus yang terdefinisi pada sub himpunan
⊂ .
Dengan menggunakan ekspansi Taylor di sekitar titik tetap ̇ maka sistem persamaan (2.7) dapat ditulis sebagai berikut:
̇ ≡ ̇ = + ( ) (2.8)
Dengan J adalah matriks Jacobi
= = ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ … ⋯ ⋮ ⋮ ⋱ ⋮ … ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤
Dan ( ) adalah suku berorde tinggi yang bersifat → ( ) = 0, dengan = − ̇ . pada sistem persamaan (2.8) disebut pelinearan sistem persamaan (2.6). [15]
Untuk lebih jelasnya dapat dilihat contoh di bawah ini.[5]
10 Maka matriks Jacobinya adalah
⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ = 6 3 − 3 0 2 −3 4 4 + 3 2 + 3 2 + 6
2.6 Nilai Eigen dan Vektor Eigen
Misalkan matriks berukuran × , maka suatu vektor tak nol di disebut vektor eigen dari jika untuk suatu skalar berlaku:
= (2.9)
Vektor disebut vektor eigen yang bersesuaian dengan nilai eigen . Untuk mencari nilai eigen dari matriks yang berukuran × , maka persamaan (2.9) dapat ditulis sebagai berikut:
( − ) = 0 (2.10)
dengan adalah matriks identitas. Persamaan (2.10) mempunyai solusi tak nol jika dan hanya jika:
( − ) = | − | = 0 (2.11)
Persamaan (2.11) disebut persamaan karakteristik dari matriks .[1] Untuk lebih jelasnya dapat dilihat contoh di bawah ini.[1]
Sistem linier
2 − =
5 − 4 =
Maka dapat ditulis dalam bentuk matriks sebagai berikut:
2 −1 5 −4 = Sehingga diidapat = 2 −1 5 −4 dan = Sehingga − = 1 0 0 1 − 2 −1 5 −4 = 0 0 − 2 −1 5 −4 = − 2 1 −5 + 4 . Maka | − | = − 2 1 −5 + 4 = 0 = ( − 2)( + 4) − (1)(−5) = 0 = + 4 − 2 − 8 + 5 = 0 = + 2 − 3 = 0
11 ( − 1)( + 3) = 0
Sehingga nilai eigen dari adalah = 1 dan = −3.
2.7 Sifat Stabilitas Titik Tetap
Secara umum sifat stabilitas titik tetap mempunyai dua perilaku sebagai berikut:[15]
1. Stabil, jika
a. Setiap nilai eigen real adalah negatif
b. Setiap komponen bagian real dari nilai eigen kompleks, lebih kecil atau sama dengan nol.
2. Tak stabil, jika
a. Ada nilai eigen real yang positif
b. Ada komponen bagian real dari nilai eigen kompleks, lebih besar dari nol. Sebagai contoh: 1. + 2 − 3 = 0 ( − 1)( + 3) = 0 2. + 1 = 0 = −1 = ±√−1
Maka didapat nilai eigen nya untuk contoh 1 adalah = 1 dan = −3. Sehingga kestabilannya bersifat tidak stabil karena ada nilai eigen yang bernilai positif yaitu = 1. Dan untuk contoh 2 adalah = 0 + dan = 0 − . Sehingga kestabilannya bersifat stabil karena bagian real dari nilai eigen kompleks adalah nol.
2.8 Metode Euler
Metode Euler adalah salah satu dari metode satu langkah yang paling tua dan paling sederhana dalam menyelesaikan persamaan diferensial. Penyelesaian persamaan diferensial biasa dengan metode Euler sangat sederhana, akan tetapi hasil penyelesaiannya sering merupakan penyelesaian pendekatan dengan nilai
12 error yang cukup besar, biasanya untuk mengurangi nilai errornya diambil partisi
h yang cukup kecil, akan tetapi hal ini akan menambah jumlah iterasinya.
Penyelesaian dengan metode Euler tidak perlu mencari turunan-turunan fungsi terlebih dahulu. Adapun rumus Euler dapat diperoleh sebagai berikut:[13]
Gambar 2.1 Rumus Euler
Persamaan garis singgung di titik ( , ) adalah:
= (2.12)
Atau
= = ( , ) (2.13)
Dan dari persamaan (2.12) dan (2.13) maka: = ( , )
− = ( − ). ( , )
Karena − = ℎ maka = + ℎ ( , ) (2.14)
Maka persamaan (2.14) disebut rumus Euler. Dengan: i = 0,1,2,...,n = hampiran sekarang = hampiran sebelumnya ℎ = ukuran langkah Sebagai contoh:[6] ( , ) = −2 + 12 − 20 + 8,5
dari 0 ≤ ≤ 1 dimana ℎ = 0.5 dan kondisi awal = 0 adalah = 1. Fungsi asli yang diberikan adalah = −0,5 + 4 − 10 + 8,5 + 1.
+ 1
+ 1
13 Sousli: Substitusi persamaan (2.14) untuk mendapatkan persamaan metode Euler.
(0,5) = (0) + (0,1) ∗ 0,5
Dimana untuk mencari (0,1) adalah sebagai berikut: (0,1) = −2(0) + 12(0) − 20(0) + 8,5 = 8,5 sehingga (0,5) = 1,0 + 8,5(0,5) = 5,25
Solusi sebenarnya pada = 0,5 adalah:
(0,5) = −0,5(0,5) + 4(0,5) − 10(0,5) + 8,5(0,5) + 1 = 3,21875 Jadi kesalahannya adalah:
= sebenarnya – taksiran
= 3,21875 − 5,25 = −2,03125. Artinya nilai kesalahannya besar. Untuk langkah kedua:
(1,0) = (0,5) + (0.5, 5.25) ∗ 0,5
= 5,25 + [−2(0,5) + 12(0,5) − 20(0,5) + 8,5] ∗ 0.5 = 5,875 Solusi sebenarnya = 1,0 adalah:
(1,0) = −0,5(1,0) + 4(1,0) − 10(1,0) + 8,5(1,0) + 1 = 3,00000 = sebenarnya – taksiran
= 3,00000 − 5,875 = −2,875. Artinya nilai kesalahannya besar
Dalam metode Euler selesaian yang diperoleh berupa urutan nilai untuk = dengan = 0, 1,2 , … , + 1. Jika urutan titik-titik ( , ) tersebut dihubungkan dengan segmen garis maka akan terbentuk bangun yang dinamakan rantai poligon. Untuk masalah nilai awal yang berbentuk:[13]
= ( , , ) = ( , , )
( ) = , ( ) =
Maka rumus Euler untuk sistem berbentuk sebagai berikut: = + ( , , )ℎ, = 0, 1, 2, … ,
= + ( , , )ℎ = 0, 1, 2, … ,
14
BAB III
KESTABILAN TITIK TETAP MODEL VIROTHERAPY DAN
RADIOVIROTHERAPY
Model yang akan dianalisis merupakan sebuah model yang dibangun berdasarkan pertumbuhan populasi sel tumor. Pada umumnya model pertumbuhan tumor tanpa perlakuan terapi dijelaskan oleh fungsi Gompertz. Model Gompertz diberikan dalam bentuk persamaan sebagai berikut:[10]
= { − ln( )} (3.1)
dengan:
( )= volume tumor pada waktu t
= laju pertumbuhan intrinsik tumor (berkaitan dengan tingkat mitosis) = faktor pertumbuhan (berkaitan dengan proses antiangiogenic)
Namun untuk beberapa tumor yang lebih umum model Bertalanffy-Richard atau generalized logistic digunakan juga untuk menjelaskan pertumbuhan pada tumor. Model Bertalanffy-Richard diberikan dalam bentuk persamaan sebagai berikut:[2]
̇ = 1 − (3.2)
dengan:
( ) = ukuran populasi sel tumor
= laju konstan pertumbuhan efektif populasi sel tumor
= parameter yang menyatakan ukuran maksimal populasi sel tumor.
= parameter yang menyatakan bentuk karakteristik pertumbuhan tumor.
15
3.1 Model Virotherapy
Menurut Bajzer dkk, pada model virotherapy mempertimbangkan tiga interaksi populasi yaitu:[3]
( ) = sel tumor tidak terinfeksi pada waktu ( ) = sel tumor yang terinfeksi virus pada waktu
( ) = partikel virus bebas yang menginfeksi pada waktu
pemodelan interaksi populasi sel tumor dan partikel virus dinyatakan dalam bentuk persamaan berikut:[3]
̇ = 1 − − ( + ) (3.3)
̇ = − (3.4)
̇ = − ( + ) (3.5)
Dengan menggunakan metode Euler maka persamaan (3.3) sampai (3.5) menjadi ̇ = ( ) 1 − ( ) ( ) − ( ( ) ( ) + ( )) lim∆ → ( ∆ ) ( ) ∆ = lim∆ → ( ) 1 − ( ) ( ) − ( ( ) ( ) + ( )) Hilangkan limit pada kedua ruas sehingga diperoleh
( ∆ ) ( ) ∆ = ( ) 1 − ( ) ( ) − ( ( ) ( ) + ( ) ( )) ( + ∆ ) − ( ) = ( ) 1 − ( ) ( ) − ( ( ) ( ) + ( ) ( )) ∆ ( + ∆ ) = ( ) + ( ) 1 − ( ) ( ) ∆ − ( ( ) ( )∆ + ( ) ( )∆ (3.6) ̇ = ( ) ( ) − ( ) lim ∆ → ( + ∆ ) − ( ) ∆ = lim∆ → ( ) ( ) − ( )
Hilangkan limit kedua ruas sehingga diperoleh ( + ∆ ) − ( ) ∆ = ( ) ( ) − ( ) ( + ∆ ) − ( ) = ( ( ) ( ) − ( ))Δ ( + ∆ ) = ( ) + ( ) ( )Δ − ( )Δ (3.7) ̇ = ( ) − ( ( ) ( ) + ( )) lim ∆ → ( + ∆ ) − ( ) ∆ = lim∆ → ( )− ( ( ) ( )+ ( ))
16 Hilangkan limit kedua ruas sehingga diperoleh
( + ∆ ) − ( )
∆ = ( )− ( ( ) ( )+ ( ))
( + ∆ ) − ( ) = ( ) − ( ( ) ( ) + ( ) Δ )
( + ∆ ) = ( ) + ( )Δ − ( ( ) ( )Δ + ( )Δ ) (3.8) dengan:
= laju pertumbuhan efektif sel yang tidak terinfeksi . = ukuran maksimal sel tumor.
= laju infeksi.
= laju sel yang bergabung.
= laju kematian efektif sel yang terinfeksi. = laju virus yang mati.
= laju produksi virus dari sel tumor yang terinfeksi.
Gambar 3.1. Skema Diagram Model Virotherapy [2]
Gambar 3.1 di atas representasi model virotherapy pada persamaan (3.3) sampai persamaan (3.5). Garis panah berwarna merah menandakan populasi bertambah atau populasi berkurang, sedangkan garis putus-putus berwarna biru menunjukkan pengaruh.
Populasi sel tumor yang tidak terinfeksi terus berkembang biak. Perkembangbiakan sel-sel ini terjadi karena pengaruh laju pertumbuhan efektif ( ), ukuran maksimal tumor ( ), dan parameter yang merupakan bentuk karakteristik pertumbuhan tumor ( ). Namun, perkembangbiakan tersebut diikuti
K, r , k
δ
y
17 oleh laju infeksi > 0 dan laju sel yang bergabung dengan sel yang terinfeksi > 0 yang mengakibatkan sel tumor yang tidak terinfeksi akan berkurang, diberikan oleh penjumlahan + . Populasi sel tumor yang terinfeksi bertambah karena dipengaruhi oleh laju infeksi. Setelah itu, beberapa sel tumor yang terinfeksi tersebut akan mengalami kematian karena pengaruh laju kematian efektif > 0. Populasi partikel virus dapat berkembang biak karena pengaruh laju produksi virus dari sel yang terinfeksi, dinyatakan dengan ( ) dimana ≥ 0. Proses ini sama seperti populasi sel yang tidak terinfeksi, setelah berkembangbiak, populasi virus akan berkurang karena pengaruh laju infeksi dan laju virus yang mati ≥ 0.[2]
Populasi awal untuk model virotherapy yaitu (0) = , (0) = 0 dan (0) = , semua parameter yang digunakan non negatif, ukuran tumor diukur sebagai volume (dalam mm3) sedangkan dalam model ini menganggap jumlah populasi sel. Volume tumor dikonversi ke populasi sel dengan asumsi bahwa 1mm3 sama dengan 106 sel tumor. Model ini menyatakan jumlah populasi sel tumor dan virus dalam , , dalam satuan 106, dan model ini menganggap bahwa semua unit waktu dinyatakan dalam hari. Untuk keberhasilan terapi model ini diperoleh ketika jumlah populasi tumor ( )= ( ) + ( ) < 1 yang artinya sel tumor tidak terdeteksi.[3]
3.2 Model Radiovirotherapy
Menurut Dingli, pada model Radiovirotherapy mempertimbangkan empat interaksi populasi yaitu: [11]
( ) = sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi pada waktu
( ) = sel tumor yang terinfeksi juga tidak rusak oleh radiasi pada waktu ( ) = sel yang dirusak oleh radiasi pada waktu
( ) = populasi partikel virus pada waktu
Pemodelan interaksi antara populasi sel tumor, virus dan terapi radiasi dinyatakan dalam bentuk persamaan sebagai berikut:[11]
18
̇ = − − (3.10)
̇ = ( + ) − (3.11)
̇ = − (3.12)
Dengan menggunakan metode Euler maka persamaan (3.9) sampai (3.12) menjadi ̇ = ( ) 1 − ( ) + ( ) + ( ) − ( ( ) ( ) + ( )) lim∆ → ( ∆ ) ( ) ∆ = lim∆ → ( ) 1 − ( )+ ( )+ ( ) − ( ( ) ( ) + ( )) Hilangkan limit kedua ruas sehingga diperoleh
( + ∆ ) − ( ) ∆ = ( ) 1 − ( )+ ( )+ ( ) − ( ( ) ( ) + ( )) ( + ∆ ) − ( ) = ( ) 1 − ( ) ( ) ( ) − ( ( ) ( ) + ( ) Δ ( + ∆ ) = ( ) + ( ) 1 − ( ) ( ) ( ) ∆ − ( ( ) ( )∆ + ( )Δ ) (3.13) ̇ = ( ) ( ) − ( ) − ( ) lim ∆ → ( + ∆ ) − ( ) ∆ = lim∆ → ( ) ( ) − ( ) − ( )
Hilangkan limit kedua ruas sehingga diperoleh ( + ∆ ) − ( ) ∆ = ( ) ( ) − ( ) − ( ) ( + ∆ ) − ( ) = ( ) ( ) − ( ) − ( ) Δ ( + ∆ ) = ( ) + ( ) ( )Δ − ( )Δ − ( )Δ (3.14) ̇ = ( ( ) + ( )) − ( ) ( ) lim ∆ → ( + ∆ ) − ( ) ∆ = lim∆ → ( ( ) + ( ))− ( ) ( )
Hilangkan limit kedua ruas sehingga diperoleh ( + ∆ ) − ( )
∆ = ( ( ) + ( ))− ( )
( )
( + ∆ ) − ( ) = ( ( ) + ( )) − ( ) ( ) Δ
19 ̇ = ( ) − ( ) lim ∆ → ( + ∆ ) − ( ) ∆ = lim∆ → ( ) − ( )
Hilangkan limit kedua ruas sehingga diperoleh ( + ∆ ) − ( )
∆ = ( ) − ( )
( + ∆ ) − ( ) = ( ( ) − ( ))Δ
( + ∆ ) = ( ) + ( )Δ − ( )Δ (3.16)
dengan:
= laju pertumbuhan efektif sel yang tidak terinfeksi. = ukuran maksimal sel tumor.
= laju infeksi.
= laju kematian efektif sel yang terinfeksi. = laju virus yang mati.
= laju produksi virus dari sel tumor yang terinfeksi. = dosis radiasi yang diserap oleh sel.
= tingkat kerusakan sel tumor.
= laju kematian efektif sel yang telah rusak
Gambar 3.2. Skema Model Radiovirotherapy [11]
K, r ,
k y
20 Gambar 3.2 di atas representasi model radiovirotherapy pada persamaan (3.9) sampai persamaan (3.12). Garis panah berwarna merah menandakan populasi bertambah atau populasi berkurang, sedangkan garis putus-putus berwarna biru menunjukkan pengaruh.
Pada model ini laju infeksi virus ke sel tumor tak terinfeksi ( ) hanya merupakan pengaruh dari populasi partikel virus dan tidak ikut dalam persamaan populasi partikel virus. Begitu juga dengan laju produksi virus dari sel tumor yang terinfeksi . Pada model radiovirotherapy ini, menunjukkan populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi. Populasi partikel virus ditunjukkan oleh , menunjukkan populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi, dan merupakan populasi sel yang rusak akibat radiasi.[11]
Populasi sel tumor yang tidak terinfeksi dan tidak rusak oleh radiasi terus berkembangbiak karena pengaruh , , . Namun, perkembangbiakan tersebut diikuti oleh laju infeksi dan tingkat kerusakan sel tumor yang tidak terinfeksi akibat radiasi yang mengakibatkan populasi sel tumor yang tidak terinfeksi akan berkurang. Untuk populasi sel tumor yang terinfeksi juga tidak rusak oleh radiasi , populasinya terus bertambah karena dipengaruhi oleh laju infeksi. Setelah itu, beberapa sel tumor yang terinfeksi tersebut akan mengalami kematian karena pengaruh laju kematian efektif dan tingkat kerusakan sel tumor yang terinfeksi akibat radiasi .[11]
Populasi partikel virus dapat berkembang biak karena pengaruh laju produksi virus dari sel yang terinfeksi, dinyatakan dengan . Proses ini sama seperti populasi sel yang tidak terinfeksi, setelah berkembangbiak, populasi virus akan berkurang karena pengaruh laju virus yang mati . Dan populasi sel yang rusak akibat radiasi akan terus bertambah karena pengaruh + . Setelah itu akan mengalami kematian efektif sel yang rusak yang dinyatakan oleh
.[11]
Populasi awal untuk model radiovirotherapy yaitu (0) = , (0) = 0, (0) = 0, dan (0) = . Dan semua parameter yang digunakan non negatif, ukuran tumor diukur sebagai volume (dalam mm3) sedangkan dalam model ini menganggap jumlah populasi sel. Volume tumor dikonversi ke populasi sel dengan asumsi bahwa 1mm3 sama dengan 106 sel tumor. Model ini menyatakan
21 jumlah populasi sel tumor dan virus dalam , , , dalam satuan 106
, dan model ini menganggap bahwa semua unit waktu dinyatakan dalam hari.[11]
3.3 Analisis Model Virotherapy
3.3.1 Menentukan Titik Tetap Model Virotherapy
Titik tetap dari persamaan (3.3) sampai (3.5) akan diperoleh dengan menetapkan ̇ = 0, ̇ = 0, dan ̇ = 0, sehingga diperoleh persamaan-persamaan di bawah ini:
1 − − ( + ) = 0 (3.17)
− = 0 (3.18)
− ( + ) = 0 (3.19)
Dari persamaan (3.17) akan diperoleh nilai sebagai berikut:
1 − − ( + ) = 0 1 − − ( + ) = 0 1 − − ( + ) = 0 = 0 ∩ 1 − = ( + ) = 0 ∩ 1 − = ( ) = 0 ∩ = 1 −( ) = 0 ∩ = = 0 ∩ = = 0 ∩ = = 0 ∩ = = 0 ∩ = −
22 Dari persamaaan (3.18) akan diperoleh nilai sebagai berikut:
− = 0
− = − =
=
Dari persamaan (3.19) akan diperoleh nilai sebagai berikut: − ( + ) = 0
− ( + ) = −
( + ) =
( + ) =
= ( )
Substitisi = 0 untuk mendapatkan nilai dan = , karena nilai = 0 maka = ( ) = 0 =
( ), karena nilai = 0 dan = 0 maka = ( )
( ( ) )= 0 Sehingga diperoleh titik tetap ( , , ) = (0,0,0)
Untuk memperoleh titik tetap ( , , ) substitusi = 0 dan = 0 ke persamaan berikut: = − = ( ) ( ) − (0) = − 0 = − 0 = | | − 0 = − 0 = (0) − 0 = 1 − 0 =
23 Sehingga diperoleh titik tetap ( , , ) = ( , 0,0)
Untuk memperoleh titik tetap ( , , ) maka dari persamaan (3.18) diperoleh nilai sebagai berikut:
− = 0 =
= (3.20)
Dari persamaan (3.19) diperoleh nilai dengan mensubstitusikan persamaan (3.20) sebagai berikut: − ( + ) = 0 − − = 0 − − = 0 − − = 0 = − = ( − ) ( − ) = = ( − ) = ( ) (3.21)
Subsitusi persamaan (3.21) ke persamaan (3.20) sehingga diperoleh nilai
= =
( )
=
( )
= ( ) =( ) (3.22)
Dari persamaan (3.17) diperoleh nilai dengan mensubtitusikan persamaan (3.21) dan (3.22) sebagai berikut:
1 − − ( + ) = 0 1 − − ( ) + = 0 ( ) + = 1 − = 1 −
24 − + = 1 − ( − + ) = 1 − = ( ) 1 − = ( ) 1 −
sehingga diperoleh titik tetap ( , , ) = ( ) , ( ) 1 − ,
( )
.
Jadi dengan menyelesaikan persamaan (3.17) sampai (3.19) diperoleh tiga titik tetap yaitu (0,0,0), ( , 0,0) dan (
) , ( ) 1 − ,
( )
. Dimana untuk ( , 0,0) mewakili kegagalan terapi dan ( ) ,
( ) 1 −
,( ) mewakili keberhasilan terapi.[3]
3.3.2 Analisis Kestabilan Titik Tetap Model Virotherapy
Untuk menganalisis kestabilan titik tetap model virotherapy hanya menganalisis dua titik tetap yaitu dan karena untuk menganalisis titik tetap penyelesaiannya sangat kompleks. Misalkan persamaan (3.3) sampai persamaan (3.5) dituliskan sebagai berikut:
∶ ̇ = 1 − − ( + )
∶ ̇ = −
∶ ̇ = − ( + )
Dengan melakukan pelinearan terhadap persamaan , , maka akan diperoleh matriks Jacobi sebagai berikut:
= ⎝ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎞ = 1 − − ( + ) = − − −
25 = − − − − = 1 − − − − = 1 − − ( + ) = − − − = − − = 1 − − ( + ) = − − − = − = − = = − = − = − = = − ( + ) = − − = − ∶ = = = − = − = − + = − + − = − − ∶ = = 0 = − = − = − + = 0 + − = 0 − = −
26 = − ( + )
= − − =
= − ( + )
= − − = − −
Sehingga diperoleh dalam matriks Jacobi sebagai berikut:
= ⎝ ⎛ 1 − + − + −1 − − − + −1 − − − − − − ⎠ ⎞ (3.23)
Analisis Kestabilan di Titik Tetap
Untuk memperoleh kestabilan sistem di titik tetap substitusi (0,0,0) ke persamaan (3.23) sehingga diperoleh matriks Jacobi sebagai berikut:
( , , ) =
0 0
0 − 0
0 −
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik
( ( 0,0,0) − )=0 sehingga diperoleh: det 0 0 0 − 0 0 − − 1 0 0 0 1 0 0 0 1 = 0 det 0 0 0 − 0 0 − − 0 0 0 0 0 0 = 0 − 0 0 0 − − 0 0 − − = 0 ( − )(− − )(− − ) = 0 − = 0 − − = 0 − − = 0 − = − − = − = = = − = − Sehingga diperoleh nilai eigennya sebagai berikut:
27 Karena parameter yang digunakan non negatif, maka 1>0 dan 2 , 3<0. Sehingga
kestabilan titik tetapnya tidak stabil.
Analisis Kestabilan di Titik Tetap
Untuk memperoleh kestabilan sistem di titik tetap substitusi ( , 0, 0) ke persamaan (3.23) maka diperoleh matriks Jacobi sebagai berikut:
( , , )=
− − − −
0 −
0 − −
Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik
( ( K ,0,0) − )=0 sehingga diperoleh : − − − − 0 − 0 − − − 1 0 0 0 1 0 0 0 1 = 0 − − − − 0 − 0 − − − 0 0 0 0 0 0 = 0 − − − − − 0 − − 0 − − − = 0 − − − − − 0 − − 0 − − − − − − − 0 − − 0 = 0 [(− − )(− − )(− − − )] + [(− − )( )(0)] + [(− )(0)( ) − [(− )( − − )(0)] − [(− − )( )( )] − [( − − )(0)(− − − )] = 0 ↔ [(− − )(− − )(− − − ) + 0 + 0] − [0 +(− − )( )( ) + 0] = 0 ↔ (− − )(− − )(− − − ) −(− − )( )( ) = 0 ↔ (− − )[(− − )(− − − ) − ( )( )] = 0 ↔ (− − )[ + + + + + − ] = 0 ↔ (− − )[ + + + + − + ] = 0 ↔ (− − )[ + ( + + ) + ( − ) + ] = 0
Dari persamaan di atas dimisalkan ( + + ) = dan ( − ) + = sehingga persamaan di atas dapat ditulis:
↔ (− − )[ + + ] = 0 − − = 0
28 = −
+ + = 0
Gunakan rumus pytaghoras untuk mendapatkan dan , = ±√ , = ± = ±
Sehingga diperoleh nilai eigen sebagai berikut: = −
= ( + + ) ( + + ) ( − ) +
= ( + + ) ( + + ) ( − ) +
Berdasarkan kondisi yang telah diperoleh maka sesuai dengan analisis kestabilan, titik tetap yang diperoleh dipengaruhi oleh laju kematian efektif sel yang terinfeksi ( ) dan laju produksi virus dari sel tumor yang terinfeksi ( ) sehingga harus diperiksa dari kondisi > , < dan = .
Untuk kasus yang pertama nilai parameter > akan menghasilkan , , < 0, sehingga dari nilai-nilai eigen yang diperoleh kestabilan titik tetapnya bersifat stabil. Kasus yang kedua nilai parameter < akan menghasilkan , < 0 dan > 0 sehingga dari nilai-nilai eigen yang diperoleh kestabilan titik tetapnya bersifat tidak stabil dan kasus yang ketiga nilai parameter = akan menghasilkan , , < 0, sehingga dari nilai-nilai eigen yang diperoleh kestabilan titik tetapnya bersifat stabil.
Berdasarkan titik tetap yang diperoleh, laju kematian sel yang terinfeksi ( ) dan laju produksi virus dari sel yang terinfeksi ( ) mempengaruhi kestabilan titik tetapnya. Jadi untuk dalam kondisi apapun kestabilannya bersifat tidak stabil sedangkan untuk dalam kondisi > dan = kestabilannya bersifat stabil sedangkan dalam kondisi < kestabilannya bersifat tidak stabil.
29
3.5 Analisis Model Radiovirotherapy
3.5.1 Menentukan Titik Tetap Model Radiovirotherapy
Titik tetap dari persamaan (3.9) sampai persamaan (3.12) akan diperoleh dengan menetapkan ̇ = 0, ̇ = 0, ̇ = 0 dan ̇ = 0 sehingga diperoleh persamaan-persamaan di bawah ini:
1 − − ( + ) = 0 (3.24)
− − = 0 (3.25)
( + ) − = 0 (3.26)
− = 0 (3.27)
Dari persamaan (3.24) akan diperoleh nilai sebagai berikut:
1 − − ( + ) = 0 1 − − ( + ) = 0 1 − − ( + ) = 0 = 0 (3.28) 1 − − ( + ) = 0 − − − = 0 = − − = = = = = − ( + ) (3.29)
Dari persamaan (3.25) akan diperoleh nilai sebagai berikut: − − = 0
30
− ( + ) = −
( + ) =
=( ) (3.30)
Dari persamaan (3.26) akan diperoleh nilai sebagai berikut: ( + ) − = 0
− = − ( + )
= ( + )
= ( ) (3.31)
Dari persamaan (3.27) akan diperoleh nilai sebagai berikut: − = 0
− = − =
= (3.32)
Substitusi persamaan (3.32) ke persamaan (3.30). Maka diperoleh sebagai berikut: = ( ) = ( ) = × ( ) = ( + ) = + − = 0 ( + − ) = 0 = ( ) = 0
Substitusi = 0 ke persamaan (3.32). Maka diperoleh sebagai berikut: = = = ( )= 0
Substitusi = 0 dan = 0 ke persamaan (3.31). Maka diperoleh sebagai berikut:
31 = ( )
1 = =
=
Substitiusi = 0, = 0 dan = ke persamaan (3.29) maka diperoleh sebagai berikut: = − ( + ) = − (0 + ) = − + = = ( ) − = −
Sehingga diperoleh titik tetap
( , , , ) = ⎝ ⎜ ⎛ , 0, , 0 ⎠ ⎟ ⎞
Untuk memperoleh titik tetap ( , , , ) maka dari persamaan (3.25) diperoleh sebagai berikut:
− − = 0 = +
= (3.33)
Dari persamaan (3.27) diperoleh sebagai berikut: − = 0
32
= (3.34)
Dari persamaan (3.26) diperoleh sebagai berikut: ( + ) − = 0
− = − ( + )
= ( + ) = ( )
= ( )
Dari persamaan (3.24) diperoleh sebagai berikut:
1 − − ( + ) = 0
= 1 − −
=
=
Substitusi persamaan (3.34) ke persamaan (3.33) maka diperoleh nilai sebagai berikut: = = = ( + )
Sehingga diperoleh titik tetap
( , , , ) = ( + ), , ( ),
Jadi dengan menyelesaikan persamaan (3.24) sampai (3.25) diperoleh dua titik tetap yaitu
⎝ ⎜ ⎛ , 0, , 0 ⎠ ⎟ ⎞ dan ( + ), , ( ), .
33
3.5.2 Analisis Kestabilan Titik Tetap Model Radiovirotherapy
Untuk analisis kestabilan titik tetap model radiovirotherapy hanya menganalisis titik tetap karena untuk menganalisis titik tetap penyelesaiannya sangat kompleks. Misalkan persamaan (3.6) sampai persamaan (3.9) dituliskan sebagai berikut:
: ̇ = 1 − − ( + )
: ̇ = − − C: ̇ = ( + ) −
: ̇ = −
Dengan melakukan pelinearan terhadap persamaan , , , maka akan diperoleh matriks Jacobi sebagai berikut:
= ⎝ ⎜ ⎜ ⎜ ⎛ ⎠ ⎟ ⎟ ⎟ ⎞ = 1 − − ( + ) = − − − = − å− å å − − â = 1 − − − − = 1 − − ( + ) = − − − ∶ = = = − = − = − + = − + − = − −
34 = − = 1 − − ( + ) = − − − = − å å = 1 − − ( + ) = − − − = − = − − = = − − = − − = − − = 0 = − − = = ( + ) − = + − = = ( + ) − = + − = = ( + ) − = + − = − = ∶ = = 0 = − = − = − + = 0 − + − = 0 − ∶ = = 0 = − = − = − + = 0 − + − = 0 −
35 = ( + ) − = + − = − ( ) = − = 0 = − = = − = 0 = − = −
Sehingga diperoleh dalam matriks Jacobi sebagai berikut:
= ⎝ ⎜ ⎜ ⎛ 1 − − − − − − − − − 0 − ( ) 0 0 − ⎠ ⎟ ⎟ ⎞ (3.35)
Analisis Kestabilan Titik Tetap
Untuk memperoleh kestabilan sistem di titik tetap substitusi
( , , , ) = ⎝ ⎜ ⎛ , 0, ,0 ⎠ ⎟ ⎞ ke persamaan (3.35) dan
memisalkan = 1 (ada pertumbuhan tumor) sehingga diperoleh matriks Jacobi sebagai berikut: = ⎝ ⎜ ⎜ ⎜ ⎛ 1 − + + − − − − 0 − − 0 0 − 0 0 − ⎠ ⎟ ⎟ ⎟ ⎞
36 Kemudian dicari nilai eigennya dengan menggunakan persamaan karakteristik
⎝ ⎜ ⎛ ⎝ ⎜ ⎛ , 0, , 0 ⎠ ⎟ ⎞ − ⎠ ⎟ ⎞ = 0 sehingga diperoleh: ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 − 2 + − + − − − − 0 − − 0 0 − − − 0 0 − ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ − 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = 0 ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 − 2 + − + − − − − 0 − − 0 0 − − − 0 0 − ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ − 0 0 0 0 0 0 0 0 0 0 0 0 ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = 0 ⎝ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎛ 1 − 2 + − + − − − − − 0 − − − 0 − − − − 0 0 − − ⎠ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎞ = 0 1 − 2 + − + − − − − − 0 − − − 0 − − − − 0 0 − − = 0 − ⎣ ⎢ ⎢ ⎢ ⎢ ⎢ ⎡ 0 − − − − − 0 − − ⎦ ⎥ ⎥ ⎥ ⎥ ⎥ ⎤ − ⎣ ⎢ ⎢ ⎢ ⎢ ⎡ 1 − 2 + − + − − − − 0 − − − 0 − − ⎦ ⎥ ⎥ ⎥ ⎥ ⎤ = 0 − 0 − − − − − − + 0 − 1 − 2 + − + − − − − − − − − 0 + 0 = 0 − − (− − − )(− − ) − − 1 − 2 + − + − − (− − − )(− − ) − = 0 (− − − )(− − ) − − −2 + − + − − (− − − )(− − ) − = 0 (− − − )(− − ) − − −2 + − + − − = 0 + + + + + − − +2 − − − + + = 0 + ( + + ) − + 2 + − − − − + = 0 + ( + + ) − = 0
37 Misalkan ( + + ) = dan = maka persamaannya dapat ditulis
+ − = 0. Gunakan rumus pytaghoras untuk mendapatkan dan , = ±√ , = ± . = ±
Sehingga diperoleh nilai eigen sebagai berikut: =
( ) ( )
= ( ) ( )
+ + − − − + = 0
Misalkan + − − − = dan = maka
persamaannya dapat ditulis + + = 0. Gunakan rumus pytaghoras untuk mendapatkan dan , = ±√ , = ±√ = ±√
Sehingga diperoleh nilai eigen sebagai berikut:
=
=
Jadi dari titik tetap
⎝ ⎜ ⎛ , 0, , 0 ⎠ ⎟ ⎞
diperoleh nilai eigen berikut:
=
( ) ( )
38
= ( ) ( )
=
=
Berdasarkan kondisi yang telah diperoleh maka sesuai dengan analisis kestabilan, titik tetap yang diperoleh dipengaruhi oleh dosis radiasi dan dosis virus sehingga diperoleh nilai eigen , , , < 0,. Jadi kestabilan titik tetapnya bersifat stabil.
39
BAB IV
SIMULASI DAN PERBANDINGAN WAKTU KESTABILAN
MODEL VIROTHERAPY DAN RADIOVIROTHERAPY UNTUK
PENYAKIT TUMOR
Berikut akan dibahas perbandingan waktu kestabilan pada dinamika populasi pertumbuhan tumor dengan model virotherapy dan radiovirotherapy dengan mensubsitusikan nilai-nilai parameter terhadap model-model tersebut yang sudah diubah dengan menggunakan metode Euler kemudian mensimulasikannya yang diselesaikan menggunakan bantuan program Matlab.
4.1 Dinamika Populasi Pertumbuhan Tumor dengan Virotherapy
Untuk mengamati pengaruh pertumbuhan populasi sel tumor dengan
virotherapy maka diperlukan kurva bidang solusi yang menunjukkan hubungan
banyaknya populasi dengan variabel waktu. Solusi numerik menggunakan
software Matlab dilakukan dengan mensubstitusikan nilai-nilai parameter ke
persamaan (3.6) sampai (3.8) sehingga diperoleh hubungan antara populasi sel tumor yang tidak terinfeksi ( ), populasi sel terinfeksi virus ( ), dan populasi partikel virus ( ) berdasarkan analisis kestabialn titik tetapnya. Pengaruh yang signifikan pada model virotherapy ini adalah laju kematian sel yang terinfeksi ( ) dan laju produksi virus dari sel yang terinfeksi ( ).
4.1.1 Dinamika populasi untuk >
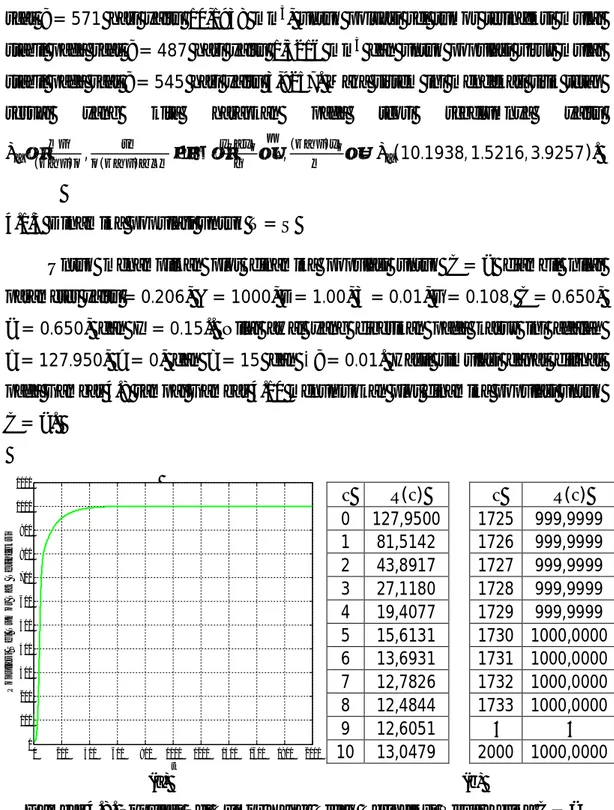
Untuk menampilkan plot dinamika populasi untuk > diambil nilai parameter yaitu = 0.206, = 1000, = 1.00, = 0.01, = 0.108, = 0.650, = 0.263, dan = 0.15. Nilai awal yang diberikan pada kasus ini adalah
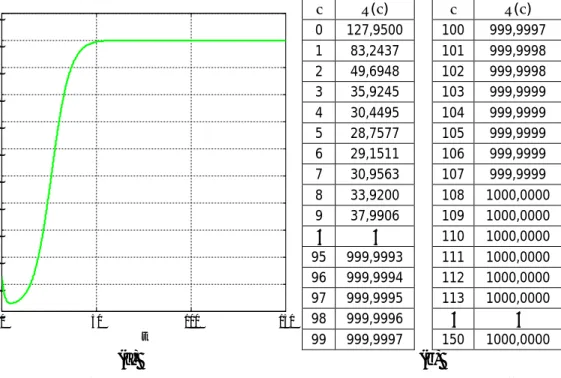
= 127.950, = 0, dan = 15 dan ∆ = 0.01. Hasil simulasi dapat dilihat pada Gambar 4.1 sampai Gambar 4.3 yang menunjukkan plot dinamika populasi untuk > .
40 ( ) ( ) 0 127,9500 100 999,9997 1 83,2437 101 999,9998 2 49,6948 102 999,9998 3 35,9245 103 999,9999 4 30,4495 104 999,9999 5 28,7577 105 999,9999 6 29,1511 106 999,9999 7 30,9563 107 999,9999 8 33,9200 108 1000,0000 9 37,9906 109 1000,0000 ⋮ ⋮ 110 1000,0000 95 999,9993 111 1000,0000 96 999,9994 112 1000,0000 97 999,9995 113 1000,0000 98 999,9996 ⋮ ⋮ 99 999,9997 150 1000,0000 (a) (b)
Gambar 4.1 Populasi Sel Tumor Yang Tidak Terinfeksi Ketika > (a). Dalam Bentuk grafik (b).Dalam Bentuk Data
Gambar 4.1 menunjukkan saat laju kematian efektif sel yang terinfeksi yang dihasilkan lebih besar dari pada laju produksi virus dari sel tumor yang terinfeksi dan populasi awal sel tumor yang tidak terinfeksi ( ) yang diberikan 127,950 mm3. Maka populasi sel tumor yang tidak terinfeksi pada = 6 hari mengalami penurunan yaitu mencapai 29,1511 mm3 ini disebabkan karena pengaruh dari populasi partikel virus yang terus menyerang sel tumor yang tidak terinfeksi namun dengan seiring berjalannya waktu populasi partikel virus mengalami penurunan sehingga mengakibatkan populasi sel tumor yang tidak terinfeksi mengalami peningkatan secara terus menerus hingga mencapai titik stabil dan mencapai ukuran maksimal tumor dimulai pada saat = 108 hari yaitu 1000 mm3. Adapun data selengkapnya dapat dilihat di lampiran B-1.
0 50 100 150 0 100 200 300 400 500 600 700 800 900 1000 1100 P o p u la s i S e l T u m o r T a k T e ri n fe k s i t
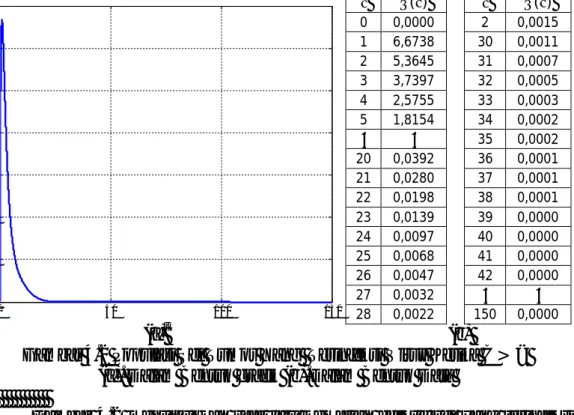
41 0 50 100 150 0 1 2 3 4 5 6 7 P o p u la s i S e l T u m o r T e ri n fe k s i V ir u s t ( ) ( ) 0 0,0000 2 0,0015 1 6,6738 30 0,0011 2 5,3645 31 0,0007 3 3,7397 32 0,0005 4 2,5755 33 0,0003 5 1,8154 34 0,0002 ⋮ ⋮ 35 0,0002 20 0,0392 36 0,0001 21 0,0280 37 0,0001 22 0,0198 38 0,0001 23 0,0139 39 0,0000 24 0,0097 40 0,0000 25 0,0068 41 0,00 00 26 0,0047 42 0,0000 27 0,0032 ⋮ ⋮ 28 0,0022 150 0,0000 (a) (b)
Gambar 4.2 Populasi Sel Tumor Yang Terinfeksi Virus Ketika > (a). Dalam Bentuk grafik (b).Dalam Bentuk Data
Gambar 4.2 menunjukkan saat laju kematian efektif sel yang terinfeksi yang dihasilkan lebih besar dari pada laju produksi virus dari sel tumor yang terinfeksi dan populasi awal sel tumor yang terinfeksi virus ( ) yang diberikan adalah 0 maka pada kasus ini populasi sel tumor yang terinfeksi virus mengalami penigkatan pada = 1 hari mencapai 6,6738 mm3
ini disebabkan oleh populasi sel tumor yang tidak terinfeksi mengalami penurunan pada awal terapi namun karena penurunan jumlah virus yang terus menerus sampai nol maka populasi sel tumor yang terinfeksi virus pun ikut menurun sampai titik stabil di nol dimulai pada saat = 39 hari ini disebabkan karena populasi sel tumor yang tidak terinfeksi mengalami peningkatan mencapai ukuran maksimal. Adapun data selengkapnya dapat dilihat di lampiran B-1.
42 ( ) ( ) 0 15,0000 21 0,0034 1 5,1484 2 0,0020 2 3,4578 23 0,0012 3 2,8602 24 0,0007 4 2,4195 25 0,0004 5 2,0073 26 0,0003 6 1,6219 27 0,0002 ⋮ ⋮ 28 0,0001 15 0,0728 29 0,0001 16 0,0451 30 0,0000 17 0,0274 31 0,0000 18 0,0164 32 0,0000 19 0,0098 ⋮ ⋮ 20 0,0058 150 0, 0000 (a) (b)
Gambar 4.3. Populasi Partikel Virus Ketika > (a). Dalam Bentuk grafik (b).Dalam Bentuk Data
Gambar 4.3 menunjukkan saat laju kematian efektif sel yang terinfeksi yang dihasilkan lebih besar dari pada laju produksi virus dari sel tumor yang terinfeksi dan populasi partikel virus ( ) yang diberikan 15 maka pada kasus ini populasi partikel virus terus menyerang populasi sel tumor tidak terinfeksi sehingga populasi sel tumor tidak terinfeksi menurun namun karena populasi partikel virus ini terus menginfeksi sel tumor sehingga mengakibatkan populasi partikel virus terus menerus menurun dimulai pada saat = 30 hari mencapai titik stabil yaitu di nol. Adapun data selengkapnya dapat dilihat di lampiran B-1.
Maka dari Gambar 4.1 sampai Gambar 4.3 ini mendekati pada titik tetap yang sesuai diharapkan pada teori sebelumnya yaitu ( , , ) = ( , 0,0) =
(1000, 0, 0) yaitu terkait dengan kegagalan terapi.
4.1.2 Dinamika populasi untuk <
Untuk menampilkan plot dinamika populasi untuk < diambil nilai parameter yaitu = 0.206, = 1000, = 1.00, = 0.01, = 0.108, = 0.263, = 0.650, dan = 0.15. Nilai awal yang diberikan pada kasus ini adalah = 127.950, = 0, dan = 15 dan ∆ = 0.01. Hasil simulasi dapat dilihat pada Gambar 4.4 sampai Gambar 4.7 menunjukkan plot dinamika populasi untuk < . 0 50 100 150 0 5 10 15 P o p u la s i P a rt ik e l V ir u s t
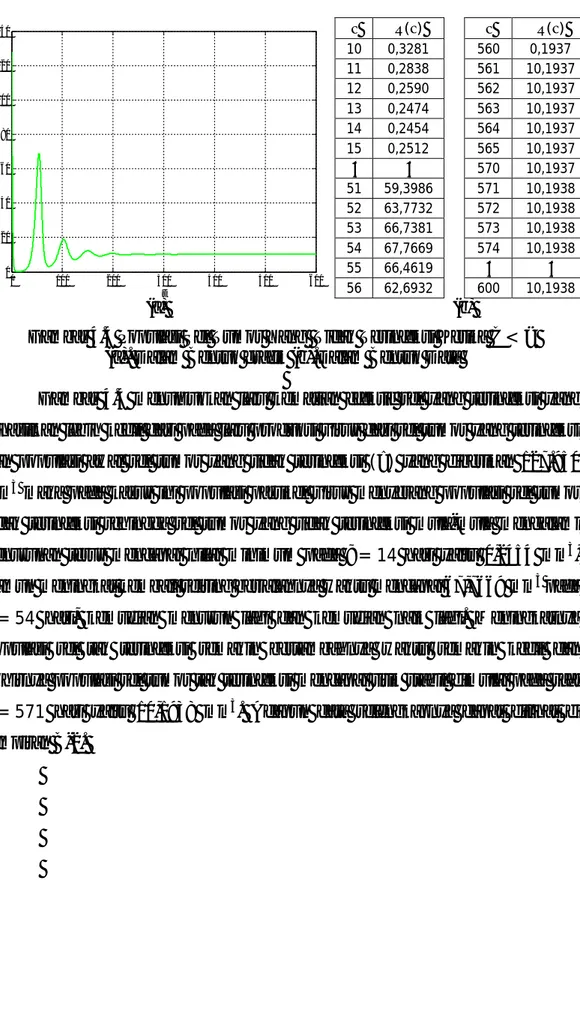
43 ( ) ( ) 10 0,3281 560 0,1937 11 0,2838 561 10,1937 12 0,2590 562 10,1937 13 0,2474 563 10,1937 14 0,2454 564 10,1937 15 0,2512 565 10,1937 ⋮ ⋮ 570 10,1937 51 59,3986 571 10,1938 52 63,7732 572 10,1938 53 66,7381 573 10,1938 54 67,7669 574 10,1938 55 66,4619 ⋮ ⋮ 56 62,6932 600 10,1938 (a) (b)
Gambar 4.4 Populasi Sel Tumor Yang Tidak Terinfeksi Ketika < (a). Dalam Bentuk grafik (b).Dalam Bentuk Data
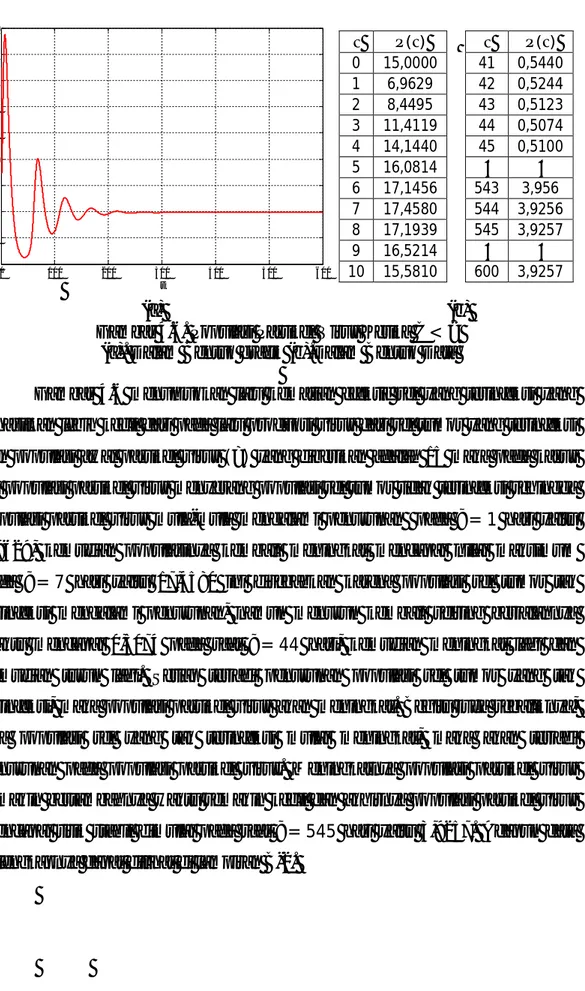
Gambar 4.4 menunjukkan laju kematian efektif sel yang terinfeksi yang dihasilkan lebih kecil dari pada laju produksi virus dari sel tumor yang terinfeksi dan populasi awal sel tumor yang tidak terinfeksi ( ) yang diberikan 127.950 mm3 maka pada kasus ini populasi partikel virus menyerang populasi sel tumor tidak terinfeksi sehingga sel tumor yang tidak terinfeksi mula-mula mengalami penurunan terus mencapai nilai minimum pada = 14 hari yaitu 0,2454 mm3, namun meningkat kembali seiring berjalannya waktu mencapai 67,7669 mm3 pada = 54 hari, kemudian menurun lagi dan kemudian naik lagi. Meningkatnya populasi sel tak terinfeksi semakin bertambahnya waktu semakin kecil dan akhirnya populasi sel tumor tak terinfeksi mencapai titik stabil dimulai pada saat
= 571 hari yaitu 10,1938 mm3
. Adapun data selengkapnya dapat dilihat di lampiran B-2. 0 100 200 300 400 500 600 0 20 40 60 80 100 120 140 t P o p u la s i S e l T u m o r T a k T e ri n fe k s i
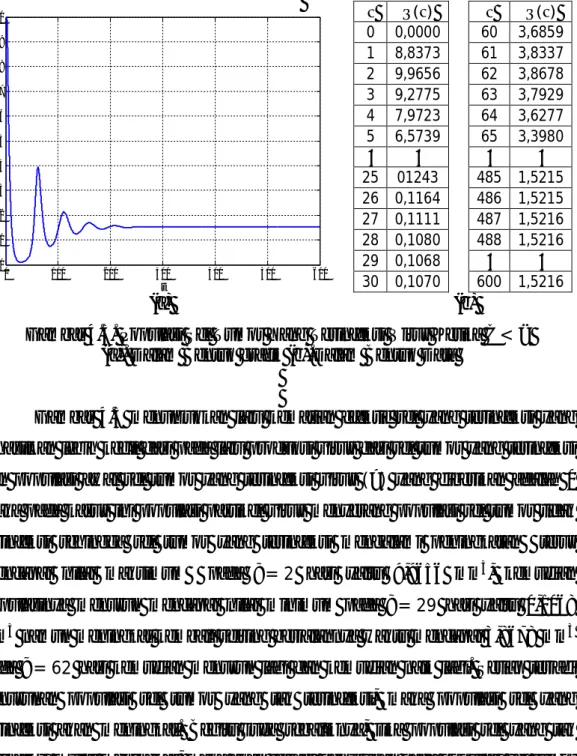
44 0 100 200 300 400 500 600 0 1 2 3 4 5 6 7 8 9 10 t P o p u la s i S e l T u m o r T e ri n fe k s i V ir u s ( ) ( ) 0 0,0000 60 3,6859 1 8,8373 61 3,8337 2 9,9656 62 3,8678 3 9,2775 63 3,7929 4 7,9723 64 3,6277 5 6,5739 65 3,3980 ⋮ ⋮ ⋮ ⋮ 25 01243 485 1,5215 26 0,1164 486 1,5215 27 0,1111 487 1,5216 28 0,1080 488 1,5216 29 0,1068 ⋮ ⋮ 30 0,1070 600 1,5216 (a) (b)
Gambar 4.5. Populasi Sel Tumor Yang Terinfeksi Virus Ketika < (a). Dalam Bentuk grafik (b).Dalam Bentuk Data
Gambar 4.5 menunjukkan laju kematian efektif sel yang terinfeksi yang dihasilkan lebih kecil dari pada laju produksi virus dari sel tumor yang terinfeksi dan populasi awal sel tumor yang terinfeksi virus ( ) yang diberikan adalah 0 maka pada kasus ini populasi partikel virus menyerang populasi sel tumor tidak terinfeksi sehingga sel tumor yang terinfeksi mengalami peningkatan terus mencapai nilai maksimum pada = 2 hari yaitu 9,9656 mm3, kemudian populasinya menurun mencapai nilai minimum pada = 29 hari yaitu 0,1068 mm3 namun meningkat kembali seiring berjalannya waktu mencapai 3,8678 mm3 pada = 62 hari kemudian menurun lagi dan kemudian naik lagi. Setiap terjadi penurunan populasi sel tumor yang tak terinfeksi, maka populasi sel yang terinfeksi akan meningkat. Begitu juga sebaliknya, jika populasi sel yang tak terinfeksi mulai meningkat, maka akan terjadi penurunan pada populasi sel tumor yang terinfeksi. Meningkatnya populasi sel terinfeksi semakin bertambahnya waktu semakin kecil dan akhirnya populasi sel tumor terinfeksi mencapai titik stabil pada saat = 487 hari yaitu 1,5216 mm3
. Adapun data selengkapnya dapat dilihat di lampiran B-2.

![Gambar 3.1. Skema Diagram Model Virotherapy [2]](https://thumb-ap.123doks.com/thumbv2/123dok/4421583.3215872/32.892.168.788.127.1124/gambar-skema-diagram-model-virotherapy.webp)
![Gambar 3.2. Skema Model Radiovirotherapy [11]](https://thumb-ap.123doks.com/thumbv2/123dok/4421583.3215872/35.892.161.734.104.1022/gambar-skema-model-radiovirotherapy.webp)