LANDASAN TEORI
2.1 Permasalahan Transportasi
2.1.1 Sejarah Permasalahan Transportasi
Masalah transportasi ini sebenarnya telah lama dipelajari dan dikembangkan sebelum lahir model program linear. Pada tahun 1939, L.V Kantorovitch mempelajari beberapa permasalahan yang berhubungan dengan model transportasi. Kemudian, pada tahun 1941, F.L. Hitchcock merumuskan model matematika dari persoalan transportasi yang kini dianggap sebagai model matematika dari persoalan transportasi yang kini dianggap sebagai model baku, sehingga sering disebut juga sebagai model Hitchcock. Ada lagi seseorang yang bernama T.C. Koopmans pada tahun 1947 banyak mempelajari hal-hal yang berhubungan dengan program transportasi (PT) atau model transportasi (MT).
2.1.2 Persoalan Transportasi
Situasi dunia yang semakin dinamis menyebabkan waktu pengambilan keputusan menjadi sangat penting. Di saat yang sama, parameter pengambilan keputusan tidak tersedia atau tersedia tetapi tidak lengkap dan jelas. Ketidakjelasan parameter pengambilan keputusan yang diambil tetap optimal. Optimasi adalah salah satu alat bantu seorang manajer dalam pengambilan keputusan.
Persoalan transportasi membicarakan masalah pendistribusian suatu komoditas atau produk dari sejumlah sumber (supply) ke sejumlah tujuan (demand, destination) dengan tujuan meminimumkan ongkos pengangkutan yang terjadi.
Ciri-ciri khusus persoalan transportasi adalah :
1. Terdapat sejumlah sumber dan sejumlah tujuan tertentu.
2. Kuantitas komoditas atau barang yang didistribusikan dari setiap sumber dan yang diminta oleh setiap tujuan, besarnya tertentu.
3. Komoditas yang dikirim atau diangkut dari suatu sumber ke suatu tujuan, besarnya sesuai dengan permintaan atau kapasitas sumber.
4. Ongkos pengangkutan komoditas dari suatu sumber ke suatu tujuan, besarnya tertentu.
Data yang dibutuhkan dalam metode transportasi adalah:
1. Level supply pada setiap daerah sumber dan level permintaan pada setiap daerah tujuan untuk kasus pendistribusian barang; jumlah produksi dan jumlah permintaan.
2. Biaya transportasi per unit komoditas dari setiap daerah sumber menuju berbagai daerah tujuan pada kasus pendistribusian; biaya produksi.
Model transportasi merupakan salah satu bentuk khusus atau variasi dari program linier yang di kembangkan khusus untuk memecahkan masalah-masalah yang berhubungan dengan transportasi (pengangkutan) dan disribusi produk atau sumber daya dari berbagai sumber (pusat pengadaan, atau titik supply) ke berbagai tujuan (titik permintaan atau pusat pemakaian) yang lebih efisien dalam hal perhitungan.
Dilihat dari model matematika persolan program linier terdapat tipe/ ciri/ karakteristik khusus pada permasalahan transportasi, yaitu:
1). Semua fungsi kendala bertanda „=‟ 2). Semua nilai aij bernilai 1 atau 0.
2.1.3 Keseimbangan transportasi
Suatu model transportasi dikatakan seimbang apabila total supply (sumber) sama dengan total demand (tujuan). Dengan kata lain:
n j j m i i b a 1 1Dalam persoalan transportasi yang sebenarnya, batasan ini tidak selalu terpenuhi atau dengan kata lain jumlah supply yang tersedia mungkin lebih besar atau lebih kecil daripada jumlah demand. Jika hal ini yang terjadi, maka model persoalan disebut sebagai model yang tidak seimbang. Batasan di atas dikemukakan hanya karena itu menjadi dasar dalam pengembangan teknik transportasi. Namun, setiap persoalan transportasi dapat dibuat seimbang dengan memasukkan kolom dummy atau baris dummy.
Jika demand melebihi supply maka dibuat suatu sumber dummy yang akan men-supply kekurangan tersebut yaitu sebanyak
n j j b 1 -
m i i a 1Sebaliknya, jika jumlah supply melebihi jumlah demand, maka dibuat suatu tujuan dummy untuk menyerap kelebihan tersebut yaitu sebanyak
n j j m i i b a 1 1
Ongkos transportasi per unit (cij) dari sumber dummy ke seluruh tujuan adalah nol. Hal ini dapat dipahami karena pada kenyataan dari sumber dummy tidak terjadi pengiriman.
2.1.4 Model Umum Permasalahan Transportasi
2.1.4.1 Asumsi Dasar
Model transportasi pada dasarnya merupakan sebuah program linier yang dapat dipecahkan oleh metode simpleks yang biasa. Tetapi strukturnya yang khusus memungkinkan pengembangan sebuah prosedur pemecahan, yang disebut teknik transportasi yang lebih efisien dalam hal perhitungan.
Asumsi dasar dari model ini adalah bahwa biaya transportasi di sebuah rute tertentu adalah proposional secara langsung dengan jumlah unit yang dikirimkan. Defenisi unit transportasi akan bervariasi bergantung pada jenis barang yang di kirimkan.
Model umum suatu persoalan transportasi dilandasi pada asumsi-asumsi berikut:
1. Bahwa suatu produk yang ingin diangkat tersedia dalam jumlah yang tetap dan diketahui.
2. Bahwa produk tersebut akan dikirim melalui jaringan transpotasi yang ada dengan memakai cara pengakutan tertentu dari pusat-pusat permintaan.
3. Bahwa jumlah permintaan di pusat permintaan pun diketahui dalam jumlah tertentu dan tetap.
4. Bahwa ongkos angkutan per-unit produk yang diangkut pun diketahui, sehingga tujuan kita untuk meminimumkan biaya total angkutan dapat tercapai.
Karena hanya ada satu jenis komoditas, pada dasarnya setiap daerah tujuan dapat menerima komoditas dari sembarang daerah sumber.
2.1.4.2 Model transportasi
Sebuah model transportasi dari sebuah jaringan dengan m sumber dan n tujuan. Sebuah sumber atau tujuan diwakili dengan sebuah node. Busur yang menghubungkan sebuah sumber dan sebuah tujuan mewakili rute pengiriman barang tersebut. Jumlah penawaran di sumber i adalah ai dan permintaan di tujuan j adalah bj. Biaya unit transportasi antara sumber i dan tujuan j adalah cij. Anggaplah Xij mewakili jumlah barang yang dikirimkan dari sumber i ke tujuan j; maka model program linier yang mewakili masalah transprotasi ini secara umum adalah sebagai berikut:
Model transportasi berusaha menentukan sebuah rencana transportasi sebuah barang dari sejumlah sumber ke sejumlah tujuan.
i =1 j =1 j = 2 i =2 j = 3 i =m j = n Data dalam model mencakup:
1. Tingkat penawaran di setiap sumber dan jumlah permintaan di setiap tujuan. 2. Biaya transportasi per unit barang dari setiap sumber ke setiap tujuan.
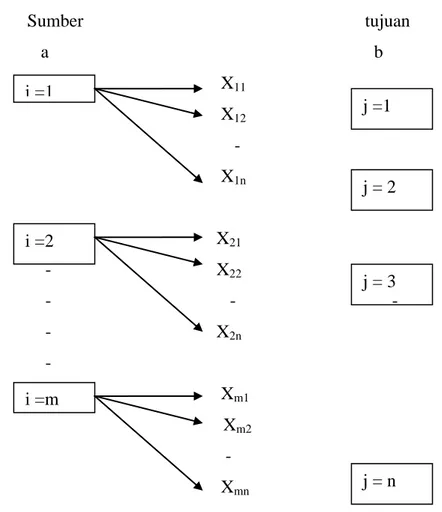
Secara diagramatik, model transportasi dapat digambarkan sebagai berikut: Misalkan ada m buah sumber dan n buah tujuan.
Sumber tujuan a b X11 X12 - X1n X21 - X22 - - - - X2n - Xm1 Xm2 - Xmn
Gambar 2.1 Diagram Model Transportasi
a. Masing-masing sumber mempunyai kapasitas ai , 𝑖 = 1, 2, 3, . . . , 𝑚.
b. Masing-masing tujuan membutuhkan komoditas sebanyak bj, 𝑗 = 1, 2, 3, . . . , 𝑛. c. Jumlah satuan (unit) yang dikirimkan dari sumber i ke tujuan j adalah sebanyak
xij.
Dengan demikian, maka formulasi program liniernya adalah sebagai berikut: Minimum; Z =
m i n j ij ijx c 1 1 Batasan:
Xij ai;i1,2,...,m
Xij bj; j1,2,...nXij 0 untuk seluruh i dan j.
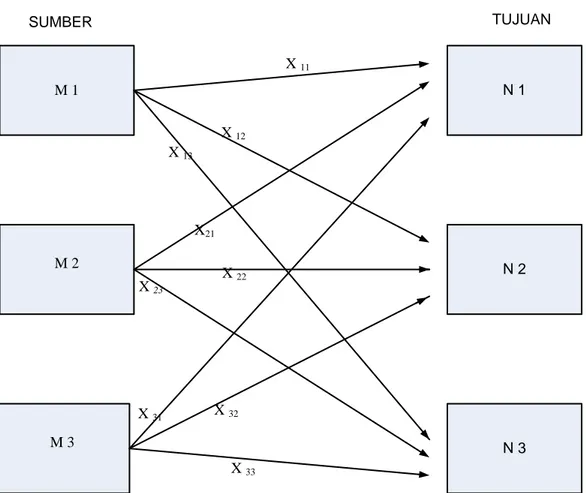
Gambar di bawah ini memperlihatkan sebuah model dari sebuah jaringan dengan 3 sumber dan 3 tujuan. Sebuah sumber atau tujuan diwakili dengan sebuah node. Busur yang menghubungkan sebuah sumber dan sebuah tujuan mewakili rute pengiriman barang tersebut. Jumlah penawaran di sumber i adalah ai dan permintaan di tujuan j adalah bj. Biaya unit transportasi antara sumber i dan tujuan j adalah cij.
Sebagai ilustrasi, jika ada 3 buah sumber dan 3 tujuan (m = 3, n = 3)
M 1 M 2 M 3 N 1 N 2 N 3 SUMBER TUJUAN X 11 X 12 X 13 X 23 X 22 X21 X 33 X 32 X 31
formulasi Minimumkan: Z = c11x11 + c11x11 + c12 x12 + c13x13 + c21x21 + c22x22 + c23x23 + c31x31 + c32x32 + c33x33 Berdasarkan pembatas: x11 + x12 + x13 = a1 x21 + x22 + x23 = a2 x31 + x32 + x33 = a3 x11 + x21 + x31 = b1 x12 + x22 + x32 = b2 x13 + x23 + x33 = b3
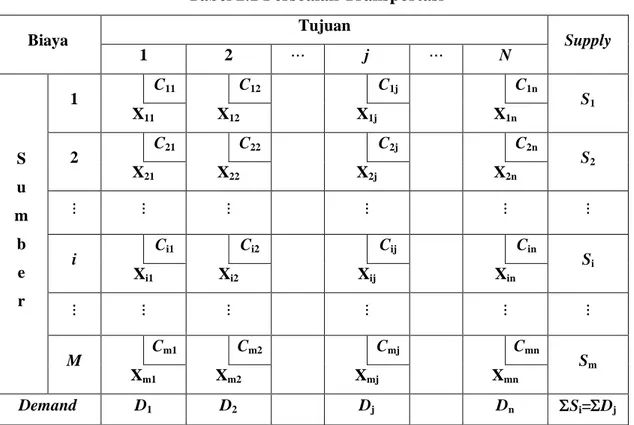
Tabel 2.1 Persoalan Transportasi
Biaya Tujuan Supply
1 2 ⋯ j ⋯ N S u m b e r 1 C11 C12 C1j C1n S1 X11 X12 X1j X1n 2 C21 C22 C2j C2n S2 X21 X22 X2j X2n ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ i Ci1 Ci2 Cij Cin Si Xi1 Xi2 Xij Xin ⋮ ⋮ ⋮ ⋮ ⋮ ⋮ M Cm1 Cm2 Cmj Cmn Sm Xm1 Xm2 Xmj Xmn Demand D1 D2 Dj Dn Si=Dj 2.1.5 Metode Pemecahan
Untuk menyelesaikan persoalan transportasi, harus dilakukan dengan langkah-langkah sebagai berikut:
1. Menentukan Solusi Fisibel Basis Awal.
2. Manentukan entering variabel dari variabel-variabel nonbasis. Bila semua variabel sudah memenuhi kondisi optimal, STOP. Bila beum lanjutkan ke langkah 3.
3. Tentukan leaving variabel diantara variabel-variabel basis yang ada, kemudian hitung solusi yang ada. Kembali ke langkah 2.
Untuk menentukan solusi basis awal terdapat 3 metode yang dapat digunakan adalah:
1. Metode pojok kiri atas pojok kanan bawah/ metode pojok barat laut/ nort west corner.
Mulai dari pojok kiri atas, alokasi sebesar x11 = min (s1, d1). Artinya bila d1< s1 maka x11= d1; jika d1> s1 maka x11 = s1, selanjutnya yang mendapat giliran untuk dialokasikan adalah x12 sebesar min (s1 – d1, d2); kalau x11 = s1 (atau d1 > s1), maka selanjutnya yang mendapat giliran untuk dialokasikan adalah x21 sebesar (d1 – s1, s2) dan seterusnya.
2. Metode ongkos (baris/ kolom) terkecil (least cost).
Prinsip cara ini adalah pemberian prioritas pengelokasian pada tempat yang mempunyai satuan ongkos terkecil.
a. Pendistribusian dimulai dari biaya terkecil dan, apabila terdapat biaya terkecil lebih dari satu, maka dipilih salah satu.
b. Setiap pendistribusian dipilih nilai sebanyak mungkin tanpa mengabaikan jumlah sumber/tujuan.
3. Metode pendekatan vogel (vogel’s approximation method’s/ VAM).
Cara ini merupakan cara yang terbaik dibandingkan dengan cara di atas. Langkah-langkah penerjaan metode diatas adalah:
a. Menghitung opportunity cost yang didasarkan pada dua biaya terkecil pada setiap baris dan kolom dan mengurangkan keduanya, hasil perhitungannya disebut dengan penalty cost.
c. Memilih biaya terkecil dari nilai penalty cost terbesar dan mendistribusikan sejumlah nilai. Baris/ kolom penalti yang sudah terpilih diabaikan untuk langkah selanjutnya.
d. Menyesuaikan jumlah permintaan dan penawaran untuk menunjukkan alokasi yang sudah dilakukan. Menghilangkan semua baris dan kolom dimana penawaran dan permintaan telah dihabiskan.
e. Apabila jumlah penawaran dan permintaan belum sesuai, maka ulangi langkah pertama sampai terisi semua.
Untuk mencari solusi optimal terdapat 2 metode yang dapat digunakan yaitu: 1. Metode batu loncatan (Stepping Stone).
Untuk menentukan entering dan leaving variable ini, terlebih dahulu harus dibuat suatu loop tertutup bagi setiap variabel nonbasis loop tersebut berawal dan berakhir pada variabel nonbasis tadi. Dimana tiap sudut loop haruslah merupakan titik-titik yang ditempati oleh variabel-variabel basis dalam tabel transportasi.
Langkah-langkah penyelesaiannya adalah sebagai berikut :
1. Apakah jumlah variabel basis sama dengan n+m-1 ? Jika kurang dari m+n-1 maka akan terjadi kemerosotan (degeneracy). STOP. Tetapi jika sama maka dapat dihitung Zij –Cij untuk sel-sel yang bukan basis, dengan cara sebagai berikut :
a. Dibuat loop tertutup bagi setiap variabel non basis dimana loop tersebut berawal dan berakhir pada variabel non basis, dan setiap titik sudut loop tersebut harus merupakan titik-titik yang ditempati oleh variabel-variabel basis dalam tabel transportasi.
b. Dihitung Zij-Cij = jumlahan para Cij pada loop dengan koefisien (+1) dan (-1)bergantian dengan koefisien variabel non basis (-1).
2. Menentukan variabel yang masuk menjadi basis (entering variable) dengan cara memilih nilai Zij-Cij yang terbesar atau Max{Zij-Cij}. (Xij masuk menjadi basis bila dan hanya bila Zij-Cij = Max{Zij-Cij}).
3. Menentukan variabel yang keluar dari basis, caranya: a. Dibuat loop yang memuat Xst.
b. Diadakan pengamatan para Cij dalam loop yang mempunyai koefisien (+1).
c. Variabel Xab yang keluar basis bila dan hanya bila Xab minimum dari langkah 3.
4. Menentukan harga variabel basis (yang berada di dalam loop yang baru/penyesuaian untuk variabel basis yang baru). Xst = Xab = Xpq sedangkan untuk variabel-variabel basis yang lain yang juga berada dalam loop. Xab(baru) = Xab + Xpq (untuk a+b = ganjil) Xab(baru) = Xab – Xpq (untuk a+b = genap).
5. Untuk variabel-variabel basis yang lain di luar loop harganya tetap. Hitung kembali nilai Zij-Cij untuk variable non basis seperti pada langkah 1.
6. Diperoleh tabel optimal jika semua Zij-Cij >0.
7. Jika masih ada nilai Zij-Cij > 0, maka dapat ditentukan kembali Entering Variable dan Leaving Variable seperti pada langkah yang ke-2.
2. Metode faktor pengali (multiplier)/ Metode MODI (Modified Distribution). Metode MODI merupakan variasi dari model Stepping Stone yang didasarkan pada rumusan dual. Perbedaannya dengan metode Stepping Stone adalah pada metode ini tidak harus menentukan semua jalur tertutup variabel non basis, kecuali pada saat akan melakukan perpindahan pengisian tabel. Dengan demikian MODI merupakan cara yang efisien untuk menghitung variabel non basis. Dalam metode MODI terdapat persamaan sebagai berikut :
Di mana : mi = Nilai setiap sel baris nj = Nilai setiap kolom
Cij = Biaya transportasi per unit
Adapun langkah-langkah dalam metode MODI adalah :
1) Mentukan nilai mi untuk setiap baris dan nilai-nilai nj untuk setiap kolom dengan menggunakan hubungan Cij = mi + nj untuk semua variabel basis dan menentukan nilai mi = 0.
2) Menghitung perubahan biaya Cij untuk setiap variabel non basis dengan menggunakan rumus Cij - mi - nj.
3) Apabila hasil perhitungan terdapat nilai Cij negatif, maka solusi belum optimal. Oleh karena itu, dipilih Xij dengan nilai Cij negatif terbesar sebagai entering variabel.
4) Mengalokasikan sejumlah nilai ke entering variabel Xij sesuai dengan proses Stepping Stone dan mengulangi langkah pertama.
2.2 Matriks
Matriks adalah sekumpulan himpunan objek (bilangan riil atau kompleks, variabel– variabel) yang disusun secara persegi panjang (yang terdiri dari baris dan kolom) yang biasanya dibatasi dengan kurung siku atau biasa. Bilangan-bilangan dalam susunan tersebut dinamakan entri dalam matriks atau disebut juga elemen atau unsur. Jika sebuah matriks memiliki m baris dan n kolom maka matriks tersebut berukuran (ordo) m x n. Matriks dikatakan bujur sangkar (square matrix) jika m = n. Dan skalar– skalarnya berada di baris ke-i dan kolom ke-j yang disebut (ij) matriks entri.
mn m m n n a a a a a a a a a A 2 1 2 22 21 1 12 11
2.2.1 Invers Matriks
Matrik A memiliki invers jika matrik A non-singular (determinan 0 dan rank r = n) , A-1 matrik adalah invers dari matrik A. Jika matrik A tidak memiliki invers, maka matrik A disebut singular. Bila matrik A dikalikan dengan matrik A-1 maka akan menghasilkan matrik identitas I, yaitu suatu matrik yang elemen-elemen diagonalnya bernilai 1. adj A A ) det( 1 1 A
Biasanya untuk matriks berukuran besar yang sering digunakan adalah IA=A-1I
2.3 Algoritma Arsham kahn
Sebelum menguraikan langkah-langkah penyelesaian dengan algoritma ini, terlebih dahulu diperkenalkan notasi-notasi yang akan dipergunakan.
PT : persoalan transportasi PL : program linear
SS : stepping-stone
GJP : Gauss-Jourdan Pivotting VB : variabel basis
HVB : himpunan variabel basis FE : fisibelitas
BP : baris pivot (baris yang ditentukan untuk variabel masuk) KP : kolom pivot (kolom yang berhubungan dengan variabel masuk) EP : elemen pivot
BT : baris terbuka (sebuah baris yang belum diisi variabel basis ; diberi label [?]
[?] : label untuk baris yang belum diisi variabel basis (baris terbuka) NSK : nilai sebelah kanan
Algoritma ini dimulai dengan persiapan dan diikuti oleh dua tahapan. Tahap pertama merupakan iterasi VB untuk membangun HVB yang mungkin fisibel atau tidak. Tahap kedua merupakan iterasi FE untuk membangun solusi yang fisibel dan optimum. Kedua tahapan ini menggunakan transformasi GJP. Akan tetapi berbeda dalam metode memilih EP. Iterasi VB menggunakan kriteria simpleks, yang dimodifikasi hanya untuk memilih baris terbuka yang belum diisi VB. Strategi ini membawa kepada tercapainya titik optimal, dan terkadang menyebabkan ketidakfisibelan. Iterasi FE, jika dibutuhkan, membawa kembali solusi kepada fisibelitas dengan menggunakan kriteria dual simpleks untuk memilih EP.
Jelas, dalam suatu persoalan transportasi yang setimbang, satu dari (m+n) konstrain adalah berlebih. Dari pada mengeliminasi konstrain secara sebarang, maka pada algoritma ini dieliminasi konstrain yang akan lebih banyak memberikan pengurangan jumlah iterasi pada tahap pertama.
Adapun dalam tahapan-tahapan ini masing-masing dapat dikelompokkan berdasarkan operasi yang menambah keefisienan dalam pengerjaannya. Langkah 0.1 dan 0.2 mengeliminasi konstrain yang akan lebih banyak mengurangi jumlah iterasi. Kelompok kedua terdiri dari tiga operasi: 1.2c, 2.2a dan 2.2d, yang bersama-sama secara progresif mengurangi ukuran tabel.
Iterasi 0 (Persiapan)
0.0 – Formulasi matriks-biaya PT
0.1 – Reduksi baris-kolom (atau reduksi kolom-baris) Dari setiap baris kurangkan terhadap biaya terkecil.
Akumulasi pengaruh dari setiap reduksi baris menjadi biaya awal. Demikian, dari setiap kolom kurangkan terhadap biaya terkecil. Akumulasi pengaruh dari setiap reduksi kolom menjadi biaya awal. 0.2 – Eliminasi konstrain berlebih
Periksa baris atau kolom yang memiliki nilai nol terbanyak Eliminasi konstrain tersebut.
Gunakan sebuah baris untuk setiap konstrain dan sebuah kolom untuk setiap variabel.
Jangan menambahkan variabel artificial 0.4– Tentukan HVB
Untuk setiap kolom yang merupakan vektor satuan, beri label baris dengan nama variabel pada kolom tersebut.
Beri label baris yang lain dengan tanda tanya (?). 0.5– Hapus kolom VB.
Iterasi 1 (Tahap VB)
1.0 – Uji terminasi iterasi HVB
Jika terdapat label (?) atau terdapat baris terbuka, maka lanjutkan iterasi VB. Jika tidak HVB telah lengkap; mulai tahap FE (langkah 2.0).
1.1 – Pilih VB dari EP
KP : Pilih nilai Cij terkecil dan tetapkan sebagai bakal kolom. BP : Pilih baris terbuka sebagai bakal baris.
EP : Pilih bakal baris dan kolom dengan K/B non-negatif terkecil.
Jika tidak ada K/B non-negatif, pilih K/B yang bernilai absolut terkecil. Jika elemen pivotnya bernilai nol, maka pilih Cij terbaik selanjutnya. 1.2 – Penambahan HVB
(a) Lakukan GJP.
(b) Ubah label baris (?) dengan nama variabel. (c) Pindahkan KP dari tabel.
Lanjutkan iterasi HVB (kembali ke 1.0)
Iterasi 2 (Tahap FE)
2.0 – Uji terminasi iterasi FE
Jika NSK non-negatif, maka tabel sudah optimal. Interpretasikan hasilnya. Jika terdapat NSK negatif maka lanjutkan iterasi FE (langkah 2.1).
2.1 – Pilih FE dari EP
BP : Baris dengan NSK paling negatif .
KP : Kolom dengan sebuah elemen negatif pada BP. Pilih kolom dengan Cij terkecil.
2.2 – Transformasi FE
(a) Simpan KP di luar tabel. (b) Lakukan PGJ biasa.
(c) Tukarkan label KP dan BP.
(d) Ganti KP baru dengan KP lama yang disimpan dalam (a). Lanjutkan iterasi FE (kembali ke 2.0)
Bagian Akhir Algoritma, tahap pertama dari algoritma ini dapat digolongkan sebagai pencarian himpunan variabel basis yang menuju kepada titik optimal. Tahap kedua, jika diperlukan, membawa kembali kepada fisibelitas.
2.4 Analisis Sensitivitas
Analisa perubahan parameter dan pengaruhnya terhadap solusi Program Linier disebut Post Optimality Analisis. Istilah post optimality menunjukkan bahwa analisa ini terjadi setelah diperoleh solusi optimal, dengan mengasumsikan seperangkat nilai parameter yang digunakan dalam model, atau analisis postoptimal (disebut juga analisis pasca optimal atau analisis setelah optimal, atau analisis kepekaan dalam suasana ketidaktahuan) merupakan suatu usaha untuk mempelajari nilai-nilai dari peubah-peubah pengambilan keputusan dalam suatu model matematika jika satu atau beberapa atau semua parameter model tersebut berubah atau menjelaskan pengaruh perubahan data terhadap penyelesaian optimal yang sudah ada.
Dapat diketahui bahwa dunia nyata yang diabstraksikan dan disimplifikasikan ke dalam model program linier, tidak sederhana seperti rumusan Program Linier sederhana tersebut. Oleh karena itu dalam dunia pengelolaan dan kehidupan dunia nyata, selalu dihadapkan pada pertanyaan-pertanyaan keragu-raguaan seperti “apa yang akan terjadi, jika” ini dan itu berubah?
Persoalan peluang dan ketidakpastiaan pertanyaan-pertanyaan tersebut harus dapat dijawab dalam rangka meyakinkan pendirian terhadap sesuatu yang akan diputuskan kelak. Dengan demikian hasil yang diharapkan tersebut adalah hasil yang
memang ”paling mungkin“ dan ”paling mendekati”, atau “perkiraan yang paling tepat”. Uji kepekaan hasil dan pasca optimal yang dapat memberikan jawaban terhadap persoalan-persoalan tersebut diatas.
Perubahan atau variasi dalam suatu persoalan program linier yang biasanya dipelajari melalui post optimality analysis dapat dipisahkan ke dalam tiga kelompok umum, yaitu :
1. Analisa yang berkaitan dengan perubahan diskrit parameter untuk melihat berapa besar perubahan dapat ditolerir sebelum solusi optimal mulai kehilangan optimalitasnya, ini dinamakan Analisa Sensitivitas. Jika suatu perubahan kecil dalam parameter menyebabkan perubahan drastis dalam solusi, dikatakan bahwa solusi adalah sangat sensitif terhadap nilai parameter itu. Sebaliknya, jika perubahan parameter tidak mempunyai pengaruh besar terhadap solusi dikatakan solusi relatif insensitif terhadap nilai parameter tersebut.
2. Analisa yang berkaitan dengan perubahan struktural. Masalah ini muncul bila persoalan program linier dirumuskan kembali dengan menambahkan atau menghilangkan kendala dan atau variabel untuk menunjukkan operasi model alternatif. Perubahan struktural ini dapat dimasukkan dalam analisa sensitivitas. 3. Analisa yang berkaitan dengan perubahan kontinu parameter untuk menentukan
urutan solusi dasar yang menjadi optimal. Diketahui model matematika persoalan program linier adalah sebagai berikut: Menentukan nilai dari X1, X2, X3, ..., Xn sedemikian rupa sehingga :
Z = C1X1 + C2X2+ .... + CjXj+ .... + CnXn =
n j j jX C 1 (Optimal)Yang kemudian disebut sebagai fungsi tujuan (objective function) dengan pembatasan (funsi kendala/syarat ikatan) :
a11 X1 + a12 X2 +...+ a1n Xn ataub1,
a21 X1 + a22 X2 +...+ a2n Xn ataub2,
am1 X1 + am2 X2 +....+ amn Xn ataubm, atau aij Xj atau bi untuk i = 1,2,3, … , m.
dan X1 0, X2 0... Xn 0atau Xj 0, dimana j = 1, 2, 3,...., n (syarat non-negatif).
Berdasarkan model matematika persoalan program linier di atas analisis sensitivitas dapat dikelompokkan berdasarkan perubahan-perubahan parameter:
1. Perubahan koefisien fungsi tujuan (Cj),
2. Perubahan koefisien teknologi (aij) (koefisien inpu-output), 3. Perubahan fungsi objektif (bi),
4. Adanya tambahan fungsi kendala baru (perubahan nilai m)
5. Adanya tambahan perubahan (variabel) pengambilan keputusan (Xj).
2.4.1 Analisis Sensitivitas Pada Persoalan Transportasi
Analisis sensitivitas pada persoalan program linear dilakukan setelah diperoleh solusi optimal karena adanya perubahan koefisien fungsi objektif. Berdasarkan perubahan tersebut maka diperiksa dampak perubahannya terhadap solusi optimal dan nilai optimal. Uji terhadap perubahan solusi optimal dan nilai optimal tersebut disebut analisis sensitivitas.
Solusi optimal adalah sebagai berikut:
* 1 * 1
,
x b Z Cb
dimana C adalah vektor koefisien dari fungsi objektif yang koefisiennya berhubungan dengan indeks variabel basis, x* adalah solusi optimal basis dan Z* adalah nilai optimal.
Analisis sensitivitas pada parameter fungsi objektif persoalan transportasi tidak dapat dilakukan dengan menggunakan metode analisis sensitivitas yang digunakan pada persoalan program linear biasa. Hal ini disebabkan, karena beberapa parameter mungkin berubah secara simultan atau serentak karena perubahan parameter harus
juga memenuhi persamaan keseimbangan model transportasi (
Si
Dj ). Untuk menguji dan mengukur nilai ini, digunakan konsep diferensial lengkap.Definisi :
Untuk fungsi y f x( ), didefinisikan:
(a) dx, disebut diferensial x, dengan hubungan dx x. (b) dy, disebut diferensial y, dengan dy f x dx( ) .
Dari definisi, diferensial peubah bebas adalah sama dengan pertambahan peubah tersebut, tetapi diferensial peubah yang bergantung tidak sama dengan pertambahan peubah tersebut.
Untuk fungsi 2 variabel bebas x dan y z, = f(x, y), didefinisikan dx x dan
dy y. Bila x berubah sedangkan y tetap, z merupakan fungsi dari x saja dan diferensial parsial z terhadap x didefinisikan sebagai d zx f x y dx( , ) x zdx
x
. Dengan cara yang sama, diferensial parsial zterhadap y didefinisikan sebagai
( , ) y y y z d z f x y d dy y
. Diferensial total dz didefinisikan sebagai jumlah diferensial parsialnya, yaitu, z z dz dx dy x y (1)
Untuk fungsi wF x y z( , , , ..., )t , diferensial total dwdidefinisikan sebagai: ... w w w w dw dx dy dz dt x y z t (2)
Andaikan bahwa, diantara nilai sebelah kanan k parameter diubah. Selanjutnya, berdasarkan sifat keseimbangan persoalan transportasi,
si djdanj j
d d
dan si si harus dipenuhi. Maka berdasarkan konsep diferensial total,
* * * * 1 2 1 2 ... i i i i B B B B m m x x x dx d d d b b b b b b (3)
Dengan memperhatikan konsep umum perubahan dalam kasus diferensial lengkap, dapat dianggap bahwa db1 b1, sehingga diperoleh * *
i i B B dx x . Dengan menggantikan * * , i B i k k dx y
db dalam persamaan (3) dan juga dengan memperhatikan perubahan dalam k parameter nilai sebelah kanan, persamaan berikut diperoleh:
* * * * ,1 1 ,2 2 ... , i B i i i k k x y y y b b b