LOGIKA MATEMATIKA PERTEMUAN 5 KALKULUS PROPOSISI

(1)

LOGIKA MATEMATIKA

PERTEMUAN 5

KALKULUS PROPOSISI

RAKA YUSUF, ST.MTI

(2)

Definisi (Proposisi)

Sebuah proposisi(proposition) atau statement ialah sebuah kalimat deklaratif yang memiliki tepat satu nilai kebenaran, yaitu: ”Benar”(B)

atau ”Salah”(S).

Kalkulus proposisi (propotional calculus) merupakan metode untuk kalkulasi menggunakan proposisi/kalimat. Dalam kalkulus proposisi yang ditinjau adalah nilai kalimat deklaratif (true/false), metode

penggabungan kalimat dan penarikan kesimpulan (kalimat) berdasarkan kalimat tersebut.

Suatu proposisi adalah sebuah variabel logika p, q, r, ... atau sebuah ungkapan yang dibangun dari variabel-variabel ini dan hubungan dengan logika (_, _, _).

(3)

Beberapa contoh proposisi dan bukan proposisi:

1. Jakarta adalah ibu kota Republik Indonesia.

2. 7 merupakan sebuah bilangan prima.

3. Manusia adalah salah satu jenis makluk di Bumi.

4. Taufik Hidayat pandai main bulu tangkis atau tennes.

5. Jika 10 habis dibagi dengan 4, maka juga habis dibagi dengan 2.

6. Mudah-mudahan anda berhasil dalam meniti karier.

7. Berolahragalah secara teratur!

8. Pergi kamu!

9. Ke Bogor.

10. Apa yang kamu lakukan?

• Kalimat deklaratif pertama, kedua dan ketiga dalam tidak memuat penghubung disebut proposisi primitip(primitif ), dan dilambangkan dengan huruf kecil: p, q, r, s.

• Kalimat deklaratif keempat dan kelima memuat penghubung ”atau” dan ”jika...maka...” disebut proposisi majemuk(composite). Kalimat keenam, ketujuh, kedelapan, kesembilan, dan sepuluh bukan proposisi.

(4)

Penghubung atau

konektif(

connective

)

Dalam logika matematika dikenal sebanyak

5 penghubung, yaitu:

•

Konjungsi(

Conjunction

)

•

Disjungsi(

Disjunction

)

•

Negasi(

Negation

)

•

Implikasi(

Implication

)

(5)

•

Konjungsi / AND /



Konjungsi p dan q dinyatakan dengan, p _ q, adalah sebuah proposisi yang bernilai benar jika proposisi p dan q keduanya bernilai benar.

Pernyataan ”p DAN q” dapat ditulis p _ q Contoh:

• p = Bumi adalah satu-satunya planet di jagat raya yang mempunyai kehidupan. (B)

• q = Satu dekade sama dengan 10 tahun. (B)

• p _ q = Bumi adalah satu-satunya planet di jagat raya yang

(6)

•

Disjungsi / OR /



Disjungsi p dan q dinyatakan dengan, p  q, adalah proposisi yang bernilai salah jika proposisi p dan q keduanya bernilai salah. Pernyataan ”p ATAU q” dapat ditulis p  q Contoh:

• p = Blaise Pascal menemukan mesin hitung.

• q = Taufik hidayat pandai bermain bulu tangkis.

• p _ q = Blaise Pascal menemukan mesin hitung atau Taufik hidayat pandai bermain bulu tangkis

(7)

•

Negasi / NOT /



Untuk sembarang proposisi, p, yang memiliki nilai kebenaran, B=S, maka negasinya ditulis sebagai, p, memiliki nilai kebenaran lawannya  p, S=B

 p = bukan p / tidak p/ tidak benar bahwa a

 p adalah benar bilamana p salah, dan _ p adalah salah bilaman p benar. Nilai kebenaran dari negasi suatu pernyataan selalu berlawanan dengan nilai kebenaran pernyataan aslinya.

Contoh:

• p = Komputer digital elektronik pertama dirakit pada abad ke dua puluh.

 __{p = Komputer digital elektronik tidak dirakit pada abad ke} dua puluh

(8)

•

Implikasi /



Implikasi dari p ke q dinyatakan dengan, p _ q, ialah proposisi yang bernilai salah jika dan hanya jika p bernilai benar dan q bernilai salah.

Proposisi p disebut anteseden(premis/hipotesa)

dan proposisi q disebut

konsekuen(konklusi/kesimpulan)

Pernyataan ”Jika p maka q” ditulis dengan notasi p _ q Contoh:

• p = Bunga mawar berwarna merah.

• q = Manusia memiliki rambut.

• p _ q = Jika Bunga mawar berwarna merah maka manusia memili rambut.

(9)

•

Bi - Implikasi /



Proposisi bersyarat penting lainnya adalah berbentuk “p jika dan hanya jika q” yang dinamakan bi-implikasi.

Ekivalensi dari p dan q dinyatakan dengan, p _ q, adalah proposisi yang bernilai benar jika proposisi p dan q

mempunyai nilai kebenaran sama. Pernyataan ”jika p dan hanya jika q” ditulis dengan notasi p _ q

Contoh:

• p = Saya pergi ke Puncak.

• q = Mobil berada di rumah.

• p _ q = Saya pergi ke Puncak jika dan hanya jika mobil berada di rumah.

(10)

Contoh soal

1. Misalkan p adalah ”Dia tinggi” dan q adalah ”Dia tampan”. Tuliskan setiap pernyataan berikut dalam bentuk simbolik dengan menggunakan p dan q (Asumsikan bahwa ”Dia rendah” berarti ”Dia tidak tinggi”.)

• Dia tinggi dan tampan.

• Dia tinggi tetapi tidak tampan.

• Salah bahwa dia rendah atu tampan.

• Dia tidak tinggi maupun tampan. JAWAB:

• p  q c.  ( p  q)

• p   q d.  p   q

2. Misalkan p adalah ”Sam orang kaya” dan q adalah ”Sam bahagia”. Berikan sebuah kalimat verbal sederhana yang menggambarkan setiap pernyataan berikut:

a. p _ q c. p _ _ q

b. _ p _ _ q d. _ p _ (p _ _ q) JAWAB:

• Sam orang miskin tetapi bahagia.

• Saya tidak kaya maupun bahagia.

• Sam orang kaya atau tidak bahagia.

(11)

3. Misalkan p adalah ”Audi berbicara bahasa Perancis” dan q adalah ” Audi berbicara bahasa Mandarin. Tuliskan setiap pernyataan berikut dalam bentuk simbolik.

• Audi berbicara bahasa Perancis atau Mandarin.

• Audi berbicara bahasa Perancis dan Mandarin.

• Audi berbicara bahasa Perancis tetapi tidak Mandarin.

• Audi tidak berbicara bahasa Perancis atau dia tidak berbicara bahasa Mandarin.

JAWAB:

a. p  q c. p   q

b. p  q d. p   q

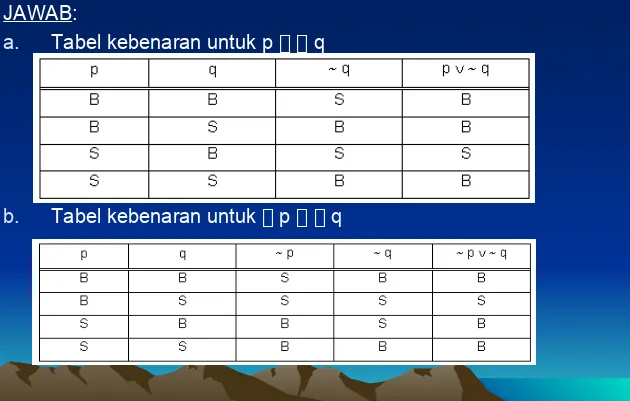
4. Buatlah tabel kebenaran dari  (p  q)!

JAWAB:

(12)

5. Buat tabel kebenaran untuk: – p _ _ q

 __p_ __q

JAWAB:

a. Tabel kebenaran untuk p _ _ q

(13)

TAUTOLOGI DAN KONTRADIKSI

•

Sebuah proposisi disebut

tautologi jika ia benar

untuk semua kasus, proposisi tautologi dicirikan

pada kolom terakhir pada tabel kebenarannya

hanya memuat B (benar).

•

Sebuah proposisi disebut

kontradiksi jika ia

salah untuk semua kasus, proposisi tautologi

dicirikan pada kolom terakhir pada tabel

kebenarannya hanya memuat S (salah).

•

Contoh Tautologi:

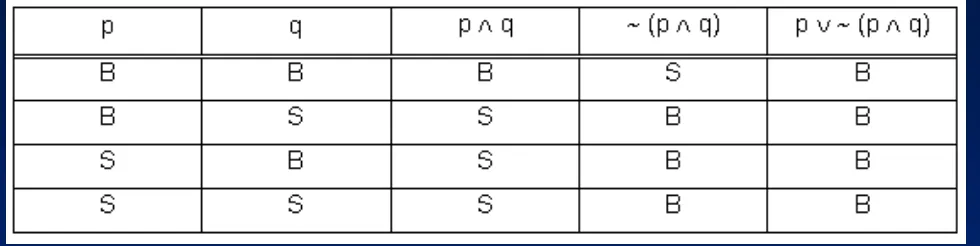
– Buktikan bahwa proposisi p



(p



q) adalah

sebuah tautologi. Buatlah tabel kebenarannya!

(14)

Karena nilai kebenaran dari p   (p  q) adalah B (benar) untuk semua

nilai p dan q maka proposisi adalah sebuah Tautologi. Contoh Kontradiksi:

1. Buktikan bahwa proposisi (p_q) _ _ (p_q) adalah sebuah Kontradiksi. Jawab

Tabel kebenaran:

Karena nilai kebenaran dari (p_q) _ _ (p_q) adalah S (salah) untuk semua nilai p

(15)

Latihan

1. Buatlah kedalam notasi simbolik proposisi-proposisi dibawah ini:

• Jika es mencair di kutub, maka permukaan air laut naik.

• Jika Amir bukan orang kaya, maka tidak mempunyai mobil.

• Mata Anda lelah jika dan hanya jika anda lama menonton televisi.

• Pemuda itu tinggi, atau pendek dan tampan.

2. Buatlah kalimat yang baik sesuai dengan notasi simbolik berikut:

• p _ q

• q _ _p

 __p_₍__q__r)  __(p__q)_

3. Buktikan bahwa proposisi _ (p _ q) _ _ p _ _q adalah sebuah tautologi. Buatlah tabel kebenarannya!