LAPORAN PRAKTIKUM FISIKA DASAR I AYUNAN DAN PERCEPATAN GRAVITASI
( M.5 )
Nama : I Dewa Putu Rega Elyana
NIM : 1311205018
Dosen : Drs. Ida Bagus Alit Paramarta, M.Si Asisten Dosen :I Gede Surya Adi Pranata
Putu Ayu Adi Susanti
Angelia Bella Kusumaningtyas
JURUSAN TEKNOLOGI INDUSTRI PERTANIAN FAKULTAS TEKNOLOGI PERTANIAN
I. Tujuan dan Obyek Percobaan 1. Mempelajari sifat ayunan 2. Menentukan kecepatan gravitasi II. Tinjauan Teori
Gerak yang terjadi secara berulang dengan selang waktu yang sama dinamakan periodik atau gerak harmonis/harmonik. Dalam kehidupan sehari-hari, gerak bolak balik benda yang bergetar terjadi tidak tepat sama karena pengaruh gaya gesekan. Gaya gesekan sendiri adalah gaya yang timbul di antara dua benda saling bersinggungan. Gaya gesekan ada dua yaitu gaya gesekan statis dan gesekan kinetik. Gerak harmonis sederhana yang dapat dijumpai dalam kehidupan sehari-hari adalah getaran benda pada ayunan sederhana.
Ayunan sederhana
Ayunan sederhana atau disebut bandul melakukan gerakan bolak balik sepanjang busur AB. Waktu yang diperlukan oleh benda untuk bergerak dari titik A ke titik A lagi disebut Satu Perioda. Sedangkan banyaknya getaran atau gerak bolak-balik yang dapat dilakukan dalam waktu satu detik disebut Frekuensi.. Pada ayunan sederhana, selain periode dan frekuensi, terdapat juga amplitudo. Amplitudo adalah perpindahan maksimum dari titik kesetimbangan.
Ayunan terdiri atas cakram yang menyerupai partikel bermassa m yang digantungkan pada seutas tali ringan dengan panjang L yang bagian atasnya tidak bergerak (diikatkan ke suatu titik). Gerak yang terjadi pada bidang vertikal dan disebabkan oleh gaya gravitasi. Saat sudut θ kecil (kurang dari 100), gerak yang terjadi sangat mirip dengan gerak osilator harmonik sederhana.
Ft=−mgsinθ=m d 2
s dt2
Dimana s adalah posisi bola ayunan yang diukur sepanjang busurnya dan tanda negatif menunjukkan bahwa gaya tangensialnya bekerja ke arah posisi setimbang (vertikal). Oleh karena s = Lθ dan L konstan, persamaan ini dapat disederhanakan menjadi :
d2θ dt2 =−
g
Lsinθ
Jika kita asumsikan nilai θ kecil, kita dapat menggunakan perkiraan sin θ ≈ θ sehingga dalam perkiraan tersebut, persamaan gerak ayunan sederhananya
Kita simpulkan bahwa gerak osilasi dengan amplitudo yang kecil ini adalah gerak harmonik sederhana. Oleh karena itu, fungsi θ dapat ditulis sebagai θ = θmaks cos(ωt+ϕ) di mana θmaks adalah posisi sudut maksimum dan frekuensi sudut ω adalah :
ω=
√
g
L
Periode geraknya adalah :
T
=
2
π
ω
=
2
π
√
L
g
Gambar Ayunan sederhan
Ayunan fisis
Bandul fisis atau Ayunan fisis merupakan sembarang benda tegar yang digantung yang dapat berayun/bergetar/berisolasi dalam bidang vertical terhadap sumbu tertentu. Bandul fisis sebenarnya memiliki bentuk yang lebih kompleks, yaitu sebagai benda tegar.
Suatu benda yang bersumbu dititik O yang berjarak d dari pusat massanya. Gaya gravitasi memberikan torsi terhadap suatu sumbu melalui O, dan besar torsi ini adalah mgd sin θ. Menggunakan bentuk rotasi dari Hukum Newton II, ∑τ = Iα, di mana I adalah momen inersia terhadap sumbu yang melalui O, kita mendapatkan :
−mgdsinθ=I d
2 θ dt2
Tanda negatif menunjukan bahwa torsi pada O cenderung menurunkan nilai θ. Artinya, gaya gravitasi menghasilkan suatu torsi pemulih. Jika kita asumsikan nilai θ kecil, perkiraan sin θ ≈ θ sekali lagi dapat kita gunakan, dan persamaan geraknya menjadi :
d2θ dt2 =−
(
mgd
Karena persamaan tersebut, maka geraknya adalah gerak harmonik sederhana,artinya
θ = θmaks cos (ωt + ),ϕ dengan θmaks adalah posisi sudut maksimumnya, dan
ω=
√
mgd
I
Periodenya adalah
T
=
2
π
ω
=
2
π
√
I
mgd
Gravitasi
Hukum Newton tentang gravitasi bumi dapat diungkapkan sebagai berikut: “Setiap partikel materi di jagat raya melakukan tarikan terhadap setiap partikel lainnya dengan suatu gaya yang berbanding langsung dengan hasil kali massa partikel-partikel itu dan berbanding terbalik dengan kuadrat jarak yang memisahkan.”
Newton, setelah mengamati hal yang sama pada bulan dan pada benda-benda yang jatuh bebas di permukaan bumi, menyimpulkan bahwa gaya tarik menarik berlaku secara universal untuk sembarang benda . Hukum gravitasi universal yang dirumuskan oleh Newton, diawali dengan beberapa pemahaman dan pengamatan empiris yang telah dilakukan oleh ilmuwan-ilmuwan sebelumnya. Mula-mula Copernicus memberikan landasan pola berpikir yang tepat tentang pergerakan planet-planet, yang semula dikira planet-planet tersebut bergerak mengelilingi bumi, seperti pada konsep Ptolemeus. Copernicus meletakkan matahari sebagai pusat pergerakan planet-planet, termasuk bumi, dalam gerak melingkarnya. Kemudian dari data hasil pengamatan yang teliti tentang pergerakan planet, yang telah dilakukan Tycho Brahe. Gravitasi dapat dirumuskan sebagai berikut :
Hukum-hukum Kepler ini adalah hukum empiris. Keplet tidak mempunyai penjelasan tentang apa yang mendasari hukum-hukumnya ini. Kelebihan Newton, adalah dia tidak hanya dapat menjelaskan apa yang mendasari hukum-hukum Kepler ini, tetapi juga menunjukkan bahwa hukum yang sama juga berlaku secara
universal untuk semua benda-benda bermassa. Bunyi masing-masing hukum Kepler :
Hukum Kepler pertama : “semua planet bergerak mengelilingi matahari dengan lintasan berupa elips dengan matahari berada pada salah satu titik apinya.”
Hukum Kepler kedua : “Dalam waktu yang sama, garis khayal yang menghubungkan planet dan matahari menyapu luasan yang sama.”
Hukum Kepler ketiga :“Kuadrat periode revolusi planet sebanding dengan pangkat tiga jarak rata-rata planet itu dari matahari.”
Hukum Gravitasi Universal
Kita dapat menjabarkan, dengan cara yang sederhana, hukum gravitasi universal dengan memulainya dari fakta-fakta empiris yang telah ditemukan Kepler. Untuk memudahkan analisa kita anggap bahwa planet-planet bergerak dalam lintasan yang berbentuk lingkaran dengan jejari r, dengan kelajuan konstan. Karena planet bergerak dalam lintasan lingkaran maka planet mengalami percepatan sentripetal yang besarnya diberikan oleh :
a =
V2T
=
dengan T adalah periode planet mengelilingi matahari. Percepatan ini tentunya disebabkan oleh suatu gaya yang mengarah ke pusat lingkaran (ke matahari). Besar gaya ini tentunya sama dengan massa planet m dikali percepatan sentripetalnya, sehingga besar gaya tadi dapat dirumuskan sebagai :
F = m
4rπ2 T2Hukum Kepler ketiga dapat kita tuliskan sebagai : T2 = kr3
dengan k adalah suatu konstanta kesebandingan. Dengan persamaan hukum Kepler ketiga ini, besar gaya dapat ditulis sebagai
F= m4π 2
k r2 =k’ m r2
dengan k’ adalah suatu konstanta. Karena gaya ini mengarah ke pusat lingkaran, yaitu ke matahari, tentunya logis bila dianggap bahwa gaya tersebut disebabkan oleh matahari.
IV. Prosedur Percobaan A. Ayunan Sederhana
Gambar 1: Ayunan sederhana 1. Ambil panjang tali tertentu
2. Ukur waktu ayunan dengan mengukur waktu yang diperlukan untuk 20 kali ayunan
3. Ulangi percobaan ini sekurang-kurangnya 3 kali dengan mengambil panjamg tali yang berlainan
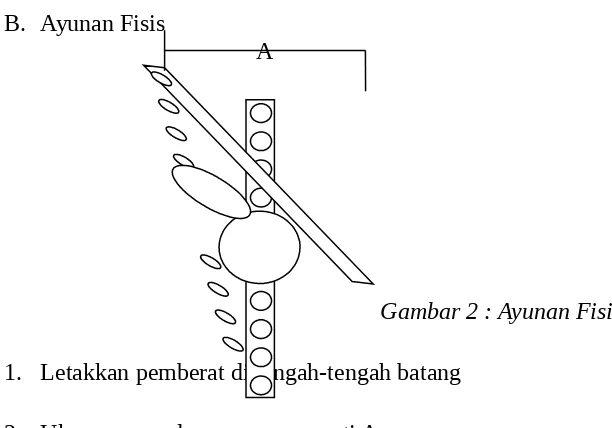
B. Ayunan Fisis
A
B
B Gambar 2 : Ayunan Fisis 1. Letakkan pemberat di tengah-tengah batang
60 36,20
VI. Analisa / Pengolahan Data
6.1. Ralat
A. Ayunan Sederhana 1. Percobaan I
L L L−L
b. Ralat Waktu (t)
T t t−t
( t−t )2
25,11 25,62 -0,521 0,262144
25,63 25,62 0,008 0,000064
25,70 25,62 0,078 0,006084
25,83 25,62 0,208 0,043264
25,84 25,62 0,218 0,047524
∑( t−t )2 =
a. Ralat panjang (L)
ΔL =
√
∑(L−LL)228,47 29,05 -0,586 0,343396
28,70 29,05 -0,356 0,126736
29,04 29,05 -0,016 0,000256
29,41 29,05 0,354 0,125316
29,66 29,05 0,604 0,364816
∑( t−t ) =
a. Ralat panjang (L)
ralat nisbi Δ LLL x 100% = 0
31,54 31,95 -0,412 0,169744
31,58 31,95 -0,372 0,138384
31,86 31,95 -0,092 0,008464
32,09 31,95 0,138 0,019044
32,69 31,95 0,738 0,544644
∑( t−t )2 =
a. Ralat panjang (L)
b. Ralat Waktu (t)
33,59 34,89 -1,302 1,695204
34,16 34,89 -0,732 0,535824
35,21 34,89 0,318 0,101124
35,65 34,89 0,758 0,574564
35,85 34,89 0,958 0,917764
∑( t
a. Ralat panjang (L)
b. Ralat Waktu (t)
T t t−t
( t−t )2
25,11 25,62 -0,512 0,262144
25,63 25,62 0,008 0,000064
25,83 25,62 0,208 0,043264
25,84 25,62 0,218 0,047524
25,70 25,62 0,078 0,006084
∑( t−t )
a. Ralat panjang (L)
L L L−L
b. Ralat Waktu (t)
T t t−t
( t−t )2
36,72 36,42 0,296 0,087616
36,20 36,42 -0,224 0,050176
36,85 36,42 0,426 0,181476
36,33 36,42 -0,094 0,008836
∑( t−t )2 =
a. Ralat panjang (L)
L L L−L
33,04 33,16 -0,126 0,015876
33,12 33,16 -0,046 0,002116
33,20 33,16 0,034 0,001156
33,16 33,16 -0,006 0,000036
33,31 33,16 0,144 0,020736
0,03992
a. Ralat panjang (L)
L L L−L
34,35 34,23 0,118 0,013924
34,20 34,23 -0,032 0,001024
34,33 34,23 0,098 0,009604
34,11 34,23 -0,122 0,014884
34,17 34,23 -0,062 0,003844
± Δt = (34,23 ± 0,04) sekon
tt
ralat nisbi ΔttL x 100% = 34,230,04 x 100% = 0,11% kebenaran = 100% - 0,11% = 99,89%
2. Percobaan IV
a. Ralat panjang (L)
L L L−L
31,16 31,19 -0,036 0,001296
31,22 31,19 0,024 0,000576
31,10 31,19 -0,096 0,009216
31,23 31,19 0,034 0,001156
31,27 31,19 0,074 0,005476
ralat nisbi ΔttL x 100% = 0,02
31,19 x 100% = 0,06% kebenaran = 100% - 0,06% = 99,94%
3. Percobaan V
a. Ralat panjang (L)
L L L−L
30,65 30,52 0,13 0,0169
30,51 30,52 -0,01 0,0001
30,71 30,52 0,19 0,0361
30,40 30,52 -0,12 0,0144
30,33 30,52 -0,19 0,0361
=
(2x3,14)2(602) 602.(36,47)2 =141978,2
4788219,2=0,03
m/s
2Percobaan 2
1759336,96=0,03
m/s
2Percobaan 3
2929232.25=0,03
m/s
2Percobaan 4
875534,49=0,04
m/s
2T = 2π
√
Lg
g =
L2+k2 ¿ (2π)2¿
¿
=
(2x3,14)2(202) 202.(30,52)2 =15775,36
372588,16=0,04
m/s
2VI.2 Grafik
a. Ayunan Sederhana
32 44 55 66 78
0 5 10 15 20 25 30 35 40
panjang tali (cm)
w
ak
tu
Grafik 1 : Grafik ayunan sederhana antara panjang tali dengan kuadrat waktu b. Ayunan Fisis
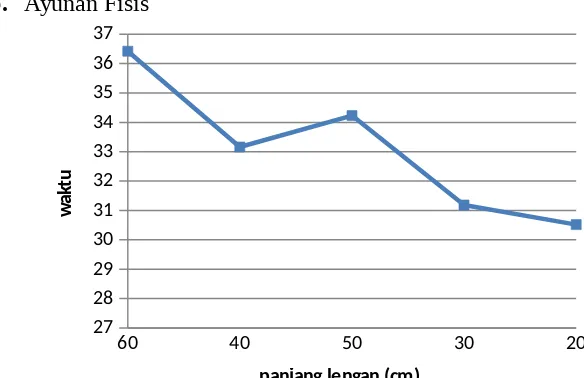
60 40 50 30 20
27 28 29 30 31 32 33 34 35 36 37
panjang lengan (cm)
w
ak
tu
Grafik 2: grafik ayunan fisis antara letak beban dengan kuadrat waktu
VII. Pembahasan
mengukur waktu yang diperlukan. Dan dilakukan sekurang-kurangnya 5 kali dengan mengambil panjang tali berlainan.
Secara teori pada bandul fisis berat beban tidak diabaikan begitu juga dengan berat batang sebagai lengan ayun. Tapi pada penuntun praktikum berat beban dan batang diabaikan. Ditinjau dari segi grafik, pada percobaan dengan ayunan sederhana dapat dianalisa bahwa kuadrat waktu ayun berbanding lurus dengan panjang tali yang digunakan pada percobaan.
Percobaan yang kedua adalah menggunakan ayunan fisis. Prosedur kerjanya adalah dengan menggunakan sebuah beban yang dipasang pada sebuah batang sebagai porosnya. Untuk mendapatkan data yang bervariasi letak beban diubah-ubah sehingga jarak kepusat massa (a) berbeda-beda.. Kemudian beban diayunkan dan dihitung waktu yang dibutuhkan untuk mencapai 20 kali ayunan. Ada beberapa faktor yang menjadi penyebab kesalahan ini, selain karena adanya kurang teliti dalam pengambilan data, ada kemungkinan kesalahan dalam menggunakan rumus. Secara teori pada bandul fisis berat beban tidak diabaikan begitu juga dengan berat batang sebagai lengan ayun.
Pada percobaan ayunan fisis yang terdiri atas sebuah batang dengan panjang L dan salah satu ujungnya sebagai poros (sumbu) yang ditengahnya diletakkan beban (pemberat) dengan massa m, percobaan dilakukan dengan cara seperti pada ayunan sederhana serta mengukur waktu ayunan. Ditinjau dari segi grafik, pada percobaan ayunan fisis berbanding lurus terhadap kuadrat waktu. Semakin jauh letak beban semakin banyak waktu yang diperlukan.
Dari percobaan tersebut data-data yang dihasilkan dapat diketahui kecepatan grafitasi dengan menggunakan rumus sebagai berikut:
T = 2π
√
Lg
VIII. Kesimpulan
Beradasarkan hasil pengamatan dan pembahasan di atas dapat disimpulkan bahwa :
1. Gerak yang terjadi secara berulang dengan selang waktu yang sama dinamakan periodik atau gerak harmonis/harmonik.
2. Ayunan sederhana adalah sistem mekanik yang menunjukkan gerak periodik .
3. Periode dan frekuensi ayunan sederhana hanya bergantung pada panjang tali dan percepatan yang diakibatkan oleh gravitasi. 4. Ayunan sederhana dengan panjang yang sama dan berada pada
lokasi yang sama (sehingga g konstan) akan berosilasi dengan periode yang sama pula.
5. Ayunan sederhana dengan panjang L mengalami gerak harmonik sederhana bila perpindahan sudut dari posisi vertikalnya kecil. Periodenya adalah
T
=
2
π
√
L
g
6. Untuk perpindahan sudut yang kecil dari posisi vertikalnya, sebuah ayunan fisis mengalami gerak harmonik sederhana disekitar poros yang tidak melewati pusat massa. Periode pada gerak tersebut adalah
T=2π
√
Imgd=2π
√
(
a2+k2)
(a.g)
7. Dari hasil perhitungan diperoleh percepatan gravitasi masing-masing ayunan sebagai berikut:
Percobaan I (g) = 2,5m/s2 Percobaan II (g) =2,07m/s2 Percobaan III (g) = 2,0 m/s2 Percobaan IV (g) = 1,75 m/s2 Percobaan V (g) = 1,31 m/s2 b. Ayunan Fisis
Beban di tengah – tengah (g) = 0,33m/s2 Beban ¾ batang (g) = 0,17m/s2
DAFTAR PUSTAKA
Bresnick, Stephen. 2002. Intisari Fisika. Erlangga : Jakarta.
Tripler, Paul A. 1998. Fisika Untuk Sains dan Teknik. Erlangga : Jakarta.
Giancoly, Douglas. 2001. Fisika. Erlangga : Jakarta.
Jewett, John. 2009. Fisika Untuk Sains dan Teknik. Salemba Teknika : Jakarta.
Devia.2009.Simpangangetaran.http://deviafisika.blogspot.com/2009/12/si mpangan-getaran.html. 11Desember2013, 20:02.