Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains Program Studi Matematika

REGRESI ROBUST DENGAN M-ESTIMASI

MAKALAH

Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Sains

Program Studi Matematika

Disusun oleh : Agnes Tri Susilawati

NIM : 053114001

PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI

UNIVERSITAS SANATA DHARMA YOGYAKARTA

ii

ROBUST REGRESSION WITH M-ESTIMASI

MAKALAH

Presented As a Partial Fulfillment of The Requirements To Obtain The Sarjana Sains Degree

In Mathematics

By :

Agnes Tri Susilawati Student Number : 053114001

MATHEMATICS STUDY PROGRAM DEPARTEMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY

SANATA DHARMA UNIVERSITY YOGYAKARTA

vi

Berdirilah dengan teguh, jangan goyah, dan giatlah selalu dalam pekerjaan Tuhan! Sebab dalam persekutuan dengan Tuhan jerih payahmu tidak sia-sia

1 Korintus 15 : 58

vii ABSTRAK

Outlier adalah pengamatan dengan nilai residual yang besar. Dengan adanya outlier, parameter-parameter dalam model regresi akan menjadi bias, oleh karena itu dibutuhkan regresi yang dapat menghasilkan model regresi yang tidak terpengaruh oleh outlier yaitu regresi robust. Regresi robust adalah alat penting untuk menganalisa data yang dipengaruhi oleh outlier sehingga dihasilkan model yang tidak terpengaruh oleh outlier.

Pada makalah ini akan dibahas pendugaan parameter dalam regresi robust dengan menggunakan metode M-Estimasi dengan fungsi bobot Huber. Pada regresi kuadrat terkecil penduga parameter β adalah β=

(

Χ′Χ

)

−1Χ′Υ sedangkan untuk regresi robust penduga parameter β adalah β=

(

Χ′W_βΧ

)

−1Χ′W_βΥ . Ketika W_β =1 model regresi robust sama dengan model regresi kuadrat terkecil. Kesukaran dalam mendapatkan penduga parameter β regresi robust bahwa W_β tergantung pada β dan

β tergantung pada W_β, sehingga untuk mendapatkan nilai β digunakan suatu iterasi yang disebut dengan iteratively reweighted least squares (IRLS).

viii ABSTRACT

Outlier is an observation data with big residual value. With attending outlier, some parameters in the regression model can be bias, so that it needs a best regression model without outlier and it is mentioned as a robust regression. The robust regression is an important tool to analyze outlier and then to obtain a regression model without outlier.

In this research we describe some predicted parameters for the robust regression using M-Estimation method through a weight formula of Huber. The least squares regression estimators of β are β=

(

Χ′Χ

)

−1Χ′Υ , whereas the robust regression estimators of β are β=

(

Χ′W_βΧ

)

−1Χ′W_βΥ .When W_β =1 the robust regression model same as with least square regression model. The difficulty in obtaining of predicted parameter β is reciprocal depending onW_β , while W_β depends on β and β depends onW_β, so that to obtain a value of β we need an iteration calculation using IRLS (iteratively reweighted least squares).

x

KATA PENGANTAR

Puji dan syukur penulis panjatkan kepada Tuhan Yesus Kristus, atas berkat dan kasih karunianya yang telah diberikan sehingga penulis dapat menyelesaikan makalah yang berjudul “ Regresi Robust dengan M-estimasi”.

Dalam proses penulisan makalah ini banyak hambatan yang dialami oleh penulis. Namun, berkat bantuan dan dukungan dari banyak pihak, akhirnya makalah ini dapat terselesaikan. Oleh karena itu penulis ingin mengucapkan terimakasih kepada:

1. Ibu Enny Murwaningtyas, S.Si, M.Si, selaku dosen pembimbing tugas akhir yang telah meluangkan waktu, pikiran, serta sabar dalam membimbing penulis selama penyusunan tugas akhir ini.

2. Yosef Agung Cahyanta, S.T., M.T. selaku Dekan Fakultas Sains dan Teknologi

3. Ibu Lusia Krismiyati Budiasih, S.Si, M. Si, selaku ketua program studi Matematika FST USD Yogyakarta yang telah banyak membantu dan memberikan saran.

4. Romo Prof. Dr. Frans Susilo, SJ, selaku dosen pembimbing akademik yang selalu setia memberikan nasehat dan saran untuk penuslis dan selaku kepala perpustakaan yang telah menyediakan fasilitas dan kemudahan selama penulis kuliah

xi

6. Bapak Zaerilus Tukija dan Ibu Erma Linda Santyas Rahayu yang telah memberikan pelayanan administrasi dan urusan-urusan akademik kepada penulis selama masih kuliah.

7. Perpustakaan USD dan Staf yang telah memberikan fasilitas dan kemudahan kepada penulis.

8. Bapak dan Ibu tercinta: Bapak F. Ngatijan dan Ibu FM. Suryati yang selalu mendoakan penulis, memberikan dukungan yang tak pernah berhenti dalam segala hal.

9. Mas Robert Lujantoro, Mbak Chrispina Lidisia Dwinursari terima kasih karna kalian telah membuat persaudaraan ini indah dan penuh makna, semoga kita dapat selalu menjaganya walau jarak memisahkan kita.

10.Simbah Handoyo Hadisuasono Kakung dan Simbah Handoyo Hadisuasono Putri terima kasih atas doanya sehingga penulis dapat berhasil sampai sekarang ini.

11.Yohan Priyambodo yang telah memberikan seluruh perhatian, pengertian, waktu, kesabaran, nasehat, dan keceriaan buat penulis. Terima kasih pula atas support, doa yang tiada henti untuk penulis, saran, pengetahuan, kebersamaan dan hari-hari yang begitu indah yag telah diberikan kepada penulis.

12.Teman-teman Kost Pink “ Maria Yuli, Maria Pudyanti, Yulia Venty, Fransiska Septiana terima kasih buat kebersamaan kita.

xii

14.Teman-teman Matematika angkatan 2005 yang sudah memberikan segala keceriaan dalam melewati kebersamaan selama di Matematika USD.

Penulis juga tidak lupa mengucapkan terima kasih kepada semua pihak yang membantu penulis dalam penulisan makalah ini.

Yogyakarta,

xiii DAFTAR ISI

Halaman

HALAMAN JUDUL ... i

HALAMAN JUDUL (INGGRIS) ... ii

HALAMAN PERSETUJUAN PEMBIMBING... iii

HALAMAN PENGESAHAN... iv

PERNYATAAN KEASLIAN KARYA... v

HALAMAN PERSEMBAHAN... vi

ABSTRAK... vii

ABSTRACT... viii

PERNYATAAN PUBLIKASI KARYA ILMIAH... ix

KATA PENGANTAR... x

DAFTAR ISI ... xiii

DAFTAR TABEL... xv

DAFTAR GAMBAR... xvi

DAFTAR LAMPIRAN... xvii

BAB I PENDAHULUAN ... ... 1

A. Latar Belakang Masalah ... 1

B. Rumusan Masalah ... 2

C. Batasan Masalah ... 3

D. Tujuan Penulisan ... 3

E. Metode Penulisan ... 3

xiv

G. Sistematika Penulisan ... 4

BAB II REGRESI LINEAR ... 5

A. Metode Maksimum Likelihood... 5

B. Model Regresi Linear Sederhana... 6

C. Metode Kuadrat Terkecil... ... 10

D. Metode Regresi Linear k_{-Variabel ... ... 14}

E. Penaksiran Metode Kuadrat Terkecil k-Variabel... ... 16

F. Penaksiran Metode Maksimum Likelihood k-Variabel.. 18

BAB III OUTLIER DAN REGRESI ROBUST……….. ….. 20

A. Outlier……….. ….. 20

B. Regresi Least Absolute Deviation (Regresi L)……….. 31

C. M-Estimator……….. 32

D. Prosedur M-Estimasi……… 36

BAB IV APLIKASI REGRESI ROBUST ……….. 49

A. Ketenagakerjaan Baja Suatu Negara di Eropa pada tahun 1974 dan 1992……….. ….. 49

B. Kerugian Penjualan Motor Bekas Suatu Dealer Motor……….. 53

BAB V PENUTUP ………... 56

A. Kesimpulan………... 56

B. Saran……….. 58

DAFTAR PUSTAKA ……… 59

xv

DAFTAR TABEL

Halaman

Tabel 3.1 Banyak barang terjual dan harga barang ...………… 24

Tabel 3.2 Kuartil dan Jangkauan...……… 26

Tabel 3.3 Kuartil dan Jangkauan...……… 28

Tabel 3.4 Banyak barang terjual dan harga barang ...………… 41

Tabel 3.5 Model regresi kuadrat terkecil dan model regresi robust... 42

Tabel 3.6 Bentuk kuadrat terkecil dan bentuk regresi robust ……….... 43

Tabel 3.7 Banyak barang terjual dan harga barang ...………… 45

Tabel 3.8 Kuartil dan Jangkauan...……… 45

Tabel 3.9 Model regresi kuadrat terkecil dan model regresi robust... 47

Tabel 3.10 Bentuk kuadrat terkecil dan bentuk regresi robust ……….... 43

xvi

DAFTAR GAMBAR

Halaman

Gambar 1.1 ……… 2

Gambar 3.1a ……… 21

Gambar 3.1b ……… 22

Gambar 3.2a ……… 22

Gambar 3.2b ……… 23

Gambar 3.3 ……… 24

Gambar 3.4 ……… 25

Gambar 3.5 ……… 26

Gambar 3.6a ……… 27

Gambar 3.6b ……… 27

Gambar 3.7a ……… 28

Gambar 3.7b ……… 29

Gambar 3.8a ……… 39

Gambar 3.8b ……… 39

Gambar 3.9 ……… 39

Gambar 3.10 ……… 46

Gambar 4.1 ……… 51

xvii

DAFTAR LAMPIRAN

Halaman

Lampiran A ……… 62

Lampiran B ……… 62

Lampiran C ……… 64

Lampiran D ……… 64

Lampiran E ……… 66

Lampiran F ……… 67

Lampiran G ……… 69

Lampiran H ……… 69

Lampiran I ……… 71

Lampiran J ……… 71

1

BAB I

PENDAHULUAN

A. Latar Belakang Masalah

Dalam suatu pengamatan, misalkan Y simbol yang akan digunakan untuk variabel tak bebas dan X simbol yang akan digunakan untuk variabel bebas, maka rumusan model regresi antara variabel Y dan X adalah:

i ip p i

i=β +βΧ + +β Χ +ε Υ 0 1 1 L

dengan: =

Υ_i variabel tak bebas, i=1,2,K,n =

Χ_ij variabel bebas, i=1,2,K,n, j=1,2,K,p

=

β koefisien regresi Χ terhadap Υ =

i

ε nilai error (galat)

Dalam regresi linear sederhana pendugaan parameter dapat menggunakan metode kuadrat terkecil, namun ketika distribusi dari ε_i tidak normal atau adanya beberapa outlier yang berpengaruh pada model maka metode kuadrat terkecil tidak dapat digunakan karena penduga parameter akan menjadi bias. Oleh karena itu harus digunakan model regresi yang lain. Regresi robust adalah alat penting untuk menganalisa data yang dipengaruhi outlier sehingga dihasilkan model yang tidak terpengaruh oleh outlier.

residual yang besar. Dalam Gambar 1.1 diperlihatkan sekumpulan data dengan titik yang keempat merupakan outlier.

Gambar 1.1. Regresi linear dengan satu outlier

Dalam makalah ini metode yang akan dibahas untuk menduga parameter dari model regresi robust adalah M-Estimasi dengan fungsi bobot Huber. Fungsi Huber merupakan fungsi parabola di sekitar titik nol dan meningkat secara linear pada

a

u

>

, dengan a adalah tuning konstan.

B. Perumusan Masalah

Berdasarkan uraian yang dikemukakan dalam latar belakang diatas, pokok permasalahan dalam makalah ini dapat dirumuskan sebagai berikut:

1. Bagaimana mendeteksi data yang memuat outlier?

2. Apa penduga parameter dari regresi robust dengan M-Estimasi?

3

C. Batasan Masalah

Pembahasan masalah dalam makalah ini dibatasi pada pembahasan mengenai regresi robust yang digunakan untuk mendapatkan model regresi yang tidak terpenga-ruh outlier. Untuk menyelesaikan masalah ini akan diduga parameter regresi robust dengan M-Estimasi menggunakan fungsi bobot Huber dengan tuning konstan

345 . 1

=

a . Pemilihan tuning konstan tidak akan dibahas dalam makalah ini. Dalam makalah ini juga tidak akan dibahas tentang distribusi dari residual, dan sifat BLUE penduga parameter.

D. Tujuan Penulisan

Tujuan penulisan makalah ini adalah:

1. Memahami outlier dan pendeteksian adanya outlier.

2. Menentukan regresi robust dengan M-Estimasi menggunakan funsi bobot Huber’s

E. Metode Penulisan

Metode penulisan makalah ini menggunakan metode studi pustaka, yaitu menggunakan buku-buku, jurnal, makalah yang telah dipublikasikan dan dari internet, sehingga tidak ditemukan hal-hal yang baru. Untuk penyelesaian masalah akan diguna-kan program MATLAB.

F. Manfaat Penulisan

1. Mendapatkan suatu penduga parameter yang dapat mengurangi pengaruh adanya outlier.

G. Sistematika Penulisan

Bab I pendahuluan berisi latar belakang masalah, perumusan masalah, batasan masalah, tujuan penulisan, metode penulisan, dan manfaat penulisan.

Bab II berisi tentang model regresi linear sederhana dan regresi berganda, metode kuadrat terkecil, maximum likelihood.

Bab III berisi tentang pengertian outlier dan cara pendeteksian adanya outlier, pengertian regresi robust, M-Estimasi, Huber’s M-Estimasi.

Bab IV berisi kasus tentang model regresi robust yang akan diselesaikan dengan metode M-Estimasi menggunakan fungsi bobot Huber.

5 BAB II REGRESI LINEAR

A. Metode Maksimum Likelihood

Dari suatu pengamatan, sejumlah pendekatan dapat diambil untuk memperoleh suatu penduga. Salah satu metode untuk memperoleh sebuah penduga adalah metode maximum likelihood (ML). Misalkan

(

Χ₁,Χ₂L,Χ_n

)

nilai yang diobservasi dalam suatu sampel random yang besarnya n. Maka fungsi likelihood sampel tersebut adalah

( )

(

)

(

) (

) (

)

(

;

)

( )

2.1 f

; f ; f ; f

; , , ,

n

1 i

i

n 2

1 2 1

∏

=

Χ =

Χ Χ

Χ =

Χ Χ Χ =

β

β β

β

β β

L L _n

f L

dengan β adalah suatu parameter yang tidak diketahui. L

( )

β adalah fungsi likelihood untuk β, dengan Χ₁,Χ₂,L,Χ_n tetap (fixed). Penduga Maximum Likelihood untuk

parameter β adalah nilai βˆ yang memaksimumkan fungsi likelihood L

( )

β .

Contoh 2.1:

Suatu eksperimen Binomial terdiri dari n percobaan yang menghasilkan observasi

(

Χ₁,Χ₂,K,Χ_i,K,Χ_n

)

dengan Χ_i=1 jika percobaan sukses dan Χ_i =0 jika percobaan gagal. Dengan menggunakan metode maximum likelihood carilah pˆ sebagai penduga dari parameter p.

Jawab:

( )

X

(

)

n X

p p p

dengan

∑

= Χ = n i i X 1

banyaknya sukses. Nilai pˆ dicari dengan menurunkan L

( )

p terhadap

p kemudian menyamakannya dengan nol. Untuk mencari turunan L

( )

p lebih baik diambil lognya (ln = log dengan bilangan pokok e).

( )

( ) (

) (

)

( )

(

)

(

)

(

)

(

) (

)

X np Xp np Xp X p X n p X p X n p X p X n p X p X n p X dp p L d p X n p X p L = − = − − = − − − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = − − + = 1 1 1 1 1 0 1 1 1 ln 1 ln ln ln

Nilai p yang membuat L

( )

p maksimum ialah

X n X n X p i = = =

∑

dengan Χ_i=1 jika percobaan sukses dan Χ_i=0 jika percobaan gagal.

Jadi penduga parameter p dengan menggunakan metode maximum likelihood ialah

n X

p=

B. Model Regresi Linear Sederhana

7

ayahnya, sedangkan anak laki-laki dari ayah yang badannya sangat pendek cenderung lebih tinggi daripada ayahnya.

Suatu fungsi dikatakan linear dalam parameter β jika β hanya dengan pangkat satu dan tidak dikalikan atau dibagi dengan parameter lain dan β berderajat satu. Suatu fungsi dikatakan linear dalam variabel X jika X hanya dengan pangkat satu dan tidak dikalikan atau dibagi dengan variabel lain dan f(X) merupakan fungsi polynomial berderajat satu. Dari penafsiran linearitas tersebut, linearitas dalam parameter dapat mengikuti perkembangan teori regresi. Jadi istilah regresi linear akan selalu berarti suatu regresi yang linear dalam parameter β, mungkin linear atau tidak dalam variabel yang menjelaskan X. Persamaan regresi adalah persamaan matematik yang memungkinkan untuk meramalkan nilai-nilai suatu variabel tak bebas dari nilai-nilai satu atau lebih variabel bebas. Beberapa contoh model regresi yang termasuk model regresi linear adalah

1. Υ_i=β₀+β₁Χ_i+ε_i

2. _i

i i=β +β _Χ +ε Υ _{0 1} 1 3. Υi=β +βΧi +εi

2 1 0

Model regresi dari pengamatan

(

Χ_i,Υ_i

)

dalam sampel akan memenuhi persamaan

i i i=β +βΧ +ε

Υ _{0 1} (2.2) dengan:

=

Υi variabel tak bebas, i=1,2,K,n =

Χ_i variabel bebas, i=1,2,K,n

=

β koefisien regresi Χ terhadap Υ

=

i

ε nilai error (galat)

Asumsi-asumsi regresi linear menurut Gauss: a. Model regresi adalah linear dalam parameter b. ε_i berdistribusi normal untuk setiap i

c. ε_i mempunyai rata-rata 0 untuk setiap i d. Variansi dari ε ₌σ2

i untuk semua xi (homokedastisitas) e. Kovariansi ε_i dan ε_j, i≠ j adalah 0

f. Variabel-variabel bebas adalah variabel yang nir-stokastik (mempunyai nilai yang tetap)

( )

i

EΧ_i =Χ_i,∀

Akibat dari asumsi d dan asumsi c yaitu:

( )

( )

( )

[

( )

]

( )

( )

2 2

2 2

2 2

2

0 ,

σ ε

ε σ

ε ε

ε σ ε

=

− =

− =

∀ =

i

i

i i

i i

E

E

E E

Var

9

Asumsi e dikenal sebagai asumsi tidak adanya korelasi berurutan atau tidak ada autokorelasi (non autokorelasi). Asumsi ini mengakibatkan nilai E

( )

εi dan E

( )

εj saling

bebas, hal ini ditunjukkan dalam penjabaran berikut ini:

(

)

[

(

( )

)

(

( )

)

]

( )

( ) ( )

( )

[

]

[

]

( )

( )

( )

0 0 0 0 , = = = + − − = + − − = − − = j i j i j i j i i j j i j i j j i i j i E E E E E E E E E E E E Cov ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε

Akibat dari asumsi f adalah:

i

Υ berdistribusi normal untuk setiap i dengan nilai harapan dan variansi:

( )

(

)

( ) (

) ( )

i i i i i i i E E E E Y E Χ + = + Χ + = + Χ + = + Χ + = 1 0 1 0 1 0 1 0 0 β β β β ε β β ε β β

( )

(

)

( )

(

)

( )

( )

2

2 1 1 0 1 0 var 0 var var var var var σ β ε β β ε β β + Χ + = + Χ + = + Χ + = i i i i i i Y

Bagian var

( )

Χ_i adalah

( )

(

( )

)

(

)

( )

0 0 var 2 2 2 = = Χ − Χ = Χ − Χ = Χ E E E E i i i i i

C. Metode Kuadrat Terkecil

Metode kuadrat terkecil adalah suatu metode pendugaan parameter dengan

meminimumkan

∑

=

n

i i

1 2

ε (jumlah residual kuadrat) sehingga diperoleh penduga

parameter βˆ₀ dan βˆ1. Penduga (estimator) dalam pendugaan parameter tersebut adalah

aturan bagaimana menghitung nilai dugaan (estimate) berdasarkan pengukuran-pengukuran yang terdapat di dalam sampel. Persamaan penduga parameter dalam regresi linear sederhana adalah

i i= + Χ

Υˆ _βˆ_{0 β}ˆ_{1 (2.3)}

Dengan mengingat kembali model regresi linear Persamaan (2.2) dan persamaan penduga parameter Persamaan (2.3), dapat dicari suatu nilai residual ε yaitu selisih antara nilai Υ yang diamati dengan nilai Υ yang diduga, yang dapat dinyatakan sebagai berikut:

( )

2.4 ˆ

ˆ ˆ

1

0 i

i i

i i i

Χ − − Υ =

Υ − Υ =

β β ε

ε

Gauss dan Legendre (Plackett 1972 dan Stigler 1981) mengatakan bahwa penduga parameter βˆ0 dan βˆ1 dapat dicari dengan metode kuadrat terkecil yaitu:

∑

=

n

i i

1 2 ˆ

min ε

β (2.5)

Prinsip kuadrat terkecil memilih βˆ₀ dan βˆ1 sedemikian rupa sehingga untuk suatu

sampel tertentu

∑

=

n

i i

1 2

ε sekecil mungkin.

Penduga parameter βˆ₀ diperoleh dengan menurunkan

(

)

∑

=

Χ − − Υ n

i

i i

1

2

1

0 ˆ

ˆ _β

11

secara parsial terhadap βˆ₀ dan menyamakan hasil yang diperoleh dengan nol sehingga didapat:

(

)

(

)

(

)

( )

2.6 ˆ ˆ ˆ ˆ ˆ ˆ ˆ ˆ 0 ˆ ˆ 0 ˆ ˆ 0 ˆ ˆ 2 0 ˆ ˆ ˆ ˆ 1 1 1 0 1 1 1 0 1 1 1 0 1 1 0 1 1 1 1 0 1 1 1 0 1 1 0 1 2 1 0 0 0 1 2 n n n n n n i i n i i n i n i i i n i n i i i n i i n i i n i i n i n i i n i i i n i i i n i i i n i i

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

= = = = = = = = = = = = = = = Χ − Υ = Χ − Υ = Χ − Υ = Χ − − Υ = Χ − − Υ = Χ − − Υ = Χ − − Υ − = Χ − − Υ ∂ ∂ = ∂ ∂ β β β β β β β β β β β β β β β β β β ε karena Υ = Υ

∑

= n n i i

1 _dan =Χ

Χ

∑

= n n i i 1

maka Persamaan (2.6) dapat ditulis dalam bentuk:

( )

2.7 ˆ ˆ 1

0 =Υ−βΧ

β

Penduga parameter βˆ1 diperoleh dengan menurunkan

(

)

∑

= Χ − − Υ n i i i 1 2 1 0 ˆ ˆ _β β

(

)

(

)

(

)

( )

2.8 ˆ ˆ 0 ˆ ˆ 0 ˆ ˆ 2 0 ˆ ˆ ˆ ˆ 1 2 1 1 0 1 1 1 0 1 1 0 1 2 1 0 1 1 1 2

∑

∑

∑

∑

∑

∑

∑

= = = = = = = Χ − Χ − Υ Χ = Χ − − Υ Χ = Χ − − Υ Χ − = Χ − − Υ ∂ ∂ = ∂ ∂ n i i n i i n i i i n i i i i n i i i i n i i i n i i β β β β β β β β β β ε

Dengan mensubstitusikan Persamaan

( )

2.7 ke Persamaan

( )

2.8 didapatkan:

(

)

( )

2.9 ˆ ˆ 1 1 ˆ ˆ ˆ ˆ 0 ˆ ˆ 0 ˆ ˆ 0 2 1 1 2 1 1 1 1 1 2 2 1 1 1 1 1 1 2 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 2 1 1 1 2 1 1 1 1 2 1 1 1 1 1 1 2 1 1 1 1 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _Χ − Χ Χ Υ − Υ Χ = Χ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _Χ Υ Χ − Χ Υ = Χ − Χ Χ Υ Χ − Χ Υ = Χ − Χ Χ Υ Χ − Χ Υ = Χ Υ + Υ Χ − = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{Χ Χ − Χ} ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{Χ Χ − Χ} + Χ Υ − Υ Χ = Χ − Χ Χ + Χ Υ − Υ Χ = Χ − Χ Χ − Υ − Υ Χ =

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

= = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = = n i i n i i n i i n i i n i i i n i i n i i n i i i n i i n i i n i i n i i n i i n i i i n i i n i i n i i n i i n i i i n i i n i i n i i i n i i n i i n i i n i i n i i n i i i n i i n i i n i i n i i i n i i n i i n i i i n n n n n n β β β β β β β β β β

13

(

)

(

)(

)

(

2.10

)

1 1 1 1 1 1 1 1 1 1 1 2 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

= = = = = = = = = = = = = = = = = = = = = = = = = = Υ − Υ Χ − Χ = Υ Χ + Χ Υ − Υ Χ − Υ Χ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{ΧΥ − ΧΥ − ΥΧ + ΧΥ} = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{ΧΥ −Χ Υ −Υ Χ + ΧΥ} = Χ Υ + Χ Υ − Χ Υ − Υ Χ = Χ Υ − Χ Υ + Χ Υ − Υ Χ = Χ Υ − Υ Χ n i i i n i i i i i n i n i i n i i n i i i n i i n i i n i i i n i i n i i n i i n i i n i i n i i n i i i n i i n i i n i i n i i n i i n i i n i i i n i i n i i n i i i n n n n n n n n n n n n n n n

Dengan menyelesaikan bagian penyebut Persamaan (2.9) didapat:

(

)

(

)

(

2.11

)

2 2 2 2 2 1 2 1 2 2 1 1 1 2 1 1 2 1 1 2 1 1 1 2 2 1 2 1 1 2 2 1 1 2

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

∑

= = = = = = = = = = = = = = = = = Χ − Χ = Χ + Χ Χ − Χ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{Χ − ΧΧ + ΧΧ} = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{Χ − Χ Χ + ΧΧ} = Χ Χ + Χ Χ − Χ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _Χ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _Χ − Χ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _Χ − Χ n i i n i i i n i n i i n i i n i i n i i n i i n i i n i i n i i n i i n i i n i i n i i n i i n i i n n n n n n n n n n n n n

Dengan mensubstitusikan Persamaan (2.10), dan (2.11) ke Persamaan (2.9) didapat penduga parameter βˆ₁ sebagai berikut:

(

)(

)

(

)

(

2.12

)

D. Model Regresi Linear k-Variabel

Secara umum model regresi linear dua-tiga variabel, dapat ditulis sebagai model regresi linear k-variabel yang meliputi variabel tak bebas Y dan k−1 variabel yang menjelaskan X₂,X₃,K,X_k dapat ditulis sebagai berikut:

N i

X X

X

Yi=β1+β2 2i+β3 3i+L+βk ki+εi =1,2,3,K, (2.13) dengan

k= banyaknya variabel bebas i= observasi ke-i

N= besarnya populasi

Persamaan (2.13) adalah bentuk ringkas untuk sekumpulan N persamaan berikut:

(

2.14

)

3 3 2 2 1 2 2 32 3 22 2 1 2 1 1 31 3 21 2 1 1 N kN k N N N k k k k X X X Y X X X Y X X X Y ε β β β β ε β β β β ε β β β β + + + + + = + + + + + = + + + + + = L K K K K K K K K K K K K K K K K K L L

Persamaan diatas dapat ditulis dengan cara lain yang lebih menjelaskan sebagai berikut:

(

2.15

)

1 1 1 1 1 1 2 1 2 1 3 2 2 32 22 1 31 21 2 1 × × × × + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ N k k N N X X X X X X X X X Y Y Y N k kN N N k k N ε β X Υ ε ε ε β β β M M M M M M L L M dengan

Υ = vektor kolom N×1 observasi atas variabel tak bebas Y

15

β = vektor kolom k×1 dari parameter yang tak diketahui β₁,β₂,K,β_k

ε = vektor kolom N×1 dari N gangguan (disturbance) ε_i

Asumsi-asumsi dalam k-variabel secara umum sama seperti asumsi dalam model regresi linear sederhana dalam notasi matriks, yaitu:

a. ε_i berdistribusi normal b. E

( )

ε_i =0

dimana ε_i dan 0 adalah vektor kolom N×1, 0 merupakan vektor nol. c. Var

( )

ε_i =σ2I

dimana I adalah matriks identitas (identity matrix) N×N

d. Cov

( )

ε_i,ε_j =0

e. Matriks X

(

N×k

)

adalah nir-stokastik, yaitu terdiri dari sekelompok angka yang tetap

f. Rank (Derajat) dari X adalah k (banyaknya kolom dalam X) dan k lebih kecil dari N(banyaknya observasi).

g. Tidak ada multikolinearitas sempurna yaitu tidak terdapat hubungan linear sempurna diantara variabel bebas Χ.

Asumsi c dapat dijabarkan sebagai berikut:

( ) ( )

[

]

⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

= ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢

⎣ ⎡

= ′

2 2

1

2 2

2 1 2

1 2

1 2 1

2 1 2 1

, , ,

N N

N

N N N

N

E E E E

E

ε ε

ε ε ε

ε ε ε

ε ε

ε ε ε

ε ε

ε ε ε

ε ε ε

M M

M

L L K M

i i ε

( )

( )

(

)

( )

( )

(

)

(

) (

)

( )

N N N N N N N E E E E E E E E E × = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = I 2 2 2 2 2 2 2 1 2 2 2 1 2 1 2 1 2 1 1 0 0 0 1 0 0 0 1 0 0 0 0 0 0 σ σ σ σ σ ε ε ε ε ε ε ε ε ε ε ε ε ε ε ε M M M L L M M M L L M M M L L

Asumsi d ditunjukkan oleh unsur-unsur di luar diagonal utama pada matriks diatas.

E. Penaksiran Metode Kuadrat Terkecil dalam k-variabel

Untuk mendapatkan penduga kuadrat terkecil dari β, mula-mula ditulis model regresi sampel k-variabel:

i ki k i

i

i X X X

Y =βˆ₁+βˆ_{2 2} +βˆ_{3 3} +L+βˆ +ε

yang dapat ditulis secara ringkas dalam notasi matriks sebagai ε

β X

Υ= ˆ+ _(2.16)

dan dalam bentuk matriks adalah

1 1 1 1 1 1 2 1 2 1 3 2 2 32 22 1 31 21 2 1 × × × × + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ + ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ N k k N N X X X X X X X X X Y Y Y N k kN N N k k N ε β X Υ ε ε ε β β β M M M M M M L L M

17

(

)

∑

∑

= − 1− 2 2 − 3 3 − − 2

2 _{ˆ ˆ ˆ ˆ}

ki k i

i i

i Y β β X β X β X

ε L (2.17)

dengan

∑

2

i

ε adalah jumlah residual kuadrat. Dalam notasi matriks, ini sama dengan

meminimumkan ε′ε karena

[

]

∑

= + + + = ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ = ′ 2 2 2 2 2 1 2 1 2 1 i N N N ε ε ε ε ε ε ε ε ε ε L ε ε

dari (2.16) diperoleh

β X Υ

ε_{= −} ˆ _(2.18)

Oleh karena itu,

(

) (

)

β X X β Υ X β 2 Υ Υ β X Υ β X Υ ε ε ˆ ˆ ˆ ˆ ˆ ′ ′ + ′ ′ − ′ = − ′ − = ′ (2.19)

Dengan sifat-sifat transpose suatu matriks, yaitu

( )

Xβˆ′=βˆ′X′, dan karena βˆ′X′Υ adalah suatu skalar (suatu angka real), bentuk itu sama dengan transposenya Υ′βˆX.

Dari Persamaan (2.19) dengan aturan penurunan matriks, dan menyamakan hasil yang diperoleh dengan nol didapatkan:

( )

(

2.20

)

ˆ ˆ ˆ ˆ ˆ Υ X β Χ X Υ X 2 β Χ X 2 β Χ X 2 Υ X 2 0 β Χ X 2 Υ X 2 β ε ε ′ = ′ ′ = ′ ′ + ′ − = ′ + ′ − = ∂ ′ ∂

dengan mengalikan di muka kedua sisi dari Persamaan (2.20) dengan invers ini, didapatkan:

(

′

) (

− ′

) (

= ′

)

− ′Υ X X X β X X X

X 1 ˆ 1 (2.21) Tetapi karena

(

X′X

) (

−1 X′X

)

=I suatu matriks identitas derajat (order) k×k, maka didapatkan:

(

XX

)

XΥ β

Iˆ= ′ −1 ′

atau

βˆ =

(

X′X

)

−1X′Υ (2.22)

F. Penaksiran Metode Likelihood dalam k-variabel

Pendugaan parameter model regresi linear sederhana dengan metode maksimum likelihood adalah sebagai berikut:

Dengan mengingat kembali model regresi linear Persamaan (2.16), Y berdistribusi normal dengan rata-rata Xˆ dan variansi β σ2. Sebagai hasilnya fungsi likelihood L

( )

β adalah

( )

( )

( ) ( ) 2 ˆ ˆ 2 1 2 1 _σ π σ β β X Υ β X Υ− ′ − − = e L _N

N (2.23)

Pendugaan parameter βˆ diperoleh dengan menurunkan L

( )

β terhadap βˆ dan menyamakan hasilnya dengan nol. Untuk memperoleh turunan L

( )

β lebih baik diambil lognya (ln = log dengan bilangan pokok e), sehingga Persamaan (2.23) menjadi

19

(

)(

)

(

)(

)

(

ΥΥ 2βXΥ βXXβ

)

β X Υ β X Υ β X Υ β X Υ ˆ ˆ ˆ 2 1 ln 2 ln 2 ˆ ˆ 2 1 ln 2 ln 2 ln ˆ ˆ 2 1 ln 2 ln 2 2 2 2 ′ ′ + ′ ′ − ′ − − − = − − − − − = − − − − − = ′ ′ σ σ π σ σ π σ σ π N N N N e N N

Hasil penurunan lnL

( )

β terhadap βˆ adalah

( )

(

)

(

)

(

)

(2.24) ˆ ˆ 0 ˆ 1 0 ˆ 2 1 0 ˆ ˆ ˆ ˆ 2 1 ln 2 ln 2 ˆ ln 2 2 2 Υ X β Χ X β Χ X Υ X β Χ X Υ X β Χ X 2 Υ X 2 β β X X β Υ X β 2 Υ Υ β ′ − = ′ ′ + ′ − = ′ + ′ − = ′ + ′ − = ∂ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− − − ′ − ′ ′ + ′ ′} ∂ = ∂ ∂ σ σ σ σ π β N N L

Dalam Persamaan (2.24) besaran yang diketahui adalah

(

X′X

)

dan X′Υ (perkalian silang antara variabel Χ dan Υ) dan yang tidak diketahui adalah βˆ. Sekarang dengan menggunakan aljabar matriks, kalau invers dari

(

X′X

)

ada, katakan

(

_′

)

−1

X

X , maka dengan mengalikan di muka kedua sisi dari Persamaan (2.24) dengan invers ini, didapatkan:

(

′

) (

− ′

) (

= ′

)

− ′Υ X X X β X X X

X 1 ˆ 1 (2.25) Tetapi karena

(

X′X

) (

−1 X′X

)

=I suatu matriks identitas derajat (order) k×k, maka didapatkan:

(

XX

)

XΥ β

Iˆ= ′ −1 ′

atau

(

XX

)

XΥ β_ˆ = ′ −1 ′

20 BAB III

OUTLIER DAN REGRESI ROBUST

Dalam suatu pengamatan, misalkan Y simbol yang akan digunakan untuk variabel bebas dan X simbol yang akan digunakan untuk variabel tak bebas, maka rumusan model regresi antara variabel Y dan X adalah:

i ip p i

i =β +β Χ + +β Χ +ε

Υ _{0 1 1} L (3.1)

Menurut asumsi regresi linear εi berdistribusi normal, namun ketika distribusi dari ε_i tidak normal atau adanya beberapa outlier yang berpengaruh pada model, maka penduga kuadrat terkecil menjadi bias sehingga kurang tepat untuk menduga parameter-parameter dalam model regresi tersebut. Oleh karena itu dibutuhkan suatu model regresi dengan parameter-parameter yang tidak terpengaruh oleh outlier. Metode pendekatan alternatif yang berguna untuk mencari parameter-parameter dalam model regresi tersebut adalah regresi robust. Regresi robust yang diperkenalkan oleh Andrews (1972) adalah alat penting untuk menganalisa data yang dipengaruhi oleh outlier sehingga dihasilkan model yang tidak terpengaruh oleh outlier.

A. Outlier

Menurut Staudte dan Snether (1990) outlier adalah suatu observasi yang jauh dari sebagian besar data. Pada regresi linear, outlier adalah pengamatan dengan nilai residual yang besar.

21

mengandung outlier akan mengganggu proses analisa data dan harus dihindari dalam banyak hal. Dalam kaitannya dengan analisa regresi, outlier dapat menyebabkan hal-hal berikut :

1. Residual yang besar dari model yang terbentuk atau E

( )

εi ≠0

2. Variansi pada data tersebut menjadi lebih besar 3. Taksiran interval memiliki rentang yang lebar

Permasalahan dengan data yang memuat outlier adalah: 1. Permasalahan dengan outlier di sumbu y

Andaikan

(

Χ₁,Υ₁

) (

,L, Χ₅,Υ₅

)

suatu pengamatan sampel dengan suatu garis L yang diperlihatkan dalam Gambar 3.1a. Jika terdapat kesalahan dalam memasukkan data, misalnya nilai Υ₄ tinggi yang akan menyebabkan adanya outlier. Maka Gambar 3.1a akan berubah seperti yang diperlihatkan dalam Gambar 3.1b yaitu titik yang keempat menjauh dari posisi aslinya (ditandai oleh lingkaran garis putus-putus). Titik ini disebut suatu outlier di sumbu y, yang mempunyai suatu pengaruh besar dengan garis L, yang sungguh berbeda dari garis L di dalam Gambar 3.1a.

Gambar 3.1. (b) Regresi linear dengan satu outlier di sumbu y. 2. Permasalahan dengan outlier di sumbu x

Andaikan

(

Χ₁,Υ₁

)

,L,

(

Χ₅,Υ₅

)

suatu pengamatan sampel dengan suatu garis L yang diperlihatkan dalam Gambar 3.2a. Jika terdapat kesalahan dalam memasukkan data, misalnya nilai Χ₁ tinggi yang akan menyebabkan adanya outlier. Maka Gambar 3.2a akan berubah seperti yang diperlihatkan dalam Gambar 3.2b yaitu titik yang pertama menjauh dari posisi aslinya (ditandai oleh lingkaran garis putus-putus). Titik ini disebut suatu outlier di sumbu x, yang mempunyai suatu pengaruh besar dengan garis L, yang sungguh berbeda dari garis L di dalam Gambar 3.2a.

23

Gambar 3.2. (b) Regresi linear dengan satu outlier di sumbu x.

Untuk mendeteksi suatu data yang memuat outlier dan menentukan batasan out-lier dalam sebuah analisa, akan digunakan 3 metode estimasi yaitu:

1. Metode Grafis (Scatter-plot)

Untuk melihat apakah terdapat outlier pada data, dapat dilakukan dengan mem-plot data. Selain itu, jika sudah didapatkan model regresi maka dapat dilakukan dengan cara memplot antara residual (ε ) dengan nilai prediksi Υˆ . Jika terdapat satu atau beberapa data yang terletak jauh dari pola kumpulan data keseluruhan maka hal ini mengindikasikan adanya outlier. Metode ini mempunyai kelemahan yaitu keputusan bahwa suatu data merupakan outlier sangat bergantung pada peneliti, karena hanya mengandalkan visualisasi grafis, untuk itu dibutuhkan seseorang yang ahli dan berpe-ngalaman dalam menginterpretasikan gambar tersebut.

Contoh 3.1

Tabel 3.1. Banyak barang yang terjual dan harga barang

Observasi X Y

1 18 770

2 16 785

3 15 790

4 12 800

5 10 810

6 7 825

7 6 830

Dengan menggunakan Metode Grafis (Scatter-plot), tentukan apakah data tersebut memuat outlier?

Jawab:

Melalui metode grafis akan diuji apakah data memuat outlier. Dengan menggunakan SPSS, scatter-plot antara nilai X dengan nilai Y ditunjukkan dalam Gambar 3.3.

Gambar 3.3. Scatter-plot

6.00 8.00 10.00 12.00 14.00 16.00 18.00

X

770.00 780.00 790.00 800.00 810.00 820.00 830.00

Y

25

Contoh 3.2

Menggunakan Contoh 3.1 dengan mengganti jumlah barang yang terjual pada observasi ke-6 dengan nilai 30. Dengan menggunakan Metode Grafis (Scatter-plot), tentukan apakah data tersebut memuat outlier?

Jawab:

Melalui metode grafis akan diuji apakah data memuat outlier. Dengan menggunakan SPSS, scatter-plot antara nilai X dengan nilai Y ditunjukkan dalam Gambar 3.4.

Gambar 3.4. Scatter-plot

5.00 10.00 15.00 20.00 25.00 30.00

X

770.00 780.00 790.00 800.00 810.00 820.00 830.00

Y

Dari Gambar 3.4. terlihat bahwa data pada observasi ke-6 jauh dari pola kumpulan data keseluruhan. Jadi data tersebut memuat outlier.

2. Boxplot

pada nilai yang kurang dari 1.5*IQR terhadap kuartil 1 dan nilai yang lebih dari 1.5*IQR terhadap kuartil 3.

Gambar 3.5. Skema identifikasi outlier menggunakan IQR atau boxplot

Contoh 3.3

Dengan menggunakan Boxplot, tentukan apakah data pada Contoh 3.1 memuat outlier?

Jawab:

Untuk keperluan ini terlebih dahulu dihitung nilai kuartil (Q) 1, 2, dan 3 serta jangkauan (IQR, Interquartile Range) seperti yang tercantum dalam Tabel 3.2

Tabel 3.2. Kuartil dan jangkauan

X Y Q1 7 785 Q2 12 800 Q3 16 825 IQR 9 40

27

Dari Tabel 3.2. outlier terletak pada daerah X < -6.5 dan X > 29.5 atau Y < 725 dan Y > 885. Karena nilai X pada data berada pada nilai -6.5 < X < 29.5 dan nilai Y pada data berada pada nilai 725 < Y < 885, maka dapat disimpulkan bahwa data tersebut tidak memuat outlier.

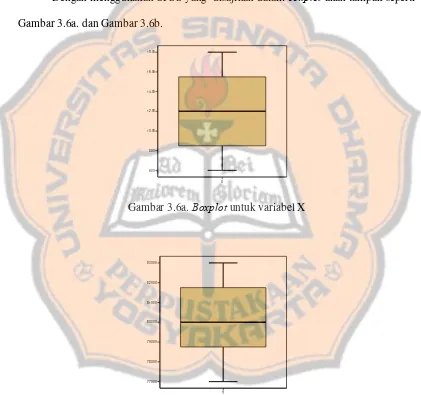
Dengan menggunakan SPSS yang disajikan dalam boxplot akan tampak seperti Gambar 3.6a. dan Gambar 3.6b.

X 6.00

8.00 10.00 12.00 14.00 16.00 18.00

Gambar 3.6a. Boxplot untuk variabel X

Y 770.00

780.00 790.00 800.00 810.00 820.00 830.00

Gambar 3.6b. Boxplot untuk variabel Y

Contoh 3.4

Dengan menggunakan Boxplot, tentukan apakah data pada Contoh 3.2 memuat outlier?

Jawab:

Untuk keperluan ini terlebih dahulu dihitung nilai kuartil (Q) 1, 2, dan 3 serta jangkauan (IQR, Interquartile Range) seperti yang tercantum dalam Tabel 3.3

Tabel 3.3. Kuartil dan jangkauan

X Y Q1 10 785 Q2 15 800 Q3 18 825

IQR 8 40

1.5*IQR 12 60

Dari Tabel 3.3. outlier terletak pada daerah X < -2 dan X > 30 atau Y < 725 dan Y > 885. Karena nilai X pada observasi ke-6 yaitu X = 30 berada pada daerah outlier maka data tersebut memuat outlier di sumbu X.

Dengan menggunakan SPSS yang disajikan dalam boxplot akan tampak seperti Gambar 3.7a. dan Gambar 3.7b.

X 5.00

10.00 15.00 20.00 25.00

30.00 6

29

Y 770.00

780.00 790.00 800.00 810.00 820.00 830.00

Gambar 3.7b. Boxplot untuk variabel Y

Dari Gambar 3.7a. terlihat bahwa data pada observasi ke-6 berada di daerah outlier. Jadi data tersebut memuat outlier di sumbu X.

3. Residual yang distudentkan (Studentized Residual)

Umumnya outlier dipengaruhi oleh pengamatan

(

Υ_i,X_i

)

pada penduga kuadrat terkecil yang tergantung pada Υ_i yang terlalu besar atau terlalu kecil dibandingkan dengan nilai X_i. Suatu metode yang sederhana dan efektif untuk mendeteksi outlier adalah analisis residual. Residual banyak memegang peranan penting dalam pengujian model regresi karena residual itu sendiri merupakan sisa pada suatu pengamatan. Residual ke-i didefinisikan sebagai berikut:

i i i =Υ −Υˆ ε

Umumnya pengamatan yang dicurigai sebagai outlier dikategorikan ke dalam pelanggaran asumsi. Maka lebih tepat jika digunakan analisis residual. Untuk mendeteksi apakah terdapat outlier atau tidak, dapat dilakukan dengan menghitung nilai

is

ε sebagai berikut:

i i is

h

s −

=

1 ε

dengan:

p n s

n

i i

− =

∑

=1

2

2

ε

p adalah banyaknya parameter

i

h (nilai laverage) adalah ukuran seberapa jauh x_i menyimpang dari nilai rata-rata X. Andaikan H matriks orthogonal dari X, dengan elemen diagonalnya h₁,K,h_n adalah

nilai leverage dari x₁,K,x_n. Matriks H memenuhi H=X′

(

X′X

)

−1X dan

(

)

i

i x x

h = _i′ X′X −1 .

Jika 2ε_is > atau ε_is <−2 untuk data kecil

(

n<30

)

dan ε_is >3.5 atau ε_is <−3.5 untuk data besar

(

n≥30

)

maka data mengandung outlier.

Contoh 3.5

Dengan menggunakan studentized residual, tentukan apakah data pada Contoh 3.1 memuat outlier?

Jawab:

Dari M-file pada program MATLAB yang ditunjukkan dalam Lampiran A diperoleh nilai

i

h = [0.4286 0.2698 0.2143 0.1429 0.1746 0.3413 0.4286]T

i

ε = [-3.0952 2.4603 2.7381 -1.4286 -0.8730 -0.0397 0.2381]T

s = 2.2800

dengan memasukkan nilai h_i, ε_i, dan s ke Persamaan (3.2) diperoleh nilai studentized residual sebagai berikut:

is

31

Karena nilai studentized residual dari data adalah −2<ε_is <2 maka dapat diyatakan bahwa data tidak memuat outlier.

Contoh 3.6

Dengan menggunakan studentized residual, tentukan apakah data pada Contoh 3.2 memuat outlier?

Jawab:

Dari M-file pada program MATLAB yang ditunjukkan dalam Lampiran B diperoleh nilai

i

h = [0.1639 0.1443 0.1431 0.1738 0.2228 0.7625 0.3896]T

i

ε = [-31.0180 -16.3205 -11.4718 -1.9256 7.7719 25.7972 27.1668]T

s = 23.7812

dengan memasukkan nilai h , _i ε_i, dan s ke Persamaan (3.2) diperoleh nilai studentized residual sebagai berikut:

is

ε = [-1.4265 -0.7419 -0.5221 -0.0891 0.3707 2.2258 1.4622]T

Karena studentized residual dari data observasi ke-6 adalah 2.2258 > 2 maka dapat di-nyatakan bahwa data memuat outlier.

B. Regresi Least Absolute Deviation (Regresi L)

Ketika error diasumsikan tidak normal, maka pendugaan parameter β menggunakan metode maximum likelihood dengan kriteria selain kuadrat terkecil. Sebagai contoh andaikan error ε_i, i=1,2,L,n saling bebas dan berdistribusi double exponensial

( )

ε σ

σ

ε i

e

f _i = −

2 1

Fungsi densitas double exponensial mempunyai puncak tertinggi σ 2

1

pada ε_i =0 dan

i

ε dapat bernilai negatif atau positif. Maka prinsip maximum likelihood untuk penduga β akan meminimumkan:

∑

=

n

i i

1

ε

yaitu jumlah harga mutlak residual, ini dinamakan regresi L₁, sedangkan metode maximum likelihood dengan kriteria kuadrat terkecil dengan distribusi error

( )

( )

₂ 12 2 ₂ 2

2πσ ε σ

ε = − e−

f _i (3.4) meminimumkan

∑

=

n

i 1 i 2

ε

yaitu jumlah kuadrat error, kuadrat terkecil diberi nama regresi L₂. Ada juga metode regresi L_p yang meminimumkan

∑

=

n

i p i

1

ε

C. M-ESTIMATOR

M-Estimator adalah tipe penduga maximum likelihood. Andaikan error berdistribusi sesuai dengan distribusi fungsi f

( )

ε , maka penduga maximum likelihood (MLE) dari β yang ditulis dengan βˆ memaksimumkan besarnya

(

)

∏ − ′

=

n

i i

Y f

1

β

33

dengan x_i′ adalah baris ke i dari Χ, i=1,2,L,n pada model Υ=Χβ+ε. Jika arg max adalah nilai yang memaksimumkan suatu fungsi, maka pernyataan diatas dapat ditulis sebagai

(

)

_⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∏ − ′ = = n i i Y f 1 max arg

ˆ _{x β}

β _i (3.6)

Jika fungsi densitas f

( )

ε selalu bernilai positif yaitu lim

( )

>0

∞ → f ε

ε , dan fungsi

ln adalah fungsi yang meningkat, maka untuk memaksimumkan f

( )

ε sama halnya dengan memaksimumkan ln f

( )

ε , sehingga diperoleh

(

)

(

) (

)

(

)

[

]

(

)

(

)

(

)

[

]

(

)

( )

3.7 1 ln max arg ln ln ln max arg ln max arg 1 ln max arg ˆ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − ′ = ′ − + + ′ − + ′ − = ′ − ⋅ ′ − ⋅ ′ − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∏ = − ′ = n i i Y f i Y f i Y f i Y f i Y f i Y f i Y f n i i Y f β i x β i x β i x β i x β i x β i x β i x β i x β L L

Jika error berdistribusi normal maka Persamaan 3.7 dapat ditulis sebagai berikut:

( )

(

)

( )

(

)

( )

(

(

)

)

( )

(

)

( )

(

)

( )

3.8 2 2 ln 2 1 max arg 2 2 ln 2 1 max arg ln 2 2 ln 2 1 max arg ln 2 ln max arg 2 ln max arg ˆ 1 2 2 1 2 1 2 2 2 1 2 2 2 1 2 2 2 2 1 2 1 2 2 2 2 1 2 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ _{− ′} − + ∑ − = ∑ _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ _{− ′} − − = ∑ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛_{− + − − ′} = ∑ _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ + = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ _⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = = = = = = ′ − − − = ′ − − − n i i n i n i i n i i n i i Y n i i Y Y Y e Y e e σ πσ σ πσ σ πσ πσ πσ σ σ β x β x β x β i i i β i x β i x

Jika _σˆ2 _{adalah penduga untuk} σ2_{, maka nilai tersebut dianggap konstan. Karena nilai}

(

)

∑

= ⎥⎦ ⎤ ⎢⎣ ⎡− n i1 2 2 ln 2 1 _πσ

pendiferensialan maka untuk memaksimumkan penduga βˆ nilai tersebut dapat diabaikan sehingga

(

)

( )

3.9 max arg ˆ 1 2 ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ′ − − =

∑

= n i i

Y xβ

β i

Jika arg min adalah nilai yang meminimumkan suatu fungsi, maka

( )

x

[

f

( )

x

]

f =argmin − max

arg , sehingga diperoleh

(

)

(

)

(

3.10

)

min arg min arg ˆ 1 2 1 2 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∑ − ′ = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ∑− − ′ − = = = n i i n i i Y Y β x β x β i i

Jadi penduga βˆ untuk distribusi normal meminimumkan

(

)

2

1

∑ − ′

=

n

i i i

Y x β (3.11)

Jika error berdistribusi tidak normal, maka pendugaan β mengikuti selain distribusi normal, andaikan error berdistribusi double exponensial maka Persamaan 3.7 dapat di-tulis sebagai berikut:

( )

( )

( )

(

)

(

)

( )

( )

35

Jika σˆ adalah penduga untuk σ maka nilai tersebut dianggap konstan. Karena nilai

( )

[

]

∑ − = n i 1 2

ln σ dan σ merupakan nilai konstan yang akan hilang dalam proses

pendiferensialan maka untuk memaksimumkan penduga βˆ nilai tersebut dapat diabaikan sehingga

(

3.13

)

min arg min arg max arg ˆ 1 1 1 ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ _′ − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′ − − − = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ′ − − =

∑

∑

∑

= = = n i i n i i n i i Y Y Y β x β x β x β i i i

Jadi penduga βˆ untuk distribusi double eksponensial meminimumkan

∑ − ′

=

n

i i i

Y

1

β

x (3.14)

Gagasan ini dapat diperluas, andaikan ρ

( )

u adalah suatu fungsi untuk u dan σ

adalah penduga parameter skala, dengan

σ iβ x′

− =Yi

u , dan ρ=−ln f

( )

ε maka Persamaan (3. 7) menjadi

(

)

(

)

(

)

_⎥ ⎦ ⎤ ⎢ ⎣ ⎡ _{− ′} = ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ _{− − ′} − = ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ∑ = − − ′ =

∑

∑

= = n i i n i i Y Y n i i Y 1 1 min arg min arg 1 max arg ˆ β x β x β i x β i i ρ ρ ρ

sehingga dapat didefinisikan suatu penduga βˆ yang meminimumkan

∑

= ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ′ n i i i Y 1 σ

ρ xβ (3.15)

6745 , 0 1 med 1 med _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − − − = h h ε ε σ

dengan

( )

⎪ ⎪ ⎪ ⎪ ⎩ ⎪ ⎪ ⎪ ⎪ ⎨ ⎧ ₊ + + = ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎜ ⎝ ⎛ gasal n untuk 2 1 genap n untuk 1 2 2 2 1 med n n n i ε ε ε ε

Dapat dilihat jika ρ

( )

u =u2 maka kriteria meminimumkan sama dengan Persamaan 3.11, jika ρ

( )

u = u maka kriteria meminimumkan sama dengan Persamaan 3.14. Dalam kasus yang specifik ini, ρ

( )

u dan distribusi dasar saling terkait. Untuk selanjutnya ρ

( )

u akan menggunakan fungsi Huber’s

( )

⎪ ⎪ ⎩ ⎪⎪ ⎨ ⎧ _≤ > − = a u a a u a u u untuk 2 2 1 u untuk 2 2 1

ρ (3.16)

dengan a adalah tuning konstan. Tuning konstan a dalam regresi robust menentukan kerobustan dan efisiensi. Tuning konstan dipilih untuk memberikan variansi asimtotik sehingga didapat effisiensi asimtotik pada distribusi normal. Dengan menggunakan efisiensi asimtotik 95% pada distribusi normal standar diperoleh tuning konstan

a = 1.345. Pembahasan tuning konstan tidak dibahas secara mendalam.

D. Prosedur M-Estimasi

37 k , 0,1,2, j 0, ˆ 1 K = = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ − ′

∑

= n i i i ij Y x σ

ψ xβ (3.17)

dengan ψ

( )

u =∂ρ ∂u dan x_ij adalah entri ke-j dari x′_i =

(

1,x_i1,x_i2,K,x_ik,

)

. Didefinisikan suatu fungsi bobot yaitu:

(

)

n , 1,2, i , ˆ ˆ K = ′ − ′ − = σ σ ψ β _β x β x i i i i i Y Y

w (3.18)

Maka bagian kiri dari Persamaan (3.17) dapat ditulis

(

)(

)

(

)

(

3.19

)

ˆ 1 ˆ 1 ˆ 1 ˆ ˆ ˆ 1 ˆ ˆ ˆ ˆ 1 1 1 1 1 1 β x β x β x β x β x β x β x β x β x i i n i ij i i n i ij i i i n i ij i i i i i i n i ij i i i i n i i i ij n i i i ij w x Y w x -Y w x -Y Y Y ψ x Y Y -Y ψ x -Y ψ x ′ − = ′ = ′ ′ − ′ − = ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ′ − ′ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ′ = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ′

∑

∑

∑

∑

∑

∑

= = = = = = β β β σ σ σ σ σ σ σ σ σ σ

Masukkan Persamaan 3.19 ke Persamaan 3.17 diperoleh

(

3.20

)

, , 2 , 1 , 0 , 0 1 1 1 1 k j Y w x w x w x Y w x i i n i ij i i n i ij i i n i ij i i n i ij K = ∑ = ′ ∑ = ′ ∑ − ∑ = = = = β β β β β x β x

Bagian kiri dari Persamaan 3.20 dalam bentuk matriks adalah

(

3.21

)

0 0 0 0 0 0 2 1 2 1 2 22 12 1 21 11 2 1 2 1 2 22 21 1 12 11 ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ n nk k k n n n nk n n k k x x x x x x x x x w w w x x x x x x x x x β β β M L M M M L L L M M M L L L M M M L L

Bagian kanan dari Persamaan 3.20 dalam bentuk matriks adalah

Dengan memasukkan Persamaan 3.21 dan 3.22 ke Persamaan 3.20 dalam bentuk matriks dapat ditulis sebagai berikut

Υ W Χ Χβ W

Χ′ _β = ′ _β (3.23)

dengan W_β adalah matriks diagonal n×n dari bobot, dengan elemen-elemen diagonal

(

w1β,w2β,K,wnβ

)

. Persamaan ini dikenal sebagai persamaan normal kuadrat terkecil

terboboti. Jika invers dari

(

Χ′W_βΧ

)

ada, katakanlah

(

Χ′W_βΧ

)

−1, maka dengan mengalikan di muka kedua sisi dari (3.23) dengan invers ini didapatkan

(

) (

) (

)

(

)

(

)

1

(

3.24

)

1 1 1 Υ W Χ Χ W Χ β Υ W Χ Χ W Χ Iβ Υ W Χ Χ W Χ β Χ W Χ Χ W Χ β β β ′ ′ = ′ ′ = ′ ′ = ′ ′ − − − − β β β β β

Dalam makalah ini W_β menggunakan bobot kriteria Huber’s. Fungsi bobot Huber’s dapat dicari dengan menurunkan fungsi ρ

( )

u Persamaan 3.16 terhadap u, sehingga diperoleh:

( )

( )

⎪ ⎩ ⎪ ⎨ ⎧ = ≤ > a u a u a u u untuk u untuk sgn

ψ (3.25)

dengan

( )

u u

∂ ∂ = ρ

ψ dan

( )

du u d

u =

sgn dimana

( )

⎪ ⎪ ⎩ ⎪ ⎪ ⎨

⎧− _<

= > = 0 jika 1 0 jika 0 0 jika 1 sgn u u u u

39

Gambar 3.8.a. Fungsi ρ

( )

u Huber

0.0 0.5 1.0

0.5 1.0

1 ₂

3 2 1 0 3

U PSI

Gambar 3.8.b. Fungsi ψ

( )

u Huber

Berdasarkan Persamaan (3.18) yaitu

( )

u u

W_β =ψ , dengan

σˆ β xi i

Y

u= − ′ maka

fungsi bobot huber’s adalah

⎪ ⎪ ⎩ ⎪⎪ ⎨

⎧ _≤

> =

a

a a

W

u untuk 1

u untuk u

β (3.26)

dengan

(

( )

)

du u d u

sgn 1 ₌

Fungsi bobot Huber disajikan dalam gambar 3.9

Fungsi bobot Huber’s merupakan sebuah matriks diagonal

(

w_1β,w_2β,K,w_nβ

)

yang tiap elemennya bernilai ⎥

⎦ ⎤ ⎢ ⎣ ⎡

u a

, 1

min . Pada umumnya M-Estimasi Huber akan

memberikan bob