Gerak Lurus Beraturan dan Gerak Lurus Be

GLB DAN

GLBB

KELOMPOK I

•

ANDHIKA PURWANTARA

(1301154097)

•

M.IKDHAR ISNAN (1301150083)

•

IRFAN MULIA T (1301150069)

•

NORMA ROSITA (1301150433)

TUJUAN

ALAT DAN BAHAN

DASAR TEORI

MOMEN INERSIA

PENGOLAHAN DATA

KESIMPULAN

TUJUAN



_{Mempelajari Gerak Lurus Beraturan}

(GLB) dan Gerak Lurus Berubah

Beraturan

(GLBB)

menggunakan

pesawat attwood



_{Menentukan Momen Inersia roda}

ALAT DAN BAHAN

1.

Pesawat attwood

lengkap

2. Jangka sorong

3. Stopwatch

DASAR TEORI

Hukum 1 newton menyatakan bahwa, jika resultan gaya yang bekerja pada suatu sistem (benda) sama dengan nol, maka sistem dalam keadaan setimbang, artinya benda tersebut akan bergerak lurus beraturan (GLB). Pada hukum II Newton, disimpulkan bahwa :

1. Arah percepatan benda sama dengan arah resultan gaya yang bekerja pada benda

2. Besarnya percepatan sebanding gayanya

3. Bila ada gaya bekerja pada benda maka benda mengalami percepatan, sebaliknya bila benda mengalami percepatan tentu ada gaya penyebabnya.

Untuk percepatan (a) yang tetap/konstan, maka berlaku persamaan gerak yang disebut sebagai gerak lurus beraturan sebagai berikut :

X = + t + dengan A

=

Jadi, GLB adalah Gerak benda pada lintasan lurus dengan kecepatan tetap tanpa ada percepatan dan GLBB adalah gerak benda pada lintasan lurus dengan percepatan atau perlambatan tetap.

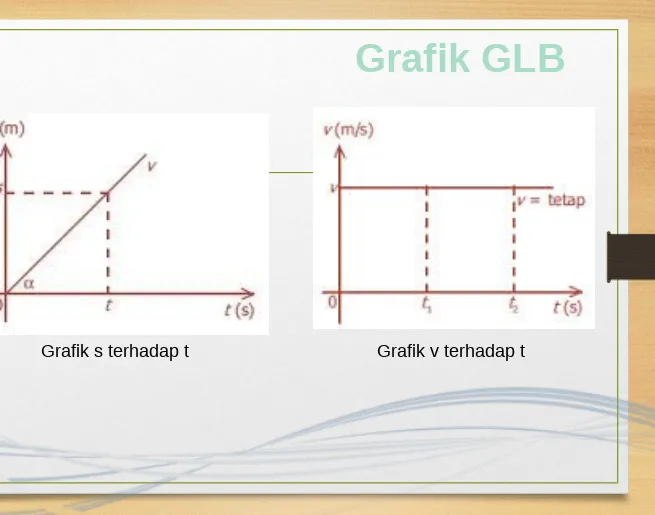
Grafik GLB

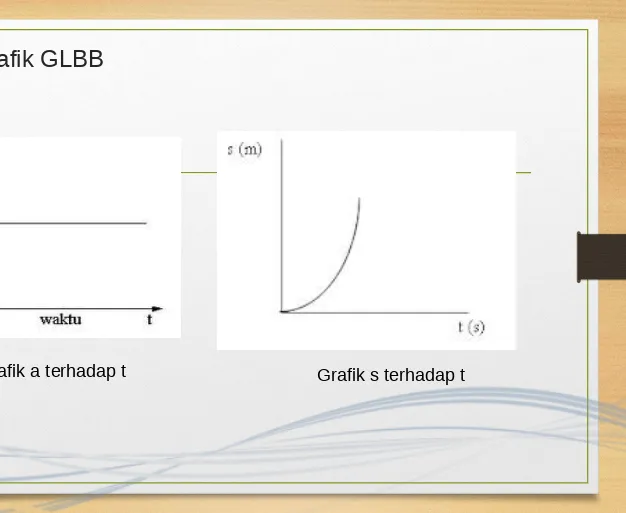
Grafik GLBB

Momen inersia adalah ukuran kelembaman suatu benda untuk berotasi terhadap porosnya. Momen inersia (I) suatu benda

terhadap poros tertentu besarnya sebanding dengan massa benda tersebut dan sebanding dengan kuadrat dari jarak benda terhadap poros.

I ~ m I ~ r2

Untuk katrol dengan beban seperti pada gambar 1 maka berlaku persamaan :

 ∑ sehingga

Dengan :

a = percepatan gerak beban (m/s2)

m = massa beban (kg)

I = momen inersia katrol (m) g = percepatan gravitasi (m/s2)

•

 

Keterangan gambar :

P = penjepit

A = kedudukan awal

B = celah penyangkut

C = landasan akhir

m

₁

= m

₂

Pada gambar : m1 dijepit di P, sementara m2 dan

m3 di A. jika m1 dilepas maka (m2 + m3) akan

turun dari A ke B dengan gerak dipercepat. Pada

saat melalui celah B, m3 akan tertinggal, maka

gerak dari B ke C merupakan gerak lurus

beraturan karena m1=m2 (m1<(m2+m3)).

PENGOLAHAN DATA

GLBB : Gerak Lurus Berubah Beraturan

NO

Dengan 1 beban dengan 2 beban Jarak AB TAB Jarak AB TAB

PENGOLAHAN DATA

Dengan 1 Beban Tambahan

•

 

3 3.6481 0,25 13.3086 0,06250.912025 4 4.2025 0,3 17.6610 0,09 1.26075

13.11

94 0,9 45.05968 0,215 3.111015

No. X1 Y1 X2 Y2 X1Y1 3 3.6481 0,25 13.3086 0,06250.912025 4 4.2025 0,3 17.6610 0,09 1.26075

13.11

94 0,9 45.05968 0,215 3.111015

a

₁

= () 2

=( )2 =

X

2

=

0.156796 m/s

2

Untuk beban 1 Tambahan, a = b =

0.156796 m/s

2

b=

y = ]

 

y = ]

PENGOLAHAN DATA

Dengan 2 Beban Tambahan

a

₁

= () 2

=( )2 =

X

2

=

0.260612m/s

2

Untuk beban 2 Tambahan, a = b =

0.260612 m/s

2

b=

y = ]

 

y = ]

HASIL PENGAMATAN GLB

“GLB” Gerak Lurus Beraturan

y = ]

= ]

y = ]

y = ]

y = = =

•

 

y = 0.2757

Maka b=0.02757

 

0.02757

= 0.02757

= 0.02757 x 4.34099 = 0,11968m/s

b

=0,11968m/s

MAKA V = {00.11968} m/s

Tingkat ketelitian = (1- %

Analisa Data Momen Inersia

I

1

=[ - (m

1

+ m

2

+ m

3

)] r

2

I

2

=[ - (m

1

+ m

2

+ m

3

+ m

4

)] r

2

= =

0.156796

= =

0.260612

Dari massa beban dan jari-jari katrol :

m

1

± m

1

= (0.0784 ± 0,005) kg

m

2

± m

2

= (0.0784 ± 0,005) kg

m

3

± m

3

= (0.0036 ± 0,005) kg. (bebantambahan 1)

m

4

± m

4

= (0.0056 ± 0,005) kg. (bebantambahan 2)

R ± R =(0.065 ± 0,0025) m

I

1

=[ -

(0.0784+ 0.0784+0.0036)kg) ] (0.0650)2 m2

I

1

= [ (0.1604)] (0.004225 m)

I

1

= 0.004225 m

2

= 0,06415kg . 0.004225 m

2

= 0.00027103 kg m

2

I

2

=[ -

0.0784+0.0784+0.0036+0.0056)KG) ] (0.0650)2 m2

I

2

= [ - 0.166kg] (0.004225 m)

I

2

= (0.004225 m

2

= 0.17925 kg x 0.004225 m

2

= 0.0007573 kg m

2

I

| |

=

Tingkat ketelitian =

=

KESIMPULAN

Pada pesawat atwood dapat diketahui

bahwa pada GLB kecepatan benda konstan,

percepatan benda = 0 dan pada GLBB

percepatan benda konstan. Pada GLB dan

GLBB hukum II Newton berlaku, yaitu jika

massa diperbesar maka kecepatan dan