BAB I PENDAHULUAN
A. LATAR BELAKANG
Investasi merupakan penempatan sejumlah dana pada saat ini dengan
harapan untuk memperoleh keuntungan di masa mendatang (Abdul
Halim,2005:4). Menurut Tandelilin (2007:5) bahwa hal yang mendasar dalam
proses keputusan investasi adalah pemahaman hubungan antara return yang diharapkan dan risiko suatu investasi. Ketidakpastian risiko membuat investor
mengambil strategi untuk membentuk portofolio. Portofolio merupakan
kombinasi atau gabungan atau sekumpulan aset, baik berupa aset riil maupun
aset finansial yang dimiliki oleh investor.
Investor selalu ingin memaksimalkan return yang diharapkan dengan tingkat risiko tertentu yang bersedia ditanggungnya, atau mencari portofolio
yang menawarkan risiko terendah dengan tingkat return tertentu dalam pembentukan portofolio. Karakteristik portofolio seperti ini disebut sebagai
portofolio yang efisien (Tandelilin,2007:74). Sedangkan portofolio yang
dipilih seorang investor dari sekian banyak pilihan yang ada pada kumpulan
portofolio efisien merupakan portofolio optimal.
Markowitz (1952) mengembangkan pembentukan portofolio yang
berusaha untuk meminimumkan risiko dan memastikan return akan lebih dari jumlah yang ditetapkan pengambil keputusan. Varians digunakan sebagai ukuran risiko dalam model Markowitz. Model Markowitz adalah model
programming. Model Markowitz yang berbentuk kuadratik dianggap tidak mudah diselesaikan oleh sebagian praktisi. Sharpe (1963) memperkenalkan
model baru untuk masalah pembentukan portofolio. Sharpe mengenalkan
risiko sistematik yang mengukur kepekaan return saham terhadap return pasar.
Model tujuan tunggal hanya mempertimbangkan satu fungsi tujuan ,
di sisi lain model multi tujuan mempertimbangkan lebih dari satu fungsi
tujuan . Salah satu teknik untuk menyelesaikan model multi- tujuan adalah
goal programming yang diperkenalkan oleh Charnes, dkk (1995). Goal programming adalah salah satu metode matematis yang dipandang sesuai untuk pemecahan masalah multi- tujuan karena melalui variabel deviasinya,
goal programming secara otomatis menangkap informasi tentang pencapaian relatif dari tujuan yang ada (Charles D & Simson, 2002). Secara umum goal programming ini digunakan untuk menyelesaikan persoalan yang memiliki multi tujuan (atau lebih dari satu tujuan ). Goal programming tidak memberikan prioritas setiap tujuan dengan kata lain setiap tujuan mempunyai
prioritas yang sama, sedangkan penyelesaian goal programming dengan memprioritaskan tujuan atau dapat dikatakan mempunyai bobot pada setiap
tujuan disebut lexicographic goal programming.
Sebagaimana diketahui dalam portofolio optimal, terdapat
permasalahan multi-tujuan. Metode goal programming dalam masalah keuangan dikembangkan oleh Lee & Lerro (1973). Pendekatan yang sama
dikenalkan Bilbao, dkk (2006), Kumar, dkk (1978), Lee & Chesser (1980).
Penelitian mengenai aplikasi model goal programming lain seperti yang dilakukan Rosita & Aran (2012) meneliti mengenai pemilihan portofolio
menggunakan goal programming. Penelitian ini membahas pembentukan portofolio dengan goal programming dari model LAD (Least Absolute Value Deviation).
Salah satu aset yang dapat dianalisis dengan model ini adalah saham.
Saham sebagai salah satu instrumen pasar modal yang paling aktif diperjual
belikan dan dapat dijadikan pilihan bagi para investor untuk mengalokasikan
dana yang dimiliki investor. Saham juga merupakan objek investasi yang
sangat rentan terhadap perubahan yang terjadi. Banyaknya saham yang
terdaftar dalam bursa sering membuat investor bingung dalam memilih saham
yang baik untuk dimasukkan ke dalam portofolionya.
Jakarta Islamic Index merupakan indeks terbaru di Bursa Efek Indonesia, indeks ini hanya memasukkan saham-saham yang memenuhi
kriteria investasi dalam syariat islam. Jakarta Islamic Index menawarkan alternatif baru investasi saham yang halal atau sesuai dengan syariat islam
kepada masyarakat. Menurut Abdul Halim (2005: 53) melihat masyarakat
Indonesia yang mayoritas adalah muslim dan terlebih lagi dengan mulai
diterimanya sistem ekonomi syariah di dunia bisnis Indonesia maka
diberlakukan Jakarta Islamic Index di Bursa Efek Indonesia. Saham syariah
kriteria syariah ( Daftar Efek Syariah yang diterbitkan oleh Bapepam-LK)
dengan mempertimbangkan kapitalisasi pasar dan likuiditas.
Berdasarkan uraian di atas, penelitian ini akan dibahas aplikasi model
goal programming dan model lexicographic goal programming untuk optimisasi portofolio saham pada Jakarta Islamic Index. Model Lee & Chesser (1980) akan digunakan dalam penyelesaian pembentukan portofolio
optimal, dimana model ini merupakan pendekatan linier goal programming yang menggunakan risiko sistematis dan tingkat keuntungan. Adapun yang
menjadi fungsi tujuan dalam penelitian ini adalah jumlah dana yang
diinvestasikan, tingkat return, tingkat risiko sistematis atau risiko pasar (beta) dan pembatasan proporsi dana setiap saham. Selanjutnya, penyelesaian model goal programming dan model lexicographic goal programming akan dibantu menggunakan sofware LINGO.
B. BATASAN MASALAH
Batasan masalah dalam skripsi ini adalah sebagai berikut:
1. Portofolio dibentuk dalam aset finansial berupa saham.
2. Kriteria yang dipertimbangkan dalam menentukan portofolio yaitu
jumlah dana yang diinvestasikan, tingkat return, tingkat risiko sistematis dan pembatasan proporsi dana setiap saham, jadi terdapat 4
tujuan dalam pembentukan portofolio saham.
C. RUMUSAN MASALAH
Adapun masalah yang dapat dirumuskan dalam skripsi ini adalah:
1. Bagaimana pembentukan portofolio saham dengan model goal programming?
2. Bagaimana pembentukan portofolio saham dengan model
lexicographic goal programming?
3. Bagaimana penerapan pembentukan portofolio saham model goal programming dan lexicographic goal programming pada pasar saham di Indonesia?
4. Bagaimana efektifitas model goal programming dan model lexicographic goal programming dalam pembentukan portofolio saham?
D. TUJUAN
1. Untuk mengetahui bagaimana pembentukan portofolio saham dengan
model goal programming.
2. Untuk mengetahui bagaimana pembentukan portofolio saham dengan
model lexicographic goal programming.
3. Untuk mengetahui penerapan pembentukan portofolio saham model
goal programming dan lexicographic goal programming pada pasar saham di Indonesia?
E. MANFAAT
Penulisan skripsi ini diharapkan dapat memberikan manfaat , antara
lain:
1. Bagi investor
Hasil penelitian ini diharapkan dapat dijadikan sebagai masukan dan
bahan pertimbangan dalam pengambilan keputusan investasi di pasar
modal.
2. Bagi Universitas
Dapat dijadikan sebagai tambahan referensi guna meningkatkan proses
belajar mengajar.
3. Bagi Mahasiswa
Dapat digunakan sebagai tambahan referensi untuk penerapan ilmu
pengetahuan khususnya di bidang pasar modal mengenai pembentukan
portofolio optimal.
4. Bagi Penulis
Menambah pengetahuan mengenai analisis pembentukan portofolio
7 BAB II KAJIAN TEORI
A. Investasi
Abdul Halim (2005:4) berpendapat bahwa investasi pada hakikatnya
merupakan penempatan sejumlah dana pada saat ini dengan harapan untuk
memperoleh keuntungan di masa yang akan datang. Pada umumnya investasi
dibedakan menjadi dua yaitu pertama investasi pada aset- aset finansial
(financial assets) berupa sertifikat deposito, commercial paper, surat berharga
yang dilakukan di pasar uang dan investasi yang dilakukan di pasar modal,
misalnya saham, obligasi, waran, opsi. Kedua investasi pada aset- aset riil
(real assets) seperti pembelian aset produktif, pendirian pabrik, pembukaan
pertambangan pembukaan perkebunan dan lainnya.
Proses investasi menunjukkan bagaimana seharusnya seorang investor
membuat keputusan investasi pada aset-aset yang dapat dipasarkan dan kapan
dilakukan, untuk itu diperlukan tahapan sebagai berikut (Abdul Halim,
2005:4) :
1. Menentukan tujuan investasi
Tiga hal yang perlu dipertimbangkan dalam tahap ini, yaitu: return yang diharapkan (expected of return), risiko (risk), dan ketersediaan jumlah dana yang akan diinvestasikan. Apabila dana cukup tersedia, maka
8
(expected return) bersifat linier, artinya semakin tinggi tingkat risiko, maka semakin tinggi pula return yang diharapkan.
2. Melakukan analisis
Tahap ini investor melakukan analisis terhadap suatu aset atau
sekelompok aset. Salah satu tujuan penilaian ini adalah untuk
mengidentifikasi aset yang salah harga (mispriced), apakah harganya terlalu tinggi atau terlalu rendah, ada dua pendekatan yang dapat
digunakan, yaitu:
a. Pendekatan Fundamental
Pendekatan ini didasarkan pada informasi-informasi yang diterbitkan
oleh emiten maupun oleh administrator bursa efek. Karena kinerja
emiten dipengaruhi oleh kondisi sektor industri dimana perusahaan
tersebut berada dan perekonomian secara makro, maka untuk
memperkirakan prospek harga sahamnya di masa mendatang harus
dikaitkan dengan faktor-faktor fundamental yang mempengaruhinya.
Jadi analisis ini dimulai dari siklus usaha perusahaan secara umum,
selanjutnya ke sektor industrinya. Akhirnya dilakukan evaluasi
terhadap kinerjanya dan saham yang diterbitkannya.
b. Pendekatan Teknikal
Pendekatan ini didasarkan pada data (perubahan) harga saham di
masa lalu sebagai upaya untuk memperkirakan harga saham di masa
mendatang. Para analisis memperkirakan pergeseran penawaran
9
mereka berusaha untuk cenderung mengabaikan risiko dan
pertumbuhan laba dalam menentukan barometer dari penawaran dan
permintaan. Namun demikian, analisis ini lebih mudah dan cepat
dibanding analisis fundamental, karena dapat secara simultan
diterapkan pada beberapa saham. Analisis ini tidak menganggap
bahwa analisis fundamental tidak berguna, namun investor
menganggap bahwa analisis fundamental terlalu rumit dan terlalu
banyak mendasarkan pada laporan keuangan emiten. Oleh karena itu,
analisis teknikal mendasarkan diri pada premis bahwa harga saham
tergantung pada penawaran dan permintaan saham itu sendiri. Data
finansial historis yang tergambar pada diagram dipelajari untuk
mendapatkan suatu pola yang berarti, dan pola tersebut digunakan
untuk memprediksi harga di masa mendatang, serta untuk
memperkirakan pergeseran individual saham maupun pergerakan
indeks pasar (market index). 3. Membentuk portofolio
Tahap ini dilakukan identifikasi terhadap aset-aset mana yang akan
dipilih dan berapa proporsi dana yang akan diinvestasikan pada
masing-masing aset tersebut.
4. Mengevaluasi kinerja portofolio
Tahap ini dilakukan evaluasi atas kinerja portofolio yang telah dibentuk,
10
pengukuran (measurement) adalah penilaian kinerja portofolio atas dasar aset yang telah ditanamkan dalam portofolio tersebut. Kedua,
perbandingan (comparison) yaitu penilaian berdasarkan pada perbandingan dua set portofolio dengan risiko yang sama.
5. Merevisi portofolio
Tahap ini merupakan tindak lanjut dari tahap evaluasi kinerja portofolio,
dari hasil evaluasi inilah selanjutnya dilakukan revisi (perubahan)
terhadap aset- aset yang membentuk portofolio tersebut jika dirasa bahwa
komposisi portofolio yang sudah dibentuk tidak sesuai dengan tujuan
investasi. Revisi tersebut dapat dilakukan secara total yaitu dilakukan
likuidasi atas portofolio yang ada, kemudian dibentuk portofolio yang
baru, atau dilakukan secara terbatas, yaitu dilakukan perubahan atas
proporsi atau komposisi dana yang dialokasikan dalam masing-masing
aset yang membentuk portofolio tersebut.
B. Saham
Saham dapat didefinisikan sebagai tanda penyertaan atau surat
kepemilikan seseorang atau badan dalam suatu perusahaan atau perusahaan
terbatas. Wujud saham berupa selembar kertas yang menerangkan bahwa
pemilik saham tersebut adalah pemilik perusahaan yang menerbitkansurat
berharga tersebut. Porsi kepemilikan ditentukan oleh seberapa besar
penyertaan yang ditanamkan di perusahaan tersebut (Tjiptono Darmadji,
11 C. Transaksi Saham
Sebelum melakukan jual beli saham, seperti layaknya membuka
rekening di bank maka terlebih dahulu harus membuka rekening disatu atau
beberapa perusahaan aset, maka secara resmi telah tercatat sebagai nasabah
dan data identitas tercatat dalam pembukuan perusahaan aset seperti nama,
alamat, nomor rekening bank dan data- data lainnya. Bersama dengan
pembukuan rekening ini, terdapat perjanjian harus ditandatangani dengan
perusahaan aset yang menyangkut hak dan kewajiban kedua belah pihak.
Pada dasarnya tidak ada batasan dana dan jumlah untuk jual beli
saham, jumlah yang diperjual-belikan adalah dalam satuan perdagangan yang
disebut lot, dalam bursa aset Indonesia satu lot berarti 100 saham, itulah batas
minimal pembelian saham. Dana yang dibutuhkan untuk bisnis saham
menjadi bervariasi karena beragamnya harga saham-saham yang tercatat di
bursa.
D. Jakarta Islamic Index
Jakarta Islamic Index (JII) adalah indeks saham yang didasarkan atas prinsip syariah. Saham dalam JII terdiri atas 30 saham yang keanggotaannya
akan terus ditinjau secara berkala berdasarkan kinerja transaksi di
perdagangan bursa, rasio- rasio keuangannya, dan ketaatannya pada prinsip-
prinsip syariah sebagaimana termaktub dalam fatwa Dewan Syariah Nasional
no 05/DSN-MU/IV/2000 tentang jual beli saham dan fatwa
40/DSN-MUI/IX/2003 tentang pasar modal, serta pedoman umum penerapan prinsip
12
Saham- saham yang masuk dalam indeks syariah adalah emiten yang
kegiatan usahanya tidak bertentangan dengan syariah seperti:
a. Usaha perjudian dan permainan yang tergolong judi atau perdagangan
yang dilarang
b. Usaha lembaga keuangan konvensional (ribawi) termasuk perbankan dan
usaha asuransi konvensional
c. Usaha yang memproduksi, mendistribusi serta memperdagangkan
makanan dan minuman yang tergolong haram
d. Usaha yang memproduksi mendistribusi dan atau menyediakan barang-
barang ataupun jasa yang merusak moral dan bersifat mudarat.
Selain kriteria di atas, dalam proses pemilihan saham yang masuk JII,
Bursa Aset Jakarta melakukan tahap- tahap pemilihan yang juga
mempertimbangkan aspek likuiditas dan kondisi keuangan emiten, yaitu:
a. Kumpulan saham dengan jenis usaha utama yang tidak bertentangan
dengan prinsip syariah dan sudah tercatat lebih dari 3 bulan (kecuali
termasuk dalam 10 kapitalisasi besar).
b. Saham yang berdasarkan laporan keuangan tahunan atau tengah tahun
memiliki rasio kewajiban terhadap aktiva maksimal 90%.
c. Enam puluh saham dari susunan saham berdasarkan urutan rata- rata
kapitalisasi pasar (market capitalization) terbesar selama satu tahun terakhir.
d. Tiga puluh saham dengan urutan berdasarkan tingkat likuiditas rata-rata
13
Evaluasi terhadap saham- saham yang masuk dalam perhitungan JII
dilakukan setiap 6 bulan sekali dengan penentuan komponen index pada awal
bulan Januari dan Juli setiap tahunnya. Sedangkan perubahan jenis usaha
emiten akan terus diawasi berdasarkan data- data publik yang tersedia.
Apabila saham- saham tersebut tidak lagi memenuhi prinsip- prinsip syariah,
otoritas akan mengeluarkannya dari JII dan kedudukannya digantikan saham
lain yang memenuhi prinsip- prinsip syariah (Muhamad Nafik, 2009:260).
Dilihat dari nilai kapitalisasinya maupun nilai indeksnya, saham-
saham yang tergabung dalam JII punya kinerja yang baik. Saham- saham JII
merupakan saham yang masuk kategori blue chips yaitu sekitar 80% , masuk kategori LQ-45 sehigga pergerakan kapitalisasi dan indeks saham- saham JII
selalu mengikuti pergerakan pasar.
E. Teori Portofolio
Portofolio merupakan kombinasi atau gabungan atau sekumpulan aset,
baik berupa aset riil maupun aset finansial yang dimiliki investor (Abdul
Halim, 2005:54). Suatu portofolio dikatakan efisien apabila portofolio
tersebut ketika dibandingkan dengan portofolio lain memberikan nilai return terbesar dengan risiko yang sama, atau memberikan nilai risiko terkecil
dengan return yang sama. Portofolio optimal adalah portofolio yang dipilih oleh investor dari kumpulan portofolio efisien. Pemilihan portofolio tersebut
14 F. Return
Return merupakan keuntungan yang diperoleh dari investasi yang dilakukan. Return dapat berupa realized return (return realisasi) yang sudah terjadi atau expected return (return ekspektasi) yang belum terjadi tetapi yang diharapkan akan terjadi di masa mendatang. Realized return penting karena digunakan sebagai salah satu alat pengukur kinerja dari suatu perusahaan.
Realized return atau return historis juga digunakan dalam menghitung expected return dan risiko di masa mendatang. Nilai realized return saham ke-i , i = 1,2,...,n , periode ke-t ,t = 1,2,..., n, dilambangkan dengan , dihitung berdasarkan data historis dengan rumus sebagai berikut :
(2.1)
Keterangan :
= realized return saham ke-i pada periode ke- t
= harga saham pada periode ke-t
= harga saham pada periode t-1
Expected return adalah tingkat keuntungan yang diharapkan oleh investor di masa mendatang, dihitung berdasarkan rata-rata yang berasal dari suatu
distribusi return sebagai berikut (Elton dan Gruber, 1995) : ∑
(2.2)
Keterangan :
= expected return saham ke-i
15
Return yang dipersyaratkan (required return) atau return minimal merupakan tingkat return minimal yang dikehendaki oleh investor atas preferensi subyektif investor terhadap risiko. Return yang dipersyaratkan diperoleh secara historis. Nilai return yang dipersyaratkan biasanya merupakan nilai mean dari expected return seluruh saham yang diinvestasikan.
Realized return portofolio adalah jumlah nilai return realisasi saham- saham di dalam portofolio (Jogiyanto, 2010 : 312) sebagai berikut:
∑ (2.3)
Keterangan :
= realized return portofolio
= proporsi saham yang diinvestasikan
Expected return portofolio merupakan rata-rata tertimbang dari expected return masing- masing saham tunggal pada portofolio. Secara matematis, return portofolio dapat ditulis sebagai berikut (Jogiyanto,2010 : 312) :
( ) ∑ (2.4)
Keterangan :
( ) = expected return portofolio
G. Risiko
Menurut Wardani (2010) risiko adalah kemungkinan penyimpangan
16
maka preferensi investor terhadap risiko dibedakan menjadi tiga (Mohammad
Samsul, 2007:356), yaitu:
1. Investor yang suka terhadap risiko (risk seeker)
Risk seeker merupakan investor yang apabila dihadapkan pada dua
pilihan investasi yang memberikan tingkat pengembalian sama dengan
risiko yang berbeda, maka ia akan lebih memilih investasi dengan risiko
yang lebih besar. Biasanya investor ini bersikap agresif dan spekulatif
dalam mengambil keputusan investasi.
2. Investor yang netral (risk neutrality)
Investor yang akan meminta kenaikan tingkat pengembalian yang sama
untuk setiap kenaikan risiko investor jenis ini umumnya cukup fleksibel
dan bersikap hati- hati dalam mengambil keputusan.
3. Investor yang tidak suka terhadap risiko (risk averter)
Investor yang apabila dihadapkan pada dua pilihan investasi yang
memberikan tingkat pengembalian yang sama dengan risiko yang
berbeda, maka ia akanlebih suka mmilih investasi dengan risiko yang
lebih kecil. Biasanya investor bersikap matang dalam menentukan pilihan
investasi.
Risiko saham ke-i diukur dengan standard deviation sebagai berikut (Jogiyanto, 2010: 229)
√∑
(2.5)
Keterangan :
17
Risiko portofolio dapat dihitung menggunakan varians dari , dapat ditulis sebagai berikut(Jogiyanto, 2010: 257):
( )
∑ ∑
( )
( )
( ) ( ) ( )
( ) ( ) ( )
( )( )
( )( )
( )
∑ ∑
Persamaan di atas dapat ditulis dalam bentuk matriks berikut:
[
]
18 Keterangan :
= varians portofolio
= kovarians saham ke-i dan ke- j
Setelah diketahui varians portofolio, dapat dihitung standard deviation yang merupakan risiko portofolio diperoleh dari akar kuadrat dari varians portofolio.
H. Beta Saham
Beta merupakan suatu pengukur volatilitas return suatu saham atau return portofolio terhadap return pasar. Beta saham ke-i mengukur volatilitas return saham ke-i dengan return pasar. Beta portofolio mengukur volatilitas return portofolio dengan return pasar, dengan demikian beta merupakan pengukur risiko sistematik (systematic risk) dari suatu saham (Jogiyanto,2010:375). Beta portofolio dapat dihitung dengan mengetahui beta
masing – masing saham terlebih dahulu. Beta saham ke-i dapat dihitung dengan rumus sebagai berikut (Jogiyanto, 2010; 383):
∑
∑ (2.7)
Keterangan :
= beta saham ke-i
= return pasar periode ke- t = return pasar
Beta portofolio ( ) merupakan rata- rata tertimbang dari beta
19
∑ (2.8)
Keterangan:
= proporsi saham ke-i = beta portofolio
Jika beta suatu saham sama dengan satu, , berarti saham
tersebut memiliki risiko yang sama dengan risiko rata- rata pasar. Misalnya,
jika IHSG naik 5%, maka harga pasar saham tersebut cenderung meningkat
5%. Sementara itu, jika , berarti saham tersebut memiliki risiko lebih
kecil dari risiko rata- rata pasar dan saham tersebut akan bergerak 0,5 kali
perubahan IHSG. Selanjutnya jika , berarti saham tersebut memiliki
risiko lebih besar dari risiko rata- rata pasar dan saham tersebut akan bergerak
1,5 kali perubahan IHSG.
Oleh karena itu, semakin besar beta , maka akan semakin peka excess return suatu saham terhadap perubahan excess return portofolio pasar, sehingga saham itu akan semakin berisiko, dengan demikian dapat dikatakan
bahwa tingkat pengembalian portofolio ditentukan oleh risiko sistematis atau
risiko pasar yang diukur dengan beta ( dan tingkat pengembalian pasar.
Beta saham mengindikasikan tingkat kepekaan saham terhadap
kondisi pasar secara umum. Jika beta suatu saham lebih besar dari beta pasar
, berarti saham tersebut memiliki risiko lebih tinggi dari risiko rata-
rata pasar, dan saham tersebut termasuk saham agresif. Sebaliknya, jika beta
suatu saham lebih kecil dari satu, berarti saham tersebut termasuk saham
20
keberanian investor dalam menanggung risiko. Semakin berani seorang
investor menanggung risiko , dia akan memilih saham- saham agresif (Abdul
Halim, 2005:74).
I. Koefisien Variasi
Dua faktor harus dipertimbangkan bersama-sama dalam melakukan
analisis investasi, yaitu expected return dan risiko saham. Koefisien variasi (coefficient of variation) dapat digunakan untuk mempertimbangkan dua faktor tersebut bersamaan (Jogiyanto,2010:290). merupakan notasi
koefisien variasi untuk saham ke-i. Rumus koefisien variasi adalah:
(2.9)
Rumus koefisien variasi dapat diartikan bahwa semakin kecil nilai
semakin baik saham tersebut. Semakin kecil menunjukkan semakin kecil
risiko saham dan semakin besar expected return. J. Indeks Sharpe
Tujuan penilaian kinerja portofolio adalah untuk mengetahui dan
menganalisis apakah portofolio yang dibentuk telah dapat meningkatkan
kemungkinan tercapainya tujuan investasi sehingga dapat diketahui
portofolio mana yang memiliki kinerja yang lebih baik jika ditinjau dari
21
(2.10)
Keterangan:
= indeks sharpe = return Portofolio = risiko portofolio
K. Pemrograman Linier
Menurut Fredick S. Hiller dan Gerald J. Lieberman, program linier
merupakan suatu model matematis untuk menggambarkan masalah yang
dihadapi. Linier berarti bahwa semua fungsi matematis dalam model ini harus
merupakan fungsi – fungsi linier. Pemrogaman merupakan sinonim untuk
kata perencanaan, dengan demikian membuat rencana kegiatan- kegiatan
untuk memperoleh hasil yang optimal, ialah suatu hasil untuk mencapai
tujuan yang ditentukan dengan cara yang paling baik (sesuai dengan model
matematis) diantara semua alternatif yang mungkin (Andi Wijaya ,2013: 9).
Program linier dikenal dua macam fungsi, yaitu:
a. Fungsi tujuan , menggambarkan apa yang ingin dicapai perusahaan dengan
menggunakan sumber daya yang ada, fungsi tujuan digambarkan dalam
bentuk maksimasi ( misalnya untuk laba, penerimaan, produksi, dan lain-
lain atau minimasi (misalnya untuk biaya) yang dinyatakan dalam notasi
Z.
b. Fungsi kendala, menggambarkan kendala- kendala yang dihadapi
22
mesin, tenaga kerja, dan lain- lain, untuk kasus program linier, kendala
yang dihadapi berjumlah dari satu kendala.
1. Asumsi – Asumsi Dasar Pemrograman Linier
Asumsi – asumsi dasar pemrograman linier diuraikan agar
penggunaan teknik pemrograman linier dapat memuaskan untuk berbagai
masalah. Adapun asumsi – asumsi dasar pemrograman linier sebagai
berikut (Pangestu Subagyo,1995:14) :
a) Kesebandingan (Proportionality)
Asumsi ini mempunyai arti bahwa naik turunnya nilai fungsi tujuan
dan penggunaan sumber atau fasilitasyang tersedia akan berubah secara
sebanding (proportional ) dengan perubahan tingkat kegiatan.
b) Penambahan (Additivity)
Nilai fungsi tujuan tiap kegiatan tidak saling mempengaruhi atau dalam
pemrograman linier dianggap bahwa kenaikan dari nilai tujuan yang
diakibatkan oleh kenaikan suatu kegiatan dapat ditambahkan tanpa
mempengaruhi bagian nilai tujuan yang diperoleh dari kegiatan lain.
c) Dapat dibagi (Divisibility)
Asumsi inimenyatakan bahwa keluaran yang dihasilkan oleh setiap
kegiatan dapat berupa jikangan pecahan. Demikian pula dengan nilai
tujuan yang dihasilkan.
d) Kepastian (Deterministic)
Semua parameter yang terdapat dalam model pemrograman linier dapat
23
2. Bentuk Umum Model Pemrograman Linier
Masalah pemrograman linier merupakan masalah optimasi
bersyarat yakni pencarian nilai maksimum atau pencarian nilai minimum
sesuatu fungsi tujuan berkenaan dengan keterbatasan – keterbatasan atas
kendala yang harus dipenuhi. Masalah- masalah tersebut secara umum
dapat dirumuskan sebagai berikut (Johannes Supranto, 1991: 44):
Fungsi tujuan meminimalkan dinotasikan dengan Z dan relasi
dalam kendala berbentuk , dapat ditulis sebagai berikut:
Meminimalkan
dengan kendala,
, i = 1,2, ... , n (2.11) Fungsi tujuan memaksimalkan dinotasikan dengan Z dan relasi dalam kendala berbentuk , dapat ditulis sebagai berikut:
Memaksimalkan
dengan kendala,
24
(2.12)
Keterangan :
: variabel keputusan ke-n
: suku tetap/ bahan mentah ke-m yang tersedia
: koefisien kendala
: koefisien ongkos ke-n
L. Metode Simpleks
Metode simpleks pertama kali diperkenalkan oleh George B. Dantzig
pada tahun 1947 dan telah diperbaiki oleh para ahli lain. Metode simpleks
adalah suatu prosedur bukan secara grafis maupun aljabar yang digunakan
untuk mencari nilai optimal dari fungsi tujuan dalam masalah-masalah
optimisasi yang terkendala. Pencarian nilai optimum dengan menggunakan
metode simpleks dilakukan proses pengulangan (iterasi) dimulai dari
penyelesaian dasar awal yang layak (feasible) hingga penyelesaian dasar akhir yang layak dimana nilai dari fungsi tujuan telah optimum. Dalam hal
ini proses pengulangan tidak dapat dilakukan lagi. Secara khusus prosedur
pengulangan mudah dipahami menggunakan operasi baris dari Gauss-Jordan.
Permasalahan model linear harus diubah kedalam bentuk kanonik sebelum
dilakukan penyelesaian menggunakan metode simpleks, perubahan tersebut
25 1. Fungsi kendala
Terdapat tiga persyaratan untuk merumuskan fungsi kendala masalah
pemrogaman linier dengan menggunakan metode simpleks, yaitu
a. Semua kendala pertidaksamaan harus dinyatakan sebagai persamaan
Sebelum penyelesaian dengan metode simpleks pertidaksamaan harus
diyatakan dalam persamaan linier. Perubahan tersebut dibedakan
menjadi tiga sesuai sifat persamaaan tersebut
1) Tanda lebih kecil dari atau sama dengan (≤)
Kendala yang mempunyai tanda lebih kecil dari atau sama dengan
harus ditambahkan dengan variabel slack ( ) non negatif disisi kiri kendala. Variabel ini untuk membuat ruas yang semula longgar
menjadi ketat sehingga sama nilainya dengan ruas yang lainnya
(B. Susanta, 1994: 69) . Contoh kendala berubah
menjadi
2) Tanda lebih besar dari atau sama dengan (≥)
Kendala yang mempunyai tanda lebih besar dari atau sama dengan (≥) harus ditambahkan dengan variabel surplus (t) non negatif
disisi kanan kendala dan ditambahkan variabel buatan atau
artificial variabel (q) disisi kiri. Variabel surplus untuk membuat
ruas yang semula longgar menjadi ketat sehingga sama nilainya
dengan ruas yang lainnya. Variabel buatan memudahkan untuk
menyelesaikan masalah awal metode simpleks. Contoh kendala
26 3) Tanda sama dengan (=)
Setiap kendala yang mempunyai tanda sama dengan (=), harus
ditambahkan dengan variabel buatan di sisi kiri kendala. Contoh
kendala berubah menjadi .
b. Sisi kanan dari suatu kendala persamaan tidak boleh negatif
Jika sebuah kendala bernilai negatif di sisi kanan, kendala tersebut
harus dikalikan -1 untuk membuat sisi kanan positif.Jika terdapat
pertidaksamaan yang sisi kanan bernilai negatif maka harus dikalikan -1
sehingga merubah tanda pertidaksamaanya juga. Contoh kendala
berubah menjadi
c. Semua variabel dibatasi nilai-nilai non negatif
Variabel-variabel yang bernilai negatif terdapat metode khusus dalam
penyelesaiannya akan tetapi tidak dibahas dalam tulisan ini. Contoh
kendala
2. Fungsi tujuan
Permasalahan model linear dapat dibedakan menjadi dua yaitu
meminimalkan atau memaksimalkan fungsi tujuan . Perubahan
masing-masing fungsi tujuan kedalam bentuk kanonik berbeda satu sama
lain,dapat dituliskan bentuk kanonik dari metode simpleks sebagai
27 a. Fungsi tujuan meminimalkan
Meminimalkan
dengan kendala
dengan dan untuk i=1,2,...,m; j=1,2,...,n (2.13)
maka bentuk kanonik metode simpleks dapat dituliskan menjadi:
(2.14)
b. Fungsi tujuan memaksimalkan
Memaksimalkan
dengan kendala
28
dengan dan untuk i=1,2,...,m; j=1,2,...,n
maka bentuk kanonik metode simpleks dapat dituliskan menjadi:
(2.16)
dimana adalah variabel slack non negatif.
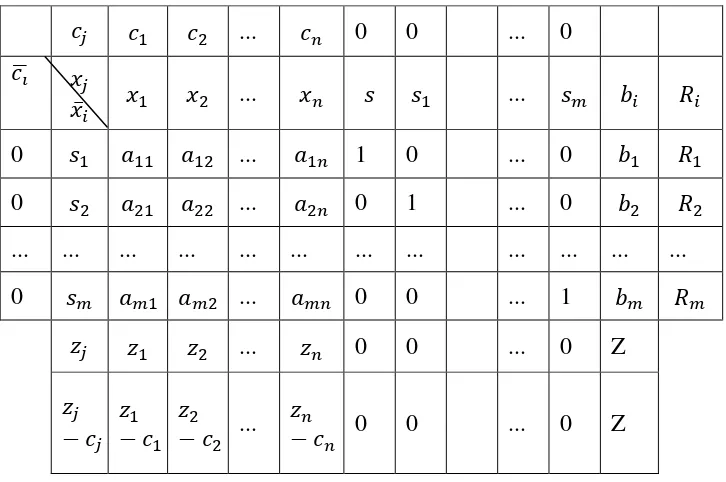
Tabel awal simpleks dengan matriks yang diperbesar dengan
penambahan variabel basis dan . Tabel awal simpleks dapat dilihat
seperti Tabel 2.1 Dumairy,2012:369).
Tabel 2. 1 Tabel Awal Simpleks Penyelesaian Program Linear
... 0 0 ... 0
̅
̅ ... ...
0 ... 1 0 ... 0
0 ... 0 1 ... 0
... ... ... ... ... ... ... ... ... ... ... ...
0 ... 0 0 ... 1
... 0 0 ... 0 Z
29 Keterangan :
= variabel fungsi tujuan
= koefisien teknis
= konstanta ruas kanan setiap kendala
= koefisien ongkos fungsi tujuan , untuk variabel slack dan surplus bernilai nol sedangkan variabel artifisial bernilai –M untuk polamemaksimalkan dan M untuk pola meminimumkan
̅ = variabel basis pada persamaan kanonik
̅ = koefisien untuk variabel dalam basis , pada awal koefisien
ini bernilai nol.
= hasil kali , dengan kolom ∑
= rasio terkecil untuk menentukan variabel keluar (baris pivot),
diperoleh dengan rumus ⁄ yang digunakan untuk
menentukan baris kunci yaitu dipilih dengan terkecil dengan
Z = nilai fungsi tujuan yang diperoleh dari ∑ ̅
Penyelesaian metode simpleks dilakukan guna memperoleh kombinasi
yang optimal dari variabel-variabel pilihan. Langkah-langkah penyelesaian
metode simpleks sebagai berikut (Dumairy, 2012:370):
1. Rumuskan dan mengubah model menjadi bentuk kanonik.
2. Bentuk tabel pertama berdasarkan keterangan tabel simplek 2.1
30
kolom yang mengandung nilai paling positif untuk kasus
maksimasi atau mengandung nilai paling negatif jika kasusnya
minimasi.
4. Tentukan baris pivot diantara baris – baris variabel yang ada,yaitu baris yang memiliki “rasio kuantitas” dengan nilai positif terkecil, baik masalah
maksimasi maupun minimasi.
5. Bentuk tabel berikutnya dengan memasukkan variabel yang masuk ke
kolom program dan mengeluarkan variabel yang keluar dari kolom
tersebut, serta lakukan transformasi baris- baris variabel.
6. Lakukan pengujian optimalitas. Ciri-ciri tabel simpleks yang sudah optimal
dibedakan menjadi
a. Pola memaksimumkan
Tabel sudah optimal jika ( ) untuk semua j b. Pola meminimumkan
Tabel sudah optimal jika ( ) untuk semua j
Selanjutnya kembali ke langkah nomor 2 dan seterusnya hingga
diperoleh penyelesaian yang optimal.Berikut merupakan contoh penyelesaian
masalah program linear menggunakan metode simpleks agar mempermudah
pemahaman (Dumairy, 2012:371).
Contoh:
Maksimumkan
Dengan kendala :
31
Berdasarkan langkah- langkah penyelesaian pemrograman linier, masalah di
atas terlebih dahulu diubah menjadi bentuk kanonik, berikut model kanonik:
Maksimumkan
Dengan kendala,
Model yang sudah berbentuk kanonik ini dapat langsung diterjemahkan
menjadi tabel simpleks pertama, dengan menempatkan variabel- variabel
semu atau slack variable sebagai variabel dasar. Langkah
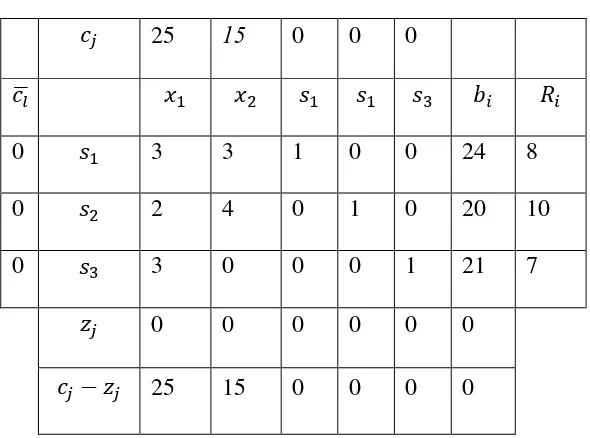
[image:31.595.165.460.494.713.2]awal disajikan pada Tabel 2.2 sebagai berikut:
Tabel 2.2 Tabel simpleks I
25 15 0 0 0
̅
0 3 3 1 0 0 24 8
0 2 4 0 1 0 20 10
0 3 0 0 0 1 21 7
0 0 0 0 0 0
32
Pada Tabel 2.2 terlihat bahwa tabel belum optimal karena masih
terdapat nilai positif pada baris .Dipilih nilai terbesar sehingga
kolom pivot pada tabel tersebut menjadi variabel yang masuk. Ternyata nilai
terbesar dimiliki oleh kolom , nilai terkecil adalah 7 pada
variabel basis sehingga keluar digantikan variabel . Perpotongan
antara kolom pivot dan baris pivot menjadi elemen pivot yang menjadi acuan
perhitungan Operasi Baris Elementer (OBE) untuk pengisian tabel simpleks
selanjutnya. Selanjutnya dilakukan dengan cara perhitungan terlebih dahulu
pada baris pivot, elemen pivot yang sebelumnya bernilai 3 diubah menjadi 1
dengan cara perhitungan baris pivot dikalikan 1/3 Sedangkan elemen di atas
elemen pivot (menjadi 0) diperoleh dengan cara, baris kedua dikurangi 2/3
dikalikan baris pivot. Sedangkan baris pertama dikurangi 1 dikalikan baris
pivot, sehingga tabel iterasi II seperti Tabel 2.3.
Tabel 2.3 Tabel simpleks iterasi II
25 15 0 0 0
̅
0 0 3 1 0 -1 3 1
0 0 4 0 1 2/3 6 1,5
25 1 0 0 0 1/3 7 --
23 0 0 0 25/3 0
33
Berdasarkan Tabel 2.3 dapat dilihat bahwa nilai tersebut belum
optimal, karena masih ada nila yang bernilai positif, sehingga harus
ditentukan kolom pivot, baris pivot dan elemen pivot. Nilai terbesar
dimiliki oleh kolom dan variabel merupakan variabel masuk. Adapun
baris pivot adalah baris karena memiliki nilai terkecil dan basis
merupakan variabel yang keluar. Sehingga keluar digantikan variabel .
Elemen pivot yang sebelumnya bernilai 3 diubah menjadi 1 dengan cara
perhitungan baris pivot dikalikan 1/3 Sedangkan elemen di bawah elemen
pivot (menjadi 0) diperoleh dengan cara, baris kedua dikurangi 4/3 dikalikan
baris pivot. Sedangkan baris ketiga dikurangi 0 dikalikan baris pivot,
[image:33.595.158.468.417.635.2]sehingga tabel iterasi II seperti Tabel 2.4.
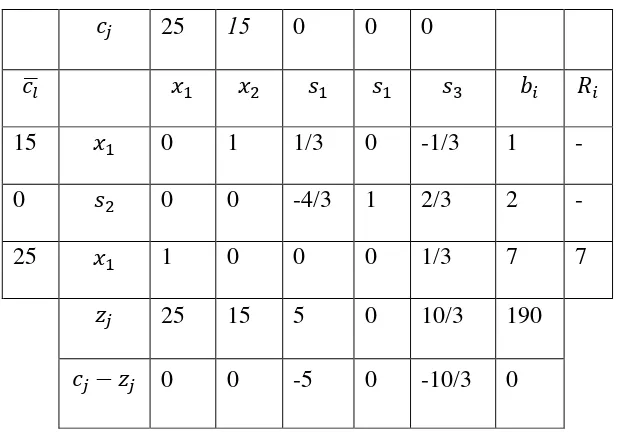
Tabel 2.4 Tabel Simpleks Iterasi Akhir
25 15 0 0 0
̅
15 0 1 1/3 0 -1/3 1 -
0 0 0 -4/3 1 2/3 2 -
25 1 0 0 0 1/3 7 7
25 15 5 0 10/3 190
0 0 -5 0 -10/3 0
Pada penyelesaian tahap ketiga ini terlihat tidak terdapat lagi unsur
34
merupakan tabel optimal. Dengan membaca tabel terakhir ini dapat
disimpulkan bahwa optimalitas tercapai pada kombinasi produksi 7 unit
dan 1 unit dengan provit maksimum 190 dan tersisa 2 unit masukan
.
M. Goal Programming
Goal programming adalah salah satu metode yang digunakan dalam pemecahan masalah program linier dengan multi-tujuan. Model umum
program linier multi tujuan dapat dituliskan sebagai berikut (Mohammed &
Hordofa, 2016:3) :
Memaksimumkan
∑
dengan kendala
∑
(2.17)
Keterangan:
= fungsi tujuan ke- i
= variabel keputusan
= koefisien
= jumlah sumber daya yang tersedia
Fungsi tujuan model goal programming selalu diekspresikan dalam bentuk minimisasi yaitu meminimalkan penyimpangan dari nilai fungsi-
35
adalah merumuskan variabel- variabel penyimpangan dari fungsi tujuan yaitu
, dituliskan sebagai berikut:
∑ (2.18)
dimana
dan
Fungsi tujuan goal programming adalah meminimalkan nilai varibel – variabel penyimpangan dari fungsi – fungsi tujuan dengan tambahan fungsi
kendala, yaitu :
∑ (2.19)
atau
∑ (2.20)
Sehingga model goal programming dari masalah (2.17) adalah (Hillier dan Lieberman, 1980: 173):
Meminimalkan
∑
dengan kendala
∑
∑
(2.21)
Keterangan:
= penyimpangan ke- i
36
= penyimpangan atas ke- i (overachievement)
Notasi adalah variabel penyimpangan yang merepresentasikan
tingkat pencapaian di bawah target ( underachievement ). Notasi adalah variabel penyimpangan yang merepresentasikan tingkat pencapaian di atas
target (overachievement ). Kedua variabel penyimpangan tersebut merupakan sepasang variabel deviasional yang berfungsi untuk menampung
penyimpangan yang akan terjadi pada nilai ruas kiri suatu persamaan kendala
terhadap nilai ruas kanannya. Agar penyimpangan tersebut minimal, artinya
nilai ruas kiri suatu persamaan kendala sebisa mungkin mendekati nilai ruas
kanannya maka variabel deviasional itu harus diminimalkan di dalam fungsi
tujuan (Siswanto, 2007: 342). Berdasarkan tujuan dapat ditentukan variabel
[image:36.595.138.490.500.618.2]deviasional yang akan diminimalkan dalam fungsi tujuan goal programming pada Tabel 2.5 berikut (Orumie dan Ebong, 2014:61):
Tabel 2.5 Stuktur Umum Goal Programming Tujuan Variabel deviasional yang diminimalkan dalam Z
Fungsi tujuan pertama (baris pertama Tabel 2.5) menyatakan bahwa
tujuan yang hendak dicapai dituangkan ke dalam dan tidak boleh
37
agar hasil tidak melebihi nilai , maka dibutuhkan variabel deviasional
untuk diminimalkan. Fungsi tujuan kedua (baris kedua Tabel 2.5) menyatakan
bahwa penyimpangan diubah nilai harus diminimalkan agar hasil
penyelesaian paling sedikit sama dengan , dengan demikian
akan diminimumkan. Fungsi tujuan terakhir (baris ketiga Tabel 2.5 )
setiap penyimpangan atas dan bawah tidak boleh dilampaui, maka
dan harus diminimumkan. Apabila kedua variabel deviasional yang
dimaksud di atas dapat diminimisasi, artinya: kedua variabel deviasional
bernilai nol, maka tujuan telah tercapai, begitu juga sebaliknya.
Pada beberapa kasus, tujuan satu akan lebih penting dengan tujuan
lainnya, maka pengambil keputusan harus menentukkan mana dari tujuan –
tujuan tersebut yang diprioritaskan. Misalkan tujuan yang paling penting
sebagai prioritas ke-1. Tujuan yang kurang begitu penting ditentukan sebagai
prioritas ke-2, demikian seterusnya. Pembagian prioritas tersebut dikatakan
sebagai pengutamaan (preemptive), yaitu mendahulukan tercapainya kepuasan pada sesuatu tujuan yang telah diberikan prioritas utama sebelum
menuju kepada tujuan-tujuan atau prioritas-prioritas berikutnya. Jadi tujuan
harus disusun dalam suatu urutan (ranking) menurut prioritasnya (Nasendi &
Affendi, 1985: 213). Model dengan memprioritaskan tujuan ini disebut
sebagai model lexicographic goal programming.
Notasi yang digunakan untuk menandai prioritas tujuan tersebut
adalah . Faktor- faktor- faktor prioritas tersebut memiliki
38
dimana >> berarti “jauh lebih penting daripada”. Berdasarkan Persamaan
(2.21) dengan memperhatikan prioritas setiap tujuan model lexicographic goal programming dapat dituliskan sebagai berikut:
Meminimalkan
dengan kendala
∑
∑
(2.22)
Keterangan :
= Prioritas ke-i
Neelavathi (2015) memaparkan langkah- langkah untuk
menyelesaikan model lexicographic goal programming, dapat diselesaikan dengan tahapan sebagai berikut :
Diasumsikan setiap fungsi tujuan mempunyai nilai optimal, langkah pertama
39 Meminimalkan
dengan kendala: Persamaan Tujuan
Fungsi Kendala
Kendala non-negatif
Nilai fungsi tujuan prioritas ke-1 akan ditambahkan pada fungsi kendala pada
prioritas ke-2. Misalkan nilai fungsi tujuan prioritas ke-1 adalah , maka
model lexicographic goal programming prioritas ke-2 adalah Meminimalkan
dengan kendala: Persamaan Tujuan
Fungsi Kendala
Kendal non-negatif
Misalkan nilai fungsi tujuan prioritas ke- 2 adalah , maka model
lexicographic goal programming prioritas ke- 3 adalah Meminimalkan
dengan kendala: Persamaan Tujuan
Fungsi Kendala
40 Meminimalkan
dengan kendala: Persamaan Tujuan
Fungsi Kendala
Kendala non-negatif
Solusi optimal prioritas ke- n menjadi solusi optimal dari masalah lexicographic goal programming pada kasus ini.
Agar lebih mudah dipahami akan diberikan kasus permasalahan
lexicographic goal programming. Misalkan terdapat 4 variabel deviasional yang akan diminimalkan, dua variabel deviasional pada prioritas ke- 1, satu
variabel deviasional prioritas ke- 2, dua variabel deviasional pada prioritas
ke- 3. Variabel deviasional berturut- turut adalah . Penyelesaian
lexicographic goal programming prioritas ke- 1 adalah Meminimalkan
dengan kendala: Persamaan Tujuan
Fungsi Kendala
Kendala non-negatif
Misalkan hasil optimal fungsi meminimalkan prioritas ke-1 yaitu , maka
41 Meminimalkan
dengan kendala: Persamaan Tujuan
Fungsi Kendala
Kendala non-negatif
Misalkan hasil optimal fungsi meminimalkan prioritas ke- 2 yaitu , maka
model lexicographic goal programming prioritas ke- 3 adalah Meminimalkan
dengan kendala: Persamaan Tujuan
Fungsi Kendala
Kendala non-negatif
Solusi optimal prioritas ke- 3 menjadi solusi optimal dari masalah
42 BAB III PEMBAHASAN
Pada bab ini akan dibahas pembentukan portofolio menggunakan metode
goal programming dan lexicographic goal programming pada empat saham yang akan dipilih menjadi kandidat portofolio dari saham- saham yang tergabung dalam
Jakarta Islamic Index (JII) periode Februari 2014 - Maret 2016. Pembentukan portofolio optimal dipilih dari 11 portofolio yang dibentuk investor. Selanjutnya
dilakukan penilaian kinerja portofolio berdasarkan perhitungan indeks sharpe guna mendapatkan portofolio optimal. Oleh karena itu, dalam bab ini terlebih
dahulu akan dibahas analisis pembentukan portofolio menggunakan metode goal programming dan lexicographic goal programming, perhitungan indeks sharpe. Pembentukan portofolio metode goal programming dan lexicographic goal programming akan dilakukan dengan menggunakan program komputer LINGO.
A. Pembentukan Model Portofolio
Pemilihan portofolio membahas permasalahan bagaimana investasi
dapat memberi keuntungan maksimal dengan risiko minimal. Menurut Abdul
Halim (2005:4), ada tiga hal yang perlu dipertimbangkan dalam investasi,
yaitu return yang diharapkan (expected of return), risiko (risk), dan ketersediaan jumlah dana yang akan diinvestasikan. Selain tiga hal tersebut
agar diversifikasi terbentuk atau investasi tidak terpusat dalam satu saham
dilakukan pembatasan proporsi setiap saham. Sehingga masalah nyata yang
43
1. Seorang investor ingin melakukan investasi pada beberapa aset saham
agar memenuhi jumlah dana yang diinvestasikan.
2. Berdasarkan jumlah dana yang diinvestasikan investor ingin
mendapatkan keuntungan yang maksimum. Investor berharap akan
mendapatkan tingkat keuntungan (expected return) lebih dari nilai DR, dimana DR adalah nilai return minimal.
3. Investor akan berhadapan dengan risiko.
4. Guna melakukan diversifikasi atau meratakan jumlah dana yang
diinvestasikan pada masing- masing saham, investor membatasi proporsi
setiap saham.
Permasalahan - permasalahan nyata tersebut akan disusun ke dalam
suatu model portofolio goal programming dan lexicographic goal programming dengan asumsi sebagai berikut:
1. Investor mempunyai jumlah dana yang diinvestasikan sebesar 1 ( =1).
2. Return portofolio yang diharapkan oleh investor diasumsikan lebih dari nilai DR. DR adalah nilai return minimal, yang diperoleh dari mean expected return seluruh saham yang diinvestasikan.
3. Investor menghendaki nilai maksimum proporsi setiap saham tidak akan
lebih dari V, nilai V yang dikehendaki antara 30% - 40% dari jumlah
dana. Setidaknya investor menginvestasikan jumlah dana sebesar D yaitu
5% setiap saham.
44
sama dengan nilai tertentu S ( . Investor memilih beta portofolio kurang dari sama dengan 0,9 ( . Hal ini berarti risiko portofolio
yang ditanggung investor memiliki risiko yang lebih kecil dari risiko
rata- rata pasar, portofolio akan bergerak kurang dari sama dengan 0,9
kali perubahan IHSG.
5. Investor akan melakukan investasi dengan urutan prioritas sebagai
berikut: risiko yang ditanggung investor >> return yang diharapkan >>
jumlah dana yang diinvestasikan >> pembatasan proporsi dana setiap
saham.
6. Tidak terjadi pinjaman (short sale).
B. Pembentukan Portofolio Model Goal Programming
Memenuhi jumlah dana yang diinvestasikan menjelaskan bahwa
proporsi saham ( , i = 1,2,...,n , seluruh n-saham akan sama dengan jumlah dana yang diinvestasikan (M0), Agar tujuan ini tercapai, maka penyimpangan di bawah dan di atas nilai M0 harus diminimalkan. Hal ini membutuhkan kehadiran variabel deviasional , sehingga fungsi tujuan pertama
adalah
∑ (3.1)
45
∑ ( (3.2)
Ukuran risiko menggunakan konsep Sharpe (1963) yaitu risiko
sistematis. Risiko sistematis atau beta saham ke-i dilambangkan dengan , i= 1, 2,...,n. Berdasarkan asumsi bahwa investor merupakan risk averter, dimana
investor tidak suka terhadap risiko, sehingga dipilih beta portofolio yang tidak
akan lebih dari S. Oleh karena itu, penyimpangan di atas nilai S harus diminimalkan agar hasil penyelesaian tidak melebihi nilai S atau paling banyak sebesar S atau dengan kata lain variabel deviasional akan diminimalkan pada fungsi tujuan goal programming, fungsi tujuan ketiga dapat dituliskan :
∑ (3.3)
Fokus dalam maksimasi dari jumlah dana yang diinvestasikan dan
return portofolio diharapkan memperoleh keuntungan yang besar (M). Penyimpangan di bawah nilai M harus diminimalkan, dengan demikian, variabel deviasional akan diminimalkan. Fungsi tujuan keempat dapat
dibentuk dalam model matematis sebagai berikut:
∑ ( (3.4)
Masalah nyata kelima menjelaskan bahwa untuk meratakan jumlah
dana yang diinvestasikan pada masing- masing saham diberikan batasan
alokasi dana pada setiap saham, dengan proporsi saham ( ) masing-masing
46
penyimpangan harus diminimalkan, oleh karena itu penyimpangan di
bawah nilai V diminimalkan pada fungsi tujuan dan juga penyimpangan diatas nilai D diminimalkan , dengan demikian fungsi tujuan keempat menjadi:
(3.5)
dan
(3.6)
Ciri khas yang menandai model goal programming adalah kehadiran variabel penyimpangan di dalam fungsi tujuan yang harus diminimalkan. Hal
ini merupakan konsekuensi logis dari tujuan kehadiran variabel
penyimpangan di dalam fungsi tujuan . Jadi, fungsi tujuan model portofolio
goal programming sebagai berikut : Meminimalkan
∑
∑ (3.7)
47 Meminimalkan
∑
∑
dengan kendala:
∑
∑ (
∑
∑ (
(3.8)
Keterangan:
= Variabel deviasional overachievment = Variabel deviasional underachievment
= Variabel keputusan, proporsi investsi yang
48 ( = Expected return saham ke-i
= Return minimal yang diinginkan investor = Risiko sistematik saham ke-i
= Risiko sistematik portofolio yang diharapkan
V = Limit investasi saham
D = Batas minimal proporsi investasi saham
Lexicographic goal programming merupakan salah satu jenis goal programming dimana terdapat pre-emptive (pengutamaan) goal programming. Misalnya tujuan yang paling penting ditentukan sebagai prioritas pertama, tujuan yang kurang begitu penting dibanding tujuan
pertama ditentukan sebagai prioritas kedua, demikian seterusnya.Jadi, harus
disusun dalam suatu urutan (ranking) menurut prioritasnya. Karena investor
merupakan risk averter , maka prioritas pertama adalah memperhatikan risiko. Penyusunan urutan (ranking) menurut prioritasnya pada pembentukan
model portofolio saham lexicographic goal programming diberikan sebuah kasus dimana investor akan melakukan investasi dengan urutan prioritas
sebagai berikut:
1. Risiko yang ditanggung investor.
2. Return yang diharapkan.
3. Jumlah dana yang diinvestasikan.
4. Pembatasan proporsi alokasi dana setiap saham.
49
Pembentukan portofolio saham lexicographic goal programming analog dengan pembentukan portofolio saham goal programming, yang membedakan adalah pada fungsi tujuan. Fungsi tujuan pada model
lexicographic goal programming mempunyai prioritas pada variabel deviasional yang diminimumkan setiap kendala. Berdasarkan masalah (3.8)
dan prioritas yang dibentuk, maka diperoleh model lexicographic goal programming sebagai berikut:
:
( ( ( (∑ ∑ )
(
dengan kendala:
∑
∑ (
∑
∑ (
50 Keterangan:
= Prioritas ke –i, dimana i= 1,2,...,n.
C. Penerapan Model dalam Membentuk Portofolio Saham JII 1. Data
Populasi dalam penelitian ini adalah seluruh perusahaan yang terdaftar
di JII selama periode pengamatan Februari 2014 – Maret 2016. Data yang
digunakan adalah data close price saham bulanan dari perusahaan – perusahaan yang stabil masuk dalam JII. Pemilihan sampel data dilakukan secara purposive sampling dengan kriteria:
1. Saham tersebut selalu masuk daftar saham yang tergabung dalam JII
selama periode Februari 2014 – Maret 2016.
2. Saham mempunyai data historical price saham bulanan yang lengkap Februari periode 2014 – Maret 2016.
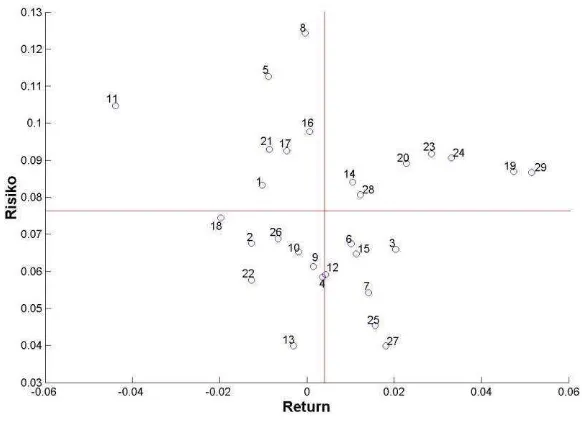
3. Termasuk saham positif yang mempunyai return lebih tinggi dan risiko lebih rendah dari pada rata- rata return dan risiko saham seluruhnya yang dapat ditunjukkan dengan scatter plot data (return dan risiko) saham JII. 4. Sampel yang diambil adalah saham- saham yang memiliki nilai koefisien
variasi terendah.
Data yang digunakan merupakan data sekunder yang diambil dari
www.finance.yahoo.com . Berikut daftar saham JII yang digunakan dalam
51
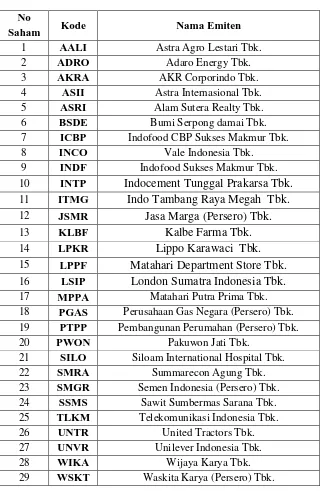
Tabel 3.1 Daftar Saham Jakarta Islamic Index
No
Saham Kode Nama Emiten
1 AALI Astra Agro Lestari Tbk.
2 ADRO Adaro Energy Tbk.
3 AKRA AKR Corporindo Tbk.
4 ASII Astra Internasional Tbk.
5 ASRI Alam Sutera Realty Tbk.
6 BSDE Bumi Serpong damai Tbk.
7 ICBP Indofood CBP Sukses Makmur Tbk.
8 INCO Vale Indonesia Tbk.
9 INDF Indofood Sukses Makmur Tbk.
10 INTP Indocement Tunggal Prakarsa Tbk.
11 ITMG Indo Tambang Raya Megah Tbk.
12 JSMR Jasa Marga (Persero) Tbk.
13 KLBF Kalbe Farma Tbk.
14 LPKR Lippo Karawaci Tbk.
15 LPPF Matahari Department Store Tbk.
16 LSIP London Sumatra Indonesia Tbk.
17 MPPA Matahari Putra Prima Tbk.
18 PGAS Perusahaan Gas Negara (Persero) Tbk.
19 PTPP Pembangunan Perumahan (Persero) Tbk.
20 PWON Pakuwon Jati Tbk.
21 SILO Siloam International Hospital Tbk.
22 SMRA Summarecon Agung Tbk.
23 SMGR Semen Indonesia (Persero) Tbk.
24 SSMS Sawit Sumbermas Sarana Tbk.
25 TLKM Telekomunikasi Indonesia Tbk.
26 UNTR United Tractors Tbk.
27 UNVR Unilever Indonesia Tbk.
28 WIKA Wijaya Karya Tbk.
29 WSKT Waskita Karya (Persero) Tbk.
2. Pemilihan Saham
52
pada periode ke-t dilambangkan dengan , perhitungan dapat menggunakan Persamaan (2.1), perhitungan realize return saham AKRA periode ke-t sebagai berikut:
Expected return masing-masing saham dapat diperoleh menggunakan rumus Persamaan (2.2), perhitungan expected return saham AKRA sebagai berikut:
( ∑
(
Risiko saham diperoleh menggunakan rumus dari Persamaan (2.5),
perhitungan risiko saham AKRA sebagai berikut :
√(( (
53
Gambar 3.1 Scatter Plot Data Return dan Risiko Saham JII
Gambar 3.1 terlihat bahwa saham-saham yang mempunyai return lebih tinggi dan risiko lebih rendah dari rata- rata adalah AKRA, BSDE,
ICBP, JSMR, LPPF, TLKM, UNVR. Selanjutnya akan dipilih empat
saham dari tujuh saham yang terpilih dengan melihat koefisien variasi
( sebagai ukuran. Koefisien variasi (coeficient of variation) dapat digunakan untuk mempertimbangkan dua faktor tersebut secara
bersamaan. Menggunakan Persamaan (2.9) dalam menghitung koefisien
variasi, koefisien variasi saham AKRA adalah
(
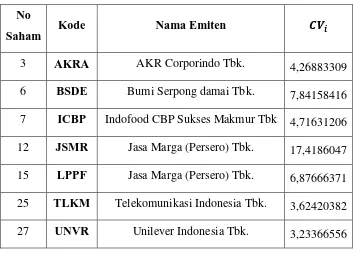
Koefisien variasi tujuh saham- saham yang terpilih lainnya dapat
dihitung dengan cara yang sama. Berikut koefisien variasi saham- saham
54
Tabel 3.2 Daftar Koefisien Variasi Saham No
Saham Kode Nama Emiten
3 AKRA AKR Corporindo Tbk. 4,26883309
6 BSDE Bumi Serpong damai Tbk. 7,84158416 7 ICBP Indofood CBP Sukses Makmur Tbk 4,71631206 12 JSMR Jasa Marga (Persero) Tbk. 17,4186047 15 LPPF Jasa Marga (Persero) Tbk. 6,87666371 25 TLKM Telekomunikasi Indonesia Tbk. 3,62420382 27 UNVR Unilever Indonesia Tbk. 3,23366556
Koefisien variasi merupakan pembagian risiko dengan expected return, dapat diartikan bahwa semakin kecil nilai semakin baik aktiva tersebut. Semakin kecil menunjukkan semakin kecil risiko saham dan
semakin besar . Dipilih empat saham yang mempunyai nilai
koefisien variasi terkecil, yaitu AKRA, ICBP, TLKM, UNVR.
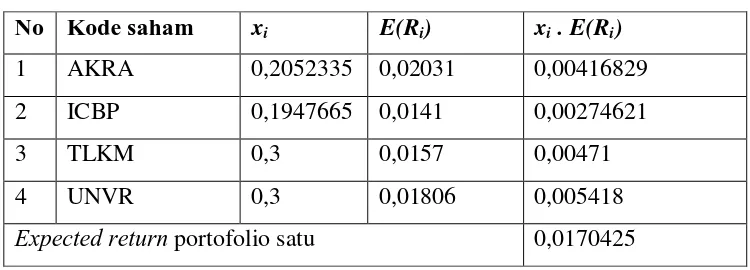
Didefinisikan proporsi saham AKRA sebagai variabel keputusan ,
proporsi saham ICBP sebagai variabel , proporsi saham TLKM sebagai
variabel , dan proporsi saham . Berdasarkan asumsi dan Persamaan (3.1),
tujuan pertama untuk model pembentukan portofolio goal programming dapat dituliskan sebagai berikut:
55
3.Menghitung Expected Return dan Beta Saham terpilih
Expected return telah dihitung sebelumnya. Sedangkan risiko yang menjadi ukuran dalam model pembentukan portofolio optimal adalah risiko
sistematik atau juga dikenal sebagai beta saham. Perhitungan beta saham
menggunakan Persamaan (2.7) dengan nilai realize return saham periode ke-i dan nilai realize return pasar ke-i dapat dilihat di Lampiran 2. Perhitungan beta saham AKRA sebagai berikut :
∑ ( ( ( (
∑ ( (
( ( ( ( (( (
1
Berikut daftar expected return dan beta empat saham yang terpilih. Tabel 3.3 Return dan Beta Saham Terpilih
Kode Saham AKRA ICBP TLKM UNVR
Return 0,02031 0,0141 0,0157 0,01806
Beta Saham 0,29031 1,294 0,73946 0,50658
4.Menghitung Return Minimal
Seperti yang telah dijelaskan sebelumnya bahwa return minimal yang diinginkan investor adalah nilai mean dari expected return seluruhsaham yang masuk dalam portofolio, perhitungan nilai DR sebagai berikut:
56
Berdasarkan return saham pada Tabel 3.3 dan telah diperoleh return minimal, dari Persamaan (3.2) maka tujuan kedua untuk model portofolio
goal programming dapat dituliskan sebagai berikut:
(3.11)
Berdasarkan beta saham pada Tabel 3.3 yang akan dijadikan sebagai
koefisien Persamaan (3.3), dan beta portofolio akan mendekati suatu nilai
( yang ditentukan investor. Penelitian ini mengasumsikan bahwa
investor merupakan risk averter yaitu investor yang tidak suka terhadap risiko, maka investor menginginkan beta portofolio kurang dari sama dengan
nilai tertentu S ( . Investor memilih beta portofolio kurang dari sama dengan 0,9 , , maka tujuan ketiga model portofolio goal programming dituliskan sebagai berikut:
(3.12)
Berdasarkan Persamaan (3.4) tujuan keempat model pembentukan
portofolio goal programming dapat dituliskan sebagi berikut:
(3.13)
5. Batasan proporsi
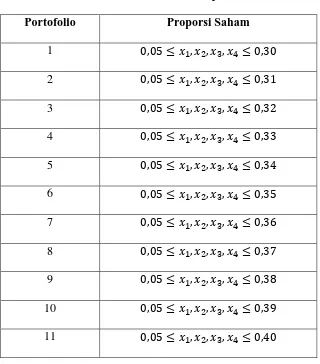
Pada portofolio ini akan dibuat 11 portofolio dengan menetapkan
terlebih dahulu asumsi pada tujuan keempat. Investor menginginkan proporsi
yang diinvestasikan pada suatu saham tidak kurang dari V yaitu 5% dan tidak lebih dari nilai D, dimana besar nilai D diantara 30% sampai 40%. Hal tersebut bertujuan agar jumlah bobot investasi yang dialokasikan sebesar
100% atau modal yang dimiliki digunakan seluruhnya dalam investasi.
57
Tabel 3.4 Batasan Proporsi Saham
Portofolio Proporsi Saham
1
2
3
4
5
6
7
8
9
10
11
Setelah diperoleh proporsi setiap saham pada masing- masing
portofolio, akan dihitung kinerja portofolio-portofolio berdasarkan
58 6.Model Goal Programming
a. Proporsi Saham pada Portofolio
Setelah semua persamaan tujuan yang diperlukan dalam
membentuk portofolio diketahui. Langkah selanjutnya akan dicari proporsi
investasi pada masing-masing saham. Model umum portofolio goal programming tanpa prioritas portofolio 1 sebagai berikut:
Meminimalkan:
dengan kendala:
Penyelesaian model untuk mendapatkan proporsi investasi
59
Lampiran 3, output LINGO penyelesaian portofolio 1 model goal programming mempunyai objective value bernilai nol, hal ini berarti bahwa semua variabel deviasional yang diminimumkan dalam fungsi
tujuan bernilai nol dengan kata lain fungsi tujuan tercapai.
Secara analog dapat diperoleh nilai masing- masing proporsi tiap
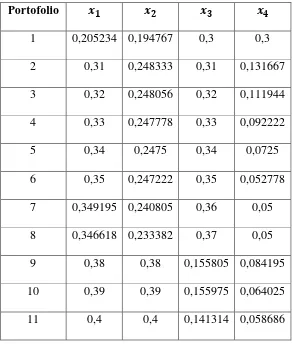
saham pada sepuluh portofolio lainnya, output lingo terlampir pada
[image:59.595.166.459.331.675.2]Lampiran 3. Diperoleh nilai proporsi investasi masing-masing portofolio seperti disajikan dalam Tabel 3.5 berikut:
Tabel 3.5 Proporsi Saham pada Portofolio Saham JII Portofolio
1 0,205234 0,194767 0,3 0,3
2 0,31 0,248333 0,31 0,131667
3 0,32 0,248056 0,32 0,111944
4 0,33 0,247778 0,33 0,092222
5 0,34 0,2475 0,34 0,0725
6 0,35 0,247222 0,35 0,052778
7 0,349195 0,240805 0,36 0,05
8 0,346618 0,233382 0,37 0,05
9 0,38 0,38 0,155805 0,084195
10 0,39 0,39 0,155975 0,064025
60
b. Risiko dan Return Portofolio Goal Programming
Setelah proporsi investasi masing-masing saham pada setiap
portofolio diketahui, langkah selanjutnya adalah menghitung nilai expected return portofolio dan risiko portofolio. Expected Return portofolio diperoleh dari Persamaan (2.4) sedangkan risiko portofolio dihitung berdasarkan
[image:60.595.142.517.312.447.2]Persamaan (2.6) . Pada portofolio 1 perhitungan nilai expected return dapat