1
BAB I
GAYA PADA BIDANG DATAR
Pada bab ini, kita akan mempelajari pengaruh gaya‐gaya yang bekerja pada
suatu partikel. Pemakaian kata “partikel” tidak berarti bahwa kita membatasi pelajaran
kita pada benda yang kecil. Yang dimaksud di sini adalah ukuran dan bentuk benda
yang ditinjau tidak banyak mempengaruhi penyelesaian masalah.
Gaya termasuk besaran vektor. Sehingga pada materi ini kita akan lebih sering
menggunakan istilah vektor sebagai pengganti besaran gaya. Karena gaya merupakan
besaran vektor, maka sebuah gaya akan ditentukan oleh besar dan arahnya.
Besarnya suatu gaya ditentukan oleh suatu satuan. Dalam SI, gaya mempunyai
satuan Newton(N), sedang sistem satuan Amerika menggunakan satuan pound(lb).
Arah gaya ditentukan dengan suatu tanda panah. Perjanjian tanda yang lazim untuk
menyatakan arah gaya dapat dilihat pada gambar 1.
Gambar 1. Perjanjian tanda arah gaya
A. GAYA PADA BIDANG DATAR
Dua buah vektor , seperti tampak pada gambar 2a dan b, yang mempunyai
besar dan garis aksi yang sama tetapi arah berbeda, akan memberikan efek yang
berlawanan bila bereaksi pada sebuah benda. X(+) X(-)
Y(+)
2
(a) (b)
30° 30°
Gambar 2
(a)
A A A
(b) (c)
P
Q
R P
Q
R
Gambar 3
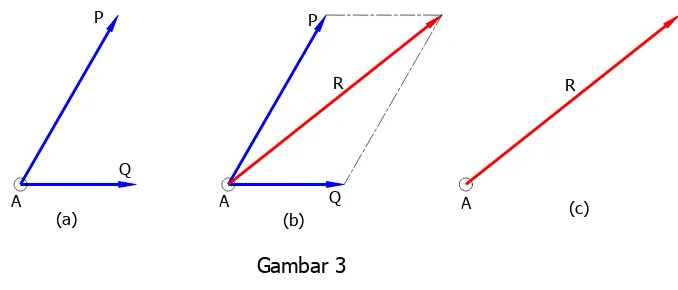
Dua buah vektor P dan Q yang bekerja pada sebuah benda A (gambar 3a) dapat
digantikan dengan sebuah vektor tunggal R yang akan memberikan efek yang sama
pada benda tersebut (gambar 3c). Vektor ini disebut vektor resultan dari vektor P dan
Q.
Dua buah vektor yang besar dan arahnya sama disebut kedua vektor itu sama,
tidak tergantung apakah keduanya mempunyai titik aksi yang sama atau berbeda
(gambar 4). Dua vektor yang besarnya sama, garis aksi sejajar tetapi berlawanan arah
disebut kedua tersebut berbeda (gambar 5).
3
A
B B
A
R
θ θ
(a) (b)
Gambar 6.
A
B B A
A+B ATAU
A+B
A
B
(a) (b) (c)
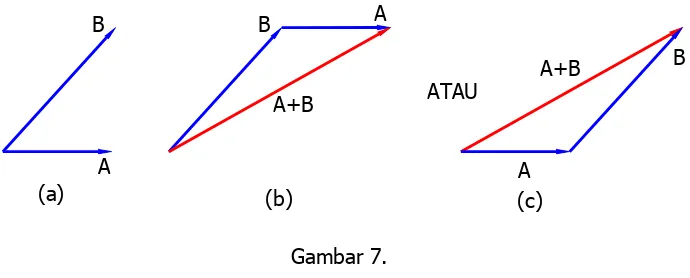
Gambar 7. B. PENJUMLAHAN DAN PENGURANGAN GAYA
Dua buah vektor gaya A dan B bekerja pada satu titik tangkap dan membentuk
sudut apit θ. Resultan atau jumlah kedua vektor tersebut dicari menggunakan hukum
jajaran genjang (gambar 6a dan b).
Besarnya resultan dapat dihitung menggunakan persamaan sebagai berikut :
R = |A B| = √A B 2AB cos θ (1)
Dari hukum jajaran genjang, dapat diturunkan cara lain untuk menentukan
jumlah dua buah vektor gaya. Metode ini dikenal dengan hukum segitiga (gambar 7a,
4
A B
-B
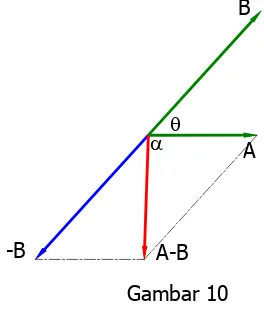
Gambar 10
θ α
A-B
Gambar 8 Gambar 9
Pengurangan vektor gaya didefinisikan sebagai penjumlahan suatu vektor yang
sama dengan arah berlawanan. Gambar 10 memperlihatkan pengurangan dua vektor A
dan B.
Besarnya A‐B dihitung menggunakan persamaan berikut ini :
A‐B =√A B 2AB cos α (2)
Dimana α = 180 ‐ θ dan cos (180 ‐ θ) = ‐ cos θ, sehingga persamaan 2 dapat diubah
menjadi :
A‐B = √A B 2AB cos θ (3)
Rumus hukum segitiga yang sering digunakan dalam perhitungan adalah
5
a b
c
α β
γ
P = 40 N
Q = 60 N
R
20
°
25
°
a
sin β
b
sin α
c
sin γ
Contoh 1.
Dua buah gaya P dan Q beraksi pada suatu paku
A. Tentukan resultannya.
Penyelesaian :
R = P Q 2PQ cos α
6
Contoh 2.
Penyelesaian :
Sebuah tiang pancang ditarik dari tanah dengan memakai dua tali seperti tampak pada gambar.
a. tentukan besar gaya P sehingga gaya resultan yang timbul pada tiang mengarah vertikal.
b. Berapa besar resultan tersebut ?.
Karena resultan kedua gaya pada tiang harus vertikal, maka gambar gaya di samping dapat diubah seperti tampak pada gambar berikut.
7
Tentukan dengan trigonometri besar dan arah resultan dua gaya seperti tampak pada gambar di samping.
R = 2002 +3002+2⋅200⋅300⋅cos70 = 413,57 lb
Untuk menghitung arah resultan gaya digunakan hukum segitiga.
8
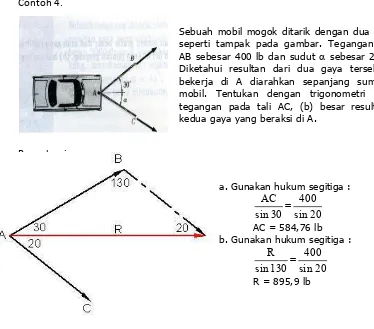
Contoh 4.
Penyelesaian :
C. KOMPONEN TEGAK LURUS SUATU GAYA
Sebuah vektor gaya dapat diuraikan dalam sebuah bidang Cartesian dalam
komponen Fx sepanjang sumbu x dan Fy sepanjang sumbu y seperti tampak pada
gambar 11.
Gambar 11
Sebuah mobil mogok ditarik dengan dua tali seperti tampak pada gambar. Tegangan di AB sebesar 400 lb dan sudut α sebesar 20°. Diketahui resultan dari dua gaya tersebut bekerja di A diarahkan sepanjang sumbu mobil. Tentukan dengan trigonometri (a) tegangan pada tali AC, (b) besar resultan kedua gaya yang beraksi di A.
a. Gunakan hukum segitiga :
20 b. Gunakan hukum segitiga :
9
Begitu juga sebaliknya, jika diketahui dua komponen gaya Fx dan Fy yang saling tegak
lurus, maka dapat dihitung resultan kedua gaya dan arah resultan gaya tersebut
menggunakan persamaan berikut :
Fx
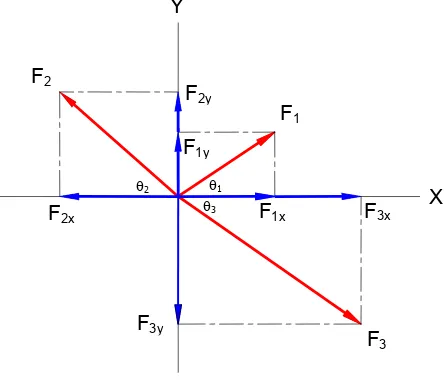
D. RESULTAN GAYA DENGAN MENAMBAH KOMPONEN X DAN Y
Tiga buah gaya F1, F2, dan F3 bekerja pada suatu bidang kartesian pada satu titik
tangkap seperti ditunjukkan pada gambar 12.
Untuk mencari resultan ketiga gaya tersebut, maka harus diuraikan masing‐
masing gaya terhadap sumbu x dan y sehingga terdapat komponen gaya‐gaya :
10
Dari komponen‐komponen gaya di atas, dapat dijumlahkan secara aljabar
terhadap sumbu x dan y, yaitu :
ΣFx = F1x‐ F2x + F3x (8)
dan
ΣFy = F1y + F2y‐ F3y (9)
sehingga resultan ketiga gaya dicari menggunakan persamaan :
∑
+∑
Tentukan komponen x dan y setiap gaya pada gambar di samping.
11
Silinder hidrolik GE menimbulkan suatu gaya P diarahkan sepanjang garis GE pada bagian DF. Diketahui P harus mempunyai komponen tegak lurus DF sebesar 600 N. Tentukan :
a. besar gaya P.
b. komponennya yang sejajar terhadap DF.
12
Penyelesaian :
E. KESETIMBANGAN SUATU PARTIKEL
Bila resultan semua gaya yang bekerja pada suatu partikel adalah nol, maka
partikel tersebut dalam keadaan setimbang. Syarat untuk mencapai keadaan
setimbang secara matematis dapat ditulis sebagai berikut ini :
ΣFx = 0 dan ΣFy = 0 (11)
contoh 8.
R = 62 +17,52 =18,5ft
Tx = - Tcos θ
= - 370 x 18,5
6
= - 120 lb
= 120 lb (ke kiri) Ty = Tsin θ
= 370 x 18,5 17,5
= 350 lb
13
Penyelesaian :
ΣFx = 0
TBC Cos 30 – TAC Cos 50 = 0
0,87 TBC = 0,64 TAC
TBC = 0,74 TAC (a)
ΣFy = 0
TAC Sin 50 + TBC Sin 30 – 400 = 0
0,77 TAC + 0,5 TBC = 400 (b)
Substitusikan (a) ke dalam (b) :
0,77 TAC + 0,5 (0,74 TAC) = 400
1,14 TAC = 400
TAC = 350,88 lb
Masukkan TAC ke dalam (a) :
TBC = 0,74 x 350,88
= 259,65 lb
TAC
TBC
TACSIN 50
TACCOS 50
TBCSIN 30
TBCCOS 30
400
X Y
14
A
30 60
W = 20 N
A
30 60
W = 20 N
T3
T1 T2
Contoh 9 :
Hitung tegangan tali T1, T2, dan T3 pada gambar berikut ini jika titik A setimbang. W
adalah berat benda.
Penyelesaian :
Diagram gaya‐gaya yang bekerja :
Tinjau benda W :
Benda ini berada pada keadaan setimbang sehingga :
T3 = W = 20 N
Tinjau titik A :
15
Substitusikan persamaan (1) ke persamaan (2), kita peroleh :
T1 3
Subtitusikan nilai T1 ke persamaan (1) untuk mendapatkan nilai T2
16
Contoh 10.
Penyelesaian :
Suatu kotak yang dapat digerakkan berikut isinya mempunyai 960 lb. Tentukan panjang rantai terpendek ACB yang dapat digunakan untuk mengangkat beban kotak tersebut bila tegangan pada rantai tidak melebihi 730 lb.
Karena berbentuk simetris, maka TAC = TBC = T.
ΣFy = 0 2T sin θ - 960 = 0 2 x 730 x sin θ = 960 sin θ = 0,658
θ = 41,1°
sehingga R =
41,1 cos
13,75
= 18,33 in
17
LATIHAN
1. Determine the magnitude of the
resultant force FR = F1 + F3 and its
direction, measured
counterclockwise from the
positive x‐axis.
2. Determine the magnitude of the
resultant force FR = F1 + F2 and its
direction, measured
counterclockwise from the
positive x‐axis
3. Resolve the force F1 into components acting the
u and v axes and determine the magnitudes of
18
4. The plate is subjected to the two forces at A and
B as shown. If θ = 60°, determine the magnitude
of the resultant of these forces and its direction
measured from the horizontal
5. Determine the magnitudes of F1 and F2 so that
the particle P is in equilibrium
6. Determine the magnitude and direction θ of F so
19
7. The device shown is used to straighten the
frames of wrecked autos. Determine the
tension of each segment of the chain, i.e., AB
and BC if the force which hydraulic cylinder
DB exerts on point B is 3,50 kN, as shown
8. Determine the force in cables AB and AC
necessary to support the 12 kg traffic
light
9. Coeds AB and AC can each sustain a maximum
tension of 800 lb. If the drum has a weight of
900 lb, determine the smallest angle θ at which
20
10. The 500 lb crate is hoisted using the ropes AB
and AC. Each rope can withstand a maximum
tension 2500 lb before it breaks. If AB always
remains horizontal, determine the smallest