STRATEGI VAKSINASI KONTINU PADA MODEL EPIDEMIK SVIR TONAAS K W Y MARENTEK

(1)

STRATEGI VAKSINASI KONTINU

PADA MODEL EPIDEMIK SVIR

TONAAS K W Y MARENTEK

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2011

(2)

PERNYATAAN MENGENAI TESIS DAN

SUMBER INFORMASI

Dengan ini saya menyatakan bahwa tesis Strategi Vaksinasi Kontinu pada Model Epidemik SVIR adalah karya saya dengan arahan dari komisi pembimbing dan belum diajukan dalam bentuk apapun kepada perguruan tinggi manapun. Sumber informasi yang berasal atau kutipan dari karya yang diterbitkan dari penulis lain telah disebutkan dalam teks dan dicantumkan dalam Daftar Pustaka di bagian akhir tesis ini.

Bogor, Agustus 2011

Tonaas Marentek

(3)

ABSTRACT

TONAAS K W Y MARENTEK. A Continuous Vaccination Strategy in the SVIR

Epidemic Model. Supervised by PAIAN SIANTURI and ALI KUSNANTO.

Vaccination is conducted to minimize the spread of a disease. The vaccination is usually done several times within a fixed time interval. In the SVIR model, it is assumed that individuals do not get immediate immunity following a vaccination program. So according to process of vaccination on SVIR model, there are two strategies, i.e. the continuous vaccination strategy (CVS) and the pulse vaccination strategy (PVS). In this study, only the CVS strategy in epidemic model SVIR is considered. Results of the study indicate that dynamics of the CVS system depends on the basic reproductive number. If the basic reproductive number is less than one, then the disease-free fixed point is asymptotically stable. It means that the disease will eventually disappear from the population. Conversely, if the basic reproductive number is greater than one, then the endemic fixed point is asymptotically stable, which means that the disease will remain exist in the population. Simulation result shows that the vaccination would minimize the spread of disease by reducing the basic reproductive number. If the time for the vaccinated recipients to obtain the immunity, as well as a possibility of vaccinated recipients to be infected are neglected, then the disease will be eradicated. This condition is called an over-evaluating effect of vaccination. Keywords: vaccination, SVIR, continuous vaccination strategy, stability

(4)

RINGKASAN

TONAAS MARENTEK. Strategi Vaksinasi Kontinu pada Model Epidemik SVIR. Dibimbing oleh PAIAN SIANTURI dan ALI KUSNANTO.

Vaksinasi merupakan metode yang umum digunakan untuk mengendalikan penyebaran penyakit antara lain cacar, campak, polio, tetanus, pertusis, TBC, hepatitis B dan lain-lain. Berdasarkan teori epidemik, penyebaran penyakit menular bisa digambarkan dalam bentuk kompartemen S, I dan R yang pertama kali dikemukakan oleh Kermark dan McKendrick pada tahun 1927. Model SVIR dianggap sebagai penambahan kompartemen V ke dalam model SIR. Pada SVIR, populasi dibagi kedalam empat kelompok yaitu, kelompok individu yang sehat tetapi rentan (S), kelompok individu yang mengalami proses vaksinasi (V), kelompok individu yang telah terinfeksi (I) dan kelompok individu yang kebal (R). Oleh karena itu, berdasarkan proses vaksinasi terdapat dua strategi yaitu strategi vaksinasi kontinu (CVS) dan strategi vaksinasi terputus (PVS). Dimana CVS adalah strategi vaksinasi dengan cara melakukan vaksinasi secara terus menerus terhadap individu-individu rentan. Sedangkan PVS adalah suatu strategi vaksinasi yang dilakukan hanya sekali atau bisa juga lebih dari sekali tetapi dengan jangka waktu tertentu.

Dalam penelitian ini hanya dibahas strategi vaksinasi kontinu. Hasil analisis kestabilan menunjukkan bahwa dinamika CVS ini sepenuhnya bergantung pada bilangan reproduksi dasar. Titik tetap bebas penyakit akan stabil asimtotik ketika bilangan reproduksi dasar kurang dari satu yang berarti bahwa penyakit tidak akan menyebar dalam populasi dan pada akhirnya penyakit akan hilang dari populasi. Sedangkan titik tetap endemik akan stabil asimtotik ketika bilangan reproduksi dasar lebih dari satu yang berarti bahwa penyakit akan tetap ada dalam populasi.

Selanjutnya, hasil matematis menunjukkan bahwa vaksinasi bermanfaat untuk pengendalian penyakit yaitu dengan mereduksi bilangan reproduksi dasarnya dan menurunkan fraksi individu yang terinfeksi. Ketika 0 yang berarti tidak dilakukan proses vaksinasi maka bilangan reproduksi dasar sistem CVS akan menjadi bilangan reproduksi dasar model SIR. Sedangkan ketika 0 yaitu proses vaksinasi dilakukan akan terdapat dua kasus yaitu kemungkinan individu yang divaksinasi terinfeksi diabaikan (₁ 0) dan kemungkinan individu yang divaksinasi masih memiliki kemungkinan terinfeksi (₁0).

Pertama, ketika kemungkinan individu penerima vaksin untuk terinfeksi diabaikan (₁0). Hal ini berarti bahwa efektifitas vaksin sangat tinggi sehingga individu yang divaksinasi tidak akan terinfeksi penyakit. Secara matematis bilangan reproduksi dasarnya yaitu R₀c akan tereduksi menjadi R₁c, sehingga untuk nilai  yang semakin besar R₁c akan mendekati nol. Dapat disimpulkan bahwa ketika efektifitas vaksin sangat tinggi, sehingga individu penerima vaksin tidak akan terinfeksi maka penyakit akan bisa diberantas dengan strategi apapun. Hal ini disebut over evaluating dimana akan menghilangkan nilai kondisi untuk memberantas penyakit dan penyakit selalu dapat diberantas dengan strategi vaksinasi apapun.

(5)

Kedua, ketika individu penerima vaksin masih memiliki kemungkinan untuk terinfeksi secara matematis bilangan reproduksi dasarnya akan sama dengan

0

c

R dan untuk  yang semakin besar R₀c akan menjadi R . Dimana ₂ R adalah ₂

kondisi yang diperlukan untuk memberantas penyakit. Jika R₂ 1 maka akan diperoleh nilai kritis ₀c

sehingga strategi vaksinasi yang harus dilakukan haruslah lebih dari ₀c

. Dari hasil simulasi kondisi atau strategi yang diperlukan untuk memberantas penyakit bergantung pada nilai-nilai parameter ₁ dan ₁. Ketika

1 1

  yang berarti bahwa efektifitas vaksin tinggi sehingga individu yang divaksinasi besar kemungkinannya mendapatkan kekebalan dari pada terinfeksi maka akan semakin melemahkan kondisi yang diperlukan untuk memberantas penyakit ( semakin kecil) atau akan semakin meningkatkan efisiensi strategi vaksinasi ini.

Hasil simulasi terhadap penyakit campak dengan menggunakkan nilai-nilai parameter yang diambil dari d’Onofrio et al. (2007) dan dengan asumsi ketika 0 bilangan reproduksi dasar R₀ 1.5. Sehingga diperoleh nilai kritis laju individu rentan yang divaksinasi. Nilai kritis ini akan lebih kecil jika kemungkinan individu yang divaksinasi untuk terinfeksi lebih kecil dari laju rata-rata individu yang divaksinasi mendapatkan kekebalan ( ₁ ₁). Sehingga minimal 0.00001710409246 atau minimal 0.001710409246% populasi rentan harus divaksinasi setiap hari untuk memberantas penyakit campak dengan strategi vaksinasi CVS.

(6)

(7)

© Hak Cipta milik Institut Pertanian Bogor, tahun 2011

Hak Cipta dilindungi Undang-Undang

1. Dilarang mengutip sebagian atau seluruh karya tulis ini tanpa mencantumkan atau menyebutkan sumber.

a. Pengutipan hanya untuk kepentingan pendidikan, penelitian, penulisan karya ilmiah, penyusunan laporan, penulisan kritik, atau tinjauan suatu masalah

b. Pengutipan tidak merugikan kepentingan yang wajar Institut Pertanian Bogor

2. Dilarang mengumumkan dan memperbanyak sebagian atau seluruh Karya tulis dalam bentuk apapun tanpa izin Institut Pertanian Bogor.

(8)

STRATEGI VAKSINASI KONTINU

PADA MODEL EPIDEMIK SVIR

TONAAS K W Y MARENTEK

Tesis

sebagai salah satu syarat untuk memperoleh gelar Magister Sains pada

Program Studi Matematika Terapan

SEKOLAH PASCASARJANA

INSTITUT PERTANIAN BOGOR

BOGOR

2011

(9)

(10)

Judul Tesis : Strategi Vaksinasi Kontinu Pada Model Epidemik SVIR Nama : Tonaas Kabul Wangkok Yohanis Marentek

NIM : G551090381

Disetujui Komisi Pembimbing

Dr. Paian Sianturi Ketua

Drs. Ali Kusnanto, M.Si. Anggota

Diketahui

Ketua Program Studi S2 Matematika Terapan

Dekan Sekolah Pascasarjana IPB

Dr. Ir. Endar H. Nugrahani, MS. Dr. Ir. Dahrul Syah, M.Sc. Agr.

(11)

PRAKATA

Puji dan syukur penulis panjatkan kepada sang Khalik Allah Tritunggal atas segala karunia-Nya sehingga karya ilmiah ini dapat diselesaikan. Tema yang dipilih dalam penelitian yang dilaksanakan sejak bulan Nopember 2010 ini adalah vaksinasi pada penyebaran penyakit, dengan judul Strategi Vaksinasi Kontinu pada Model Epidemik SVIR.

Terima kasih penulis ucapkan kepada Bapak Dr. Paian Sianturi dan Bapak Drs. Ali Kusnanto, M.Si masing-masing selaku ketua dan anggota Komisi Pembimbing, serta bapak Dr. Jaharuddin, M.Si selaku Penguji Luar Komisi dan selaku dosen Program Studi Matematika Terapan yang telah banyak memberikan saran. Ucapan terima kasih juga penulis sampaikan pada seluruh keluarga atas segala doa dan kasih sayangnya. Semoga karya ilmiah ini bermanfaat.

Bogor, Agustus 2011

(12)

RIWAYAT HIDUP

Penulis dilahirkan di Manado Sulawesi Utara pada tanggal 3 Januari 1981 dari bapak Wempie Marentek (Alm) dan ibu Yohana Laykesso. Penulis merupakan putra ketujuh dari tujuh bersaudara.

Tahun 1998 penulis lulus dari SMU Negeri 5 Balikpapan dan pada tahun yang sama menempuh pendidikan di Program Studi Teknik Sipil, Fakultas Teknik UNSRAT Manado, namun pada tahun 2002 penulis pindah di program studi Matematika, FMIPA UNSRAT Manado, lulus pada tahun 2007. Tahun 2008 sampai 2009, penulis menjadi karyawan bank Danamon Manado. Tahun 2009, penulis diterima di Program Studi Matematika Terapan pada Sekolah Pascasarjana Institut Pertanian Bogor.

(13)

DAFTAR ISI

Halaman

DAFTAR GAMBAR ……… xi

DAFTAR TABEL ………..………. xii

DAFTAR LAMPIRAN ………. xiii

I PENDAHULUAN ………... 1

1.1 Latar Belakang ……….. 1

1.2 Tujuan Penelitian ………... 2

1.3 Metode Penelitian ……….. 2

II LANDASAN TEORI ………. 3

2.1 Sistem Persamaan Diferensial ………... 3

2.2 Titik Tetap ……….… 3

2.3 Kondisi Routh-Hurwitz ………. 5

2.4 Bilangan Reproduksi Dasar ………... 6

III MODEL MATEMATIKA PENYEBARAN PENYAKIT ……… 7

3.1 Model SIR ……….. 7

3.2 Model SVIR dan Strategi Vaksinasi Kontinu ……… 8

IV HASIL DAN PEMBAHASAN ………... 11

4.1 Penentuan Titik Tetap ………... 11

4.2 Analisis Kestabilan ……… 12

4.2.1 Kestabilan Titik Tetap Bebas Penyakit ………..… 12

4.2.2 Kestabilan Titik Tetap Endemik ……….... 13

4.3 Efek Dari Strategi Vaksinasi CVS ……… 17

4.3.1 Kasus ₁ 0 ……….……… 18

4.3.2 Kasus ₁ 0……….………. 20

V KESIMPULAN DAN SARAN ………. 24

5.1 Kesimpulan ………... 24

5.2 Saran ………. 24

DAFTAR PUSTAKA………. 25

(14)

DAFTAR TABEL

Halaman 1 Kondisi Kestabilan Titik Tetap ……….……….. 15 2 Bilangan Reproduksi Dasar ………..…….. 18

(15)

DAFTAR GAMBAR

Halaman 1 Diagram transfer penyebaran penyakit model SIR ………... 7 2 Diagram transfer penyebaran penyakit model SVIR

dengan strategi CVS ………... 9 3 _{Dinamika populasi S, V, I dan R dengan}

0 0.520833 1

c

R …...…... 15

4 Dinamika populasi S, V, I dan R dengan R₀c 1.17187 1 …..……... 16 5 _{Dinamika populasi I terhadap waktu dengan}

0 0.520833

c

R ………….... 16

6 Bilangan Reproduksi Dasar pada kasus ₁ 0 ……..………...… 19 7 Dinamika populasi S, V, I dan R, pada kasus 1 0

dan R₀c 0.97132 1 ………... 19 8 Dinamika populasi S, V, I dan R, pada kasus ₁ 0

dan R₀c 1.18077 1 ………..……….……….. 20 9 Bilangan Reproduksi Dasar pada kasus ₁ 0 ………..…...…... 21 10 Bilangan Reproduksi Dasar untuk memberantas penyakit

pada kasus 1 0 dan 1 1……… ₂₁

11 Bilangan Reproduksi Dasar untuk memberantas penyakit

(16)

DAFTAR LAMPIRAN

Halaman

1 Bukti Teorema 1 Kriteria Routh-Hurwitz ………... 28

2 Program mencari titik tetap strategi vaksinasi CVS ………...…… 29

3 Mencari nilai a a₁, ₂ dan a₃ ………. 31

4 Dinamika Populasi untuk R₀ 0.520833 ………..… 32

5 Dinamika Populasi untuk R0 1.17187 …... 33

6 Dinamika Populasi I untuk R0 0.520833 ……….….. 34

7 Sifat-sifat Matematis Bilangan Reproduksi Dasar ………..……..…. 35

8 Kondisi Bilangan Reproduksi Dasar untuk memberantas penyakit …...… 36

9 Dinamika Populasi S, V, I dan R untuk kasus 1 0 dan R₀c 0.97132 1 ……….……….. 37

10 Dinamika Populasi S, V, I dan R untuk kasus 1 0 dan R₀c 1.18077 1 ………... ………...….…. 38

11 Kondisi Bilangan Reproduksi Dasar untuk memberantas penyakit pada kasus ₁ 0 dan ₁ ₁………...……….. 39

12 Kondisi Bilangan Reproduksi Dasar untuk memberantas penyakit pada kasus 1 0 dan 1 1 ………...………. 40

(17)

1

I PENDAHULUAN

1.1 Latar Belakang

Vaksinasi merupakan metode yang umum digunakan untuk mengendalikan penyebaran penyakit seperti cacar, campak, polio, tetanus, pertusis, TBC, hepatitis B dan lain-lain. Sekarang ini vaksinasi rutin disediakan di semua negara-negara berkembang terhadap semua penyakit. Pemberantasan penyakit cacar yang terakhir terlihat dalam kasus alami pada tahun 1977 telah dianggap sebagai keberhasilan paling spektakuler vaksinasi (Anonym, 2005).

Menurut Ramali & Pamoentjak (2005), vaksin merupakan suspensi bibit penyakit yang hidup tetapi telah dilemahkan atau dimatikan untuk menimbulkan kekebalan aktif terhadap suatu penyakit sehingga dapat mencegah atau mengurangi pengaruh infeksi oleh organisme alami. Sedangkan untuk menyelesaikan proses vaksinasi biasanya ada jadwal yang berbeda untuk penyakit yang berbeda ataupun untuk penerima vaksin yang berbeda.

Berdasarkan teori epidemik dari Kermark & McKendrick yang dikemukakan pertama kali pada tahun 1927, penyebaran penyakit menular biasanya dapat digambarkan secara matematis oleh model-model kompartemen seperti model SIR atau SIRS dengan setiap huruf mengacu pada kompartemen dimana individu dapat berada. Oleh karena itu vaksinasi juga dapat dianggap sebagai penambahan kompartemen secara alami ke dalam model epidemik dasar

SIR sehingga modelnya akan menjadi SVIR dimana populasi dibagi ke dalam

empat kelompok yaitu, kelompok individu yang sehat tetapi rentan (S), kelompok individu yang mengalami proses vaksinasi (V), kelompok individu yang terinfeksi (I) dan kelompok individu yang telah sembuh dari penyakit atau individu yang telah mendapatkan kekebalan terhadap penyakit baik secara alami ataupun akibat dari vaksinasi (R).

Model penyebaran penyakit SVIR ini, berdasarkan prosesnya terdapat dua strategi vaksinasi yaitu strategi vaksinasi yang kontinu (CVS) dan strategi vaksinasi yang terputus (PVS). Dimana strategi CVS dapat dikenali sebagai perilaku dari individu-individu rentan yang dilakukan vaksinasi secara terus menerus sedangkan strategi PVS adalah suatu proses vaksinasi yang dilakukan

(18)

2

hanya sekali atau bisa juga lebih dari sekali tetapi dengan jangka waktu tertentu yang telah ditetapkan (musiman).

Pada penelitian ini, hanya akan dibahas strategi vaksinasi kontinu (CVS) pada model epidemik SVIR.

1.2 Tujuan Penelitian

Tujuan dari penelitian ini adalah :

1. Mengkaji strategi vaksinasi kontinu pada model epidemik SVIR.

2. Mengkaji efek dari strategi vaksinasi kontinu dengan menganalisis secara matematis.

3. Simulasi efek vaksinasi kontinu terhadap jenis penyakit campak yang sesuai dengan model SVIR.

1.3 Metode Penelitian

Dalam penelitian ini akan dilakukan dengan pendekatan matematis dan studi literatur. Langkah-langkah yang akan dilaksanakan dalam penelitian ini:

1. Menganalisis strategi vaksinasi kontinu dengan menentukan kesetimbangannya, memeriksa kestabilannya dan menentukan bilangan reproduksi dasarnya.

2. Menganalisis secara matematis efek dari strategi vaksinasi kontinu berdasarkan bilangan reproduksi dasarnya.

3. Mengimplementasikan dengan cara melakukan simulasi terhadap penyakit campak yang sesuai dengan model SVIR dengan menggunakan perangkat lunak Mathematica 7.0.

(19)

3

II LANDASAN TEORI

2.1 Sistem Persamaan Diferensial (SPD)

Definisi 1 (SPD Linear)

Suatu SPD yang dinyatakan sebagai

0

, (0)

dx

x Ax b x x

dt  (2.1)

dengan A adalah matriks koofisien konstan berukuran n n dan b vektor konstan. Sistem tersebut dinamakan sistem persamaan diferensial linear orde 1 dengan kondisi awal x(0) x₀. Jika b 0 sistem dikatakan homogen dan dikatakan takhomogen jika b 0.

(Tu 1994) Definisi 2 (SPD Tak Linear)

Suatu SPD yang dinyatakan sebagai

x f t x( , ) (2.2)

dengan x = dan f(t,x) = dimana f merupakan

fungsi tak linear pada disebut sistem persamaan diferensial tak linear.

(Braun 1983) Definisi 3 (SPD Mandiri)

Misalkan diberikan suatu SPD orde 1 sebagai berikut :

, x n (2.3) dengan f merupakan fungsi kontinu bernilai real dari x dan mempunyai turunan parsial kontinu. Persamaan (2.3) disebut persamaan diferensial mandiri (autonomous) karena tidak memuat t secara eksplisit di dalamnya.

(Tu 1994)

2.2 Titik Tetap

Definisi 4 (Titik Tetap)

(20)

4

(2.4) Titik x disebut titik tetap atau titik kritis ataupun disebut juga titik kesetimbangan jika f x( ) 0.

(Tu 1994) Definisi 5 (Titik Tetap Stabil)

Misalkan x adalah titik tetap SPD mandiri dan x(t) adalah solusi dengan nilai awal dengan x . Titik x dikatakan titik tetap stabil, jika untuk setiap , terdapat , sedemikian sehingga

x

₀

x

r

, maka solusi x(t) memenuhi x untuk setiap t>0.

(Vershulst 1990) Definisi 6 (Titik Tetap Stabil Asimtotik Lokal)

Titik x dikatakan titik tetap stabil asimtotik jika titik x stabil dan terdapat

0 sedemikian sehingga jika x x0 maka lim ( )

t x t x, dengan x0 x(0). (Szidarovzky & Bahill 1998) Definisi 7 (Nilai Eigen dan Vektor Eigen)

Misalkan A adalah matriks n n, suatu vektor tak nol x di dalam n

disebut vektor eigen dari A , jika suatu skalar yang disebut nilai eigen dari A berlaku :

Ax x (2.5) Vektor x disebut vektor eigen yang bersesuaian dengan nilai eigen yang berukuran n n, maka persamaan (2.5) dapat dituliskan sebagai berikut :

(A I x) 0 (2.6) dengan I adalah matriks identitas. Persamaan (2.5) memiliki solusi tak nol jika dan hanya jika det(A I) 0 yang disebut dengan persamaan karakteristik.

(Anton 1995) Analisis Kestabilan Titik Tetap

Analisa kestabilan untuk setiap titik tetap yang berbeda untuk setiap nilai eigen yakni :

(21)

5

1. Sistem x Ax adalah stabil jika dan hanya jika setiap nilai eigen dari A

bagian realnya bernilai negatif.

2. Sistem x Ax adalah tidak stabil jika dan hanya jika minimal satu nilai eigen dari A bagian realnya bernilai positif.

(Borrelli & Coleman 1998)

2.3 Kondisi Routh Hurwitz

Misalkan bilangan-bilangan real, . Semua

nilai eigen dari persamaan karakteristik ( 1) ( 2)

1 2

( ) k k k ... k 0

p a a a

mempunyai bagian real yang negatif jika determinan dari matriks H_j adalah positif. Selanjutnya didefinisikan matriks Hurwitz H_j sebagai berikut

Hj dengan H_j (h_lm) dan 2

1 , untuk 2

0 , untuk 2

ata

, untuk 0

2 u 2

l m lm

a

l

m

k

l

m

l

m

l

k

m

h

semua nilai eigen dari persamaan karakteristik mempunyai bagian real yang negatif (titik tetap stabil) jika dan hanya jika determinan dari semua matriks Hurwitz positif, yaitu :Hj 0, untuk j 1, 2,...,ksehingga menurut kondisi Routh-Hurwitz untuk suatu k, k =2,3,4 disebutkan bahwa titik tetap stabil jika

dan hanya jika (untuk k =2,3,4),

1. k=2, 2. k=3, 3. k=4,

(Edelstein-Keshet 1998) Untuk kasus k 3, kriteria Routh-Hurwitz disajikan dalam teorema berikut.

(22)

6

Teorema 1

Misalkan A,B,C bilangan real. Bagian real dari setiap nilai eigen persamaan karakteristik p( = + adalah negatif jika dan hanya jika

A,C bernilai positif dan AB>C.

Bukti : (Lampiran 1)

2.4 Bilangan Reproduksi Dasar

Bilangan Reproduksi Dasar ) adalah rata-rata banyaknya individu rentan yang terinfeksi secara langsung oleh individu lain yang sudah terinfeksi bila individu yang terinfeksi tersebut masuk ke dalam populasi yang seluruhnya masih rentan.

Kondisi yang akan timbul adalah salah satu diantara kemungkinan berikut : 1. Jika , maka penyakit akan menghilang.

2. Jika R₀ 1, maka penyakit akan menetap (endemik).

3. Jika , maka penyakit akan meningkat menjadi wabah.

(23)

7

III MODEL MATEMATIKA PENYEBARAN PENYAKIT

3.1 Model SIR

Model dasar yang digunakan untuk menggambarkan penyebaran penyakit adalah model epidemik SIR. Model SIR ini dikemukakan oleh Kermark & McKendrick pada tahun 1927 sebagai model dasar dari pengembangan pemodelan epidemiologi. Model ini mempunyai tiga kompartemen yang menggambarkan proses penyebaran penyakit pada suatu populasi. Kompartemen-kompartemen tersebut adalah : Susceptible (S) yaitu kelompok individu yang sehat tetapi dapat terinfeksi penyakit, Infected (I) yaitu kelompok individu yang terinfeksi dan dapat sembuh dari penyakit dan Recovered (R) yaitu kelompok individu yang telah sembuh dan kebal dari penyakit. Menurut Hethcote (2000), diasumsikan bahwa adalah laju rekrutmen dan laju kematian alami dari populasi, adalah laju infeksi atau laju transmisi penularan penyakit ketika individu rentan bersinggungan/kontak dengan individu yang terinfeksi dan adalah laju pemulihan individu yang terinfeksi dan individu-individu yang pulih atau sembuh yang diasumsikan memiliki kekebalan (kekebalan alami) terhadap penyakit. Asumsi-asumsi tersebut dapat digambarkan ke dalam bentuk kompartemen-kompartemen pada Gambar 1 berikut.

Gambar 1 Diagram transfer penyebaran penyakit model SIR

Dari kompartemen pada Gambar 1 di atas dapat disusun model matematika yang dituliskan sebagai berikut :

(3.1) dS S SI dt dI SI I I dt dR I R dt

dengan semua parameter pada sistem (3.1) adalah bernilai positif.

R

(24)

8

3.2 Model SVIR dan Strategi Vaksinasi Kontinu (CVS)

Berdasarkan teori epidemik dari Kermark dan McKendrick, penyebaran penyakit menular dapat digambarkan secara matematis oleh model-model kompartemen SIR dengan setiap huruf mengacu pada kompartemen dimana individu berada. Oleh karena itu Vaksinasi juga dapat dianggap sebagai penambahan kompartemen V secara alami ke dalam model epidemik dasar SIR.

Kribs-Zaleta & Velasco-Hernandez (2000), menambahkan kompartemen V ke dalam model SIS dan mempelajari penyakit pertusis dan TBC, sedangkan Arino et al. (2003) menambahkan kompartemen V ke dalam model SIRS, Kribs-Zaleta & Martcheva (2002) mempelajari efek dari kampanye vaksinasi pada penyebaran suatu penyakit non-fatal seperti hepatitis A dan hepatitis B, baik pada tahap infeksi akut ataupun kronis. Alexander et al. (2004) dan Shim (2006) menggunakan model SVIR untuk mempelajari model dinamika penyakit influenza (flu) dengan vaksinasi.

Semua model kontinu di atas yang berasumsi bahwa individu memperoleh kekebalan setelah divaksinasi dan waktu bagi individu mendapatkan kekebalan atau waktu untuk menyelesaikan proses vaksinasi diabaikan. Pada kenyataannya segera setelah individu yang rentan memulai proses vaksinasi, individu itu akan berbeda dengan individu yang rentan tetapi individu yang divaksinasi harus dibedakan dengan individu yang pulih karena telah mendapatkan kekebalan akibat divaksinasi ataupun kekebalan setelah sembuh dari penyakit.

Oleh karena itu, dengan mempertimbangkan vaksinasi dalam model dasar

SIR, model SVIR ini mengasumsikan bahwa individu yang divaksinasi tidak

mendapatkan kekebalan segera artinya bahwa individu yang divaksinasi masih memungkinkan terinfeksi atau individu dalam V akan pindah ke R saat mendapatkan kekebalan akibat divaksinasi.

Strategi vaksinasi kontinu pada model SVIR ini berdasar pada model dasar

SIR untuk suatu penyakit yang tidak menyebabkan kematian (non fatal) misalkan

penyakit campak. Menurut Alexander et al. (2004), Arino et al. (2004), Kribz-Zaleta & Velasco-Hernandez (2000) total populasi akan berada pada tingkat konstan, maka strategi vaksinasi kontinu ini mengasumsikan bahwa adalah laju rekrutmen dan laju kematian alami dari populasi, adalah laju

(25)

9

transmisi/penularan penyakit ketika individu yang rentan berinteraksi dengan individu yang terinfeksi dan adalah laju pemulihan individu yang terinfeksi dan individu yang pulih diasumsikan memiliki kekebalan alami terhadap penyakit. Xianning et al. (2007) memperkenalkan strategi vaksinasi kontinu pada model epidemik SVIR. Strategi vaksinasi kontinu pada model SVIR secara matematis adalah penambahan kompartemen V pada model dasar SIR, dimana V adalah kelompok baru yang dibagi dari kelompok S dan menunjukkan kepadatan individu yang telah memulai proses vaksinasi. Individu dalam V memerlukan waktu untuk mendapatkan tingkat proteksi terhadap penyakit selama proses vaksinasi dan akan berpindah ke R saat mendapatkan kekebalan. Oleh karena itu, berdasarkan diagram transfer kompartemen model SIR maka dapat digambarkan diagram transfer model kompartemen sebagai berikut dengan asumsi :

a) adalah laju dimana individu yang rentan dipindahkan ke dalam proses vaksinasi.

b) ₁ adalah laju rata-rata (1 / ₁ adalah waktu rata-rata) bagi individu yang mengalami proses vaksinasi untuk memperoleh kekebalan.

c) Sebelum memperoleh kekebalan, individu masih memiliki kemungkinan terinfeksi dengan laju transmisi adalah ₁. Diasumsikan 1 lebih kecil dari

karena individu yang memperoleh vaksinasi mungkin memiliki kekebalan parsial selama proses vaksinasi.

Gambar 2 Diagram transfer penyebaran penyakit model SVIR dengan strategi CVS

R

S

I

V

(26)

10

Asumsi-asumsi diatas dapat dituliskan dalam bentuk persamaan diferensial berikut : 1 1 1 1 (3.2) dS S SI S dt dV S VI V V dt dI SI VI I I dt dR V I R dt

(27)

11

IV HASIL DAN PEMBAHASAN

4.1 Penentuan Titik Tetap

Analisis titik tetap pada sistem persamaan diferensial sering digunakan untuk menentukan suatu solusi yang tidak berubah terhadap waktu (solusi konstan). Titik tetap dari persamaan diferensial (3.2) akan diperoleh dengan

menentukan dS 0,dV 0,dI 0 dt dt dt dan 0 dR dt . Karena persamaan , dan dS dV dI

dt dt dt tidak bergantung pada persamaan dR dt , maka (3.2) dapat direduksi menjadi : 1 1 1 (4.1) dS S SI S dt dV S VI V V dt dI SI VI I I dt

sehingga akan diperoleh persamaan-persamaan di bawah ini :

1 1 1 0 0 (4.2) 0 dS S SI S dt dV S VI V V dt dI SI VI I I dt

dengan menyelesaikan secara bersamaan maka akan diperoleh dua titik tetap yaitu titik tetap bebas penyakit dan titik tetap endemik.

1. Titik tetap bebas penyakit 0 0 0 0

1

( , , ) , , 0

E S V I

2. Titik tetap endemik E (S V I, , ) dengan

1 1 1 1

, S

S V

I I I I

dan I adalah akar positif dari 2

1 2 3 ( ) g I A I A I A dengan : 1 ( ) 1 A

(28)

12 2 1 1 1 3 1 1 1 ( ) ( ) ( ) ( )( )( ) ( ) A A 4.2 Analisis Kestabilan

Misalkan pada persamaan (4.1) dinotasikan sebagai berikut :

1 1 1 ( , , ) ( , , ) ( , , ) (4.3) f S V I g S V S SI S VI V V SI VI I S h S V I I I

dengan melakukan pelinearan persamaan-persamaan di atas akan diperoleh matriks Jacobi sebagai berikut.

1 1 1 1 1 0 ( , , ) f f f S V I g g g J S V I V S V I h h h S V I I S I I I S V

4.2.1 Kestabilan Titik Tetap Bebas Penyakit

Pelinearan pada titik tetap E₀ akan menghasilkan matriks Jacobi sebagai berikut : 0 0 0 0 1 0 1 1 0 0 0 J E V S S V

sehingga akan diperoleh nilai eigen dengan menyelesaikan persamaan karakteristik det J E₀ I 0.

Persamaan karakteristik dari J E₀ adalah :

1 1 2 0 1 0 3 1 2 1 3 0 1 0 0 1 0 0 0 0 0 ( ) c 1 S V S V S V R dengan

(29)

13 0 1 0 1 0 1 (4.4) ( ) c S V R

yang selanjutnya disebut sebagai bilangan reproduksi dasar penyebaran penyakit pada strategi vaksinasi CVS.

Perhatikan bahwa nilai eigen yang kesemuanya adalah bilangan real akan negatif jika R₀c 1. Jadi kestabilan di titik tetap bebas penyakit bergantung pada

0

c

R . Kondisi stabil yang dipenuhi ketika 0 1

c

R dimana 0

c

R disini merupakan

bilangan reproduksi dasar individu yang terinfeksi secara langsung oleh individu lain yang sudah terinfeksi bila individu yang terinfeksi tersebut masuk kedalam populasi yang seluruhnya masih rentan. Kondisi stabil asimtotik ketika R₀c 1 karena individu yang terinfeksi hanya akan menularkan kurang dari satu individu baru yang terinfeksi yang artinya penyakit akan menghilang dari populasi. Sebaliknya, ketika ₀c 1

R merupakan kondisi yang tidak stabil karena penyakit dapat bertahan dan meningkat dalam populasi.

4.2.2 Kestabilan Titik Tetap Endemik

Pelinearan pada titik tetap E akan menghasilkan matriks Jacobi sebagai berikut : 1 1 1 1 1 1 1 0 0 0 J E V S S I S I I I S V S I I V V

Jika semua nilai eigen yang diperoleh dari matriks Jacobi J E

mempunyai bagian real negatif, maka solusi titik tetap endemik adalah stabil. Nilai eigen tersebut dapat ditentukan dengan menghitung det J E I 0

(30)

14 3 2 1 2 3 0 (4.5) a a a dengan 1 22 23 11 13 11 12 2 2 2 1 32 33 31 33 21 22 2 2 2 1 3 1 0 0 det 0 S a trace J E S V J J J J J J a V I S I J J J J J J V S I V I a J E S I V S

Berdasarkan kriteria Routh-Hurwitz kondisi kestabilan sistem (3.2) pada titik tetap endemik akan stabil jika dan hanya jika persamaan (4.5) memenuhi syarat-syarat berikut :

a1 0, a2 0 dan a a1 2 a3.

Perhatikan bahwa koefisien-koefisien pada persamaan (4.5) bernilai positif, berarti untuk memeriksa kestabilan titik tetap endemik cukup dibuktikan bahwa a a₁ ₂ a₃ 0. Sehingga : 2 2 1 2 3 1 1 2 2 2 1 1 2 2 2 2 1 1 0 S a a a S I V I S I S V V V S I S I V I S I S V V V S I S I S I S I S V V

berdasarkan kriteria Routh-Hurwits maka disimpulkan titik tetap endemik E

adalah stabil asimtotik jika titik tetap endemik ini ada.

Berikut ini akan ditunjukkan bahwa keberadaan titik tetap E akan dipengaruhi oleh ₀c

R yaitu akan ada jika ₀c 1

R . Nilai I adalah akar positif dari

2 1 2 3 ( ) g I A I A I A dengan 1 1 2 1 1 1 3 1 1 1 ( ) ( ) ( ) ( ) ( )( )( ) ( ) A A A Karena 0 1 1 c R maka persamaan 2 1 2 3 ( )

(31)

15

2

1 2 4 0

( ) (1 c)

g I A I A I A R dengan A4 ( )( )( 1) 0.

Keberadaan titik tetap endemik yaitu E dimana I adalah akar real yang bernilai positif dari persamaan 2

1 2 4 0

( ) (1 c)

g I A I A I A R terpenuhi jika 0 1

c

R . Jadi

titik tetap endemik E akan ada dan stabil jika R₀c 1. Tabel 1 Kondisi Kestabilan Titik Tetap

Kondisi E ₀ E

0

1

c

R

Stabil asimtotik Tidak ada

0

1

c

R

Tidak stabil Stabil asimtotik

Tabel 1 menunjukkan bahwa dinamika sistem pada strategi vaksinasi CVS adalah sepenuhnya ditentukan oleh bilangan reproduksi dasar. Ketika R₀c 1 titik tetap bebas penyakit E₀ akan stabil asimtotik yang berarti bahwa penyakit tidak akan menyebar dalam populasi atau dengan kata lain pada akhirnya penyakit akan hilang dari populasi. Ketika R₀c 1 titik tetap endemik E akan stabil asimtotik yang berarti bahwa penyakit akan tetap ada dan menyebar dalam populasi.

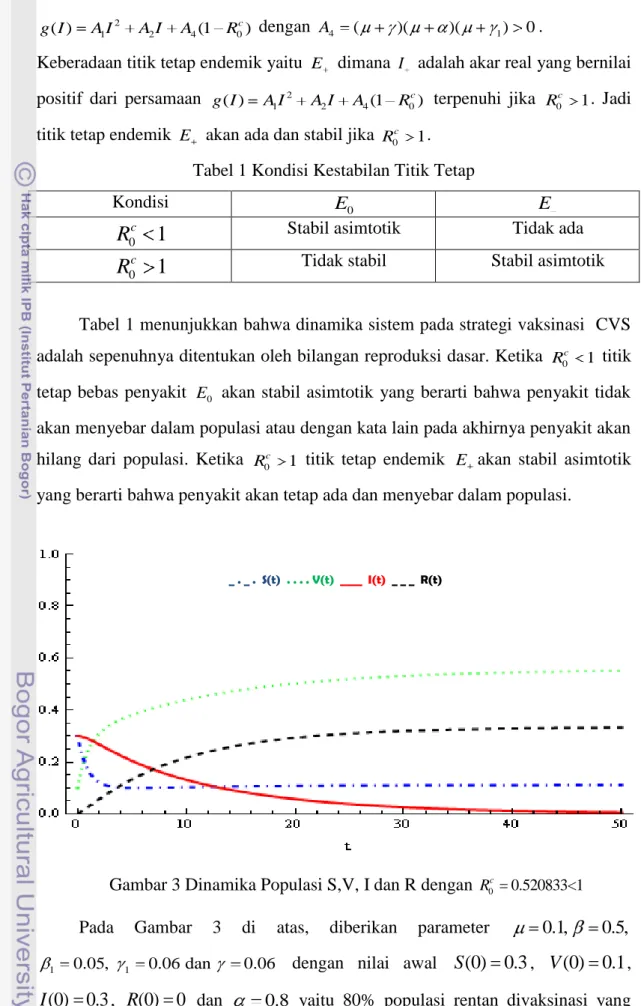
Gambar 3 Dinamika Populasi S,V, I dan R dengan 0 0.520833<1

c

R

Pada Gambar 3 di atas, diberikan parameter 0.1, 0.5,

1 0.05, 1 0.06 dan 0.06 dengan nilai awal S(0) 0.3, V(0) 0.1,

(0) 0.3

I , R(0) 0 dan 0.8 yaitu 80% populasi rentan divaksinasi yang

(32)

16

menyebabkan R₀c 0.520833 terlihat bahwa kurva S, V, I dan R akan menuju ke titik tetapnya yaitu (0.111111, 0.555556, 0, 0.333333). Kurva I akan menuju nol dan stabil yang artinya bahwa pada akhirnya penyakit akan hilang dari populasi. Program untuk menampilkan Gambar 3 dapat dilihat pada lampiran 4.

Gambar 4 Dinamika Populasi S,V, I dan R dengan 0 1,17187 1

c

R

Sedangkan pada gambar 4, dengan 0.2 yaitu 20% populasi rentan divaksinasi yang menyebabkan R₀c 1.17187 kurva S, V, I dan R akan menuju titik tetapnya yaitu (0.285714, 0.34632, 0.1, 0.267966). Kurva I akan stabil menuju 0.1 yang artinya bahwa penyakit akan tetap ada dalam populasi. Progam untuk menampilkan Gambar 4 dapat dilihat pada lampiran 5.

Gambar 5 Dinamika Populasi I terhadap waktu dengan 0 0.520833

c R 0 10 20 30 40 50 0.0 0.1 0.2 0.3 0.4 0.5 0.6 t _ . _ . S(t) . . . . V(t) ____ I(t) _ _ _ R(t)

(33)

17

Pada Gambar 5, diberikan nilai awal yang berbeda yaitu

(0) 0.3, (0) 0.4, (0) 0.5 dan (0) 0.6

I I I I terlihat pada akhirnya kurva I

yaitu populasi yang terinfeksi akan stabil menuju nol untuk t yang semakin besar sehingga nilai awal tidak berpengaruh jika ₀c 1

R berapapun nilai awalnya, pada akhirnya akan menuju nol. Program untuk menampilkan Gambar 5 dapat dilihat pada lampiran 6.

4.3 Efek Dari Strategi Vaksinasi CVS

Hasil analisis pada strategi vaksinasi CVS menunjukkan bahwa dinamika sistem sepenuhnya ditentukan oleh bilangan reproduksi dasar. Sehingga efek dari vaksinasi bergantung pada bilangan reproduksi dasarnya.

Secara matematis diuraikan sifat-sifat bilangan reproduksi dasar strategi vaksinasi CVS sebagai berikut :

1. Ketika 0 yang berarti tidak ada vaksinasi, maka ₀c

R akan tereduksi

menjadi ₀c ₀ ₀

R R yang adalah bilangan reproduksi dasar model

SIR.

2. Ketika 0, maka akan terdapat dua kasus, yaitu :

i. Kasus ₁ 0 yang berarti bahwa individu yang divaksinasi tidak akan terinfeksi maka bilangan reproduksi dasarnya menjadi

1

0| 0 1

( )( )

c c

R R dan untuk nilai yang semakin besar

maka R akan mendekati nol. ₁c

ii. Kasus ₁ 0 yang berarti bahwa individu yang divaksinasi masih memiliki kemungkinan untuk terinfeksi maka bilangan reproduksi dasarnya adalah sama dengan ₀c

R dan untuk nilai yang semakin besar

maka R₂ akan mendekati nilai 1 1 ( )( ) .

Sehingga untuk menganalisa efek dari strategi vaksinasi CVS diasumsikan bahwa tanpa vaksinasi penyakit akan endemik atau tetap ada dalam populasi

(34)

18

Tabel 2 Bilangan Reproduksi Dasar

Untuk mengamati efek dari strategi vaksinasi CVS ini perlu diimplementasikan kedalam suatu contoh penyakit yang sesuai dengan model

SVIR dalam hal ini penyakit campak. Sehingga dilakukan simulasi komputer

dengan bantuan perangkat lunak Mathematica 7.0 dengan nilai-nilai parameter yang diambil dari d’Onofrio et al (2007).

1. merupakan laju rekrutmen atau laju kematian alami manusia, yakni

0.0 1

0003653/h 1

75 365 ari

L , dimana L adalah angka harapan

hidup.

2. 1 0.143/hari

D , D 7hari adalah waktu rata-rata individu yang

terinfeksi mendapatkan kekebalan.

3. Dimisalkan R₀ 1.5 maka diperoleh nilai 0.215/hari adalah waktu rata-rata individu yang rentan terinfeksi sebelum mengalami proses vaksinasi.

4.3.1 Kasus ₁ 0

Dimisalkan individu yang divaksinasi tidak akan terinfeksi ( ₁ 0) yang berarti bahwa efektivitas vaksin sangat tinggi. Secara matematis ₀c

R akan sama dengan ₁c

R yang akan menuju ke nol untuk nilai yang semakin besar. Karena

1

limRc 0 maka dapat disimpulkan bahwa penyakit bisa diberantas dengan

Kasus 0 0 1 0 1 0| 0 1 1 ( )( ) lim 0 c c c R R R 0

R

1 0 1 0 1 0 2 lim c c R R R

(35)

19

strategi CVS. Namun jika kemungkinan bagi penerima vaksin terinfeksi diabaikan, hal ini dapat menyebabkan over evaluating dari efek vaksinasi CVS.

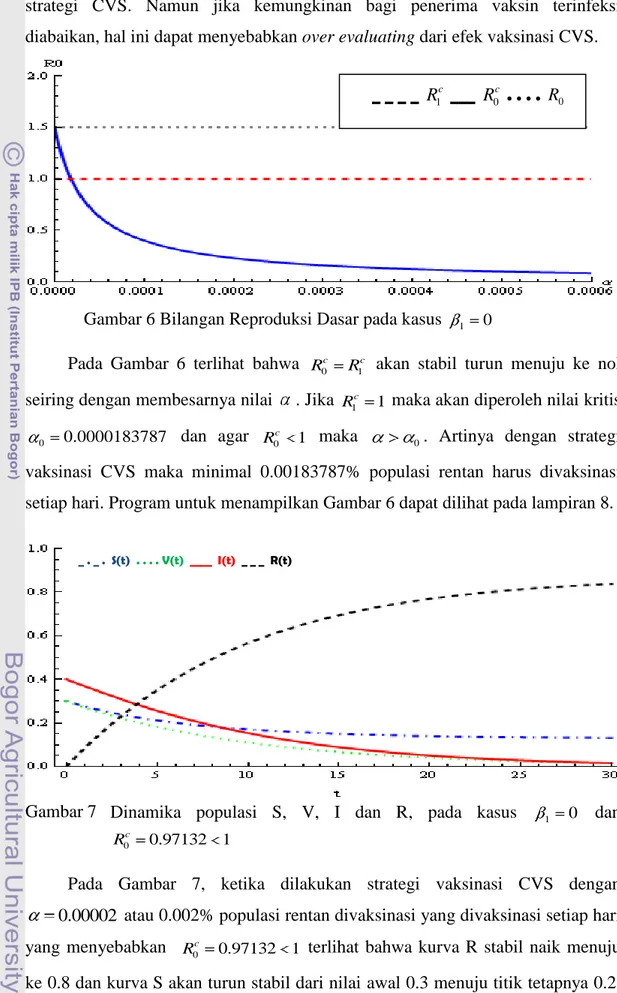
Gambar 6 Bilangan Reproduksi Dasar pada kasus ₁ 0 Pada Gambar 6 terlihat bahwa ₀c ₁c

R R akan stabil turun menuju ke nol

seiring dengan membesarnya nilai . Jika R₁c 1 maka akan diperoleh nilai kritis

0 0.0000183787 dan agar 0 1

c

R maka ₀. Artinya dengan strategi vaksinasi CVS maka minimal 0.00183787% populasi rentan harus divaksinasi setiap hari. Program untuk menampilkan Gambar 6 dapat dilihat pada lampiran 8.

Gambar 7 Dinamika populasi S, V, I dan R, pada kasus ₁ 0 dan

0 0.97132 1

c

R

Pada Gambar 7, ketika dilakukan strategi vaksinasi CVS dengan

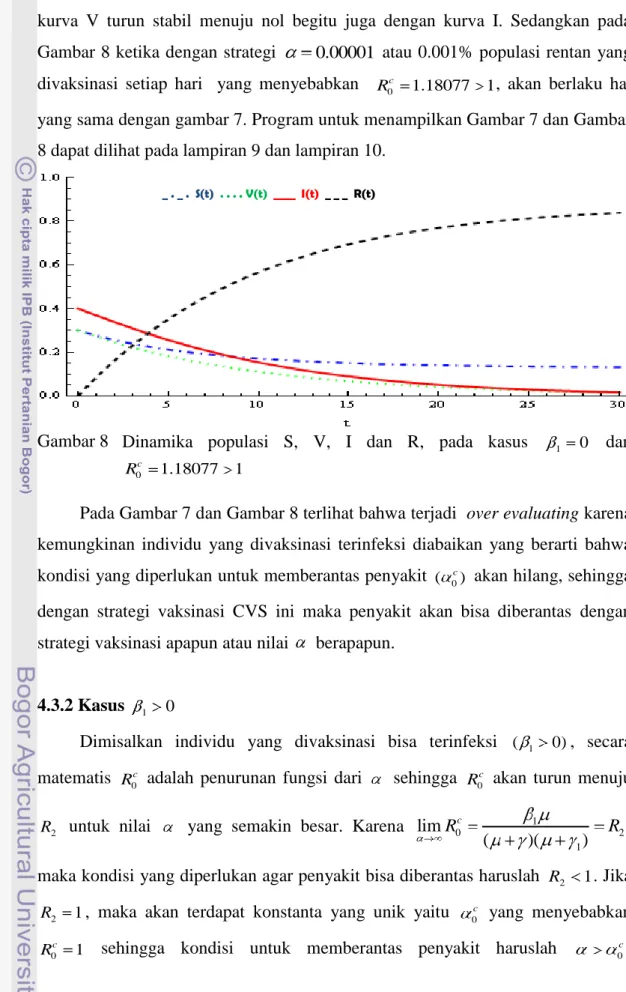
0.00002 atau 0.002% populasi rentan divaksinasi yang divaksinasi setiap hari yang menyebabkan R₀c 0.97132 1 terlihat bahwa kurva R stabil naik menuju ke 0.8 dan kurva S akan turun stabil dari nilai awal 0.3 menuju titik tetapnya 0.2,

_ _ _ _ ₁c

R ___ R . . . . ₀c R0

(36)

20

kurva V turun stabil menuju nol begitu juga dengan kurva I. Sedangkan pada Gambar 8 ketika dengan strategi 0.00001 atau 0.001% populasi rentan yang divaksinasi setiap hari yang menyebabkan ₀c 1.18077 1

R , akan berlaku hal

yang sama dengan gambar 7. Program untuk menampilkan Gambar 7 dan Gambar 8 dapat dilihat pada lampiran 9 dan lampiran 10.

Gambar 8 Dinamika populasi S, V, I dan R, pada kasus 1 0 dan 0 1.18077 1

c

R

Pada Gambar 7 dan Gambar 8 terlihat bahwa terjadi over evaluating karena kemungkinan individu yang divaksinasi terinfeksi diabaikan yang berarti bahwa kondisi yang diperlukan untuk memberantas penyakit ( ₀c) akan hilang, sehingga dengan strategi vaksinasi CVS ini maka penyakit akan bisa diberantas dengan strategi vaksinasi apapun atau nilai berapapun.

4.3.2 Kasus ₁ 0

Dimisalkan individu yang divaksinasi bisa terinfeksi ( ₁ 0), secara matematis ₀c

R adalah penurunan fungsi dari sehingga 0

c

R akan turun menuju

2

R untuk nilai yang semakin besar. Karena 1

0 2 1 lim ( )( ) c R R ,

maka kondisi yang diperlukan agar penyakit bisa diberantas haruslah R₂ 1. Jika

2 1

R , maka akan terdapat konstanta yang unik yaitu ₀c_{yang menyebabkan}

0 1

c

R sehingga kondisi untuk memberantas penyakit haruslah ₀c_.

(37)

21

Sebaliknya jika R₂ 1 maka R₀c R₂ 1 yang mengakibatkan penyakit tidak bisa diberantas untuk setiap nilai .

Kasus ketika ₁ 0 dan ₁ ₁

Pada kasus ini diasumsikan ₁ 0.5 0.1075 dan ₁ 0.1

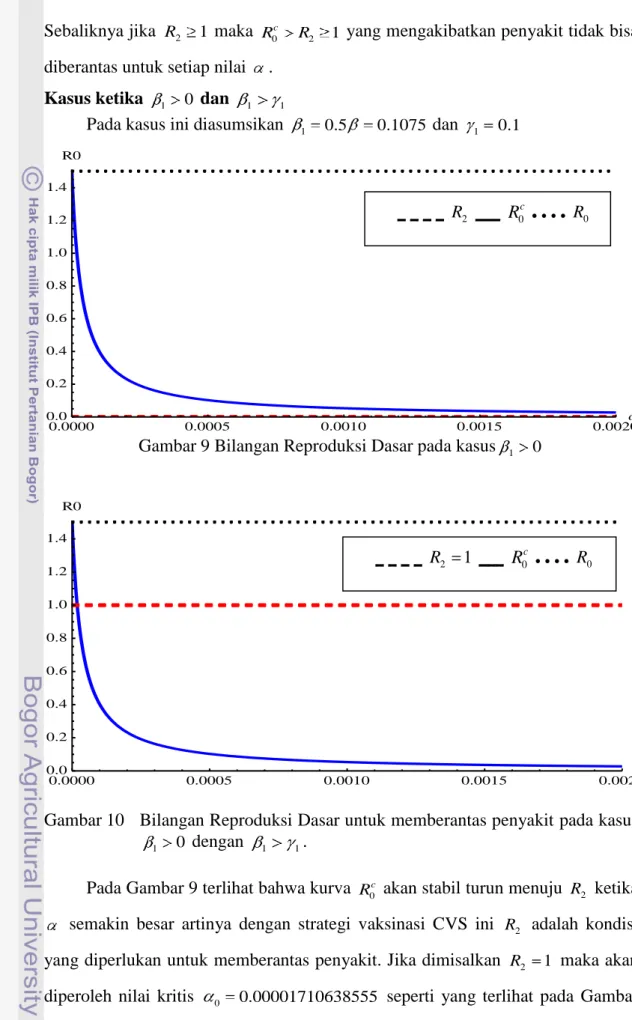
Gambar 9 Bilangan Reproduksi Dasar pada kasus ₁ 0

Gambar 10 Bilangan Reproduksi Dasar untuk memberantas penyakit pada kasus

1 0 dengan 1 1.

Pada Gambar 9 terlihat bahwa kurva ₀c

R akan stabil turun menuju R2 ketika

semakin besar artinya dengan strategi vaksinasi CVS ini R₂ adalah kondisi yang diperlukan untuk memberantas penyakit. Jika dimisalkan R₂ 1 maka akan diperoleh nilai kritis ₀ 0.00001710638555 seperti yang terlihat pada Gambar

0.0000 0.0005 0.0010 0.0015 0.0020 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 R0 0.0000 0.0005 0.0010 0.0015 0.0020 0.0 0.2 0.4 0.6 0.8 1.0 1.2 1.4 R0 _ _ _ _ R₂ ___ R . . . . ₀c R0 _ _ _ _ R₂ 1 ___ R . . . . ₀c R0

(38)

22

10. Sehingga haruslah minimal 0.001710638555% dari populasi rentan harus divaksinasi setiap hari agar penyakit bisa diberantas. Program untuk menampilkan Gambar 9 dan Gambar 10 dapat dilihat pada lampiran 11.

Kasus ketika ₁ 0 dan ₁ ₁

Pada kasus ini diasumsikan ₁ 0.25 0.0525 dan ₁ 0.1

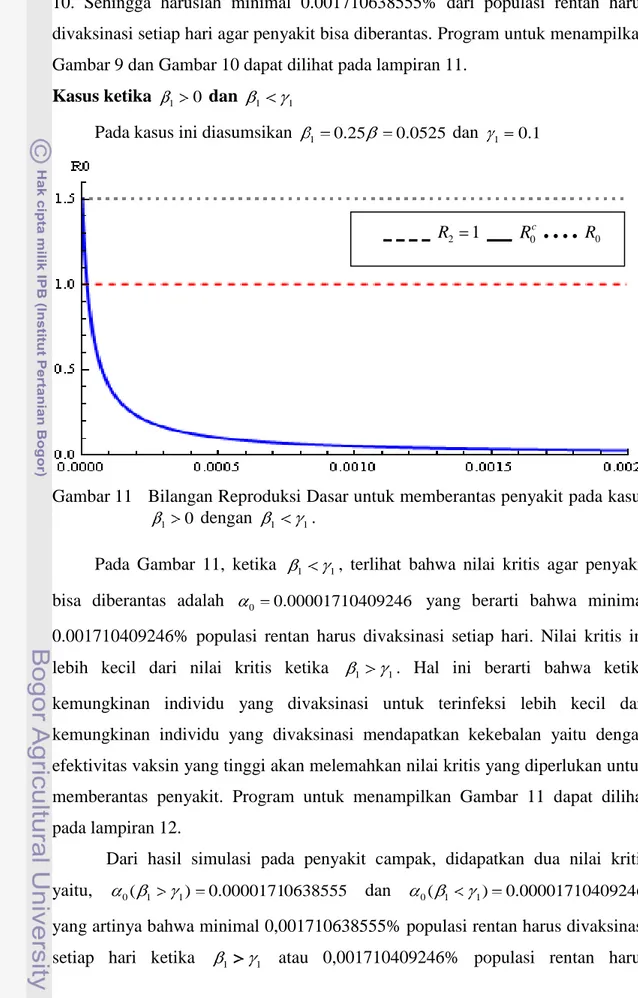
Gambar 11 Bilangan Reproduksi Dasar untuk memberantas penyakit pada kasus

1 0 dengan 1 1.

Pada Gambar 11, ketika ₁ ₁, terlihat bahwa nilai kritis agar penyakit bisa diberantas adalah ₀ 0.00001710409246 yang berarti bahwa minimal 0.001710409246% populasi rentan harus divaksinasi setiap hari. Nilai kritis ini lebih kecil dari nilai kritis ketika ₁ ₁. Hal ini berarti bahwa ketika kemungkinan individu yang divaksinasi untuk terinfeksi lebih kecil dari kemungkinan individu yang divaksinasi mendapatkan kekebalan yaitu dengan efektivitas vaksin yang tinggi akan melemahkan nilai kritis yang diperlukan untuk memberantas penyakit. Program untuk menampilkan Gambar 11 dapat dilihat pada lampiran 12.

Dari hasil simulasi pada penyakit campak, didapatkan dua nilai kritis yaitu, ₀( ₁ ₁) 0.00001710638555 dan ₀( ₁ ₁) 0.00001710409246 yang artinya bahwa minimal 0,001710638555% populasi rentan harus divaksinasi setiap hari ketika ₁ ₁ atau 0,001710409246% populasi rentan harus

(39)

23

divaksinasi setiap hari ketika ₁ ₁ , terlihat bahwa ketika efektifitas vaksin semakin tinggi yang menyebabkan pengurangan nilai ₁ dan kenaikan nilai ₁ akan semakin melemahkan nilai kritis yang diperlukan untuk memberantas penyakit.

Dari hasil analisis matematis dan simulasi didapatkan nilai parameter ₁ dan ₁ sangat mempengaruhi nilai R₂, dimana ₁ adalah laju individu yang divaksinasi terinfeksi dan 1 / ₁ adalah waktu rata-rata penerima vaksin mendapatkan kekebalan penuh, nilai kedua parameter ini ditentukan oleh efektifitas vaksin. Jika vaksin semakin efektif maka nilai ₁ akan semakin meningkat dan mengurangi nilai ₁ sehingga nilai R₂ akan semakin kecil yang artinya melemahkan kondisi yang diperlukan untuk memberantas penyakit.

Vaksinasi sangat membantu untuk mengendalikan penyebaran penyakit dengan dapat menurunkan bilangan reproduksi dasarnya dan mengurangi fraksi individu yang terinfeksi pada tahap endemik. Tapi ada kondisi yang diperlukan agar penyakit bisa diberantas. Jika kemungkinan bagi individu penerima vaksin untuk terinfeksi diabaikan, hal ini dapat menyebabkan over evaluating dari efek vaksinasi yang berarti bahwa kondisi yang diperlukan untuk memberantas penyakit akan hilang, sehingga penyakit akan bisa diberantas dengan strategi apapun atau nilai berapapun. Efektifitas strategi vaksinasi bergantung pada kemungkinan penerima vaksin untuk terinfeksi kecil ( ₁ kecil) atau waktu untuk mendapatkan kekebalan singkat ( ₁ besar). Jadi semakin tinggi efektifitas vaksin akan semakin melemahkan kondisi yang diperlukan untuk memberantas penyakit.

(40)

24

V KESIMPULAN DAN SARAN 5.1 Kesimpulan

Berdasarkan hasil dan pembahasan, hasil analisis yang telah dilakukan pada model matematika strategi vaksinasi kontinu (CVS) diperoleh dua titik tetap yaitu titik tetap bebas penyakit dan titik tetap endemik. Dari analisis kestabilan, dinamika CVS ini sepenuhnya bergantung pada bilangan reproduksi dasar. Ketika bilangan reproduksi dasarnya kurang dari satu maka titik tetap bebas penyakit akan stabil asimtotik yang berarti bahwa penyakit tidak akan menyebar dalam populasi atau pada akhirnya penyakit akan hilang dari populasi. Jika bilangan reproduksi dasarnya lebih dari satu maka titik tetap endemik akan stabil asimtotik yang berarti bahwa penyakit akan tetap ada dan menyebar dalam populasi.

Selanjutnya, dari analisis matematis dan simulasi terhadap efek dari strategi vaksinasi CVS diperoleh kesimpulan sebagai berikut :

1. Vaksinasi bermanfaat untuk mengendalikan penyebaran penyakit yaitu dengan mereduksi bilangan reproduksi dasarnya dan menurunkan fraksi individu yang terinfeksi pada tahap endemik.

2. Ketika kemungkinan bagi individu penerima vaksin untuk terinfeksi diabaikan, maka kondisi yang diperlukan untuk memberantas penyakit akan hilang (over

evaluating), sehingga penyakit akan bisa diberantas dengan strategi apapun.

3. Strategi yang diperlukan untuk memberantas penyakit bergantung pada kemungkinan individu penerima vaksin terinfeksi ( ₁ kecil) dan individu penerima vaksin mendapatkan kekebalan ( ₁ besar). Ketika kemungkinan individu penerima vaksin terinfeksi itu lebih kecil dari pada kemungkinan individu penerima vaksin mendapatkan kekebalan ( ₁ ₁) maka efektifitas vaksinasi akan semakin baik. Dengan kata lain, semakin tinggi efektifitas vaksin maka akan semakin melemahkan kondisi yang diperlukan untuk memberantas penyakit.

5.2 Saran

Penelitian ini perlu dilanjutkan dengan strategi vaksinasi yang berbeda yaitu strategi vaksinasi terputus (Pulse Vaccination Strategy-PVS) dan membandingkannya dengan strategi CVS, yang telah dibahas disini.

(41)

25

DAFTAR PUSTAKA

Anonym. 2005. Immunization against diseases of public health importance. http://www.who.int/mediacentre/factsheets/fs288/en/index.html/

Anton H. 1995. Aljabar Linear Elementer (Edisi ke-5). Pantur Silaban & I Nyoman Susila,penerjemah. Jakarta : Erlangga.

Alexander ME, Bowman C, Moghadas SM, Summers R, Gumel AB, Sahai BM. 2004. A Vaccination Model for Transmission Dynamics of Influenza. SIAM J. Appl. Dyn. Syst. 3, 503-524

Arino J, Mccluskey CC, van den Driessche P. 2003. Global results for an

epidemic model with vaccination that exhibits backward bifurcation.

SIAM J. Appl. Math. 64, 260–276.

Blyuss KB, Kyrichko YN. 2005. On a basic model of a two-disease epidemic.

Elsevier applied Mathematics and computation. 160 : 177-187

Borelli RL, Coleman CS. 1998. Differential Equations. John Wiley and Sons, Inc. USA.

Braun M. 1983. Differential equation and their applications. New York : Springer-Verlag

d’Onofrio A, Manfredi P, Salinelli E. 2007. Vaccinating behaviour, information,

and the dynamics of SIR vaccine preventable diseases. Theor. Popul. Biol.

71, 301–317

Edelstein-Keshet L. 1998. Mathematical Models in Biology. New York : Random House.

Hethcote HW. 2000. The mathematics of infectious diseases. SIAM rev.42. 599-653

Kermack M, McKendrick A. 1927. Contribution to the Mathematical Theory of

Epidemics, Part I. Proc. Roy. A 115, 700-721.

Kribs-Zaleta CM, Velasco-Hernandez JX. 2000. A Simple Vaccination model with

Multiple endemic states. Math. Biosci. 164, 183-201.

Kribs-Zaleta CM, Martcheva M. 2002. Vaccination Strategies and backward

bifurcation in an age-since-infection structured model. Math. Biosci.

(42)

26

Ramali, Pamoentjak. 2005. Arti dan Keterangan istilah. Kamus Kedokteran.cet.26. Jakarta

Shim E. 2006. A Note on epidemic models with infective immigrants and

vaccination. Math. Biosci. Eng. 3, 557-566.

Szidarovszky F, Bahill AT. 1998. Linear System Theory. Second edition. Florida : CRC Press.

Tu PNV. 1994. Dynamic systems : An introduction with application in economics

and biology. New York : Springer-Verlag

Verhulst F. 1990. Nonlinear differential equation and Dynamical system. Springer-Verlag., Heidelberg, Germany

Xianning L, Yasuhiro T, Shingo I, 2007. SVIR models with vaccination strategies. Shiuzuka University, Hammamatsu 432-9561, Japan

(43)

27

(44)

28

Lampiran 1

Bukti teorema 1 kriteria Routh Hurwitz

Misalkan A, B, C bilangan riil. Bagian riil dari setiap nilai eigen persamaan karakteristik _p_{( )} 3 _A 2 _B _C ₀_{adalah jika dan hanya jika A, C}

bernilai positif dan AB C. Bukti :

Dari persamaan 3 2

( ) 0

p A B C , maka

0 1, 1 , 2 , 3

a a A a B a C dan a_i 0 jika i selainnya. Berdasarkan kriteria

Routh-Hurwitz, maka bagian riil dari setiap akar polimonial

3 2

( )

p A B C adalah jika dan hanya jika detHj 0, untuk

1, 2,3 j dengan 1 1 1 3 2 2 1 3 3 2 1 3 det 0 det 0 1 1 0 0 det 1 0 0 H a A A a a A C H AB C a B a a A C H a a a 2 1 0 0 0 B ABC C A C Dari (1), diperoleh A 0 Dari (2), diperoleh AB C 0 Dari (3), diperoleh 2 ( ) 0

ABC C C AB C , karena AB C 0 sehingga

diperoleh C 0.

Dengan demikian diperoleh bahwa bagian riil dari semua akar persamaan karakteristik _p_{( )} 3 _A 2 _B _C_{adalah negatif jika dan hanya jika A, C}

bernilai positif dan AB C.

(45)

29

Lampiran 2

Program mencari titik tetap strategi vaksinasi CVS Dengan mathematica 7.0 1 1 1 [{0 ( * ) ( * * ) ( * ), 0 ( * ) ( * * ) ( * ) ( * ), 0 ( * * ) ( * * ) ( * ) ( * )}, { , , }] / / Solve s s i s s v i v v s i v i i i s v i Simplify    2 2 1 1 1 1 1 1 1 1 1 1 1 2 1 1 2 2 1 1 1 1 1 1 1 1 {{ ( 2 ( ) (4 ( ) ( ( )) (( ( ) ( )) ( )( )) )), ( ( 4 i v 2 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 1 1 1 1 1 ( ) ( ( )) (( ( ) ( )) ( )( )) )) / (2 ( ( ))), ( (4 ( ) ( ( )) (( ( ) ( ) ) ( )( s 2 1 1 1 2 2 1 1 1 1 1 1 1 1 2 1 1 1 1 1 2 2 1 1 1 1 1 )) )) / (2 ( ( )))} 1 { ( 2 ( ) (4 ( ) ( ( )) (( ( ) ( )) ( )( )) )), ( i v ₁ ₁ 2 1 1 1 1 1 1 1 1 2 2 1 1 1 1 1 1 1 1 1 1 (4 ( ) ( ( )) (( ( ) ( )) ( )( )) )) / (2 ( ( ))), ( (4 ( ) ( ( )) (( ( ) ( s 2 1 1 1 1 1 )) ( )( )) )) / (2 ( ( )))}, { , 0, }} ( )( ) v i s 0 0 0 0 1 ( , , ) , , 0 E S V I ( , , ) E S V I dengan

(46)

30 S I 1 1 1 1 S V I I I 2 1 1 1 2 1 1 1 2 2 2( ) 4 ( ) ( ( ) ( ) ) I

(47)

31

Lampiran 3

Mencari nilai a a₁, ₂ dan a₃

1 tr( ( )) 0 S S a J E S V S V 22 23 11 13 11 12 2 32 33 31 33 21 22 1 2 1 1 2 2 2 1 0 0 0 J J J J J J a J J J J J J S S V S S V a S I I V a V I S I V 3 1 3 1 1 1 1 2 2 2 1 3 1 det ( ) 0 0 0 0 a J E S S V S V a I S V I S V I S I V I a S I V S

(48)

32

Lampiran 4

Dinamika Populasi untuk R₀ 0.520833

Perintah ini digunakan untuk menggambarkan simulasi pada Gambar 3 

=0.1; =0.5; 1=0.05; =0.06; 1=0.06; =0.8; R0c=( )/((+)(+))+(1  )/((+1)(+)(+)) 0.520833

bidsol=NDSolve[{-( s[t])-( s[t] i[t])-( s[t])s'[t],( s[t])-(1 v[t] i[t])-(1 v[t])-( v[t])v'[t],( s[t] i[t])+(1 v[t] i[t])-( i[t])-v[t])-( i[t])i'[t],(1 v[t])+( i[t])-v[t])-( r[t])r'[t], s[0]0.3,v[0]0.1,i[0]0.3,r[0]0},{s[t],v[t],i[t],r[t]},{t,0,100000}] {{s[t]InterpolatingFunction[{{0.,100000.}},<>][t],v[t]InterpolatingFunction[{{0., 100000.}},<>][t],i[t]InterpolatingFunction[{{0.,100000.}},<>][t],r[t]Interpolatin gFunction[{{0.,100000.}},<>][t]}} Anis1=Plot[s[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Blue,Thick}]; Anis2=Plot[v[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Green,Thick}]; Anis3=Plot[i[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Red,Thick}]; Anis4=Plot[r[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Black,Thick}]; Show[Anis1,Anis2,Anis3,Anis4]

(49)

33

Lampiran 5

Dinamika Populasi untuk R₀ 1.17187

=0.1; =0.5; 1=0.05; =0.06; 1=0.06; =0.2; R0c=( )/((+)(+))+(1  )/((+1)(+)(+)) 0.520833

bidsol=NDSolve[{-( s[t])-( s[t] i[t])-( s[t])s'[t],( s[t])-(1 v[t] i[t])-(1 v[t])-( v[t])v'[t],( s[t] i[t])+(1 v[t] i[t])-( i[t])-v[t])-( i[t])i'[t],(1 v[t])+( i[t])-v[t])-( r[t])r'[t], s[0]0.3,v[0]0.1,i[0]0.3,r[0]0},{s[t],v[t],i[t],r[t]},{t,0,100000}] {{s[t]InterpolatingFunction[{{0.,100000.}},<>][t],v[t]InterpolatingFunction[{{0., 100000.}},<>][t],i[t]InterpolatingFunction[{{0.,100000.}},<>][t],r[t]Interpolatin gFunction[{{0.,100000.}},<>][t]}} Anis1=Plot[s[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Blue,Thick}]; Anis2=Plot[v[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Green,Thick}]; Anis3=Plot[i[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Red,Thick}]; Anis4=Plot[r[t]/.bidsol,{t,0,100},PlotRange{0,0001},FrameLabel{"t"},Frame{{ True,False},{True,False}},PlotStyle{Dashed,Black,Thick}]; Show[Anis1,Anis2,Anis3,Anis4]

(50)

34

Lampiran 6

Dinamika Populasi I untuk R₀ 0.520833

1=0.8;2=0.8;3=0.8;4=0.8;

R0c1=( )/((+1)(+))+(1 1 )/((+1)(+1)(+)) 0.520833

bidsol1=NDSolve[{-( s[t])-( s[t] i[t])-(1 s[t])s'[t],(1 s[t])-(1 v[t] i[t])-(1 v[t])-( v[t])v'[t],( s[t] i[t])+(1 v[t] i[t])-( i[t])-( i[t])i'[t], s[0]0.3,v[0]0.1,i[0]0.3},{s[t],v[t],i[t]},{t,0,100000}];

Tonas1=Plot[i[t]/.bidsol1,{t,0,100},PlotRangeAll,FrameLabel{"t"},Frame{{Tru e,False},{True,False}},PlotStyle{Dashed,Blue,Thick}];

Tonas2=Plot[i[t]/.bidsol2,{t,0,100},PlotRangeAll,FrameLabel{"t"},Frame{{Tru e,False},{True,False}},PlotStyle{Dashed,Red,Thick}];

Tonas3=Plot[i[t]/.bidsol3,{t,0,100},PlotRangeAll,FrameLabel{"t"},Frame{{Tru e,False},{True,False}},PlotStyle{Dashed,Green,Thick}];

Tonas4=Plot[i[t]/.bidsol4,{t,0,100},PlotRangeAll,FrameLabel{"t"},Frame{{Tru e,False},{True,False}},PlotStyle{Dashed,Black,Thick}];

(51)

35

Lampiran 7

Sifat-sifat Matematis Bilangan Reproduksi Dasar

1 0 1 0 1 1 0| 0 ( )( ) ( )( )( ) ( )( ) c c c R R R R Jelas bahwa, ₁c ₀c R R . Karena 1 maka : 0 1 1 2 1 [( ) ] 0 ( ) ( )( ) c R 0 0| 0 0 c c R R R . 1 0 2 limRc 0, limRc R 1 0 2 1 lim ( )( ) c R R .

(52)

36

Lampiran 8

Kondisi Bilangan Reproduksi Dasar untuk memberantas penyakit Perintah ini digunakan untuk menggambarkan simulasi pada Gambar 6  =0.00003653;=0.215;1=0;=0.143;1=0.1; r0=/(+) 1.50311 r0c=( )/((+)(+))+(1  )/((+)(+)(+1)) 0.0000549087/(0.00003653 +) r1c=( )/((+)(+)) 0.0000549087/(0.00003653 +) r2=(1 )/((+)(+1)) 0 plot1=Plot[r1c,{,0,0.001},PlotStyle{Dashed,Blue,Thick},PlotRange{{0,0.001},{ 0,2}},AxesLabel{"","R0"}]; plot2=Plot[r0,{,0,0.001},PlotStyle{Dashed,Black,Thick},PlotRange{{0,0.001},{ 0,2}},AxesLabel{"","R0"}]; r3=1 plot3=Plot[r3,{,0,0.001},PlotStyle{Dashed,Red,Thick},PlotRange{{0,0.001},{0, 2}},AxesLabel{"","R0"}]; Show[plot1,plot2,plot3]

(53)

37

Lampiran 9

Dinamika Populasi S, V, I dan R untuk kasus ₁ 0 dan ₀c 0.97132 1

R

=0.00003653;=0.215;1=0;=0.143;1=0.1;=0.00002;

(54)

38

Lampiran 10

Dinamika Populasi S, V, I dan R untuk kasus ₁ 0 dan R₀c 1.18077 1 Perintah ini digunakan untuk menggambarkan simulasi pada Gambar 8 

=0.00003653;=0.215;1=0;=0.143;1=0.1;=0.00001;

(55)

39

Lampiran 11

Kondisi Bilangan Reproduksi Dasar untuk memberantas penyakit pada

kasus ₁ 0 dan ₁ ₁

Perintah ini digunakan untuk menggambarkan simulasi pada Gambar 9 dan Gambar 10  =0.00003653;=0.215;1=0.1075;=0.143;1=0.1; r0=/(+) 1.50311 r0c=( )/((+)(+))+(1  )/((+)(+)(+1)) 0.0000549087/(0.00003653 +)+(0.000274443 )/(0.00003653 +) r2=(1 )/((+)(+1)) 0.000274443 plot1=Plot[r0,{,0,0.002},PlotStyle{Dashed,Black,Thick},PlotRange{{0,0.002},{ 0,1.6}},AxesLabel{"","R0"}]; plot2=Plot[r0c,{,0,0.003},PlotStyle{Dashed,Blue,Thick},PlotRange{{0,0.003},{ 0,1.6}},AxesLabel{"","R0"}]; plot3=Plot[r2,{,0,0.003},PlotStyle{Dashed,Red,Thick},PlotRange{{0,0.003},{0, 0.001}},AxesLabel{"","R0"}]; Show[plot1,plot2,plot3]