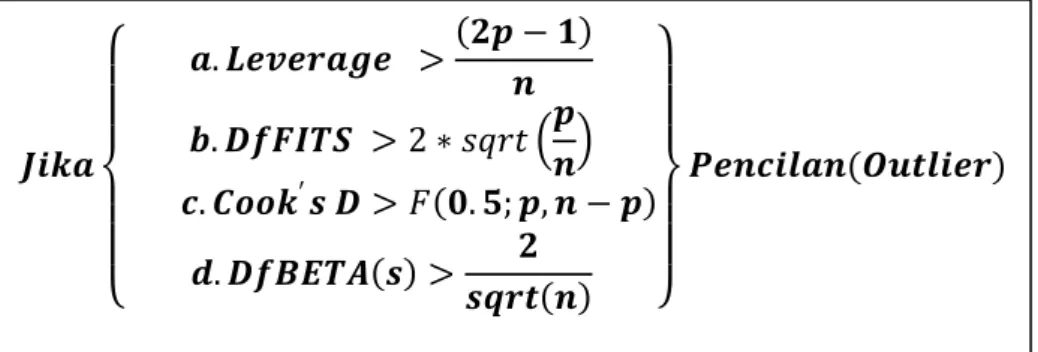BAB 2
LANDASAN TEORI
2.1 Regresi Linier
Analisis regresi digunakan untuk mengetahui hubungan antara variabel terikat (Y) dengan satu atau lebih variabel bebas (X). Menurut Hair et al (2009) regresi linear sederhana dapat efektif dengan ukuran sampel sebanyak 20 observasi. Menurut
Nawari (2010), model regresi linier untuk satu variabel bebas yaitu model regresi
linier sederhana, dinyatakan dalam persamaan berikut:
𝑌𝑌𝑖𝑖 = 𝛽𝛽0+ 𝛽𝛽1𝑋𝑋𝑖𝑖+ 𝜀𝜀𝑖𝑖 2.1 Keterangan: i = 1, 2, ..., 𝑁𝑁 Yi = variabel terikat Xi = variabel bebas 𝛽𝛽0, 𝛽𝛽1 = parameter regresi 𝜀𝜀𝑖𝑖 = sisaan/galat
Nilai 𝛽𝛽0 dan 𝛽𝛽1 adalah parameter regresi yang tidak diketahui nilainya dan akan dicari nilai estimasinya.
Model penduga regresi linier sederhana untuk persamaan 2.1 adalah sebagai berikut:
𝑌𝑌�𝑖𝑖 = 𝛽𝛽̂0+ 𝛽𝛽̂1𝑋𝑋𝑖𝑖 2.2
Keterangan:
𝑌𝑌�𝑖𝑖 = nilai 𝑌𝑌𝑖𝑖 yang diestimasi 𝛽𝛽̂0, 𝛽𝛽̂1 = penduga parameter
2.2 Metode Kuadrat Terkecil
Metode kuadrat terkecil merupakan salah satu penduga parameter (nilai 𝛽𝛽̂0, 𝛽𝛽̂1) model regresi linier sederhana. Menurut Sembiring (1995), metode kuadrat terkecil merupakan metode yang meminimumkan jumlah kuadrat sisa (selisih antara data yang sebenarnya dengan data dugaan dari model regresi yang terbentuk). Dari persamaan regresi linier sederhana 2.1, nilai residu (sisaan) ke-i pada model yaitu:
𝜀𝜀𝑖𝑖 = 𝑌𝑌𝑖𝑖 − 𝑌𝑌�𝑖𝑖 2.3
𝜀𝜀𝑖𝑖 = 𝑌𝑌𝑖𝑖 − ( 𝛽𝛽̂0+ 𝛽𝛽̂1𝑋𝑋𝑖𝑖) 2.4
Prinsip dasar metode kuadrat terkecil adalah meminimumkan jumlah kuadrat sisaan yang dinyatakan sebagai berikut:
Minimum ∑𝑛𝑛𝑖𝑖=1 𝜀𝜀𝑖𝑖2 2.5 ∑𝑛𝑛𝑖𝑖=1 𝜀𝜀𝑖𝑖2 = ∑ �𝑌𝑌𝑛𝑛𝑖𝑖=1 𝑖𝑖 − 𝑌𝑌�𝑖𝑖�2 = ∑ �𝑌𝑌𝑛𝑛𝑖𝑖=1 𝑖𝑖 − ( 𝛽𝛽̂0+ 𝛽𝛽̂1𝑋𝑋𝑖𝑖 )�2 ∑𝑛𝑛𝑖𝑖=1 𝜀𝜀𝑖𝑖2 = ∑ �𝑌𝑌𝑛𝑛𝑖𝑖=1 𝑖𝑖 − 𝛽𝛽̂0− 𝛽𝛽̂1𝑋𝑋𝑖𝑖 �2 2.6 Keterangan: 𝑌𝑌𝑖𝑖 = data sebenarnya 𝑌𝑌�𝑖𝑖 = data dugaan 𝛽𝛽̂0, 𝛽𝛽̂1 = penduga parameter 𝜀𝜀𝑖𝑖2 = sisaan kuadrat
Andaikan ∑𝑛𝑛𝑖𝑖=1 𝜀𝜀𝑖𝑖2 dinotasikan dengan 𝑃𝑃, 𝑃𝑃 merupakan fungsi dari nilai 𝛽𝛽̂0 dan 𝛽𝛽̂1 sehingga nilai-nilai 𝑃𝑃 dapat ditentukan dengan menurunkan persamaan (2.6) terhadap 𝛽𝛽̂0 dan 𝛽𝛽̂1 kemudian menyamakan tiap turunannya dengan nol, diperolehlah nilai sebagai berikut:
𝑃𝑃 = ∑𝑁𝑁 𝜀𝜀2
𝑖𝑖=1 = ∑ �𝑌𝑌𝑁𝑁𝑖𝑖=1 𝑖𝑖− 𝛽𝛽̂0− 𝛽𝛽̂1𝑋𝑋𝑖𝑖 �2
𝜕𝜕𝑃𝑃 𝜕𝜕𝛽𝛽�0= 0 − 2 ∑ 𝑌𝑌𝑖𝑖 𝑁𝑁 𝑖𝑖=1 − 0 + 2 ∑ �𝛽𝛽̂𝑁𝑁𝑖𝑖=1 0+ 𝛽𝛽̂1𝑋𝑋𝑖𝑖�= 0 𝜕𝜕𝑃𝑃 𝜕𝜕𝛽𝛽�0= − ∑ 𝑌𝑌𝑖𝑖 𝑁𝑁 𝑖𝑖=1 + ∑ �𝛽𝛽̂𝑁𝑁𝑖𝑖=1 0+ 𝛽𝛽̂1𝑋𝑋𝑖𝑖� = 0 ∑𝑛𝑛𝑖𝑖=1𝑌𝑌𝑖𝑖 = 𝑁𝑁𝛽𝛽̂0+ 𝛽𝛽̂1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖 2.7 dan 𝜕𝜕𝑃𝑃 𝜕𝜕𝛽𝛽�1= 0 − 0 − 2 ∑ 𝑌𝑌𝑖𝑖𝑋𝑋𝑖𝑖 𝑁𝑁 𝑖𝑖=1 + 2 ∑ �𝛽𝛽̂0𝑁𝑁𝑖𝑖=1 + 𝛽𝛽̂1𝑋𝑋𝑖𝑖�𝑋𝑋𝑖𝑖 = 0 𝜕𝜕𝑃𝑃 𝜕𝜕𝛽𝛽�1= − ∑ 𝑌𝑌𝑖𝑖𝑋𝑋𝑖𝑖 𝑁𝑁 𝑖𝑖=1 + ∑ �𝛽𝛽̂𝑁𝑁𝑖𝑖=1 0+ 𝛽𝛽̂1𝑋𝑋𝑖𝑖�𝑋𝑋𝑖𝑖 = 0 ∑𝑁𝑁𝑖𝑖=1𝑌𝑌𝑖𝑖𝑋𝑋𝑖𝑖 = 𝛽𝛽̂0∑𝑖𝑖=1𝑁𝑁 𝑋𝑋𝑖𝑖+ 𝛽𝛽̂1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖2 2.8
Dari persamaan 2.7 maka akan dicari nilai 𝛽𝛽̂0 sebagai berikut: ∑𝑁𝑁𝑖𝑖=1𝑌𝑌𝑖𝑖 = 𝑁𝑁𝛽𝛽̂0+ 𝛽𝛽̂1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖
𝛽𝛽̂0 = ∑𝑁𝑁𝑖𝑖=1𝑌𝑌𝑖𝑖− 𝛽𝛽̂𝑁𝑁1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖
𝛽𝛽̂0 = 𝑌𝑌� − 𝛽𝛽̂1𝑋𝑋� 2.9
Selanjutnya, dari persamaan 2.8, akan dicari nilai 𝛽𝛽̂1 sebagai berikut: ∑𝑁𝑁𝑖𝑖=1𝑌𝑌𝑖𝑖𝑋𝑋𝑖𝑖 = 𝛽𝛽̂0∑𝑖𝑖=1𝑁𝑁 𝑋𝑋𝑖𝑖+ 𝛽𝛽̂1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖2 = �∑𝑁𝑁𝑖𝑖=1𝑌𝑌𝑖𝑖−𝛽𝛽�1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖 𝑁𝑁 � ∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖 + 𝛽𝛽̂1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖2 = ∑𝑁𝑁𝑖𝑖=1𝑌𝑌𝑖𝑖∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖 𝑁𝑁 − 𝛽𝛽�1�∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖�2 𝑁𝑁 + 𝛽𝛽̂1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖2 ∑𝑁𝑁𝑖𝑖=1𝑌𝑌𝑖𝑖𝑋𝑋𝑖𝑖
−
∑ 𝑌𝑌𝑖𝑖∑ 𝑋𝑋𝑖𝑖 𝑁𝑁 𝑖𝑖=1 𝑁𝑁 𝑖𝑖=1 𝑁𝑁 = − 𝛽𝛽�1�∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖�2 𝑁𝑁 + 𝛽𝛽̂1∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖2 = 𝛽𝛽̂1�−𝑁𝑁1(∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖)2+ ∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖2�maka diperolehlah 𝛽𝛽̂1 yaitu:
𝛽𝛽̂1 =∑ 𝑌𝑌𝑖𝑖𝑋𝑋𝑖𝑖 𝑁𝑁 𝑖𝑖=1 −∑ 𝑌𝑌𝑖𝑖 ∑ 𝑋𝑋𝑖𝑖 𝑁𝑁 𝑖𝑖=1 𝑁𝑁 𝑖𝑖=1 𝑁𝑁 ∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖2−𝑁𝑁1�∑𝑁𝑁𝑖𝑖=1𝑋𝑋𝑖𝑖�2 2.10
2.3 Rataan Kuadrat Sisa (Mean Square Error)
Menurut Sembiring (1995), salah satu untuk menentukan kecocokan model dengan rataan kuadrat sisa 𝑠𝑠2, jika semakin kecil rataan kuadrat sisanya maka
semakin baik modelnya. Ukuran ini memperhitungkan banyaknya parameter dalam model melalui pembagian dengan derajat kebebasannya. Untuk menentukan rataan kuadrat sisa dinyatakan dalam rumus sebagai berikut:
𝑠𝑠2 = 𝐽𝐽𝐽𝐽𝐽𝐽 𝑛𝑛−𝑝𝑝 =
𝐽𝐽𝐽𝐽𝐽𝐽 −𝐽𝐽𝐽𝐽𝐽𝐽
𝑛𝑛−𝑝𝑝 2.11
Keterangan:
JKS = Jumlah Kuadrat Sisa
JKT = Jumlah Kuadrat Total = ∑(𝑌𝑌𝑖𝑖 − 𝑌𝑌�)2 JKR = Jumlah Kuadrat Regresi = ∑(𝑌𝑌�𝑖𝑖 − 𝑌𝑌�)2 𝑛𝑛 = Banyaknya sampel
𝑝𝑝 = Banyaknya parameter 𝑌𝑌𝑖𝑖 = Data sebenarnya 𝑌𝑌�𝑖𝑖 = Data dugaan
𝑌𝑌� = Rataan data sebenarnya
2.4 Pencilan
2.4.1 Pengertian Pencilan
Menurut Sembiring (1995), secara umum pencilan ialah data yang tidak mengikuti pola umum model.
2.4.2 Dampak Pencilan
Menurut Soemartini (2007), keberadaan data pencilan akan mengganggu dalam proses analisis data dan harus dihindari dalam banyak hal. Salah satu penyebab tidak terpenuhi asumsi kenormalan galat adalah pencilan (Gujarati, 1991). Dalam kaitannya dengan analisis regresi, pencilan dapat menyebabkan hal-hal berikut: 1. Residual yang besar dari model yang terbentuk
2. Varians pada data tersebut menjadi lebih besar 3. Taksiran interval memiliki rentang yang lebar
2.4.3 Pendeteksian Pencilan
Menurut Soemartini (2007) beberapa metode dan nilai yang dapat digunakan untuk mendeteksi ada atau tidak adanya pencilan ialah sebagai berikut:
1. Metode Grafik
Metode grafik merupakan salah satu cara pendeteksian pencilan yang mudah dipahami karena menampilkan data secara grafis (gambar) tanpa melibatkan perhitungan yang rumit. Namun, kelemahan metode ini yaitu yang menentukan data tersebut sebagai pencilan atau tidak tergantung pada kebijakan (judgement) peneliti, karena metode ini hanya mengandalkan visualisasi gambar. Pendeteksian pencilan dengan metode grafik di antaranya ialah:
a. Diagram Pencar (Scatter Plot)
Metode ini dilakukan dengan cara memplot data dengan observasi ke-𝑖𝑖 (𝑖𝑖 = 1, 2, …, 𝑛𝑛). Selain itu, setelah diperoleh model regresi maka dapat dilakukan dengan cara memplot antara residual (𝑒𝑒) dengan nilai prediksi Y (𝑌𝑌�). Jika terdapat satu atau beberapa data yang terletak jauh dari pola kumpulan data keseluruhan maka hal ini mengindikasikan adanya pencilan.
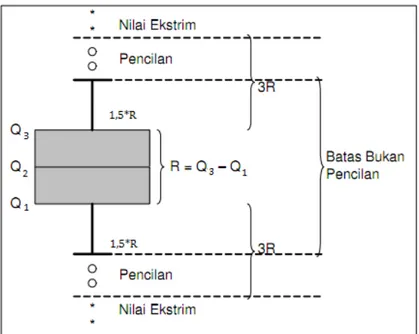
b. Boxplot
Metode boxplot merupakan metode yang paling umum yaitu dengan menggunakan nilai kuartil dan jangkauan. Jangkauan (IQR, Interquartile Range) didefinisikan sebagai selisih kuartil 1 terhadap kuartil 3, atau IQR = 𝑸𝑸𝟑𝟑− 𝑸𝑸𝟏𝟏. Pendeteksian pencilan dapat ditentukan jika nilai yang kurang dari 1,5*IQR terhadap kuartil 1 dan nilai yang lebih dari 1,5*IQR terhadap kuartil 3.
Gambar 2.1 Skema Identifikasi Data Pencilan dengan IQR atau Box Plot
2. Leverage Values, DFFITS, Cook’s Distance, dan DfBETA(s)
Cara mendeteksi pencilan dapat juga dengan menentukan nilai Leverage, DFFITS, Cook’s Distance, dan DfBETA(s). Definisi dari masing-masing nilai tersebut ialah sebagai berikut:
a. Leverage Values; menampilkan nilai leverage (pengaruh) terpusat.
b. DFFITS atau Standardized DfFIT; menampilkan nilai perubahan dalam harga yang diprediksi bilamana case tertentu dikeluarkan dan sudah distandarkan.
c. Cook’s Distance; menampilkan nilai jarak Cook.
d. DfBETA(s); menampilkan nilai perubahan koefisien regresi sebagai hasil perubahan yang disebabkan oleh pengeluaran case tertentu. Digunakan untuk mendeteksi pencilan pada variabel bebas.
Ketentuan dalam pendeteksian pencilan dengan nilai-nilai tersebut adalah:
Gambar 2.2 Kriteria Pengambilan Keputusan Adanya Pencilan atau Tidak
Keterangan:
n = jumlah observasi (sampel). p = jumlah parameter.
2.5 Regresi Robust
Menurut Drafer dan Smith (1981), penolakan begitu saja suatu pencilan bukanlah prosedur yang bijaksana, adakalanya pencilan memberikan informasi yang tidak bisa diberikan oleh titik data lainnya. Metode kuadrat terkecil (MKT) merupakan metode yang baik untuk menduga 𝛽𝛽 pada model regresi linier. Tetapi jika dalam penelitian diketahui terdapat pengamatan yang merupakan pencilan, maka penggunaan MKT akan menghasilkan kesimpulan yang tidak sempurna. Sebagai alternatif digunakan regresi robust.
Secara umum robust memiliki arti kekar. Regresi robust merupakan alat yang penting untuk menganalisis data yang terkontaminasi oleh pencilan dan memberikan hasil yang lebih fleksibel. Regresi robust tetap menggunakan seluruh data, tetapi dengan memberikan bobot yang kecil untuk data pencilan (Soemartini, 2007: 12). Regresi robust digunakan untuk mendeteksi pencilan dan memberikan hasil terhadap adanya pencilan (Chen, 2002).
𝑱𝑱𝑱𝑱𝑱𝑱𝑱𝑱 ⎩ ⎪ ⎪ ⎨ ⎪ ⎪ ⎧ 𝑱𝑱. 𝑳𝑳𝑳𝑳𝑳𝑳𝑳𝑳𝑳𝑳𝑱𝑱𝑳𝑳𝑳𝑳 >(𝟐𝟐𝟐𝟐 − 𝟏𝟏)𝒏𝒏 𝒃𝒃. 𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫 > 2 ∗ 𝑠𝑠𝑠𝑠𝑠𝑠𝑠𝑠 �𝟐𝟐𝒏𝒏� 𝒄𝒄. 𝑪𝑪𝑪𝑪𝑪𝑪𝑱𝑱′𝒔𝒔 𝑫𝑫 > 𝐹𝐹(𝟎𝟎. 𝟓𝟓; 𝟐𝟐, 𝒏𝒏 − 𝟐𝟐) 𝒅𝒅. 𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫𝑫(𝒔𝒔) >𝒔𝒔𝒔𝒔𝑳𝑳𝒔𝒔(𝒏𝒏)𝟐𝟐 ⎭⎪⎪ ⎬ ⎪ ⎪ ⎫ 𝑷𝑷𝑳𝑳𝒏𝒏𝒄𝒄𝑱𝑱𝑷𝑷𝑱𝑱𝒏𝒏(𝑶𝑶𝑶𝑶𝒔𝒔𝑷𝑷𝑱𝑱𝑳𝑳𝑳𝑳)
2.5.1 Regresi Robust Penduga-S
Penduga-S (Scale) pertama kali diperkenalkan oleh Rousseeuw dan Yohai (1984) di mana metode ini merupakan keluarga high breakdown point yaitu ukuran umum proporsi dari data pencilan yang dapat ditangani sebelum pengamatan tersebut mempengaruhi model prediksi. Disebut penduga-S karena mengestimasi berdasarkan skala. Skala yang digunakan adalah simpangan baku sisaan.
Pendugaan koefisien regresi pada model regresi linier dengan MKT dilandasi pada peubah 𝜀𝜀𝑖𝑖 = 𝑌𝑌𝑖𝑖 − 𝑌𝑌�𝑖𝑖 pada persamaan:
∑𝑛𝑛𝑖𝑖=1𝑥𝑥𝑖𝑖𝑒𝑒𝑖𝑖 = 0 2.12
Bentuk yang lebih umum dari pendugaan parameter pada model regresi adalah pemecahan terhadap:
∑𝑛𝑛𝑖𝑖=1𝜓𝜓(𝑢𝑢𝑖𝑖)𝑥𝑥𝑖𝑖 = 0 2.13
Di mana
𝑢𝑢𝑖𝑖 = 𝑐𝑐𝐽𝐽𝑒𝑒𝑖𝑖 2.14
Dengan S didefinisikan sebagai:
𝐽𝐽𝑚𝑚 = 𝑚𝑚𝑒𝑒𝑚𝑚𝑖𝑖𝑚𝑚𝑛𝑛|𝑒𝑒𝑖𝑖|, 𝑖𝑖 = 1, 2, . . . , 𝑛𝑛 2.15 Di mana 𝑒𝑒𝑖𝑖 adalah sisaan yang diperoleh dari MKT.
Penyelesaian koefisien regresi pada persamaan 2.13 disebut dengan penduga-M dan dapat diselesaikan dengan MKT terboboti berikut:
β * = (X’WX)-1
X’WY
di mana W (matriks diagonal 𝑛𝑛𝑥𝑥𝑛𝑛) = diagonal utama [𝑤𝑤1, 𝑤𝑤2, … , 𝑤𝑤𝑛𝑛], 𝑤𝑤𝑖𝑖 merupakan pembobot pengamatan ke-𝑖𝑖 (Myers, 1990).
Jika 𝑤𝑤𝑖𝑖 = 𝜓𝜓(𝑢𝑢𝑖𝑖)
𝑢𝑢𝑖𝑖 maka persamaan 2.13 menjadi:
Tahapan iterasi dalam penaksiran koefisien regresi (Winahju, 2010) adalah:
1. Dihitung penaksir β, dinotasikan b menggunakan least square, sehingga didapatkan yˆi,0 dan εi,0 = yi −yˆi,0, (i = 1, 2, ... n) yang diperlakukan sebagai
nilai awal (yi adalah hasil eksperimen).
2. Dari nilai-nilai residual ini dihitung σ , dan pembobot awal wˆ0 i,0 =
) ( ) ( * 0 , * 0 , i i ε ε ψ . Nilai ψ(εi*) dihitung sesuai fungsi Huber, dan εi,0* = εi,0 /
0
ˆ σ .
3. Disusun matrik pembobot berupa matrik diagonal dengan elemen w1,0 , w2,0 , . .
. , wn,0 , dinamai W0.
4. Dihitung penaksir koefisien regresi: bRobust ke 1 = (XT W0 X)-1 XT W0 Y 5. Dengan menggunakan bRobust ke 1 dihitung pula
∑
= − n i i i y y 1 1 , | ˆ | atau
∑
= n i i 1 1 . | |ε .6. Selanjutnya langkah 2 sampai dengan 5 diulang sampai didapatkan
∑
= n i m i 1 . | |ε konvergen. Nilai
∑
= n i m i 1 . ||ε yang konvergen adalah selisih antara 𝑏𝑏𝑚𝑚+1 dan 𝑏𝑏𝑚𝑚 mendekati 0; 𝑚𝑚 = banyak iterasi.
Persamaan 2.15 menunjukkan bahwa penduga-M hanya menggunakan median pada pembentukan nilai pembobot. Kelemahan median adalah kurangnya pertimbangan pada pola sebaran data dan bukan merupakan fungsi dari keseluruhan data. Rousseeuw dan Yohai (1984) memperkenalkan penduga-S yang merupakan pengembangan dari penduga-M. Penduga-S menggunakan simpangan baku sisaan untuk mengatasi kelemahan dari median. Menurut Salibian dan Yohai (2006) penduga-S (𝛽𝛽̂𝐽𝐽) dinyatakan dalam bentuk rumus sebagai berikut:
𝛽𝛽̂𝐽𝐽 = min ∑𝑛𝑛𝑖𝑖=1𝜌𝜌 �𝐽𝐽𝑒𝑒𝑠𝑠𝑖𝑖� atau
𝛽𝛽̂𝐽𝐽 = min ∑𝑛𝑛𝑖𝑖=1𝜌𝜌 �𝑦𝑦𝑖𝑖−𝑋𝑋𝐽𝐽𝑠𝑠𝑖𝑖𝑖𝑖𝛽𝛽𝑖𝑖� 2.17
Penyelesaian persamaan 2.17 adalah dengan cara menurunkannya terhadap 𝛽𝛽 sehingga,
𝜕𝜕𝛽𝛽�𝐽𝐽
𝜕𝜕𝛽𝛽 = ∑𝑛𝑛𝑖𝑖=1𝑋𝑋𝑖𝑖𝑖𝑖𝜓𝜓� 𝑒𝑒𝑖𝑖
𝐽𝐽𝑠𝑠� = 0 2.18
𝜓𝜓 disebut fungsi pengaruh yang merupakan turunan dari 𝜌𝜌, sedangkan 𝐽𝐽𝑠𝑠 didefinisikan sebagai:
𝐽𝐽𝑠𝑠 = �𝑛𝑛 ∑𝑛𝑛𝑖𝑖=1(𝑒𝑒𝑖𝑖𝑀𝑀)2− �∑𝑛𝑛𝑖𝑖=1𝑒𝑒𝑖𝑖𝑀𝑀�2
𝑛𝑛(𝑛𝑛−1) 2.19
Di mana 𝑒𝑒𝑖𝑖𝑀𝑀 adalah sisaan yang diperoleh melalui penduga-M. Persamaan 2.18 dapat diselesaikan melalui MKT terboboti secara iterasi yang disebut Iteratively Reweighted Least Squares (Iterasi kuadrat terkecil terboboti kembali). Sisaan awal yang digunakan pada penduga-S adalah sisaan yang diperoleh dari penduga-M. Selanjutnya dikatakan bahwa Iterasi kuadrat terkecil terboboti kembali merupakan proses pendugaan melalui metode kuadrat terkecil terboboti dilanjutkan dengan menghitung sisaan dan pembobot 𝑤𝑤(𝑢𝑢𝑖𝑖) yang baru dan dilakukan pendugaan secara berulang-ulang sampai konvergen. Kekonvergen tercapai jika perubahan jumlah mutlak sisaan, ∑𝑛𝑛𝑖𝑖=1|𝜀𝜀𝑖𝑖:𝑚𝑚| dari iterasi terakhir ke iterasi berikutnya kurang dari 0,01 (Salibian dan Yohai, 2006).
Fungsi 𝜌𝜌 pada persamaan 2.17 disebut fungsi kriteria 𝜌𝜌 disarankan memakai fungsi obyektif berikut (Tukey, 1977, dalam Chen, 2002):
𝜌𝜌(ui) = � c2[1−�1−(ui c)2� 3 ] 6 , |𝑢𝑢𝑖𝑖| ≤ c c2 6, |𝑢𝑢𝑖𝑖| > c 2.20
dengan fungsi pengaruh:
𝛹𝛹(𝑢𝑢𝑖𝑖) = 𝜌𝜌′(𝑢𝑢𝑖𝑖) = �𝑢𝑢𝑖𝑖(1 − (uci)2)2, |𝑢𝑢𝑖𝑖| ≤ c 0, |𝑢𝑢𝑖𝑖| > c Oleh karena 𝑤𝑤𝑖𝑖 = 𝛹𝛹(𝑢𝑢𝑖𝑖) (𝑢𝑢𝑖𝑖) , sehingga: 𝑤𝑤𝑖𝑖 = �[1 − ( ui c)2]2, |𝑢𝑢𝑖𝑖| ≤ c 0, |𝑢𝑢𝑖𝑖| > c 2.21 Rousseeuw dan Leroy (1987) menyarankan nilai 𝑐𝑐 = 1,547 agar mendapatkan nilai breakdown point 50%. Fungsi pengaruh atau penimbang ini disebut fungsi Tukey atau bisquare weight atau biweight. Selanjutnya diterangkan juga bahwa secara umum ide dalam biweight adalah bahwa sisaan yang kecil mendapatkan
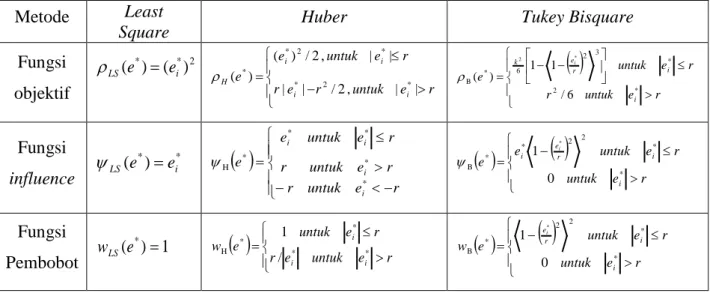
bobot yang besar. Secara ringkas, fungsi obyektif dan pembobot dari estimator Least Square, Huber, dan Tukey Bisquare dapat dilihat pada Tabel 2.1.
Tabel 2.1 Fungsi Objektif, Fungsi Influence dan Fungsi Pembobot untuk Least Square, Huber, dan Tukey Bisquare
Metode Least
Square Huber Tukey Bisquare
Fungsi objektif 2 * * ) ( ) ( i LS e = e ρ > − ≤ = r e untuk r e r r e untuk e e i i i i H | | , 2 / | | | | , 2 / ) ( ) ( * 2 * * 2 * * ρ
( )
> ≤ − − = r e untuk r r e untuk e i i r e k i * 2 * 3 2 6 * B 6 / 1 1 ) ( * 2 ρ Fungsi influence * * ) ( i LS e =e ψ( )
− < − > ≤ = r e untuk r r e untuk r r e untuk e e i i i i * * * * * H ψ( )
( )
> ≤ − = r e untuk r e untuk e e i i r e i i * * 2 2 * * B 0 1 * ψ Fungsi Pembobot ( ) 1 * = e wLS( )
> ≤ = r e untuk e r r e untuk e w i i i * * * * H / 1( )
( )
> ≤ − = r e untuk r e untuk e w i i r ei * * 2 2 * B 0 1 *Sumber: Fox (2002), Montgomery (1992)
Langkah-langkah menentukan regresi robust penduga-S (Salibian dan Yohai, 2006) adalah sebagai berikut:
a. Didapatkan vektor penduga awal 𝑏𝑏1, 𝑏𝑏2, … , 𝑏𝑏𝑝𝑝 dari model regresi dengan MKT didapatkan galat 𝑒𝑒𝑖𝑖0.
b. Dari sisaan awal dihitung 𝐽𝐽𝑀𝑀 sesuai persamaan (2.15) untuk mendapatkan 𝑢𝑢𝑖𝑖 berdasarkan persamaan (2.14).
c. Menghitung nilai 𝑤𝑤𝑖𝑖 sesuai persamaan (2.21).
d. Dengan menggunakan MKT terboboti didapatkan penduga kuadrat terkecil terboboti:
β * = (X’WX)-1
X’WY
e. Menjadikan sisaan langkah (d) sebagai sisaan awal pada langkah (b), sehingga didapatkan nilai 𝐽𝐽𝑀𝑀 dan pembobot 𝑤𝑤𝑖𝑖 yang baru.
f. Iterasi diulang sampai didapatkan kekonvergenan sehingga diperoleh 𝑏𝑏0𝑀𝑀, 𝑏𝑏1𝑀𝑀, … , 𝑏𝑏𝑝𝑝𝑀𝑀 yang merupakan penduga-M sehingga didapatkan sisaan 𝑒𝑒𝑖𝑖𝑀𝑀.
g. Dari sisaan yang diperoleh pada langkah (f), dihitung robust 𝐽𝐽𝑠𝑠 sesuai persamaan(2.19) untuk mendapatkan nilai 𝑢𝑢𝑖𝑖 sesuai persamaan (2.14).
h. Menghitung nilai 𝑤𝑤𝑖𝑖 sesuai persamaan (2.21).
i. Digunakan MKT terboboti untuk mendapatkan penduga kuadrat terkecil terboboti:
β * = (X’WX)-1
X’WY
j. Menjadikan sisaan yang diperoleh pada langkah (i) sebagai sisaan pada langkah (g), sehingga didapatkan nilai 𝐽𝐽𝑠𝑠 dan pembobot 𝑤𝑤𝑖𝑖 yang baru.
k. Iterasi ulang sampai didapatkan kekonvergenan sehingga diperoleh 𝑏𝑏0𝐽𝐽, 𝑏𝑏1𝐽𝐽, … , 𝑏𝑏𝑝𝑝𝐽𝐽 yang merupakan penduga-S.
2.5.2 Regresi Robust Penduga Least Trimmed Squares (LTS)
Least Trimmed Squares (LTS) merupakan metode penduga regresi robust yang menggunakan konsep pengepasan metode kuadrat terkecil (ordinary least squares) untuk meminimumkan jumlah kuadrat sisaan (Akbar dan Maftukhah, 2007). Menurut Rousseeuw dan Leroy (1987), penduga LTS (𝛽𝛽̂) dinyatakan dalam bentuk rumus sebagai berikut:
𝛽𝛽̂𝐿𝐿𝐽𝐽𝐽𝐽 = min ∑ (𝑠𝑠ℎ 2)𝑖𝑖:𝑛𝑛
𝑖𝑖=1 2.22
Keterangan:
(𝑠𝑠2)1:𝑛𝑛 ≤ (𝑠𝑠2)2:𝑛𝑛 ≤ … ≤ (𝑠𝑠2)𝑛𝑛:𝑛𝑛 = sisaan kuadrat yang diurutkan ℎ =𝑛𝑛2+𝑝𝑝+12 = 𝑛𝑛+𝑝𝑝+12
n = banyaknya sampel p = banyaknya parameter
Jumlah h menunjukkan sejumlah subset data dengan kuadrat fungsi obyektif terkecil. Nilai h pada persamaan akan membangun breakdown point yang besar sebanding dengan 50%. Kuadrat sisa pada persamaan (2.22) berasal dari persamaan estimasi regresi linier menggunakan konsep metode kuadrat terkecil dengan banyaknya sisaan kuadrat (𝑒𝑒2)𝑖𝑖:𝑛𝑛 yang akan diolah adalah sebanyak h residual.