1
BAB I
PENDAHULUAN
I.1. Latar Belakang
Indonesia merupakan salah satu negara di dunia dengan peradaban masa lampau yang sangat megah. Peninggalan peradaban masa lampau tersebut masih dapat dinikmati hingga saat ini. Salah satu peninggalan masa lampau yang mudah diketahui berupa peninggalan fisik. Peninggalan fisik yang paling banyak tersebar berupa candi, baik Candi Hindu maupun Candi Budha dengan berbagai kelengkapan didalamnya. Salah satu Candi Hindu yang terkenal di Indonesia ialah Candi Prambanan.
Candi Prambanan merupakan warisan budaya jaman Kerajaan Mataram Hindu yang bertempat di sekitar Yogyakarta. Secara geografis Candi Prambanan terletak di lintang 7o 45’ 8” LS dan di bujur 110o 29’ 30” BT. Candi tersebut dibangun pada abad ke-9 masehi oleh Raja Mataram Hindu. Situs Candi Prambanan sudah diakui oleh UNESCO sebagai salah satu situs warisan dunia yang harus dilestarikan. Candi Prambanan terletak di dataran luas di kaki Gunung Merapi dan berada di wilayah aliran Sungai Opak (Anonim, 2011).
Sungai Opak merupakan salah satu sungai yang memiliki mata air di lereng Gunung Merapi. Sungai Opak merupakan suatu bentang alam yang menjadi bagian dari Sesar Opak. Sesar Opak merupakan sesar utama dengan arah sesar Barat Daya – Timur Laut (Sulaeman, dkk., 2008). Arah sesar seperti ini mengindikasikan bahwa Sesar Opak termasuk jenis sesar mendatar dengan arah ke kiri (Sulaeman, dkk., 2008). Sesar ini memanjang dari kawasan Pantai Parangtritis hingga ke sebelah timur Kota Yogyakarta (Abidin, dkk., 2009), dengan lebar zona sesar diperkirakan sekitar 2,5 km (Wicaksono, 2014). Sesar Opak merupakan penyebab terjadinya gempa bumi di Yogyakarta pada tanggal 27 Mei 2006 dengan kedalaman 10 km dan magnitud 6,3 SR (Sulaeman, dkk., 2008).
Mengingat Candi Prambanan merupakan situs budaya yang harus dilestarikan dan karena lokasinya yang terletak di daerah rawan gempa, maka perlu dilakukan
pemantauan secara kontinyu. Salah satu metode yang digunakan adalah pemantauan deformasi aspek geometrik dengan metode Geodesi. Pemantauan dilakukan pada titik-titik pantau Candi Prambanan.
Sesudah terjadi gempa bumi tahun 2006, Balai Pelestarian Cagar Budaya (BPCB) Yogyakarta melakukan pengukuran stabilisasi candi dengan mengukur titik-titik pantau yang tersebar di area candi. Pengukuran dilakukan menggunakan kerangka pengukuran berupa poligon tertutup, sehingga ketelitian pengukuran hanya berdasarkan pada nilai kesalahan linier poligon (Basuki, 2006). Perhitungan hasil pengukuran dilakukan menggunakan metode Bowditch. Metode ini meratakan kesalahan ke seluruh hasil pengukuran, baik pengukuran jarak maupun pengukuran sudut. Pengukuran menggunakan metode ini sudah dilakukan sejak tahun 1999, dimana saat itu terdapat pengukuran stabilisasi tubuh Candi Prambanan, namun pemantauan ini tidak dilakukan secara kontinyu oleh BPCB Yogyakarta sehingga data pemantauan Candi Prambanan tidak terdapat di setiap epoch.
Analisis deformasi dengan menggunakan hitung perataan kuadrat terkecil metode parameter baru dimulai pada perhitungan epoch 2011 dan 2013. Proses ini tidak dilakukan untuk epoch 1999 dan 2001 sehingga pemantauan deformasi Candi Prambanan terbatas pada epoch setelah Gempa Yogyakarta tahun 2006. Pemantauan belum menyeluruh pada epoch sebelum dan sesudah Gempa Yogyakarta 2006. Oleh karena itu perlu dilakukan penelitian selanjutnya untuk menganalisis deformasi sebelum dan sesudah gempa.
Penelitian ini merupakan kelanjutan penelitian sebelumnya yang dilakukan untuk menganalisis deformasi yang terjadi pada setiap titik pantau. Perbedaan dari penelitian sebelumnya terdapat pada data yang digunakan dan metode analisis yang digunakan. Penelitian ini menggunakan data pemantauan stabilisasi Candi Prambanan pada epoch 1999, 2001, 2011, 2013 dan 2015. Data pemantauan tahun 1999 dan 2001 diasumsikan mewakili data pemantauan sebelum terjadi gempa bumi 2006. Analisis dilakukan menggunakan hitung perataan kuadrat terkecil metode
I.2. Identifikasi Masalah
Berdasarkan latar belakang yang ada, dalam penelitian ini permasalahan utama dirumuskan sebaga berikut :
1. Belum ada kajian deformasi secara komprehensif sebelum dan sesudah Gempa Yogyakartan tahun 2006, oleh karena itu belum diperoleh nilai koordinat yang merepresentasikan kondisi sebelum dan sesudah Gempa Yogyakarta tahun 2006.
2. Pemrosesan data pengukuran Candi Prambanan belum dilakukan sesuai prosedur dalam analisis deformasi aspek geometrik.
1.3. Pertanyaan Penelitian
Berdasarkan permasalahan yang sudah diidentifikasi, maka pertanyaan yang muncul terkait penelitian ini dapat dijabarkan sebagai berikut :
1. Berapa nilai koordinat dan ketelitian titik-titik pantau Candi Prambanan, khususnya pada Candi Siwa setelah dilakukan analisis menggunakan
epoch 1999, 2001 yang merepresentasikan data sebelum gempa bumi
tahun 2006 serta epoch 2011, 2013 dan 2015 yang merepresentasikan data setelah gempa bumi tahun 2006?
2. Apakah terjadi deformasi secara signifikan pada tubuh Candi Prambanan, khususnya Candi Siwa serta berapa jarak pergeseran antar dua epoch dan kemana arah pergeserannya?
1.4. Pembatasan Masalah
Berdasarkan latar belakang dan tujuan yang telah dirumuskan pembatasan penelitian ini dijabarkan sebagai berikut :
1. Objek penelitian ini adalah Candi Siwa yang merupakan candi terbesar di kompleks Candi Prambanan.
2. Perhitungan parameter deformasi horisontal yang terjadi menggunakan data ukuran epoch 1999, 2001 (epoch sebelum gempa bumi tahun 2006), 2011, 2013 dan 2015 (epoch setelah gempa bumi tahun 2006).
3. Jaring titik pantau berupa poligon tertutup delapan titik dengan data ukuran sudut dan jarak pada delapan titik pantau tersebut.
4. Pada proses perhitungan menggunakan kerangka dasar relatif yang tidak memiliki titik ikat di lapangan.
5. Analisis deformasi menggunakan uji kesebangunan jaring, uji pergeseran titik dan uji signifikansi parameter.
1.5. Tujuan Penelitian
Berdasarkan pertanyaan penelitian yang telah diajukan, maka tujuan penelitian ini dapat dirumuskan sebagai berikut:
1. Teridentifikasi deformasi horisontal aspek geometrik pada jaring pemantauan Candi Prambanan dengan data terestris sebelum dan sesudah Gempa Yogyakarta tahun 2006.
2. Teridentifikasi nilai koordinat titik-titik pantau Candi Prambanan khususnya Candi Siwa beserta nilai ketelitiannya pada epoch 1999, 2001 (epoch sebelum gempa bumi tahun 2006), 2011, 2013 dan 2015 (epoch setelah gempa bumi tahun 2006).
3. Teridentifikasi titik-titik pantau yang mengalami deformasi secara signifikan.
4. Teridentifikasi besaran dan arah pergerakan titik pantau deformasi Candi Prambanan, khususnya Candi Siwa.
1.6. Manfaat Penelitian
Berdasarkan penelitian ini dapat dirumuskan manfaat dari penelitian sebagai berikut:
1. Untuk bidang keilmuwan, penelitian ini diharapkan sebagai studi kasus pemanfaatan metode hitung kuadrat terkecil pada analisis deformasi bangunan, khususnya deformasi pada peninggalan kebudayaan.
2. Untuk Balai Pelestarian Cagar Budaya Yogyakarta, penelitian ini diharapkan sebagai acuan penentuan konservasi yang dilakukan pada
tubuh candi agar meminimalisir kemungkinan negatif yang terjadi akibat gempa bumi maupun akibat dari pergeseran tubuh candi sendiri.
1.7. Tinjauan Pustaka
Penelitian studi deformasi pada bangunan peninggalan bersejarah seperti candi sudah dilakukan di berbagai tempat. Penelitian pada Candi Prambanan dilakukan sejak tahun 1984 oleh BPCB Yogyakarta, namun dokumen yang ditemukan pada epoch 1999. Pada dokumen tersebut diketahui bahwa pemantaun stabilitas Candi Prambanan menggunakan delapan titik yang tersebar di sekitar Candi Siwa. Penelitian difokuskan pada Candi Siwa disebabkan Candi Siwa merupakan candi terbesar dan termegah, namun dasar Candi Siwa sangat kecil untuk menopang tubuh candi di atasnya sehingga dibutuhkan pengamatan yang seksama di Candi Siwa. Pengukuran stabilitas Candi Siwa menggunakan metode triangulaterasi pada delapan titik poligon tersebut. Pada epoch 1999 pengukuran dilakukan menggunakan alat ukur sudut, jarak dan elevasi, sehingga didapatkan nilai koordinat 3D dalam sistem koordinat lokal dengan titik awal di SI. Koordinat titik SI didefinisikan dengan nilai koordinat (600,000 ; 600,000) m serta elevasi 153,496 m. Hasil pengolahan data menggunakan metode Bowditch pada epoch 1999 dan setelah dilakukan perbandingan dengan data 1997 maka didapatkan hasil bahwa memang terjadi pergeseran sebesar 7 mm di titik SIV dan SV (BPCB, 1999).
Penelitian selanjutnya dilakukan pada epoch 2001. Pengukuran stabilitas ini dilakukan karena pada tanggal 25 Mei 2001 telah terjadi gempa bumi di selatan Pulau Jawa sehingga perlu ada pengukuran pemantauan stabilitas di Candi Siwa. Proses pengukuran ini menggunakan delapan titik poligon yang sudah tersebar di sekitar Candi Siwa sebelumnya menggunakan metode triangulaterasi. Pengukuran menggunakan alat ukur sudut, jarak dan elevasi, sehingga didapatkan nilai koordinat 3D pada setiap titik poligon. Pada epoch 2001 nilai koordinat tetap didefinisikan dalam sistem koordinat lokal dengan titik awal di SI seperti pada pengukuran stabilitas epoch 1999. Hasil pengolahan data menggunakan metode Bowditch pada
terdapat pergeseran sebesar 4 mm pada arah horisontal dan pergeseran sebesar 5 mm pada arah vertikal (BPCB, 2001).
Penelitian lainnya yang menggunakan data epoch 2011 dan 2013 diketahui bahwa titik poligon yang digunakan memanfaatkan titik-titik poligon sebelumnya. Metode yang digunakan pada penelitian ini menggunakan metode triangulaterasi. Alat akuisisi data pada epoch 2011 dan 2013 hanya menggunakan alat pengukur sudut dan jarak sehingga nilai koordinat yang didapatkan hanya 2D atau hanya dalam arah horisontal. Pada epoch 2011 dan 2013 nilai koordinat tidak didefinisikan dengan nilai koordinat lokal, melainkan sudah menggunakan nilai koordinat global dengan titik ikat poligon pada Titik Tinggi Geodesi (TTG) 836 dan BM Boulevard. Proses pengukuran titik ikat poligon menggunakan metode ekstraterestris. Proses pengolahan data menggunakan metode hitung kuadrat terkecil terkendala minimum. Hasil analisis data didapatkan hasil bahwa telah terjadi pergeseran minimum pada titik SII sebesar 3,642 ± 4,490 mm dengan arah timur laut dan pergeseran maksimum sebesar 10,746 ± 5,657 mm pada titik SIII dengan arah timur laut. Nilai pergeseran ini belum menunjukkan adanya pergeseran secara signifikan setelah dilakukan uji statistik menggunakan tabel Fisher pada tingkat kepercayaan 95% (Wicaksono, 2014).
Penelitian ini dilaksanakan menggunakan lima epoch yang berbeda dengan peralatan akuisisi data yang berbeda. Agar penelitian ini berkesinambungan dengan analisis deformasi pada epoch 2011 dan 2013, maka penelitian ini juga memfokuskan pada pergeseran 2D Candi Siwa. Perhitungan menggunakan prinsip hitung perataan kuadrat terkecil metode inner constraint. Uji global memanfaatkan tabel Fisher dengan derajat kepercayaan tertentu. Apabila uji global ditolak maka langkah selanjutnya ialah melakukan uji blunder untuk mengetahui apakah terdapat blunder pada data pengamatan. Setelah dilakukan uji blunder maka langkah selanjutnya melakukan analisis pergeseran yang meliputi uji kesebangunan jaring dan uji pergeseran titik-titik pantau Candi Siwa dengan memanfaatkan tabel Fisher. Apabila dalam proses analisa pergeseran diketahui bahwa titik-titik pantau Candi Siwa mengalami pergeseran, maka perlu dilakukan uji signifikansi parameter. Uji ini memanfaatkan tabel t-student.
1.8. Landasan Teori
I.8.1. Gejala Dinamika Bumi
Ilmu Geodesi merupakan ilmu kebumian yang salah satu tujuannya untuk menyelenggarakan dan memelihara kerangka dasar geodetik 3D nasional dan global di daratan. Penyelenggaraan dan pemeliharaan kerangka dasar memperhatikan aspek waktu dalam pemantauan kerangka tersebut (Widjajanti, N., 1997). Pemantauan kerangka dasar geodetik diperlukan untuk memantau berbagai gejala dinamika bumi yang terjadi. Pembagian gejala dinamika bumi tersebut dapat dijabarkan sebagai berikut (Rais, 1984) :
1. Skala global. Pembagian pada skala ini menunjukkan pergerakan bumi secara keseluruhan yang diakibatkan oleh pergerakan antar lempeng, rotasi bumi dan gerakan kutub.
2. Skala regional. Pembagian pada skala ini menunjukkan pergerakan bumi dalam skala yang lebih kecil dari skala global (hanya beberapa kilometer). Pergerakan pada skala ini dapat ditemui pada gejala deformasi regional, gerakan sesar dan geologi regional.
3. Skala lokal. Skala ini menunjukkan adanya gejala dinamika bumi pada skala kecil. Pembagian pada skala ini sering disebut dengan deformasi, termasuk didalamnya ialah gerakan tanah, perubahan muka air tanah dan dampak medan geomagnetik dan geolistrik lokal.
Penafsiran deformasi dalam praktiknya lebih ditujukan pada pengertian secara luas tanpa memperhatikan pembagian skala yang sudah ditetapkan, tetapi pada dasarnya deformasi merupakan pergerakan titik pada suatu benda yang bersifat absolut maupun relatif.
Deformasi sendiri memiliki beberapa parameter yang merepresentasikan bagaimana deformasi itu terjadi. Salah satu parameter deformasi tersebut adalah pergeseran. Pada jenis deformasi ini yang menjadi fokus adalah pergeserannya beserta komponen pergeseran. Komponen pergeseran adalah jarak pergeseran dan arah pergeseran.
1.8.2. Survei Deformasi
Menurut Widjajanti (2001) deformasi merupakan pergerakan suatu titik pada benda secara absolut maupun relatif yang diakibatkan oleh pergerakan lempeng bumi. Pergerakan relatif dikaji dari pergerakan suatu titik relatif terhadap titik lainnya yang diasumsikan tidak mengalami pergerakan. Sedangkan untuk pergerakan absolut dikaji dari pergerakan titik itu sendiri.
Penentuan besaran dan arah dari deformasi yang terjadi pada suatu benda, maka diperlukan kerangka dasar pemantauan deformasi yang dapat dibagi menjadi dua jenis yaitu :
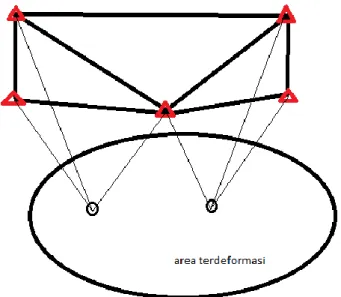
1. Kerangka dasar absolut. Suatu kerangka dasar pemantauan deformasi dikatakan sebagai kerangka dasar absolut apabila titik-titik ikat yang berfungsi sebagai titik-titik referensi terletak di luar area objek pengamatan deformasi. Ilustrasi kerangka dasar absolut ditunjukkan pada Gambar I.1 berikut.
Gambar I. 1. Kerangka dasar absolut (modifikasi Kuang, 1996)
Kerangka dasar absolut bertujuan untuk menentukan pergeseran titik relatif terhadap titik acuan yang didefinisikan tidak mengalami pergeseran (Widjajanti, 1997).
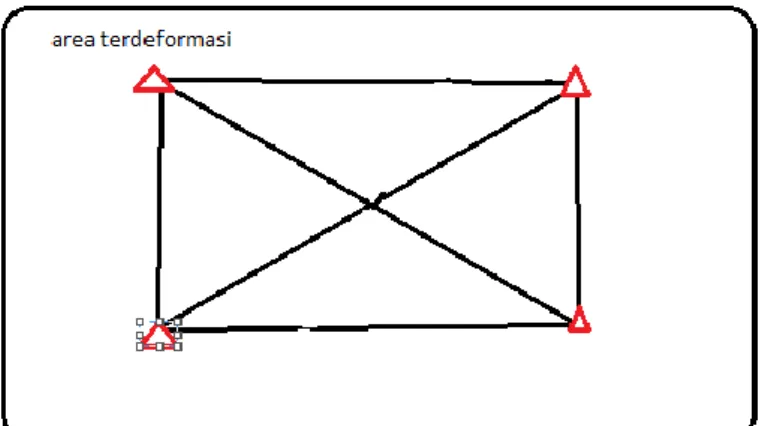
2. Kerangka dasar relatif. Suatu kerangka dasar pemantauan deformasi dikatakan sebagai kerangka dasar relatif apabila titik-titik ikat yang
berfungsi sebagai titik referensi terletak dalam area pemantauan deformasi, sehingga titik ini ikut mengalami deformasi. Ilustrasi kerangka dasar relatif ditunjukkan pada Gambar I.2 berikut.
Gambar I. 2. Kerangka dasar relatif (modifikasi Kuang, 1996) Pada kerangka dasar relatif analisis deformasi bertujuan untuk menentukan pergeseran relatif antar blok. Tahapan analisis deformasi pada kerangka dasar relatif dijabarkan sebagai berikut (Widjajanti, 1997):
1. Pemilihan titik-titik objek untuk pergeseran titik tunggal dengan mengabaikan titik-titik lainnya.
2. Perancangan model deformasi.
3. Pengujian model deformasi melalui uji statistik. 1.8.3. Jaring Kontrol Horisontal
Berdasarkan SNI 19-6724-2002 tentang Jaring Kontrol Horisontal (2002), pengertian jaring kontrol horisontal merupakan kumpulan titik kontrol horisontal yang saling terikat dengan pengukuran jarak maupun sudut, nilai koordinatnya ditentukan menggunakan metode pengamatan tertentu dalam suatu sistem referensi koordinat horisontal yang telah ditetapkan.
Jaring kontrol horisontal ketelitiannya tergantung dari pendefinisian orde dan kelas jaring kontrol horisontalnya. Orde jaringan merupakan suatu atribut yang memberikan nilai karakteristik ketelitian atau akurasi suatu jaring yaitu tingkat kedekatan jaring terhadap titik kontrol yang sudah ada dan dijadikan referensi (BSN, 2002). Kelas jaringan merupakan atribut yang memberikan karakteristik ketelitian
internal (tingkat presisi) dari suatu jaring, nilai ketelitian internal ini didapat melalui proses perataan terkendala minimum (BSN, 2002). Penggunaan jaring kontrol horisontal sangat banyak, tidak lagi hanya berkisar sebagai jaring kontrol pemetaan, namun pengembangannya dapat digunakan sebagai kerangka dasar pemantauan deformasi serta studi lainnya yang terkait. Metode pengukuran jaring kontrol horisontal dapat menggunakan metode terestris maupun metode ekstraterestris. Pengukuran secara terestris pada jaring kontrol horisontal dapat menggunakan metode poligon, triangulasi, trilaterasi, triangulaterasi, pemotongan ke muka dan pemotongan ke belakang (Basuki, 2006).
1.8.4. Metode Triangulaterasi
Metode triangulaterasi merupakan metode pengukuran kerangka kontrol horisontal yang tujuannya untuk menentukan nilai koordinat titik-titik kontrol horisontal dengan melakukan pengukuran semua jarak dan sudut di setiap titik-titik pengamatan (Yulaikhah, 2013).
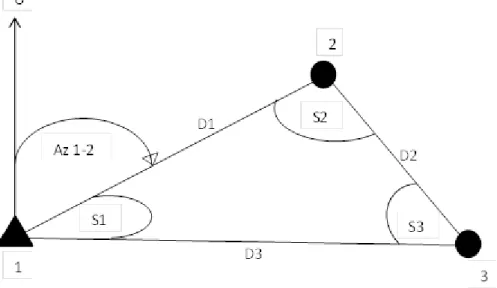
Gambar I. 3. Jaring triangulaterasi Keterangan Gambar I.3 :
: titik yang diketahui nilai koordinatnya, : titik yang akan dicari nilai koordinatnya, D1, D2, D3 : jarak antar titik,
Az 1-2 : sudut jurusan titik 1-2, S1, S2, S3 : sudut horisontal,
Perhitungan triangulaterasi menggunakan konsep dasar hitungan poligon tertutup seperti persamaan (I.1) dan (I.2).
X2 = X1 + D1 sin Az1-2 + koreksi absis (ΔX) ...(I.1) Y2 = Y1 + D1 cos Az1-2 + koreksi ordinat (ΔY) ...(I.2)
1.8.5. Hitung Perataan Kuadrat Terkecil
Setiap pengukuran yang dilakukan selalu dihinggapi kesalahan yang bersifat acak (random). Untuk meminimalisir nilai kesalahan acak ini dibutuhkan suatu metode yang dapat menentukan nilai parameter tertentu. Hitung perataan merupakan metode yang mampu menyelesaikan permasalahan tersebut.
Hitung perataan merupakan suatu metode untuk menentukan nilai koreksi yang harus diberikan pada hasil pengukuran, sehingga hasil pengukuran tersebut memenuhi suatu syarat geometri (Wolf, 1980). Syarat geometri merupakan suatu kondisi yang harus dipenuhi dari hubungan suatu pengukuran dengan pengukuran lainnya.
Hitung perataan kuadrat terkecil memiliki berbagai cara penyelesaian, salah satunya adalah metode parameter. Pada metode ini nilai parameter yang dicari memiliki hubungan linier. Apabila nilai parameter yang dicari belum memiliki hubungan linier, maka perlu dilakukan proses linierisasi menggunakan deret Taylor (Hadiman, 1991). Hasil dari proses linierisasi ini merupakan sebuah model matematik yang berfungsi sebagai persamaan pengamatan dalam proses perhitungan. Ciri khas dari hitung perataan adalah jumlah pengukuran yag dilakukan melebihi jumlah parameter yang ditentukan nilainya, sehingga menimbulkan ukuran lebih (Wolf, 1980).
Penyelesaian menggunakan metode ini dilakukan dengan cara mencari nilai hasil penjumlahan kuadrat residunya (VTPV) minimum, sehingga tidak muncul suatu
nilai hitungan lainnya yang bernilai lebih kecil dari nilai kuadrat residunya (VTPV)
(Hadiman, 1991). Prinsip perhitungan menggunakan metode hitung perataan kuadrat terkecil menekankan adanya pengamatan lebih sehingga didapatkan nilai derajat
kebebasan suatu data. Derajat kebebasan (r) dapat ditentukan dengan persamaan (I.3).
r = n – u ...(I.3) Dalam hal ini :
n : jumlah ukuran,
u : jumlah parameter yang ditentukan nilainya.
Penyusunan model matematis hitung perataan menjadi sangat penting. Model matematis yang digunakan seperti pada persamaan (I.4) dan (I.5).
La = F(Xa) ...(I.4) F(Xa) = F(Xo + X) ...(I.5) Nilai estimasi pengamatan ditentukan dari persamaan (I.6).
La = Lb + V ...(I.6) Lb + V = F(Xo + X) ...(I.7) Dalam hal ini :
La : nilai estimasi pengamatan, Xa : nilai estimasi parameter, Lb : nilai pengamatan,
F : selisih nilai estimasi pengamatan dengan nilai pengamatan, V : residu atau koreksi pengamatan,
Xo : nilai pendekatan parameter, X : nilai koreksi parameter
Penentuan matriks residu untuk mendapatkan nilai koreksi terbaik dibentuk dengan menggunakan persamaan (I.8).
V = AX – F ...(I.8) Dalam hal ini, elemen matriks untuk tiap-tiap persamaan (I. 8) yaitu :
V : vektor residu yang elemen matriksnya terdiri atas besaran-besaran koreksi ukuran (v1, v2, ... , vn) dengan dimensi (n x 1),
A : matriks desain yang elemen matriksnya terdiri atas koefisien-koefisien parameter (a1.1, a1.2, ... , an.u) dengan dimensi (n x u),
X : vektor parameter yang elemen matriksnya terdiri atas parameter yang dicari nilainya (x1, x2, ... , xn) dengan dimensi (u x 1),
F : vektor sisa yang elemen matriksnya terdiri atas selisih dari tiap konstanta persamaan linier (a1.0, a2.0, ... , an.0) dengan besaran ukuran (l1, l2, ... , ln) yang
bersesuaian dengan dimensi (n x 1).
Penentuan nilai estimasi terbaik menggunakan persamaan (I.9).
X = (ATPA)-1 ATPF ...(I.9) Dalam hal ini :
P : matriks bobot pengamatan
1.8.6. Penerapan Hitung Kuadrat Terkecil pada Kerangka Dasar Relatif
Hitung perataan kuadrat terkecil metode parameter dapat menjadi suatu dasar untuk proses perhitungan pada kerangka dasar relatif. Dikarenakan kerangka dasar relatif tidak memiliki suatu titik referensi maka perhitungan menjadi lebih kompleks dari proses perhitungan hitung perataan kuadrat terkecil metode parameter pada umumnya. Pengembangan dari metode parameter salah satunya adalah perataan metode inner constraint.
Perataan metode inner constraint mampu mengatasi permasalahan yang timbul ketika metode parameter digunakan untuk melakukan perhitungan kerangka dasar relatif. Permasalahan mendasar pada kerangka dasar relatif adanya kekurangan datum geodetik pada kerangkanya (Widjajanti, 1997). Hal ini menjadikan matriks normal (ATPA) menjadi singular yang berarti bahwa determinan matriks normal tersebut sama dengan nol dan apabila dilakukan proses inversi menghasilkan nilai matriks yang tidak terdefinisi (Widjajanti, 1997). Proses pemecahan permasalahan tersebut dijelaskan pada bagian selanjutnya.
1.8.7. Hitung Perataan Metode Inner Constraint
Hitung perataan metode inner constraint merupakan suatu metode hitung perataan yang berbasiskan pada metode parameter. Penerapan metode ini digunakan pada jaring relatif dengan kondisi yang telah dijelaskan sebelumnya bahwa kondisi jaring tidak memiliki titik ikat di lapangan. Penggunaan metode ini sudah dijelaskan pada bagian sebelumnya dimana kondisi matriks normal memiliki nilai determinan sama dengan nol atau disebut dengan matriks singular. Faktor timbulnya matriks
singular disebabkan belum terdefinisinya sistem koordinat yang digunakan pada jaring pemantauan deformasi atau disebut juga dengan rank deficiency.
Rank deficiency pada setiap sistem koordinat berbeda-beda tergantung dari
jenis sistem koordinat yang digunakan pada jaringnya. Secara umum terdapat tiga jenis sistem koordinat yang sering digunakan, sehingga rank deficiency setiap sistem koordinat sebagai berikut (Soeta’at, 1996):
a. Sistem koordinat 1D. Rank deficiency pada sistem koordinat ini sebesar d = 1, sehingga untuk mendefinisikan sistem koordinat pada sistem koordinat ini membutuhkan satu titik sebagai referensi tinggi.
b. Sistem koordinat 2D. Rank deficiency pada sistem koordinat ini sebesar d = 4, sehingga untuk mendefinisikan sistem koordinat pada sistem koordinat ini membutuhkan dua titik referensi atau empat unsur terdefinisi.
c. Sistem koordinat 3D. Rank deficiency pada sistem koordinat ini sebesar d = 7, sehingga untuk mendefinisikan sistem koordinat pada sistem koordinat ini membutuhkan tiga titik referensi atau minimal membutuhkan tujuh unsur terdefinisi.
Pada metode inner constraint untuk mengatasi permasalahan kekurangan datum membutuhkan suatu matriks “kondisi” atau matriks E. Persamaan umum untuk menyelesaikan matriks X yang merupakan matriks koreksi pada metode inner
constraint diselesaikan dengan persamaan (I.10).
𝑋 = (𝐴𝑇𝑃𝐴 + 𝐸𝑇𝐸)−1 𝐴𝑇𝑃𝐹 ...(I.10) Persamaan (I.10) menjelaskan bahwa nilai matriks X sangat bergantung pada nilai dari matriks E atau matriks kondisi tersebut. Matriks E ini sangat penting karena menjadi solusi untuk menyelesaikan matriks normal yang singular. Metode ini dikatakan sebagai metode inner constraint apabila memenuhi persyaratan sebagai berikut (Soeta’at,1996) :
𝐴 𝐸𝑇 = 0 ...(I.11) Bentuk umum matriks E pada sistem koordinat 2D sebagai berikut (Caspary, 1987):
𝐸 = [ 1 0 0 1 𝑌1 −𝑋1 𝑋1 𝑌1 1 0 0 1 𝑌2 −𝑋2 𝑋2 𝑌2 … … 1 0 0 1 𝑌𝑛 −𝑋𝑛 𝑋𝑛 𝑌𝑛 ] ...(I.12) Secara geometrik, baris pertama dan kedua pada matriks E merupakan besaran translasi pada arah x dan y. Pada baris ketiga menunjukkan rotasi pada arah vertikal sedangkan baris keempat menentukan nilai penskalaan pada data observasi yang diberikan pada koordinat pendekatan. Apabila pada data observasi memiliki informasi mengenai datum, pembentukan matriks E ini dapat diabaikan (Caspary, 1987).
Penentuan nilai estimasi terbaik menggunakan hitung perataan kuadrat terkecil metode inner constraint menggunakan persamaan (I.13).
X = (ATPA + ETE)-1 ATPF ...(I.13) Persamaan (I.14) digunakan untuk melakukan perhitungan matriks varian kovarian (∑𝑥𝑥) :
∑ 𝑥𝑥 = 𝜎̂02(𝐴𝑇𝑃𝐴 + 𝐸𝑇𝐸)−1 ...(I.14) Dimana 𝜎̂02 merupakan nilai varian aposteori yang didefinisikan menggunakan persamaan (I.15) :
𝜎̂02 =𝑉𝑇𝑃𝑉
𝑛−𝑢 ...(I.15) Akar elemen-elemen diagonal matriks ∑𝑥𝑥 merupakan nilai ketelitian dari setiap parameter yang bersesuaian. Penentuan nilai ketelitian estimasi residu dilakukan dengan perhitungan varian kovarian residu menggunakan persamaan (I.16) ∑VV = 𝜎̂𝑜2 ( P-1 – A(ATPA+ETE)-1 AT) ... ...(I.16) Akar elemen-elemen diagonal matriks ∑VV merupakan nilai ketelitian setiap residu pengamatan yang bersesuaian.
1.8.9. Linierisasi Persamaan Pengamatan
Persamaan non-linier merupakan suatu persamaan apabila dilakukan proses penurunan terhadap parameter menghasilkan turunan kedua yang tidak sama dengan nol. Contoh persamaan non-linier ini adalah persamaan pengamatan sudut dan jarak. Kedua persamaan tersebut menghasilkan suatu persamaan non-linier. Persamaan
linier dihasilkan dari proses linierisasi terhadap kedua persamaan tersebut menggunakan deret Taylor.
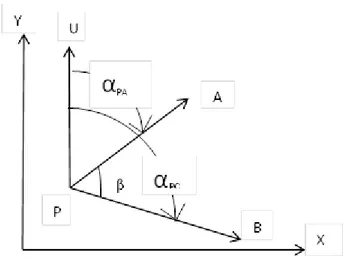
1.8.9.1. Linierisasi persamaan pangamatan sudut dengan deret Taylor. Sudut merupakan selisih bacaan arah horisontal ke titik A dengan selisih bacaan arah horisontal ke titik B. Sudut ini terbentuk dari selisih azimut di suatu titik seperti pada Gambar I.4 berikut.
Gambar I. 4. Sudut horisontal yang dibentuk dari titik A, P dan B
Azimut 𝛼𝑃𝐴 dan azimut 𝛼𝑃𝐵 merupakan model fungsional 2D (X,Y). Penentuan besaran nilai pengamatan sudut, model matematiknya seperti persamaan (I.17)
𝛽 = 𝑎𝑟𝑐 tan𝑋𝐵−𝑋𝑃
𝐵−𝑌𝑃 − 𝑎𝑟𝑐 tan
𝑋𝐴−𝑋𝑃
𝑌𝐴−𝑌𝑃 ...(I.17)
Pada persamaan (I.17), nilai XA, YA, XP, YP, XB, YB merupakan parameter yang nilainya dicari, maka nilai turunan model matematik terhadap setiap parameter sebagai persamaan (I.18) s.d. (I.23).
1. Turunan terhadap XA 𝜕𝛽 𝜕𝑋𝐴= −(𝑌𝐴−𝑌𝑃) (𝑋𝐴−𝑋𝑃)2+(𝑌𝐴−𝑌𝑃)2 ...(I.18) 2. Turunan terhadap YA 𝜕𝛽 𝜕𝑌𝐴= (𝑋𝐴−𝑋𝑃) (𝑋𝐴−𝑋𝑃)2+(𝑌𝐴−𝑌𝑃)2 ...(I.19)
3. Turunan terhadap XP 𝜕𝛽 𝜕𝑋𝑃= −(𝑌𝐶−𝑌𝑃) (𝑋𝐶−𝑋𝑃)2+(𝑌𝐶−𝑌𝑃)2+ 𝑌𝐴−𝑌𝑃 (𝑋𝐴−𝑋𝑃)2+(𝑌𝐴−𝑌𝑃)2 ...(I.20) 4. Turunan terhadap YP 𝜕𝛽 𝜕𝑌𝑃= (𝑋𝐶−𝑋𝑃) (𝑋𝐶−𝑋𝑃)2+(𝑌𝐶−𝑌𝑃)2− 𝑋𝐴−𝑋𝑃 (𝑋𝐴−𝑋𝑃)2+(𝑌𝐴−𝑌𝑃)2 ...(I.21) 5. Turunan terhadap XB 𝜕𝛽 𝜕𝑋𝐵= (𝑌𝐵−𝑌𝑃) (𝑋𝐵−𝑋𝑃)2+(𝑌𝐵−𝑌𝑃)2 ...(I.22) 6. Turunan terhadap YB 𝜕𝛽 𝜕𝑌𝐵 = −(𝑋𝐵−𝑋𝑃) (𝑋𝐵−𝑋𝑃)2+(𝑌𝐵−𝑌𝑃)2 ...(I.23)
1.8.9.2. Linierisasi persamaan pangamatan jarak dengan deret Taylor. Jarak merupakan selisih koordinat antara dua titik. Geometri pengukuran jarak antara dua titik seperti Gambar I.5 berikut.
Gambar I. 5. Jarak antara titik 1 dengan titik 2
Model matematik jarak sebagai persamaan (I.24). 𝐷12= √(𝑋2− 𝑋1)2+ (𝑌
2− 𝑌1)2 ...(I.24) Persamaan (I.24) diturunkan terhadap setiap parameter X1, Y1, X2, Y2 sebagai persamaan (I.25) s.d. (I.28).
1. Turunan terhadap X1 𝜕𝐷 𝜕𝑋1 = −(𝑋2−𝑋1) √(𝑋2−𝑋1)2+(𝑌2−𝑌1)2= −(𝑋2−𝑋1) 𝐷12 ...(I.25) 2. Turunan terhadap Y1 𝜕𝐷 𝜕𝑌1 = −(𝑌2−𝑌1) √(𝑋2−𝑋1)2+(𝑌2−𝑌1)2 = −(𝑌2−𝑌1) 𝐷12 ...(I.26) 3. Turunan terhadap X2 𝜕𝐷 𝜕𝑋2 = (𝑋2−𝑋1) √(𝑋2−𝑋1)2+(𝑌2−𝑌1)2= (𝑋2−𝑋1) 𝐷12 ...(I.27) 4. Turunan terhadap Y2 𝜕𝐷 𝜕𝑌2 = (𝑌2−𝑌1) √(𝑋2−𝑋1)2+(𝑌2−𝑌1)2 = (𝑌2−𝑌1) 𝐷12 ...(I.28) 1.8.10. Bobot
Bobot pengamatan merupakan suatu perbandingan ketelitian antara suatu besaran pengamatan dengan besaran pengamatan lainnya. Nilai bobot didefinisikan sebagai suatu nilai yang berbanding terbalik dengan besaran varian pengukuran (Mikhail dan Gracia, 1981).
Pemberian niai bobot pengamatan terhadap ukuran menjadi sangat penting sebab suatu besaran pengamatan memiliki ketelitian yang berbeda satu dengan yang lain. Oleh sebab itu bobot pengamatan harus diberikan agar sesuai dengan ketelitian setiap pengukuran. Bobot ditentukan dengan persamaan (I.29).
𝑃 = 𝜎̂02 ∑Lb-1
...(I.29) Dalam hal ini ;
P : bobot pengamatan, 𝜎̂02 : varian apriori, ∑Lb-1
: varian pengukuran.
Karena setiap pengamatan tidak saling berkorelasi, maka bobot pengamatan merupakan suatu matriks diagonal sebagai berikut :
∑Lb-1 = [ 1 𝜎112 0 0 0 𝜎1 222 0 0 0 𝜎1 332 ]
: invers matriks varian kovarian pengamatan
Berdasarkan matriks invers varian kovarian pengamatan tersebut, maka dibentuk suatu matriks bobot sebagai persamaan (I.30).
𝑃 = 𝜎̂02 [ 1 𝜎112 0 0 0 𝜎1 222 0 0 0 𝜎1 332 ] ...(I.30)
1.8.10.1. Varian pengukuran sudut. Varian pengukuran sudut dibentuk oleh persamaan (I.32) (Mikhail dan Gracie (1981).
𝜎𝐵2 = 𝜎
𝐵𝐶 2 + 𝜎𝐵𝑅 2 + 𝜎𝐵𝑃 2 + 𝜎𝐵𝑇 2 ...(I.32) Dalam hal ini :
𝜎𝐵2 : varian total sudut ukuran,
𝜎𝐵𝐶 : kesalahan akibat pemusatan alat ukur dan target,
𝜎𝐵𝑅 : kesalahan akibat pembacaan pada skala piringan horisontal, 𝜎𝐵𝑃 : kesalahan akibat pembidikan,
𝜎𝐵𝑇 : kesalahan akibat penempatan target. Dalam hal ini :
𝜎𝐵𝐶 2 = {𝜎𝐶12 𝐷12 + 𝜎𝐶22 𝐷22 + 𝜎𝐶32 𝐷12 𝐷22 (𝐷1 2+ 𝐷 22 − 2𝐷1𝐷2cos 𝛽} 𝜌"2 ...(I.33) (Kuang, 1996)
Dalam hal ini :
𝜎𝐶1, 𝜎𝐶2 : kesalahan pemusatan target satu dan target dua 𝜎𝐶3 : kesalahan pemusatan alat ukur
𝐷1, 𝐷2 : jarak ke target satu dan target dua 𝛽 : sudut ukuran
𝜌 : 206265” 𝜎𝐵𝑅 2 = 𝜎
𝑅2⁄ (untuk teodolit repetisi) 2𝑛2
𝜎𝑅 = 3 x d (ketelitian piringan horisontal 10” s.d. 1”) 𝑑 : pembacaan terkecil piringan horisontal
𝜎𝐵𝑃 2 = 𝜎 𝑃2⁄ 𝑛 𝜎𝑃 = 60" 𝑀⁄
M : perbesaran teropong alat ukur teodolit n : jumlah pengamatan
𝜎𝐵𝑇 2 = 𝐷12+ 𝐷22
𝐷12 𝐷 22 𝜎𝑇
𝜎𝑇2 : ketelitian target
1.8.10.2. Varian pengukuran jarak. Nilai varian pengukuran jarak harus ditentukan terlebih dahulu yang nantinya digunakan untuk menyusun matriks bobot. Perhitungan nilai varian pengukuran jarak menggunakan persamaan (I.31) (Mikhail dan Gracie, 1981) :
𝜎𝐷2 = 𝑎2 + 𝑏2. 𝐷2 ...(I.31) Dalam hal ini :
𝜎𝐷2 : varian total jarak pengukuran,
𝑎2 : ketelitian jarak yang tidak tergantung jarak pengukuran (mm), 𝑏2 : ketelitian relatif alat (ppm),
𝐷2 : jarak (km).
I.8.11. Iterasi
Iterasi merupakan suatu metode yang digunakan secara berulang untuk menyelesaikan permasalahan perhitungan matematik. Iterasi dimulai setelah mendapatkan nilai pendekatan terhadap matriks X (X0). Nantinya nilai matriks X yang baru dijadikan sebagai nilai pendekatan pada hitung perataan berulang (Uotila, 1988).
Pada proses perhitungan hitung perataan kuadrat terkecil dimana persamaan pengamatan merupakan fungsi persamaan non-linier dan selanjutnya dilakukan proses linierisasi menggunakan deret Taylor proses iterasi menjadi sangat penting. Deret Taylor yang dalam proses linierisasi persamaan non-linier hanya berhenti pada turunan pertama persamaan, memerlukan proses ini agar menghasilkan nilai estimasi terbaik.
X = N+ (ATPF)
𝑋𝑎 = 𝑋0+ 𝑋 ...(I.34) Iterasi pertama menggunakan nilai Xa sebagai nilai pendekatan, sedangkan untuk hitungan kedua nilai pendekatan menggunakan nilai matriks parameter yang baru (X1).
X1 = Xa
Xa1 = X1 + Xa ... ...(I.35) Syarat penghentian iterasi sebagai berikut (Uotila, 1988) :
1. 𝑋̂ mendekati atau sama dengan nol, dimana nilai i semakin besar. 𝑖 2. Selisih 𝑉𝑖 − 𝑉𝑖−1 mendekati nol.
3. Nilai 𝑉𝑖𝑇𝑃𝑉
𝑖 stabil. 1.8.12. Uji Global
Uji global merupakan salah satu langkah pengujian terhadap data yang dilakukan setelah proses hitung perataan. Uji ini dilakukan untuk mengetahui apakah data mengandung kesalahan tak acak yang berpengaruh besar terhadap data pengamatan setiap kala. Uji global menggunakan prinsip pengujian nilai varian aposteori ( ˆ2
o
) dengan varian apriori ( 2 o
). Pengujian ini menggunakan tabel Fisher untuk menentukan apakah data ditolak atau diterima. Tahap pengujian dilakukan sebagai berikut (Widjajanti, 1997):
1. Menyusun hipotesis : Ho : ˆ2 2 o o ...(I.36) Ha : ˆo2 o2 ...(I.37)
2. Menetapkan taraf uji (𝛼0).
3. Menentukan nilai batas F 1-αo,∞, r dari tabel fungsi Fisher dengan argumen αo dan r (r = derajat kebebasan).
4. Melakukan uji hipotesis nol (Ho). Ho ditolak apabila memenuhi persyaratan pada persamaan (I.38).
r o o F , , 1 2 2 ˆ ...(I.38) Penolakan pada nilai hipotesis nol mengindikasikan adanya kemungkinan bahwa pengukuran dipengaruhi oleh kesalahan tak acak yang mengakibatkan perubahan terhadap nilai rata-rata dan nilai pengukuran tidak mengikuti sebaran normal. Apabila dalam tahap ini hipotesis nol ditolak, maka langkah selanjutnya adalah melakukan data snooping terhadap data pengukuran.
1.8.13. Data Snooping
Data snooping merupakan suatu cara dalam metode hitung perataan kuadrat terkecil untuk menemukan data yang dihinggapi kesalahan tak acak dengan melakukan penyusunan ulang hipotesis nol (Ho) dan Ha (Widjajanti, 1997). Langkah melakukan data snooping sebagai berikut (Widjajanti, 1997) :
1. Menyusun hipotesis
Ho : hasil pengamatan yang tidak dihinggapi kesalahan tidak acak Ha : hasil pengamatan yang dihinggapi kesalahan tidak acak 2. Menetapkan taraf uji (αo).
3. Menentukan nilai batas F1/21-αo,∞,r menggunakan tabel Fisher.
4. Melakukan uji hipotesis nol (Ho). (Ho) diterima apabila memenuhi persyaratan pada persamaan (I.39).
2 / 1 , 1 , 1 o F wi ...(I.39)
Dalam hal ini : 𝑊𝑖 = 𝜎𝑉𝑖
𝑉𝑖 ...(I.40)
𝑉𝑖 : koreksi pengamatan ke-i
𝜎𝑉𝑖 : simpangan baku koreksi pengamatan ke-i
Apabila Ho diterima maka dapat disimpulkan bahwa data pengamatan tidak dihinggapi kesalahan tidak acak sehingga data tidak perlu dihilangkan atau dilakukan pengukuran ulang. Apabila Ho ditolak maka dapat disimpulkan bahwa data dihinggapi kesalahan tidak acak sehingga data yang ditolak tidak diikutkan dalam perhitungan atau dilakukan pengukuran ulang (Widjajanti, 1997).
Uji statistik tersebut menghasilkan suatu luaran berupa nilai koordinat beserta ketelitiannya tanpa ada data yang mengandung kesalahan tak acak. Proses selanjutnya ialah melakukan analisis deformasi. Analisis deformasi terdiri atas dua tahapan, yaitu uji kesebangunan jaring dan uji pergeseran titik pantau.
1.8.14. Model Persamaan Pergeseran Horisontal
Hasil dari proses hitung kuadrat terkecil berupa data koordinat 2D (X dan Y) untuk setiap epoch data dan varian aposteori setiap epoch. Data tersebut menjadi data masukan dalam analisis pergeseran horisontal. Model hitungan pergeseran horisontal
setiap epoch dimodelkan dengan besaran pergeseran (d). Pergeseran dua epoch pengamatan ditentukan dengan persamaan (I.41) dan (I.42).
dX = X(j) – X(i) ...(I.41) dY = Y(j) – Y(i) ...(I.42) Besaran pergeseran tersebut tidak bisa digunakan sebagai representasi pergeseran suatu absis dan ordinat apabila tidak memiliki ketelitian yang ditunjukkan dengan besaran simpangan baku pergeseran absis dan besaran simpangan baku pergeseran ordinat. Ketelitian pergeseran absis dan ketelitian pergeseran ordinat ditentukan dengan persamaan (I.43) dan (I.44).
𝜎𝑑𝑋 = √𝜎𝑋(𝑗)2 + 𝜎𝑋
(𝑖)2 ...(I.43)
𝜎𝑑𝑌 = √𝜎𝑌
(𝑗)2 + 𝜎𝑌(𝑖)2 ...(I.44)
Jarak pergeseran horisontal diperoleh dari rumus phytagoras dengan mengurangkan nilai absis dan ordinat menggunakan persamaan (I.45).
d = √𝑑𝑋2 + 𝑑𝑌2 ...(I.45) Jarak pergeseran tersebut tidak dapat menjelaskan pergeseran suatu titik apabila tidak memiliki besaran ketelitian. Untuk mendapatkan nilai ketelitian pergeseran suatu titik ditentukan dengan prinsip hitung perambatan kesalahan acak sebagai persamaan (I.46).
σd2 = (𝜕𝑑 𝜕𝑑𝑋) 2 𝜎2 𝑑𝑋 + ( 𝜕𝑑 𝜕𝑑𝑌) 2 𝜎2 𝑑𝑌 ... ...(I.46)
Setiap nilai koordinat yang dihasilkan pada tiap epoch memiliki nilai kesalahan sebesar V (residu), sehingga untuk melakukan analisis pergeseran horisontal menggunakan persamaan (I.47) dan (I.48).
dX = X(j) + VX (j) – (X(i) + VX (i)) ... ...(I.47) dY = Y(j) + VY (j) – (Y(i) + VY (i)) ... ...(I.48)
Persamaan (I.47) dan (I.48) yang nantinya digunakan untuk melakukan analisis deformasi horisontal.
Arah pergeseran dari suatu titik dapat direpresentasikan menggunakan besaran sudutnya. Persamaan (I.49) digunakan untuk merepresentasikan arah pergeserannya.
𝛼 = atan ((𝑋(𝑌𝑗𝑗− 𝑋− 𝑌𝑖𝑖))) ... ...(I.49)
1.8.15. Uji Kesebangunan Jaring
Uji kesebangunan jaring merupakan langkah analisis deformasi yang menggunakan uji global. Tujuan uji ini ialah untuk menganalisis apakah terdapat pergeseran pada bentuk jaring pantau. Penolakan hipotesis nol (Ho) pada uji ini menandakan bahwa ada pergeseran pada jaring, sehingga perlu dilakukan uji selanjutnya yaitu uji pergeseran titik pantau (Widjajanti, 1997).
Tahapan melakukan uji kesebangunan jaring sebagai berikut (Widjajanti, 1997) :
1) Membentuk persamaan (I.50) yang merupakan pergeseran horisontal untuk proses analisis deformasi.
𝑈𝑑 𝑉𝑑 + 𝑑 = 0 ...(I.50) Dalam hal ini,
𝑈𝑑 : matriks koefisien koreksi pengamatan, 𝑉𝑑 : pergeseran koordinat titik objek, 𝑑 : vektor pergeseran titik pantau.
2) Menghitung nilai korelat pergeseran K dengan persamaan (I.51).
K = ( Ud Qd UdT )-1 d ... ...(I.51) 𝑄𝑑 = [𝑄(𝑗) 0 0 𝑄(𝑘)] Q(j) = 𝑁+ (𝑗) Q(k) = 𝑁+ (𝑘)
Q(j) : matriks kofaktor parameter pada epoch pertama,
Q(k) : matriks kofaktor parameter pada epoch kedua.
3) Menghitung nilai koreksi koordinat pergesaran titik objek 𝑉𝑑, 𝑉̅𝑑 dengan persamaan (I.52) dan (I.53).
𝑉𝑑 = − 𝑄𝑑 𝑈𝑑𝑇 (𝑈
𝑑 𝑄𝑑 𝑈𝑑𝑇)−1 𝑑 ...(I.52) 𝑉̅𝑑 = 𝑄𝑑−1 𝑉𝑑 ...(I.53) 4) Menghitung varian nilai pergeseran dengan persamaan (I.54) dan (I.55).
Varian apriori pergeseran : 2 σˆ σˆ σ ) k ( 2 0 ) j ( 2 0 2 d 0 + = ...(I.54)
Varian aposteriori pergeseran :
r V Q V σˆ d -1 d T d 2 d 0 = ...(I.55) 5) Menyusun hipotesis :
Ho : bentuk jaring tidak mengalami perubahan (𝜎̂𝑜𝑑2 = 𝜎 𝑜𝑑2 ) Ha : bentuk jaring mengalami perubahan (𝜎̂𝑜𝑑2 > 𝜎
𝑜𝑑2 ) 6) Menetapkan taraf uji (𝛼0).
7) Menentukan nilai batas F1- , ,f
0
dari tabel fungsi Fisher dengan argumen
𝛼0 dan f (f : jumlah persamaan syarat).
8) Melakukan uji hipotesis nol (Ho). Ho ditolak apabila memenuhi persyaratan pada persamaan (I.56).
f d d F1- ,∞, 2 0 2 0 0 ˆ ... ...(I.56)
1.8.16. Uji Pergeseran Titik Pantau
Uji pergeseran titik pantau dilakukan apabila Ho pada uji kesebangunan ditolak pada derajat kebebasan tertentu. Widjajanti (1997) menerangkan bahwa tujuan uji ini untuk menentukan lokasi titik yang mengalami pergeseran. Pengujian pada setiap titik menggunakan prinsip data snooping. Apabila Ho pada uji ini diterima maka titik tidak mengalami pergeseran, namun apabila Ho ditolak pada derajat kebebasan tertentu maka titik mengalami pergeseran atau deformasi.
Tahap melakukan uji pergeseran titik objek sebagai berikut (Widjajanti, 1997) :
1. Menyusun hipotesis :
Ho : koordinat titik ke-i tidak mengalami pergeseran Ha : koordinat titik ke-i mengalami pergeseran 2. Menentukan taraf uji (𝛼0).
3. Menentukan nilai batas 𝐹1−𝛼0,∞,𝑓 dari tabel fungsi Fisher dengan argumen 𝛼0.
𝑁𝑑 = 𝑈𝑑𝑇 (𝑈
𝑑 𝑄𝑑 𝑈𝑑𝑇)−1 𝑈𝑑 ...(I.57) 𝑊𝑑𝑖= 𝑄𝑑𝑖−1 𝑉𝑑𝑖
𝜎𝑜𝑑 √𝑁𝑑𝑖 ...(I.58)
5. Melakukan uji hipotesis nol (Ho). Ho ditolak apabila memenuhi persyaratan pada persamaan (I.59).
|𝑊𝑑𝑖| > 𝐹1−𝛼0,∞,1 ...(I.59)
1.8.17. Uji Signifikansi Parameter
Uji ini merupakan tahapan tambahan uji statistik pada titik observasi yang berguna untuk mengetahui apakah pergerakan titik tersebut secara signifikan atau tidak. Uji ini dilakukan setelah uji pergeseran titik, apabila dari uji pergeseran titik diketahui bahwa suatu titik mengalami pergeseran, maka perlu dikethaui apakah pergeserannya secara signifikan atau tidak. Uji signifikansi parameter ini menggunakan tabel t-student dengan tahapan sebagai berikut :
1. Menyusun hipotesis :
Ho : titik ke-i tidak mengalami pergeseran secara signifikan Ha : titik ke-i mengalami pergeseran secara signifikan
2. Menentukan vektor pergeseran titik-titik pantau candi yang merupakan selisih absis dan ordinat dari koordinat titik pantau.
𝑑𝑥𝑖 = 𝑥𝑖(1)− 𝑥𝑖(2) ...(I.60) 𝑑𝑦𝑖 = 𝑦𝑖(1)− 𝑦𝑖(2) ...(I.61) 3. Menghitung nilai uji untuk setiap koordinat titik pantau dari dua epoch
pengukuran. 𝑡𝑥𝑖 = | 𝑥𝑖 (1)− 𝑥 𝑖 (2) √(𝜎𝑥𝑖(1))2+ (𝜎𝑥𝑖(2))2 | ...(I.62) 𝑡𝑦𝑖 = | 𝑦𝑖(1)− 𝑦𝑖(2) √(𝜎𝑦𝑖(1))2+ (𝜎𝑦𝑖(2))2 | ...(I.63)
4. Menentukan taraf uji 𝛼𝑜.
5. Menentukan nilai 𝑡(𝛼𝑜,𝑟) dari tabel fungsi distribusi t-student dengan argumen 𝛼𝑜 dan derajat kebebasan r.
6. Melakukan uji hipotesis nol (Ho). Ho diterima apabila memenuhi persyaratan pada persamaan (I.64) dan (I.65).
𝑡𝑥𝑖 < 𝑡(𝛼𝑜,𝑟) ...(I.64)
𝑡𝑦𝑖 < 𝑡(𝛼𝑜,𝑟) ...(I.65)
Penerimaan Ho menunjukkan bahwa titik ke-i tidak mengalami pergeseran secara signifikan. Sedangkan penolakan pada Ho menunjukkan bahwa titik ke-i mengalami pergeseran secara signifikan
I.9. Hipotesis
Deformasi pada tubuh Candi Prambanan khususnya Candi Siwa bergeser dengan arah horisontal. Nilai koordinat sebelum gempa Yogyakarta tahun 2006 memiliki nilai yang tidak berbeda secara signifikan dan nilai ketelitian berkisar dalam fraksi milimeter dengan nilai 1 mm s.d. 3 mm. Namun pada epoch transisi antara sebelum dan sesudah gempa bumi tahun 2006 nilai ketelitian melebihi 3 mm berdasarkan penelitian Wicaksono (2014). Berdasarkan laporan penelitian yang dilakukan oleh BPCB tahun 1999 dan 2001 serta penelitian yang dilakukan oleh Wicaksono (2014) diketahui bahwa pergeseran horisontal Candi Prambanan berkisar 4 mm s.d. 10 mm. Namun pada epoch transisi terdapat nilai pergeseran yang lebih besar dari 10 mm dikarenakan adanya gempa bumi tahun 2006.