PENGEMBANGAN TEOREMA MORLEY PADA SEGIEMPAT

Journal of Medives Volume 2, No. 1, 2018, pp. 41-50 http://e-journal.ikip-veteran.ac.id/index.php/matematika/article/view/526

PENGEMBANGAN TEOREMA MORLEY PADA SEGIEMPAT

Fabelia Andani Barutu*, Mashadi, Sri Gemawati

Program Studi Magister Matematika Universitas Riau *fabeliaandani.b@gmail.com

Diterima: Nopember 2017. Disetujui: Desember 2017. Dipublikasikan: Januari 2018

ABSTRAK

Pada umumnya teorema Morley diberlakukan pada segitiga, dalam tulisan ini akan dikembangkan ide teorema Morley untuk bangun datar dengan sisi yang lebih banyak (dalam hal ini segi empat) dan menentukan rumus panjang sisi segiempat Morley tersebut. Segiempat yang dibahas yakni persegi, persegi panjang, belah ketupat, layang-layang, dan trapesium sama kaki. Pembuktian dalam tulisan ini menggunakan cara yang lebih sederhana dengan konsep kesebangunan dan konsep trigonometri.

Kata kunci: Teorema Morley, konsep kekongruenan, trigonometri.

ABSTRACT

Morley’s Theorem generally applies in triangle. This paper applied Morley’s Theorem in quadrilateral to determine the side lenght of Morley’s quadrilateral. Quadrilaterals discussed in this paper are square, rectangle rhombus, kite, and isoscelestrapezium. Simpler way is used to prove by applying congruence and trigonometric concepts.

Keywords: Morley’s Theorem, congruence concept, trigonometry.

How to Cite: Barutu, F.A., Mashadi., & Gemawati, S. (2018). Pengembangan Teorema Morley pada Segiempat. Journal of Medives, 2(1), 41-50.

PENDAHULUAN

Menurut (Oakley & Baker, 2014) menyatakan bahwa teorema Morley berkaitan dengan tokoh yang bernama Frank Morley (1899), yang merupakan profesor Matematika di Haverford College. Salah satu artikel yang membahas tentang teorema Morley adalah (Peters, 1941) yang menyatakan bahwa Morley menemukan sebuah teorema yang diberi nama “Teorema Morley”. Teorema tersebut dinyatakan sebagai berikut.

Teorema Morley

Diberikan sebarang ∆ . Setiap sudut ∆ yakni ∠ , ∠ , dan ∠

dibangun trisektor. Trisektor yang berdekatan akan berpotongan di satu titik yakni titik , , dan . Jika titik-titik perpotongan tersebut dihubungkan maka terbentuk ∆ sama sisi. Segitiga tersebut disebut dengan segitiga Morley.

Gambar 1. Teorema Morley pada Segitiga Sebarang

Morley menyatakan jika ∆

adalah sebarang dan terdapat trisektor pada ∠ , ∠ , dan ∠ kemudian trisektor yang berdekatan bertemu di titik , , dan , maka ∆ sama sisi (Walls, 2008). Misalkan pada ∠ dibentuk trisektor yang disebut garis dan ,

pada ∠ dibentuk trisektor yang disebut garis dan , dan pada ∠ dibentuk trisektor yang disebut garis dan , maka perpotongan trisektor yang ber-dekatan itu ialah garis dan yang berpotongan dititik , garis dan yang berpotongan dititik , dan garis dan yang berpotongan dititik . Sehingga jika titik , , dan dihubung-kan, maka akan membentuk ∆ sama sisi (Gambar 1).

Beberapa bukti dari Teorema Morley dengan sudut pandang yang berbeda telah ditemukan oleh matema-tikawan seperti (Donolato, 2013), (Stonebridge, 2009), dan (Coghetto, 2015). Dalam (Donolato, 2013) dinyatakan bahwa panjang sisi segitiga Morley adalah

8 sin( ) sin( ) sin( ),

dengan =

∠ , = ∠

, =∠ , dan

= ∠ . Setiap segitiga mempunyai sudut luar dan sudut jauh yang masing-masing disebut dengan sudut eksterior dan remote interior (Mashadi, 2015[a]). Selanjutnya (Kuruklis, 2014) dan (McCartin, 2010) memberikan kasus yang berkaitan dengan teorema Morley yang berbunyi bahwa segitiga Morley dapat terbentuk dari trisektor sudut eksternal segitiga sebarang.

Tulisan ini akan membahas pene-rapan dan pengembangan teorema Mor-ley pada segiempat yang berlaku untuk persegi, persegi panjang, belah ketupat, layang-layang, dan trapesium sama kaki. Ide pembuktiannya adalah dengan menggunakan konsep kekongruenan dan trigonometri yang dibahas dalam (Mashadi, 2015[b]; Mashadi, 2016) dan materi yang diajarkan di SMP dan SMA.

HASIL DAN PEMBAHASAN

Berikut ini adalah hasil dan pembahasan pengembangan teorema Morley pada persegi, persegi panjang, belah ketupat, layang-layang, dan trapesium sama kaki.

Teorema Morley pada Persegi

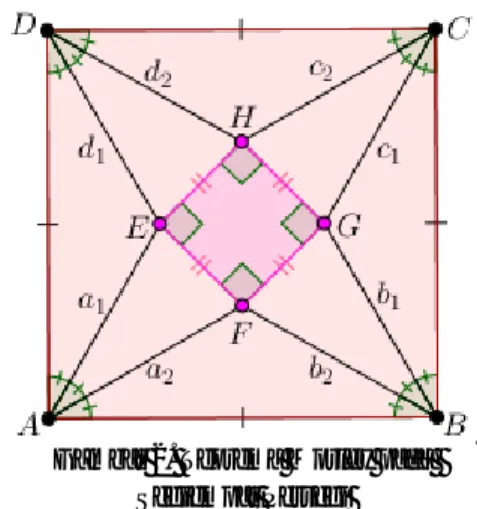
Terdapat persegi , kemudian dibangun trisektor pada keempat sudutnya, pada setiap sudut akan terdapat dua garis bagi yang membagi sudut menjadi tiga bagian yang sama besar. Garis-garis trisektor tersebut akan berpotongan dengan garis trisektor yang terdekat, sehingga terdapat empat titik perpotongan, jika keempat titik potong tersebut dihubungkan maka terbentuk segiempat (Gambar 2).

Gambar 2. Teorema Morley pada Segiempat Persegi

Teorema 1

Terdapat segiempat persegi. Setiap sudut persegi dibentuk trisektor yang membagi setiap sudut menjadi tiga sudut yang sama besar. Misalkan titik E, F, G, dan H adalah titik perpotongan antara garis trisektor dan , garis trisektor dan , garis trisektor dan , dan garis trisektor dan . Jika

keempat titik potong tersebut dihubung-kan maka adalah persegi.

Bukti (Kekongruenan)

Akan dibuktikan bahwa

adalah persegi dengan menunjukkan

= = = dan besar keem-pat sudutnya adalah 90°. Akan ditunjuk-kan dengan konsep kekongruenan. Pada persegi jelas bahwa besar

∠ =∠ = 90°. Sehingga dapat

ditunjukkan ∆ ≅ ∆ ≅ ∆ ≅

∆ yang mengakibatkan ∆ ≅

∆ ≅ ∆ ≅ ∆ sehingga

= = = .

Selanjutnya untuk membuktikan bahwa keempat sudut pada segiempat adalah 90°. Pada ∆ , terdapat

∠ dan ∠ yang masing-masing besarnya 30°. Besar sudut pada segitiga berjumlah 180°, sehingga

∠ = 120°. (1)

Pada ∆ terdapat ∠ yang besarnya 30° karena merupakan sudut trisektor pada persegi dan merupakan segitiga sama kaki, sehingga

∠ = ∠ = 75°. (2)

Kemudian pada ∆ berlaku hal yang sama yakni ∠ = 30°, sehingga

∠ = ∠ = 75°. (3)

Besar ∠ diperoleh dengan cara mensubtitusikan persamaan (1), (2), dan (3) ke persamaan berikut.

∠ = 360°−

(∠ + ∠ +∠ )

= 360°−(120° + 75° + 75°) = 90°.

Selanjutnya, dengan cara yang sama akan diperoleh ∠ = ∠ =

∠ = 90°.

Berdasarkan uraian diatas diperoleh bahwa keempat sudut pada segiempat

ialah 90°. Karena keempat sisi pada segiempat sama panjang dan keempat sudut pada segiempat

90°, terbukti bahwa segiempat

adalah persegi yang disebut dengan persegi Morley.

Teorema 2

Panjang sisi persegi Morley adalah

2− √3 , dengan merupakan panjang sisi persegi .

Bukti (Aturan Cosinus)

Misalkan panjang sisi = =

= = dan ∠ =∠ =∠ =

∠ = 90°. Berdasarkan konsep trisektor pada ∠ dan ∠ maka diperoleh ∆

sama kaki dengan besar sudut kakinya

30° dan panjang = . Berdasar-kan dalil Phytagoras dapat diperoleh

= √3 . Terdapat empat segitiga sama kaki yakni ∆ , ∆ , ∆ , dan ∆ dengan semua panjang kaki-kaki segitiga tersebut ialah

= = = = =

= = = √3 (4)

dan ∠ =∠ =∠ =

∠ = 30°.

Dengan menerapkan aturan cosinus pada segitiga sama kaki , diperoleh

= + −

2. . . ∠30°,

= + − √3 . .

Oleh karena = = maka

= + − √3 . ,

= (2− √3),

= 2− √3 .

Teorema Morley pada Persegi Panjang

Konstruksi Teorema Morley pada persegi panjang sama seperti konstruksi Teorema Morley pada bangun datar yang lainnya (Gambar 3).

Teorema 3

Terdapat segiempat persegi panjang. Pada setiap sudut persegi panjang dibentuk trisektor yang membagi setiap sudut menjadi tiga sudut yang sama besar. Misalkan titik E, F, G, dan H

adalah titik perpotongan antara garis trisektor dan , garis trisektor dan , garis trisektor dan , dan garis trisektor dan . Jika keempat titik potong tersebut dihubungkan maka membentuk belah ketupat .

Gambar 3. Teorema Morley pada Persegi Panjang

Bukti (Kekongruenan)

Akan dibuktikan bahwa

adalah belah ketupat dengan menunjuk-kan panjang sisi = = = ,

besar ∠ =∠ , dan ∠ =

∠ . Besar ∠ =∠ = 90°, maka besar sudut trisektornya ialah 30°, sehingga dapat ditunjukkan bahwa

∆ ≅ ∆ dan ∆ ≅ ∆ .

∆ ≅ ∆ ≅ ∆ ≅ ∆ yang

mengakibatkan = = = .

Selanjutnya untuk menunjukkan

bahwa ∠ =∠ dan ∠ =

∠ . Perhatikan ∆ dan ∆ . Diketahui besar ∠ =∠ =

∠ =∠ = 30°, sehingga besar

∠ =∠ . Perhatikan ∆ dan

∆ , berdasarkan konsep kekongruen-an sisi-sudut-sisi ∆ ≅ ∆

sehingga ∠ =∠ . Perhatikan

∆ dan ∆ , berdasarkan konsep kekongruenan sisi-sudut-sisi ∆ ≅ ∆ sehingga ∠ =∠ . Misal-kan besar ∠ =∠ = , ∠ =∠ = , dan ∠ = ∠ = sehingga diperoleh ∠ =∠ +∠ +∠ , ∠ = + + , (5) dan ∠ =∠ +∠ +∠ , ∠ = + + . (6)

Berdasarkan persamaan (5) dan (6) besar ∠ =∠ . Dengan cara yang sama diperoleh ∠ =∠ . Karena keempat sisi pada segiempat sama panjang serta besar ∠ =∠ dan

∠ =∠ terbukti bahwa

segiempat adalah belah ketupat yang disebut dengan belah ketupat Morley.

Teorema 4

Panjang sisi belah ketupat Morley adalah + − √3 , dengan merupakan panjang persegi panjang dan merupakan lebar persegi panjang .

Bukti (Aturan Cosinus)

Misalkan panjang sisi = =

dan = = . Terdapat empat segitiga sama kaki yakni ∆ , ∆ ,

∆ dan ∆ . Panjang sisi yang sama panjang pada ∆ dan ∆ adalah

= = = = √3 . (7) Panjang sisi yang sama panjang pada

∆ dan ∆ adalah

= = = = √3 . (8) Pada segitiga sebarang besar

∠ = 30° dengan menggunakan

aturan cosinus dan mensubtitusikan persamaan (7) dan (8) maka diperoleh

= + − 2. . . cos (30°) = 1 3√3 + 1 3√3 − 2 √3 √3 √3 = + − √3 .

Panjang sisi belah ketupat EFGH adalah

+ − √3 .

Teorema Morley pada Belah Ketupat

Teorema Morley pada belah ketupat tentang trisektor yang dibentuk pada setiap sudut belah ketupat

yang saling berpotongan sehingga membentuk persegi panjang

(Gambar 4).

Teorema 5

Terdapat segiempat belah ketupat. Pada setiap sudut belah ketupat dibentuk trisektor yang membagi setiap sudut menjadi tiga sudut yang sama besar. Misalkan titik E, F, G, dan H

trisektor dan , garis trisektor , dan , garis trisektor dan , dan garis trisektor dan . Jika keempat titik potong tersebut dihubungkan maka terbentuk persegi panjang .

Gambar 4. Teorema Morley pada Belah Ketupat

Bukti (Kekongruenan)

Akan dibuktikan bahwa

adalah persegi panjang dengan menunjukkan panjang sisi = ,

= , dan besar ∠ =∠ =∠ =

∠ = 90°. Akan ditunjukkan dengan konsep kekongruenan. Besar ∠ =

∠ dan ∠ =∠ , sehingga dapat ditunjukkan ∆ ≅ ∆ ≅ ∆ ≅ ∆ . Dari hasil itu juga akan mudah ditunjukkan ∆ ≅ ∆ dan

∆ ≅ ∆ yang mengakibatkan

= dan = .

Selanjutnya akan ditunjukkan besar sudut pada segiempat adalah 90°. Besar keempat sudut pada belah ketupat berjumlah 360°, sehingga 2 + 2 = 360° + = 180°. (9) Pada ∆ diperoleh ∠ = 180°−1 3( + ).

Subtitusikan persamaan (9) diperoleh

∠ = 180°− (180°),

= 120°. (10)

Karena ∆ merupakan segitiga sama kaki maka ∠ =∠ , sehingga

∠ =1

2 180°−3

= 90°− . (11) Karena ∆ juga merupakan segitiga sama kaki maka ∠ =∠ , sehingga

∠ =1

2 180°−3

= 90°− . (12) Diketahui besar ∠ yaitu

∠ = 360°− ∠

−∠ − ∠ . (13) Subtitusikan persamaan (10), (11), dan (12) persamaan (13), maka diperoleh

∠ = 360°−(120°)

− 90°− − 90°−

= 360°−120°−90°−90° +

( + ).

Subtitusikan persamaan (9) sehingga diperoleh

∠ = 360°−120°−90°−90° +

(180°)

= 90°.

Dengan cara yang sama diperoleh

∠ =∠ =∠ = 90°.

Karena = , = , dan besar

∠ =∠ =∠ =∠ = 90° terbukti

bahwa segiempat adalah persegi panjang yang disebut dengan persegi panjang Morley.

Teorema 6

Jika merupakan persegi panjang Morley pada belah ketupat dengan panjang sisi , maka =

= 2 sin dan = =

2 sin .

Bukti (Aturan Sinus)

Misalkan panjang sisi = = = = . Oleh karena ∆ sama kaki, maka diketahui

= √3 . (13) Dengan menggunakan aturan sinus pada

∆ dan mensubtitusikan persamaan (10) dan (13) maka diperoleh

=

(∠ ) √

=

° √

=

√

= 2 sin .

Oleh karena ∆ ≅ ∆ maka dengan cara yang sama diperoleh juga panjang sisi = 2 sin .

Diketahui ∆ sama kaki, maka diperoleh

= √3 . (14) Dengan menggunakan aturan sinus pada

∆ dan mensubtitusikan persamaan (10) dan (14) maka diperoleh

=

(∠ ) √

=

( °) √

=

√ = 2 sin( ).

Karena ∆ ≅ ∆ maka dengan cara yang sama diperoleh juga panjang sisi = 2 sin .

Teorema Morley pada Layang-layang

Teorema Morley pada segiempat layang-layang adalah tentang trisektor yang dibentuk pada setiap sudut layang-layang akan saling berpotongan dan membentuk trapesium sama kaki

(Gambar 5).

Gambar 5. Teorema Morley pada Layang-layang

Teorema 7

Terdapat segiempat layang-layang. Pada setiap sudut layang-layang dibentuk trisektor yang membagi setiap sudut menjadi tiga sudut yang sama besar. Misalkan titik E, F, G, dan H

adalah titik perpotongan antara garis trisektor dan , garis trisektor dan , garis trisektor dan , dan garis trisektor dan . Jika keempat titik potong tersebut dihubungkan maka membentuk trapesium sama kaki .

Bukti (Kekongruenan)

Akan dibuktikan adalah trapesium sama kaki dengan menunjuk-kan panjang sisi = dan besar

∠ =∠ dengan menggunakan konsep kekongruenan. Diketahui besar

ditunjukkan ∆ ≅ ∆ dan

∆ ≅ ∆ . Dari hasil itu juga akan mudah ditunjukkan ∆ ≅ ∆ yang mengakibatkan = .

Selanjutnya akan ditunjukkan bahwa besar ∠ =∠ . Perhatikan

∆ dan ∆ . Diketahui besar

∠ =∠ karena ∆ ≅ ∆ .

Pada ∆ dan ∆ , diketahui besar

∠ =∠ karena ∆ ≅ ∆ .

Kemudian ∆ merupakan segitiga sama kaki karena panjang sisi =

sehingga besar sudut pada kaki-kakinya sama besar yakni ∠ =∠ . Berdasarkan tiga pasang sudut yang sama besar tersebut maka besar ∠ =

∠ . Karena = , dan besar

∠ =∠ terbukti bahwa segi-empat adalah trapesium sama kaki yang disebut dengan trapesium sama kaki Morley.

Teorema 8

Jika merupakan trapesium sama kaki Morley pada layang-layang

dengan = = , maka

= =

( ) ( ).

Bukti (Aturan Sinus)

Misalkan panjang sisi = =

dan = = . Pada ∆ dengan menggunakan aturan sinus diperoleh

= (∠ ) = ° ( ) = ( ) . (15)

Perhatikan ∆ , dengan menggunakan aturan sinus dan mensubtitusikan persamaan (15) maka diperoleh

=

(∠ )

=

sin 3 sin1 3( + ) ( )

=

sin 1 3( + ) sin ( )

.

Oleh karena ∆ ≅ ∆ , maka dengan cara yang sama diperoleh juga panjang sisi = sin 3 sin 3

( ) sin ( ).

Teorema Morley pada Trapesium Sama Kaki

Teorema Morley pada segiempat trapesium sama kaki menjelaskan tentang trisektor yang dibentuk pada setiap sudut

trapesium akan saling

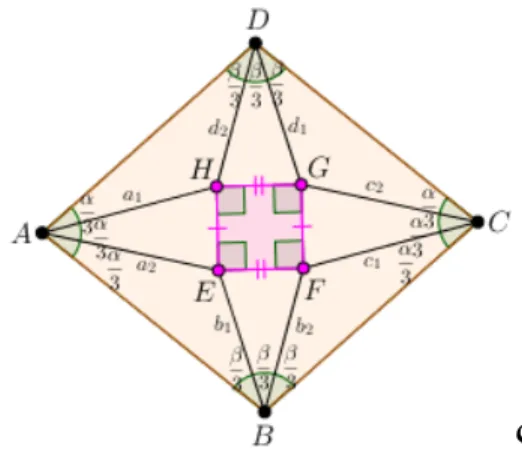
berpotongan dan membentuk segiempat layang-layang (Gambar 6).

Gambar 6. Teorema Morley pada Trapesium Sama Kaki

Teorema 9

Diketahui segiempat adalah trapesium sama kaki. Pada setiap sudut trapesium sama kaki dibentuk trisektor yang membagi setiap sudut menjadi sama besar. Misalkan titik E, F, G, dan H

adalah titik perpotongan antara garis trisektor dan , garis trisektor dan , garis trisektor dan , dan garis trisektor dan . Jika keempat titik potong tersebut dihubungkan maka membentuk layang-layang .

Bukti (Kekongruenan)

Akan dibuktikan adalah layang-layang dengan menunjukkan panjang sisi = , = dan besar ∠ =∠ dengan meng-gunakan konsep kekongruenan. Besar

∠ =∠ dan ∠ =∠ ,

sehingga dapat ditunjukkan ∆ ≅ ∆ . Dari hasil itu juga dengan mudah dibuktikan ∆ ≅ ∆ dan ∆ ≅ ∆ yang mengakibatkan =

dan = .

Selanjutnya akan ditunjukkan besar

∠ =∠ . Berdasarkan konsep kekongruenan, karena ∆ ≅ ∆ , maka besar ∠ =∠ . Dimisalkan

∠ =∠ = . Karena ∆ ≅

∆ , maka besar ∠ =∠ . Dimisalkan besar ∠ =∠ = . Karena ∆ ≅ ∆ , maka besar

∠ =∠ . Dimisalkan ∠ =

∠ = . Karena terdapat 3 pasang sudut yang sama besar maka ∠ =

∠ . Karena = , = , dan besar ∠ =∠ terbukti bahwa segiempat adalah layang-layang yang disebut dengan layang-layang Morley.

Teorema 10

Jika adalah layang-layang Morley yang diperoleh dari trapesium dengan = = , =∠ , =∠ , ∠ = , dan ∠ = , maka = = √ ( ) dan = = √ ( ) .

Bukti (Aturan Sinus)

Pada pembuktian Teorema 10 ini digunakan konsep trigonometri untuk menunjukkan panjang sisi = . Misalkan panjang sisi = = . Besar keempat sudut pada trapesium sama kaki berjumlah 360°, sehingga

2 + 2 = 360°

+ = 180°. (16) Pada ∆ dengan menggunakan aturan sinus dan mensubtitusikan persamaan (16) diperoleh

=

(∠ )

=

° ( )

=

( )

=

( °)

=

√

= √ . (17) Perhatikan ∆ , dengan menggunakan aturan sinus dan mensubtitusikan persamaan (17) maka diperoleh

=

(∠ )

=

2√3 3 ( )

= √ sin 3 sin 3 3sin ( ) .

Diketahui ∆ ≅ ∆ , maka dengan cara yang sama diperoleh juga panjang sisi = √ sin3 sin 3

3sin ( ) .

Pada ∆ dengan menggunakan aturan sinus diperoleh

=

(∠ ).

Dengan cara yang sama maka diperoleh

= √ . (18) Perhatikan ∆ , dengan menggu-nakan aturan sinus dan mensubtitusikan persamaan (18) maka diperoleh

=

(∠ )

=

2√3 3 ( )

= √ sin 3 sin 3 3 sin( ) .

Diketahui ∆ ≅ ∆ , maka dengan cara yang sama diperoleh juga panjang sisi = √ sin 3 sin3

3 sin( ) .

PENUTUP

Dari Teorema Morley pada segiempat khusus terbentuk segiempat Morley yang khusus juga yang dapat dilihat pada Tabel 1.

Tabel 1. Segiempat Morley yang terbentuk

Segiempat ABCD

Segiempat Morley EFGH

Persegi Persegi Persegi Panjang Belah Ketupat Belah Ketupat Persegi Panjang Layang-Layang Trapesium Sama Kaki Trapseium Sama Kaki Layang-Layang

Teorema Morley pada segiempat khusus ini dapat diterapkan ke pembelajaran siswa SMP dan SMA

karena pembuktian menggunakan cara yang simpel dan mudah karena pembuktiannya menggunakan prinsip kekongruenan dan trigonometri yang telah diajarkan di sekolah menengah.

DAFTAR PUSTAKA

Coghetto, R. (2015). Morley’s trisector theorem. Formalized Mathematics. 23 (2), 75-79.

Donolato, C. (2013). A vector based proof of Morley’s trisector theorem. Forum Geometricorum. 13, 233-235.

Kuruklis, S. A. (2014). Trisectors like Bisectors with equilaterals instead of Points. Cubo A Mathematical Journal. 16 (2), 71-110.

Mashadi. (2015)[a]. Geometri Edisi

Kedua. UR Press. Pekanbaru.

Mashadi. (2015)[b]. Geometri Lanjut. UR Press. Pekanbaru.

Mashadi. (2016). Pengajaran

Matematika. UR Press.

Pekanbaru.

McCartin, B. J. (2010). Mysteries of The Equilateral Triangle. Hikari Ltd: Michigan.

Oakley, C. O. & Baker, J. C. 2014. The Morley Trisector Theorem.

Mathematical Association of

America. 85 (9), 737-745.

Peters, J. W. (1941). The Theorem of Morley. National Mathematics Magazine. 16 (3), 119-126.

Stonebridge, B. (2009). A simple geometric proof of Morley’s trisector theorem. Applied Probability Trust. 2-4.

Walls, N. (2008). An Elementary Proof of Morley’s Trisector Theorem.

Edinburgh Mathematical Notes. 34, 12-13.