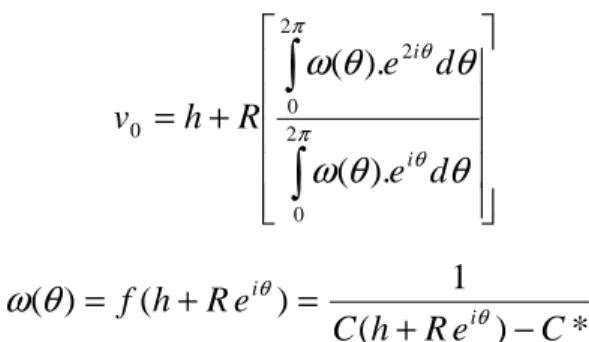BAB 4 Implementasi. Kasus 1. Diberikan suatu persamaan

BAB 4

Implementasi

Pada bab ini akan diperlihatkan bagaimana proses penyelesaian ekplisit persamaan transenden dengan menyelesaikan beberapa kasus yang sering ditemukan dalam kehidupan sehari-hari, dengan 2 cara yaitu : metode yang penulis kerjakan dan dibandingkan dengan metode secant atau Newton-Raphson.

Kasus 1.

Diberikan suatu persamaan ztanz =B. Persamaan ini muncul dari penyelesaian deret takhingga masalah konduksi panas transien (transient heat conduction) berdimensi satu. Carilah akar positif z dari persamaan tersebut.

Penyelesaian :

Persamaan tersebut dapat ditulis sebagai :ztanz−B=0atau

z B z= tan atau 0 cos sinz−B z= z (4.1) karena (4.1) tak memiliki titik singular, maka dicari dari kebalikannya. Maka z B z z z f cos sin 1 ) ( − = ) (z

f memiliki titik singular di z= z₀, dimana z tergantung nilai B, dan ₀ )

(z

f analitik di suatu titik di z , karena memiliki turunan terhadap B 0

Karena f(z)mempunyai titik singular di z =z₀, maka rumus ekplisit pada (3.6) berlaku.               + =

∫

∫

ρ θ π θ

θ

θ

ω

θ

θ

ω

2 0 2 0 2 0 ) ( ) ( d e d e R h z i i

dengan ) cos( ) sin( ) ( 1 ) ( ) (

θ

θ _{θ θ θ}

ω

i i i i e R h B e R h e R h e R h f + − + + = + =

Lakukan diskritisasi dengan metode kuadratur Gauss, maka diperoleh :

( )

( ). , 0, 1, 2,... 1 0 2 0 ± ± = =

∑

∫

− = n e d e N n i n i θn π θ

_θ

_ω

_θ

θ

ω

Dari anggapan bahwa z adalah real sehingga penulis gambarkan tanz dan

z B

, di R , seperti pada gambar 4.1 di bawah ini, maka terlihat bahwa pilihan yang 2 cocok untuk lintasan tertutup C adalah lingkaran dengan jari-jari R=π/4 dan

pusat 

π

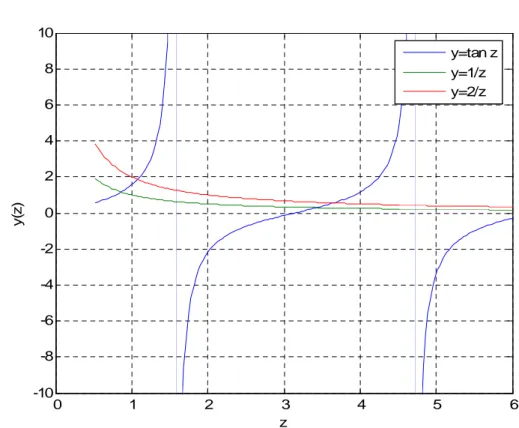
     − = 4 3 n h_n 0 1 2 3 4 5 6 -10 -8 -6 -4 -2 0 2 4 6 8 10 z y (z ) y=tan z y=1/z y=2/z

Gambar 4.1. Grafik Persamaan tan z= B/z, dengan B= 1 dan B=2

Dengan mengambil B=2 , R=π/4, h=π /4(n=1), dan N=32 titik diperoleh akarnya 1,0769

Sedangkan untuk n=2atau 4 5

π

=

h , R=π/4,B=2diperoleh akarnya 3,6436, dan seterusnya tergantung pada pengambilan n atau pusatnya h.

Program matlabnya dibawah ini.

function kasus1 clear clc x=[pi/16:pi/16:2*pi] h=pi/4 r=pi/4 %r=3.*pi/16 %h=5*pi/4 z=h+r*exp((j*x)) f=1./(z.*sin(z)-2*cos(z)) g=exp(j.*x) a=f.*g temp=fft(a)./fft(f) format z= h+r.*temp akar=z(32)

Apabila kita bandingkan dengan metode secant dengan nilai awal z0 =complex(0.3)

dan z1 =complex(0.2), maka diperoleh setelah 8 iterasi akarnya 1,0769. Tabel 4.1 Hasil perhitungan dengan metode Secant

untuk persamaan ztanz=B Iterasi(k) Akar(z) Galat Relatif

1 2,1520 0.9071 2 0.9782 1.2000 3 1.0902 0.1028 4 1.0766 0.0126 5 1.0769 2.1368 e-004 6 1.0769 4.1938 e-007 7 1.0769 1.4549 e-011 8 1.0769 0

Program secantnya sebagai berikut :

function secan1 format clc clear z0=complex(0.3); z1=complex(0.2); f1=z1*sin(z1)-2*cos(z1); f0=z0*sin(z0)-2*cos(z0); delta=1e-11; epsilon=1e-11;

for k=1:10000 z2=z1-(f1*(z1-z0)/(f1-f0)) galat=abs((z2-z1)/z2) z0=z1; z1=z2; f0=f1; f1=z1*sin(z1)-2*cos(z1); if(galat<delta), break, end end

k z2 z1

Kasus 2

Persamaan di bawah ini adalah persamaan panjang gelombang maksimum tenaga emisi untuk radiasi Black-body:

5 ) 5

( −z ez = (4.2) akan dicari akar dari persamaan tersebut.

Penyelesaian:

Persamaan (4.2) dapat ditulis sebagai (5−z)ez −5=0

Karena (4.2) tidak mempunyai titik singular maka diubah ke bentuk kebalikannya menjadi 5 ) 5 ( 1 ) ( − − = z e z z

f sehingga dapat ditentukan titik singularnya yaitu

pada z=0. Tetapi jika penulis gambarkan pada gambar 4.3 antara

) 5 ( 5 z − dan z

e akan saling beririsan pada 2 lokasi, yaitu pada z=0,solusi trivial, sedangkan solusi z yang lain berada sangat dekat sebelah kiri dari ₀ z =5, maka diperoleh 2 singularitas yaitu pada z=0dan z =z₀. Singularitas dapat dihapuskan dengan mengalikan f(z) dengan z(z−z0) sehingga teorema integral Cauchy berlaku dan rumus (3.7) atau (3.8). dapat digunakan untuk mencari akar persamaan di atas, dengan rumus di bawah ini.

              =

∫

∫

π θ π θ

θ

θ

ω

θ

θ

ω

2 0 2 2 0 3 0 ) ( ) ( d e d e R z i i

Ambil h=0 dan R=5, diperoleh akarnya z= 4.9654 dan programnya berikut:

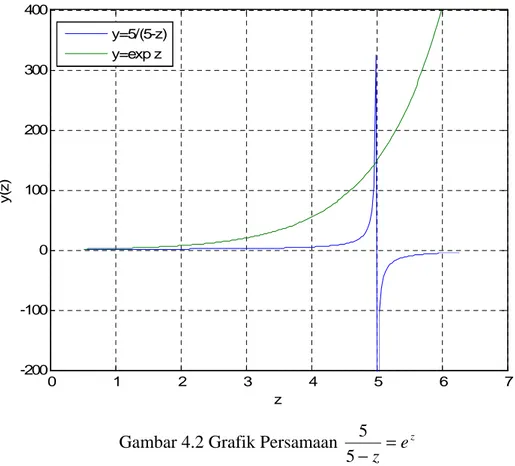
function kasus2 clear clc x=[pi/16:pi/16:2*pi] h=0 r=5 z=h+r*exp((j*x)) f=exp(j.*x)./((5-z).*exp(z)-5) g=exp(j.*x) a=f.*g temp=fft(a)./fft(f) z=r.*temp format akar=z(32) 0 1 2 3 4 5 6 7 -200 -100 0 100 200 300 400 z y (z ) y=5/(5-z) y=exp z

Gambar 4.2 Grafik Persamaan ez z =

− 5

Jika diselesaikan dengan metode Secant dengan mengambil nilai awal )

5 ( 0 complex

z = dan z₀ =complex(3) diperoleh akar setelah 11 iterasi adalah 4.9651. selengkapnya dapat dilihat dalam tabel berikut :

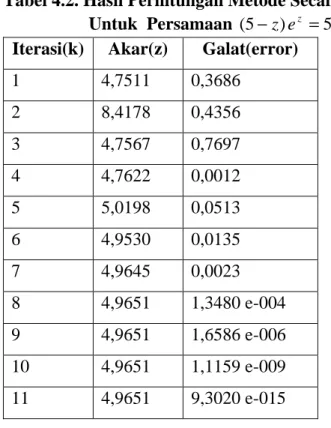
Tabel 4.2. Hasil Perhitungan Metode Secant Untuk Persamaan (5−z)ez =5

Iterasi(k) Akar(z) Galat(error)

1 4,7511 0,3686 2 8,4178 0,4356 3 4,7567 0,7697 4 4,7622 0,0012 5 5,0198 0,0513 6 4,9530 0,0135 7 4,9645 0,0023 8 4,9651 1,3480 e-004 9 4,9651 1,6586 e-006 10 4,9651 1,1159 e-009 11 4,9651 9,3020 e-015 Kasus 3. Diberikan persamaan

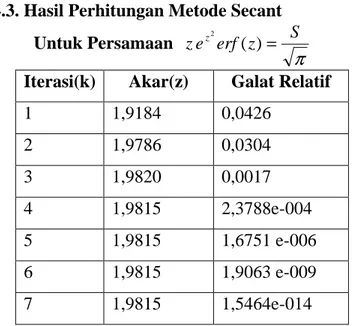
π

S z erf e z z2 ( )= (4.3) Persamaan ini dijumpai dalam masalah proses pembekuan suatu cairan murni,

akan dicari kapan titik beku terjadi. Secara matematika ini sama dengan mencari akar real positif dari persamaan

Penyelesaian :

Persamaan (4.3) dapat ditulis sebagai zez2 erf(z)

π

−S =0, tetapi tidak memiliki titik singular, maka kita ubah menjadi kebalikannya

S z erf e z z f z − = π ) ( 1 ) ( 2 (4.4)

Bentuk(4.4) memiliki titik singular pada titik z= z0 yang tergantung pada nilai S Ruas kiri persamaan (4.3) merupakan fungsi genap. Oleh karena itu, maka akan mempunyai 2 penyelesaian yang berlawanan tanda tetapi besarnya sama. Tanpa mengurangi keumuman kita fokus pada sumbu real positif.

Pada sumbu real untuk z≥2, maka dt e z erf z t

∫

− = 0 2 2 ) ( π , misalkan 2 x t = , dt dx 2 1 = = e dx z x

∫

− 0 2 2 1 . 2 2 π . = e dx z x

∫

− 0 2 _. 2 2 2 π =         −

_∫

∫

∞ − − ∞ − − dx e dx e x z x 0 2 2 2 2 2 1 2 1 . 2 π π

[

( ) 1/2

]

. 2 ) (z = N z − erf dimana N(z)=        

∫

∞ − − z x dx e 2 2 2 1 .

π merupakan fungsi momutatif distribusi normal standar.

Untuk z≥2, nilai N(z)≈1, maka ,

1 ) (z ≈

erf untuk z≥2

Untuk membantu dalam pemilihan pusat dan jari-jari yang penulis berikan, maka gambarkan persamaan tersebut dalam bentuk eksplisitnya yaitu

π z

S z erf

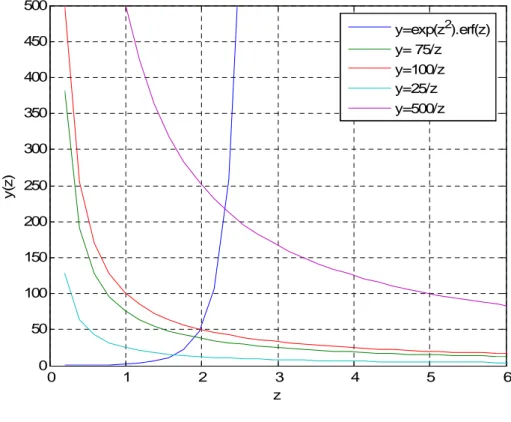
Ruas kiri persamaan (4.3) akan memdekati 100 untuk z=2.Oleh karena itu untuk S ≤100 π , pilih h=1 dan R=1, misalkan S =100 π akan diperoleh akarnya z = 1,9864, untuk S =75 π , maka z = 1,8401,dan untuk S =25 π , maka z= 1,6815. dan seterusnya.

0 1 2 3 4 5 6 0 50 100 150 200 250 300 350 400 450 500 z y (z ) y=exp(z2).erf(z) y= 75/z y=100/z y=25/z y=500/z

Gambar 4.3 Grafik Persamaan :

π z S z erf ez2 ( )=

Nilai-nilai tersebut diperoleh dengan pemograman matlab berikut :

function kasus3 clear format %clc x=[0+pi/16:(pi/16):2*pi]; h=1; r=1; S=100*sqrt(pi); z1=real(h+r*exp((j.*x))); z=(h+r*exp((j.*x))); %z=(h+r*exp((j.*x))); f=1./(z.*exp(z.^2).*erf(z1)*(sqrt(pi))-S); g=exp(j.*x); a=f.*g; qq=[fft(a);fft(f)]; temp=fft(a)./fft(f);

z=h+r.*temp; akar=z(32)

dan jika menggunakan metode secant untuk S =100 π dengan nilai awal )

1 ( 0 complex

z = dan z₁ =complex(2), dengan 8 iterasi diperoleh akarnya 1,9815 Hasil selengkapnya dapat di lihat pada tabel 4.3

Tabel 4.3. Hasil Perhitungan Metode Secant Untuk Persamaan π S z erf e z z2 ( )=

Iterasi(k) Akar(z) Galat Relatif

1 1,9184 0,0426 2 1,9786 0,0304 3 1,9820 0,0017 4 1,9815 2,3788e-004 5 1,9815 1,6751 e-006 6 1,9815 1,9063 e-009 7 1,9815 1,5464e-014

Untuk S yang besar, penyelesaiannya dapat diperoleh dengan pemisalan 1

) (z ≈

erf , sehingga persamaan (4.3) menjadi : π z S ez2 = , ln 2       = ⇔ π z S z dengan syarat π π S z z S _{> ⇔ >} 1 π ln ln ln 2 = − − ⇔ z S z π ln ln ln 2 + = − ⇔ z z S

Karena S besar , maka z pun membesar, akibatnya z2 >>lnz,sehingga 2

2

lnz z

z + ≈ artinya lnz diabaikan terhadap z . 2

maka _            ≅ π S z ln (4.5)

Jika h dimisalkan sebagai _            = π S h ln = 2,4929 dari S =500 π dan R = 0,2, maka akarnya diperoleh 2,3183. lihat gambar 4.3

Kasus 4

Pencarian nilai volatilitas dari persamaan Black-Scholes dalam rumus mencari nilai opsi call Eropa :

) 2 ( . ) 1 ( . ) , (S t S N d Ke ( )N d C = − −rT−t (4.6) dengan ) ( ) ( 2 1 ln 1 2 t T v t T v r K S d − −       + +       = π v d t T v t T v r K S d = − − −       ₋ +       = 1 ) ( ) ( 2 1 ln 2 2

∫

∞ − − = xe d x N

η

π

η 2 1 2 1 ) ( dimana

S= harga saham (Stock Price), K= Strike Price, r = suku bunga(Interes rate), T= maturity time, t= waktu awal, dan v = volatilitas.

Penyelesaian :

Karena yang dicari adalah nilai volatilitas, maka C(S,t)=C(v) dan C* adalah nilai opsi call Eropa yang diberikan atau diketahui dari pasar opsi,

Sehingga persamaan (4.6) menjadi *

) (v C

C = atau C(v)−C*=0 (4.7) Untuk mencari akar persamaan (4.7) harus dibentuk kebalikan nya, yaitu

* ) ( 1 ) ( C v C v f − =

Penyelesaian selanjutnya, karena f(z)mempunyai titik singular yang dapat dihapuskan pada v yang tergantung pada nilai C*, maka Penyelesaian eksplisit 0 rumus 1 berlaku yaitu :

              + =

∫

∫

π θ π θ

θ

θ

ω

θ

θ

ω

2 0 2 0 2 0 ). ( ). ( d e d e R h v i i = + = ( ) ) (θ θ ω i e R h f * ) ( 1 C e R h C + iθ −

Bentuk dalam kurung besar adalah perbandingan dari koefisien kedua dan kesatu deret Fourier eksponensial sehingga dapat dicari dengan bantuan algoritma FFT. pada Matlab.

Jika masalah di atas digambarkan secara eksplisit yaitu C(v) = C* seperti pada gambar 4.4 berikut

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1 0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 v y (v ) CStar z=c(v)

Gambar 4.4 Grafik C(v) = C*, dengan C* = 0,2 S=2, K=2, r=0.03, T=1

Dan program matlabnya function kasus4a clear clc r=0.03;S=2;K=2;T=1; %r=0.03;S=3;K=1;T=3; H=0.15; R=0.4; x=[pi/16:pi/16:2*pi]; v=real(H+R*exp(j*x)) d1=(log(S/K)+(r+0.5*v.^2)*(T))/(sqrt(T)) d2=d1-v*sqrt(T); N1=0.5*(1+erf(d1/sqrt(2))); N2=0.5*(1+erf(d2/sqrt(2))); f=1./(S*N1-K*exp(-r*(T))*N2-0.2); g=real(exp(j.*x)) a=f.*g temp=real(fft(a)./fft(f)) z= H+R.*temp akarnya=z(32)

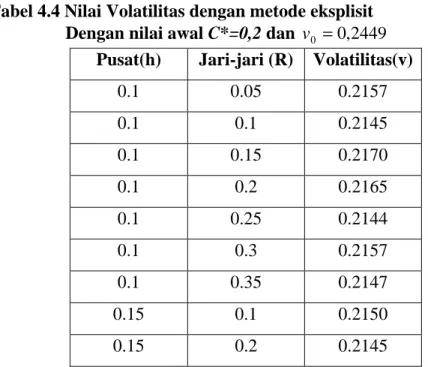
Dengan memasukan nilai S = 2, K =2, r=0.03,T=1, C*= 0.2 , h=0,1 dan R=0.15 dengan banyak titik N=32, maka diperoleh nilai volatilitasnya = 0,2145

Dengan merubah-rubah pusat dan jari-jari, akan tetap mendekati nilai tersebut asalkan masih berada dalam batas kesingularan, seperti dapat dilihat dalam tabel di bawah ini.

Tabel 4.4 Nilai Volatilitas dengan metode eksplisit Dengan nilai awal C*=0,2 dan v0 =0,2449

Pusat(h) Jari-jari (R) Volatilitas(v)

0.1 0.05 0.2157 0.1 0.1 0.2145 0.1 0.15 0.2170 0.1 0.2 0.2165 0.1 0.25 0.2144 0.1 0.3 0.2157 0.1 0.35 0.2147 0.15 0.1 0.2150 0.15 0.2 0.2145

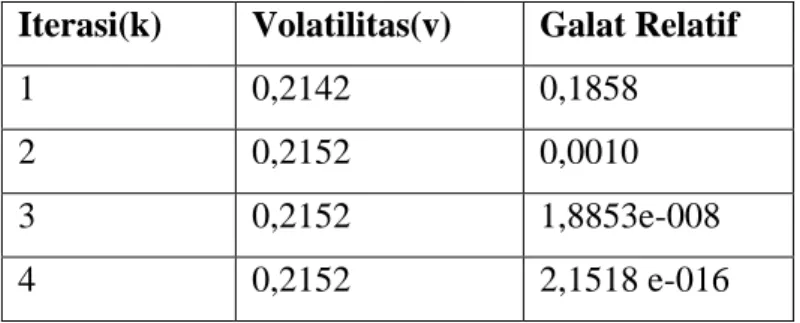
Jika dibandingkan dengan menggunakan metode Newton dan nilai awal volatilitasv_o =0,4 maka setelah iterasi ke-4 nilai volatilitasnya = 0,2152. Nilai selengkapnya yangdiperoleh ditullis dalam tabel 4.5.

Tabel 4.5. Hasil Perhitungan dengan Metode Newton-Raphson Untuk Persamaan C(S,t)=S.N(d1)−K.e−r(T−t)N(d2)

Iterasi(k) Volatilitas(v) Galat Relatif

1 0,2142 0,1858

2 0,2152 0,0010

3 0,2152 1,8853e-008

4 0,2152 2,1518 e-016

Perhitungannya menggunakan pemograman matlab berikut :

function v=newton2() clc;

r=0.03;S=2;K=2;T=1;

%simulasi dan uji model

%---%v1=0.1;

%[CTrue,Cdelta,P,Pdelta]=ch8(S,K,r,v1,T);

%disp('nilai Eropean Call Option adalah'),disp(CTrue); %CTrue=CTrue; %dalam hal CTrue= CStar

%---CStar = 0.2 v=0.4

%vhat = sqrt(2*abs(log(S/K)+r*T)/T);

disp('nilai volatility awal adalah'),disp(v);

%akan dicari sigma* %metode Newton %t=0; %if max(S-K*exp(-r*(T-t)),0) <= Cst < S tol = 1e-11; % v = vhat vdiff = 1; k=0;

while (vdiff >= tol & k < 100) k = k+1

%Cvega = S*sqrt(T-t)*1/sqrt(2*pi)*exp((1/2)*d1^2);

increment = (C-CStar)/Cvega; v = v - increment; %Fsigma = increment-Cst vdiff = abs(increment)

disp('Nilai volatility baru adalah = '),disp(v); end

%end

%disp('Nilai volatility baru adalah = '),disp(v); %plot(Fsigma,k);

Program Newton-Raphson ini menggunakan program fungsi Ch8(S,K,r,v1,T) sebagai berikut

function[C,Cdelta,P,Pdelta]=ch8(S,K,r,v,T)

%algoritma black scholes untuk European Option

if T > 0 d1=(log(S/K)+(r+0.5*v^2)*(T))/(v*sqrt(T)); d2=d1-v*sqrt(T); N1=0.5*(1+erf(d1/sqrt(2))); N2=0.5*(1+erf(d2/sqrt(2))); C=S*N1-K*exp(-r*(T))*N2; Cdelta=N1; else C=max(S-K,0); Cdelta=0.5*(sign(S-K)+1); end

dan program ch10(S,K,r,v,T) berikut

function[C,Cdelta,Cvega,P,Pdelta,Pvega]=ch10(S,K,r,v,T)

%algoritma black scholes untuk European Option

if T > 0 d1=(log(S/K)+(r+0.5*v^2)*(T))/(v*sqrt(T)) d2=d1-v*sqrt(T); N1=0.5*(1+erf(d1/sqrt(2))); N2=0.5*(1+erf(d2/sqrt(2))); C=S*N1-K*exp(-r*(T))*N2; Cdelta=N1; Cvega=S*sqrt(T)*exp(-0.5*d1^2)/sqrt(2*pi); else C=max(S-K,0); Cdelta=0.5*(sign(S-K)+1); Cvega=0; end