Sejarah Logika
Logika dimulai sejak Thales (624 SM - 548 SM ), filsuf Yunani pertama yang meninggalkan segala dongeng, takhayul, dan cerita-cerita isapan jempol dan berpaling kepada akal
budi untuk memecahkan rahasia alam semesta.
PENGERTIAN
1. Logika matematika adalah Ilmu yang mempelajari tentang cara berpikir yang logis/masuk akal
2.Logika matematika adalah ilmu yang digunakan untuk menentukan nilai kebenaran dari suatu pernyataan atau penarikan kesimpulan
Kontradiksi
Biimplikasi p ↔ q
I. PERNYATAAN
1.
Pengertian
Pernyataan adalah adalah suatu kalimat
yang bernilai
benar
saja atau
salah saja
.
Dengan kata lain, tidak sekaligus
kedua-duanya.
Pernyataan disebut juga kalimat
tertutup.
Contoh :
Tentukan mana yang merupakan
pernyataan dan yang bukan pernyataan
1. 9 adalah bilangan prima pernyataan
Salah
2. 27 merupakan bilangan kelipatan 9 pernyataan
Benar
3. Siapakah yang tidak mengerjakan PR ? Bukan pernyataan
Lambang pernyataan:
p, q, r , dst. (huruf kecil)
Nilai kebenaran pernyataan : B (benar)
S (salah)
Contoh :
2. INGKARAN/NEGASI
Lambang : “ “ atau “ …. “ dibaca : bukan/tidak
Contoh :
Tentukanlah negasi dari pernyataan berikut 1. p : 3+ 4 = 7
p : 3 + 4 7
Tidak benar bahwa 3 + 4 = 7 2. q : Semua Siswa berbaju putih
q : Tidak semua siswa berbaju putih
q : Beberapa siswa tidak berbaju putih q : Ada siswa yang tidak berbaju putih
Table kebenaran ingkaran
p ~p
B S
Kontradiksi
Biimplikasi
3. Pernyataan Majemuk
1. Disjungsi
Uci membeli sandal merah atau sepatu basket
2. Konjungsi :
Ayah membaca koran sripo dan ekspres
3. Implikasi
Jika hari ini adalah hari Sabtu maka siswa memakai seragam pramuka
4. Biimpilkasi
Adhan membawa pensil 2B jika dan
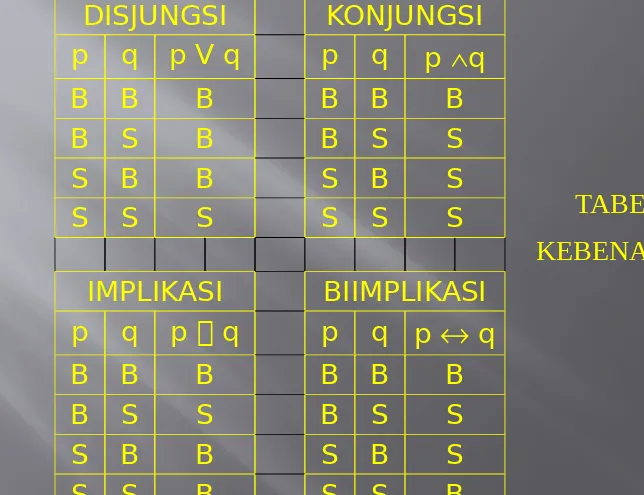
DISJUNGSI KONJUNGSI
p q p V q p q p q
B B B B B B
B S B B S S
S B B S B S
S S S S S S
IMPLIKASI BIIMPLIKASI
p q p q p q p q
B B B B B B
B S S B S S
S B B S B S
S S B S S B
TABEL
IMPLIKASI
~q ~p p ~q
~p ~q
q p
p q
KONVERS INVERS
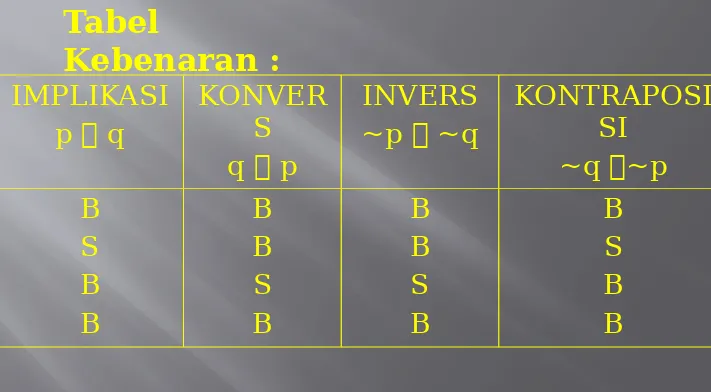
Tabel
Kebenaran :
IMPLIKASI p q
KONVER S
q p
INVERS ~p ~q
KONTRAPOSI SI
Contoh
Tentukanlah konvers, invers, kontraposisi dan ingkaran dari pernyataan “Jika ABC segitiga sama sisi maka semua sisinya sama panjang“
Diketahui :
p : ABC segitiga sama sisi
Jawab :
Konvers : q p
Jika semua sisinya sama panjang maka ABC segitiga sama sisi
Invers : ~p q :
Jika ABCD bukan segitiga sama sisi maka semua sisinya tidak sama panjang
Kontraposisi : ~q p
Jika semua sisinya tidak sama panjang maka ABC bukan segitiga sama sisi
Ingkaran : p ~q
ABC segitiga sama sisi dan semua sisinya tidak
II. PENARIKAN KESIMPULAN
Istilah
1. Premis
2. Konklusi
3. Argumen
Pola
Konklusi sebaiknya diturunkan dari
premis-premis, kalau premis yang
digunakan benar, maka konklusi akan bernilai benar.
Keabsahan argumen dapat ditunjukkan
Contoh: Tunjukan dengan table
kebenaran !
Premis 1 : p
q
Premis 2 : p
Konklusi : q
Jawab :
{(p
q)
p}
q benar
2. Pola Penarikan Kesimpulan
a. Modus Ponens.
Premis 1 : p
q
Premis 2 : p
Konklusi : q
Dibaca : Jika diketahui p
q benar
Contoh
Premis 1 : Jika 2 + 3 = 5, maka 5 > 4
Premis 2 : 2 + 3 = 5
b. Moduls Tollens.
Premis 1 : p
q
Premis 2 :
q
Konklusi :
p
Dibaca : Jika diketahui p
q benar
dan
q benar , maka
disimpulkan
Contoh
Premis 1 : Jika hari hujan, maka cuaca
dingin
Premis 2 : Cuaca tidak dingin
3. Prinsip Silogisma.
Premis 1 : p
q
Premis 2 : q
r
Konklusi : p
r
Dibaca: Jika diketahui p
q benar dan
q
r benar, maka
disimpulkan
Contoh:
Premis 1 : Jika Maher seorang siswa SMK maka Maher melaksanakan PSG
Premis 2 : Jika Maher melaksanakan PSG maka Maher belajar di industri minimal 3 bulan
Latihan 1
Diketahui p : Tuti gadis cantik q : Tuti gadis pandai
Tulislah pernyataan yang benar dari a. q d. p q
b. p q e. p q c. p q
Jawab:
a. Tuti bukan gadis cantik
b. Tuti gadis cantik dan tidak pandai c. Tuti bukan gadis cantik atau pandai d. Jika tuti gadis cantik maka pandai
Latihan 2
Tentukan nilai kebenaran dari pernyataan di
bawah ini :
a. Tidak benar 2 + 7 9
b. 30 atau 40 habis dibagi 6
c. Jika Jakarta Ibukota Indonesia maka Jakarta di Pulau Madura
Tentukan konvers, invers, kontraposisi da ingkaran dari pernyataan-pernyataan ” Jika ABC suatu segitiga sebangun maka sudut-sudut seletaknya sama”
Jawab :
konvers: Jika sudut-sudut seletaknya sama maka ABC suatu segitiga sebangun
Invers: Jika ABC bukan suatu segitiga sebangun maka sudut-sudut seletaknya tidak sama” Kontraposisi : ”Jika sudut-sudut seletaknya tidak
sama maka ABC bukan suatu segitiga sebangun
Ingkaran: ”ABC suatu segitiga sebangun dan sudut-sudut seletaknya tidak sama”
Buatlah tabel kebenaran dari : a. (p q)
b. p (q p)
5. Mana yang merupakan modus Ponens, Tollens atau Silogisma :
a. Premis 1:Jika Ibu pergi maka adik menangis Premis 2: Adik tidak menangis
Konklusi: Ibu tidak pergi
b. Premis 1: Jika log 10 = 1 maka 2log 8 = 3
Premis 2: log 10 = 1 Konklusi: 2log 8 = 3
c. Premis 1: Jika Aldi seorang programer IT maka
Aldi memahami flowchart
Premis 2:Jika Aldi memahami flowchart maka Aldi mampu mengoperasikan komputer
c. Premis 1: Jika semua masyarakat resah maka
harga bbm naik
Premis 2:Harga BBM naik atau harga bahan pokok naik
Premis 3: Harga bahan pokok naik