PENINGKATAN KEMAMPUAN KONEKSI MATEMATIS DAN KEMANDIRIAN BELAJAR SISWA DENGAN PENDEKATAN PEMBELAJARAN METAKOGNITIF DI SEKOLAH MENENGAH PERTAMA.

(1)

DAFTAR ISI

Halaman

HALAMAN JUDUL ………. i

HALAMAN PENGESAHAN ………... ii

PERNYATAAN ………. iii

PERSEMBAHAN ………. iv

KATA PENGANTAR ………. v

ABSTRAK ………. ix

ABSTRACT ………. x

DAFTAR ISI ………. xi

DAFTAR TABEL ………. xiii

DAFTAR GAMBAR ………. xix

DAFTAR LAMPIRAN ………. xxi

BAB I PENDAHULUAN ……… 1

A. Latar Belakang Masalah ………... 1

B. Rumusan Masalah ………... 12

C. Tujuan Penelitian ………... 14

D. Manfaat Penelitian ………... 16

E. Definisi Operasional Variabel _………. ₁₇

BAB II KAJIAN PUSTAKA ……… 20

A. Pendekatan Metakognitif ... 20

B. Belajar dalam Kelompok Kecil ………... 33

C. Koneksi Matematis ……… 41

D. Kemampuan Koneksi Matematis ... 44

E. Kemandirian Belajar Siswa ... 48

F. Mengembangkan Kemandirian Belajar Siswa ... 56

G. Karakteristik Siswa Sekolah Menengah Pertama ... 60

H. Teori Belajar yang Mendasari ... 68

I. Pembelajaran Konvensional ... 80

J. Penelitian yang Relevan ……... 82

K. Hipotesis Penelitian ……….. 88

BAB III METODE PENELITIAN ……… 89

A. Jenis dan Desain Penelitian ……… 89

(2)

ii

C. Pengembangan Instrumen dan Teknik

Pengumpulan Data ...………... 104

D. Teknik Analisis Data ……… 140

E. Prosedur Pelaksanaan Penelitian ……….. 144

F. _{Waktu Pelaksanaan Penelitian dan} Indikator Kinerja _……….. ₁₄₉

BAB IV HASIL PENELITIAN DAN PEMBAHASAN ………. 150

A. Analisis Data Kemampuan Awal Matematika (KAM) …. 152 B. Analisis Data Kemampuan Koneksi Matematis ... 164

C. Analisis Data Kemandirian Belajar Siswa ……... 194

D. Analisis Data Hasil Kerja Siswa ... 222

E. Pembahasan Hasil Penelitian ... 235

1. Pendekatan Pembelajaran Metakognitif ... 237

2. Keunggulan, Keterbatasan, dan Tantangan Pembelajaran PPMG dan PPMK ... 3. Level Sekolah ...………... 246 254 4. Kemampuan Awal Matematika (KAM) ... ... 5. Kemandirian Belajar Siswa dalam Matematika Berdasarkan Pembelajaran, Level Sekolah, dan KAM .. 256 259 BAB V KESIMPULAN, IMPLIKASI, KETERBATASAN, DAN REKOMENDASI ... 269

A. Kesimpulan _……….. ₂₆₉

B. Implikasi _……….. ₂₇₃

C. Keterbatasan _……….. ₂₇₅

D. Rekomendasi _……….. ₂₇₆

(3)

iii

DAFTAR TABEL

Tabel Judul Halaman

2.1 Struktur Pengajaran Model Pencapaian Kosep ... 75

2.2 Ringkasan Penelitian tentang Metakognisi dan Problem Solving ... 86

3.1. Keterkaitan antara Kemampuan Koneksi Matematis, Kelompok Pembelajaran, Level Sekolah, dan Kemampuan Awal Matematika ……... 92

3.2. Keterkaitan antara Kemandirian Belajar, Kelompok Pembelajaran, Level Sekolah, dan Kemampuan Awal Matematika ……... 93

3.3 Sampel Penelitian Berdasarkan Peringkat Sekolah ... 98

3.4. Uji Normalitas Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 12 Bandung ……... 99

3.5. Uji Homogenitas Varians Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 12 Bandung ……... 99

3.6. Uji Kesetaraan Data Kemampuan Awal Matematika Siswa Ketiga Kelas VIII SMPN 12 Bandung ……... 100

3.7. Uji Normalitas Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 15 Bandung ……... 101

3.8. Uji Homogenitas Varians Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 15 Bandung ……... 101

3.9. Uji Kesetaraan Data Kemampuan Awal Matematika Siswa Ketiga Kelas VIII SMPN 15 Bandung ……... 102

3.10. Uji Normalitas data KAM Siswa Kedua Level Sekolah Berdasarkan Tiga Pendekatan Pembelajaran ……... 103

3.11 Uji Perbedaan Data Kemampuan Awal Matematika Siswa Berdasarkan Level Sekolah ... 103

3.12 Analisis Statistik ANOVA Validitas Muka ... 111

3.13 Analisis Statistik ANOVA Validitas Isi ... 112

(4)

iv

3.15. Hasil Analisis Reliabilitas ……... 116

3.16. Sebaran Sampel Penelitian ……... 117

3.17. Analisis Validitas Muka dengan Cochran’s ……... 119

3.18. Analisis Validitas Isi dengan Cochran’s ……... 120

3.19. Interpretasi Nilai Koefisien Korelasi r xy ... 125

3.20. Hasil Pertimbangan Validitas Butir Soal Pretes Kemampuan Koneksi Matematis (KKM) ……... 125

3.21. Hasil Perhitungan Validitas Butir Soal Postes Kemampuan Koneksi Matematis (KKM) ... 126

3.22. Interpretasi Koefisien Reliabilitas ...…... 127

3.23. Rekapitulasi Hasil Ujicoba Tes Kemampuan Koneksi Matematis (KKM) ……... 128

3.24. Distribusi Respon Siswa untuk Pernyataan Positif Nomor 1 dan Pernyataan Negatif Nomor 3 ……... 130

3.25 Perhitungan Skor Skala Kemandirian Belajar Siswa untuk Pernyataan Positif Nomor 1 ……... 132

3.26. Perhitungan Skor Skala Kemandirian Belajar Siswa untuk Pernyataan Negatif Nomor 3 ……... 132

3.27. Skor Setiap Item Skala Kemandirian Belajar Siswa ……... 134

3.28. Keterkaitan antara Masalah, Hipotesis, Kelompok Data dan Jenis Statistik yang digunakan dalam Analisis Data ……... 142

4.1. Sebaran Sampel Penelitian ...…… 151

4.2. Deskripsi Data KAM Berdasarkan Pendekatan Pembelajaran dan Level Sekolah _……... ₁₅₄

4.3. Deskripsi Data KAM ketiga Pendekatan Pembelajaran untuk Setiap Kategori KAM ……... 155

(5)

v

4.5. Uji Homogenitas Varians untuk

Ketiga Kelompok Pembelajaran ……... 159 4.6. Uji Perbedaan Data KAM Siswa antar Kedua Level

Sekolah ... 160 4.7. Uji Kesetaraan Data KAM Berdasarkan

Pendekatan Pembelajaran ……... 161

4.8. Uji Homogenitas Varians dari Levene terhadap Data KAM Siswa Ketiga Kelompok Pembelajaran

untuk Setiap Level Sekolah ……... 162

4.9. Uji Kesetaraan Data KAM Ketiga Kelompok

Pembelajaran untuk Setiap Sekolah ... 163 4.10. Deskripsi Data KKM Siswa Ketiga Kelompok

Pembelajaran ……... 164

4.11. Uji Normalitas Data N-Gain KKM Siswa Ketiga

Kelompok Pembelajaran …….. 166

4.12. Uji Signifikansi Peningkatan KKM Siswa

Ketiga Kelompok Pembelajaran ……... 167 4.13. Uji Homogenitas Varians dari Levene terhadap

Data N-Gain KKM Siswa Ketiga Kelompok

Pembelajaran ... 169

4.14 Uji Signifikansi Perbedaan KKM Siswa antara

Ketiga Kelompok Pembelajaran ……... 170

4.15. Skor N-Gain Kemampuan Koneksi Matematis

(KKM) ……... 170

4.16. Deskripsi Data KKM Siswa Ketiga Kelompok

Pembelajaran untuk Setiap Level Sekolah ... 171 4.17. Uji Normalitas Data N-Gain KKM Siswa Kedua Level

Sekolah …… 173

4.18. Uji Signifikansi Peningkatan KKM Siswa Ketiga Kelompok Pembelajaran untuk Setiap Level

(6)

vi

4.19. Uji Homogenitas Varians Data N-Gain KKM Siswa Ketiga Kelompok Pembelajaran untuk Setiap Level

Sekolah ……... 174

4.20. Uji Signifikansi Perbedaan Peningkatan KKM Siswa antara Ketiga Kelompok Pembelajaran Berdasarkan

Level Sekolah ……... 176

Sekolah Level Tinggi ... 176

4.22 Skor N-Gain Kemampuan Koneksi Matematis

Sekolah Level Sedang ... 177

4.23. Deskripsi Data KKM Siswa Ketiga Kelompok

Pembelajaran untuk Setiap Kategori KAM ... 178 4.24. Uji Normalitas Data N-Gain KKM Siswa Ketiga

Pembelajaran untuk Setiap Kategori KAM ……... 180 4.25. Uji Signifikansi Peningkatan KKM Siswa

KetigaKelompok Pembelajaran untuk Setiap

Kategori KAM ……... 181

4.26. Uji Homogenitas Varians dari Levene terhadap Data N-Gain KKM Siswa Ketiga Kelompok Pembelajaran

untuk Setiap Kategori KAM ...……... 182

4.27. Uji Signifikansi Perbedaan Peningkatan KKM Siswa Ketiga Kelompok Pembelajaran untuk

Setiap Kategori KAM _...…... ₁₈₃

Kategori KAM ... 184

4.29. Uji Homogenitas Varians Data Peningkatan KKM Siswa ditinjau dari Interaksi antara Pebelajaran dengan Level

Sekolah ...….. 185

4.30. Uji Interaksi antara Pendekatan Pembelajaran dengan

(7)

vii

4.31. Uji Homogenitas Varians Data Peningkatan KKM Siswa

ditinjau dari Interaksi antara Pebelajaran dengan KAM ... 189 4.32. Uji Interaksi antara Pendekatan Pembelajaran dengan

KAM terhadap Peningkatan KKM ... 191 4.33. Deskripsi Data Kemandirian Belajar Siswa (KBS)

Ketiga Kelompok Pembelajaran ... 194 4.34. Uji Normalitas Data N-Gain KKM Siswa Ketiga

Kelompok Pembelajaran …... 196

4.35. Uji Signifikansi Peningkatan KBS Ketiga

Kelompok Pembelajaran ……... 197

4.36. Uji Homogenitas Varians dari Levene terhadap Data

N-Gain KBS Ketiga Kelompok Pembelajaran ... 198 4.37. Uji Signifikansi Perbedaan Peningkatan KBS antara

Ketiga Kelompok Pembelajaran ……... 199

4.38. Deskripsi Data KBS Ketiga Kelompok

Pembelajaran untuk Setiap Level Sekolah ……... 200 4.39. Uji Normalitas Data N-Gain KBS kedua Level

Sekolah ... 202

4.40. Uji Signifikansi Peningkatan KBS Ketiga Kelompok

Pembelajaran untuk Setiap Level Sekolah ……... 203 4.41. Uji Homogenitas Varians dari Levene terhadap Data

N-Gain KBS Ketiga Kelompok Pembelajaran untuk

Setiap Level Sekolah ……... 203

4.42. Uji Signifikansi Perbedaan Peningkatan KBS Ketiga

Kelompok Pembelajaran Berdasarkan Level Sekolah ... 205 4.43. N-Gain Kemandirian Belajar Siswa ... 205 4.44. Deskripsi Data KBS Ketiga Kelompok Pembelajaran

untuk Setiap Kategori KAM ... 206

4.45. Uji Normalitas Data N-Gain KBS Ketiga Kelompok Pembelajaran untuk Setiap Kategori

(8)

viii

4.46. Uji Signifikansi Peningkatan KBS Ketiga Kelompok

Pembelajaran untuk Setiap Kategori KAM ... 209 4.47. Uji Homogenitas Varians dari Levene terhadap Data

N-Gain KBS Ketiga Kelompok Pembelajaran untuk

Setiap Kategori KAM …… 210

4.48. Uji Signifikansi Perbedaan Peningkatan KBS Ketiga

Kelompok Pembelajaran untuk Setiap Kategori KAM …. 211 4.49 Uji Homogenitas Varians Data Peningkatan KBS

ditinjau dari Interaksi antara Pembelajaran dengan

Level Sekolah ...… 212

4.50. Uji Interaksi antara Pendekatan Pembelajaran dengan

Level Sekolah terhadap Peningkatan KBS …… 214 4.51. Uji Homogenitas Varians Data Peningkatan KBS

ditinjau dari Interaksi antara Pembelajaran dengan KAM ... 217 4.52. Uji Interaksi antara Pendekatan Pembelajaran dengan

KAM terhadap Peningkatan KBS ……... 218

4.53. Rangkuman Pengujian Hipotesis Penelitian …….. 221 4.54. Rata-rata Setiap Aspek KKM Siswa ditinjau dari

Pendekatan Pembelajaran ……... 223

4.55. Hasil Pengklasifikasian Siswa Merasa Senang

(9)

ix

DAFTAR GAMBAR

Gambar Judul Halaman

1.1. Koneksi Berbagai Konsep ……… 4

1.2. Koneksi Antar Konsep ……… 7

2.1. Kurikulum Matematika Singapora …………. 21

2.2. Aktivitas Berpikir Siswa dalam Menyelesaikan Masalah …………. 22

2.3. Pengembangan KKM, KBS, Perswepsi terhadap Pembelajaran …………... 24

2.4. Metakognitif Grup …………. 30

2.5. Metakognitif Klasikal …………... 30

2.6. Siswa Menyelesaikan Masalah dengan Inisiatif Sendiri ... 31

2.7. Rasa Percaya Diri Siswa di Deoan Kelas ... 32

2.8. Keterkaitan antar Konsep ... 44

2.9. Siklus Kemandirian Belajar ... 53

2.10. Tingkat Inisiatif Kemandirian Belajar ... 55

2.11. Proses Perkembangan Kognisi dari Piaget _... 69

2.12. Contoh dan non Contoh Gambar Garis Lurus ...…… 73

2.13. Penanaman Konsep Gradien dan Garis Lurus …………. 74

4.1. Rata-rata Skor KAM Berdasarkan Level Sekolah …………. 155

4.2. Rata-rata Skor KAM Berdasarkan Kategori KAM ………... 155

4.3. Normalisasi Skor KAM ………... 158

(10)

x

Gambar Judul Halaman

4.5. Peningkatan N-Gain KKM Berdasarkan

Pembelajaran ………… 165

4.6. Peningkatan N-Gain KKM Berdasarkan

Pembelajaran dan Gabungan ………… 168

4.7. Peningkatan N-Gain KKM Siswa

Berdasatkan Level Sekolah …………. 172

4.8. Peningkatan N-Gain KKM Siswa

Berdasarkan Kategori KAM …………. 179

4.9. Interaksi antara Pendekatan Pembelajaran dengan Level Sekolah terhadap

Peningkatan N-Gain KKM …………... 188

4.10. Interaksi antara Pendekatan Pembelajaran dengan KAM terhadap Peningkatan N-Gain

KKM …………. 191

4.11. Perbandingan Peningkatan KKM …………... 193 4.12. Rata-rata Skor Kemandirian Belajar Siswa (KBS) ... 195 4.13. Peningkatan N-Gain KBS ... 195 4.14. Peningkatan N-Gain KBS Berdasarkan

Pembelajaran dan Gabungan ... 197 4.15. Peningkatan N-Gain KBS Berdasarkan

Kategori KAM ... 215

(11)

xi

DAFTAR LAMPIRAN

Lampi

ran Judul Halaman

A-1. Lembar Pertimbangan ... 293 A-2. Hasil Pertimbangan Tes Kemampuan Awal

Matematis ……… 297

A-3. Hasil Pertimbangan Tes Kemampuan

Koneksi Matematis ………... 299 A-4. Hasil Uji Validitas dan Reliabilitas Data Ujicoba

Tes Kemampuan Awal matematis ……… 300

A-5. Hasil Uji Validitas dan Reliabilitas Data Ujicoba

Tes Kemampuan Koneksi Matematis ……… 304

A-6. Kisi-Kisi dan Skala Kemandirian Belajar Siswa ……… 308 A-7. Data Hasil Ujicoba Skala Kemandirian Belajar Siswa …… 312 A-8. Pemberian Skor Tiap Item Skala Kemandirian

Belajar Siswa ………... 315

A-9. Rekapitulasi Data Ujicoba Skala Kemandirian

Belajar Siswa Setelah Pembobotan ………... 317 A-10. Hasil Uji Validitas dan Reliabilitas Skala

Kemandirian Belajar Siswa ………... 320 B-1. Rencana Pelaksanaan Pembelajaran (Kelas Eksperimen) …. 322 B-2. Tes Kemampuan Awal Matematis (KAM) ….... 335 B-3. Tes Kemampuan Koneksi Matematis ... 342 B-4. Skala Sikap Kemandirian Belajar Siswa ... 352 B-5. Pedoman Wawancara dengan Siswa,

(12)

xii

Lampiran Judul Halaman

B-8. Angket Profil Siswa ... 415

B-9. Angket Perasaan Siswa ... 416 C-1. Nilai Kemampuan Koneksi

Matematis Siswa ... 417 C-2 Data Uji Interaksi ... 439 D-1. Hasil Analisis Data Kemampuan Awal Matematika

Siswa Kelas 8 SMP Negeri 12 Bandung ... 444 D-2. Data Hasil Penelitian: KAM, Pretes, Postes dan

N-Gain (Keseluruhan) dan Uji Normalitas KAM Kedua

Level Sekolah …… 447

E. Dokumentasi Penelitian …… 451

F. Surat Izin Penelitian dan Surat Keterangan Pelaksanaan

Penelitian ... 553

(13)

BAB I PENDAHULUAN

A. Latar Belakang Masalah

Menulis merupakan bagian yang integral dari pembelajaran matematika. Dengan tulisan dapat disampaikan hasil pikiran kita kepada orang lain, dan orang lainpun mengetahui apa yang sedang dikerjakan. Demikian juga halnya dengan jawaban soal matematika yang ditulis siswa. Dari jawaban tersebut, guru tahu tentang jawaban siswa, jalan pikiran siswa dan yang tidak kalah penting lagi, guru dapat melihat apakah siswa sudah memahami masalah atau belum.

Salah satu strategi untuk meningkatkan pemahaman siswa dalam memecahkan masalah adalah memposisikan sektor pembelajaran sebagai alat utama dalam peningkatan mutu pendidikan. Dalam pendidikan matematika, harus diakui penguasaan siswa terhadap konsep, fakta, prinsip maupun kemampuan matematika masih sangat rendah. O’Neil & Brown (1997) menyatakan bahwa dalam rangka membangun strategi untuk memecahkan masalah, metakognisi memegang peranan penting sebagai proses di mana seseorang berpikir tentang pikirannya dalam rangka membangun strategi tersebut. Sedangkan pendapat para ahli lain seperti Ridley, Schutz, Glanz & Weinstein (1992) mengenai kemampuan metakognisi adalah bahwa :

"Metacognitive skills include taking conscious control of learning,

planning and selecting strategies, monitoring the progress of learning,

correcting errors, analyzing the effectiveness of learning strategies, and

(14)

2

Pada prinsipnya jika dikaitkan dengan proses belajar, kemampuan metakognitif adalah kemampuan seseorang dalam mengontrol proses belajarnya, mulai dari tahap perencanaan, memilih strategi yang tepat sesuai masalah yang dihadapi, kemudian memonitor kemajuan dalam belajar dan secara bersamaan mengoreksi jika ada kesalahan yang terjadi selama memahami konsep, menganalisis keefektifan dari strategi yang dipilih dan bagian akhir sebagai bentuk upaya refleksi, biasanya seseorang yang memiliki kemampuan metakognitif yang baik selalu mengubah kebiasaan belajar dan juga strateginya jika diperlukan, karena mungkin hal itu tidak cocok lagi dengan keadaan tuntutan lingkungan dalam mengembangkan kemampuannya.

Nilai-nilai dari kebiasaan belajar siswa dan pentingnya mengontrol proses belajar matematika sangat ditekankan dalam lembar kerja siswa (LKS) yang dirancang dan difasilitasi. Hal ini diupayakan agar siswa dapat dilatih keterampilan metakognitifnya, yaitu siswa beraktivitas melalui kegiatan pemecahan masalah di kelas secara interaktif dalam bentuk diskusi, menjelaskan, mengajukan pertanyaan dan solusinya serta merefleksi dan menyimpulkan secara lisan maupun tulisan di LKS. Kegiatan seperti ini dapat melibatkan siswa sehingga siswa memiliki pengalaman yang bermakna dan apabila dilatih secara rutin akan terbentuk kemandirian belajar siswa baik di sekolah maupun di rumah.

(15)

3

Teachers of Mathematics (NCTM) yaitu (problem solving), penalaran dan bukti

(reasoning and proof), komunikasi (communication), representasi (representation) dan koneksi (connections). Proses pembelajaran matematika yang memfasilitasi pengembangan kemampuan ini dapat melatih siswa mengembangkan potensi berpikir secara maksimal. Sumarmo (2005) mengemukakan bahwa kemampuan-kemampuan di atas disebut dengan daya matematik (mathematical power) atau keterampilan matematika (doing math).

Dengan mengacu pada lima standar kemampuan NCTM di atas, maka Depdiknas menyusun tujuan pembelajaran matematika sebagai berikut (1) koneksi antar konsep dalam matematika dan penggunaannya dalam memecahkan masalah, (2) penalaran, (3) pemecahan masalah, (4) komunikasi dan representasi, dan (5) faktor afektif. Kemampuan-kemampuan ini merupakan kemampuan yang strategis yang menjadi tujuan pembelajaran matematika. Standar Kurikulum di China tahun 2006 untuk sekolah dasar dan menengah juga menekankan pentingnya koneksi matematik dalam bentuk aplikasi matematika, koneksi antara matematika dengan kehidupan nyata, dan penyinergian matematika dengan pelajaran lain (http://www.apecneted.org).

(16)

4

terpisah dari masalah yang terjadi dalam kehidupan, ada manfaatnya pada bidang lain selain matematika. Tanpa koneksi matematika maka siswa harus belajar dan mengingat terlalu banyak konsep dan prosedur matematika yang saling terpisah (NCTM, 2000: 275). Konsep-konsep dalam bilangan pecahan, presentase, rasio, dan perbandingan linear merupakan salah satu contoh topik-topik yang dapat dikait-kaitkan. Fisher (1980: 60) mengemukakan bahwa membuat koneksi antar konsep adalah suatu cara bagi kita untuk memahami sesuatu. Hal ini senada dengan yang dikemukakan Daniels dan Anghileri (1994: 91) bahwa bila kita mengerti sesuatu, hal itu berarti kita telah membuat suatu koneksi terkait dengan sesuatu itu. Pendapat Fisher dan Daniels menujukkan bahwa ada hubungan timbal balik antara koneksi dan daya ingat. Untuk bisa melakukan koneksi terlebih dahulu kita harus ingat permasalahannya, sedangkan untuk mengerti permasalahan, kita harus mampu membuat koneksi dengan topik-topik yang terkait dengan permasalahan. Berikut disajikan gambaran hasil temuan dalam pra-penelitian dimana siswa di minta untuk menyelesaikan soal berikut :

Gambar 1.1. Koneksi berbagai konsep

Selidiki apakah kedua garis (garis k dan garis l) berpotongan, jika ya tentukan titik potongnya !

Tentukan persamaan garis k dan garis l ?

k

l y = ... x + ...?

?

y = ... x + ... ? X

(17)

5

Sebagian besar siswa menjawab garis k dan garis l berpotongan, karena siswa dapat memperkirakan apabila kedua garis tersebut diperpanjang maka kedua garis tersebut berpotongan, namun cukup banyak juga siswa tidak bisa menentukan persamaan garis k dan garis l, akibatnya tidak dapat menentukan titik

potongnya. Hal ini mengindikasikan bahwa siswa belum memahami konsep (1) memaknai atau membuat sketsa grafik fungsi aljabar sederhana pada sistem

koordinat Cartesius, (2) menentukan gradien, persamaan dan grafik garis lurus, (3) menyelesaikan sistem persamaan linear dua variable. Lebih spesifik lagi diduga bahwa siswa belum terbiasa mengaitkan berbagai representasi konsep dan prosedur dalam gradien, persamaan dan grafik garis lurus, juga pengaruh dari karakteristik siswa, kemampuan awal yang dimikinya bahkan lebih luas lagi dimana siswa sekolah, apakah sekolah siswa di level biasa biasa saja atau sekolah di level baik atau bertaraf internasional.

(18)

6

spesifik dan sistematik, yang pada intinya adalah bagaimana cara memfasilitasi siswa belajar, pengalaman apa yang harus disediakan dan bagaimana cara mengorganisasi pengalaman tersebut agar diperoleh pengaruh yang berarti. Tidak dipungkiri bahwa apabila siswa mampu mengkaitkan pengalaman yang diperolehnya sendiri yaitu ide-ide matematika maka pemahaman matematikanya akan semakin dalam dan bertahan lama karena mereka mampu melihat keterkaitan antar topik dalam matematika, dengan konteks selain matematika, dan dengan pengalaman hidup sehari-hari (NCTM, 2000: 64).

Keterkaitan antar konsep atau prinsip dalam matematika memegang peranan yang sangat penting dalam mempelajari matematika. Dengan pengetahuan itu maka siswa memahami matematika secara lebih menyeluruh dan lebih mendalam. Selain itu dalam menghafal juga semakin sedikit akibatnya belajar matematika menjadi lebih mudah dan bermakna. Berikut adalah contoh koneksi antar konsep dalam matematika dengan mengaitkan antara konsep kesejajaran dua garis, kesamaaan gradien, dan menggambar grafik pada koordinat Cartesius. Soal yang diberikan kepada siswa kelas 2 SMP semester 1, misalnya:

Dari soal ini diharapkan pada siswa muncul beberapa konsep yang mendukung solusi dari permasalahan ini. Misalnya apa konsep gradien sebuah garis lurus, bagaimana kedudukan gradien dari dua garis sejajar, syarat dua garis

Selidiki apakah garis y = 2x + 1 sejajar dengan garis y = 2x – 4.

(19)

7

berpotongan dan kapan dua garis mempunyai himpunan penyelesaian ? Ilustrasi dari beberapa konsep di atas dapat dikaitkan seperti pada Gambar 1.2 berikut.

Gambar 1.2. Koneksi antar konsep

Berdasarkan Gambar 1.2 di atas, untuk melakukan pengkaitan sebagaimana ilustrasi di atas maka konsep-konsep dalam matematika terlihat menjadi satu kesatuan yang utuh untuk digunakan secara bersamaan dalam menyelesaikan masalah, sehingga pembelajarannya lebih bermakna (meaningfull learning).

Selanjutnya, Madnesen (1983) dan Sheal (1989) mengemukakan bahwa kebermaknaan interaksi belajar tergantung bagaimana belajar dalam kegiatan pembelajaran. Jika belajar hanya dengan membaca kebermaknaan bisa mencapai 10%, dari mendengar 20%, dari melihat 30%, mendengar dan melihat 50%, mengatakan-komunikasi mencapai 70%, dan belajar dengan melakukan dan mengkomunikasikan besarnya mencapai 90%, faktor keterbatasan sangat berpengaruh terhadap daya serap.

Dari uraian di atas implikasi terhadap pembelajaran adalah bahwa kegiatan pembelajaran identik dengan aktivitas siswa secara optimal. Kenyataan di

Konsep 1.

Gradien sebuah garis lurus.

Konsep 2.

Dua garis sejajar.

Konsep 3.

Dua garis perpotongan.

Konsep 4.

Himpunan Penyelesaian.

Konsep 5.

Koordinat Cartesius.

x y

1

2 y = 2x + 1

(20)

8

lapangan, karakteristik pembelajaran matematika saat ini lebih mengacu pada tujuan jangka pendek (lulus ujian sekolah, kabupaten/kota, atau nasional), materi kurang membumi, lebih fokus pada kemampuan prosedural, komunikasi satu arah, pengaturan ruang kelas monoton, low-order thinking skills, bergantung kepada buku paket, lebih dominan soal rutin, dan pertanyaan tingkat rendah (Shadiq dalam Kadir, 2010: 6). Pembelajaran matematika seperti ini dikenal dengan pembelajaran konvensional.

(21)

9

Menyadari pentingnya suatu strategi dan pendekatan pembelajaran untuk dapat mengembangkan potensi berpikir dalam kemampuan koneksi matematis siswa, melalui tahapan perencanaan, memilih strategi yang tepat, memonitor dan merefleksi maka mutlak diperlukan adanya pembelajaran matematika yang lebih banyak melibatkan siswa secara aktif dalam proses pembelajaran. Hal ini dapat terwujud melalui suatu bentuk pembelajaran yang dirancang sedemikian rupa sehingga mencerminkan keterlibatan siswa secara aktif dalam merespon kesadaran metakognisinya.

Selain faktor pembelajaran, ada faktor lain yang juga dapat diduga berkontribusi terhadap kemampuan matematis siswa dan terhadap sikap siswa dalam belajar matematika, yaitu kelompok kemampuan awal matematika (KAM) siswa, yang dapat digolongkan ke dalam kelompok baik, cukup, dan kurang. Seseorang yang memiliki KAM baik, rasa percaya dirinya tinggi sebaliknya seseorang yang memiliki KAM rendah kurang percaya diri, selalu bertanya pada temannya dalam menyelesaikan masalah. Selain KAM diduga berkontribusi juga suasana hati atau perasaan siswa dalam mengikuti pembelajaran di kelas maupun di luar kelas. Seorang siswa dengan hati atau perasaan yang nyaman berpotensi memberi hasil belajar yang baik, sedangkan seorang siswa dengan hati atau perasaan yang gelisah kecenderungan berdampak hasil belajar yang kurang.

(22)

10

pembelajaran tersebut, seperti : (1) respon dan partisipasi aktif dan (2) umpan balik yang bersifat korektif terhadap miskonsepsi (Arnawa, 2006). Siswa yang memiliki KAM kategori cukup atau kurang membutuhkan waktu dalam menerima ilmu baru dalam proses perkembangan metakognisinya.

Perkembangan dalam psikologi bidang pendidikan khususnya matematika berjalan sangat pesat, salah satunya adalah perkembangan konsep metakognisi (metacognition) yang pada intinya menggali pemikiran orang tentang berpikirnya ”thinking about thinking”.

(23)

11

masalah, juga hanya membaca buku-buku pelajaran kalau diperintah oleh gurunya.

Temuan dari hasil pra-penelitian, hasil observasi dan beberapa kajian teori mendalam serta hasil penelitian yang memfokuskan pada penggunaan pendekatan pembelajaran yang berpusat pada pikiran siswa mendorong peneliti untuk menggali secara komprehensif pendekatan pembelajaran yang dapat melatih ketrampilan berpikir siswa dengan memberikan beberapa pengalaman-pengalaman belajar. Seseorang yang terbiasa dengan aktivitas melatih ketrampilan berpikir dengan mengaitkan beberapa konsep berpengaruh terhadap kemampuan koneksi matematis. Pengalaman belajar yang memfokuskan pada bagaimana merencanakan pemecahan masalah, melaksanakan rencana dengan cara mandiri dan mengevaluasi hasil belajarnya memberi kesan yang positif bagi siswa apabila didekati dengan pendekatan pembelajaran yang bermakna. Berdasarkan analisis penulis, titik awal dalam pembelajaran matematika pada setiap penelitian belum memanfaatkan potensi siswa dalam pikirannya khususnya dalam upaya peningkatan kemampuan koneksi matematis dan kemandirian belajar siswa.

(24)

12

B. Rumusan Masalah

Berdasarkan latar belakang masalah, masalah utama yang dikaji dalam penelitian adalah pengaruh pembelajaran pendekatan metakognitif terhadap kemampuan koneksi matematis dan terbentuknya kemandirian belajar siswa, yang dibandingkan dengan pengaruh pembelajaran biasa yang menggunakan metode ceramah atau ekspositori terhadap kemampuan koneksi matematis dan kemandirian belajar siswa.

Masalah ini dapat disajikan lebih rinci menjadi beberapa submasalah, yaitu:

a. Apakah terdapat peningkatan kemampuan koneksi matematis dan kemandirian dalam belajar matematika siswa melalui pendekatan pembelajaran metakognitif baik secara grup maupun secara klasikal serta belajar melalui pendekatan pembelajaran biasa.

b. Apakah terdapat perbedaan kemampuan koneksi matematis siswa antara yang memperoleh pendekatan pembelajaran metakognitif grup (PPMG), pendekatan pembelajaran metakognitif klasikal (PPMK) dan pembelajaran biasa (PB), ditinjau dari keseluruhan siswa?

c. Apakah terdapat perbedaan kemampuan koneksi matematis siswa antara yang memperoleh pembelajaran PPMG, PPMK, dan pembelajaran PB, ditinjau dari level sekolah (tinggi dan sedang)?

(25)

13

e. Apakah terdapat interaksi antara pendekatan pembelajaran (PPMG,PPMK,PB) dengan peringkat sekolah (tinggi dan sedang) dalam peningkatan kemampuan koneksi matematis siswa?

f. Apakah terdapat interaksi antara pendekatan pembelajaran (PPMG,PPMK,PB) dengan kemampuan awal matematik (KAM) dalam peningkatan kemampuan koneksi matematis siswa?

g. Apakah terdapat perbedaan kemandirian belajar siswa antara yang memperoleh pendekatan pembelajaran metakognitif grup (PPMG), pendekatan pembelajaran metakognitif klasikal (PPMK) dan pembelajaran biasa (PB), ditinjau dari keseluruhan siswa?

h. Apakah terdapat perbedaan kemandirian belajar siswa antara yang memperoleh pembelajaran PPMG, PPMK dan pembelajaran PB, ditinjau dari level sekolah (tinggi dan sedang)?

i. Apakah terdapat perbedaan kemandirian belajar siswa antara yang memperoleh pembelajaran PPMG, PPMK, dan pembelajaran PB, ditinjau dari kemampuan awal matematika siswa (KAM baik, KAM cukup, dan KAM kurang)?

j. Apakah terdapat interaksi antara pendekatan pembelajaran dengan level sekolah dalam peningkatan kemandirian belajar siswa terhadap matematika? k. Apakah terdapat interaksi antara pendekatan pembelajaran dengan kemampuan

(26)

14

l. Bagaimana kualitas kemampuan koneksi matematis dan kemandirian dalam belajar siswa yang belajar melalui pendekatan metakognitif baik secara grup maupun klasikal dibandingkan dengan belajar melalui pembelajaran biasa? m. Bagaimana perasaan siswa terhadap pembelajaran dengan pendekatan

metakognitif?

C. Tujuan Penelitian

Berdasarkan rumusan masalah di atas, tujuan penelitian ini adalah:

a. Menelaah secara komprehensif peningkatan kemampuan koneksi matematis dan kemandirian belajar siswa yang belajar melalui pendekatan pembelajaran metakognitif grup (PPMG), pendekatan pembelajaran metakognitif klasikal (PPMK) dan pembelajaran konvensional atau pembelajaran biasa (PB).

b. Menelaah secara komprehensif perbedaan kemampuan koneksi matematis siswa antara yang memperoleh pendekatan pembelajaran dengan metakognitif grup (PPMG), pendekatan pembelajaran dengan metakognitif klasikal (PPMK) dan pembelajaran biasa (PB), ditinjau dari keseluruhan siswa.

c. Menelaah secara komprehensif perbedaan kemampuan koneksi matematis siswa antara yang memperoleh pembelajaran PPMG, pembelajaran PPMK dan pembelajaran PB, ditinjau dari level sekolah (tinggi dan sedang).

(27)

15

e. Menelaah secara komprehensif interaksi antara pendekatan pembelajaran (PPMG,PPMK,PB) dengan level sekolah (tinggi dan sedang) dalam peningkatan kemampuan koneksi matematis siswa.

f. Menelaah secara komprehensif interaksi antara pendekatan pembelajaran (PPMG,PPMK,PB) dengan kemampuan awal matematika (KAM) dalam peningkatan kemampuan koneksi matematis siswa.

g. Menelaah secara komprehensif perbedaan kemandirian belajar siswa dalam matematika antara yang memperoleh pembelajaran PPMG, PPMK dan pembelajaran PB, ditinjau dari keseluruhan siswa.

h. Menelaah secara komprehensif perbedaan kemandirian belajar siswa dalam matematika antara yang memperoleh pembelajaran PPMG, PPMK dan pembelajaran PB, ditinjau dari level sekolah (tinggi dan sedang),

i. Menelaah secara komprehensif perbedaan kemandirian belajar siswa dalam matematika antara yang memperoleh pembelajaran PPMG, PPMK dan pembelajaran PB, ditinjau dari kemampuan awal matematika (KAM baik, KAM cukup, dan KAM kurang).

j. Menelaah secara komprehensif interaksi antara pendekatan pembelajaran dan level sekolah dalam peningkatan kemandirian belajar matematika siswa.

k. Menelaah secara komprehensif interaksi antara pendekatan pembelajaran dengan kemampuan awal matematika dalam peningkatan kemandirian belajar siswa terhadap matematika.

(28)

16

D. Manfaat Penelitian

Penelitian ini diharapkan dapat bermanfaat bagi:

a. Siswa, karena pendekatan metakognitif, kemampuan dalam koneksi matematik siswa dan kemandirian belajar siswa membutuhkan suatu perencanakan, mengontrol dan refleksi diri yang menyediakan suatu pengalaman berkaitan dengan situasi kontekstual dalam dunia nyata, sehingga apabila siswa telah menyelesaikan studinya, mereka dapat menjadi expert dalam pemecahan masalah matematik.

b. Guru yang mengajar, mendapat pengalaman nyata untuk menerapkan pendekatan metakognitif untuk digunakan mengembangkan kemampuan koneksi matematis dan kemandirian belajar siswa.

c. Peneliti, merupakan pengalaman berharga dimana penelitian ini merupakan rujukan bagi langkanya teori mengenai pendekatan metakognitif dan/atau teori kemandirian belajar siswa dalam bidang matematika dan pendidikan matematika, kemampuan bermatematika dan latar belakang siswa, khususnya di Indonesia, sehingga membuka suatu wawasan penelitian bagi para ahli matematika untuk mengembangkannya.

(29)

17

E. Definisi Operasional Variabel

Dalam penelitian ini digunakan beberapa istilah. Karena hampir setiap istilah dapat mempunyai makna dan interpretasi yang berbeda-beda, maka diperlukan definisi operasional dari istilah yang digunakan dalam penelitian ini. 1. Koneksi matematis yang dimaksud merupakan koneksi (keterkaitan) antara

topik yang sedang dibahas dengan topik lainnya. Koneksi disini bisa antar topik matematika, dengan mata pelajaran lain atau dengan kehidupan sehari-hari dalam dunia nyata.

2. Kemampuan koneksi matematis yang dimaksud adalah kemampuan siswa dalam membuat hubungan antar konsep matematika (dalam hal ini persamaan garis lurus yang terdiri dari menentukan gradien, persaman dan grafik garis lurus dan sistem persaman linear dua variabel meliputi menyelesaikan sistem persaman linear dua variabel, membuat model matematika, dan menyelesaikan model matematika), antara pelajaran matematika dengan pelajaran lain atau dengan masalah kehidupan sehari-hari dalam dunia nyata.

(30)

18

tantangan; mencari dan memanfaatkan sumber belajar yang relevan; memilih dan menerapkan strategi belajar; mengevaluasi proses dan hasil belajar; dan keyakinan tentang dirinya sendiri.

4. Pembelajaran matematika dengan pendekatan metakognitif adalah penyajian pembelajaran yang menanamkan kepada siswa suatu proses bagaimana merancang (planning), memonitor (monitoring), serta mengevaluasi (evaluation) informasi atau pengetahuan yang dimiliki untuk kemudian dikembangkan menjadi tindakan (action) dalam menyelesaikan suatu masalah matematika. Penyajian pelajaran dalam tiga tahapan, yaitu : (1) diskusi awal; (2) siswa bekerja secara mandiri berlatih mengajukan dan menjawab pertanyaan metakognitifnya dalam menyelesaikan masalah matematis; dan (3) refleksi dan membuat simpulan atas apa yang dilakukan di kelas dengan menjawab pertanyaan.

5. Pertanyaan metakognitif adalah pertanyaan yang dapat diajukan oleh guru dalam upaya menemukan konsep matematika pada suatu permasalahan; memfokuskan pertanyaan tersebut kepada pemahaman masalah, pengembangan hubungan antara pengetahuan yang lalu dan sekarang, penggunaan strategi penyelesaian masalah yang tepat. Pertanyaan metakognitif yang dapat diajukan siswa adalah sebagai berikut:

a. Pertanyaan pemahaman (Comprehension Question); b. Pertanyaan koneksi (Connection Question);

(31)

19

(32)

BAB III

METODE PENELITIAN

A. Jenis dan Desain Penelitian

Penelitian ini dikategorikan sebagai penelitian kuasi-eksperimen karena penelitian ini dilakukan dalam setting sosial dan berasal dari suatu lingkungan yang telah ada yaitu siswa dalam kelas, dengan memberikan perlakuan di kelas eksperimen berupa pembelajaran dengan pendekatan metakognitif grup (PPMG) dan pembelajaran dengan pendekatan metakognitif klasikal (PPMK) kepada subjek penelitian untuk selanjutnya ingin mengetahui lebih jauh pengaruh perlakuan tersebut dan pembelajaran biasa (PB) di kelas kontrol. Di dalam kelompok kontrol ini sampel tidak diberlakukan khusus, hanya dibelajarkan dengan pembelajaran biasa (konvensional), waktu dan bahan ajar sama yang membedakannya hanya pada cara atau metodenya.

(33)

90

pengetahuan awal matematika siswa (baik, cukup, dan kurang). Desain penelitian ini menggunakan desain kelompok kontrol pretes-postes (atau tes awal dan tes akhir), sebagai berikut.

(Ruseffendi, 2005 : 50)

Keterangan:

A : Pemilihan sampel secara acak sekolah untuk tiap kelompok sekolah dan secara

acak kelas pada masing-masing kelompok sekolah

X1 : Perlakuan berupa pembelajaran dengan Pendekatan Metakognitif secara Grup (PPMG)

X2 : Perlakuan berupa pembelajaran dengan Pendekatan Metakognitif secara Klasikal (PPMK)

O : Tes awal dan tes akhir kemampuan koneksi matematis

Ketiga kelas sampel tersebut tidak dibentuk dengan cara menempatkan secara acak subjek-subjek penelitian ke dalam kelas-kelas sampel tersebut, melainkan menggunakan kelas-kelas yang ada. Pada disain ini, berarti pemilihan sampel dilakukan secara acak kelas (A). Ketiga kelas diberikan perlakukan berbeda, yakni PPMG (X1) di kelas eksperimen 1 (untuk sekolah SMPN 12 Bandung kelas VIII-C dan untuk SMPN 15 kelas VIII-A), dengan PPMK (X2) di kelas eksperimen 2 (untuk sekolah SMPN 12 Bandung kelas VIII-D dan untuk SMPN 15 kelas VIII-B), dan dengan PB (X3) di kelas kontrol (untuk sekolah SMPN 12 Bandung kelas VIII-E dan untuk SMPN 15 kelas VIII-C). Bahan ajar yang diberikan ketiga kelas sama, yang membedakannya terletak pada pendekatan atau sajiannya. Siswa ketiga kelas juga diberi tes kemampuan awal matematis (KAM) berguna untuk melihat kemampuan prasyarat siswa dan untuk mengelompokkan siswa dalam pembelajaran yang terlebih dahulu dikonsultasikan

(34)

91

untuk diskusikan dengan guru agar homogenitas antar kelompok dan heterogenitas di dalam kelompok tetap terpenuhi, karena guru kelas yang mengajar selama ini sudah mengetahui karakteristik masing-masing siswa dan punya banyak pengalaman. Selain itu, siswa di ketiga kelas juga diberikan angket kemandirian belajar.

(35)

92

Penelitian ini dilakukan di SMP Negeri kelas VIII semester 1 mulai bulan Juli sampai bulan Desember 2010, sementara studi pendahuluan dilakukan pada bulan Maret 2010 yang terdiri dari SMPN 12 Bandung dalam kategori cluster 1 (level tinggi), SMPN 15 Bandung cluster 2 (level sedang) berdasarkan lokasi, luas tanah, peringkat, sarana prasyarana dan input dari nilai maximum dan nilai minimum masuk.

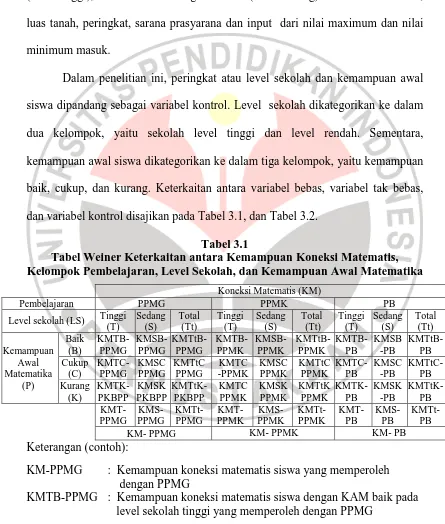
Dalam penelitian ini, peringkat atau level sekolah dan kemampuan awal siswa dipandang sebagai variabel kontrol. Level sekolah dikategorikan ke dalam dua kelompok, yaitu sekolah level tinggi dan level rendah. Sementara, kemampuan awal siswa dikategorikan ke dalam tiga kelompok, yaitu kemampuan baik, cukup, dan kurang. Keterkaitan antara variabel bebas, variabel tak bebas, dan variabel kontrol disajikan pada Tabel 3.1, dan Tabel 3.2.

Tabel 3.1

Tabel Weiner Keterkaitan antara Kemampuan Koneksi Matematis, Kelompok Pembelajaran, Level Sekolah, dan Kemampuan Awal Matematika

Koneksi Matematis (KM)

Pembelajaran PPMG PPMK PB

Level sekolah (LS) Tinggi (T)

KM-PPMG : Kemampuan koneksi matematis siswa yang memperoleh dengan PPMG

(36)

93

KMTtB-PKBPP : Kemampuan koneksi matematis siswa dengan KAM baik yang memperoleh dengan PPMG

KMT-PPMK : Kemampuan koneksi matematis siswa pada level sekolah tinggi yang memperoleh dengan PPMK

KMSB-PB : Kemampuan koneksi matematis siswa dengan KAM baik pada level sekolah sedang yang memperoleh dengan PB

KMTtK-PB : Kemampuan koneksi matematis siswa dengan KAM kurang yang memperoleh dengan PB

Tabel 3.2

Tabel Weiner Keterkaitan antara Kemandirian Belajar,

Kelompok Pembelajaran, Level Sekolah, dan Kemampuan Awal Matematika Kemandirian Belajar (KB)

Pembelajaran PPMG PPMK PB

Level sekolah (LS) Tinggi (T)

KB-PPMG : Kemampuan kemandirian belajar siswa yang memperoleh dengan PPMG

KBTB-PPMG : Kemampuan kemandirian belajar siswa dengan KAM baik pada level sekolah tinggi yang memperoleh dengan PPMG KBTtB-PKBPP : Kemampuan kemandirian belajar siswa dengan KAM baik

yang memperoleh dengan PPMG

KBT-PPMK : Kemampuan kemandirian belajar siswa pada level sekolah tinggi yang memperoleh dengan PPMK

KBSB-PB : Kemampuan kemandirian belajar siswa dengan KAM baik pada level sekolah sedang yang memperoleh dengan PB KBTtK-PB : Kemampuan kemandirian belajar siswa dengan KAM kurang

(37)

94

Desain penelitian kualitatif digunakan untuk mengeksplorasi lebih jauh keterlaksanaan pendekatan PPMG, PPMK dan PB dalam upaya peningkatan kemampuan koneksi matematis, dan pembentukan kemandirian belajar siswa SMP yang diteliti. Data diperoleh berdasarkan informasi dari guru dan siswa yang mendapat pendekatan PPMG dan PPMK dan beberapa tokoh masyarakat yang diwawancarai serta lembar observasi. Untuk menganalisis lebih dalam keterhubungan berbagai informasi yang diperoleh, maka dilakukan triangulasi. Triangulasi data dilakukan dengan mengaitkan berbagai informasi yang diperoleh, seperti hasil kerja siswa terhadap tes yang diberikan, observasi, dan wawancara dengan siswa, guru, dan tokoh masyarakat bertujuan untuk memperoleh kekurangan atau mengsinergikan kedalaman dalam menganalisis data.

B. Populasi dan Sampel Penelitian

(38)

95

pendekatan metakognitif yaitu merencanakan, mengontrol dan mengevaluasi pikiran. (3) Tingkat perkembangan kognitif siswa juga sudah pada awal fase formal operasional (>12 th) yaitu awal pembentukan (pemikiran belum terpola) dalam berpikir abstrak dan berpikir ilmiah yang sangat dibutuhkan sebagai pondasi ke depan, sehingga adanya relevansinya dengan karakteristik pendekatan metakognitif dan masih dapat ditingkatkan kemampuan koneksi matematis yang berkarakter berpikir tingkat tinggi serta aspek kemandirian belajar yang dikembangkan membutuhkan pengalaman-pengalaman matematik yang dapat mereka rasakan sendiri dan dapat digunakan di kelas, (4) selain itu mempertimbangkan pengalaman belajar siswa relatif belum banyak berpikir formal atau masih awal berpikir formal dibandingkan kelas di atasnya, sehingga diharapkan awal pembentukan kebiasaan belajar mereka berdasarkan karakteristik pendekatan metakognitif dalam mengembangkan kemandirian belajar siswa, dapat memberi dampak yang positif bagi siswa dalam pengaturan diri dan mengenali kesalahannya bagi perkembangannya.

(39)

96

karena mengingat pada level ini kemampuan akademik siswanya relatif heterogen, mulai dari yang terendah sampai dengan yang tertinggi dapat terwakili.

Dari masing-masing peringkat sekolah dipilih secara acak satu sekolah. Dengan kata lain, terdapat dua sekolah yang mewakili masing-masing peringkat sekolah. Selanjutnya, dari dua sekolah ini dipilih secara acak tiga kelas sebagai sampel penelitian. Dengan demikian, unit sampel dalam penelitian ini adalah kelas, bukan individu siswa untuk menggeneralisasi. Pemilihan kelas-kelas relatif homogen, artinya semua kelas dipandang mempunyai kemampuan setara atau ekuivalen.

Dalam hal ini, sampel penelitian dipilih SMP kelas VIII. Sedangkan pemilihan siswa SMP sebagai subyek penelitian ini didasarkan pada pertimbangan keragaman kemampuan akademik, tingkatan berpikir siswa, dan kondisi perkembangan fisik dan psikologis mereka yang masih berada pada awal berpikir formal atau transisi dari berpikir konkret ke berpikir abstrak sehingga mereka memiliki kesiapan dalam pembentukan pondasi berpikir abstrak dan kemandirian belajar mereka yang menjadi fokus kajian penelitian ini.

(40)

97

masing-masing tiga kelas (kelas eksperimen 1, kelas eksperimen 2, dan kelas kontrol) yang mewakili setiap peringkat sekolah.

Berdasarkan pertimbangan pengambilan sampel di atas, maka langkah-langkah penentuan sampel penelitian ini adalah sebagai berikut:

1. Mendaftar beberapa SMP Negeri yang memiliki sekolah cluster 1 (level tinggi), cluster 2 (level sedang) dan memiliki jumlah kelas lebih dari tiga. 2. Mengambil secara acak dengan teknik strata (stratified sampling) satu SMP

Negeri yang level tinggi dan satu SMP Negeri dengan level sedang 3. Mengambil secara acak tiga kelas VIII pada masing-masing SMP terpilih. 4. Menentukan secara acak kelas dengan teknik kelompok (cluster random

sampling) yang mendapat pembelajaran dengan pendekatan metakognitif grup

(kelas eksperimen 1), kelas yang mendapat pembelajaran dengan pendekatan metakognitif klasikal (kelas eksperimen 2), dan kelas yang mendapat pembelajaran konvensional (kelas kontrol).

5. Pada masing-masing kelompok siswa akan dilakukan pengelompokan kembali berdasarkan KAM yang dimilikinya, KAM siswa dikelompok menjadi tiga yaitu KAM baik, KAM cukup, dan KAM kurang. KAM siswa didasarkan pada tes yang diberikan di awal penelitian.

Menentukan pengkategorian KAM dengan menggunakan kriteria, kriteria pengelompokkan berdasarkan skor rata-rata (x) dan simpangan baku (sb) yaitu:

a. siswa kategori baik : total nilai KAM ≥

−

x + sb b. siswa kategori cukup :

−

x - sb ≤ total nilai KAM < − x + sb c. siswa kategori kurang : total nilai KAM <

(41)

98

Prosedur pengambilan subyek sampel di atas disajikan pada Gambar 3.1 berikut: Gambar 3.1. Prosedur Pengambilan Sampel

Acak Acak

Pemilihan kelompok sampel beserta ukurannya disajikan secara ringkas pada Tabel 3.3 berikut.

Tabel 3.3

Sampel Penelitian Berdasarkan Level Sekolah

Level Sekolah Sekolah Kelompok Subjek Ukuran Sampel

Tinggi

Siswa sampel sebanyak 262 ini sudah cukup representatif sesuai dengan pendapat (Ruseffendi, 2005:104) yang menyatakan bahwa banyaknya siswa untuk penelitian percobaan (eksperimen) paling sedikit 30 orang perkelompok.

SMP Negeri 12 Bandung yang dipilih secara acak memiliki delapan kelas VIII selanjutnya dipilih secara acak kelas sebanyak tiga kelas dengan jumlah

(42)

99

siswa 42 orang (kelas C), 42 orang (kelas D), dan 42 orang (kelas VIII-E) dan SMP negeri 15 Bandung yang dipilih secara acak memiliki tujuh kelas VIII selanjutnya dipilih secara acak kelas sebanyak tiga kelas terdiri dari 44 siswa (kelas VIII-A), 45 siswa (kelas VIII-B), dan 46 siswa (kelas VIII-C). Hasil uji normalitas data (uji Kolmogorov-Smirnov-Z) menunjukkan bahwa data kemampuan awal matematika siswa pada ketiga kelas ini berdistribusi normal sebagaimana dapat dilihat pada Tabel 3.4. Hasil lengkap uji ini dapat dilihat pada lampiran D-1.

Tabel 3.4

Uji Normalitas Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 12 Bandung

Kelas n Rata-rata Simpangan Baku Sig. Keterangan

VIII-C 42 21,857 4,337 0,11 Normal

VIII-D 42 21,238 4,853 0,20 Normal

VIII-E 42 22,048 5,070 0,18 Normal

Tabel 3.4. menunjukkan bahwa nilai probabilitas atau nilai significance (sig.) ketiga kelas lebih besar dari ≥ = 0,05. Ini berarti data kemampuan awal matematika siswa ketiga kelas berdistribusi normal. Sementara itu, hasil uji homogenitas varians data kemampuan awal matematika siswa ketiga kelas dengan uji levene menunjukkan bahwa nilai significance (sig.) yaitu 0,54 lebih besar dari

≥ = 0,05. Ini berarti varians data ketiga kelas adalah homogen sebagaimana dapat dilihat pada Tabel 3.5. Hasil lengkap uji ini dapat dilihat pada lampiran D-1.

Tabel 3.5

Uji Homogenitas Varians Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 12 Bandung

Levene Statistic dk 1 dk 2 Sig.

(43)

100

Selanjutnya, hasil uji ANOVA satu jalur menunjukkan bahwa nilai significance (sig.) adalah 0,86 lebih besar dari ≥ = 0,05. Ini berarti tidak ada perbedaan secara signifikan rata-rata kemampuan awal matematika siswa dari ketiga kelas VIII tersebut pada taraf signifikansi ≥ = 0,05 sebagaimana ditunjukkan oleh Tabel 3.6. Hasil lengkap uji ini dapat dilihat pada Lampiran D-1.

Tabel 3.6

Uji Kesetaraan Data Kemampuan Awal Matematika Siswa Ketiga Kelas VIII SMPN 12 Bandung

Sum of

Squares df Mean Square F Sig.

Between Groups 6,492 2 3,246 0,155 0,86

Within Groups 2571,167 123 20,904

Total 2577,659 125

Tabel 3.6 menunjukkan bahwa nilai significance (sig.) adalah 0,86 lebih besar dari 0,025. Hal ini berarti bahwa tidak terdapat perbedaan rata-rata kemampuan awal matematika siswa ketiga kelas VIII SMPN 12 Bandung pada taraf signifikansi ≥ = 0,05. Oleh karena itu, dapat diambil secara acak ketiga kelas ini yaitu kelas VIII-C dijadikan sebagai kelas eksperimen yang mendapat pembelajaran dengan pendekatan metakognitif grup (PPMG), kelas VIII-D sebagai kelas eksperimen yang mendapat pembelajaran dengan pendekatan metakognitif klasikal (PPMK) dan kelas VIII-E sebagai kelas kontrol (PB) yang mendapat pembelajaran dengan pendekatan biasa.

(44)

101

ini berdistribusi normal sebagaimana dapat dilihat pada Tabel 3.7. Hasil lengkap uji ini dapat dilihat pada Lampiran D-2.

Tabel 3.7

Uji Normalitas Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 15 Bandung

Kelas n Rata-rata Simpangan Baku Sig. Keterangan

VIII-A 45 22,000 3,405 0,200 Normal

VIII-B 45 20,600 4,287 0,200 Normal

VIII-C 46 20,457 3,053 0,200 Normal

Tabel 3.7 menunjukkan bahwa data kemampuan awal matematika siswa ketiga kelas berdistribusi normal pada taraf signifikansi ≥ = 0,05. Sementara itu, hasil uji homogenitas varians data kemampuan awal matematika siswa ketiga kelas dengan uji Levene menunjukkan bahwa varians data ketiga kelas adalah homogen sebagaimana dapat dilihat pada Tabel 3.8. Hasil lengkap uji ini dapat dilihat pada Lampiran D-3.

Tabel 3.8

Uji Homogenitas Varians Data Kemampuan Awal Matematika Siswa Kelas VIII SMPN 15 Bandung

Levene

Statistic dk 1 dk 2 Sig.

1.908 2 133 0,152

(45)

102

Tabel 3.9

Uji Kesetaraan Data Kemampuan Awal Matematika Siswa Ketiga Kelas VIII SMPN 15 Bandung

Sum of

Squares df Mean Square F Sig.

Between Groups 65,758 2 32,879 2,516 0,085

Within Groups 1738,213 133 13,069

Total 1803,971 135

Tabel 3.9 menunjukkan bahwa nilai significance sig. = 0,085 lebih besar dari 0,025. Hal ini berarti bahwa tidak terdapat perbedaan rata-rata kemampuan awal matematika siswa ketiga kelas VIII SMPN 15 Bandung pada taraf signifikansi ≥ = 0,05. Oleh karena itu, dapat dijadikan sampel penelitian ketiga kelas yang diambil secara acak kelas, kelas VIII-A sebagai kelas dengan pembelajaran PPMG, kelas VIII-B sebagai kelas dengan pembelajaran PPMK, dan kelas VIII-C sebagai kelas dengan pembelajaran PB.

(46)

103

Tabel 3.10

Uji Normalitas Data KAM Siswa Kedua Level Sekolah Berdasarkan Tiga Pendekatan Pembelajaran Level

Sekolah Statistik

Pendekatan Gabungan

(PPMG+PPMK+PB)

PPMG PPMK PB

Tinggi

N 42 42 42 126

KS-Z 0,123 0,110 0,115 0,114

Sig. 0,114 0,200 0,183 0,000

H0 Diterima Diterima Diterima Ditolak

Sedang

N 45 45 46 136

KS-Z 0,100 0,094 0,89 0,085

Sig. 0,200 0,200 0,200 0,018

H0 Diterima Diterima Diterima Ditolak

Dilanjutkan dengan uji non parametric Tests yaitu Uji Mann-Whitney U digunakan untuk membandingkan dua sampel independen dengan skala ordinal atau skala interval tetapi data tidak berdistribusi normal. Sebagaimana hasil uji Mann-Whitney U yang ditampilkan pada Tabel 3.11. Hasil lengkap uji ini dapat dilihat pada Lampiran D3.

Tabel 3.11

Uji Perbedaan Data Kemampuan Awal Matematika Siswa Berdasarkan Level Sekolah

Skor KAM LevSek

Mann-Whitney U 7050,500

Wilcoxon W 16366,500

Z -2,484

Asymp. Sig. (2-tailed) 0,013

(47)

104

kemampuan awal matematika siswa sekolah level tinggi sebesar 22,103 lebih besar dari pada rata-rata pengetahuan awal matematika siswa sekolah level sedang sebesar 21,259 dengan skor total 40. Perbedaan rata-rata ini disamping akibat dari level sekolah diduga kesiapan dan keseriusan siswa dalam menjawab soal tes KAM tersebut juga pengetahuan awal siswa terhadap materi relasi dan fungsi yang di tes-kan.

Di samping melibatkan siswa kelas VIII pada kedua sekolah SMPN 12 Bandung dan SMPN 15 Bandung, juga dilibatkan empat orang guru matematika dari kedua sekolah tersebut sebagai observer dan lima orang ahli pendidikan matematika sebagai validator perangkat pembelajaran dan instrumen yang digunakan dalam penelitian ini.

C. Pengembangan Instrumen dan Teknik Pengumpulan Data

(48)

105

1. Instrumen Tes Kemampuan Awal Matematika (KAM)

Kemampuan awal matematika adalah berupa pengetahuan yang dimiliki siswa dan dibawa ke dalam proses belajar sebelum perlakuan pembelajaran dalam penelitian ini berlangsung. Tes KAM diperuntukan kepada seluruh kelas VIII di level sekolah tinggi dan level sekolah sedang, dengan tujuan melihat kesetaraan atau ekuivalensi sampel. Hasil KAM digunakan untuk mengetahui pengetahuan siswa sebelum pembelajaran berlangsung, pengelompokan siswa, dan untuk menjawab terkait dengan rumusan masalah yang telah ditetapkan. KAM siswa diukur dengan menggunakan seperangkat soal tes yang diadobsi dari soal-soal latihan setiap pokok bahasan yang ada pada buku-buku pelajaran matematika SMP kelas VIII semester 1 dan sesuai dengan Kurikulum Tingkat Satuan Pendidikan (KTSP).

(49)

106

KTSP. Banyaknya tes KAM terdiri 20 soal benbentuk objektif dengan empat pilihan dan dua soal berbentuk uraian yang mencakup materi sesuai dengan silabus matematika SMP kelas VIII awal semester 3 yang terkait dengan topik yang diajarkan yaitu persamaan garis lurus dan SPLDV, yaitu :

1. Faktorisasi Suku Aljabar : mengelompokkan suku-suku sejenis dari suatu suku banyak, menyederhanakan suku banyak, menentukan hasil kali suatu bilangan dengan suku dua, menentukan hasil kali suku satu dengan suku dua dan menentukan hasil kali suku dua dengan suku dua dan menentukan perpangkatan suku dua.

2. Relasi dan Fungsi : menjelaskan dan menyatakan masalah sehari-hari yang berkaitan dengan fungsi, menyatakan suatu fungsi yang terkait dengan kejadian sehari-hari dan menggambar grafik fungsi dalam koordinat Cartesius.

(50)

107

Sebelum tes digunakan dalam penelitian, terlebih dahulu dilakukan uji validitas untuk melihat validitas isi dan validitas muka. Uji validitas isi dan validitas muka dilakukan oleh para penimbang yang dianggap ahli dan mempunyai pengalaman mengajar dalam bidang pendidikan matematika. Untuk mengukur validitas isi, dilakukan pertimbangan berdasarkan pada kesesuaian soal dengan kriteria aspek-aspek KAM, kesesuaian soal dengan materi ajar kelas VIII, dan kesesuaian tingkat kesukaran untuk siswa kelas tersebut. Untuk mengukur validitas muka, pertimbangan dilakukan berdasarkan pada kejelasan soal tes dari segi bahasa dan redaksi, sajian, serta akurasi gambar atau ilustrasi.

Uji validitas isi dan validitas muka dilakukan oleh empat orang penimbang yang berlatar belakang pendidikan S2 pendidikan matematika (sedang menempuh jenjang pendidikan S3) dan satu orang penimbang yang berlatar belakang pendidikan S2 pendidikan matematika. Kelima orang penimbang tersebut diminta untuk memberikan pertimbangannya terhadap soal KAM. Lembar pertimbangan KAM secara lengkap disajikan pada Lampiran A-1. Selanjutnya berdasarkan pertimbangan para validator ada beberapa revisi soal KAM. Revisi KAM oleh validator disajikan berikut:

Perbaikan butir-butir soal berdasarkan komentar atau saran perbaikan para penilai, disajikan sebagai berikut.

Soal 1 (Semula)

Secara umum, relasi diartikan sebagai .... a. hubungan beberapa himpunan.

(51)

108

d. pemetaan.

Para penilai menyarankan untuk mengganti kalimat “Secara umum, relasi diartikan sebagai...” dengan “apa yang dimaksud dengan relasi...”. Hal ini akan memberikan kejelasan bagi siswa. Berikut adalah rumusan soal setelah diperbaiki. Soal 1 (Setelah diperbaiki)

Apa yang dimaksud dengan relasi.... a. hubungan beberapa himpunan.

b. hubungan antara anggota satu himpunan dengan anggota himpunan lain. c. fungsi.

d. pemetaan. Soal 4 (Semula)

Perhatikan diagram-diagram panah berikut.

Para penilai menyarankan untuk mengganti kalimat “Pada diagram di atas...” dengan “Pada diagram panah di atas...”. Hal ini akan memberikan kejelasan bagi siswa. Berikut adalah rumusan soal setelah diperbaiki.

Perhatikan diagram-diagram panah berikut.

(52)

109

Pada diagram panah di atas, yang bukan merupakan fungsi adalah ....

a. (i) dan (ii) b. (i) dan (iii) c. (ii) dan (iii) d. (iii) dan (iv) Soal 10 (Semula)

Fungsi f didefinisikan oleh f(x) = 2x2 – x + 1 dengan domain {–1, 0, 1}. Daerah hasil fungsi tersebut adalah ....

a. {4, -1, 2} b. {–4, –1, 2} c. {4, 1, –2} d. {–4, 1, 2} Para penilai menyarankan untuk mengecek kembali jawaban. Berikut adalah rumusan soal setelah diperbaiki.

Soal 10 (Setelah diperbaiki)

Fungsi f didefinisikan oleh f(x) = 2x2 – x + 1 dengan domain {–1, 0, 1}. Daerah hasil fungsi tersebut adalah ....

(53)

110

Soal 11 (Semula)

Diketahui f : x → –2x + 9. Jika p → 15, nilai p adalah .... a. – 3 b. – 2 c. 2 d. 3

Para penilai menyarankan untuk merubah format penyajian dari “Diketahui f : x → –2x + 9. Jika p → 15, nilai p adalah...” menjadi “Diketahui f (x) = –2x + 9.

Jika f (x) = 15, nilai x adalah ....Berikut adalah rumusan soal setelah diperbaiki. Soal 11 (Setelah diperbaiki)

Diketahui f (x) = –2x + 9. Jika f (x) = 15, nilai x adalah .... a. – 3 b. – 2 c. 2 d. 3

Soal 20 (Semula)

Perhatikan gambar di bawah ini !

(x-3) cm x cm (x+5) cm x cm

Diketahui persegi panjang dan persegi di atas mempunyai luas yang sama. Tulislah persamaan dalam x dan selesaikanlah! kemudian tentukan keliling masing-masing gambar di atas?

Para penilai menyarankan untuk format pengetikan x dan cm dengan font atau huruf italic hal ini berdasarkan aturan bahwa variabel harus di ketik miring dan perubahan aspek kalimat dan format penyajian. Berikut adalah rumusan soal setelah diperbaiki.

(54)

111

Soal 21 (Setelah diperbaiki) Perhatikan gambar di bawah ini !

(x-3) cm x cm (x+5) cm x cm

Gambar persegi panjang dan persegi di atas mempunyai luas yang sama. Tulislah persamaan luas dua bangun tersebut dalam x dan selesaikanlah! Kemudian tentukan keliling masing-masing gambar di atas?

Hasil pertimbangan mengenai validitas muka dan validitas isi KAM secara lengkap disajikan pada Lampiran A-2.

Hasil pertimbangan terhadap validitas muka dianalisis dengan menggunakan statistic Q-Cochran yang bertujuan untuk mengetahui keseragaman para penimbang terhadap tes KAM ditinjau dari segi bahasa dan redaksi, sajian, serta akurasi gambar atau ilustrasi. Hasil dianalisis dengan menggunakan statistic Q-Cochran disajikan pada Tabel 3.12 berikut:

Tabel 3.12.

Analisis Statistik ANOVAValidasi Muka Sum of

Squares df Mean Square Cochran's Q Sig

Between People 0,364 21 0,017

Within People Between Items 0,145 4 0,036 8,000 0,09

Residual 1,455 84 0,017

Total 1,600 88 0,018

Total 1,964 109 0,018

(55)

112

Dari hasil pengolahan data berdasarkan pertimbangan para validator diperoleh asymp. Sig. = 0,09 atau probabilitas lebih besar dari 0,05. Jadi pada taraf signifikansi ≥ = 5% dapat disimpulkan bahwa para penimbang melakukan pertimbangan yang seragam terhadap tiap butir tes KAM dari segi validitas muka mencakup aspek (1) kejelasan dari segi bahasa/redaksional yang digunakan dan (2) kepatutan/kepantasan/kemenarikan dari penampilan sajian instrumen.

Hasil pertimbangan validitas isi juga dianalisis dengan menggunakan statistic Q-Cochran yang bertujuan untuk mengetahui keseragaman para penimbang terhadap tes KAM ditinjau dari kesesuaian dari materi pokok yang diberikan sesuai kisi-kisi instrumen, tujuan yang ingin dicapai, aspek kemampuan yang diukur, indikator kemampuan yang diukur dan tingkat kesukaran untuk siswa SMP kelas VIII semester 3. Hasil pertimbangan validitas isi dianalisis dengan menggunakan statistic Q-Cochran disajikan pada Tabel 3.13 berikut:

Tabel 3.13.

Analisis Statistik ANOVAValidasi Isi

Sum of Squares df Mean Square Cochran's Q Sig

Between People 3,755 21 0,179

Within People Between Items 0,055 4 0,014 1,714 0,79

Residual 2,745 84 0,033

Total 2,800 88 0,032

Total 6,555 109 0,060

(56)

113

mencakup (1) kesesuaian butir soal dengan aspek kemampuan awal matematis yang diukur (kisi-kisi) dan (2) kesesuaian dengan tingkat perkembangan atau kemampuan siswa dalam memahami kalimat.

Selanjutnya perangkat tes KAM diujicobakan secara terbatas pada enam orang siswa (2 orang siswa berkemampuan baik, 2 orang siswa berkemampuan cukup, dan 2 orang siswa berkemampuan kurang) di luar sampel penelitian tetapi telah menerima (yaitu kelas IX) materi yang diteskan. Ujicoba terbatas ini dilakukan untuk mengetahui tingkat keterbacaan bahasa sekaligus memperoleh gambaran apakah butir-butir soal yang akan diteskan dapat dipahami dengan baik oleh siswa. Dari hasil ujicoba terbatas diperoleh gambaran bahwa semua soal dapat dipahami dengan baik oleh siswa.

Setelah itu soal KAM diujicobakan di SMP Negeri 29 Bandung kelas VIII-B. Hasil ujicoba validitas tes dianalisis menggunakan Pearson Correlation dengan kriteria jika nilai significance atau sig (2-tailed) lebih kecil dari α_{= 0,05}

maka instrumen butir tes valid, hasil lengkap disajikan pada Tabel 3.14 berikut:

Tabel 3.14. Hasil Analisis Validitas

No. Soal Statistik Total Keterangan

KAM-1 Pearson Correlation .839(**) Valid

Sig. (2-tailed) .000

N 35

(57)

114

N 35

KAM-12 Pearson Correlation .215 Tidak Valid

N 35

KAM-16 Pearson Correlation .102 Tidak Valid

N 35