Informasi Dokumen
- Penulis:
- Antonius Setyo Hartanto
- Pengajar:
- Ibu Lusia Krismiyati Budiasih, S.Si., M.Si.
- Sekolah: Universitas Sanata Dharma
- Mata Pelajaran: Matematika
- Topik: Penyelesaian Numerik Persamaan Laplace dan Persamaan Poisson dalam Pelat Persegi Panjang dan Pelat Cakram dengan Metode Beda-Hingga
- Tipe: skripsi
- Tahun: 2008
- Kota: Yogyakarta
Ringkasan Dokumen
I. Pendahuluan
Pendahuluan dalam skripsi ini menjelaskan latar belakang permasalahan yang dihadapi dalam penyelesaian persamaan diferensial parsial, khususnya persamaan Laplace dan Poisson. Penulis mengemukakan pentingnya pemahaman mengenai kedua persamaan ini dalam konteks aliran panas dua dimensi dalam pelat persegi panjang dan pelat cakram. Selain itu, penulis juga merumuskan masalah, menetapkan tujuan, dan menjelaskan manfaat dari penelitian ini. Dengan demikian, pembaca diharapkan dapat memahami konteks dan signifikansi penelitian yang dilakukan.
1.1 Latar Belakang Masalah
Latar belakang permasalahan mencakup penjelasan tentang persamaan diferensial parsial yang sering muncul dalam masalah fisika. Penulis memberikan ilustrasi tentang bagaimana persamaan Laplace dan Poisson digunakan untuk menganalisis perambatan panas dalam pelat yang dipanaskan. Dengan menjelaskan konteks ini, penulis menekankan pentingnya metode numerik dalam menyelesaikan masalah yang tidak dapat dipecahkan secara analitik.
1.2 Tujuan Masalah
Tujuan penelitian ini adalah untuk memberikan pemahaman tentang cara penyelesaian persamaan Laplace dan Poisson secara numerik dengan metode Beda-Hingga. Penulis bertujuan untuk menunjukkan langkah-langkah yang diperlukan dalam penerapan metode ini, serta memberikan contoh aplikasi yang relevan dalam konteks aliran panas dua dimensi. Hal ini diharapkan dapat membantu mahasiswa dan peneliti dalam memahami teknik penyelesaian numerik.
II. Persamaan Diferensial Parsial dan Metode Gauss-Seidel
Bagian ini membahas tentang definisi dan karakteristik dari persamaan diferensial parsial, serta jenis-jenisnya. Penulis menjelaskan bahwa persamaan Laplace dan Poisson merupakan contoh dari persamaan diferensial parsial linear yang sering digunakan dalam masalah fisika. Selain itu, penulis juga membahas metode iterasi Gauss-Seidel sebagai salah satu teknik untuk menyelesaikan sistem persamaan linear yang muncul dari metode Beda-Hingga.
2.1 Persamaan Diferensial Parsial
Persamaan diferensial parsial (PDP) adalah persamaan yang melibatkan turunan parsial dari fungsi yang tidak diketahui. Dalam konteks ini, penulis menjelaskan bagaimana PDP digunakan untuk memodelkan berbagai fenomena fisik, seperti aliran panas dan difusi. Penjelasan ini penting untuk memberikan dasar teoritis yang kuat bagi pembaca mengenai konsep yang akan dibahas lebih lanjut.
2.2 Metode Iterasi Gauss-Seidel
Metode Gauss-Seidel adalah teknik numerik yang digunakan untuk menyelesaikan sistem persamaan linear. Penulis menjelaskan langkah-langkah dalam menerapkan metode ini, serta kondisi-kondisi yang diperlukan agar metode ini konvergen. Pemahaman tentang metode ini sangat penting bagi mahasiswa yang ingin menerapkan teknik numerik dalam penyelesaian masalah matematis.
III. Penyelesaian Persamaan Laplace dan Persamaan Poisson Secara Numerik
Bagian ini fokus pada penerapan metode Beda-Hingga untuk menyelesaikan persamaan Laplace dan Poisson secara numerik. Penulis menjelaskan langkah-langkah yang harus diambil untuk membangun grid, menerapkan pendekatan Beda-Hingga, dan menyelesaikan sistem persamaan linear yang dihasilkan. Contoh aplikasi yang diberikan membantu pembaca untuk memahami bagaimana teori diterapkan dalam praktik.
3.1 Metode Beda-Hingga
Metode Beda-Hingga adalah teknik numerik yang digunakan untuk mendiskretisasi persamaan diferensial. Penulis menjelaskan proses pembuatan grid dan bagaimana nilai-nilai pada grid digunakan untuk mendekati solusi dari persamaan diferensial. Penjelasan ini sangat relevan bagi mahasiswa yang belajar tentang analisis numerik dan aplikasinya dalam rekayasa.
3.2 Penyelesaian Numerik untuk Persamaan Laplace
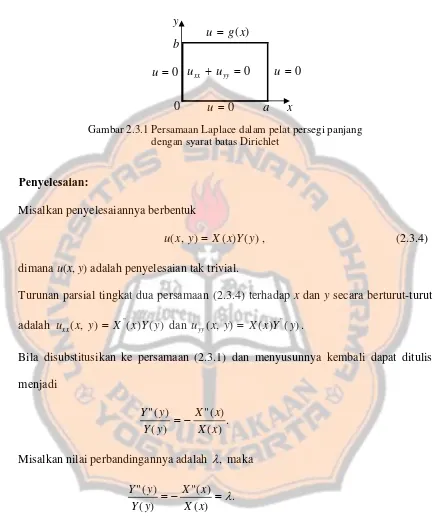
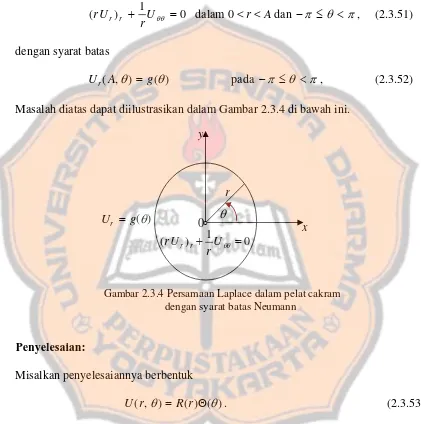
Penyelesaian numerik untuk persamaan Laplace dilakukan dengan menerapkan metode Beda-Hingga pada pelat persegi panjang dan cakram. Penulis memberikan detail tentang bagaimana syarat batas diterapkan dan bagaimana solusi dihitung. Contoh yang diberikan bertujuan untuk memfasilitasi pemahaman praktis tentang penerapan metode ini.
IV. Penutup
Bagian penutup menyajikan kesimpulan dari penelitian ini, menegaskan kembali pentingnya metode numerik dalam menyelesaikan persamaan Laplace dan Poisson. Penulis juga memberikan saran untuk penelitian lebih lanjut, yang dapat mencakup eksplorasi metode numerik lainnya atau aplikasi dalam konteks yang berbeda. Hal ini diharapkan dapat memotivasi pembaca untuk terus belajar dan menerapkan pengetahuan yang telah diperoleh.
4.1 Kesimpulan
Kesimpulan merangkum hasil penelitian dan menunjukkan bahwa metode Beda-Hingga adalah alat yang efektif untuk menyelesaikan persamaan Laplace dan Poisson. Penulis menekankan bahwa pemahaman yang baik tentang teori dan teknik numerik sangat penting untuk aplikasi di dunia nyata.
4.2 Saran
Penulis memberikan saran untuk penelitian lebih lanjut, termasuk eksplorasi metode numerik lain yang dapat digunakan untuk masalah yang lebih kompleks. Saran ini bertujuan untuk mendorong pengembangan pengetahuan dan keterampilan dalam analisis numerik.