BAB I PENDAHULUAN
A. LATAR BELAKANG
Ilmu termodinamika merupakan ilmu yang berupaya untuk memprediksi perpindahan energi yang mungkin terjadi antara material atau benda sebagai akibat dari perbedaan suhu (Holman, 2010 : 1). Ilmu termodinamika mengajarkan bahwa transfer energi yang dimaksud didefinisikan sebagai panas. Ilmu perpindahan panas tidak hanya menjelaskan bagaimana energi panas dapat ditransfer, akan tetapi juga untuk memprediksi tingkat dimana pertukaran berlangsung di bawah kondisi tertentu. Menurut jenis perambatannya, perpindahan panas digolongkan menjadi tiga yaitu perpindahan panas secara konduksi, konveksi dan radiasi.
2
energi listrik. Bahan bakar yang diubah menjadi energi panas dalam bentuk uap bertekanan dan bersuhu tinggi, energi panas tersebut diubah menjadi energi mekanik dalam bentuk putaran, dari energi panas yang diubah menjadi energi mekanik tersebut dihasilkan energi listrik.
Pada kebanyakan kasus, untuk menggambarkan keadaan fisis dari perpindahan panas digunakan model matematika yang disebut dengan persamaan diferensial dimana besaran-besarannya berubah terhadap ruang dan waktu. Pada salah satu kasus persamaan untuk perpindahan panas disebut dengan persamaan panas. Definisi dari persamaan diferensial adalah suatu persamaan yang memuat turunan dari satu atau lebih variabel terikat (Dependent Variable) terhadap satu atau lebih dari variabel bebas (Independent Variable). (Zill, Wright, & Cullen, 2012 : 2) Persamaan diferensial digolongkan menjadi dua yaitu persamaan diferensial biasa dan persamaan diferensial parsial. Untuk menyelesaikan persamaan diferensial dapat dilakukan secara analitik maupun secara numerik. Dalam menyelesaikan persamaan panas secara analitik terdapat 3 jenis syarat batas yaitu syarat batas Dirichlet, Neumann dan Robin. Ketiga syarat batas tersebut masing-masing memiliki kondisi suhu di titik awal dan titik akhir yang berbeda.
penelitian tersebut, penyelesaian analitik dari persamaan panas dimensi satu yang telah diteliti akan dihampiri menggunakan metode numerik. Persamaan dimensi satu menarik untuk menjadi bahan yang akan diteliti karena persamaan panas dimensi satu merupakan persamaan panas dengan dimensi paling dasar, sebelum meneliti lebih lanjut ke persamaan panas dengan dimensi lebih tinggi.
Metode numerik adalah teknik yang digunakan untuk memformulasikan persoalan matematika sehingga dapat dipecahkan dengan operasi perhitungan atau aritmetika biasa (tambah, kurang, kali, dan bagi) (Munir, Rinaldi, 2010 : 5). Terdapat beberapa metode numerik untuk menyelesaikan persamaan panas antara lain Finite Difference Methods, Finite Element Methods, dan Finite Volume Methods (Metode Volume Hingga). Secara garis besar metode volume hingga menggunakan bentuk integral dari persamaan. Penyelesaian yang diperoleh dibagi kedalam sejumlah kontrol volume yang berhingga, dan persamaan umum yang telah terintegral terhadap kontrol volume dan waktu akan diaplikasikan pada tiap kontrol volume. Dalam proses penyelesaian persamaan panas dimensi satu dengan metode volume hingga terdapat beberapa skema yang dapat digunakan antara lain UDS (Upwind Difference Scheme), CDS (Central Difference Scheme), LUDS (Linier Upwind Difference Scheme), QUICK (Quadratic Upwind Difference Scheme).
4
mengkaji tentang pola sebaran air panas dari spray pond dengan metode volume hingga untuk mengetahui suhu air yang berada pada spray pond apakah dapat dialirkan ke sungai tanpa mengganggu biota sungai. Hasil dari penelitian tersebut adalah dibutuhkan tekanan air yang tinggi agar proses penurunan suhu air panas yang dikeluarkan dari spray pond semakin banyak dan penyebaran air semakin luas. Selain itu peneliti lain yang membahas tentang metode volume hingga adalah Setyo Budi Utami (2008) yang membahas bagaimana penyelesaian persamaan matematika dari distribusi panas dengan metode volume hingga dan diperoleh perubahan konsentrasi distribusi aliran panas dipengaruhi oleh kecepatan, panjang penampang dan lebar penampang. Penambahan rata-rata kecepatan menyebabkan semakin pendek daerah penyebaran panas serta penambahan lebar penampang dan panjang penampang menyebabkan adanya kenaikan konsentrasi penyebaran panas. Berdasarkan latar belakang dan penelitian-penelitian yang telah dilakukan, pada Tugas Akhir Skripsi ini penulis mengambil judul “PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN METODE VOLUME HINGGA”.
B. IDENTIFIKASI MASALAH
Dari penjabaran latar belakang, dapat diidentifikasi beberapa masalah sebagai berikut:
2. Persamaan matematis dari masalah fisika mayoritas berupa persamaan diferensial parsial.
3. Penyelesaian persamaan diferensial parsial dapat diperoleh secara analitik, namun langkah-langkah yang cukup rumit dapat menjadi hambatan.
4. Penyelesaian analitik yang berupa fungsi matematika masih harus dihitung lagi untuk mendapatkan hasil akhir.
5. Terdapat beberapa metode numerik yang dapat digunakan untuk menyelesaikan persamaan dari permasalahan fisika tersebut namun dengan langkah-langkah yang cukup panjang juga.
C. PEMBATASAN MASALAH
Batasan masalah dalam penelitian ini adalah sebagai berikut:
1. Jenis perpindahan panas yang akan dibahas adalah perpindahan panas secara konduksi,
2. Persamaan panas yang akan dibahas adalah persamaan panas dimensi satu, 3. Penyelesaian panas secara analitik dan numerik hanya mengambil satu syarat
batas yaitu syarat batas Robin (campuran),
6
D. RUMUSAN MASALAH
Berdasarkan latar belakang dan pembatasan masalah yang telah dijabarkan di atas, permasalahan yang akan dikaji dalam penelitian ini adalah sebagai berikut. 1. Bagaimana model matematika persamaan panas dimensi satu?
2. Bagaimana penyelesaian analitik persamaan panas dimensi satu dengan metode separasi variabel?
3. Bagaimana penyelesaian numerik persamaan panas dimensi satu dengan metode volume hingga?
4. Bagaimana perbandingan penyelesaian analitik dan penyelesaian numerik dari persamaan panas dimensi satu?
E. TUJUAN
Berdasarkan penjabaran latar belakang hingga RUMUSAN masalah, maka diperoleh tujuan dari penelitian ini adalah sebagai berikut.
1. Memodelkan persamaan panas dimensi satu,
2. Menyelesaikan persamaan panas dimensi satu secara analitik menggunakan metode separasi variabel,
3. Menyelesaikan persamaan panas dimensi satu secara numerik menggunakan metode volume hingga,
F. MANFAAT
Berdasarkan tujuan penelitian yang hendak dicapai, maka penelitian ini diharapkan mempunyai manfaat atau kegunaan sebagai berikut:
1. Bagi Mahasiswa
a) Menambah pengetahuan tentang penurunan model panas dimensi satu, b) Dapat menyelesaikan persamaan panas dimensi satu secara analitik
dengan nilai awal dan syarat batas yang telah ditentukan,
c) Dapat menyelesaikan persamaan panas dimensi satu secara numerik dengan metode volume hingga,
d) Menambah pengetahuan tentang bagaimana perbandingan dari penyelesaian analitik dan penyelesaian numerik dalam menyelesaikan persamaan panas dimensi satu.
2. Bagi Universitas
a) Diharapkan hasil dari penelitian ini dapat menambah bahan referensi bagi Universitas Negeri Yogyakarta, khususnya untuk jurusan Pendidikan Matematika tentang penyelesaian analitik dan numerik dari persamaan panas dimensi satu.
3. Bagi Pembaca
8 BAB II KAJIAN TEORI
Pada bab II akan dibahas beberapa teori yang menjadi landasan dalam pembahasan pada bab III. Teori – teori dan beberapa kajian matematika yang akan dirangkum pada bab ini antara lain tentang perpindahan panas, persamaan diferensial yang terdiri dari persamaan diferensial biasa dan persamaan diferensial parsial, teorema integral rata-rata, penyelesaian persamaan diferensial parsial dan metode volume hingga untuk menyelesaikan persamaan panas dimensi satu secara numerik. Berikut adalah penjelasan lebih lanjutnya.
A. PERPINDAHAN PANAS
Definisi 2.1 PERPINDAHAN PANAS
Ilmu termodinamika adalah ilmu yang berupaya untuk memprediksi perpindahan energi yang mungkin terjadi antara material atau benda sebagai akibat dari perbedaan suhu. (Holman, 2010 : 1)
Definisi 2.2 PERPINDAHAN PANAS SECARA KONDUKSI
Perpindahan panas secara konduksi adalah perpindahan panas dari suhu yang tinggi menuju suhu yang lebih rendah karena interaksi antar partikel. (Bergman, Lavine, Incropera, & Dewitt, 2011 : 3)
Konduksi merupakan perpindahan panas melalui materi tetap seperti penampang logam yang diilustrasikan pada Gambar 2.1. Panas merambat atau berpindah dari suhu yang tinggi menuju suhu yang lebih rendah tanpa diikuti perpindahan partikel-partikel. Menurut Hukum Fourier atau juga yang sering disebut dengan Hukum Konduksi Panas menyatakan bahwa besar aliran panas pada saat melalui suatu material adalah sebanding dengan negatif dari perubahan suhu dan ketebalan benda. Dengan kata lain besar aliran panas menurut Hukum Fourier dapat dituliskan sebagai berikut.
= (−�� ) (2.1)
10
Konduktifitas panas pada benda padat memiliki berbagai nilai numerik, hal tersebut tergantung pada jenis material padat tersebut apakah merupakan konduktor yang relatif baik dalam menerima panas atau berfungsi sebagai isolator.
Menurut Holman (2010), terdapat beberapa sifat dalam proses perambatan panas. Sifat-sifat tersebut antara lain sebagai berikut.
1. Panas hanya mengalir dari suhu yang tinggi menuju suhu yang lebih rendah, 2. Kecepatan perambatan panas dipengaruhi oleh konduktifitas bahan
penyusunnya,
3. Kecepatan perambatan panas juga dipengaruhi oleh ketebalan batang logam, luas penampang, panjang bahan dan volume bahan.
Penampang logam
Arah aliran panas
= =
−��
B. PERSAMAAN DIFERENSIAL Definisi 2.3 PERSAMAAN DIFERENSIAL
Persamaan diferensial adalah persamaan yang memuat satu atau lebih turunan fungsi dari variabel terikat terhadap satu atau lebih variabel bebas. (Zill, Wright, & Cullen, 2012 : 2)
Berdasarkan jenisnya, persamaan diferensial dibedakan menjadi dua yaitu persamaan diferensial biasa dan persamaan diferensial parsial. Definisi dari kedua jenis persamaan diferensial tersebut adalah sebagai berikut.
Definisi 2.4 PERSAMAAN DIFERENSIAL BIASA
Persamaan diferensial parsial adalah persamaan diferensial yang memuat turunan biasa dari satu atau lebih variabel terikat terhadap satu variabel bebas. (Zill, Wright, & Cullen, 2012 : 2)
Definisi 2.5 PERSAMAAN DIFERENSIAL PARSIAL
Persamaan diferensial parsial adalah persamaan diferensial yang memuat turunan parsial dari satu atau lebih variabel terikat terhadap dua atau lebih variabel bebas. (Zill, Wright, & Cullen, 2012 : 2)
Berikut adalah beberapa contoh untuk persamaan diferensial biasa dan persamaan diferensial biasa.
Contoh 2.1
+ = (2. 2)
12
� � =
�
� (2. 4)
Dari Contoh 2.1 serta mengacu pada Definisi 2.4 dan Definisi 2.5, Persamaan (2.2) dan Persamaan (2.3) termasuk kedalam jenis persamaan diferensial biasa. Pada Persamaan (2.2), terdapat satu variabel tak bebas y dan satu variabel bebas . Begitu pula pada Persamaan (2.3), terdapat dua variabel tak bebas yaitu dan serta satu variabel bebas yaitu . Sedangkan untuk Persamaan (2.4) termasuk kedalam jenis persamaan diferensial parsial dengan variabel tak bebas dan variabel bebas dan .
Persamaan diferensial juga dibedakan berdasarkan ordernya, berikut adalah pejelasannya.
Definisi 2.6 ORDER DARI PERSAMAAN DIFERENSIAL
Urutan (order) persamaan diferensial (baik ODE atau PDE) adalah urutan turunan tertinggi dalam persamaan. (Zill, Wright, & Cullen, 2012 : 3)
Secara umum persamaan diferensial orde pertama dapat ditulis sebagai berikut.
, , = (2. 5)
Begitu pula untuk persamaan diferensial orde- , secara umum ditulis sebagai berikut.
� , , ′, . . . , = (2. 6)
dengan menyatakan turunan y terhadap yang ke-n.
Berikut adalah beberapa contoh persamaan dengan orde yang berbeda. Contoh 2.2
+ = (2. 8)
− = (2. 9)
berdasarkan Definisi (2.6), Persamaan (2.7) merupakan persamaan diferensial orde satu. Persamaan (2.7) dan Persamaan (2.8) merupakan persamaan diferensial orde dua.
Klasifikasi persamaan diferensial selanjutnya adalah berdasarkan linieritasnya. Klasifikasi berdasarkan kelinieran suatu persamaan diferensial adalah sebagai berikut.
Definisi 2.7 PERSAMAAN DIFERENSIAL LINIER
Persamaan diferensial biasa orde-n dikatakan linier jika F adalah linier di
Berikut adalah beberapa contoh persamaan diferensial linier. Contoh (2.3)
14
" − ′ + = (2. 13)
+ − = (2. 14)
berdasarkan definisi (2.7), Persamaan (2.12) Merupakan persamaan linier orde pertama. Persamaan (2.13) merupakan persamaan linier orde kedua dan Persamaan (2.14) merupakan persamaan diferensial linier orde 2.
C. TEOREMA NILAI RATA-RATA INTEGRAL
Teorema nilai rata-rata integral pada kasus ini akan digunakan untuk menentukan integral dari titik pusat kontrol volume.
TEOREMA (2.1) TEOREMA NILAI RATA-RATA INTEGRAL Jika fungsi f kontinu pada interval [ , ] dengan ∈ [ , ], maka,
� =∫ − (2. 15)
(Varberg, Purcell, & Rigdon, 2007:253)
D. PENYELESAIAN PERSAMAAN DIFERENSIAL PARSIAL
Penyelesaian dari persamaan diferensial parsial akan dicari dengan menerapkan syarat batas tertentu dan menggunakan beberapa teori yang dipakai hingga mendapat penyelesaian umumnya.
1. MASALAH NILAI AWAL DAN SYARAT BATAS
≤ . Diberikan , yang merupakan suhu di seluruh posisi pada saat sama dengan nol, hal tersebut dikatakan sebagai nilai awal.
Selanjutnya akan dibahas tentang masalah syarat batas. Menurut (Humi & Miller, 1992 : 42), untuk persamaan diferensial parsial orde 2 terdapat 3 syarat batas yang dapat digunakan yaitu sebagai berikut :
a) Syarat batas Dirichlet
Syarat batas dirichlet merupakan nilai-nilai yang tidak diketahui dari suatu fungsi pada bagian perbatasan. Dengan kata lain, syarat batas dirichlet adalah mempertahankan suhu pada posisi = dan posisi = supaya tetap nol derajat celcius. Apabila diberikan , merupakan suhu di pada saat , maka syarat batas dirichlet secara matematis dapat dituliskan sebagai berikut.
, = , =
dengan > .
b) Syarat batas Neumann
Syarat batas Neumann merupakan syarat batas yang nilai-nilai perubahan suhu pada posisi = dan posisi = dipertahankan nol. Apabila diberikan
, merupakan suhu di pada saat , maka syarat batas neumann secara matematis dapat dituliskan sebagai berikut.
� ,
� =
� ,
� =
dengan > .
c) Syarat batas Robin
16
diberikan , merupakan suhu di pada saat , maka syarat batas robin secara matematis dapat dituliskan sebagai berikut.
� ,
� = , =
dengan > .
2. MASALAH STURM-LIOUVILLE Definisi 2.9
Diberikan persamaan diferensial orde dua sebagai berikut,
[ ′ ]′+ [ + � ] = (2. 16) Persamaan (2.18) disebut dengan Masalah Sturm-Liouville Reguler. Menyelesaikan Masalah Sturm-Liouville Reguler artinya mencari nilai dari � yang disebut sebagai Nilai Eigen. Nilai dari � yang sesuai penyelesaian nontrivial disebut dengan Fungsi Eigen. (Agarwal & O'Regan, 2009 : 145)
Secara umum, akar-akar karakteristik dari suatu persamaan diferensial linier orde 2 dibedakan menjadi 3, yaitu:
Dimisalkan akar dari persamaan karakteristik pada Persamaan (2.16) adalah dan , maka penyelesaian umum dari Persamaan (2.16) sebagai berikut.
= ℎ + � ℎ
2. Akar karakteristik riil sama/kembar
Dimisalkan akar dari persamaan karakteristik pada Persamaan (2.16) adalah , maka penyelesaian umum dari Persamaan (2.16) sebagai berikut.
= +
3. Akar karakteristik bilangan kompleks
Dimisalkan akar dari persamaan karakteristik pada Persamaan (2.16) adalah
+ � dan − � , maka penyelesaian umum dari Persamaan (2.16) sebagai berikut.
= + �
(Ross, 2004) Contoh 2.3
Akan dicari penyelesaian umum dari masalah Sturm Liouville pada pada persamaan berikut ini.
′′ + = (2. 19)
Persamaan karakterisktik dari Persamaan (2.19) adalah,
+ = (2. 20)
dengan menggunakan rumus , = − ±√ − , diperoleh.
18 penyelesaian umum dari Persamaan (2.19) adalah.
= + �
Contoh 2.4
Akan dicari penyelesaian umum dari masalah Sturm Liouville pada persamaan berikut ini.
′′ − = (2. 21)
Persamaan karakterisktik dari Persamaan (2.21) adalah.
− = (2. 22)
− + =
= dan = −
Akar-akar dari Persamaan Karakteristik (2.22) adalah = dan = − , dimana dan merupakan bilangan riil. Sehingga diperoleh penyelesaian umum dari Persamaan (2.21) adalah.
= ℎ + � ℎ
Akan dicari penyelesaian umum dari masalah Sturm Liouville pada persamaan berikut ini.
′′ + ′ + = (2. 23)
Persamaan karakterisktik dari Persamaan (2.23) adalah.
+ + = (2. 24)
+ + =
= − dan = −
Akar-akar dari Persamaan Karakteristik (2.24) adalah = − dan = − , dimana dan merupakan bilangan riil yang sama besar. Sehingga diperoleh penyelesaian umum dari Persamaan (2.23) adalah.
= − + −
3. METODE SEPARASI VARIABEL Definisi 2.10
Diberikan perasamaan diferensial,
= , (2. 25)
dengan fungsi f pada Persamaan (2.25) dapat dipisah menjadi fungsi dalam x dikalikan fungsi dalam y, atau dapat dituliskan sebagai berikut.
= ℎ (2. 26)
20
Langkah-langkah untuk menyelesaikan suatu persamaan dengan menggunakan metode separasi variabel menurut (Humi & Miller, 1992:113) sebagai berikut.
1. Menentukan penyelesaian dari persamaan diferensial dalam bentuk , = . Dimana variabel hanya muncul dalam fungsi , sedangkan merupakan fungsi dari saja.
2. Menentukan konstanta pemisah misalnya �, dengan � merupakan bilangan riil.
3. Akan diselesaikan terlebih dahulu masalah nilai eigen dimana persamaan memiliki dua kondisi batas. Namun, karena nilai dari konstanta pemisah variabel (�) belum diketahui dan ditentukan bahwa � harus riil maka masalah nilai eigen akan dicari dengan melihat kondisi dari konstanta � yaitu � < ,
� = , � > .
4. Menentukan nilai eigen dan fungsi eigen.
5. Menyelesaikan persamaan untuk variabel yang lain dnegan menggunakan nilai eigen yang diperoleh pada langkah sebelumnya.
6. Untuk mendapatkan penyelesaian akhir, setelah diperoleh dan maka akan dikalikan dengan . Hal ini terjadi karena pada langkah 1 telah diasumsikan bahwa penyelesaian dari persamaan yang diselesaikan adalah , = . Berikut adalah contoh separasi variabel untuk menyelesaikan persamaan Laplace.
�
1. Menentukan penyelesaian dari persamaan diferensial dalam bentuk
, = . Dimana variabel hanya muncul dalam fungsi , sedangkan merupakan fungsi dari saja.
Diberikan penyelesaian untuk , = , apabila disubstitusikan pada Persamaan (2.27) maka diperoleh bentuk sebagai berikut.
′′ + ′′ = (2.32)
Apabila Persamaan (2.32) dikelompokkan sesuai variabelnya, maka diperoleh bentuk sebagai berikut.
′′
= − ′′ (2.33)
2. Menentukan konstanta pemisah misalnya �, dengan � merupakan bilangan riil.
Diambil konstanta pemisah �, sehingga Persamaan (2.33) menjadi. ′′
= − ′′ = � (2.34)
22
′′ − � = (2.35)
′′ + � = (2.36)
3. Akan diselesaikan terlebih dahulu masalah nilai eigen dimana persamaan memiliki dua kondisi batas. Namun, karena nilai dari konstanta pemisah variabel (�) belum diketahui dan ditentukan bahwa � harus riil maka masalah nilai eigen akan dicari dengan melihat kondisi dari konstanta � yaitu � < ,
� = , � > .
Dari Persamaan (2.35) akan dicari kemungkinan nilai � yang memenuhi sebagai berikut.
Kemungkinan I untuk nilai � = > , sehingga Persamaan (2.35) menjadi,
′′ − = (2.37)
Penyelesaian umum dari Persamaan (2.37) adalah.
′′ = (2.38) Apabila kedua ruas pada Persamaan (2.38) diintegralkan, maka diperoleh hasil sebagai berikut.
Penyelesaian umum dari Persamaan (2.39) adalah,
= + �
dengan syarat batas,
24
= + �
=
= → = + �
= + �
= �
Agar diperoleh penyelesaian non-trivial maka ≠ , sehingga nilai � =
.
� =
� = sin
= , = , , , … (2.40)
4. Menentukan nilai eigen dan fungsi eigen.
Nilai dari pada Persamaan (2.40) bergantung pada , sehingga = . Sehingga.
=
=
Karena nilai dari = + � , dengan = . Sehingga
= � . Karena nilai bergantung pada , hal ini berakibat pada
nilai yang juga bergantung pada . Sehingga diperoleh fungsi eigen sebagai
berikut.
5. Menyelesaikan persamaan untuk variabel yang lain dengan menggunakan nilai eigen yang diperoleh pada langkah sebelumnya.
Dengan menggunakan nilai dari konstanta pemisah yang telah diperoleh, maka Persamaan (2.36) dapat ditulis sebagai berikut.
′′ + � =
′′ − = (2.42)
Penyelesaian umum dari Persamaan (2.47) adalah,
= + � (2.43)
Agar diperoleh penyelesaian non-trivial maka ≠ , sehingga nilai � =
.
� ℎ =
� ℎ = sinh
= , = , , , … (2.44)
26
=
=
Karena nilai dari = ℎ + � ℎ , dengan = . Sehingga
= � ℎ . Karena nilai bergantung pada , hal ini berakibat pada
nilai yang juga bergantung pada . Sehingga diperoleh fungsi eigen sebagai
berikut.
= � ℎ = , , , …. (2.45)
6. Untuk mendapatkan penyelesaian akhir, setelah diperoleh dan maka akan dikalikan dengan . Hal ini terjadi karena pada langkah 1 telah diasumsikan bahwa penyelesaian dari persamaan yang diselesaikan
adalah , = .
Nilai dan yang bergantung pada berakibat pada penyelesaian
, yang bergantung pula pada , sehingga:
, = .
+ ∑∞ { + � } fourier konvergen pada pada . Sebaliknya, apabila diskontinu di maka deret fourier konvergen pada.
+ + − (Humi & Miller, 1992:75).
Contoh 2.7
Akan ditentukan deret Fourier dari = { < <
< <
28
= ∫
= ∫ + ∫
= [ ] + [ ]
=
=
= ∫
= ∫ + ∫
= ∫ + ∫
= ( sin ) + ( sin )
= ( sin ) + ( sin )
=
= ∫ � ( )
30
E. METODE VOLUME HINGGA
Metode volume hingga merupakan salah satu metode numerik untuk menyelesaikan persamaan diferensial parsial pada masalah-masalah fisis. Pada dasarnya metode volume hingga adalah mengubah masalah persamaan diferensial menjadi sebuah sistem dalam persamaan aljabar. Metode volume hingga sering digunakan untuk mencari pendekatan terhadap penyelesaian analitik dari suatu persamaan diferensial parsial. Dibandingkan dengan metode beda hingga, metode volume hingga memiliki beberapa kelebihan sebagai berikut :
1. Diskritisasi terhadap ruang yang fleksibel. Apabila terdapat suatu bidang yang akan didiskritisasi, maka bidang tersebut dipartisi ke dalam ukuran lebih kecil yang sering disebut dengan kontrol volume. Partisi tersebut dapat berbentuk tidak beraturan untuk mengurangi kesalahan geometri dan partisi dapat dibuat lebih rinci untuk mendapat penyelesaian yang mendekati penyelesaian analitik.
2. Persamaan ditulis dalam bentuk integral yang seringkali berasal dari hukum-hukum fisika.
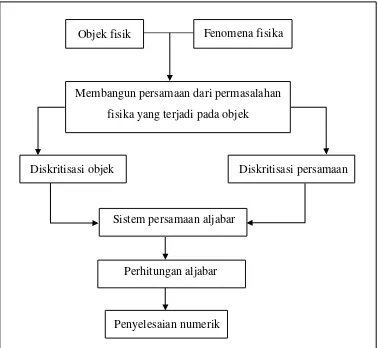
Langkah-langkah dalam menyelesaikan suatu persamaan diferensial parsial dengan metode volume hingga hampir mirip dengan finite difference method ataupun finite element method. Menurut (Moukalled, et al : 2016), adapun tahap-tahap dalam menyelesaikan persamaan diferensial parsial dengan metode volume hingga secara garis besar dapat dilihat dari Gambar 2.2 berikut.
Langkah awal dalam metode volume hingga adalah menurunkan persamaan matematik untuk fenomena fisika yang dialami oleh suatu objek. Setelah ditentukan persamaan matematik (dalam hal ini persamaan matematik yang dimaksud adalah
Penyelesaian numerik Perhitungan aljabar
Membangun persamaan dari permasalahan fisika yang terjadi pada objek
Objek fisik Fenomena fisika
Sistem persamaan aljabar
Diskritisasi persamaan Diskritisasi objek
32
persamaan diferensial parsial) untuk permasalahan fisika tersebut, lalu dilakukan diskritisasi terhadap objek (benda). Benda akan dibagi menjadi beberapa kontrol volume (dipartisi menjadi beberapa bagian dengan panjang yang sama). Sehingga akan terdapat beberapa titik yang mewakili tiap kontrol volume tersebut.
Langkah selanjutnya setelah menentukan kontrol volume adalah melakukan diskritisasi terhadap persamaan matematik yang telah diperoleh. Kedua ruas persamaan matematik diintegralkan terhadap waktu dan terhadap kontrol volume. Hingga diperoleh suatu sistem persamaan aljabar. Dengan diperoleh sistem persamaan aljabar maka akan diperoleh juga matrik dari sistem persamaan aljabar. Untuk mendapat penyelesaian numerik maka dilakukan penyelesaian terhadap matrik untuk mendapat nilai dari variabel terikat.
BAB III
HASIL DAN PEMBAHASAN
Pada bab ini akan dibahas penurunan model persamaan panas dimensi satu. Setelah itu akan ditentukan penyelesaian persamaan panas dimensi satu secara analitik dengan metode variabel terpisah. Selanjutnya penyelesaian analitik dari persamaan panas dimensi satu akan dihampiri dengan penyelesaian numerik menggunakan metode volume hingga. Berikut penjelasan lebih lanjut.
A. PENURUNAN PERSAMAAN PANAS DIMENSI SATU
Ilmu termodinamika merupakan salah satu bidang ilmu yang banyak digunakan di industri-industri dalam perencanaan macam-macam alat seperti boiler, heater dan ruang bakar. Terdapat tiga jenis perambatan panas yaitu perambatan panas secara konduksi, konveksi dan radiasi. Perambatan panas secara konduksi yaitu perpindahan panas dari suhu yang tinggi menuju suhu yang lebih rendah tanpa disertai dengan perpindahan partikel-partikelnya. Sedangkan perpindahan panas secara konveksi yaitu perpindahan panas yang terjadi antara permukaan padat dengan fluida dimana proses perpindahan panas melalui perpindahan massa fluida. Selanjutnya perpindahan panas secara radiasi yaitu perpindahan panas tanpa melalui zat perantara, artinya panas dipancarkan oleh sumber panas dan terpancar ke segala arah.
34
perpindahan partikel-partikelnya. Pada sub-bab ini, akan dibahas bagaimana penurunan persamaan panas dimensi satu secara konduksi yang terjadi pada benda padat.
Diberikan sebuah batang logam dengan panjang terbentang disepanjang sumbu seperti pada Gambar (3.1). Batang logam dipartisi menjadi beberapa bagian kecil dan dipilih satu bagian kecil yang akan mewakili sebagai kontrol volume. Dalam proses penurunan persamaan panas dimensi satu, akan diasumsikan beberapa hal sebagai berikut.
1. Luas penampang batang logam adalah konstan, 2. Jumlah kalor pada seluruh bagian adalah konstan, 3. Batang logam terbuat dari bahan yang homogen,
4. Batang logam terisolasi sempurna diseluruh permukaannya, sehingga tidak ada kalor yang dapat melewati permukaan batang logam,
5. Aliran panas merambat dari suhu yang tinggi menuju suhu yang lebih rendah, Panas jenis dan konduksi termal adalah konstan.
Selanjutnya, akan ditinjau partisi batang logam sebesar ∆ . Diberikan � merupakan total energi panas dan , yaitu jumlah energi panas per satuan
Gambar 3.1 Batang logam dengan energi panas yang mengalir searah sumbu-x
x=
= + ∆
volume yang selanjutnya disebut dengan massa jenis panas. Apabila massa jenis panas adalah konstan di seluruh volume dari batang logam, maka jumlah energi panas pada ∆ merupakan hasil dari massa jenis panas dan volume. Sehingga secara matematis dapat dirumuskan sebagai berikut.
, =�
dengan = ∆ , sehingga.
, =�∆
� = , ∆ (3.1)
Perubahan panas pada interval [ , + ∆ ] terjadi apabila terdapat aliran panas di sepanjang titik hingga + ∆ . Berdasarkan Hukum Konservasi Panas, dasar proses aliran panas adalah laju perubahan panas sama dengan energi panas yang mengalir per satuan waktu ditambah energi panas yang dihasilkan dari dalam batang logam per satuan waktu. Karena batang logam bersifat homogen dan terisolasi diseluruh permukaannya maka tidak ada panas yang dihasilkan dari dalam batang logam. Sehingga diperoleh rumusan laju perubahan panas sebagai berikut.
�
� , ∆ (3.2)
Pada Gambar (3.1) perambatan panas pada batang logam terdapat perbedaan suhu antara kedua ujung batang logam, yaitu , dan + ∆ , dengan
, > + ∆ , . Sehingga untuk energi panas yang merambat pada
potongan logam per satuan waktu adalah sebagai berikut.
36
Selanjutnya akan dicari hubungan antara laju perubahan panas dan energi panas yang merambat pada potongan logam. Menurut Holman (2010), laju difusi diberikan oleh Hukum Fick, yang menyatakan bahwa fluks berbanding lurus dengan laju perubahan panas. Sehingga diperoleh rumusan sebagai berikut.
�
� , ∆ =
�
� , ∆ = (3.4)
Apabila Persamaan (3.4) dibagi dengan , maka akan menjadi seperti berikut.
∆ �� ( , ) = � (3.5)
Selanjutnya, apabila Persamaan (3.5) dibagi dengan ∆ , maka diperoleh. �
� ( , ) = �∆ (3.6)
logam adalah . Sehingga total energi panas pada potongan logam dapat ditulis sebagai.
� = ∆ (3.8)
karena = dan = ∆ , sehingga Persamaan (3.8) dapat ditulis menjadi.
� = ∆ , (3.9)
Kemudian, apabila Persamaan (3.1) dan Persamaan (3.9) disederhanakan, diperoleh hasil sebagai berikut.
, ∆ = ∆ ,
, = ∆ ∆ ,
, = , (3.10)
Apabila Persamaan (3.10) disubstitusikan pada Persamaan (3.7) diperoleh hasil. �
� , =�
�
� (3.11)
Menurut Hukum Fourier, laju perambatan panas yang melewati permukaan bidang berbanding lurus dengan perubahan suhu yang melewati potongan logam dan ketebalan dinding. Dengan kata lain dapat dituliskan sebagai berikut.
= − ∆ ∆ , (3.12)
Pada Persamaan (3.12), merupakan konduktivitas termal. Dengan pendekatan ∆ → maka Persamaan (3.12) berubah menjadi.
= lim∆ → − ∆ ∆ ,
= − ∆ →lim ∆ ∆ ,
38
Apabila Persamaan (3.13) disubstitusikan pada Persamaan (3.11) maka diperoleh.
Misalkan = , sehingga Persamaan (3.13) dapat ditulis menjadi. � ,
�
=
� ,
� (3.15)
Kemudian Persamaan (3.15) disebut Persamaan Panas Dimensi Satu..
Gambar 3.2 apabila diilustrasikan pada bidang koordinat kartesius dengan pembanding suhu terhadap sumbu x, maka akan tampak pada Gambar 3.3.
Selanjutnya akan ditentukan penyelesaian dari persamaan panas dimensi satu menggunakan metode separasi variabel. Diberikan persamaan panas dimensi satu sebagai berikut.
� ,
� =
� ,
� , ≤ ≤ dengan > (3.16)
, = , =
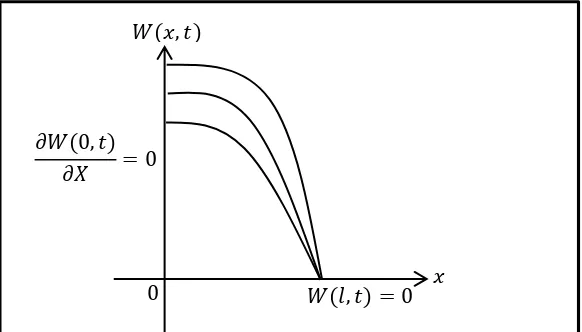
Gambar 3.2 Ilustrasi syarat batas Robin (Campuran) pada penampang logam
Gambar 3.3 Distribusi suhu terhadap sumbu-x
� ,
� =
40
Apabila Persamaan (3.17) dan Persamaan (3.18) disubstitusikan pada Persamaan (3.16) maka diperoleh.
′ = ′′ (3.19)
Akan dilakukan pemisahan variabel, dimana persamaan yang mengandung variabel x dikelompokkan pada ruas kanan dan persamaan yang mengandung variabel t akan dikelompokkan pada ruas kiri.
�′
dari Persamaan (3.21) diperoleh masalah Sturm-Liouville sebagai berikut. ′
�′
� = −λ (3.22)
′′
= −λ (3.23)
Kemudian akan diselesaikan terlebih dahulu untuk Persamaan (3.22). ′′
= −λ
′′ = −λ
′′ + λ = (3.24)
karena nilai dari konstanta pemisah λ belum diketahui dan ditentukan bahwa λ harus riil. Maka akan ditinjau 3 kemungkinan nilai untuk λ.
Kemungkinan I. Untuk nilai λ = −� < , sehingga Persamaan (3.24) menjadi.
′′ − � = (3.25)
Penyelesaian umum dari Persamaan (3.25) adalah.
42 ℎ � =
Karena � ≠ dan ≠ maka nilai ℎ � ≠ , hal tersebut berakibat pada nilai = . Sehingga untuk λ = −� < diperoleh penyelesaian trivial.
Kemungkinan II. Untuk nilai λ = , sehingga Persamaan (3.24) menjadi.
′′ = (3.26)
Penyelesaian umum dari Persamaan (3.26) adalah. = +
Karena nilai = dan = sehingga diperoleh penyelesaian trivial.
Kemungkinan III. Untuk nilai λ = � > , sehingga Persamaan (3.24) menjadi.
′′ + � = (3.27)
Penyelesaian umum dari Persamaan (3.27) adalah. = cos � + sin �
Dengan syarat batas ′ = , diperoleh.
′ = −� sin � + � cos �
� =
Supaya diperoleh penyelesaian non-trivial, maka. cos � =
cos � = cos − , dengan n = 1, 2, 3, ...
� = − , dengan n = 1, 2, 3, ... (3.28) Karena nilai � bergantung pada , maka � = � . Sehingga Persamaan (3.28) dapat ditulis sebagai berikut.
� = − , n = 1, 2, 3, ... (3.29)
44 ′
= −λ
′
= − ( − )
′
= − ( − )
′ = − ( − )
′ = − ( − )
= − ( − )
= − ( − )
Kedua ruas akan diintegralkan, dan diperoleh hasil sebagai berikut,
∫ = − ∫ ( − )
ln| | = − ( − ) +
= − − +
= − − ×
= − − ×
= − �−� (3.31)
Karena nilai dan bergantung pada n, hal tersebut berakibat pada nilai , yang juga bergantung pada n. Sehingga penyelesaian dari , dapat ditulis sebagai berikut.
, = ( − ) − −
, = ∑ ( − ) − −
∞
=
dengan = ∫
�− � �
∫ cos �−� .
Selanjutnya akan dicari penyelesaian dari ∫ − .
∫ ( − )
= ∫ ( − )
= − � ( − )]
= ( − � ( − )) −
= − � ( − )
Karena nilai � − = − + , sehingga diperoleh hasil.
∫ ( − ) = −− +
46
∫ cos ( − )
= ∫ ( − ) ( − )
Dengan menggunakan sifat = cos + + cos − , diperoleh bentuk sebagai berikut.
= ∫ ( ( − ) + )
= ∫ ( − ) +
= − � ( − ) + ]
= ( − � ( − ) + ) − ( − � + )
=
Sehingga hasil dari =∫
�− � �
∫ cos �−� adalah.
=
− +
−
= −− + ×
= −− +
, = ∑ − +
− (
−
) − −
∞
=
, = ∑∞= − −�+ − − �−� (3.32)
Diketahui panjang logam adalah . , maka Persamaan (3.32) menjadi sebagai berikut.
, = ∑∞= − −�+ .− − �−. (3.33)
48
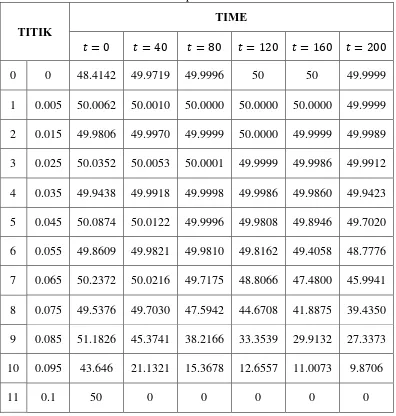
Tabel 3.1 Hasil penyelesaian analitik persamaan panas dimensi satu dengan metode separasi variabel
TITIK
TIME
= = = = = =
0 0 48.4142 49.9719 49.9996 50 50 49.9999
1 0.005 50.0062 50.0010 50.0000 50.0000 50.0000 49.9999 2 0.015 49.9806 49.9970 49.9999 50.0000 49.9999 49.9989 3 0.025 50.0352 50.0053 50.0001 49.9999 49.9986 49.9912 4 0.035 49.9438 49.9918 49.9998 49.9986 49.9860 49.9423 5 0.045 50.0874 50.0122 49.9996 49.9808 49.8946 49.7020 6 0.055 49.8609 49.9821 49.9810 49.8162 49.4058 48.7776 7 0.065 50.2372 50.0216 49.7175 48.8066 47.4800 45.9941 8 0.075 49.5376 49.7030 47.5942 44.6708 41.8875 39.4350 9 0.085 51.1826 45.3741 38.2166 33.3539 29.9132 27.3373 10 0.095 43.646 21.1321 15.3678 12.6557 11.0073 9.8706
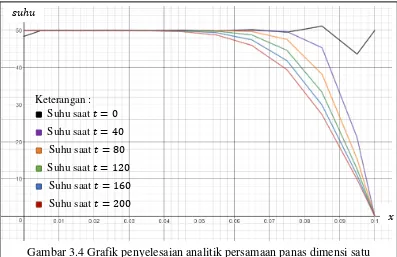
Apabila penyelesaian analitik diplot dalam bentuk grafik, maka hasilnya sebagai berikut.
Dari Gambar 3.4 dapat dilihat bahwa suhu di sebarang pada saat = berkisar pada angka 50, hal tersebut sesuai dengan nilai awal yang diterapkan pada kasus ini. Pada saat > suhu mulai mengalami penurunan secara bertahap hingga mencapai di titik = . . hal tersebut juga sesuai dengan syarat batas yaitu
. , = dengan > .
C. PENYELESAIAN NUMERIK PERSAMAAN PANAS DIMENSI SATU DENGAN METODE VOLUME HINGGA
1. PROSES DALAM METODE VOLUME HINGGA
Diberikan sebuah lilin dan batang logam homogen dengan panjang . . Lilin diletakkan di bawah batang logam di posisi sebelah kiri, setelah itu lilin
Gambar 3.4 Grafik penyelesaian analitik persamaan panas dimensi satu ℎ
Suhu saat =
Suhu saat =
Suhu saat =
Suhu saat =
Suhu saat =
50
dinyalakan beberapa waktu lalu dimatikan. Dalam kasus ini, perubahan suhu pada posisi = dipertahankan nol derajat dan suhu pada posisi = . dipertahankan nol derajat, panas hanya mengalir dari suhu tinggi menuju suhu yang lebih rendah. Akan ditentukan penyelesaian dari persamaan panas dimensi satu pada batang logam menggunakan metode volume hingga. Diberikan persamaan panas dimensi satu sebagai berikut.
� ,
� =
� ,
� , ≤ ≤ . dengan >
(3.34)
dengan nilai awal.
, = ; ≤ ≤ . (3.34a)
dan syarat batas,
, = , > (3.34b)
. , = , > (3.34c)
Diasumsikan ∆ merupakan waktu perambatan panas dari � menuju � + ∆ . Sehingga interval waktu perambatan panas pada kontrol volume adalah [ , + ∆ ]. Dari Gambar 3.5 akan ditunjukkan sistem kontrol volume yang lebih detail sebagai berikut.
Selanjutnya, karena , merupakan fungsi atas dan yang dalam hal ini sebagai posisi dan sebagai waktu. Apabila Persamaan 3.33 diintegralkan terhadap
dengan interval [ �, � + ∆ ], sehingga Persamaan (3.33) menjadi.
� �+ ∆ .
Gambar 3.5 Ilustrasi kontrol volume pada batang logam
� � + ∆
� � +
� −
∆ = .
52 sehingga Persamaan (3.35) menjadi.
∫ ∫ ( � � , )
Apabila diasumsikan besar suhu pada titik � merupakan besar suhu pada seluruh kontrol volume �. Maka ruas kiri dari Persamaan (3.36) dapat diselesaikan sebagai berikut.
Persamaan (3.37) terlebih dahulu akan diintegralkan terhadap waktu, sehingga diperoleh hasil sebagai berikut.
∫ ∫ �� � �
Proses pengintegralan berlanjut dengan mengintegralkan Persamaan 3.38 terhadap kontrol volume dan diperoleh hasil sebagai berikut.
= ∫ +∆ − �
�+∆
= +∆ − ] �� merupakan suhu di � pada waktu . Setelah diperoleh hasil integral dari ruas kiri Persamaan 3.36, selanjutnya akan ditentukan hasil integral dari ruas kanan Persamaan 3.36 sebagai berikut.
54
Teorema integral rata-rata digunakan untuk memperoleh hasil dari � � | �+∆
dan �
� | �, sehingga diperoleh hasil sebagai berikut. � Persamaan 3.40 adalah sebagai berikut.
∫ ∫ ��
Apabila Persamaan 3.39 dan Persamaan 3.41 disubstitusikan pada Persamaan 3.33 maka diperoleh hasil sebagai berikut.
saat + ∆ , atau bisa juga dengan menggunakan kombinasi suhu pada saat dan + ∆ . Selanjutnya dilakukan aproksimasi menggunakan parameter � dimana ≤ � ≤ . Sehingga diperoleh asumsi integral suhu terhadap waktu sebagai berikut.
� = ∫ +∆ � = [� � + − � � ]∆ (3.44)
dimana,
� 1
�� � ∆
�+ � ∆ �∆
Dengan mengaplikasikan Persamaan 3.44 ke dalam Persamaan 3.43 diperoleh hasil sebagai berikut.
( �− � )∆ ∆
=
(� �+ − �
∆ − �−∆ �− + − � �+∆− � − � −∆ �− ) ∆
∆
( � − � )∆
∆
= (� ( �+∆− �− �−∆ �− ) +
− � �+∆− � − � −∆ �− )
56
2. PENYELESAIAN KASUS PERSAMAAN PANAS DIMENSI SATU DENGAN METODE VOLUME HINGGA
Diberikan suatu permasalahan, sebuah batang logam dengan panjang . . Batang logam dipartisi menjadi 10 kontrol volume, dengan jarak antar titik pusat kontrol volume ∆ = . . Dalam kasus ini diketahui persamaan panas dimensi satu sesuai dengan Persamaan (3.33), dengan nilai awal , =
. Syarat batas dari kasus ini adalah , = dan . , = . Telah diketahui pula bahwa = × dan = . Dengan menggunakan Explicit Method untuk teknik diskritisasi, maka nilai untuk � adalah � = sehingga diperoleh hasil persamaan umum dari solusi kasus ini sebagai berikut.
( � − � )∆
Menurut (Versteeg & Malalasekera, 1995 : 175), untuk menentukan time step pada metode eksplisit harus memenuhi aturan sebagai berikut.
∆ < ∆ (3.47)
Dari Pertidaksamaan (3.47) maka diperoleh batas untuk time step sebagai berikut.
∆ < ∆
∆ < × × .
∆ <
∆
Untuk mengetahui suhu pada masing-masing kontrol volume, akan dicari persamaan aljabar untuk masing-masing titik pusat kontrol volume dengan menggunakan persamaan awal yaitu Persamaan (3.46).
62
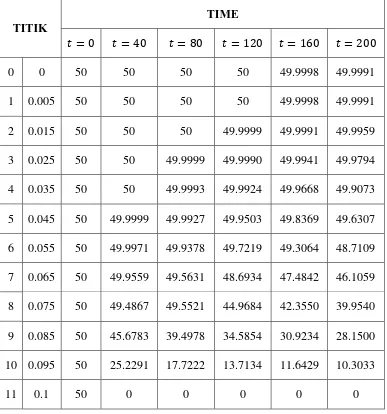
Tabel 3.2 Hasil penyelesaian numerik persamaan panas dimensi satu dengan metode volume hingga
TITIK
TIME
= = = = = =
0 0 50 50 50 50 49.9998 49.9991
1 0.005 50 50 50 50 49.9998 49.9991
2 0.015 50 50 50 49.9999 49.9991 49.9959
3 0.025 50 50 49.9999 49.9990 49.9941 49.9794 4 0.035 50 50 49.9993 49.9924 49.9668 49.9073 5 0.045 50 49.9999 49.9927 49.9503 49.8369 49.6307 6 0.055 50 49.9971 49.9378 49.7219 49.3064 48.7109 7 0.065 50 49.9559 49.5631 48.6934 47.4842 46.1059 8 0.075 50 49.4867 49.5521 44.9684 42.3550 39.9540 9 0.085 50 45.6783 39.4978 34.5854 30.9234 28.1500 10 0.095 50 25.2291 17.7222 13.7134 11.6429 10.3033
11 0.1 50 0 0 0 0 0
64
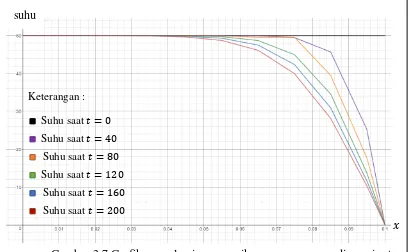
Dari Gambar 3.7 dapat dilihat bahwa suhu di sebarang pada saat = adalah 50, hal tersebut sesuai dengan nilai awal yang diterapkan pada kasus ini. Pada saat >
suhu mulai mengalami penurunan secara bertahap hingga mencapai di titik = . . Hal tersebut juga sesuai dengan syarat batas yaitu . , = dengan > .
suhu
Gambar 3.7 Grafik penyelesaian numerik persamaan panas dimensi satu Suhu saat =
Suhu saat =
Suhu saat =
Suhu saat =
Suhu saat =
D. PERBANDINGAN PENYELESAIAN ANALITIK DAN PENYELESAIAN NUMERIK PERSAMAAN PANAS DIMENSI SATU Setelah diperoleh penyelesaian analitik dan penyelesaian numerik dari persamaan panas dimensi satu, selanjutnya akan dilihat bagaimana perbandingan dari kedua penyelesaian tersebut. Perbandingan akan ditampilkan dalam bentuk grafik pada yang telah dipilih, selain itu akan dihitung pula rata-rata error relatif pada masing-masing . Menurut (Rinaldi Munir, 2010 : 24), error relatif berasosiasi dengan seberapa dekat solusi hampiran terhadap solusi sejatinya. Error relatif dapat diperoleh dengan rumusan sebagai berikut :
�� = | − ̂| (3.49)
dimana �� merupakan error relatif, merupakan nilai dari solusi analitik dan ̂ merupakan nilai hampiran (nilai dari solusi numerik). Hasil dari perbandingan solusi analitik dan numerik adalah sebagai berikut.
1. Perbandingan solusi analitik dan solusi numerik persamaan panas dimensi satu saat = .
Hasil dari penyelesaian analitik dan numerik pada saat = dapat dilihat pada tabel berikut ini.
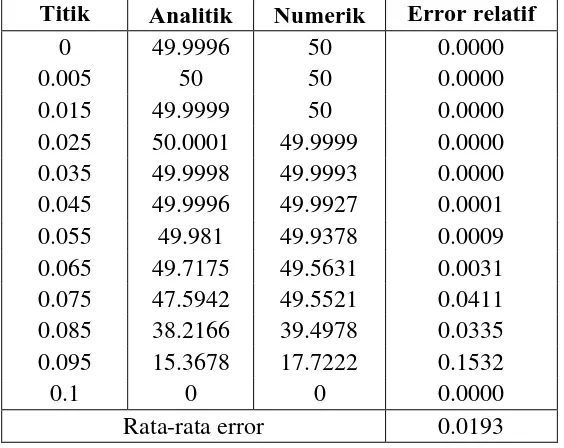
Tabel 3.3 Hasil penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Titik Analitik Numerik Error relatif
66
0.065 50.2372 50 0.0047
0.075 49.5376 50 0.0093
0.085 51.1826 50 0.0231
0.095 43.646 50 0.1456
0.1 50 50 0.0000
Rata-rata error 0.0185
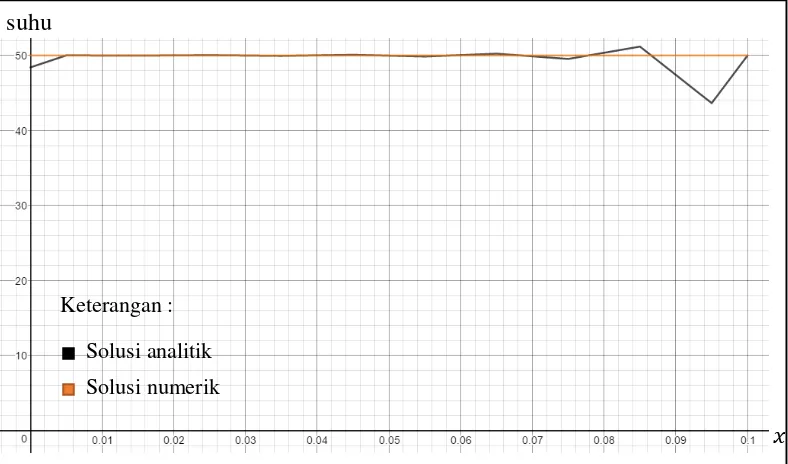
Berdasarkan Tabel 3.3 akan dilihat perbandingan dari kedua penyelesaian berupa grafik dua dimensi sebagai berikut.
Berdasarkan Gambar 3.8 dapat dilihat bahwa suhu di sebarang pada saat = berkisar pada angka 50 dengan rata-rata error relatif sebesar . . Hal ini sesuai dengan nilai awal yang ditentukan pada kasus ini. Penyelesaian secara analitik dan numerik tidak dapat memberikan hasil yang sama, akan tetapi metode numerik dapat mendekati hasil perhitungan dari metode suhu
Gambar 3.8 Grafik perbandingan penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Solusi analitik
analitik. Maka dari itu, terdapat beberapa perbedaan bentuk grafik dari kedua solusi karena hasil penyelesaian yang memang tidak sama persis.
2. Perbandingan solusi analitik dan solusi numerik persamaan panas dimensi satu saat = .
Hasil dari penyelesaian analitik dan numerik pada saat = dapat dilihat pada Tabel 3.4.
Tabel 3.4 Hasil penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Titik Analitik Numerik Error relatif
0 49.9996 50 0.0000
Rata-rata error 0.0193
68
Berdasarkan Gambar 3.9 batang logam mulai mengalami penurunan suhu, hal ini dapat dilihat dari grafik yang menuju ke nol dengan rata-rata error . . Rata-rata error relatif mengalami kenaikan sebesar . dikarenakan sistem yang telah berjalan pada saat > , sedangkan pada saat = sistem belum berjalan dan masih menggunakan nilai awal. Grafik untuk = menunjukkan hal yang sesuai dengan syarat batas . , = . Pada >
. , terjadi perbedaan suhu antara solusi analitik dan solusi numerik, namun dari perbedaan tersebut kedua solusi tersebut sama-sama menuju ke nol pada
= . .
suhu
Gambar 3.9 Grafik perbandingan penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Solusi analitik
3. Perbandingan solusi analitik dan solusi numerik persamaan panas dimensi satu saat = .
Hasil dari penyelesaian analitik dan numerik pada saat = dapat dilihat pada Tabel 3.5.
Tabel 3.5 Hasil penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Titik Analitik Numerik Error relatif
0 50 49.9998 0.0000
Rata-rata error 0.0089
70
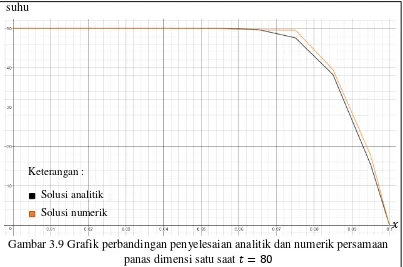
Berdasarkan Gambar 3.10 dapat dilihat bahwa terdapat perbedaan solusi dari kedua penyelesaian, namun tidak sebesar pada saat = . Rata-rata error relatif saat = adalah . , rata-rata error mengalami penurunan sebesar . . Keseluruhan dari kedua solusi hampir sama, dengan memenuhi syarat batas yang telah ditentukan.
4. Perbandingan solusi analitik dan solusi numerik persamaan panas dimensi satu saat = .
Hasil dari penyelesaian analitik dan numerik pada saat = dapat dilihat pada Tabel 3.6.
suhu
Gambar 3.10 Grafik perbandingan penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Solusi analitik
Tabel 3.6 Hasil penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Titik Analitik Numerik Error relatif 0 49.9999 49.9991 0.0000
Rata-rata error 0.0077
Berdasarkan Tabel 3.6 akan dilihat perbandingan dari kedua penyelesaian berupa grafik dua dimensi sebagai berikut.
suhu
Gambar 3.11 Grafik perbandingan penyelesaian analitik dan numerik persamaan panas dimensi satu saat =
Solusi analitik
72
Berdasarkan Gambar 3.11 dapat dilihat apabila penyelesaian dari kedua metode memiliki hasil yang hampir sama pada = dan rata-rata error sebesar . . Rata-rata error relatif mengalami penurunan sebesar . dari rata-rata error pada sebelumnya. Tidak terlihat adanya jarak antara dua grafik garis masing-masing solusi. Suhu pada saat = mulai mengalami penurunan di > . , hingga mencapai nol pada = . .
BAB IV PENUTUP A. KESIMPULAN
Dari hasil pembahasan pada BAB III, maka penulis dapat menyimpulkan beberapa hal sebagai berikut:
1. Model persamaan panas dimensi satu adalah sebagai berikut. � ,
� =
� , �
dimana menggambarkan posisi titik antara hingga . , merupakan suhu pada posisi saaat waktu . merupakan difusi thermal. 2. Penyelesaian analitik persamaan panas dimensi satu dengan nilai awal
syarat batas robin adalah sebagai berikut.
, = ∑ − +
3. Langkah-langkah metode volume hingga dalam menyelesaikan persamaan panas dimensi satu adalah:
a. Membagi objek ke dalam beberap kontrol volume.
b. Melakukan diskritisasi pada persamaan dengan mengintegralkan kedua ruas persamaan terhadap kontrol volume dan terhadap waktu.
c. Diperoleh sistem persamaan aljabar.
74
Dari persamaan panas dimensi satu dengan nilai awal , sistem persamaan aljabar yang diperoleh sebagai berikut.
= +
= + +
= + +
= + +
= + .
4. Setelah melihat 4 contoh grafik penyelesaian analitik dan numerik persamaan panas dimensi satu, dapat dilihat bahwa metode numerik dengan volume hingga dapat digunakan untuk mendekati solusi analitik dengan baik. Grafik juga menunjukkan apabila penyelesaian memenuhi nilai awal yaitu , = , serta memenuhi syarat batas pula yaitu , = dan . , = .
B. SARAN
76
DAFTAR PUSTAKA
Agarwal, R. P., & O'Regan, D. (2009). Ordinary and Partial Differential Equations. New York: Springer Science+Business Media.
Ahmadi. (2016). Tinjauan Kasus Persamaan Panas Dimensi Satu Secara Analitik. Skripsi. Yogyakarta.
Bergman, T. L., Lavine, A. S., Incropera, F. P., et al. (2011). Fundamental of Heat and Mass Transfer 7th Edition. Jefferson City: John Wiley and Sons Inc. Budi Utami, Setyo. (2008). Analisa Distribusi Aliran Panas pada Sebuah Pelat
Besi dengan Menggunakan Metode Volume Hingga. Surabaya : Institut Teknologi Sepuluh Nopember.
Fatihah, Novian Nur. (2015). Pemodelan Sebaran Air Panas Spray Pond di Pabrik Gula Menggunakan Metode Volume Hingga. Jember: Digital Repository UNEJ.
Humi, M., & Miller, W. B. (1991). Boundary Value Problems and Partial Differential Equations. Boston: PWS-Kent.
Holman, J. P. (2010). Heat Transfer 10th edition. New York: McGraw-Hill. Moukalled, F., Mangani, L., & Darwish, M. (2016). The Finite Volume Method in
Computational Fluid Dynamics. Fluid Mechanics and Its Applications. Switzerland: Springeer International Publishing.
Munir, Rinaldi. (2010). METODE NUMERIK. Bandung: Informatika.
Ross, S. L. (2004). Differential Equation (third edition). New York: John Wiley&Sons Inc.
Varberg, D., Purcell, E., & Rigdon, S. (2007). Calculus (9th Edition). New Jersey: Prentice Hall.
Versteeg, H., & Malalasekera, W. (1995). An Introduction to Computational Fluid Dynamics the Finite Volume Method. New York: John Wiley and Sons, Inc.
77
80
Lampiran 2. M-script untuk mendeskripsikan Persamaan (3.33)
function y = step(x,t,n) k=10/(10^7);
m=(2*n)-1;
y=(200/pi)*((((-1)^(n+1))/m)*(cos((m*pi*x)/0.2))*((2.71828182846)^((-1)*(t*k*((m*pi)/0.2)^2))));
Lampiran 3. M-Script penyelesaian persamaan panas dimensi satu
function y = panas(x,t) y=step(x,t,1);
i
PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN METODE VOLUME HINGGA
HALAMAN JUDUL
TUGAS AKHIR SKRIPSI
Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta
untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana Sains
Oleh :
Ardila Dewi Setyarsi NIM. 12305141002
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA
PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN
Pada umumnya masalah persamaan differensial parsial terlalu rumit apabila diselesaikan secara analitik, salah satunya adalah kasus pada persamaan panas dimensi satu. Pada kasus ini, akan diketahui bagaimana memodelkan persamaan panas dimensi satu, yang selanjutnya persamaan panas dimensi satu akan diselesaikan secara analitik menggunakan separasi variabel dan syarat batas robin. Selain penyelesaian analitik, persamaan panas dimensi satu akan diselesaikan secara numerik menggunakan metode volume hingga dengan syarat batas robin. Dari kedua penyelesaian yang telah diperoleh akan dilihat bagaimana perbandingan antara kedua penyelesaian tersebut.
Penyelesaian analitik dari persamaan panas diperoleh dengan menggunakan teknik separasi variabel dan menerapkan syarat batas robin. Sedangkan penyelesaian numerik untuk persamaan panas dimensi satu diperoleh menggunakan metode volume hingga dimana persamaan panas dimensi satu akan diintegralkan terhadap kontrol volume dan waktu. Persamaan panas yang telah diintegralkan menghasilkan sistem persamaan aljabar untuk selanjutnya diperoleh suhu pada masing-masing kontrol volume.
Hasil akhir dari penelitian ini adalah metode volume hingga dapat mendekati penyelesaian analitik dengan baik. Hal tersebut dapat dilihat dari hasil perbandingan suhu kedua penyelesaian tersebut yang berupa grafik. Perbandingan yang disajikan dalam bentuk grafik menunjukkan nilai awal dari kedua penyelesaian sesuai dengan yang telah ditentukan yaitu , = . Suhu di setiap pada saat dari kedua metode tersebut hasilnya saling beriringan. Kemudian penyelesaian analitik dan penyelesaian numerik berakhir pada suhu nol
di = . .
MOTTO
Tak ada yang tidak mungkin selagi masih ada niat, usaha dan
do’a.
(@ardila_ds)
Do’a tanpa usaha adalah bohong. Usaha tanpa do’a adalah
sombong.
(anonym)
Allah tidak membebani seseorang itu melainkan sesuai dengan
kesanggupannya.
(Q.S. Al-Baqarah : 286)
Selalu ada kekuatan dari belakang, ketika uluran tangan tak mampu melawan.
vii
PERSEMBAHAN
Teruntuk
Bapak dan Ibuk tersayang, yang selalu memberi semangat dan
do’a tanpa henti. Kalian alasanku bertahan, kalian alasanku
berjuang.
Mas Dian dan Mbak Garin, saudara dan ipar yang Tuhan berikan untukku.
Putri, Asnay, Kanthy, Fulan, Ebby, Ryan, Desi Tuparman Orang-orang yang telah menemaniku membuat kenangan di setiap
sudut Jogja.
Keluarga Jodoh Pasti Bertamu
Yang membuat ku merasa memiliki keluarga baru di Jogja. Keluarga besar LIMUNY
Tempat lain dimana aku bisa pulang. Keluarga MATSUB 2012
Terimakasih untuk kebersamaan dan kerjasamanya
Semua pihak yang tidak dapat disebutkan satu persatu yang telah membantu selesainya skripsi ini. Kalian gula dalam segelas espresso ku, membuat semua pahitku menjadi sesuatu
yang manis.
KATA PENGANTAR
Puji syukur penulis panjatkan kepada Allah SWT, berkat rahmat dan karunia-Nya penulis dapat menyelesaikan Tugas Akhir Skripsi yang berjudul
“PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN METODE VOLUME HINGGA”. Tugas Akhir Skripsi ini disusun untuk memenuhi salah satu syarat kelulusan guna meraih gelar Sarjana Sains pada Program Studi Matematika di FMIPA Universitas Negeri Yogyakarta.
Skripsi ini tidak dapat selesai tanpa bantuan dan bimbingan dari beberapa pihak. Penulis mengucapkan terimakasih kepada:
1. Bapak Dr. Hartono, selaku Dekan Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta,
2. Bapak Dr. Ali Mahmudi, selaku Ketua Jurusan Pendidikan Matematika Universitas Negeri Yogyakarta,
3. Bapak Dr. Agus Maman Abadi, selaku Ketua Program Studi Matematika Universitas Negeri Yogyakarta,
4. Ibu Fitriana Yuli Saptaningtyas, M.Si. selaku dosen pembimbing yang telah memberikan arahan serta motivasi kepada penulis dalam penyusunan skripsi ini,
ix
6. Seluruh dosen Jurusan Pendidikan Matematika Universitas Negeri Yogyakarta yang telah memberikan ilmu kepada penulis.
7. Orangtua dan keluarga yang selalu memberi semangat dan doa yang tak pernah putus,
8. Teman-teman Matematika Subsidi 2012 yang telah memberi semangat dan motivasi kepada penulis,
9. Teman-teman operator LIMUNY atas kebersamaan dan kerjasamanya 10. Seluruh pihak yang telah memberi dukungan, motivasi dan bantuan kepada
penulis dalam menyelesaikan skripsi ini.
Penulis sadar akan adanya kekurangan dan kesalahan dalam penulisan tugas akhir skripsi ini. Oleh karena itu, penulis menerima kritik dan saran yang bersifat membangun. Semoga penulisan tugas akhir skripsi ini dapat bermanfaat bagi pembaca dan pihak yang terkait.
Yogyakarta, April 2017 Penulis
DAFTAR ISI
BAB I PENDAHULUAN ... 1 A. LATAR BELAKANG ... 1 B. IDENTIFIKASI MASALAH ... 4 C. PEMBATASAN MASALAH ... 5 D. RUMUSAN MASALAH ... 6 E. TUJUAN ... 6 F. MANFAAT ... 7
xi
BAB III HASIL DAN PEMBAHASAN ... 33 A. PENURUNAN PERSAMAAN PANAS DIMENSI SATU ... 33 B. PENYELESAIAN ANALITIK PERSAMAAN PANAS DIMENSI
SATU ... 38 C. PENYELESAIAN NUMERIK PERSAMAAN PANAS DIMENSI
SATU DENGAN METODE VOLUME HINGGA ... 49
D. PERBANDINGAN PENYELESAIAN ANALITIK DAN
PENYELESAIAN NUMERIK PERSAMAAN PANAS DIMENSI SATU ... 65
BAB IV PENUTUP ... 73 A. KESIMPULAN ... 73 B. SARAN ... 74
DAFTAR TABEL
Tabel 3.1 Hasil penyelesaian analitik persamaan panas dimensi satu dengan metode separasi variabel ... 49 Tabel 3.2 Hasil penyelesaian numerik persamaan panas dimensi satu dengan metode volume hingga ... 64 Tabel 3.3 Hasil penyelesaian analitik dan numerik persamaan panas dimensi satu saat = ... 66 Tabel 3.4 Hasil penyelesaian analitik dan numerik persamaan panas dimensi satu saat = ... 68 Tabel 3.5 Hasil penyelesaian analitik dan numerik persamaan panas dimensi satu
xiii
DAFTAR GAMBAR
Gambar 2.1 Aliran panas melalui penampang logam ... 11 Gambar 2.2 Bagan alur metode volume hingga ... 32 Gambar 3.1 Batang logam dengan energi panas yang mengalir searah sumbu- 35 Gambar 3.2 Ilustrasi syarat batas Robin (Campuran) pada penampang logam. ... 40 Gambar 3.3 Distribusi suhu terhadap sumbu- ... 40 Gambar 3.4 Grafik penyelesaian analitik persamaan panas dimensi satu ... 50 Gambar 3.5 Ilustrasi kontrol volume pada batang logam ... 52 Gambar 3.6 Kontrol volume pada batang logam ... 52 Gambar 3.7 Grafik penyelesaian numerik persamaan panas dimensi satu ... 65 Gambar 3.8 Grafik perbandingan penyelesaian analitik dan numerik persamaan
panas dimensi satu saat = ... 67 Gambar 3.9 Grafik perbandingan penyelesaian analitik dan numerik persamaan
panas dimensi satu saat = ... 69 Gambar 3.10 Grafik perbandingan penyelesaian analitik dan numerik persamaan
panas dimensi satu saat = ... 71 Gambar 3.11 Grafik perbandingan penyelesaian analitik dan numerik persamaan
DAFTAR LAMPIRAN
xv
DAFTAR SIMBOL
: Besar aliran panas : Konduktivitas panas
, : Suhu di pada waktu : Panjang logam
� : Konstanta pemisah
, : Jumlah energi panas per satuan volume
: Simbol untuk posisi di sepanjang batang logam
� : Suhu di � pada waktu
i
PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN METODE VOLUME HINGGA
HALAMAN JUDUL
TUGAS AKHIR SKRIPSI
Diajukan kepada Fakultas Matematika dan Ilmu Pengetahuan Alam Universitas Negeri Yogyakarta
untuk Memenuhi Sebagian Persyaratan guna Memperoleh Gelar Sarjana Sains
Oleh :
Ardila Dewi Setyarsi NIM. 12305141002
PROGRAM STUDI MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS NEGERI YOGYAKARTA
PENYELESAIAN PERSAMAAN PANAS DENGAN ANALITIK DAN
Pada umumnya masalah persamaan differensial parsial terlalu rumit apabila diselesaikan secara analitik, salah satunya adalah kasus pada persamaan panas dimensi satu. Pada kasus ini, akan diketahui bagaimana memodelkan persamaan panas dimensi satu, yang selanjutnya persamaan panas dimensi satu akan diselesaikan secara analitik menggunakan separasi variabel dan syarat batas robin. Selain penyelesaian analitik, persamaan panas dimensi satu akan diselesaikan secara numerik menggunakan metode volume hingga dengan syarat batas robin. Dari kedua penyelesaian yang telah diperoleh akan dilihat bagaimana perbandingan antara kedua penyelesaian tersebut.
Penyelesaian analitik dari persamaan panas diperoleh dengan menggunakan teknik separasi variabel dan menerapkan syarat batas robin. Sedangkan penyelesaian numerik untuk persamaan panas dimensi satu diperoleh menggunakan metode volume hingga dimana persamaan panas dimensi satu akan diintegralkan terhadap kontrol volume dan waktu. Persamaan panas yang telah diintegralkan menghasilkan sistem persamaan aljabar untuk selanjutnya diperoleh suhu pada masing-masing kontrol volume.
Hasil akhir dari penelitian ini adalah metode volume hingga dapat mendekati penyelesaian analitik dengan baik. Hal tersebut dapat dilihat dari hasil perbandingan suhu kedua penyelesaian tersebut yang berupa grafik. Perbandingan yang disajikan dalam bentuk grafik menunjukkan nilai awal dari kedua penyelesaian sesuai dengan yang telah ditentukan yaitu , = . Suhu di setiap pada saat dari kedua metode tersebut hasilnya saling beriringan. Kemudian penyelesaian analitik dan penyelesaian numerik berakhir pada suhu nol
di = . .
MOTTO
Tak ada yang tidak mungkin selagi masih ada niat, usaha dan
do’a.
(@ardila_ds)
Do’a tanpa usaha adalah bohong. Usaha tanpa do’a adalah
sombong.
(anonym)
Allah tidak membebani seseorang itu melainkan sesuai dengan
kesanggupannya.
(Q.S. Al-Baqarah : 286)
Selalu ada kekuatan dari belakang, ketika uluran tangan tak mampu melawan.
vii
PERSEMBAHAN
Teruntuk
Bapak dan Ibuk tersayang, yang selalu memberi semangat dan
do’a tanpa henti. Kalian alasanku bertahan, kalian alasanku
berjuang.
Mas Dian dan Mbak Garin, saudara dan ipar yang Tuhan berikan untukku.
Putri, Asnay, Kanthy, Fulan, Ebby, Ryan, Desi Tuparman Orang-orang yang telah menemaniku membuat kenangan di setiap
sudut Jogja.
Keluarga Jodoh Pasti Bertamu
Yang membuat ku merasa memiliki keluarga baru di Jogja. Keluarga besar LIMUNY
Tempat lain dimana aku bisa pulang. Keluarga MATSUB 2012
Terimakasih untuk kebersamaan dan kerjasamanya
Semua pihak yang tidak dapat disebutkan satu persatu yang telah membantu selesainya skripsi ini. Kalian gula dalam segelas espresso ku, membuat semua pahitku menjadi sesuatu
yang manis.