PENYELESAIAN NUMERIS PERSAMAAN ADVEKSI-DIFUSI MENGGUNAKAN SKEMA LAX-WENDROFF DAN
BEDA HINGGA TAK STANDAR
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Diani Pratama Putri NIM: 163114020
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
i
PENYELESAIAN NUMERIS PERSAMAAN ADVEKSI-DIFUSI MENGGUNAKAN SKEMA LAX-WENDROFF DAN
BEDA HINGGA TAK STANDAR
Tugas Akhir
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Oleh:
Diani Pratama Putri NIM: 163114020
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
ii
NUMERICAL SOLUTION OF ADVECTION-DIFFUSION EQUATION USING LAX-WENDROFF AND NONSTANDARD
FINITE DIFFERENCE SCHEMES
Final Project
Presented as Partial Fulfillment of the
Reguirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written by: Diani Pratama Putri Student ID: 163114020
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
v
HALAMAN PERSEMBAHAN
“He has made everything beautiful in its time. Also He has put eternity in their hearts, except that no one can find out the work that God does
from beginning to end.” Ecclesiastes 3:11
Karya ini ku persembahkan untuk: Tuhan Yesus Kristus yang senantiasa memberikan berkat dan penyertaan-Nya disetiap langkah saya dan kedua orang tua tercinta, Petrus Marsana dan
Prihartiningsih, serta adek saya Dinda dan Dia, yang selalu mendoakan saya.
viii ABSTRAK
Persamaan adveksi-difusi adalah salah satu persamaan diferensial parsial. Persamaan adveksi-difusi dapat diselesaikan secara analitis dan numeris, namun secara umum penyelesaian secara analitis sulit untuk ditentukan. Oleh karena itu, dalam tugas akhir ini, penulis akan membahas persamaan adveksi-difusi yang akan diselesaikan menggunakan metode numeris. Metode numeris yang digunakan adalah skema Lax-Wendroff dan skema beda hingga tak standar. Kedua metode yang digunakan untuk menyelesaikan persamaan adveksi-difusi tersebut akan disimulasikan menggunakan perangkat lunak MATLAB. Simulasi persamaan adveksi-difusi satu dimensi ini akan dilakukan pada contoh yang sudah diketahui memiliki penyelesaian analitis. Berdasarkan simulasi skema Lax-Wendroff memberikan hasil yang baik dan efisien. Skema beda hingga tak standar juga memberikan hasil yang baik. Namun demikian, skema Lax-Wendroff memberikan hasil yang akurat dibandingkan skema beda hingga tak standar.
Kata kunci: Persamaan adveksi-difusi, persamaan diferensial parsial, skema Lax-Wendroff, skema beda hingga tak standar.
ix ABSTRACT
Advection-diffusion equation is a partial differential equation. This equation can be solved either analytically or numerically, but in general, analytical solution is difficult to obtain. Therefore, in this work, we discuss about solving the advection-diffusion equation using numerical methods. Numerical methods that we use in this project are the Lax-Wendroff and nonstandard finite difference schemes. These two methods to solve the advection-diffusion equation are programmed in the MATLAB software. The simulation of this one-dimensional advection-diffusion equation will be performed on known intances of their analytical solutions. Based on simulation the Lax-Wendroff scheme gives good and efficient results. Nonstandard finite difference scheme also gives good results. However, Lax-Wendroff scheme gives accurate results compared Lax-Wendroff scheme.
Keyword: Advection-diffusion equation, partial differential equation, Lax-Wendroff scheme, nonstandard finite difference scheme.
xii DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERSEMBAHAN. ... v
PERNYATAAN KEASLIAN KARYA ... vi
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... vii
ABSTRAK ... viii
ABSTRACT ... ix
KATA PENGANTAR ... x
DAFTAR ISI ... xii
BAB I PENDAHULUAN ... 1 A. Latar Belakang... 1 B. Rumusan Masalah ... 2 C. Batasan Masalah ... 2 D. Tujuan Penulisan ... 2 E. Manfaat Penulisan ... 3 F. Metode Penulisan ... 3 G. Sistematika Penulisan ... 3
BAB II PERSAMAAN DIFERENSIAL DAN HAL-HAL TERKAIT ... 5
A. Turunan... 5
B. Deret Taylor... 8
C. Klasifikasi Persamaan Diferensial ... 10
D. Pendekatan Numeris Persamaan Diferensial ... 12
E. Klasifikasi Persamaan Diferensial Parsial ... 17
F. Metode Beda Hingga ... 18
G. Metode Beda Hingga Skema Eksplisit ... 20
BAB III SKEMA NUMERIS UNTUK PERSAMAAN ADVEKSI-DIFUSI 21 A. Hukum Kekekalan ... 21
xiii
B. Persamaan Adveksi ... 23
C. Persamaan Difusi ... 24
D. Skema Eksplisit untuk Persamaan Adveksi-Difusi ... 25
E. Skema Beda Hingga Tak Standar untuk Persamaan Adveksi-Difusi ... 27
F. Kondisi Persamaan Adveksi-Difusi untuk Skema Lax-Wendroff dan Beda Hingga Tak Standar ... 29
BAB IV HASIL SIMULASI ... 31
A. Pembahasan Hasil ... 31
B. Perbandingan Galat ... 37
C. Kestabilan Metode Numeris ... 41
BAB V PENUTUP ... 44
A. Kesimpulan ... 44
B. Saran ... 44
DAFTAR PUSTAKA ... 45
1 BAB I PENDAHULUAN
A. Latar Belakang
Masalah pencemaran lingkungan seperti pada sungai, pantai, air tanah, dan atmosfer dapat dinyatakan ke dalam model matematika. Salah satu model matematika yang mengambarkan proses transportasi dan difusi adalah persamaan adveksi-difusi satu dimensi. Pemodelan matematika pada transportasi panas, polutan dan bahan tersuspensi dalam air dan tanah melibatkan persamaan diferensial (Karahan, 2008).
Persamaan diferensial adalah suatu persamaan yang memuat satu atau lebih turunan dari fungsi yang tidak diketahui. Persamaan diferensial dapat diklasifikasikan menjadi dua yaitu persamaan diferensial biasa dan persamaan diferensial parsial. Persamaan diferensial biasa adalah suatu persamaan dengan turunan biasa sedangkan persamaan diferensial parsial adalah suatu persamaan yang melibatkan turunan parsial (Boyce dan DiPrima, 1986). Persamaan difusi adalah termasuk bentuk persamaan diferensial parsial. Persamaan adveksi-difusi adalah persamaan yang memuat persamaan adveksi dan persamaan adveksi-difusi. Persamaan adveksi-difusi yang akan dibahas dalam tugas akhir ini berbentuk (Appadu, 2013) 𝜕𝑢 𝜕𝑡 + 𝑎 𝜕𝑢 𝜕𝑥= 𝛼 𝜕2𝑢 𝜕𝑥2, 0 < 𝑥 < 𝐿, 0 < 𝑡 ≤ 𝑇. kondisi awal 𝑢(𝑥, 0) = 𝑓(𝑥),
dan kondisi batas
𝑢(0, 𝑡) = 𝑔(𝑡), 0 < 𝑡 ≤ 𝑇, 𝑢(𝐿, 𝑡) = ℎ(𝑡), 0 < 𝑡 ≤ 𝑇.
dengan 𝑓, 𝑔, ℎ fungsi-fungsi yang diketahui. Di sini, 𝑎 dan 𝛼 adalah konstanta positif.
Persamaan adveksi-difusi merupakan persamaan yang memuat sifat persamaan adveksi dan persamaan difusi. Persamaan adveksi merupakan persamaan linear orde satu atau persamaan gelombang satu arah. Persamaan
difusi adalah representasi dari perpindahan molekul-molekul kimia dari bagian yang berkonsentrasi tinggi ke bagian yang berkonsentrasi rendah (LeVeque, 1992). Masalah-masalah tersebut sering dijumpai pada kualitas udara, oseanografi, meteorologi, dan lain-lain. Oleh karena itu, penyelesaian persamaan ini perlu dicari agar masalah-masalah tersebut dapat diselesaikan dengan baik.
Dalam prakteknya, mencari penyelesaian analitis sering kali sangat sulit dilakukan. Oleh karena itu, persamaan adveksi-difusi akan diselesaikan secara numeris dengan menggunakan skema Lax-Wendroff dan skema beda hingga tak standar. Kedua metode ini diyakini telah terbukti sebagai pendekatan yang efisien untuk menyelesaikan persamaan adveksi-difusi ini.
B. Rumusan Masalah
Perumusan masalah yang akan dibicarakan pada tugas akhir ini adalah sebagai berikut:
1. Bagaimana mencari penyelesaian persamaaan adveksi-difusi dengan metode numeris?
2. Bagaimana membandingkan kedua metode penyelesaian tersebut untuk mengetahui mana yang lebih baik?
C. Batasan Masalah
Pembahasan masalah dalam tugas akhir ini akan dibatasi pada menyelesaikan persamaaan adveksi-difusi berdimensi satu berdasarkan skema Lax-Wendroff dan skema beda hingga tak standar.
D. Tujuan Penulisan
Tujuan dari penulisan tugas akhir ini, yaitu:
1. Menyelesaikan persamaaan adveksi-difusi dengan metode numeris.
2. Membandingkan hasil simulasi numeris antara skema Lax-Wendroff dan skema beda hingga tak standar pada penyelesaian persamaan adveksi-difusi.
E. Manfaat Penulisan
Manfaat yang dapat diperoleh dari penulisan pada tugas akhir ini adalah mengetahui metode mana yang lebih baik untuk persamaaan adveksi-difusi. Dengan adanya tugas akhir ini penulis dapat menerapkan dalam kehidupan sehari-hari.
F. Metode Penulisan
Metode penulisan yang digunakan dalam penyusunan tugas akhir ini adalah studi pustaka, yaitu dengan mempelajari buku-buku dan jurnal. Selain itu dilakukan praktik numeris dengan menggunakan program MATLAB. G. Sistematika Penulisan BAB I PENDAHULUAN A. Latar Belakang B. Rumusan Masalah C. Batasan Masalah D. Tujuan Penulisan E. Manfaat Penulisan F. Metode Penulisan G. Sistematika Penulisan
BAB II PERSAMAAN DIFERENSIAL HAL-HAL TERKAIT A. Turunan
B. Deret Taylor
C. Klasifikasi Persamaan Diferensial
D. Pendekatan Numeris Persamaan Diferensial E. Klasifikasi Persamaan Diferensial Parsial F. Metode Beda Hingga
G. Metode Beda Hingga Skema Eksplisit
BAB III SKEMA NUMERIS UNTUK PERSAMAAN ADVEKSI-DIFUSI A. Hukum Kekekalan
B. Persamaan Adveksi C. Persamaan Difusi
D. Skema Eksplisit untuk Persamaan Adveksi-Difusi
E. Skema Beda Hingga Tak Standar untuk Persamaan Adveksi-Difusi F. Kondisi Persamaan Adveksi-Difusi untuk Skema Lax-Wendroff
dan Beda Hingga Tak Standar BAB IV HASIL SIMULASI
A. Pembahasan Hasil B. Perbandingan Galat
C. Kestabilan Metode Numeris BAB V PENUTUP
A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
5 BAB II
PERSAMAAN DIFERENSIAL DAN HAL-HAL TERKAIT
Pada bab ini akan dibahas mengenai landasan teori dari tugas akhir ini. Landasan teori yang digunakan dalam tugas akhir ini adalah turunan, deret Taylor, klasifikasi persamaan diferensial, pendekatan numeris persamaan diferensial, metode beda hingga, dan metode beda hingga skema eksplisit.
A. Turunan
Dalam subbab ini akan dijelaskan definisi turunan dan contoh dari turunan. Definisi 2.1
Fungsi 𝑓′ (dibaca “𝑓 aksen”) didefinisikan dengan rumus
𝑓′(𝑥) = lim ℎ→0
𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ
yang merupakan turunan dari fungsi 𝑓 pada titik 𝑥 dengan syarat limitnya ada (Anton dkk, 2012).
Contoh 2.1
Tentukan turunan 𝑓′(𝑥) apabila diketahui 𝑓(𝑥) = 𝑥2 di 𝑥 = 2. Penyelesaian: 𝑓′(2) = lim ℎ→0 𝑓(2 + ℎ) − 𝑓(2) ℎ = lim ℎ→0 (2 + ℎ)2− 22 ℎ = lim ℎ→0 22+ 2 ∙ 2ℎ + ℎ2− 22 ℎ = lim ℎ→0 2 ∙ 2ℎ + ℎ2 ℎ
= lim
ℎ→0(2 ∙ 2 + ℎ) = 4.
Contoh 2.2
Tentukan turunan 𝑓′(𝑥) apabila diketahui 𝑓(𝑥) = 𝑥3− 𝑥. Penyelesaian: 𝑓′(𝑥) = lim ℎ→0 𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ = lim ℎ→0 [(𝑥 + ℎ)3− (𝑥 + ℎ)] − [𝑥3− 𝑥] ℎ = lim ℎ→0 [𝑥3+ 3𝑥2ℎ + 3ℎ2𝑥 + ℎ3− 𝑥 − ℎ] − [𝑥3− 𝑥] ℎ = lim ℎ→0 3𝑥2ℎ + 3ℎ2𝑥 + ℎ3− ℎ ℎ = lim ℎ→0(3𝑥 2+ 3ℎ𝑥 + ℎ2− 1) = 3𝑥2− 1. Contoh 2.3
Tentukan turunan 𝑓′(𝑥) apabila diketahui 𝑓(𝑥) = 𝑥3− 𝑥2+ 1. Penyelesaian: 𝑓′(𝑥) = lim ℎ→0 𝑓(𝑥 + ℎ) − 𝑓(𝑥) ℎ = lim ℎ→0 [(𝑥 + ℎ)3− (𝑥 + ℎ)2 + 1] − [𝑥3− 𝑥2+ 1] ℎ = lim ℎ→0 [𝑥3+ 3𝑥2ℎ + 3ℎ2𝑥 + ℎ3− 𝑥2− 2𝑥ℎ − ℎ2+ 1 − 𝑥3+ 𝑥2− 1] ℎ = lim ℎ→0 3𝑥2ℎ + 3ℎ2𝑥 + ℎ3− 2𝑥ℎ − ℎ2 ℎ
= lim ℎ→0(3𝑥
2+ 3ℎ𝑥 + ℎ2− 2𝑥 − ℎ) = 3𝑥2− 2𝑥.
Definisi 2.2
Definisi turunan di atas dapat ditulis sebagai berikut:
Jika ditulis 𝑤 = 𝑥 + ℎ, maka ℎ = 𝑥 − 𝑤 dan ℎ mendekati 0 jika dan hanya jika 𝑤 mendekati 𝑥. Jadi, didapat
𝑓′(𝑥) = lim 𝑤→𝑥
𝑓(𝑤) − 𝑓(𝑥) 𝑤 − 𝑥
jika nilai limitnya ada.
Contoh 2.4
Contoh ini diambil dari buku Howard Anton, dkk (2012). Gunakan definisi 2.2 untuk mencari 𝑓′(𝑥) jika 𝑓(𝑥) = 𝑥
𝑥+1 Penyelesaian: 𝑓′(𝑥) = lim 𝑤→𝑥 𝑓(𝑤) − 𝑓(𝑥) 𝑤 − 𝑥 = lim 𝑤→𝑥 (𝑤 + 1) − (𝑤 𝑥 + 1)𝑥 𝑤 − 𝑥 = lim 𝑤→𝑥[ 𝑤(𝑥 + 1) − 𝑥(𝑤 + 1) (𝑤 + 1)(𝑥 + 1) ∙ 1 𝑤 − 𝑥] = lim 𝑤→𝑥[ 𝑤 − 𝑥 (𝑤 + 1)(𝑥 + 1)∙ 1 𝑤 − 𝑥] = lim 𝑤→𝑥[ 1 (𝑤 + 1)(𝑥 + 1)] = 1 (𝑥 + 1)(𝑥 + 1) = 1 (𝑥 + 1)2.
Teorema 2.1
Jika fungsi 𝑓 mempunyai turunan atau terdiferensial di 𝑥0, maka fungsi 𝑓 kontinu di 𝑥0.
Bukti dapat dilihat pada buku berjudul Calculus karangan Howard Anton, dkk (2012).
B. Deret Taylor
Dalam subbab ini akan dijelaskan deret Taylor dan hampiran metode numeris (Chapra dan Canale, 2010).
Teorema 2.2
Misalkan 𝑓 adalah suatu fungsi yang punya turunan ke 𝑛 + 1, yaitu 𝑓(𝑛+1) pada interval [𝑎, 𝑏], dan 𝑥0 ∈ [𝑎, 𝑏]. Untuk setiap 𝑥 ∈ [𝑎, 𝑏] ada 𝜉(𝑥) diantara 𝑥0 dan 𝑥 dengan 𝑓(𝑥) = 𝑃𝑛(𝑥) + 𝑅𝑛(𝑥), (2.1) dimana 𝑃𝑛(𝑥) = 𝑓(𝑥0) + 𝑓′(𝑥0)(𝑥 − 𝑥0) + 𝑓′′(𝑥0) 2! (𝑥 − 𝑥0) 2+ ⋯ +𝑓 (𝑛)(𝑥 0) 𝑛! (𝑥 − 𝑥0) 𝑛 dan 𝑅𝑛(𝑥) =𝑓 (𝑛+1)(𝜉(𝑥)) (𝑛 + 1)! (𝑥 − 𝑥0) 𝑛+1
Persamaan (2.1) secara umum dapat ditulis ke dalam bentuk seperti berikut
𝑓(𝑥𝑖+1) = 𝑓(𝑥𝑖) + 𝑓′(𝑥𝑖)(𝑥𝑖+1− 𝑥𝑖) + 𝑓′′(𝑥𝑖) 2! (𝑥𝑖+1− 𝑥𝑖) 2+ ⋯ +𝑓 (𝑛)(𝑥 𝑖) 𝑛! (𝑥𝑖+1− 𝑥𝑖) 𝑛+ 𝑅 𝑛(𝑥) dimana 𝑅𝑛(𝑥) = 𝑓(𝑛+1)(𝜉(𝑥)) (𝑛+1)! (𝑥𝑖+1− 𝑥𝑖) 𝑛+1, atau 𝑓(𝑥𝑖+1) = 𝑓(𝑥𝑖) + 𝑓′(𝑥𝑖)ℎ + 𝑓′′(𝑥𝑖) 2! ℎ 2+ ⋯ +𝑓 (𝑛)(𝑥 𝑖) 𝑛! ℎ 𝑛+ 𝑅 𝑛(𝑥) dengan ℎ = 𝑥𝑖+1− 𝑥𝑖.
𝑅𝑛(𝑥) =𝑓(𝑛+1)(𝑛+1)!(𝜉(𝑥))ℎ𝑛+1.
Contoh 2.5
Hampiri fungsi 𝑓(𝑥) = sin (𝑥) ke dalam deret Taylor di sekitar 𝑥0 = 1.
Penyelesaian
Akan ditentukan turunan sin (𝑥) terlebih dahulu sebagai berikut: 𝑓(𝑥) = sin(𝑥), 𝑓′(𝑥) = cos(𝑥), 𝑓′′(𝑥) = −sin(𝑥), 𝑓′′′(𝑥) = −cos(𝑥), 𝑓(4)(𝑥) = sin(𝑥), ⋮ dan seterusnya.
Maka, dengan menggunakan teorema (2.2), sin (𝑥) dihampiri dengan deret Taylor sebagai berikut:
sin(𝑥) = sin(1) + cos(1)(𝑥 − 1) +(−sin(1))
2! (𝑥 − 1)
2+(−cos(1))
3! (𝑥 − 1) 3
+ ⋯
Bila dimisalkan ℎ = 𝑥 − 1, maka diperoleh
sin(𝑥) = sin(1) + cos(1)ℎ +(−sin(1)) 2! ℎ
2 +(−cos(1)) 3! ℎ
3+ ⋯
= 0.8415 + 0.5403ℎ − 0.4208ℎ2− 0.0901ℎ3+ ⋯
Kasus khusus adalah bila fungsi diperluas di sekitar 𝑥0 = 0, maka deretnya dinamakan deret Maclaurin, yang merupakan deret Taylor baku. Deret Taylor yang dipotong sampai suku tingkat ke- 𝑛 dinamakan deret Taylor terpotong dan dinyatakan oleh: 𝑓(𝑥) = 𝑓(𝑥0) + 𝑓′(𝑥 0)(𝑥 − 𝑥0) + 𝑓′′(𝑥 0) 2! (𝑥 − 𝑥0) 2+ ⋯ +𝑓(𝑛)(𝑥0) 𝑛! (𝑥 − 𝑥0) 𝑛 + 𝑅𝑛(𝑥) yang dalam hal ini,
𝑅𝑛(𝑥) =𝑓
(𝑛+1)(𝜉(𝑥))
(𝑛 + 1)! (𝑥 − 𝑥0) 𝑛+1
disebut galat atau sisa (residu).
C. Klasifikasi Persamaan Diferensial
Dalam subbab ini akan dijelaskan definisi persamaan diferensial, persamaan diferensial biasa, persamaan diferensial parsial, derajat (order) dan persamaan diferensial linier/taklinier (Boyce & DiPrima, 1986).
Definisi 2.3
Persamaan diferensial adalah suatu persamaan yang melibatkan turunan satu atau banyak turunan dari fungsi yang tidak diketahui.
Contoh 2.6
Beberapa contoh di bawah ini merupakan persamaan diferensial: 𝑑2𝑦 𝑑𝑥2+ sin(𝑥 + 𝑦) = sin 𝑥 (2.2) 𝑑𝑦 𝑑𝑥= 𝑒 −𝑥− 2𝑦 (2.3) 𝜕2𝑢 𝜕𝑥2+ 𝜕2𝑢 𝜕𝑦2+ 𝜕2𝑢 𝜕𝑧2 = 0 (2.4) Definisi 2.4
Persamaan diferensial biasa adalah suatu persamaan yang melibatkan turunan biasa pada satu variabel bebas atau beberapa variabel.
Contoh 2.7
Contoh persamaan diferensial biasa ditunjukkan oleh persamaan (2.2) dan (2.3). Persamaan (2.2) adalah persamaan diferensial biasa dengan 𝑦 sebagai variabel terikat dan 𝑥 sebagai variabel bebas. Persamaan (2.3) adalah persamaan diferensial biasa dengan 𝑦 sebagai variabel terikat dan 𝑥 sebagai variabel bebas.
Definisi 2.5
Persamaan diferensial parsial adalah suatu persamaan yang melibatkan turunan parsial pada satu variabel bebas atau beberapa variabel.
Contoh 2.8
Contoh persamaan diferensial parsial ditunjukkan oleh persamaan (2.4). Persamaan (2.4) adalah persamaan diferensial parsial dengan 𝑢 sebagai variabel terikat dan 𝑥, 𝑦, 𝑧 sebagai variabel bebas.
Definisi 2.6
Orde dari persamaan diferensial didefinisikan sebagai tingkat tertinggi dari turunan yang muncul pada persamaan diferensial. Persamaan umum dari orde 𝑛 berbentuk
𝐹(𝑥, 𝑦, 𝑦′, … , 𝑦(𝑛)) = 0 (2.5) disebut persamaan diferensial biasa berorde 𝑛.
Contoh 2.9
Persamaan (2.2) adalah contoh persamaan diferensial biasa orde dua. Persamaan (2.3) adalah contoh persamaan diferensial biasa orde satu. Persamaan (2.4) adalah contoh persamaan diferensial parsial orde dua.
Definisi 2.7
Sebuah persamaan (2.5) disebut linier jika fungsi 𝐹 adalah fungsi linier dari variabel 𝑦, 𝑦′, … , 𝑦(𝑛). Bentuk umum persamaan diferensial linier orde ke-𝑛 dinyatakan
𝑎0(𝑥)𝑦(𝑛)+ 𝑎
1(𝑥)𝑦(𝑛−1)+ ⋯ 𝑎𝑛(𝑥)𝑦 = 𝑔(𝑥). (2.6) dengan 𝑎0 tidak sama dengan 0.
Contoh 2.10
Diambil dari buku Strauss (1992):
Persamaan (2.7) adalah persamaan diferensial biasa linier orde dua. Persamaan (2.7) dengan 𝑦 sebagai variabel terikat dan turunannya terjadi hanya pangkat satu saja dan tidak ada perkalian 𝑦.
Definisi 2.8
Sebuah persamaan diferensial biasa yang tidak memiliki bentuk (2.6) disebut persamaan diferensial biasa tak linier.
Contoh 2.11
Contoh persamaan biasa tak linier (Strauss, 1992): 𝑑3𝑦 𝑑𝑥3+ 2𝑒 𝑥 𝑑2𝑦 𝑑𝑥2+ 𝑦 𝑑𝑦 𝑑𝑥= 𝑥 4 (2.8)
Persamaan (2.8) adalah persamaan tak linier karena terdapat suku 𝑦𝑑𝑦 𝑑𝑥 yang melibatkan perkalian dengan variabel terikat pada turunan pertamanya.
D. Pendekatan Numeris Persamaan Diferensial
Dalam subbab ini akan dibahas mengenai penurunan numeris beserta contohnya dan penjelasan tiga pendekatan numeris dalam menghitung turunan numeris yaitu hampiran beda maju, hampiran beda mundur, hampiran beda pusat. Tiga Pendekatan untuk Menghitung Turunan Numeris
Misal diberikan nilai-nilai 𝑥 di 𝑥0− ℎ, 𝑥0, dan 𝑥0+ ℎ, serta nilai fungsi untuk nilai-nilai 𝑥 tersebut. Dalam hal ini 𝑥1 = 𝑥0+ ℎ dan 𝑥−1 = 𝑥0− ℎ. Terdapat tiga pendekatan dalam menghitung nilai 𝑓′(𝑥0).
1. Hampiran beda maju
Diketahui fungsi 𝑦 = 𝑓(𝑥0). Turunan 𝑓′(𝑥0) didefinisikan oleh
𝑓′(𝑥0) = lim ℎ→0 𝑓(𝑥0+ ℎ) − 𝑓(𝑥0) ℎ ≈𝑓(𝑥0+ ℎ) − 𝑓(𝑥0) ℎ
2. Hampiran beda mundur
𝑓′(𝑥0) = lim ℎ→0 𝑓(𝑥0) − 𝑓(𝑥0− ℎ) ℎ ≈𝑓(𝑥0) − 𝑓(𝑥0− ℎ) ℎ
3. Hampiran beda pusat
Diketahui fungsi 𝑦 = 𝑓(𝑥0). Turunan 𝑓′(𝑥0) didefinisikan oleh
𝑓′(𝑥0) = lim ℎ→0 𝑓(𝑥0+ ℎ) − 𝑓(𝑥0− ℎ) 2ℎ ≈ 𝑓(𝑥0+ ℎ) − 𝑓(𝑥0− ℎ) 2ℎ
Tafsiran geometri dari ketiga pendekatan di atas diperlihatkan pada Gambar 2.1
a). Hampiran beda mundur
b). Hampiran beda pusat
𝑥0− ℎ 𝑥0 𝑓(𝑥) 𝑥 ℎ 𝑥0− ℎ 𝑥0+ ℎ 𝑓(𝑥) 𝑥 2ℎ 𝑥0
c). Hampiran beda maju
Gambar 2.1. Tiga pendekatan dalam perhitungan turunan numeris
Pada Gambar 2.1 memberikan ilustrasi berdasarkan pendekatan beda maju, beda mundur, dan beda pusat. Pendekatan beda maju, dimana titik yang digunakan ialah saat 𝑥0 dan 𝑥1 = 𝑥0+ ℎ dengan ℎ = 𝑥1− 𝑥0. Pendekatan beda mundur, dimana titik yang digunakan ialah saat 𝑥0 dan 𝑥−1 = 𝑥0 − ℎ dengan ℎ = 𝑥0− 𝑥−1. Pendekatan beda pusat, dimana titik yang digunakan ialah saat 𝑥1 = 𝑥0+ ℎ dan 𝑥−1= 𝑥0− ℎ dengan ℎ = 𝑥1− 𝑥0 dan ℎ = 𝑥0− 𝑥−1.
Penurunan Rumus Turunan dengan Deret Taylor
Misalkan diberikan titik-titik (𝑥𝑖, 𝑓𝑖), 𝑖 = 0,1,2, … , 𝑛, yang dalam hal ini 𝑥𝑖 = 𝑥0+ 𝑖ℎ
dan
𝑓𝑖 = 𝑓(𝑥𝑖)
Selanjutnya, akan dihitung 𝑓′(𝑥), yang dalam hal ini 𝑥 = 𝑥0+ 𝑠ℎ, 𝑠 ∈ ℝ dengan ketiga pendekatan yang sudah disebutkan di atas (maju, mundur, pusat)
1. Hampiran beda maju Uraikan 𝑓(𝑥𝑖+1) di sekitar 𝑥𝑖 𝑓′(𝑥 𝑖+1) = 𝑓(𝑥𝑖) + 𝑓′(𝑥𝑖)ℎ + 𝑓′′(𝑥𝑖) 2! ℎ 2+ ⋯ (2.9) 𝑓′(𝑥𝑖) ≅𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖) ℎ + 𝑂(ℎ) ℎ = 𝑥𝑖+1− 𝑥𝑖. 𝑥0 𝑥0+ ℎ 𝑓(𝑥) 𝑥 ℎ
dalam hal ini 𝑂(ℎ) =ℎ 2𝑓
′′(𝑡), 𝑥
𝑖 < 𝑡 < 𝑥𝑖+1. 2. Hampiran beda mundur
Deret Taylor dapat diekspansi mundur untuk menghitung nilai sebelumnya berdasarkan nilai sekarang sehingga diperoleh:
𝑓(𝑥𝑖−1) = 𝑓(𝑥𝑖) − 𝑓′(𝑥𝑖)ℎ +
𝑓′′(𝑥𝑖) 2! ℎ
2− ⋯ (2.10)
Jika kita memotong deret Taylor setelah turunan orde satu pada persamaan (2.10) maka akan diperoleh:
𝑓′(𝑥𝑖) ≅ 𝑓(𝑥𝑖) − 𝑓(𝑥𝑖−1) ℎ + 𝑂(ℎ) = ∇𝑓𝑖 ℎ dimana 𝑂(ℎ) = ℎ 2𝑓 ′′(𝑡), 𝑥
𝑖−1< 𝑡 < 𝑥𝑖 sebagai error dan ∇𝑓𝑖 sebagai beda mundur.
3. Hampiran beda pusat
Pendekatan beda pusat diperoleh dengan mengurai ekspansi deret Taylor maju dengan ekspansi deret Taylor mundur atau mencari rata-rata beda maju dan beda mundur.
Kurangkan persamaaan (2.9) dan persamaaan (2.10) sehingga diperoleh 𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖−1) = 2𝑓′(𝑥 𝑖)ℎ + 𝑓(3)(𝑥𝑖) 3! ℎ 3+ ⋯ atau 2𝑓′(𝑥𝑖)ℎ = 𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖−1) − 𝑓(3)(𝑥𝑖) 3! ℎ 3+ ⋯
Kedua ruas dibagi dengan 2ℎ sehingga diperoleh
𝑓′(𝑥𝑖) = 𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖−1) 2ℎ − 𝑓(3)(𝑥𝑖) 6 ℎ 2− ⋯ atau 𝑓′(𝑥𝑖) =𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖−1) 2ℎ + 𝑂(ℎ 2) dimana 𝑂(ℎ2) = −ℎ2 6 𝑓 (3)(𝑡), 𝑥 𝑖−1< 𝑡 < 𝑥𝑖+1.
Rumus Turunan Kedua Dengan Deret Taylor 1. Hampiran beda pusat
Tambahkan hampiran beda maju dan hampiran beda mundur
𝑓(𝑥𝑖+1) + 𝑓(𝑥𝑖−1) = 2𝑓(𝑥𝑖) + 𝑓′′(𝑥𝑖)ℎ2+ 𝑓(4)(𝑥𝑖) 12 ℎ 4+ ⋯ 𝑓(𝑥𝑖+1) − 2𝑓(𝑥𝑖) + 𝑓(𝑥𝑖−1) = 𝑓′′(𝑥𝑖)ℎ2+ 𝑓(4)(𝑥𝑖) 12 ℎ 4+ ⋯ 𝑓′′(𝑥𝑖) = 𝑓(𝑥𝑖+1) − 2𝑓(𝑥𝑖) + 𝑓(𝑥𝑖−1) ℎ2 − 𝑓(4)(𝑥𝑖) 12 ℎ 2 jadi, 𝑓′′(𝑥 𝑖) = 𝑓(𝑥𝑖+1) − 2𝑓(𝑥𝑖) + 𝑓(𝑥𝑖−1) ℎ2 + 𝑂(ℎ2) 2. Hampiran beda mundur
Dengan cara yang sama seperti turunan kedua hampiran beda pusat di atas diperoleh
𝑓′′(𝑥𝑖) =
𝑓(𝑥𝑖−2) − 2𝑓(𝑥𝑖−1) + 𝑓(𝑥𝑖)
ℎ2 + 𝑂(ℎ)
3. Hampiran beda maju
Dengan cara yang sama seperti turunan kedua hampiran beda pusat di atas diperoleh
𝑓′′(𝑥𝑖) =
𝑓(𝑥𝑖+2) − 2𝑓(𝑥𝑖+1) + 𝑓(𝑥𝑖)
ℎ2 + 𝑂(ℎ)
Menentukan Orde Galat
Dalam penurunan rumus turunan numeris dengan deret Taylor, rumus galat dalam penurunan rumus turunan numeris dapat langsung diperoleh dengan bantuan deret Taylor.
Contoh:
Rumus galat dari rumus turunan numeris hampiran beda pusat
𝑓′(𝑥𝑖) =𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖−1)
2ℎ + 𝑬
𝑬 = 𝑓′(𝑥𝑖) − 𝑓(𝑥𝑖+1) − 𝑓(𝑥𝑖−1) 2ℎ = 𝑓′(𝑥𝑖) − 1 2ℎ[(𝑓(𝑥𝑖) + 𝑓 ′(𝑥 𝑖)ℎ + 𝑓′′(𝑥𝑖) 2! ℎ 2+𝑓 ′′′(𝑥 𝑖) 3! ℎ 3+ ⋯ ) − (𝑓(𝑥𝑖) − 𝑓′(𝑥 𝑖)ℎ + 𝑓′′(𝑥𝑖) 2! ℎ 2+𝑓 ′′′(𝑥 𝑖) 3! ℎ 3+ ⋯ )] = 𝑓′(𝑥𝑖) − 1 2ℎ(2ℎ𝑓′(𝑥𝑖) + 𝑓′′′(𝑥𝑖) 3! ℎ 3+ ⋯ ) = 𝑓′(𝑥𝑖) − 𝑓′(𝑥𝑖) −𝑓 ′′′(𝑥 𝑖) 6 ℎ 2+ ⋯ = −𝑓 ′′′(𝑥 𝑖) 6 ℎ 2+ ⋯ = −ℎ 2 6 𝑓 (3)(𝑡), 𝑥 𝑖−1< 𝑡 < 𝑥𝑖+1 = 𝑂(ℎ2)
E. Klasifikasi Persamaan Diferensial Parsial
Persamaan diferensial parsial linear berderajat dua dapat dituliskan ke dalam bentuk umum yaitu (LeVeque, 2007):
𝐴𝜕 2𝑢 𝜕𝑥2 + 𝐵 𝜕2𝑢 𝜕𝑦2+ 𝐶 𝜕2𝑢 𝜕𝑥𝜕𝑦+ 𝐷 = 0
Dimana 𝐴, 𝐵, dan 𝐶 adalah fungsi dari 𝑥 dan 𝑦. Sedangkan 𝐷 adalah fungsi dari 𝑥, 𝑦, 𝑢,𝜕𝑢
𝜕𝑥, dan 𝜕𝑢
𝜕𝑦. Persamaan diferensial parsial linear berderajat dua dan fungsi dua variable bebas (𝑥, 𝑦) dapat dikelompokkan menjadi tiga kategori berdasarkan nilai diskriminan yaitu:
a. Persamaan diferensial parsial dikatakan persamaan eliptik jika nilai diskriminan 𝐵2− 4𝐴𝐶 < 0
Salah satu contoh persamaan eliptik adalah persamaan Laplace dalam bentuk 𝜕
2𝑇 𝜕𝑥2+
𝜕2𝑇 𝜕𝑦2= 0
b. Persamaan diferensial parsial dikatakan persamaan parabolik jika nilai diskriminan 𝐵2− 4𝐴𝐶 = 0
Salah satu contoh persamaan parabolik adalah persamaan konduksi panas dalam bentuk 𝜕𝑇
𝜕𝑡 = 𝑘 𝜕2𝑇 𝜕𝑥2
c. Persamaan diferensial parsial dikatakan persamaan hiperbolik jika nilai diskriminan 𝐵2− 4𝐴𝐶 > 0
Salah satu contoh persamaan hiperbolik adalah persamaan gelombang
dalam bentuk 𝜕 2𝑦 𝜕2𝑥 = 1 𝑐2 𝜕2𝑦 𝜕𝑡2
F. Metode Beda Hingga
Metode beda hingga adalah salah satu metode numerik yang digunakan untuk menyelesaikan persamaan diferensial parsial. Untuk menyelesaikan persamaan tersebut metode beda hingga memanfaatkan deret Taylor dengan cara mengaproksimasi atau melalui pendekatan turunan-turunan persamaan diferensial parsial menjadi sistem persamaan linier.
Metode beda hingga memberikan nilai fungsi 𝑢 = 𝑢(𝑥, 𝑡) pada domain [0, 𝐿] × [0, 𝑇]. Dengan domain [0, 𝐿] × [0, 𝑇] yang dibagi menjadi beberapa bagian persegi panjang yang sama sisi: ∆𝑥 = ℎ dan ∆𝑡 = 𝑘 sehingga (Smith, 1985)
𝑥𝑖 = 𝑖 ∙ ℎ, 𝑖 = 0, ±1, ±2, … , 𝑀 dan
𝑡𝑛 = 𝑛 ∙ 𝑘, 𝑛 = 0,1,2, … , 𝑁
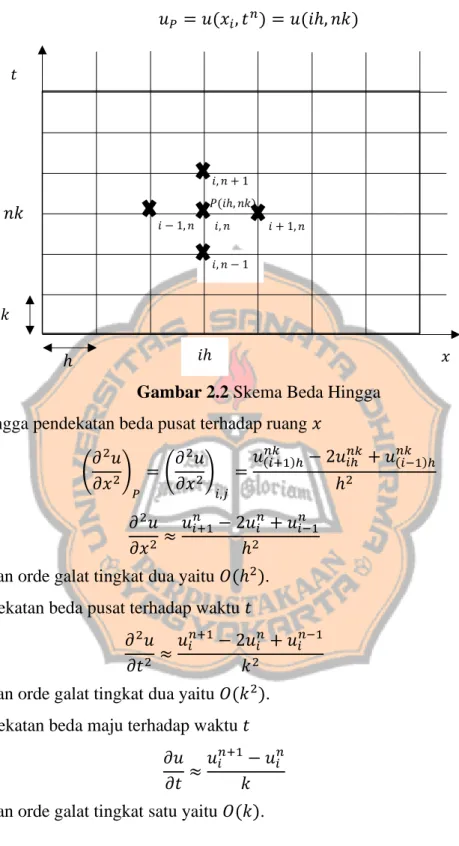
Misalkan 𝑥 = 𝑥𝑖, 𝑡 = 𝑡𝑛 dan pendekatan numeriknya pada titik (𝑥𝑖, 𝑡𝑛), dinotasikan dengan 𝑃(𝑖ℎ, 𝑛𝑘)
𝑖, 𝑛 − 1 𝑖, 𝑛 𝑖, 𝑛 + 1 𝑖 − 1, 𝑛 𝑖 + 1, 𝑛 𝑃(𝑖ℎ, 𝑛𝑘) 𝑢𝑃 = 𝑢(𝑥𝑖, 𝑡𝑛) = 𝑢(𝑖ℎ, 𝑛𝑘) ℎ
Gambar 2.2 Skema Beda Hingga Sehingga pendekatan beda pusat terhadap ruang 𝑥
(𝜕 2𝑢 𝜕𝑥2) 𝑃 = (𝜕 2𝑢 𝜕𝑥2) 𝑖,𝑗 = 𝑢(𝑖+1)ℎ 𝑛𝑘 − 2𝑢 𝑖ℎ 𝑛𝑘 + 𝑢 (𝑖−1)ℎ𝑛𝑘 ℎ2 𝜕2𝑢 𝜕𝑥2 ≈ 𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛 + 𝑢𝑖−1𝑛 ℎ2 (2.11)
dengan orde galat tingkat dua yaitu 𝑂(ℎ2). Pendekatan beda pusat terhadap waktu 𝑡
𝜕2𝑢 𝜕𝑡2 ≈
𝑢𝑖𝑛+1− 2𝑢𝑖𝑛 + 𝑢𝑖𝑛−1 𝑘2
(2.12)
dengan orde galat tingkat dua yaitu 𝑂(𝑘2). Pendekatan beda maju terhadap waktu 𝑡
𝜕𝑢 𝜕𝑡 ≈
𝑢𝑖𝑛+1− 𝑢𝑖𝑛 𝑘
(2.13)
dengan orde galat tingkat satu yaitu 𝑂(𝑘). 𝑘
𝑛𝑘
𝑖ℎ 𝑥
G. Metode Beda Hingga Skema Eksplisit
Diketahui dari persamaan (2.13) dan (2.11) berbentuk (Smith, 1985) 𝜕𝑢
𝜕𝑡 = 𝜕2𝑢 𝜕𝑥2 atau dapat dituliskan
𝑢𝑖𝑛+1− 𝑢𝑖𝑛
𝑘 =
𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛 + 𝑢𝑖−1𝑛 ℎ2
dimana 𝑢 adalah solusi eksak dari pendekatan persamaan turunan, 𝑥𝑖 = 𝑖 ∙ ℎ, 𝑖 = 0, ±1, ±2, … , 𝑀
dan
𝑡𝑛 = 𝑛 ∙ 𝑘, 𝑛 = 0,1,2, … , 𝑁 sehingga skema eksplisitnya dapat ditulis
𝑢𝑖𝑛+1 = 𝑟𝑢𝑖−1𝑛 + (1 − 2𝑟)𝑢𝑖𝑛+ 𝑟𝑢𝑖+1𝑛 , dimana 𝑟 = ∆𝑡
∆𝑥2 = 𝑘
ℎ2 dan diberikan rumus untuk mengetahui nilai suhu 𝑢𝑖
𝑛+1 yang
tidak diketahui pada titik (𝑖, 𝑛 + 1) ketika diketahui suhu di sepanjang waktu ke 𝑛. Oleh karena itu kita dapat menghitung nilai suhu pada saat suhu 𝑡 = 𝑘 dan nilai awal 𝑡 = 0.
Jadi skema eksplisit ini adalah menentukan nilai suhu yang tidak diketahui di waktu yang akan datang dari nilai suhu yang sudah diketahui di waktu saat ini.
21 BAB III
SKEMA NUMERIS UNTUK PERSAMAAN ADVEKSI-DIFUSI
Dalam bab ini akan dibahas solusi numeris untuk menyelesaikan persamaan adveksi-difusi dengan menggunakan skema Lax-Wendroff dan skema beda hingga tak standar.
A. Hukum Kekekalan
Hukum kekekalan muncul dari prinsip fisika dapat dilihat dengan menurunkan persamaan kekekalan massa dalam masalah dinamika gas satu dimensi. Misalkan aliran dalam tabung dimana sifat dari gas yaitu kepadatan dan kecepatan diasumsikan konstan di setiap bagian lintasan dari tabung. Asumsikan 𝑥 jarak sepanjang tabung, 𝜌(𝑥, 𝑡) adalah massa jenis dari gas di titik 𝑥 dan waktu 𝑡. Kepadatan didefinisikan dari massa total gas di setiap titik sepanjang 𝑥1 hingga 𝑥2 maka diperoleh integral kepadatan, yaitu (LeVeque, 1992):
massa pada [𝑥1, 𝑥2] dengan waktu 𝑡 = ∫ 𝜌(𝑥, 𝑡) 𝑑𝑥𝑥2
𝑥1 . (3.1)
Misalkan 𝑣(𝑥, 𝑡) adalah kecepatan dari gas pada titik 𝑥 dan waktu 𝑡. Diberikan laju aliran, atau fluks dari gas yang melewati titik 𝑥, yaitu:
massa aliran pada (𝑥, 𝑡) = 𝜌(𝑥, 𝑡)𝑣(𝑥, 𝑡). (3.2) Laju perubahan massa [𝑥1, 𝑥2] diberikan selisih fluks pada 𝑥1 dan 𝑥2:
𝑑
𝑑𝑡∫ 𝜌(𝑥, 𝑡) 𝑑𝑥 𝑥2
𝑥1
= 𝜌(𝑥1, 𝑡)𝑣(𝑥1, 𝑡) − 𝜌(𝑥2, 𝑡)𝑣(𝑥2, 𝑡). (3.3)
Kemudian mengintegralkan persamaan pada waktu 𝑡1 hingga 𝑡2, dengan diberikan massa pada [𝑥1, 𝑥2] di waktu 𝑡2 > 𝑡1 sehingga massa pada waktu 𝑡1 dan total (integral) fluks pada setiap batas selama periode, diperoleh:
∫ 𝜌(𝑥, 𝑡2) 𝑑𝑥 𝑥2 𝑥1 = ∫ 𝜌(𝑥, 𝑡1) 𝑑𝑥 + 𝜌(𝑥1, 𝑡)𝑣(𝑥1, 𝑡)𝑑𝑡 𝑥2 𝑥1 − 𝜌(𝑥2, 𝑡)𝑣(𝑥2, 𝑡)𝑑𝑡. (3.4)
Dari persamaan (3.4) asumsikan 𝜌(𝑥, 𝑡) dan 𝑣(𝑥, 𝑡) fungsi terdiferensial sehingga gunakan 𝜌(𝑥, 𝑡2) − 𝜌(𝑥, 𝑡1) = ∫ 𝜕 𝜕𝑡𝜌(𝑥, 𝑡)𝑑𝑡 𝑡2 𝑡1 (3.5) dan 𝜌(𝑥2, 𝑡)𝑣(𝑥2, 𝑡) − 𝜌(𝑥1, 𝑡)𝑣(𝑥1, 𝑡) = ∫ 𝜕 𝜕𝑥 𝑥2 𝑥1 (𝜌(𝑥, 𝑡)𝑣(𝑥, 𝑡))𝑑𝑥 (3.6)
pada persamaan (3.4) menjadi
∫ ∫ {𝜕 𝜕𝑡𝜌(𝑥, 𝑡) + 𝜕 𝜕𝑥(𝜌(𝑥, 𝑡)𝑣(𝑥, 𝑡))} 𝑥2 𝑥1 𝑡2 𝑡1 𝑑𝑥𝑑𝑡 = 0 (3.7)
berlaku untuk setiap titik pada [𝑥1, 𝑥2] dan interval waktu pada [𝑡1, 𝑡2]. Persamaan (3.7) menyimpulkan integral dari kekekalan massa harus bernilai nol, yaitu:
𝜌𝑡+ (𝜌𝑣)𝑥 = 0. (3.8) Hukum kekekalan (3.8) dapat diselesaikan secara terpisah hanya jika kecepatan 𝑣(𝑥, 𝑡) dikenal sebagai fungsi dari 𝜌(𝑥, 𝑡). Sehingga 𝜌𝑣 adalah fungsi dari 𝜌 dan dapat dituliskan 𝜌𝑣 = 𝑓(𝜌). Persamaan kekekalan massa (3.8) menjadi hukum kekekalan skalar untuk 𝜌, yaitu:
𝜌𝑡+ 𝑓(𝜌)𝑥= 0. (3.9) Persamaan (3.8) dapat diselesaikan secara khusus dengan persamaan kekekalan momentum dan kekekalan energi. Persamaan dinamika gas untuk kasus persamaan Euler adalah
(𝜌𝑣)𝑡+ (𝜌𝑣2+ 𝑝)
𝑥 = 0 kekekalan momentum (3.10) 𝐸𝑡+ (𝑣(𝐸 + 𝜌))𝑥 = 0 kekekalan energi (3.11) Persamaan (3.11) melibatkan kuantitas lain yaitu tekanan 𝑝, dimana 𝜌, 𝜌𝑣, dan 𝐸 adalah kuantitas kekekalan.
Jika diberikan vektor 𝑢 ∈ ℝ3
𝑢(𝑥, 𝑡) = [ 𝜌(𝑥, 𝑡) 𝜌(𝑥, 𝑡)𝑣(𝑥, 𝑡) 𝐸(𝑥, 𝑡) ] = [ 𝑢1 𝑢2 𝑢3], (3.12)
maka sistem persamaan (3.8), (3.10), (3.11) dapat ditulis menjadi
dimana 𝑓(𝑢) = [ 𝜌𝑣 𝜌𝑣2+ 𝑝 𝑣(𝐸 + 𝑝) ] = [ 𝑢2 𝑢22/𝑢1 + 𝑝(𝑢) 𝑢2(𝑢3+ 𝑝(𝑢))/𝑢1 ], (3.14)
Secara umum integral dari hukum kekekalan dapat ditulis 𝑑
𝑑𝑡∫ 𝑢(𝑥, 𝑡)𝑑𝑥 = 𝑓(𝑢(𝑥1, 𝑡)) − 𝑓(𝑢(𝑥2, 𝑡)) 𝑥2
𝑥1
(3.15)
untuk semua 𝑥1, 𝑥2, 𝑡. Ekivalensi dengan integral pada 𝑡1 hingga 𝑡2, yaitu:
∫ 𝑢(𝑥, 𝑡2) 𝑑𝑥 𝑥2 𝑥1 = ∫ 𝑢(𝑥, 𝑡1) 𝑑𝑥 + ∫ 𝑓(𝑢 𝑡2 𝑡1 (𝑥1, 𝑡))𝑑𝑡 𝑥2 𝑥1 − ∫ 𝑓(𝑢 𝑡2 𝑡1 (𝑥2, 𝑡)𝑑𝑡 (3.16) untuk semua 𝑥1, 𝑥2, 𝑡1, 𝑡2. B. Persamaan Adveksi
Sebelum masuk ke dalam persamaan adveksi, kita dapat melihat contoh dari persamaan kekekalan massa (3.8) dalam kasus ini 𝑣 diketahui fungsi dari 𝜌(𝑥, 𝑡). Dalam hal ini tidak berlaku dalam kasus dinamika gas tetapi berlaku dalam model sederhana arus lalu lintas di sepanjang jalan raya. Dimana 𝜌 adalah kepadatan kendaraan dan kecepatan mengemudi diasumsikan hanya bergantung pada kepadatan lokal (LeVeque, 1992).
Fungsi fluks yang bergantung pada 𝑥, 𝜌 dan 𝑡,
𝑓(𝜌, 𝑥, 𝑡) = 𝜌𝑣(𝑥, 𝑡). (3.17) Jika kecepatan konstan, 𝑣(𝑥, 𝑡) = 𝑎, maka 𝑓(𝜌) = 𝑎𝜌 dan persamaan (3.8) dapat ditulis
𝜌𝑡+ 𝑎𝜌𝑥 = 0. (3.18)
Persamaan (3.18) adalah persamaan linear adveksi atau persamaan gelombang satu arah. Solusi persamaan untuk 𝑡 ≥ 0 dengan kondisi awal
diasumsikan 𝜌𝑜 diketahui
𝜌(𝑥, 𝑡) = 𝜌𝑜(𝑥 − 𝑎𝑡). (3.20) Jika profil awal hanya bergerak ke hilir dengan kecepatan 𝑎, maka bentuknya tidak berubah. Persamaan (3.20) penyelesaian untuk nilai awal 𝜌𝑜(𝑥) pada saat waktu 0.
C. Persamaan Difusi
Diberikan contoh konsentrasi profil bergerak ke hilir, yang secara fisika konsentrasi profil tidak berubah. Sehingga dalam kasus ini terjadi perpaduan antara difusi dan adveksi. Perpaduan disebabkan oleh turbulensi dalam cairan yang diabaikan pada model satu dimensi yang sederhana ini. Difusi molekuler terjadi dalam aliran yang bergerak dengan kecepatan konstan. Kecepatan pada kasus ini adalah kecepatan rata-rata makroskopik molekul. Molekul meninggalkan secara acak dan kecepatan didistribusikan secara rata-rata. Molekul-molekul kimia mengalami gerakan acak sehingga molekul-molekul bergerak dari konsentrasi tinggi dan menuju ke konsentrasi yang rendah. Sehingga hukum kekekalan dapat dimodifikasi dengan pendekatan fungsi fluks (LeVeque, 1992).
Pertimbangkan fluks bahan kimia yang melewati beberapa titik 𝑥 dalam tabung. Tambahkan fluks adveksi 𝑎𝜌 dan juga fluks bersih karena konsentrasi profil tidak rata pada titik 𝑥. Fluks ditentukan oleh Hukum Fourier dari konduksi panas yang mengatakan fluks difusi sebanding dengan gradien konsentrasi
Fluks difusi= −𝐷𝜌𝑥 (3.21) Dengan koefisien difusi 𝐷 > 0 bergantung pada variansi dari komponen acak dari kecepatan partikel. Persamaan (3.21) tanda minus berarti fluks bersih bergerak dari konsentrasi tinggi. Kemudian mengabungkan fluks difusi dengan fluks adveksi
𝑓(𝜌, 𝜌𝑥) = 𝑎𝜌 − 𝐷𝜌𝑥 (3.22) dan hukum kekekalannya menjadi
𝜌𝑡+ (𝑎𝜌 − 𝐷𝜌𝑥)𝑥 = 0 (3.23) asumsikan 𝐷 konstan
Persamaan (3.24) merupakan persamaan adveksi-difusi secara khusus.
D. Skema Eksplisit untuk Persamaan Adveksi-Difusi
Pada bagian ini akan dibahas mengenai persamaan adveksi-difusi dengan metode beda hingga dalam skema eksplisit (Paskalia, 2014)
Persamaan adveksi-difusi satu dimensi yang bersifat parabolik 𝜕𝑢 𝜕𝑡 + 𝑎 𝜕𝑢 𝜕𝑥 = 𝛼 𝜕2𝑢 𝜕𝑥2, 0 < 𝑥 < 𝐿, (3.25) kondisi awal 𝑢(𝑥, 0) = 𝑓(𝑥), dan kondisi batas
𝑢(0, 𝑡) = 𝑔(𝑡), 0 < 𝑡 ≤ 𝑇, 𝑢(𝐿, 𝑡) = 𝑞(𝑡), 0 < 𝑡 ≤ 𝑇. Secara umum 𝑥𝑖 = (ℎ)𝑖 𝑖 = 0, ±1, ±2, … , 𝑀 dan 𝑡𝑛 = (𝑘)𝑛 𝑛 = 0,1,2, … , 𝑁 dimana ℎ = ∆𝑥, ℎ = 𝐿/𝑀 dan 𝑘 = ∆𝑡, 𝑘 = 𝑇/𝑁.
Misalkan 𝑥 = 𝑥𝑖, 𝑡 = 𝑡𝑛 dan pendekatan numerik pada titik (𝑥
𝑖, 𝑡𝑛) dinotasikan dengan 𝑢𝑖𝑛 = (𝑥𝑖, 𝑡𝑛). Banyaknya langkah untuk ruang dinotasikan dengan 𝑀 dengan 𝑀 ∈ 𝑍+ dan jumlah langkah untuk waktu adalah 𝑁 dengan 𝑁 ∈ 𝑍+.
Dalam menyelesaikan persamaan adveksi-difusi skema eksplisit dipertimbangkan pendekatan dari turunan persamaan adveksi-difusi yang menggabungkan bobot waktu 𝜃.
Dipilih beda maju untuk mendikritisasi langkah waktu 𝜕𝑢
𝜕𝑡 sehingga diperoleh 𝜕𝑢
𝜕𝑡 =
𝑢𝑖𝑛+1− 𝑢𝑖𝑛 𝑘 Pendekatan terhadap langkah ruang 𝜕𝑢
𝜕𝑥 dan 𝜕2𝑢
𝜕𝑥2 akan didiskritisasi dengan turunan pertama dan kedua beda pusat. Turunan pertama beda pusat 𝜕𝑢
𝜕𝑥 diperoleh 𝜕𝑢
𝜕𝑥=
𝑢𝑖+1𝑛 − 𝑢𝑖−1𝑛 2ℎ
dan mengambil setengah beda mundur pada waktu 𝑡𝑛 𝜕𝑢
𝜕𝑥=
𝑢𝑖𝑛− 𝑢𝑖−1𝑛 ℎ Sehingga diperoleh pendekatan untuk 𝜕𝑢
𝜕𝑥 yaitu 𝜕𝑢 𝜕𝑥= 1 2ℎ[𝑢𝑖 𝑛− 𝑢 𝑖−1𝑛 + 𝑢𝑖+1𝑛 − 𝑢𝑖−1𝑛 ] kedua ruas dikali 𝑎(𝑖, 𝑛) diperoleh
𝑎𝜕𝑢 𝜕𝑥 = 𝑎 { 𝜃 2ℎ[𝑢𝑖 𝑛− 𝑢 𝑖−1 𝑛 ] +1 − 𝜃 2ℎ [𝑢𝑖+1 𝑛 − 𝑢 𝑖−1 𝑛 ]}
dimana 𝜃 faktor bobot.
Turunan kedua beda pusat 𝜕 2𝑢
𝜕𝑥2 dapat diaproksimasi dengan 𝜕2𝑢 𝜕𝑥2 = 𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛+ 𝑢𝑖−1𝑛 ℎ2 Sehingga pendekatan 𝜕 2𝑢 𝜕𝑥2 dapat dituliskan 𝛼𝜕 2𝑢 𝜕𝑥2 = 𝛼 [ 𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛+ 𝑢𝑖−1𝑛 ℎ2 ]
Dipandang dari persamaan (3.25) persamaan adveksi-difusi diperoleh 𝑢𝑖𝑛+1− 𝑢𝑖𝑛 𝑘 + 𝑎 { 𝜃 2ℎ[𝑢𝑖 𝑛− 𝑢 𝑖−1 𝑛 ] +1 − 𝜃 2ℎ [𝑢𝑖+1 𝑛 − 𝑢 𝑖−1 𝑛 ]} = 𝛼 [𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛+ 𝑢𝑖−1𝑛 ℎ2 ]
Kedua ruas dikalikan 𝑘 maka diperoleh
𝑢𝑖𝑛+1− 𝑢𝑖𝑛+ 𝑎𝑘 {𝜃 2ℎ[𝑢𝑖 𝑛− 𝑢 𝑖−1𝑛 ] + 1 − 𝜃 2ℎ [𝑢𝑖+1 𝑛 − 𝑢 𝑖−1𝑛 ]} = 𝛼𝑘 [𝑢𝑖+1 𝑛 − 2𝑢 𝑖 𝑛 + 𝑢 𝑖−1𝑛 ℎ2 ] (3.26) atau 𝑢𝑖𝑛+1− 𝑢𝑖𝑛+𝑎𝑘𝜃 2ℎ [𝑢𝑖 𝑛− 𝑢 𝑖−1 𝑛 ] +𝑎𝑘(1 − 𝜃) 2ℎ [𝑢𝑖+1 𝑛 − 𝑢 𝑖−1𝑛 ] =𝛼𝑘 ℎ2[𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛 + 𝑢𝑖−1𝑛 ] (3.27)
𝑢𝑖𝑛+1= 𝑢𝑖𝑛−𝑎𝑘𝜃 2ℎ (𝑢𝑖 𝑛) −2𝛼𝑘 ℎ2 (𝑢𝑖 𝑛) +𝑎𝑘𝜃 2ℎ (𝑢𝑖−1 𝑛 ) +𝑎𝑘(1 − 𝜃) 2ℎ (𝑢𝑖−1 𝑛 ) +𝛼𝑘 ℎ2(𝑢𝑖−1𝑛 ) − 𝑎𝑘(1 − 𝜃) 2ℎ (𝑢𝑖+1 𝑛 ) +𝛼𝑘 ℎ2(𝑢𝑖+1𝑛 ) (3.28) 𝐶𝑟 =𝑎𝑘
ℎ merupakan bilangan Courant dan 𝑃𝑒 = 𝑎ℎ
𝛼 merupakan bilangan Peclet, sehingga skema ekplisitnya dapat ditulis
𝑢𝑖𝑛+1 =1 2[2 ( 𝐶𝑟 𝑃𝑒) + 𝐶𝑟(1 + 𝜃)] (𝑢𝑖−1 𝑛 ) + [1 − 2 (𝐶𝑟 𝑃𝑒) − 𝐶𝑟𝜃] (𝑢𝑖 𝑛) +1 2[2 ( 𝐶𝑟 𝑃𝑒) − 𝐶𝑟(1 − 𝜃)] (𝑢𝑖+1 𝑛 ) (3.29)
untuk 1 ≤ 𝑖 ≤ 𝑀 − 1 dan 1 ≤ 𝑖 ≤ 𝑁 − 1 (Karahan, 2008).
Skema Lax-Wendroff untuk Persamaan Adveksi-Difusi
Dari persamaan (3.29) untuk 𝜃 = 𝐶𝑟 diperoleh skema Lax-Wendroff (Karahan, 2008) 𝑢𝑖𝑛+1 =1 2[2 ( 𝐶𝑟 𝑃𝑒) + 𝐶𝑟 + (𝐶𝑟) 2] (𝑢 𝑖−1𝑛 ) + [1 − 2 ( 𝐶𝑟 𝑃𝑒) − (𝐶𝑟) 2] (𝑢 𝑖𝑛) +1 2[2 ( 𝐶𝑟 𝑃𝑒) − 𝐶𝑟 + (𝐶𝑟) 2] (𝑢 𝑖+1 𝑛 ) (3.30)
E. Skema Beda Hingga Tak Standar untuk Persamaan Adveksi-Difusi Dipandang persamaan adveksi-difusi pada persamaan (3.25), yaitu
𝑢𝑡+ 𝑎𝑢𝑥 = 𝛼𝑢𝑥𝑥 dimana 𝛼 adalah positif konstan.
Secara umum
𝑥𝑖 = (ℎ)𝑖 𝑖 = ⋯ , −1,0,1,2, … (3.31) dan
𝑡𝑛 = (𝑘)𝑛 𝑛 = 0,1,2, … dimana ℎ = ∆𝑥 dan 𝑘 = ∆𝑡.
Misalkan 𝑥 = 𝑥𝑖, 𝑡 = 𝑡𝑛 dan pendekatan numerik pada titik (𝑥
𝑖, 𝑡𝑛) dinotasikan dengan
Dari persamaan (3.25) mempunyai 3 sub persamaan dengan 𝑎 = 1 (Mickens, 1991 & 2000)
𝑢𝑡+ 𝑢𝑥= 0, (3.33)
𝑢𝑡 = 𝛼𝑢𝑥𝑥, (3.34)
𝑢𝑥 = 𝛼𝑢𝑥𝑥. (3.35)
Berdasarkan persamaan (3.33) skema beda hingga secara eksak diperoleh 𝑢𝑖𝑛+1− 𝑢𝑖𝑛
𝑘 +
𝑢𝑖𝑛− 𝑢𝑖−1𝑛 ℎ = 0
(3.36)
kemudian untuk persamaan (3.35) memiliki dua penyelesaian yang bebas linear yaitu
𝑢(1)(𝑥) = 1 𝑢(2)(𝑥) = 𝑒𝑥/𝛼 dan skema beda hingga secara eksak diperoleh sebagai berikut
|
𝑢𝑛 1 eℎ𝑛/𝛼 𝑢𝑛+1 1 eℎ(𝑛+1)/𝛼 𝑢𝑛+2 1 eℎ(𝑛+2)/𝛼
| = 0
Menggunakan aturan minor dan kofaktor diperoleh
𝑢𝑛(eℎ(𝑛+2)/𝛼− eℎ(𝑛+1)/𝛼) − 𝑢𝑛+1(𝑒ℎ(𝑛+2)/𝛼− eℎ𝑛/𝛼) + 𝑢𝑛+2(−eℎ𝑛/𝛼− eℎ(𝑛+1)/𝛼) = 0
(3.37)
setelah melakukan operasi aljabar pada persamaan (3.37) diperoleh (3.38) dengan 𝑘 = ℎ 𝑢𝑖𝑛 − 𝑢𝑖−1𝑛 ℎ = 𝛼 ( 𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛+ 𝑢𝑖−1𝑛 𝛼ℎ(exp(ℎ/𝛼) − 1)) (3.38) Sehingga 𝑢𝑖𝑛+1− 𝑢𝑖𝑛 𝑘 + 𝑢𝑖𝑛− 𝑢𝑖−1𝑛 ℎ = 𝛼 ( 𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛 + 𝑢𝑖−1𝑛 𝛼ℎ(exp(ℎ/𝛼) − 1)) (3.39)
Kemudian dari persamaan (3.39) pindahkan 𝑢𝑖 𝑛−𝑢 𝑖−1 𝑛 ℎ ke ruas kanan 𝑢𝑖𝑛+1− 𝑢𝑖𝑛 𝑘 = 𝛼 ( 𝑢𝑖+1𝑛 − 2𝑢𝑖𝑛+ 𝑢𝑖−1𝑛 𝛼ℎ(exp(ℎ/𝛼) − 1)) − 𝑢𝑖𝑛− 𝑢𝑖−1𝑛 ℎ Kedua ruas dikali 𝑘, diperoleh
𝑢𝑖𝑛+1− 𝑢𝑖𝑛 = 𝛼𝑘 𝛼ℎ(exp(ℎ/𝛼) − 1)(𝑢𝑖+1 𝑛 − 2𝑢 𝑖𝑛+ 𝑢𝑖−1𝑛 ) − 𝑘 ℎ(𝑢𝑖 𝑛− 𝑢 𝑖−1𝑛 )
atau dapat ditulis 𝑢𝑖𝑛+1− 𝑢𝑖𝑛 = 𝛽1(𝑢𝑖+1𝑛 − 2𝑢 𝑖𝑛+ 𝑢𝑖−1𝑛 ) − 𝛼1(𝑢𝑖𝑛− 𝑢𝑖−1𝑛 ) dengan 𝛼1 = 𝑘 ℎ, 𝛽1 = 𝛼1 exp(ℎ/𝛼)−1.
Kedua ruas dapat dijumlahkan 𝑢𝑖𝑛 𝑢𝑖𝑛+1 = 𝛽1(𝑢𝑖+1𝑛 − 2𝑢
𝑖𝑛+ 𝑢𝑖−1𝑛 ) − 𝛼1(𝑢𝑖𝑛− 𝑢𝑖−1𝑛 ) + 𝑢𝑖𝑛 = 𝛽1𝑢𝑖+1𝑛 − 2𝛽1𝑢𝑖𝑛+ 𝛽1𝑢𝑖−1𝑛 − 𝛼1𝑢𝑖𝑛+ 𝛼1𝑢𝑖−1𝑛 + 𝑢𝑖𝑛 atau
𝑢𝑖𝑛+1 = 𝛽1𝑢𝑖+1𝑛 + 𝑢𝑖𝑛(1 − 2𝛽1− 𝛼1) + 𝑢𝑖−1𝑛 (𝛽1+ 𝛼1) (3.40)
F. Kondisi Persamaan Adveksi-Difusi untuk Skema Lax-Wendroff dan Beda Hingga Tak Standar
Dalam subbab ini akan disajikan kondisi persamaan adveksi-difusi yang dalam Bab IV akan diselesaikan menggunakan skema Lax Wendroff dan beda hingga tak standar yang disimulasikan menggunakan MATLAB.
Diketahui solusi eksak persamaan adveksi-difusi (Appadu, 2013)
𝑢(𝑥, 𝑡) = 0.025
√0.000625 + 0.02𝑡exp [−
(𝑥 + 0.5 − 𝑡)2 (0.00125 + 0.04𝑡)]
(3.41)
sehingga diperoleh kondisi awal
𝑢(𝑥, 0) = exp [−(𝑥 + 0.5) 2 0.00125 ]
(3.42)
0 ≤ 𝑥 ≤ 𝐿 = 1 dan 0 ≤ 𝑡 ≤ 𝑇 = 1 dan kondisi batas
𝑢(0, 𝑡) = 0.025 √0.000625 + 0.02𝑡exp [− (0.5 − 𝑡)2 (0.00125 + 0.04𝑡)] (3.43) 𝑢(1, 𝑡) = 0.025 √0.000625 + 0.02𝑡exp [− (1.5 − 𝑡)2 (0.00125 + 0.04𝑡)] (3.44)
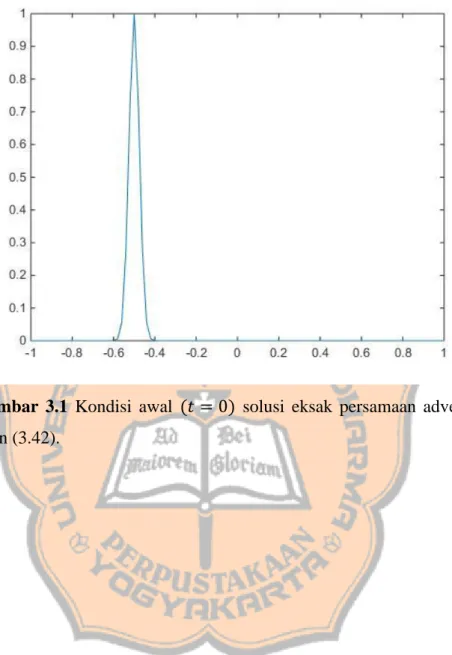
Dalam program MATLAB, kondisi awal persamaan adveksi-difusi pada persamaan (3.41) ditunjukkan pada Gambar 3.1. Di sini 𝑎 = 1 dan 𝛼 = 0.01.
Gambar 3.1 Kondisi awal (𝑡 = 0) solusi eksak persamaan adveksi-difusi persamaan (3.42).
31 BAB IV HASIL SIMULASI
Dalam bab ini akan dibahas hasil simulasi numeris dan perbandingan galat dengan menggunakan skema Lax-Wendroff dan skema beda hingga tak standar pada persamaan adveksi-difusi. Simulasi numeris untuk setiap skema akan dilakukan dengan program MATLAB.
Dalam perhitungan galat penulis menggunakan rumus Galat = 1
𝑀∑ |𝑢𝑒𝑥(𝑖) − 𝑢(𝑖)| 𝑀
𝑖=1 ,
dimana 𝑢𝑒𝑥(𝑖) adalah hasil eksak di titik 𝑥𝑖, 𝑢(𝑖) adalah hasil numeris di titik 𝑥𝑖, 𝑀 adalah banyaknya sel untuk mendiskretkan domain ruang 𝑥.
A. Pembahasan Hasil
Pada bagian ini akan dipaparkan hasil simulasi numeris persamaan adveksi-difusi menggunakan skema Lax-Wendroff. Berikut grafik hasil simulasi numeris persamaan adveksi-difusi
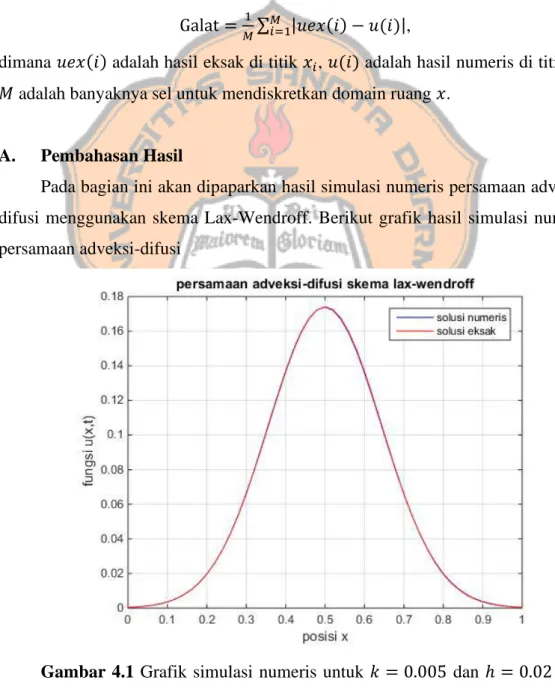
Gambar 4.1 Grafik simulasi numeris untuk 𝑘 = 0.005 dan ℎ = 0.02 pada waktu 𝑡 = 1.
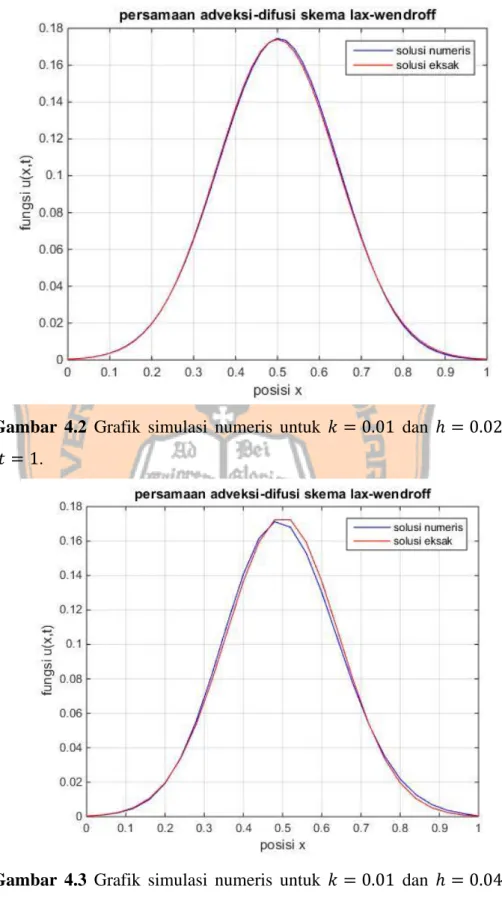
Gambar 4.2 Grafik simulasi numeris untuk 𝑘 = 0.01 dan ℎ = 0.02 pada waktu 𝑡 = 1.
Gambar 4.3 Grafik simulasi numeris untuk 𝑘 = 0.01 dan ℎ = 0.04 pada waktu 𝑡 = 1.
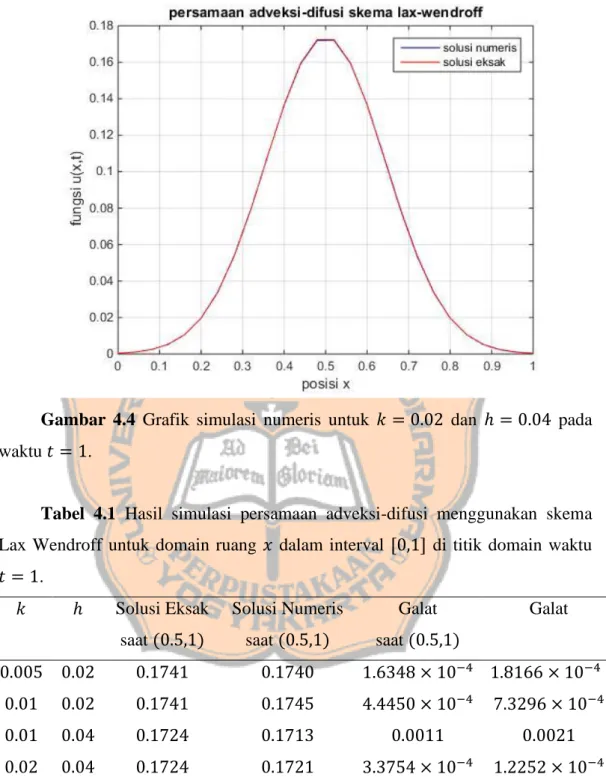
Gambar 4.4 Grafik simulasi numeris untuk 𝑘 = 0.02 dan ℎ = 0.04 pada waktu 𝑡 = 1.
Tabel 4.1 Hasil simulasi persamaan adveksi-difusi menggunakan skema Lax Wendroff untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1. 𝑘 ℎ Solusi Eksak saat (0.5,1) Solusi Numeris saat (0.5,1) Galat saat (0.5,1) Galat 0.005 0.02 0.1741 0.1740 1.6348 × 10−4 1.8166 × 10−4 0.01 0.02 0.1741 0.1745 4.4450 × 10−4 7.3296 × 10−4 0.01 0.04 0.1724 0.1713 0.0011 0.0021 0.02 0.04 0.1724 0.1721 3.3754 × 10−4 1.2252 × 10−4
Gambar 4.1 sampai Gambar 4.4 memperlihatkan secara geometris simulasi numeris persamaan adveksi-difusi. Dari keempat grafik solusi numeris Gambar 4.1 merupakan grafik yang paling mendekati dan hampir berhimpit dengan grafik solusi eksaknya. Dengan kata lain, Gambar 4.1 dengan 𝑘 = 0.005 dan ℎ = 0.02
memberikan selisih solusi numeris dan solusi eksak yang paling kecil. Namun demikian penyelesaian numeris persamaan adveksi-difusi tidak dapat dilihat secara geometris saja. Oleh karena itu, perlu dilakukan perhitungan galat dari persamaan adveksi-difusi yang ditunjukkan pada Tabel 4.1.
Pada Tabel 4.1 penyelesaian numeris persamaan adveksi-difusi 𝑘 = 0.005 dan ℎ = 0.02 menghasilkan nilai yang paling dekat dengan solusi eksak. Di sini, dilakukan pembulatan empat angka di belakang koma terhadap hasil simulasi numeris. Artinya, semakin kecil nilai 𝑘 dan ℎ, solusi numeris Lax-Wendroff semakin akurat.
Selanjutnya pada bagian sebelumnya telah dilihat hasil simulasi numeris persamaan adveksi-difusi menggunakan skema Lax-Wendroff. Hasil simulasi numeris skema beda hingga tak standar disimulasikan dengan program MATLAB. Berikut grafik hasil simulasi numeris untuk persamaan adveksi-difusi menggunakan skema beda hingga tak standar.
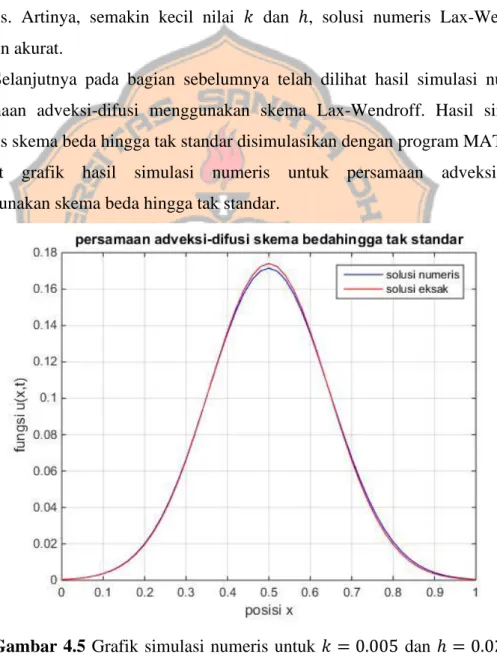
Gambar 4.5 Grafik simulasi numeris untuk 𝑘 = 0.005 dan ℎ = 0.02 pada waktu 𝑡 = 1.
Gambar 4.6 Grafik simulasi numeris untuk 𝑘 = 0.01 dan ℎ = 0.02 pada waktu 𝑡 = 1.
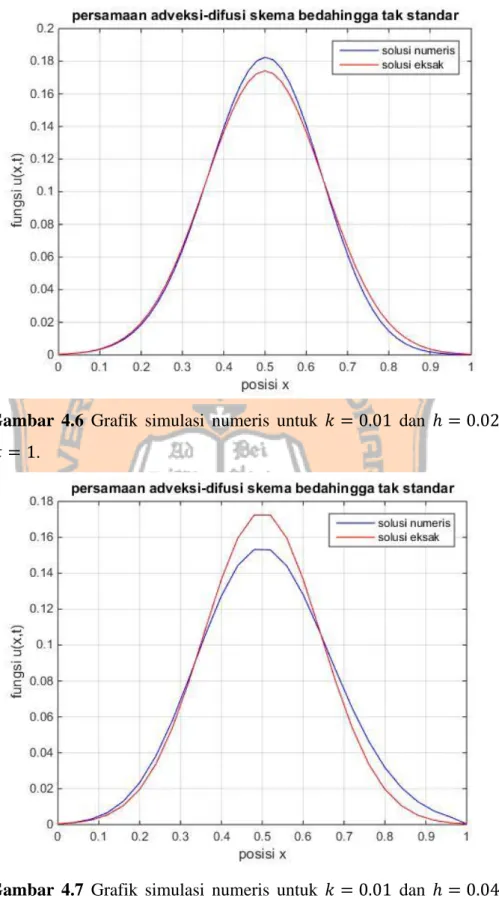
Gambar 4.7 Grafik simulasi numeris untuk 𝑘 = 0.01 dan ℎ = 0.04 pada waktu 𝑡 = 1.
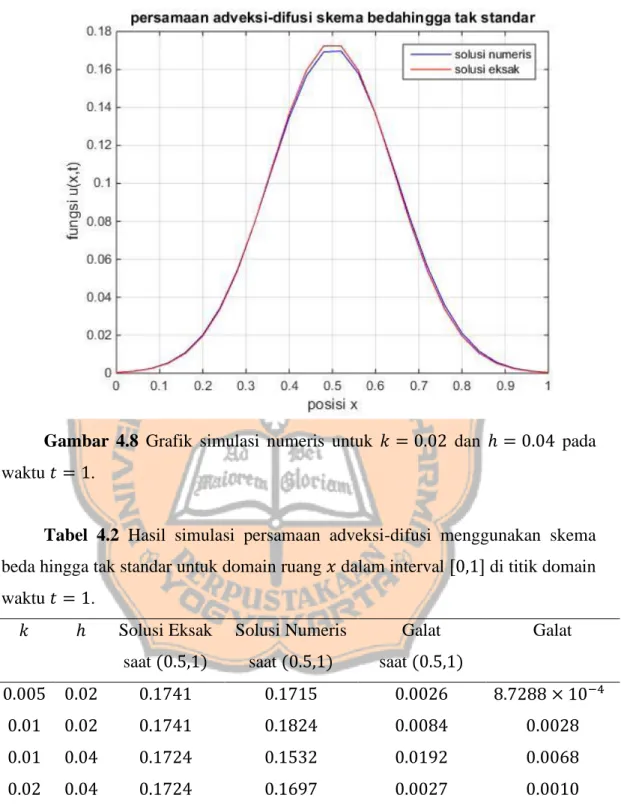
Gambar 4.8 Grafik simulasi numeris untuk 𝑘 = 0.02 dan ℎ = 0.04 pada waktu 𝑡 = 1.
Tabel 4.2 Hasil simulasi persamaan adveksi-difusi menggunakan skema beda hingga tak standar untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1. 𝑘 ℎ Solusi Eksak saat (0.5,1) Solusi Numeris saat (0.5,1) Galat saat (0.5,1) Galat 0.005 0.02 0.1741 0.1715 0.0026 8.7288 × 10−4 0.01 0.02 0.1741 0.1824 0.0084 0.0028 0.01 0.04 0.1724 0.1532 0.0192 0.0068 0.02 0.04 0.1724 0.1697 0.0027 0.0010
Gambar 4.5 sampai Gambar 4.8 memperlihatkan secara geometris simulasi numeris persamaan adveksi-difusi. Dari keempat grafik solusi numeris Gambar 4.5 merupakan grafik yang paling mendekati dan hampir berhimpit dengan grafik solusi eksaknya. Dengan kata lain, Gambar 4.5 dengan 𝑘 = 0.005 dan ℎ = 0.02
memberikan selisih solusi numeris dan solusi eksak yang paling kecil. Namun demikian penyelesaian numeris persamaan adveksi-difusi tidak dapat dilihat secara geometris saja. Oleh karena itu, perlu dilakukan perhitungan galat dari persamaan adveksi-difusi yang ditunjukkan pada Tabel 4.2.
Pada Tabel 4.2 penyelesaian numeris persamaan adveksi-difusi 𝑘 = 0.005 dan ℎ = 0.02 menghasilkan nilai yang paling dekat dengan solusi eksak. Dari Tabel 4.2 tersebut dapat disimpulkan bahwa semakin kecil nilai 𝑘 dan nilai ℎ maka akan memberikan hasil galat yang lebih akurat. Di sini, dilakukan pembulatan empat angka di belakang koma terhadap hasil simulasi numeris.
B. Perbandingan Galat
Pada subbab ini akan dibahas mengenai galat hasil simulasi numeris persamaan adveksi-difusi skema Lax-Wendroff dan skema beda hingga tak standar. Berikut ini merupakan galat hasil simulasi numeris persamaan adveksi-difusi.
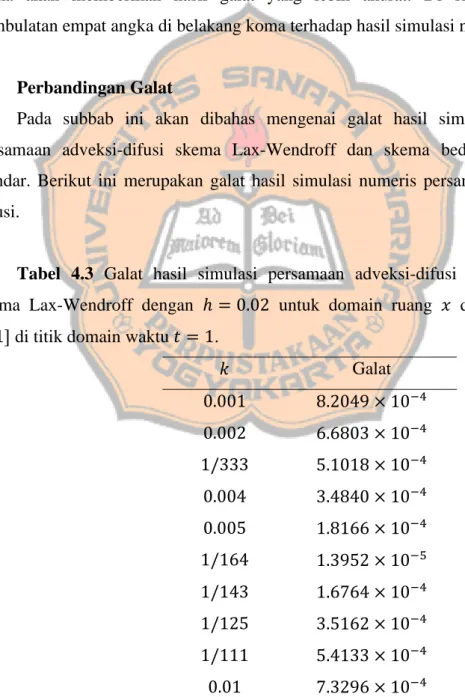
Tabel 4.3 Galat hasil simulasi persamaan adveksi-difusi menggunakan skema Lax-Wendroff dengan ℎ = 0.02 untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1.
𝑘 Galat 0.001 8.2049 × 10−4 0.002 6.6803 × 10−4 1/333 5.1018 × 10−4 0.004 3.4840 × 10−4 0.005 1.8166 × 10−4 1/164 1.3952 × 10−5 1/143 1.6764 × 10−4 1/125 3.5162 × 10−4 1/111 5.4133 × 10−4 0.01 7.3296 × 10−4
Dari Tabel 4.3 dapat dilihat hasil galat dari simulasi persamaan adveksi-difusi menggunakan skema Lax-Wendroff dengan ℎ = 0.02, 𝑘 = 1/164 ≈ 0.00601 merupakan galat terkecil.
Tabel 4.4 Galat hasil simulasi persamaan adveksi-difusi menggunakan skema beda hingga tak standar dengan ℎ = 0.02 untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1.
𝑘 Galat 0.001 0.0035 0.002 0.0028 1/333 0.0022 0.004 0.0015 0.005 8.7288 × 10−4 1/164 1.1717 × 10−4 1/143 5.2775 × 10−4 1/125 0.00126 1/111 0.0020 0.01 0.0028
Dari Tabel 4.4 dapat dilihat hasil galat dari simulasi persamaan adveksi-difusi menggunakan skema beda hingga tak standar dengan ℎ = 0.02, 𝑘 = 1/164 ≈ 0.00601 merupakan galat terkecil. Selanjutnya dari Tabel 4.3 dan Tabel 4.4 dapat dilihat bahwa skema Lax-Wendroff merupakan skema yang efisien dalam menyelesaikan persamaan adveksi-difusi. Sehingga dari hasil galat 𝑘 = 1/164 ≈ 0.00601 skema Lax-Wendroff memiliki galat yang paling terkecil dibandingkan skema beda hingga tak standar.
Tabel 4.5 Galat hasil simulasi persamaan adveksi-difusi menggunakan skema Lax-Wendroff dengan 𝑘 = ℎ/8 untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1.
ℎ 𝑘 Galat 0.1 0.1/8 0.0137 0.05 0.05/8 0.0047 0.025 0.025/8 0.0010 0.0125 0.0125/8 1.4729 × 10−4 0.00625 0.00625/8 2.0830 × 10−5 0.003125 0.003125/8 3.4291 × 10−5 0.0015625 0.0015625/8 𝑖𝑛𝑓
Dari Tabel 4.5 dapat dilihat hasil galat dari simulasi persamaan adveksi-difusi menggunakan skema Lax-Wendroff dengan nilai langkah ruang ℎ diperkecil setengah dari nilai ℎ sebelumnya dan 𝑘 = ℎ/8 memberikan hasil galat yang semakin mengecil. Untuk ℎ = 0.0015625, galatnya tak berhingga jika diterapkan untuk 𝑘 = ℎ/8.
Tabel 4.6 Galat hasil simulasi persamaan adveksi-difusi menggunakan skema Lax-Wendroff dengan 𝑘 = ℎ/16 untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1.
ℎ 𝑘 Galat 0.1 0.1/16 0.0146 0.05 0.05/16 0.0052 0.025 0.025/16 0.0013 0.0125 0.0125/16 2.6670 × 10−4 0.00625 0.00625/16 3.8240 × 10−5 0.003125 0.003125/16 4.9393 × 10−6 0.0015625 0.0015625/16 8.5144 × 10−6
Dari Tabel 4.6, dapat dilihat hasil galat dari simulasi persamaan adveksi-difusi menggunakan skema Lax-Wendroff dengan nilai langkah ruang ℎ diperkecil setengah dari nilai ℎ sebelumnya dan 𝑘 = ℎ/16 memberikan hasil galat yang semakin mengecil.
Tabel 4.7 Galat hasil simulasi persamaan adveksi-difusi menggunakan skema beda hingga tak standar dengan 𝑘 = ℎ/8 untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1.
ℎ 𝑘 Galat 0.1 0.1/8 0.0222 0.05 0.05/8 0.0124 0.025 0.025/8 0.0041 0.0125 0.0125/8 6.8711 × 10−4 0.00625 0.00625/8 9.6743 × 10−4 0.003125 0.003125/8 1.6492 × 10−4 0.0015625 0.0015625/8 𝑖𝑛𝑓
Dari Tabel 4.7 dapat dilihat hasil galat dari simulasi persamaan adveksi-difusi menggunakan skema beda hingga tak standar dengan nilai langkah ruang ℎ diperkecil setengah dari nilai ℎ sebelumnya dan 𝑘 = ℎ/8 memberikan hasil galat yang semakin mengecil. Untuk ℎ = 0.0015625, galatnya tak berhingga jika diterapkan untuk 𝑘 = ℎ/8.
Tabel 4.8 Galat hasil simulasi persamaan adveksi-difusi menggunakan skema beda hingga tak standar dengan 𝑘 = ℎ/16 untuk domain ruang 𝑥 dalam interval [0,1] di titik domain waktu 𝑡 = 1.
ℎ 𝑘 Galat 0.1 0.1/16 0.0231 0.05 0.05/16 0.0136 0.025 0.025/16 0.0050 0.0125 0.0125/16 0.0012 0.00625 0.00625/16 1.8334 × 10−4 0.003125 0.003125/16 2.366 × 10−5 0.0015625 0.0015625/16 4.1165 × 10−5
Dari Tabel 4.8 dapat dilihat hasil galat dari simulasi persamaan adveksi-difusi menggunakan skema beda hingga tak standar dengan nilai langkah ruang ℎ diperkecil setengah dari nilai ℎ sebelumnya dan 𝑘 = ℎ/16 memberikan hasil galat yang semakin mengecil.
Dapat dilihat dari Tabel 4.5 sampai Tabel 4.8 metode dikatakan stabil jika dan hanya jika galat dari solusi yang dihasilkan oleh metode tersebut tidak membesar menuju tak berhingga seiring berjalannya waktu, 𝑘 harus diambil cukup kecil. Karena keterbatasan masa studi, seberapa kecil 𝑘 harus diambil tidak dibahas dalam tugas akhir ini. Dengan demikian untuk kasus ini, solusi numeris akan lebih akurat jika menggunakan skema Lax-Wendroff.
C. Kestabilan Metode Numeris
Pada subbab ini akan dilihat bahwa sebuah metode dapat dikatakan stabil apabila galat dari solusi yang dihasilkan oleh metode tidak membesar seiring dengan berjalannya waktu.
Gambar 4.9 Grafik simulasi numeris skema Lax-Wendroff untuk 𝑘 = ℎ = 0.02 pada waktu 𝑡 = 1.
Gambar 4.10 Grafik simulasi numeris skema beda hingga tak standar untuk 𝑘 = 2ℎ = 0.04 pada waktu 𝑡 = 1.
Dapat dilihat Gambar 4.9 dan Gambar 4.10 hasil simulasi numeris skema Lax-Wendroff dan skema beda hingga tak standar jika 𝑘 diambil terlalu besar atau sama dengan ℎ maka model solusi akan rusak sehingga metode tersebut tidak stabil. Dalam tugas akhir ini tidak membahas teori kestabilan metode numeris.
44 BAB V PENUTUP
Pada bab ini akan diberikan kesimpulan dari pembahasan pada bab-bab sebelumnya serta saran penelitian berikutnya.
A. Kesimpulan
Dalam tugas akhir ini, penulis telah berhasil memodelkan persamaan difusi ke dalam persamaan adveksi-difusi dengan hukum kekekalan massa. Persamaan adveksi-difusi diselesaikan dengan skema Lax-Wendroff dan skema beda hingga tak standar. Setiap skema dalam pengambilan nilai bobot ruang dan waktu sangat mempengaruhi keakuratan hasil solusi numeris. Selain itu pemilihan langkah waktu juga mempengaruhi hasil solusi numeris dan galatnya. Setelah melakukan pengamatan dan membandingkan hasil galat. Skema Lax-Wendroff dan skema beda hingga tak standar memberikan hasil yang baik dan efisien. Skema Lax-Wendroff memberikan hasil pendekatan solusi numeris dengan solusi eksaknya sangat kecil untuk langkah waktu yang cukup kecil. Namun, skema Lax-Wendroff lebih rumit dalam perumusan. Skema beda hingga tak standar merupakan skema yang mudah dalam perumusan. Kedua metode sama-sama menghasilkan galat yang cukup kecil. Akan tetapi, dalam kasus ini skema Lax-Wendroff memberikan hasil yang lebih akurat dibandingkan skema beda hingga.
B. Saran
Penulis sadar bahwa masih banyak kekurangan dalam penulisan tugas akhir ini. Oleh karena itu penulis berharap, kelak ada yang melanjutkan penelitian ini menggunakan skema lain yang memberikan hasil yang lebih akurat.
45
DAFTAR PUSTAKA
Anton, H., Birens, I. and Davis, S. (2012). Calculus Early Transcendentals. 10th ed., Hoboken: John Wiley & Sons, Inc.
Appadu, A. R. (2013). Numerical Solution of the 1D Advection-Diffusion Equation Using Standard and Nonstandard Finite Difference Schemes. Journal of Applied Mathematics, 2013.
Boyce, W. E and DiPrima, C. R. (1986). Elementary Differential Equation. Canada: John Wiley & Sons, Inc.
Chapra, S. C., and Canale, R. P. (2010). Numerical Methods for Engineers. 6th ed., American: The McGraw-Hill Companies.
Karahan, H. (2008). Solution of Weighted Finite Difference Techniques With the Advection-Diffusion Equation Using Spreadsheets. Computer Applications in Engineering Education, 16: 147-156.
LeVeque, R. J. (1992). Finite-Volume Methods for Consevation Laws. 2nd ed., Birkhäuser-Verlag: Basel.
LeVeque, R. J. (2007). Finite Difference Methods for Ordinary and Partial Differential Equations Steady-State and Time-Dependent Problems. United States of America: SIAM.
Mickens, R. E. (1991). Analysis of a new finite-difference scheme for the linear advection-diffusion equation. Journal of Sound and Vibration, 146: 342-344. Mickens, R. E. (2000). Applications of Nonstandard Finite Difference Schemes.
Singapura: World Scientific Publishing.
Paskalia, M. 2014. “Penyelesaian Numeris Persamaan Adveksi-Difusi menggunakan Metode Beda Hingga”. Skripsi. Universitas Sanata Dharma, Yogyakarta.
Smith, G. D. (1985). Numerical Simulation of Partial Differential Equation: Finite Difference Methods. 3rd ed., Oxford University Press: New York.. Strauss, W. A. (1992). Partial Differential Equations. New York: John Wiley &
LAMPIRAN
Berikut ini adalah kode program MATLAB untuk solusi numeris menggunakan skema Lax-Wendroff dan skema beda hingga tak standar.
1. Kondisi Awal solusi Persamaan Adveksi-Difusi close all
clear all
format long
%data
L=1; %batas nilai x akhir
dx=0.02; %langkah ruang
x=-L:dx:L; %diskritisasi ruang
M=length(x); %banyaknya elemen dalam ruang diskrit
%%kondisi awal for i=1:M u(i)=exp(-1*(x(i)+0.5)^2/0.00125); end figure(1) plot(x,u) xlim([-1 1]) ylim([0 1])
2. Skema Lax-Wendroff untuk Persamaan Adveksi-Difusi close all
clear all
format long
%data
L=1; %batas nilai x akhir
T=1; %batas nilai t akhir
dt=0.005; %langkah waktu
x=0:dx:L; %diskritisasi ruang
t=0:dt:T; %diskritisasi waktu
c=1; %kecepatan
M=length(x); %banyaknya elemen dalam ruang diskrit
N=length(t); %banyaknya elemen dalam waktu diskrit
u=zeros(1,M); %penyimpanan hasil kondisi awal
u0=zeros(1,M); %penyimpanan hasil Langkah waktu sebelumnya
uex=zeros(1,M); %menyimpan hasil solusi exact %nilai koefisien
D=0.01; %koefisien difusi
Cr=c*dt/dx; %bilangan courant
Pe=c*dx/D; %bilangan peclet
CP=Cr/Pe;
x0=0.5; %titik tengah gausian pulse
teta=Cr; %faktor pembobot waktu
t=0; %time %kondisiawal for i=1:M u(i)=exp(-1*(x(i)+0.5)^2/0.00125); end %perhitugan for n=1:N-1; u0=u; t=t+dt
%menghitung solusi ujung
u(1)=0.025/sqrt(0.000625+0.02*t)*exp(-1*(0.5-t)^2/(0.00125+0.04*t));
u(M)=0.025/sqrt(0.000625+0.02*t)*exp(-1*(1.5-t)^2/(0.00125+0.04*t));
for i=2:M-1 %solusi numerik
u(i)=(0.5*(2*CP+Cr*(1+teta))*u0(i-1))+((1-
2*CP-(Cr*teta))*u0(i))+(0.5*(2*CP-Cr*(1-teta))*u0(i+1)); end
for i=1:M %solusi eksak
uex(i)=0.025/sqrt(0.000625+0.02*t)*exp(-1*(x(i)+0.5-t)^2/(0.00125+0.04*t)); end figure(2) plot(x,u,'b-',x,uex,'r'); grid on pause(000.1)
error=sum(abs(uex-u))/M; %menghitung error
end
%plot solusi
xlabel('posisi x')
ylabel('fungsi u(x,t)')
title('persamaan adveksi-difusi skema eksplisit') legend('solusi numeris','solusi eksak')
sa=max(uex); %solusi eksak
sn=max(u); %solusi numerik
disp('solusi eksak solusi numerik error') disp([sa sn error])
3. Skema Beda Hingga Tak Standar untuk Persamaan Adveksi-Difusi close all
clear all
%data
L=1; %batas nilai x akhir
T=1; %batas nilai t akhir
dx=0.02; %langkah ruang
dt=0.005; %langkah waktu
x=0:dx:L; %diskritisasi ruang
t=0:dt:T; %diskritisasi waktu
c=0.01; %koefisien difusi
M=length(x); %banyaknya elemen dalam ruang diskrit
N=length(t); %banyaknya elemen dalam waktu diskrit
u=zeros(1,M); %penyimpanan hasil kondisi awal
u0=zeros(1,M); %penyimpanan hasil Langkah waktu sebelumnya
uex=zeros(1,M); %menyimpan hasil solusi exact %nilai koefisien a=dt/dx; b=a/(exp(dx/c)-1); t=0; %time %kondisiawal for i=1:M u(i)=exp(-1*(x(i)+0.5)^2/0.00125); end %perhitugan for n=1:N-1; u0=u; t=t+dt
%menghitung solusi ujung
u(1)=0.025/sqrt(0.000625+0.02*t)*exp(-1*(0.5-t)^2/(0.00125+0.04*t));
u(M)=0.025/sqrt(0.000625+0.02*t)*exp(-1*(1.5-t)^2/(0.00125+0.04*t));
for i=2:M-1 %solusi numerik
u(i)=(b+a)*u0(i-1)+(1-2*b-a)*u0(i)+b*u0(i+1);
end
for i=1:M %solusi eksak
uex(i)=0.025/sqrt(0.000625+0.02*t)*exp(-1*(x(i)+0.5-t)^2/(0.00125+0.04*t)); end figure(2) plot(x,u,'b-',x,uex,'r'); grid on pause(000.1)
error=sum(abs(uex-u))/M; %menghitung error
end
%plot solusi
xlabel('posisi x')
ylabel('fungsi u(x,t)')
title('persamaan adveksi-difusi skema bedahingga
tak standar')
legend('solusi numeris','solusi eksak') sa=max(uex); %solusi eksak
sn=max(u); %solusi numerik
disp('solusi eksak solusi numerik error') disp([sa sn error])