PENYELESAIAN PERSAMAAN GELOMBANG AIR DANGKAL DENGAN BEBERAPA METODE NUMERIS
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Disusun oleh:
Ilga Purnama Sari NIM: 123114023
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
2016
i
PENYELESAIAN PERSAMAAN GELOMBANG AIR DANGKAL DENGAN BEBERAPA METODE NUMERIS
SKRIPSI
Diajukan untuk Memenuhi Salah Satu Syarat Memperoleh Gelar Sarjana Matematika
Program Studi Matematika
Disusun oleh:
Ilga Purnama Sari NIM: 123114023
PROGRAM STUDI MATEMATIKA JURUSAN MATEMATIKA FAKULTAS SAINS DAN TEKNOLOGI
UNIVERSITAS SANATA DHARMA YOGYAKARTA
2016
ii
SOLUTION TO THE SHALLOW WATER WAVE EQUATIONS WITH SOME NUMERICAL METHODS
A THESIS
Presented as Partial Fulfillment of the
Requirements to Obtain the Degree of Sarjana Matematika Mathematics Study Program
Written by:
Ilga Purnama Sari Student ID: 123114023
MATHEMATICS STUDY PROGRAM DEPARTMENT OF MATHEMATICS FACULTY OF SCIENCE AND TECHNOLOGY
SANATA DHARMA UNIVERSITY YOGYAKARTA
2016
iii
iv
v
vi
vii ABSTRAK
Persamaan gelombang air dangkal adalah persamaan yang memodelkan aliran air di tempat terbuka. Persamaan gelombang air dangkal seringkali disebut sistem Saint-Venant yang diturunkan dari hukum kekekalan massa dan momentum.
Dalam skripsi ini, persamaan gelombang air dangkal diselesaikan menggunakan beberapa metode, yaitu metode volume hingga, metode beda hingga grid kolokasi dan metode beda hingga grid selang-seling. Metode volume hingga bekerja dengan cara membagi domain ruang menjadi sebanyak berhingga sel, kemudian dihitung rata-rata kuantitas untuk masing-masing sel. Metode beda hingga grid kolokasi dikerjakan secara implisit yaitu membagi domain ruang menjadi sebanyak berhingga titik, kemudian persamaan gelombang air dangkal didiskretkan dan membentuk sebuah sistem persamaan linear. Terakhir, metode beda hingga grid selang-seling bekerja dengan cara membagi domain perhitungan ruang secara selang-seling. Kedalaman air dihitung pada grid dengan indeks bilangan bulat dan kecepatan air dihitung pada grid dengan indeks pecahan.
Penggunaan metode yang tepat akan menghasilkan solusi yang akurat untuk persamaan gelombang air dangkal.
Penelitian ini menguji beberapa metode numeris yang bisa digunakan untuk menyelesaikan persamaan gelombang air dangkal satu dimensi. Pengujian dilakukan menggunakan simulasi numeris. Analisis hasil simulasi dilakukan dengan observasi hasil simulasi di setiap metode dan membandingkannya dengan hasil solusi eksak.
viii ABSTRACT
The shallow water wave equations model water flows in an open channel.
The shallow water wave equations are often called the Saint-Venant system derived from the conservations of mass and momentum.
In this thesis, the shallow water wave equations are solved using several methods, the Lax-Friedrichs finite volume method, collocation grid finite difference method and staggered grid finite difference method. The finite volume method works by dividing the spatial domain into a finite number of cells, then calculating the average quantity for each cell. The collocation grid finite difference method divides the spatial domain into a finite number of computational points for the shallow water equation discretization and forms a linear system of equations.
Finally, the staggered grid finite difference method works by discretising the computational domain into staggered spatial partitions. The staggered finite diference means that we approximate the quantities of interest of the shallow water equations on different cells. In the staggered formulation, water depth is calculated at full grid points and water velocity is calculated at half grid points. The appropriate method will produce an accurate solution for the shallow water wave equations.
This study examines several numerical methods for solving the one dimensional shallow water wave equations. We investigate the performance of these numerical methods using numerical simulations. Analysis of simulation results are done by observing the results of each method and comparing the numerical results with the exact solution.
ix DAFTAR ISI
HALAMAN JUDUL ... i
HALAMAN JUDUL DALAM BAHASA INGGRIS ... ii
HALAMAN PERSETUJUAN PEMBIMBING ... iii
HALAMAN PENGESAHAN ... iv
HALAMAN PERNYATAAN KEASLIAN KARYA ... v
LEMBAR PERNYATAAN PERSETUJUAN PUBLIKASI... vi
ABSTRAK ... vii
ABSTRAK DALAM BAHASA INGGRIS ... viii
DAFTAR ISI ... ix
BAB I PENDAHULUAN ... 1
A. Latar Belakang ... 1
B. Rumusan Masalah ... 4
C. Pembatasan Masalah ... 5
D. Tujuan Penulisan ... 5
E. Metode Penulisan ... 5
F. Manfaat Penulisan ... 6
G. Sistematika Penulisan ... 6
BAB II PERSAMAAN DIFERENSIAL ... 8
x
A. Integral ... 8
B. Klasifikasi Persamaan Diferensial ... 11
C. Nilai Eigen dan Vektor Eigen ... 15
D. Persamaan Diferensial Hiperbolik ... 16
E. Penurunan Numeris ... 18
F. Karakteristik Persamaan Gelombang Air Dangkal ... 25
BAB III METODE NUMERIS UNTUK PERSAMAAN GELOMBANG AIR DANGKAL ... 28
A. Solusi Eksak Persamaan Gelombang Air Dangkal ... 28
B. Penurunan Persamaan Gelombang Air Dangkal Satu Dimensi ... 29
C. Masalah Bendungan Bobol ... 35
D. Metode Volume Hingga Lax-Friedrichs ... 37
E. Metode Beda Hingga Grid Kolokasi ... 44
F. Metode Beda Hingga Grid Selang-Seling ... 53
BAB IV PERBANDINGAN BEBERAPA METODE NUMERIS DALAM PENYELESAIAN MODEL GELOMBANG AIR DANGKAL ... 57
A. Metode Volume Hingga Lax-Friedrichs ... 58
B. Metode Beda Hingga Grid Kolokasi ... 62
C. Metode Beda Hingga Grid Selang-Seling ... 66
BAB V PENUTUP ... 71
xi
A. Kesimpulan ... 71
B. Saran ... 72
DAFTAR PUSTAKA ... 73
LAMPIRAN ... 74
1 BAB I PENDAHULUAN
Dalam bab ini akan dijelaskan latar belakang, rumusan dan pembatasan masalah, tujuan dan manfaat penulisan, juga akan disertakan sistematika penulisan.
A. Latar Belakang
Persamaan diferensial merupakan persamaan yang menghubungkan suatu fungsi beserta turunan-turunannya. Banyak masalah fisis yang dapat diselesaikan dengan persamaan diferensial. Masalah fisis merupakan masalah yang berhubungan dengan hukum alam yang dibahas dalam ilmu fisika. Masalah fisis seperti fluida dapat diselesaikan dengan menggunakan persamaan diferensial parsial.
Fluida merupakan zat yang dapat mengalir. Zat itu dapat berupa gas atau cairan. Aliran fluida merupakan salah satu masalah fisis yang sering dijumpai dalam kehidupan sehari-hari. Masalah yang sudah pernah ada adalah terjadinya bencana alam seperti bobolnya bendungan air atau tsunami. Bencana alam tersebut disebabkan oleh aliran air dalam skala besar. Aliran tersebut dapat dimodelkan secara matematis (Crowhurst, 2013; Crowhurst dan Li, 2013).
Model gelombang air yang sudah ada salah satunya adalah model gelombang air dangkal atau Shallow Water Wave Equations. Dangkal dalam arti matematis adalah amplitudo gelombang jauh lebih kecil dibandingkan panjang gelombangnya.
Dengan demikian, nilai perbandingan antara amplitudo gelombang (𝑎) dengan panjang gelombang (𝜆) ditulis 𝜆𝑎 ≪ 1.
Penyelesaian persamaan gelombang air dangkal memiliki dua komponen penting yang tidak diketahui yaitu kedalaman dan kecepatan air, dengan ℎ(𝑥, 𝑡) adalah kedalaman air dan 𝑢(𝑥, 𝑡) adalah kecepatan air. Di sini, 𝑡 adalah variabel yang menyatakan waktu dan 𝑥 adalah variabel yang menyatakan ruang satu dimensi. Persamaan gelombang air dangkal dalam bentuk sistem persamaan diferensial parsial dinyatakan oleh dua persamaan simultan, yaitu
ℎ𝑡+ (𝑢ℎ)𝑥 = 0 (1.1)
dan
(𝑢ℎ)𝑡+ (𝑢2ℎ +1
2𝑔ℎ2)𝑥= −𝑔ℎ𝑧𝑥 (1.2)
dengan 𝑧(𝑥) adalah ketinggian tanah, dan 𝑔 adalah konstanta percepatan gravitasi.
Ilustrasi gelombang air dangkal ditunjukkan dalam Gambar 1.1.
Gambar 1.1: Gelombang air dangkal dan variabel-variabel terkait dalam persamaan gelombang air dangkal.
𝜆
x y
𝑤(𝑥, 𝑡)
Pada skripsi ini akan diselesaikan persamaan gelombang air dangkal terkait dengan masalah bendungan bobol. Masalah bendungan bobol memiliki beberapa asumsi, syarat awal dan syarat batas yang akan dibahas lebih lanjut pada Bab III.
Ilustrasi bendungan air dapat dilihat pada Gambar 1.2.
Gambar 1.2: Bendungan air
Secara umum, solusi persamaan gelombang air dangkal tersebut cukup sulit untuk dicari secara analitis, sehingga diperlukan cara lain untuk memecahkannya.
Metode numeris adalah salah satu cara untuk memperoleh solusi persamaan gelombang air dangkal tersebut. Banyak metode numeris yang telah dikembangkan sebelumnya untuk memecahkan solusi persamaan tersebut, mulai dari metode karakteristik, metode beda hingga, metode elemen hingga, metode volume hingga dan sebagainya. Metode beda hingga dikembangkan berdasarkan diskritisasi langsung dari persamaan diferensial yang dipandang (LeVeque, 1992). Metode beda hingga unggul dalam kemudahan komputasi. Dalam tugas akhir ini akan dibahas penyelesaian persamaan gelombang air dangkal dengan metode beda hingga dan metode volume hingga, karena perumusan kedua metode tersebut sederhana.
Bendungan air Permukaan air
Permukaan air ℎ1
ℎ0
𝑥
Metode beda hingga terbagi atas dua model yaitu model grid kolokasi dan model grid selang-seling. Pada grid kolokasi ditentukan nilai pendekatan untuk semua variabel ℎ dan 𝑢 yang tidak diketahui secara bersamaan. Pada grid selang- seling ditentukan pendekatan variabel ℎ dan 𝑢 secara selang-seling. Salah satu referensi tentang grid kolokasi adalah LeVeque (1992). Salah satu referensi tentang grid selang-seling adalah Stelling dan Duinmeijer (2003).
Penelitian ini akan membandingkan hasil perhitungan terbaik antara metode volume hingga, metode beda hingga grid kolokasi dan metode beda hingga grid selang-seling. Dari ketiga metode tersebut diperoleh hasil perhitungan terbaik yang dapat memperbaiki metode beda hingga dengan tidak ada getaran semu (artificial oscillation) pada hasil simulasi aliran air. Fokus penelitian ini adalah
mengembangkan metode numeris dengan metode beda hingga dan volume hingga untuk menyimulasikan aliran air.
B. Rumusan Masalah
Permasalahan yang dirumuskan dalam skripsi ini ada empat, yaitu:
1. Bagaimana memodelkan gelombang air dangkal?
2. Bagaimana menyelesaikan dan menyimulasikan persamaan gelombang air dangkal dengan menggunakan metode volume hingga?
3. Bagaimana menyelesaikan dan menyimulasikan persamaan gelombang air dangkal dengan menggunakan metode beda hingga grid kolokasi?
4. Bagaimana menyelesaikan dan menyimulasikan persamaan gelombang air dangkal dengan menggunakan metode beda hingga grid selang-seling?
C. Pembatasan Masalah
Pembahasan masalah dalam skripsi ini akan dibatasi pada memodelkan gelombang air dangkal satu dimensi dan mencari penyelesaian persamaan gelombang air dangkal dengan metode beda hingga dan volume hingga.
D. Tujuan Penulisan
Skripsi ini mempunyai dua tujuan, yaitu:
1. Merumuskan dan menyelesaikan persamaan gelombang air dangkal dengan beberapa metode numeris, yaitu metode volume hingga Lax-Friedrichs, metode beda hingga grid kolokasi dan metode beda hingga grid selang-seling.
2. Membandingkan beberapa hasil simulasi numeris menggunakan metode volume hingga Lax-Friedrichs, metode beda hingga grid kolokasi dan metode beda hingga grid selang-seling. Dari hasil simulasi tersebut kemudian dipilih hasil yang terbaik yang memuat galat yang paling kecil.
3. Menyimulasikan metode volume hingga Lax-Friedrichs, metode beda hingga grid kolokasi dan metode beda hingga grid selang-seling untuk masalah bendungan bobol.
E. Metode Penulisan
Metode penulisan yang digunakan adalah studi pustaka dari buku-buku dan jurnal serta praktek simulasi numeris.
F. Manfaat Penulisan
Dengan memodelkan persamaan gelombang air, kita dapat 1. Menyimulasikan terjadinya banjir.
2. Memperkirakan daerah mana saja yang akan tenggelam.
3. Memperkirakan kecepatan dan kedalaman air pada daerah tersebut.
G. Sistematika Penulisan
Sistematika penulisan tugas akhir ini adalah sebagai berikut:
BAB I PENDAHULUAN A. Latar Belakang Masalah B. Rumusan Masalah C. Batasan Masalah D. Metode Penulisan E. Tujuan Penulisan F. Manfaat Penulisan
BAB II PERSAMAAN DIFERENSIAL A. Integral
B. Klasifikasi Persamaan Diferensial C. Nilai eigen dan vektor eigen D. Persamaan Diferensial Hiperbolik E. Penurunan Numeris
F. Karakteristik Persamaan Gelombang Air Dangkal
BAB III METODE NUMERIS UNTUK PERSAMAAN GELOMBANG AIR DANGKAL
A. Solusi Eksak Persamaan Gelombang Air Dangkal
B. Penurunan Persamaan Gelombang Air Dangkal Satu Dimensi C. Masalah Bendungan Bobol
D. Metode Volume Hingga Lax-Friedrichs
E. Metode Beda Hingga Grid Kolokasi F. Metode Beda Hingga Grid Selang-Seling
BAB IV PERBANDINGAN BEBERAPA METODE NUMERIS DALAM PENYELESAIAN MODEL GELOMBANG AIR DANGKAL
A. Metode Volume Hingga Lax-Friedrichs B. Metode Beda Hingga Grid Kolokasi C. Metode Beda Hingga Grid Selang-Seling BAB V PENUTUP
A. Kesimpulan B. Saran
DAFTAR PUSTAKA LAMPIRAN
8 BAB II
PERSAMAAN DIFERENSIAL
Landasan teori skripsi ditulis dalam bab ini. Landasan teori tersebut meliputi:
integral, klasifikasi persamaan diferensial, nilai eigen dan vektor eigen, persamaan diferensial hiperbolik, penurunan numeris, dan karakteristik persamaan gelombang air dangkal.
A. Integral
Pada bagian ini dibahas mengenai integral yang meliputi definisi dan contoh dari integral tentu dan aturan Leibniz.
Definisi 2.1
Jika diberikan suatu fungsi 𝑓(𝑥) pada suatu interval 𝐼 dan berlaku 𝐹′(𝑥) = 𝑓(𝑥), untuk suatu 𝐹(𝑥), maka 𝐹(𝑥) adalah anti turunan dari 𝑓(𝑥). Dengan kata lain 𝐹′(𝑥) = 𝑓(𝑥).
Contoh 2.1
Carilah suatu anti turunan dari 𝑓(𝑥) = 2𝑥2 pada (−∞, ∞).
Penyelesaian:
Fungsi 𝐹(𝑥) = 2𝑥3 bukan anti turunannya karena turunan 2𝑥3 adalah 6𝑥2. Tetapi hal ini menyarankan 𝐹(𝑥) =23𝑥3, yang memenuhi 𝐹′(𝑥) =233𝑥2 = 2𝑥2. Dengan demikian, suatu anti turunan dari 𝑓 adalah 23𝑥3.
Anti turunan dinotasikan dengan ∫ … 𝑑𝑥. Notasi tersebut menunjukkan anti turunan terhadap 𝑥. Anti turunan biasanya disebut integral tak tentu.
Integral Tentu
Perhatikan Gambar 2.1 berikut ini.
Gambar 2.1: Ilustrasi fungsi satu variabel
Untuk menghitung luasan dibawah kurva 𝑦 = 𝑓(𝑥) pada interval [𝑎, 𝑏], dapat dihitung dengan cara aproksimasi yaitu dengan membagi interval [𝑎, 𝑏] menjadi 𝑛 subinterval. Subinterval tersebut memiliki panjang yang sama yaitu 𝑏−𝑎𝑛 untuk 𝑛 >
0. Setelah membagi interval menjadi 𝑛 subinterval kemudian menghitung total jumlah luasan dari masing-masing persegi panjang yang dibentuk oleh masing- masing subinterval tersebut. Hal ini diperoleh dengan memilih 𝑥0, 𝑥1, … , 𝑥𝑛 dengan 𝑎 = 𝑥0, 𝑏 = 𝑥𝑛, dan
𝑥𝑖 − 𝑥𝑖−1= 𝑏 − 𝑎 𝑛 𝑦
𝑎 𝑏 𝑥
𝑦 = 𝑓(𝑥)
untuk 𝑖 = 1,2, … , 𝑛. Andaikan panjang masing-masing subinterval yaitu 𝑏−𝑎𝑛 dinotasikan dengan
∆𝑥 = 𝑥𝑖 − 𝑥𝑖−1.
Luas daerah dibawah kurva diaproksimasikan dengan total luas daerah yang dibentuk oleh masing-masing subinterval, aproksimasi luas di bawah kurva adalah 𝐴1+ 𝐴2+ ⋯ + 𝐴𝑛. Artinya total luas tersebut yang dapat ditulis
𝑓(𝑢1)∆𝑥 + 𝑓(𝑢2)∆𝑥 + ⋯ + 𝑓(𝑢𝑛)∆𝑥 = ∑ 𝑓(𝑢𝑖)∆𝑥
𝑛
𝑖=1
yang disebut jumlahan Riemann fungsi 𝑓 pada interval [𝑎, 𝑏], sebagai pendekatan luas daerah di bawah kurva 𝑦 = 𝑓(𝑥) dan diatas sumbu 𝑥. Di sini, 𝑢𝑖 ∈ [𝑥𝑖−1, 𝑥𝑖].
Semakin banyak subinterval yang digunakan, artinya ∆𝑥 → 0 maka semakin baik pula aproksimasi luasan tersebut dan semakin dekat dengan luasan yang sebenarnya. Dengan demikian,
Luas daerah = lim
∆𝑥→0∑ 𝑓(𝑢𝑖)∆𝑥.
𝑖
Definisi 2.2
Andaikan 𝑓 fungsi yang terdefinisi pada [𝑎, 𝑏]. Integral tentu 𝑓 dari 𝑎 sampai 𝑏 dinotasikan ∫ 𝑓(𝑥)𝑑𝑥𝑎𝑏 , adalah
∫ 𝑓(𝑥)𝑑𝑥
𝑏 𝑎
= lim
∆𝑥→0∑ 𝑓(𝑢𝑖)∆𝑥.
𝑖
Aturan Leibniz
Teorema 2.1
Aturan Leibniz untuk satu variabel:
Jika 𝑓 adalah fungsi kontinu pada interval [𝑎, 𝑏] dan jika 𝑢(𝑥) dan 𝑣(𝑥) adalah fungsi yang dapat diturunkan terhadap 𝑥 yang nilainya terletak di interval [𝑎, 𝑏], maka
𝑑
𝑑𝑥∫ 𝑓(𝑡)𝑑𝑡
𝑣(𝑥) 𝑢(𝑥)
= 𝑓(𝑣(𝑥))𝑑𝑣
𝑑𝑥− 𝑓(𝑢(𝑥))𝑑𝑢 𝑑𝑥
Teorema 2.2
Aturan Leibniz untuk dua variabel:
Jika 𝑓(𝑥, 𝑡) adalah fungsi sedemikian sehingga turunan parsial dari 𝑓 terhadap 𝑡 ada dan kontinu, maka
𝑑
𝑑𝑥∫ 𝑓(𝑥, 𝑡)𝑑𝑡
𝑣(𝑥) 𝑢(𝑥)
= ∫ 𝜕𝑓
𝜕𝑥𝑑𝑡
𝑣(𝑥) 𝑢(𝑥)
+ 𝑓(𝑣(𝑥), 𝑥) 𝑑
𝑑𝑥𝑣(𝑥) − 𝑓(𝑢(𝑥), 𝑥) 𝑑
𝑑𝑥𝑢(𝑥).
Bukti dapat dilihat pada buku karangan David. B dan George. C yang berjudul Basic Partial Differential Equations.
B. Klasifikasi Persamaan Diferensial
Berikut ini dibahas tentang klasifikasi persamaan diferensial. Klasifikasi persamaan diferensial yang dibahas meliputi definisi dan contoh persamaan
diferensial, persamaan diferensial biasa, persamaan diferensial parsial, orde persamaan diferensial dan kelinearan suatu persamaan diferensial.
Definisi 2.3
Persamaan diferensial adalah persamaan yang melibatkan variabel-variabel tak bebas dan turunan-turunannya terhadap variabel-variabel bebas.
Contoh 2.2
Persamaan di bawah ini merupakan contoh persamaan diferensial:
𝑑2𝑦
𝑑𝑥2+ 𝑥𝑦 (𝑑𝑦 𝑑𝑥)
2
= 0 (2.1)
𝑑4𝑥
𝑑𝑡4 + 5𝑑2𝑥
𝑑𝑡2 + 3𝑥 = sin 𝑡 (2.2)
𝜕𝑣
𝜕𝑠 +𝜕𝑣
𝜕𝑡 = 𝑣 (2.3)
𝜕2𝑢
𝜕𝑥2 +𝜕2𝑢
𝜕𝑦2 +𝜕2𝑢
𝜕𝑧2 = 0. (2.4)
Definisi 2.4
Persamaan diferensial biasa adalah persamaan diferensial yang melibatkan turunan biasa beserta satu atau lebih variabel tak bebas terhadap satu variabel bebas.
Contoh 2.3
Persamaan (2.1) dan (2.2) adalah persamaan diferensial biasa. Pada persamaan (2.1) variabel 𝑥 adalah suatu variabel bebas, dan variabel 𝑦 adalah variabel tak bebas. Pada persamaan (2.2), variabel 𝑡 adalah variabel bebas, dengan 𝑥 adalah variabel tak bebasnya.
Definisi 2.5
Persamaan diferensial parsial adalah persamaan diferensial yang melibatkan turunan parsial dari satu atau lebih variabel tak bebas terhadap lebih dari satu variabel bebas.
Contoh 2.4
Persamaan (2.3) dan (2.4) adalah persamaan diferensial parsial. Pada persamaan (2.3), variabel 𝑠 dan 𝑡 adalah variabel bebas dan 𝑣 adalah variabel tak bebasnya. Pada persaman (2.4) terdapat tiga variabel bebas yaitu 𝑥, 𝑦, dan 𝑧. Pada persamaan (2.4) variabel tak bebasnya adalah 𝑢.
Definisi 2.6
Orde dari persamaan diferensial adalah tingkat tertinggi dari turunan yang terkandung dalam persamaan diferensial.
Contoh 2.5
Persamaan diferensial biasa (2.1) adalah persamaan diferensial orde kedua, karena tingkat tertinggi dari turunan pada persamaan tersebut adalah dua.
Persamaan (2.2) adalah persamaan diferensial biasa orde keempat. Persamaan (2.3) termasuk persamaan diferensial parsial orde pertama. Persamaan (2.4) merupakan persamaan diferensial parsial orde kedua.
Definisi 2.7
Suatu persamaan diferensial biasa orde ke-𝑛 𝐹(𝑥, 𝑦, 𝑦′, 𝑦′′, … , 𝑦(𝑛)) = 0
dikatakan linear jika 𝐹 merupakan suatu fungsi linear dari variabel 𝑦, 𝑦′, 𝑦′′, … , 𝑦(𝑛); definisi yang sama juga berlaku untuk persamaan diferensial parsial. Secara umum persamaan diferensial biasa linear orde 𝑛 dituliskan sebagai
𝑎0(𝑥)𝑦(𝑛)+ 𝑎1(𝑥)𝑦(𝑛−1)+ ⋯ + 𝑎𝑛(𝑥)𝑦 = 𝑏(𝑥) (2.5) dengan 𝑎0 tidak sama dengan nol.
Contoh 2.6
Persamaan diferensial biasa berikut keduanya linear. Pada kedua persamaan berikut, variabel 𝑦 adalah variabel tak bebas. Perhatikan bahwa 𝑦 dan turunan- turunannya terjadi dengan pangkat satu saja dan tidak ada perkalian dari 𝑦 dan/ atau turunan dari 𝑦.
𝑑2𝑦
𝑑𝑥2+ 5𝑑𝑦
𝑑𝑥+ 6𝑦 = 0 (2.6)
𝑑4𝑦
𝑑𝑥4+ 𝑥2𝑑3𝑦
𝑑𝑥3+ 𝑥3𝑑𝑦
𝑑𝑥= 𝑥𝑒𝑥. (2.7)
Definisi 2.8
Suatu persamaan diferensial biasa yang tidak memiliki bentuk (2.5) dinamakan persamaan diferensial biasa tak linear.
Contoh 2.7
Persamaan diferensial biasa berikut semuanya tak linear:
𝑑2𝑦
𝑑𝑥2+ 5𝑑𝑦
𝑑𝑥+ 6𝑦2 = 0 (2.8)
𝑑2𝑦
𝑑𝑥2+ 5 (𝑑𝑦 𝑑𝑥)
3
+ 6𝑦 = 0 (2.9)
𝑑2𝑦
𝑑𝑥2+ 5𝑦𝑑𝑦
𝑑𝑥+ 6𝑦 = 0 (2.10)
Persamaan (2.8) tak linear karena variabel tak bebas 𝑦 terdapat pada pangkat kedua dalam bentuk 6𝑦2. Persamaan (2.9) juga tak linear karena terdapat bentuk 5 (𝑑𝑦𝑑𝑥)3 yang melibatkan pangkat tiga pada turunan pertama. Persamaan (2.10) tak
linear karena pada bentuk 5𝑦𝑑𝑦𝑑𝑥 melibatkan perkalian terhadap variabel tak bebas dan turunan pertamanya.
C. Nilai Eigen dan Vektor Eigen
Berikut dibahas mengenai definisi dan contoh dari nilai eigen dan vektor eigen.
Definisi 2.9
Jika 𝐴 adalah matriks 𝑛 × 𝑛, maka vektor tak nol 𝐱 di ℝ𝑛 disebut vektor eigen dari 𝐴 jika 𝐴𝒙 merupakan perkalian skalar dengan 𝐱 atau dapat ditulis
𝐴𝐱 = 𝜆𝐱
untuk suatu skalar 𝜆. Skalar 𝜆 disebut nilai eigen dari 𝐴 dan 𝐱 disebut vektor eigen yang bersesuaian dengan 𝝀.
Contoh 2.8
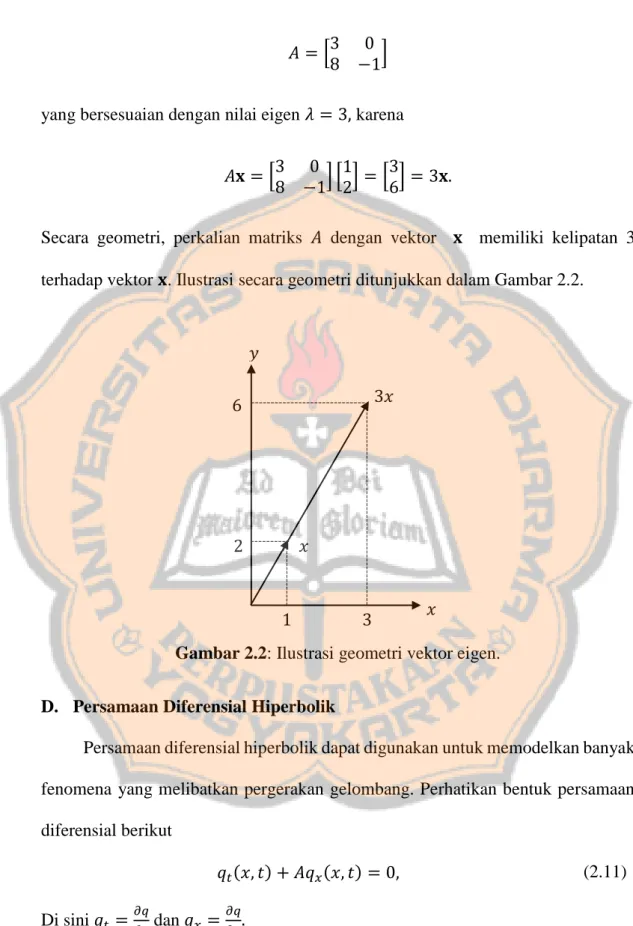
Vektor 𝐱 = [1
2] adalah vektor eigen dari
𝐴 = [3 0 8 −1] yang bersesuaian dengan nilai eigen 𝜆 = 3, karena
𝐴𝐱 = [3 0
8 −1] [12] = [36] = 3𝐱.
Secara geometri, perkalian matriks 𝐴 dengan vektor 𝐱 memiliki kelipatan 3 terhadap vektor 𝐱. Ilustrasi secara geometri ditunjukkan dalam Gambar 2.2.
Gambar 2.2: Ilustrasi geometri vektor eigen.
D. Persamaan Diferensial Hiperbolik
Persamaan diferensial hiperbolik dapat digunakan untuk memodelkan banyak fenomena yang melibatkan pergerakan gelombang. Perhatikan bentuk persamaan diferensial berikut
𝑞𝑡(𝑥, 𝑡) + 𝐴𝑞𝑥(𝑥, 𝑡) = 0, (2.11) Di sini 𝑞𝑡= 𝜕𝑞𝜕𝑡 dan 𝑞𝑥= 𝜕𝑞𝜕𝑥.
3𝑥
1 3
6
2 𝑥
𝑥 𝑦
Dalam kasus yang paling sederhana yaitu koefisien konstan dan linear. Dalam hal ini 𝑞 ∶ ℝ × ℝ → ℝ𝑛 adalah vektor dengan 𝑛 komponen yang menyatakan fungsi yang tidak diketahui (tekanan, kecepatan, dan sebagainya) yang ingin ditentukan, dan 𝐴 suatu konstan merupakan matriks real berukuran 𝑛 × n. Andaikan 𝐴 = 𝑢̅
suatu konstan yang menyatakan kecepatan perambatan (aliran pada pipa satu dimensi misalnya), maka persamaan (2.11) menjadi
𝑞𝑡(𝑥, 𝑡) + 𝑢̅𝑞𝑥(𝑥, 𝑡) = 0, (2.12) persamaan ini disebut persamaan adveksi.
Persamaan 𝑞𝑡(𝑥, 𝑡) + 𝐴𝑞𝑥(𝑥, 𝑡) = 0 adalah persamaan hiperbolik, jika matriks 𝐴 memiliki nilai eigen real dan berkorespondensi dengan 𝑛 vektor eigen yang bebas linear. Artinya, semua vektor dalam ℝ𝑛 dapat secara tunggal diuraikan sebagai kombinasi linear dari nilai-nilai eigen tersebut. Secara formal definisi persamaan diferensial hiperbolik sebagai berikut.
Definisi 2.10
Suatu sistem linear dengan bentuk
𝑞𝑡+ 𝐴𝑞𝑥 = 0
dikatakan hiperbolik jika matriks 𝐴 yang berukuran 𝑛 × n dapat didiagonalkan dengan nilai eigen real.
Secara khusus untuk persamaan adveksi, diketahui bahwa 𝐴 = 𝑢̅, yang merupakan suatu konstanta real. Jadi 𝐴 dapat didiagonalkan oleh nilai 𝐴 itu sendiri dan nilai eigen dari 𝐴 adalah 𝐴 itu sendiri. Dengan demikian, persamaan adveksi merupakan persamaan diferensial hiperbolik. Keterangan lengkap tentang
persamaan diferensial hiperbolik dapat ditemukan dalam buku karangan LeVeque (2004).
E. Penurunan Numeris
Pada subbab ini dibahas mengenai penurunan numeris beserta contohnya dan penjelasan mengenai tiga hampiran dalam menghitung turunan numerik yaitu hampiran beda maju, hampiran beda mundur dan hampiran beda pusat.
Definisi 2.11
Suatu turunan fungsi didefinisikan dengan
𝑓′(𝑥) = lim
∆𝑥→0
𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥)
∆𝑥 .
Seringkali fungsi 𝑓(𝑥) tidak diketahui secara eksplisit, tetapi hanya diketahui beberapa titik data saja. Seringkali 𝑓(𝑥) diketahui secara eksplisit tetapi karena bentuknya yang sangat rumit sehingga untuk menentukan fungsi turunannya juga sulit, misalnya pada fungsi-fungsi berikut ini:
(a). 𝑓(𝑥) =√cos(2𝑥2) + 𝑥 tan(3𝑥) sin(𝑥) + 𝑒𝑥− 2𝑥
cos(𝑥) ,
(b). 𝑓(𝑥) = 𝑥𝑒(2𝑥+2)ln(4𝑥2).
Perhitungan nilai turunan pada fungsi (a) dan (b) dapat dikerjakan secara numerik.
Nilai turunan yang diperoleh merupakan nilai hampiran dan diharapkan nilai galatnya sekecil mungkin.
Tiga Hampiran dalam Menghitung Turunan Numerik
Turunan adalah limit dari hasil bagi pengurangan dua buah nilai yang besar 𝑓(𝑥 + ∆𝑥) − 𝑓(𝑥) dan membaginya dengan bilangan yang kecil (∆𝑥). Misal diberikan nilai-nilai 𝑥 di 𝑥0− ∆𝑥, 𝑥0, dan 𝑥0+ ∆𝑥, serta nilai fungsi untuk nilai- nilai 𝑥 tersebut. Titik-titik yang diperoleh adalah (𝑥−1, 𝑓−1), (𝑥0, 𝑓0), dan (𝑥1, 𝑓1), yang dalam hal ini 𝑥−1= 𝑥0− ∆𝑥 dan 𝑥1 = 𝑥0+ ∆𝑥. Terdapat tiga hampiran dalam menghitung nilai 𝑓′(𝑥0):
1. Hampiran Beda Maju
Diketahui fungsi 𝑦 = 𝑓(𝑥0). Akan ditunjukkan 𝑓′(𝑥0) dengan hampiran beda maju.
𝑓′(𝑥0) = lim
∆𝑥→0
𝑓(𝑥0+ ∆𝑥) − 𝑓(𝑥0)
∆𝑥
≈𝑓(𝑥0+ ∆𝑥) − 𝑓(𝑥0)
∆𝑥
= 𝑓1− 𝑓0
∆𝑥 .
2. Hampiran Beda Mundur
Diketahui fungsi 𝑦 = 𝑓(𝑥0). Akan ditunjukkan 𝑓′(𝑥0) dengan hampiran beda mundur.
𝑓′(𝑥0) = lim
∆𝑥→0
𝑓(𝑥0) − 𝑓(𝑥0− ∆𝑥)
∆𝑥
≈𝑓(𝑥0) − 𝑓(𝑥0− ∆𝑥)
∆𝑥
= 𝑓0− 𝑓1
∆𝑥 .
3. Hampiran Beda Pusat
Diketahui fungsi 𝑦 = 𝑓(𝑥0). Akan ditunjukkan 𝑓′(𝑥0) dengan hampiran beda pusat.
𝑓′(𝑥0) = lim
∆𝑥→0
𝑓(𝑥0+ ∆𝑥) − 𝑓(𝑥0− ∆𝑥) 2∆𝑥
≈𝑓(𝑥0+ ∆𝑥) − 𝑓(𝑥0− ∆𝑥) 2∆𝑥
= 𝑓1− 𝑓−1 2∆𝑥 .
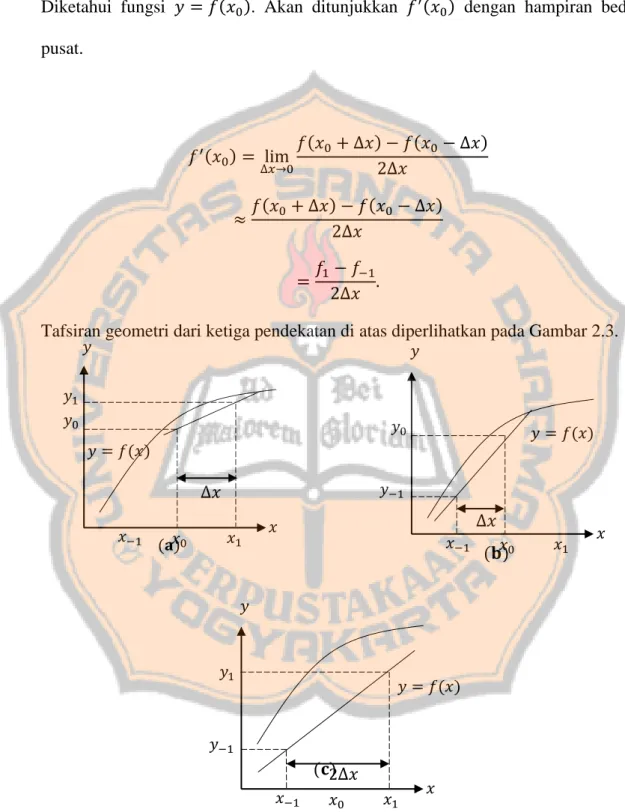
Tafsiran geometri dari ketiga pendekatan di atas diperlihatkan pada Gambar 2.3.
Gambar 2.3: Tiga pendekatan dalam perhitungan numeris; (a) Hampiran beda maju, (b) Hampiran beda mundur, dan (c) Hampiran beda pusat.
𝑦
𝑥0 𝑥1 𝑥 𝑥−1
∆𝑥
𝑦 = 𝑓(𝑥) 𝑦0
𝑦−1 𝑦
𝑥0 𝑥1 𝑥 𝑥−1
∆𝑥 𝑦 = 𝑓(𝑥)
𝑦0 𝑦1
𝑦
𝑥0 𝑥1 𝑥 𝑥−1
2∆𝑥
𝑦 = 𝑓(𝑥) 𝑦1
𝑦−1
(𝐚) (𝐛)
(𝐜)
Penurunan Rumus Turunan dengan Deret Taylor
Misalkan diberikan titik-titik (𝑥𝑖, 𝑓𝑖), 𝑖 = 0,1,2,3, … , 𝑛, yang dalam hal ini 𝑥𝑖 = 𝑥0+ 𝑖∆𝑥
dan
𝑓𝑖 = 𝑓(𝑥𝑖).
Selanjutnya akan dihitung 𝑓′(𝑥) yang dalam hal ini 𝑥 = 𝑥0+ 𝑠∆𝑥, 𝑠 ∈ 𝑅 dengan ketiga pendekatan yang disebutkan di atas (maju, mundur, pusat).
1. Hampiran Beda Maju Uraikan 𝑓(𝑥𝑖+1) di sekitar 𝑥𝑖: 𝑓(𝑥𝑖+1) = 𝑓(𝑥𝑖) +(𝑥𝑖+1− 𝑥𝑖)
1! 𝑓′(𝑥𝑖) +(𝑥𝑖+1− 𝑥𝑖)2
2! 𝑓′′(𝑥𝑖) + ⋯
dengan mensubtitusikan (𝑥𝑖+1− 𝑥𝑖) = ∆𝑥 dan penulisan 𝑓(𝑥𝑖+1) dapat ditulis 𝑓𝑖+1 diperoleh
𝑓𝑖+1= 𝑓𝑖 + ∆𝑥𝑓𝑖′+∆𝑥2
2 𝑓𝑖′′+ ⋯ (2.13)
atau dapat ditulis
∆𝑥𝑓𝑖′= 𝑓𝑖+1− 𝑓𝑖 −∆𝑥2
2 𝑓𝑖′′− ⋯
kedua ruas dibagi dengan ∆𝑥 sehingga diperoleh 𝑓𝑖′= 𝑓𝑖+1− 𝑓𝑖
∆𝑥 −∆𝑥
2 𝑓𝑖′′− ⋯
karena ∆𝑥2 𝑓𝑖′′− ⋯ merupakan bilangan yang sangat kecil dan tidak begitu mempengaruhi nilai 𝑓𝑖′ sehingga dapat ditulis
𝑓𝑖′= 𝑓𝑖+1− 𝑓𝑖
∆𝑥 + 𝑂(∆𝑥)
yang dalam hal ini, 𝑂(∆𝑥) =∆𝑥2 𝑓′′(𝑡), 𝑥𝑖 < 𝑡 < 𝑥𝑖+1.
Untuk nilai-nilai 𝑓 di 𝑥0 dan 𝑥1 persamaan rumusnya menjadi:
𝑓0′ =𝑓1− 𝑓0
∆𝑥 + 𝑂(∆𝑥).
Dalam hal ini 𝑂(∆𝑥) =∆𝑥2 𝑓′′(𝑡), 𝑥𝑖 < 𝑡 < 𝑥𝑖+1 menyatakan penurunan numeris secara beda maju memiliki tingkat keakuratan tingkat satu atau ditulis 𝑂(∆𝑥).
2. Hampiran Beda Mundur Uraikan 𝑓(𝑥𝑖−1) di sekitar 𝑥𝑖: 𝑓(𝑥𝑖−1) = 𝑓(𝑥𝑖) +(𝑥𝑖+1− 𝑥𝑖)
1! 𝑓′(𝑥𝑖) +(𝑥𝑖+1− 𝑥𝑖)2
2! 𝑓′′(𝑥𝑖) + ⋯
dengan mensubtitusikan (𝑥𝑖+1− 𝑥𝑖) = ∆𝑥 dan penulisan 𝑓(𝑥𝑖−1) dapat ditulis 𝑓𝑖−1 diperoleh
𝑓𝑖−1= 𝑓𝑖 − ∆𝑥𝑓𝑖′+∆𝑥2
2 𝑓𝑖′′− ⋯ (2.14)
atau dapat ditulis
∆𝑥𝑓𝑖′= 𝑓𝑖 − 𝑓𝑖−1+∆𝑥2
2 𝑓𝑖′′− ⋯
kedua ruas dibagi dengan ∆𝑥 sehingga diperoleh 𝑓𝑖′= 𝑓𝑖− 𝑓𝑖−1
∆𝑥 −∆𝑥
2 𝑓𝑖′′+ ⋯
karena ∆𝑥2 𝑓𝑖′′− ⋯ merupakan bilangan yang sangat kecil dan tidak begitu mempengaruhi nilai 𝑓𝑖′ sehingga dapat ditulis
𝑓𝑖′= 𝑓𝑖− 𝑓𝑖−1
∆𝑥 + 𝑂(∆𝑥)
yang dalam hal ini, 𝑂(∆𝑥) = −∆𝑥2 𝑓′′(𝑡), 𝑥𝑖−1< 𝑡 < 𝑥𝑖.
Untuk nilai-nilai 𝑓 di 𝑥0 dan 𝑥−1 persamaan rumusnya menjadi:
𝑓0′ =𝑓0− 𝑓−1
∆𝑥 + 𝑂(∆𝑥)
Dalam hal ini 𝑂(∆𝑥) = −∆𝑥2 𝑓′′(𝑡), 𝑥𝑖+1< 𝑡 < 𝑥𝑖 menyatakan penurunan numeris secara beda mundur memiliki tingkat keakuratan tingkat satu atau ditulis 𝑂(∆𝑥).
3. Hampiran Beda Pusat
Kurangkan persamaan (2.13) dengan persamaan (2.14) diperoleh:
𝑓𝑖+1− 𝑓𝑖−1= 𝑓𝑖 + ∆𝑥𝑓𝑖′+∆𝑥2
2 𝑓𝑖′′+ ⋯ − (𝑓𝑖 − ∆𝑥𝑓𝑖′+∆𝑥2
2 𝑓𝑖′′− ⋯ ) dengan menggunakan operasi penjumlahan dan pengurangan diperoleh 𝑓𝑖+1− 𝑓𝑖−1= 2∆𝑥𝑓𝑖′+∆𝑥3
3 𝑓𝑖′′′+ ⋯ atau dapat ditulis
2∆𝑥𝑓𝑖′= 𝑓𝑖+1− 𝑓𝑖−1−∆𝑥3
3 𝑓𝑖′′′− ⋯
Kedua ruas dibagi dengan 2∆𝑥 sehingga diperoleh 𝑓𝑖′= 𝑓𝑖+1− 𝑓𝑖−1
2∆𝑥 −∆𝑥2
6 𝑓𝑖′′′− ⋯ karena ∆𝑥
2
6 𝑓𝑖′′′− ⋯ merupakan bilangan yang sangat kecil dan tidak begitu mempengaruhi nilai 𝑓𝑖′ sehingga dapat ditulis
𝑓𝑖′= 𝑓𝑖+1− 𝑓𝑖−1
2∆𝑥 + 𝑂(∆𝑥2),
yang dalam hal ini, 𝑂(∆𝑥2) = −∆𝑥62𝑓′′′(𝑡), 𝑥𝑖−1< 𝑡 < 𝑥𝑖+1. Untuk nilai-nilai 𝑓 di 𝑥−1 dan 𝑥1 persamaan rumusnya menjadi:
𝑓0′ =𝑓1− 𝑓−1
2∆𝑥 + 𝑂(∆𝑥2)
Dalam hal ini 𝑂(∆𝑥2) = −∆𝑥62𝑓′′′(𝑡), 𝑥𝑖−1< 𝑡 < 𝑥𝑖+1 menyatakan penurunan numeris secara beda pusat yang memiliki tingkat keakuratan tingkat dua atau ditulis 𝑂(∆𝑥2). Perhatikan bahwa hampiran beda pusat lebih baik daripada dua hampiran sebelumnya, sebab orde galatnya adalah 𝑂(∆𝑥2).
Menentukan Orde Galat
Pada penurunan rumus turunan numeris dengan deret Taylor, rumus galat dalam penurunan rumus turunan numeris tersebut dapat langsung diperoleh. Tetapi dengan polinom interpolasi harus dicari rumus galat tersebut dengan bantuan deret Taylor.
Contoh 2.9
Tentukan rumus galat dan orde dari rumus turunan numeris hampiran beda pusat:
𝑓′(𝑥0) =𝑓1− 𝑓−1 2∆𝑥 + 𝐸
Nyatakan 𝐸 (galat) sebagai ruas kiri persamaan, lalu ekspansi rusa kanan dengan deret Taylor di sekitar 𝑥0:
𝐸 = 𝑓′(𝑥0) −𝑓1 − 𝑓−1 2∆𝑥
=𝑓0′−2∆𝑥1 [(𝑓0+ ∆𝑥𝑓0′+∆𝑥22𝑓0′′+∆𝑥63𝑓0′′′+ ⋯ ) − (𝑓0− ∆𝑥𝑓0′+
∆𝑥2
2 𝑓0′′−∆𝑥63𝑓0′′′+ ⋯ )]
=𝑓0′−2∆𝑥1 (2∆𝑥𝑓0′+∆𝑥33𝑓0′′′+ ⋯ ) =𝑓0′− 𝑓0′−∆𝑥62𝑓0′′′+ ⋯
=−∆𝑥62𝑓0′′′+ ⋯
=−∆𝑥62𝑓0′′′, 𝑥−1< 𝑡 < 𝑥1
= 𝑂(∆𝑥2).
Jadi, hampiran beda pusat memiliki galat 𝐸 = −∆𝑥62𝑓0′′′, 𝑥−1< 𝑡 < 𝑥1, dengan orde 𝑂(∆𝑥2).
F. Karakteristik Persamaan Gelombang Air Dangkal Dipandang persamaan gelombang air dangkal
ℎ𝑡+ (𝑢ℎ)𝑥 = 0 (2.15)
(ℎ𝑢)𝑡+ (𝑢2ℎ +1
2𝑔ℎ2)𝑥= 0. (2.16)
Gabungan persamaan (2.15) dan (2.16) dalam suatu sistem persamaan gelombang air dangkal yaitu
[ ℎℎ𝑢]
𝑡+ [ ℎ𝑢 ℎ𝑢2+1
2𝑔ℎ2]
𝑥
= 0 (2.17)
Jika diasumsikan ℎ dan 𝑢 halus (smooth), maka persamaan (2.16) dapat disederhanakan dengan memperluas turunan-turunannya dan menggunakan (2.15)
untuk menggantikan bentuk ℎ𝑡. Kemudian dengan menghilangkan beberapa bentuk, persamaan (2.16) menjadi
𝑢𝑡+ [1
2𝑢2+ 𝑔ℎ]𝑥= 0. (2.18)
Pada persamaan (2.15) dan (2.18) memiliki bentuk yang bergantung dengan konstanta 𝑔. Bentuk tersebut dapat disubtitusi dengan variabel 𝜑 = 𝑔ℎ. Sehingga sistem persamaan air dangkal menjadi
[𝑢
𝜑]𝑡+ [𝑢2 2 + 𝜑
𝑢𝜑 ]
𝑥
= 0 (2.19)
Sistem persamaan tersebut ekuivalen dengan sistem persamaan (2.17) untuk solusi yang halus. Namun ada catatan penting bahwa manipulasi yang dilakukan di atas bergantung pada kehalusan pada masalah. Kedua sistem dari hukum konservasi tidak ekuivalen dalam menghitung shock waves. Sistem yang tepat untuk digunakan adalah sistem persamaan (2.17) yang berasal dari persamaan integral asli. Untuk mempelajari shock waves digunakan persamaan (2.17) dan diambil
𝑞(𝑥, 𝑡) = [ ℎ
ℎ𝑢] = [𝑞1
𝑞2] , 𝑓(𝑞) = [ ℎ𝑢 ℎ𝑢2+1
2𝑔ℎ2] = [
𝑞2 (𝑞2)2
𝑞1 +1
2𝑔(𝑞1)2].
Untuk solusi halus (smooth), persamaan tersebut dapat ditulis secara ekuivalen dalam bentuk quasilinear
𝑞𝑡+ 𝑓′(𝑞)𝑞𝑥 = 0 Dengan matriks Jacobian 𝑓′(𝑞) adalah
𝑓′(𝑞) = [
0 1
(𝑞2)2 𝑞1 +1
2𝑔(𝑞1)2 2𝑞2 𝑞1
] = [ 0 1
−𝑢2 + 𝑔ℎ 2𝑢].
(2.20)
Nilai eigen dari 𝑓′(𝑞) adalah
𝜆1 = 𝑢 − √𝑔ℎ, 𝜆2 = 𝑢 + √𝑔ℎ (2.21)
Dengan vektor eigen
𝑟1 = [ 1
𝑢 − √𝑔ℎ] , 𝑟2 = [ 1 𝑢 + √𝑔ℎ].
(2.22)
Nilai eigen dan vektor eigen adalah fungsi 𝑞 untuk sistem nonlinear. Jika diinginkan gelombang dengan amplitudo yang sangat kecil, maka persamaan (2.17) dapat dilinearkan terlebih dahulu untuk mendapatkan sistem yang linear. Keterangan lengkap tentang karakteristik persamaan air dangkal dapat ditemukan dalam buku karangan LeVeque (2004).
28 BAB III
METODE NUMERIS UNTUK PERSAMAAN GELOMBANG AIR DANGKAL
Dalam bab ini akan dijelaskan metode volume hingga, metode beda hingga grid kolokasi dan metode beda hingga grid selang-seling. Metode tersebut digunakan untuk menyelesaikan masalah bendungan air bobol, terkait dengan persamaan gelombang air dangkal.
A. Solusi Eksak Persamaan Gelombang Air Dangkal
Galat perhitungan pada penurunan numeris diperoleh dengan mengurangkan solusi numeris dengan solusi eksak. Berikut adalah solusi eksak yang akan digunakan dalam perhitungan simulasi numeris pada MATLAB:
ℎ(𝑥) =
{
ℎ1, jika 𝑥 ≤ −𝑡√𝑔ℎ1 ℎ3 = 4
9𝑔(√𝑔ℎ1− 𝑥
2𝑡)2, jika − 𝑡√𝑔ℎ1 < 𝑥 ≤ 𝑡(𝑢2− √𝑔ℎ2) ℎ2 =ℎ0
2 (√1 +8𝜉̇2
𝑔ℎ0− 1) , jika 𝑡(𝑢2− √𝑔ℎ2) < 𝑥 < 𝑡𝜉̇
ℎ0, jika 𝑥 ≥ 𝑡𝜉̇
dan
𝑢(𝑥) =
{
0, jika 𝑥 ≤ −𝑡√𝑔ℎ1 𝑢3 = 2
3(√𝑔ℎ1+𝑥
𝑡)2, jika − 𝑡√𝑔ℎ1 < 𝑥 ≤ 𝑡(𝑢2− √𝑔ℎ2) 𝑢2 = 𝜉̇ −𝑔ℎ0
4𝜉̇ (√1 + 8𝜉̇2
𝑔ℎ0) , jika 𝑡(𝑢2− √𝑔ℎ2) < 𝑥 < 𝑡𝜉̇
0, jika 𝑥 ≥ 𝑡𝜉̇
dengan ℎ(𝑥) adalah kedalaman air pada titik 𝑥 dan 𝑢(𝑥) adalah kecepatan air pada titik 𝑥. Notasi 𝜉̇ adalah konstanta kecepatan shock untuk 𝑡 > 0, yaitu
𝜉̇ = 2√𝑔ℎ1+𝑔ℎ0
4𝜉̇ (1 + √1 +8𝜉̇2
𝑔ℎ0) − [2𝑔ℎ0√1 +8𝜉̇2
𝑔ℎ0− 2𝑔ℎ0]
12
.
Solusi eksak ini diambil dari Thesis karangan Mungkasi dengan judul Finite Volume Methods for the One Dimensional Shallow Water Equations (2008).
B. Penurunan Persamaan Gelombang Air Dangkal Satu Dimensi
Persamaan gelombang air dangkal dideskripsikan dari gerak fluida. Ada dua jenis gerak fluida yang dideskripsikan, yaitu Langrangian dan Eulerian. Deskripsi Langrangian berpusat pada partikel individu, dan pergerakannya diamati sebagai fungsi dari waktu. Posisi, kecepatan dan percepatan setiap partikel dinotasikan dengan 𝑠(𝑥0, 𝑡), 𝑢(𝑥0, 𝑡), dan 𝑎(𝑥0, 𝑡), kemudian kuantitasnya misalnya massa, momentum dan energi dapat dihitung. Pada kasus ini 𝑥0 merupakan titik awal atau penamaan partikel.
Deskripsi Eulerian merupakan sebuah alternatif yang dapat diikuti setiap partikel fluida secara terpisah. Kemudian dilakukan pengamatan untuk kecepatan partikel yang melewati setiap titik identifikasi pada domain ruang yang diamati.
Laju perubahan kecepatan ketika partikel melewati setiap titik dapat diamati dengan
𝜕𝑢(𝑥,𝑡)
𝜕𝑥 , dan perubahan kecepatan terhadap waktu pada setiap titik tertentu dapat diamati oleh 𝜕𝑢(𝑥,𝑡)𝜕𝑡 . Dalam deskripsi Eulerian, sifat aliran (seperti kecepatan) merupakan fungsi dari ruang dan waktu.
Persamaan air dangkal ini terdiri dari dua persamaan. Persamaan pertama diturunkan dari hukum konservasi massa dan persamaan kedua diturunkan dari hukum konservasi momentum. Berikut ini akan diuraikan penurunan persamaan gelombang air dangkal atau biasa disebut Shallow Water Wave Equations.
a. Hukum Kekekalan Massa
Hukum kekekalan massa berarti massa tersebut tidak dapat diciptakan atau dimusnahkan. Hal ini berarti massa total pada keseluruhan sistem sama setiap saat.
Terdapat beberapa asumsi yang terlibat dalam penurunan persamaan hukum kekekalan massa. Pertama, aliran air diasumsikan tenang artinya tidak ada gangguan dari luar dan kecepatannya diabaikan. Kedua, densitas 𝜌 air pada setiap titik adalah konstan sehingga air mampat. Selain itu diasumsikan bahwa tempat air kedap atau tertutup rapat karena massa adalah kekal. Oleh karena itu, massa pada setiap volume kontrol (yaitu volume tertentu atau kolam air yang diamati) hanya dapat berubah ketika aliran melintasi batas-batas volume kontrol.
Secara umum, aliran air dapat diilustrasikan pada Gambar 1.1. Notasi yang digunakan yaitu 𝑥 menyatakan variabel jarak sepanjang aliran air, 𝑡 menyatakan variabel waktu, 𝑧(𝑥) adalah topografi tanah, ℎ(𝑥, 𝑡) adalah kedalaman air di titik 𝑥 dan pada waktu 𝑡, 𝑤(𝑥, 𝑡) = 𝑧(𝑥) + ℎ(𝑥, 𝑡) adalah ketinggian air mutlak disebut
stage, dan 𝑢(𝑥, 𝑡) adalah kecepatan aliran air di titik 𝑥 dan pada waktu 𝑡. Massa total 𝑚 pada air di setiap volume kontrol [𝑥1, 𝑥2] ditentukan oleh
𝑚 = ∫ 𝜌ℎ(𝑥, 𝑡)𝑑𝑥
𝑥2 𝑥1
(3.1)
Pernyataan ini dapat diperoleh sebagai berikut. Kepadatan massa terhadap kedalaman 𝜌̅ di sebarang titik (𝑥, 𝑡) adalah 𝜌ℎ(𝑥, 𝑡) yang dapat dihitung dengan mengintegralkan 𝜌 dari 𝑧(𝑥) ke 𝑤(𝑥, 𝑡), yaitu
𝜌̅(𝑥, 𝑡) = ∫ 𝜌 𝑑𝑦
𝑤(𝑥,𝑡) 𝑧(𝑥)
= 𝜌ℎ(𝑥, 𝑡).
Akibatnya, pengintegralan 𝜌ℎ(𝑥, 𝑡) dari 𝑥1 ke 𝑥2 mengarah ke massa total di volume kontrol seperti yang dinyatakan dalam (3.1). Tingkatan aliran air yang melewati setiap titik (𝑥, 𝑡) terhadap kedalaman air disebut flux massa 𝑓1, yaitu
𝑓1 = 𝜌̅(𝑥, 𝑡)𝑢(𝑥, 𝑡) (3.2)
= 𝜌ℎ(𝑥, 𝑡)𝑢(𝑥, 𝑡)
Dengan menggunakan (3.2) dan asumsi bahwa massa dapat berubah hanya karena aliran yang melewati batas volume kontrol, dapat ditentukan bahwa
∫ 𝜌ℎ(𝑥, 𝑡 + ∆𝑡)𝑑𝑥 =𝑥2
𝑥1
∫ 𝜌ℎ(𝑥, 𝑡)𝑑𝑥𝑥2
𝑥1
+ ∫ 𝜌ℎ(𝑥1, 𝑠)𝑢(𝑥1, 𝑠)𝑑𝑠 −
𝑡+∆𝑡 𝑡
∫ 𝜌ℎ(𝑥2, 𝑠)𝑢(𝑥2, 𝑠)𝑑𝑠
𝑡+∆𝑡 𝑡
(3.3)
berlaku untuk setiap volume kontrol. Hal ini berarti bahwa massa pada setiap langkah 𝑡 + ∆𝑡 adalah sama dengan massa pada waktu 𝑡 ditambah pergerakan flux
yang masuk dan dikurangi dengan flux yang keluar dari volume kontrol selama periode ∆𝑡. Ilustrasi dari kontinuitas massa ditunjukkan pada Gambar 3.1.
Gambar 3.1: Aliran air yang masuk dan keluar dari volume kontrol.
Misalkan ∆𝑥 dan ∆𝑡 adalah kuantitas yang sangat kecil, yaitu ∆𝑥 = 𝑥2− 𝑥1. Dengan menggunakan perluasan Taylor, persamaan (3.3) dapat ditulis
𝜌ℎ(𝑥, 𝑡 + ∆𝑡)∆𝑥
= 𝜌ℎ(𝑥, 𝑡)∆𝑥 + 𝜌ℎ (𝑥 −∆𝑥
2 , 𝑡) 𝑢 (𝑥 −∆𝑥 2 , 𝑡) ∆𝑡
− 𝜌ℎ (𝑥 +∆𝑥
2 , 𝑡) 𝑢 (𝑥 +∆𝑥
2 , 𝑡) ∆𝑡 + 𝑂((∆𝑡)3) + 𝑂((∆𝑥)3).
Dengan mengabaikan bentuk 𝑂((∆𝑡)3) dan 𝑂((∆𝑥)3) persamaan terakhir di atas ekuivalen dengan
𝜌ℎ(𝑥, 𝑡 + ∆𝑡) − 𝜌ℎ(𝑥, 𝑡)
∆𝑡 = −
(𝜌ℎ𝑢)|
(𝑥+∆𝑥
2 ,𝑡)− (𝜌ℎ𝑢)|
(𝑥−∆𝑥 2 ,𝑡)
∆𝑥
(3.4)
Persamaan (3.4) dibagi dengan 𝜌 kemudian ∆𝑥 dan ∆𝑡 diaproksimasikan menuju nol sehingga persamaan (3.4) menjadi
ℎ𝑡+ (𝑢ℎ)𝑥 = 0. (3.5)
Persamaan (3.5) disebut persamaan hukum kekekalan massa.
𝑢̅
𝑥1 𝑥2
𝑢
b. Hukum Kekekalan Momentum
Hukum kedua Newton menyatakan bahwa perubahan momentum dari suatu sistem sama dengan total gaya yang bekerja. Berdasarkan hukum Newton tersebut, maka dapat ditulis
𝐹 =𝑑𝑝 𝑑𝑡.
Gaya 𝐹 didefinisikan sebagai laju perubahan momentum 𝑝 terhadap waktu 𝑡.
Momentum total dari perpindahan air pada volume kontrol dari 𝑥1 ke 𝑥2 pada waktu 𝑡 dinotasikan dengan 𝑝(𝑡), yaitu
𝑝(𝑡) = ∫𝑥2(𝑡)𝜌ℎ(𝑥, 𝑡)𝑢(𝑥, 𝑡)𝑑𝑥
𝑥1(𝑡)
(3.6)
Dengan mengasumsikan tekanan hidrostatik, gaya pada titik 𝑥1 dan 𝑥2 di atas kedalaman air pada waktu 𝑡 adalah
𝐹1(𝑡) =1
2𝜌𝑔ℎ2(𝑥1(𝑡), 𝑡)
𝐹2(𝑡) = −1
2𝜌𝑔ℎ2(𝑥2(𝑡), 𝑡)
Dengan 𝑔 > 0 adalah konstanta yang menyatakan percepatan gravitasi. Lebih lanjut, gaya pada ∆𝑧 seperti yang ditunjukkan pada Gambar 3.2, yaitu
∆𝐹3 = −𝜌𝑔ℎ(𝑥, 𝑡)∆𝑧
Atau dapat ditulis dengan
∆𝐹3 = −𝜌𝑔ℎ(𝑥, 𝑡)∆𝑧
∆𝑥∆𝑥
Dan karena gaya melalui dasar volume kontrol maka
𝐹3 = ∫ −𝜌𝑔ℎ(𝑥, 𝑡)𝑧𝑥𝑑𝑥
𝑥2 𝑥1
.
Oleh karena itu, gaya total di atas volume kontrol dinyatakan dengan 𝐹 yang merupakan jumlahan dari 𝐹1, 𝐹2, dan 𝐹3, yaitu
𝐹 = 1
2𝜌𝑔ℎ2(𝑥1(𝑡), 𝑡) −1
2𝜌𝑔ℎ2(𝑥2(𝑡), 𝑡) − ∫ 𝜌𝑔ℎ(𝑥, 𝑡)𝑑𝑧 𝑑𝑥𝑑𝑥
𝑥2 𝑥1
(3.7)
Turunan pertama dari 𝑝 terhadap 𝑡 adalah 𝑑𝑝
𝑑𝑡 = 𝑑
𝑑𝑡∫ 𝜌ℎ(𝑥, 𝑡)𝑢(𝑥, 𝑡)𝑑𝑥
𝑥2 𝑥1
Dengan menggunakan aturan Leibniz, turunan hasil integral pada persamaan terakhir di atas dapat ditulis
𝑑𝑝
𝑑𝑡 = ∫ 𝜕
𝜕𝑡𝜌ℎ(𝑥, 𝑡)𝑢(𝑥, 𝑡)𝑑𝑥
𝑥2 𝑥1
+ 𝜌ℎ(𝑥2(𝑡), 𝑡)𝑢2(𝑥2(𝑡), 𝑡)
− 𝜌ℎ(𝑥1(𝑡), 𝑡)𝑢2(𝑥1(𝑡), 𝑡)
(3.8)
Menurut hukum kedua Newton tentang gerak, hasil dari persamaan (3.8) sama dengan persamaan (3.7). Oleh karena itu, untuk periode-∆𝑡 dapat ditulis
∫ ∫ (𝜌ℎ𝑢)𝑡 𝑑𝑥 𝑑𝑡
𝑥2(𝑡) 𝑥1(𝑡) 𝑡+∆𝑡 𝑡
+ ∫𝑡+∆𝑡𝜌ℎ(𝑥2(𝑡), 𝑡)𝑢2(𝑥2(𝑡), 𝑡)𝑑𝑡
𝑡
− ∫𝑡+∆𝑡𝜌ℎ(𝑥1(𝑡), 𝑡)𝑢2(𝑥1(𝑡), 𝑡)𝑑𝑡
𝑡
= ∫ 1
2𝜌𝑔ℎ2(𝑥1(𝑡), 𝑡) 𝑑𝑡
𝑡+∆𝑡 𝑡
∫ 1
2𝜌𝑔ℎ2(𝑥2(𝑡), 𝑡) 𝑑𝑡
𝑡+∆𝑡 𝑡
− ∫ ∫ 𝜌𝑔ℎ(𝑥, 𝑡)𝑧𝑥 𝑑𝑥 𝑑𝑡
𝑥2(𝑡) 𝑥1(𝑡) 𝑡+∆𝑡 𝑡
(3.9)
Dengan cara yang sama seperti (3.3), persamaan (3.9) dapat ditulis
(ℎ𝑢)𝑡+ (ℎ𝑢2+1 2𝑔ℎ2)
𝑥 = −𝑔ℎ𝑧𝑥 Yang biasa disebut dengan persamaan kekekalan momentum.
Dengan demikian, persamaan gelombang air dangkal seringkali disebut sistem Saint-Venant. Persamaan tersebut dapat ditulis sebagai dua persamaan simultan
{
ℎ𝑡+ (𝑢ℎ)𝑥 = 0 (ℎ𝑢)𝑡+ (ℎ𝑢2+1
2𝑔ℎ2)
𝑥 = −𝑔ℎ𝑧𝑥
(3.10)
di sini variabel x menyatakan arah aliran air.
C. Masalah Bendungan Bobol
Diketahui persamaan gelombang air dangkal dengan topografi horizontal
𝑞𝑡+ 𝑓(𝑞)𝑥 = 0 (3.11)
Dengan kuantitas dan flux berturut-turut adalah
𝑞 = [ ℎ
𝑢ℎ] dan 𝑓(𝑞) = [ 𝑢ℎ 𝑢2ℎ + 1
2𝑔ℎ2]
dengan 𝑥 adalah variabel ruang, 𝑡 adalah variabel waktu, ℎ = ℎ(𝑥, 𝑡) adalah kedalaman air, 𝑢 = 𝑢(𝑥, 𝑡) adalah kecepatan air dan 𝑔 = 9,81 adalah percepatan gravitasi. Semua kuantitas diasumsikan dalam satuan SI.
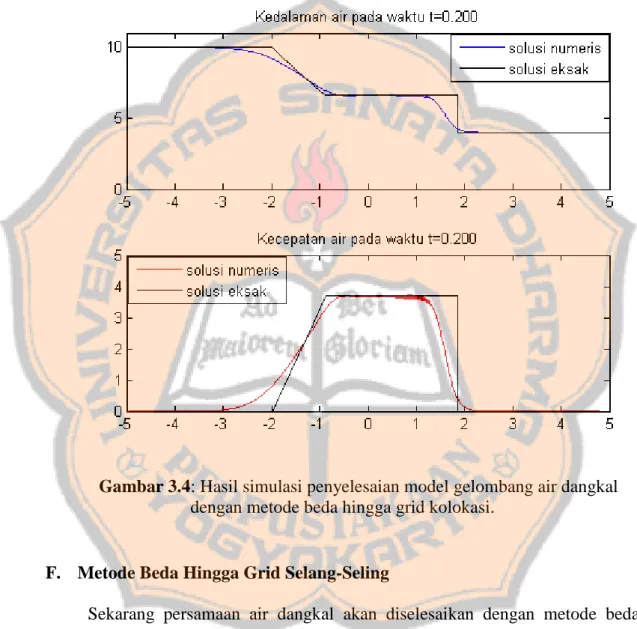
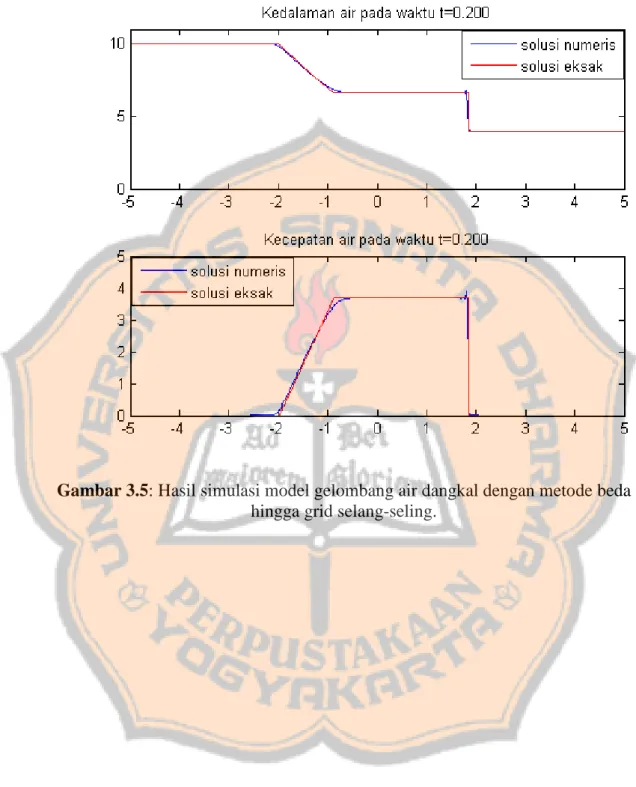
Akan disimulasikan solusi masalah bendungan bobol dengan metode volume hingga Lax-Friedrics, metode beda hingga grid kolokasi dan metode beda hingga grid selang-seling dengan menggunakan MATLAB (kondisi awal adalah "air yang tenang" seperti yang ditunjukkan pada Gambar 3.2). Pada kasus ini dianggap dinding bendungan ditarik ke atas secara instan.
Gambar 3.2: Bendungan air
Dinding bendungan air berada di titik 𝑥 = 0 dan kedalaman awal air adalah
ℎ(𝑥, 0) = {ℎ1, jika 𝑥 < 0 ℎ0, jika 𝑥 > 0
dan kecepatan awal aliran air adalah
Bendungan air Permukaan air
Permukaan air ℎ1 = 10
ℎ0 = 4
𝑥
𝑢(𝑥, 0) = 0, untuk semua 𝑥.
Diambil domain ruang [−5,5]. Simulasi pada program dihentikan pada 𝑡 = 0.2.
Pada kasus ini diasumsikan massa jenis konstan, tidak ada turbulen dan fluida ideal.
D. Metode Volume Hingga Lax-Friedrichs
Pada bagian ini dibahas mengenai skema metode volume hingga, perhitungan flux secara numeris dalam metode volume hingga dan solusi numeris metode volume hingga Lax-Friedrichs.
1.1. Skema Metode Volume Hingga
Persamaan diferensial parsial hukum kekekalan yang bersifat hiperbolik adalah
𝑞𝑡+ 𝑓(𝑞)𝑥 = 0 atau ditulis
𝜕
𝜕𝑡𝑞(𝑥, 𝑡) +𝜕𝑥𝜕 𝑓(𝑞(𝑥, 𝑡)) = 0.
Misalkan domain pada ruang didiskretkan menjadi sebanyak berhingga kontrol volume (interval) atau sel sebagai berikut:
dengan ∆𝑥 = 𝑥𝑖−1− 𝑥𝑖 atau ∆𝑥 = 𝑥𝑖+1
2− 𝑥𝑖−1
2. Domain waktu didiskretkan menjadi
𝑡𝑛 = 𝑛 ∙ ∆𝑡 𝑥𝑖−3
2
𝑥𝑖−1 𝑥𝑖 𝑥𝑖+1
𝑥𝑖−1
2 𝑥𝑖+1
2
𝑥𝑖+3 2