Data kualitatif adalah data yang berbentuk kata-kata, bukan dalam bentuk angka. Data kualitatif diperoleh melalui berbagai macam teknik pengumpulan data misalnya wawancara, analisis dokumen, diskusi terfokus, atau observasi. Data kuantitatif adalah data yang
berbentuk angka atau bilangan. Sesuai dengan bentuknya, data kuantitatif dapat diolah atau dianalisis menggunakan teknik perhitungan matematika atau statistika.
Syarat data yang baik yaitu obyektif, representative, mempunyai tingkat kesalahan yang kecil, harus tepat waktu, relevan.
2. Distribusi Frekuensi Kelompok
Data yang berukuran besar (n > 30) lebih tepat disajikan dalam tabel distribusi frekuensi kelompok, yaitu cara penyajian data yang datanya disusun dalam kelas-kelas tertentu. Langkah-langkah penyusunan tabel distribusi frekuensi adalah sebagai berikut.
Langkah ke-1 menentukan Jangkauan (J) = Xmax - Xmin
Langkah ke-2 menentukan banyak interval (K) dengan rumus "Sturgess" yaitu: K= 1 + 3,3 log n dengan n adalah banyak data. Banyak kelas harus merupakan bilangan bulat positif hasil pembulatan ke bawah.
Langkah ke-3 menentukan panjang interval kelas (I) dengan menggunakan rumus: J
I = –––– K
Langkah ke-4 menentukan batas-batas kelas. Data terkecil harus merupakan batas bawah interval kelas pertama atau data terbesar adalah batas atas interval kelas terakhir.
Langkah ke-5 memasukkan data ke dalam kelas-kelas yang sesuai dan menentukan nilai frekuensi setiap kelas dengan sistem turus.
Kuartil, Rata-rata Ukur, dan Rata-rata Harmonik
29 Sep
STATISTIKA EKONOMI I
BAB V
KUARTIL
Kuartil (K) adalah nilai-nilai yang membagi serangkaian data atau suatu frekuensi menjadi empat bagian yang sama.
Menurut Sudijono, 2006:112. Dalam dunia statistik, yang dimaksud dengan kuartil ialah titik atau skor atau nilai yang membagi seluruh distribusi frekuensi kedalam empat bagian yang sama besar, yaitu masing-masing sebesar 1/4N.
Dalam buku Suharyadi dan Purwanto SH, Kuartil diartikan sebagai ukuran letak yang membagi data yang telah diurutkan atau data yang berkelompok menjadi 4 bagian sama besar atau setiap bagian dari kuartil sebesar 25%. Kuartil 1 (K1) membagi data sebelah kiri sebesar25% dan sebelah kanan 75%. Kuartil 2 (K2) membagi data menjadi 2 bagian yang sama yaitu sisi kanan dan sisi kiri sebesar 50%, jika kurva berbentuk simetris maka K2 sama dengan Median. K3 membagi data sebelah kiri sebesar 75% dan sebelah kanan 25%.
RUMUS
Untuk mencari Q1,Q2 dan Q3 digunakan rumus sebagai berikut:
untuk data tunggal
Qn = kuartil yang ke-n. karena titik kuartil ada tiga buah, maka n dapat diisi dengan bilangan: 1,2, dan 3.
1 = lower limit ( batas bawah nyata dari skor atau interval yang mengandung Qn).
N= Number of cases.
Fkb= frekuensi kumulatif yang terletak dibawah skor atau interval yang mengandung Qn.
Fi= frekuensi aslinya (yaitu frekuensi dari skor atau interval yang mengandung Qn).
istilah skor berlaku untuk data tunggal.
istilah interval berlaku untuk data kelompok.
Contoh perhitungan kuartil untuk data tunggal
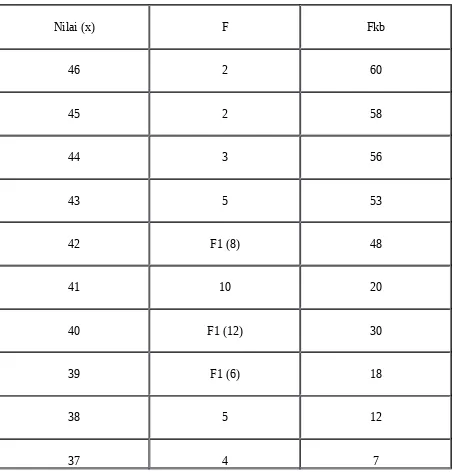
Misalkan dari 60 orang siswa MAN Jurusan IPA diperoleh nilai hasil EBTA bidang studi Fisika sebagaimana tertera pada table distribusi frekuensi berikut ini. Jika kita ingin mencari Q1, Q2, dan Q3 (artinya data tersebut akan kita bagi dalam empat bagian yang sama besar), maka proses perhitungannya adalah sebagai berikut:
Table 3.11. Distribusi frekuensi nilai hasil Ebta dalam bidang studi fisika dari 60 orang siswa MAN jurusan ipa, dan perhitungan Q1, Q2, dan Q3.
Nilai (x) F Fkb
46 2 60
45 2 58
44 3 56
43 5 53
42 F1 (8) 48
41 10 20
40 F1 (12) 30
39 F1 (6) 18
38 5 12
36 2 3
35 1 1
Titik Q1= 1/4N = ¼ X 60 = 15 ( terletak pada skor 39). Dengan demikian dapat kita ketahui: 1= 38,50; fi = 6; fkb = 12
Q1= 1 + ( n/4N-fkb) = 38,50 +(15-12) Fi 6
= 38,50 +0,50 = 39
Titik Q2= 2/4N = 2/4 X 60 = 30 ( terletak pada skor 40). Dengan demikian dapat kita ketahui: 1= 39,50; fi = 12; fkb = 18
Q2 = 1 + ( n/4N-fkb) = 39,50 +(30-18) Fi 12
= 39,50 +1,0 = 40,50
Titik Q3= 3/4N = 3/4 X 60 = 45 ( terletak pada skor 42). Dengan demikian dapat kita ketahui: 1= 41,50; fi = 8; fkb = 40
Q3 = 1 + ( n/4N-fkb) = 41,50 +(45-40) Fi 8
= 41,50+ 0,625 = 42,125
Contoh perhitungan kuartil untuk data kelompok
Titik Q1= 1/4N = ¼ X 80 = 20 ( terletak pada interval 35-39). Dengan demikian dapat
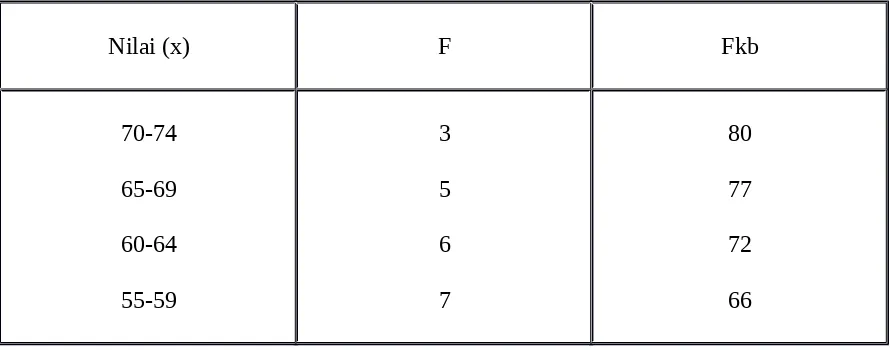
Titik Q2= 2/4N = 2/4 X 80 = 40 ( terletak pada interval 45-49). Dengan demikian dapat kita ketahui: 1= 44,50; fi = 17; fkb = 35, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi = 44,50 +(40-35) X5 Fi 17
= 44,50 +1.47 = 45,97
Titik Q3= 3/4N = 3/4 X 80 = 60 ( terletak pada interval 55-59). Dengan demikian dapat kita ketahui: 1= 54,50; fi = 7; fkb = 59, i= 5.
Q1 = 1 + ( n/4N-fkb) Xi = 54,50 +(55-59) X5 Fi 7
= 54,50 + 0,71 = 55,21
Tabel 3.12. distribusi frekuensi skor-skor hasil EBTA bidang studi tata buku dari 80 orang siswa man jurusan ips, berikut perhitungan Q1,Q2, dan Q3.
50-54
Diantara kegunaan kuartil adalah untuk mengetahui simetris (normal) atau a simetrisnya suatu kurva. Dalam hal ini patokan yang kita gunakan adalah sebagai berikut:
1. Jika Q3-Q2 = Q2- Q1 maka kurvanya adalah kurva normal.
2. Jika Q3-Q2 > Q2- Q1 maka kurvanya adalah kurva miring/ berat ke kiri(juling positif).
3. Jika Q3-Q2 < Q2- Q1 maka kurvanya adalah kurva miring/ berat ke kanan(juling negatif).
DESIL
DESIL
Desil adalah ukuran letak yang membagi data yang telah diurutkan atau data berkelompok menjadi 10 bagian yang sama besar, atau setiap bagian dari desil sebesar 10%.
Ukuran Letak
Rumus Ukuran Letak
Data Tunggal Data Berkelompok
Desil 1 (D1) [1(n+1)]/10 1n/10
Desil 2 (D2) [2(n+1)]/10 2n/10
…. … …
Desil 9 (D9) [9(n+1)]/10 9n/10
CONTOH SOAL
PENYELESAIAN D1 = nilai ke 1(13 + 1) 10
= nilai ke-14/10
= nilai ke-14/10, berarti X1 + 4/10(X2 – X1) = 30 + 4/10(35 – 30)
= 32
D2 = nilai ke 2(13 + 1) 10
= nilai ke-28/10, berarti X2 + 8/10 (X3 – X2) = 35 + 8/10 (40 – 35)
` = 39
D9 = nilai ke 9(13 + 1) 10
= nilai ke-126/10, berarti X12 + 6/10 (X13 – X12) = 95 + 6/10 (100 – 95)
= 98
Rumus Desil data berkelompok Rumus Desil :
Keterangan :
n = banyak data
F = frekuensi kumulatif kelas sebelum kelas desil
f = frekuensi kelas desil
b = tepi bawah kelas
l = lebar kelas
PRESENTIL
Presentil adalah ukuran letak yang membagi data yang telah diurutkan atau data yang berkelompok menjadi 100 bagian yang sama besar, atau setiap bagian dari desil sbesar 1%.
Ukuran Letak
Rumus Ukuran Letak
Data Tunggal Data Berkelompok
Presentil 1 (P1) [1(n+1)]/100 1n/100
Presentil 2 (P2) [2(n+1)]/100 2n/100
…. … …
Presentil 99 (D9) [99(n+1)]/100 99n/100
Apabila data sudah disusun mulai dari yang terkecil (X1) sampai yang terbesar (Xn), maka rumus persentil adalah sebagai berikut :
i(n + 1) 100
Pi = nilai yang ke , i = 1, 2, …, 99 Untuk data berkelompok
Keterangan :
Pi = persentil ke-i
n = banyaknya data
F = frekuensi kumulatif kelas sebelum kelas persentil
f = frekuensi kelas persentil
l = lebar kelas
Contoh penggunaan rumus yang hampir sama dengan sedikit perubahan dalam rumus yang disebutkan….
Menentukan Presentil 40 dari tabel berikut.. tabel nilai siswa kelas XII IPS
RATA-RATA UKUR
Rata-Rata Ukur (Geometric Mean)
Untuk gugus data positif x1, x2, …, xn, rata-rata geometrik adalah akar ke-n dari hasil perkalian unsur-unsur datanya. Secara matematis dapat dinyatakan dengan formula berikut:
Keterangan:
U = rata-rata ukur (rata-rata geometrik) n = banyaknya sampel
Π = Huruf kapital π (pi) yang menyatakan jumlah dari hasil kali unsur-unsur data.
Rata-rata geometrik sering digunakan dalam bisnis dan ekonomi untuk menghitung rata-rata tingkat perubahan, rata-rata tingkat pertumbuhan, atau rasio rata-rata untuk data berurutan tetap atau hampir tetap atau untuk rata-rata kenaikan dalam bentuk persentase.
1. Rata-Rata Ukur data Tunggal
Contoh 1:
Berapakah rata-rata ukur dari data 2, 4, 8?
Jawab:
atau:
keterangan
xi = tanda kelas (nilai tengah)
fi = frekuensi yang sesuai dengan xi
Contoh 2:
Tentukan rata-rata ukur dari tabel distribusi frekuensi pada Contoh 3 di atas!
Jawab:
Kelas ke- Nilai Ujian fi xi log xi fi.log xi 1 31 – 40 2 35.5 1.5502 3.1005 2 41 – 50 3 45.5 1.6580 4.9740 3 51 – 60 5 55.5 1.7443 8.7215 4 61 – 70 13 65.5 1.8162 23.6111 5 71 – 80 24 75.5 1.8779 45.0707 6 81 – 90 21 85.5 1.9320 40.5713 7 91 – 100 12 95.5 1.9800 23.7600
8 Jumlah 80 149.8091
Rata-Rata Harmonik
Rata-rata harmonik dari suatu kumpulan data x1, x2, …, xn adalah kebalikan dari nilai rata-rata hitung (aritmetik mean). Secara matematis dapat dinyatakan dengan formula berikut:
Secara umum, rata-rata harmonik jarang digunakan. Rata-rata ini hanya digunakan untuk data yang bersifat khusus. Misalnya,rata-rata harmonik sering digunakan sebagai ukuran tendensi sentral untuk kumpulan data yang menunjukkan adanya laju perubahan, seperti kecepatan. 1. Rata-Rata Harmonik data Tunggal
Jawab:Apabila kita menghitungnya dengan menggunakan rumus jarak dan kecepatan, tentu
hasilnya 13.5 km/jam!
Apabila kita gunakan perhitungan rata-rata hitung, hasilnya tidak tepat!
Pada kasus ini, lebih tepat menggunakan rata-rata harmonik:
2. Rata-Rata Harmonil Distribusi Frekuensi
Contoh 2:
Berapa rata-rata Harmonik dari tabel distribusi frekuensi pada table berikut
Jawab:
Kelas ke- Nilai Ujian fi xi fi/xi 1 31 – 40 2 35.5 0.0563
2 41 – 50 3 45.5 0.0659
3 51 – 60 5 55.5 0.0901
4 61 – 70 13 65.5 0.1985
5 71 – 80 24 75.5 0.3179
6 81 – 90 21 85.5 0.2456
7 91 – 100 12 95.5 0.1257