BAB II TINJAUAN PUSTAKA - Tekuk Profil Baja Siku Sama Sisi dan Tidak Sama Sisi ( Teori dan Eksperimental )

BAB II

TINJAUAN PUSTAKA

2. 1 Teori Tekuk 2. 1. 1 Latar Belakang

Kolom merupakan batang tekan tegak yang bekerja untuk menahan balok

balok loteng, rangka atap, lintasan crane dalam bangunan pabrik dan sebagainya

yang untuk seterusnya akan melimpahkan semua beban tersebut ke pondasi.

Dengan berbagai macam sebutan, seperti kolom, tiang, tonggak, dan

batang desak, batang ini pada hakekatnya jarang sekali mengalami tekanan aksial

saja. Apabila sebuah batang lurus dibebani gaya tekan aksial dengan pemberian

beban semakin lama semakin tinggi, maka pada batang tersebut akan mengalami

perubahan. Perubahan dari keadaan sumbu batang lurus menjadi sumbu batang

melengkung dinamakan tekuk.

Pada hakekatnya batang yang hanya memikul tekan aksial saja jarang

dijumpai dalam struktur namun bila pembebanan diatur sedemikian rupa hingga

pengekangan (restrain) rotasi ujung dapat diabaikan atau beban dari batang

batang yang bertemu diujung kolom bersifat simetris dan pengaruh lentur sangat

kecil dibandingkan dengan tekanan langsung maka batang tekan dapat

direncanakan dengan aman sebagai kolom yang dibebani secara konsentris.

Dari mekanika bahan diketahui bahwa hanya kolom yang sangat pendek

dapat dibebani hingga mencapai tegangan lelehnya, sedangkan keadaan yang

bahan batang sepenuhnya tercapai. Keadaan demikian yang kita sebut dengan

tekuk (buckling). Jadi pengetahuan tentang kestabilan batang tekan perlu bagi

pembaca yang merencanakan struktur baja.

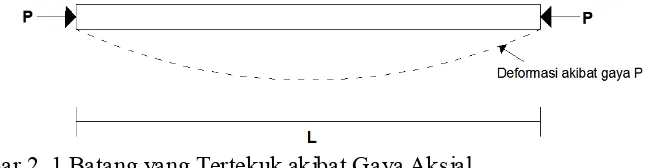
Gambar 2. 1 Batang yang Tertekuk akibat Gaya Aksial

Latar belakang tekuk kolom pertama kali dikemukakan oleh Leonhard

Euler pada tahun 1759. Batang dengan beban konsentris yang semula lurus dan

semua seratnya tetap elastis hingga tekuk terjadi akan mengalami lengkungan

yang kecil pada gambar 2. 1. Walaupun Euler hanya menyelidiki batang yang

dijepit disalah satu ujung dan bertumpu sederhana (simply supported) di ujung

yang lainnya, logika yang sama dapat diterapkan pada kolom yang berperletakan

sendi, yang tidak memiliki pengekangan rotasi dan merupakan batang dengan

kekuatan tekuk terkecil. Kita akan mendapatkan rumus rumus gaya kritis yang

dapat diterima oleh suatu batang sebelum tekuk terjadi.

Pendekatan Euler pada umumnya tidak digunakan untuk perencanaan

karena tidak sesuai dengan percobaan, dalam praktek kolom dengan panjang

umum tidak sekuat seperti yang dinyatakan oleh rumus rumus Euler.

Considere dan Esengger pada tahun 1889 secara terpisah menemukan

bahwa sebagian dari kolom dengan panjang yang umum menjadi inelastis

sebelum tekuk terjadi dan harga E yang dipakai harus memperhitungkan adanya

mereka menyadari bahwa sesungguhnya kolom dengan panjang yang umum akan

hancur akibat tekuk inelastis dan bukan akibat tekuk elastis.

Akan tetapi pengertian yang menyeluruh tentang kolom dengan beban

konsentris baru dicapai pada tahun 1946 ketika Shanley menjabarkan teori yang

sekarang ternyata benar. Ia mengemukakan bahwa hakekatnya kolom masih

mampu memikul beban aksial yang lebih besar walaupun telah melentur, tetapi

kolom mulai melentur pada saat mencapai beban yang disebut beban tekuk, yang

menyertakan pengaruh inelastisitas pada sejumlah atau semua serat penampang

lintang.

Untuk menentukan kekuatan kolom dasar, kondisi kolom perlu didealisir

dengan beberapa anggapan. Mengenai bahan, kita dapat menganggap :

1. Sifat tegangan regangan tekan sama diseluruh titik pada penampang.

2. Tidak ada tegangan internal seperti akibat pendinginan setelah

penggilingan (rolling).

3. Kolom lurus sempurna dan prismatis.

4. Resultan beban bekerja melalui sumbu pusat batang sampai batang mulai

melentur.

5. Kondisi ujung harus statis tertentu sehingga panjang antara sendi sendi

ekivalen dapat ditentukan.

6. Teori lendutan yang kecil seperti pada lenturan yang umum berlaku dan

gaya geser dapat diabaikan.

7. Puntiran atau distorsi pada penampang lintang tidak terjadi selama

Setelah anggapan anggapan diatas dibuat, sekarang disetujui bahwa

kekuatan suatu kolom dapat dinyatakan sebagai:

= =

Dimana :

σkr = tegangan rata rata pada penampang

Et = modulus tangen pada P/A

= angka kelangsingan efektif (ujung sendi ekivalen)

Seperti yang kita tahu batang tekan yang panjang akan runtuh akibat tekuk

elastis dan batang tekan yang pendek yang buntak dapat dibebani sampai bahan

meleleh atau bahkan sampai daerah pengerasan regangan (strain hardening). Pada

keadaan yang umum, kehancuran akibat tekuk terjadi setelah sebagian penampang

melintang meleleh, keadaan ini disebut dengan tekuk inelastis.

Tekuk murni akibat beban aksial sesungguhnya hanya terjadi apabila

anggapan dari (1) sampai (7) diatas berlaku. Kolom biasanya merupakan satu

kesatuan dengan struktur, dan pada hakekatnya tidak dapat berlaku secara

independent. Dalam praktek, tekuk diartikan sebagai pembatasan antara lendutan

stabil dan tidak stabil pada batang tekan: jika bukan kondisi sesaat yang terjadi

pada batang langsing elastis yang diisolir. Banyak insinyur menyebut “beban

tekuk praktis” ini sebagai “beban batas ultimate”.

2. 1. 2 Keruntuhan Batang Tekan

akibat tekuk elastis. Pada keadaan umum kehancuran akibat tekan terjadi diantara

keruntuhan akibat kelelehan bahan akibat tekuk elastis, setelah bagian penampang

melintang meleleh, keadaan ini disebut tekuk inelastis (inelastic buckling).

Ada tiga jenis keruntuhan batang tekan, yaitu:

1. Keruntuhan akibat tegangan yang terjadi pada penampang telah melalui

materialnya.

2. Keruntuhan akibat batang tertekuk elastis (elastic buckling). Keadaan ini

terjadi pada bagian konstruksi yang langsing. Disini hukum Hooke masih

berlaku bagi serat penampang dan tegangan yang terjadi tidak melebihi batas

proporsional.

3. Keruntuhan akibat melelehnya sebagian serat disebut tekuk inelastic (inelastic

buckling). Kasus keruntuhan semacam ini berada diantara kasus (1) dan kasus

(2), dimana pada saat menekuk sejumlah seratnya menjadi inelastis maka

modulus elastisitasnya ketika tertekuk lebih kecil dari harga awalnya.

2. 1. 3 Tegangan Residu

Keberadaan tegangan residu dalam profil sangat mempengaruhi kekuatan

tekuknya. Pengaruh ini diperhitungkan dengan mengambil tegangan residu

maksimum rata rata sebesar 0,3 dari tegangan lelehnya.

Tegangan residu (residual stresses) adalah tegangan yang tertinggal tetap

dalam profil setelah selesai profil dibentuk, meskipun belum ada beban luar yang

bekerja padanya.

Menurut hasil penelitian/penyelidikan, tegangan residu ini timbul oleh

1. Pendinginan setelah proses hot rolling.

2. Cold bending atau cambering selama fabrikasi.

3. Pengelasan.

2. 1. 4 Kelangsingan Batang Tekan ( λ )

Kelangsingan batang tekan ini tergantung dari jari jari kelembaman (i) dan

panjang tekuk (Lk). Karena batang mempunyai dua jari jari kelembaman,

umumnya akan terdapat dua harga λ. Yang menentukan ialah harga λ yang

terbesar (atau dengan i yang terkecil). Panjang tekuk (Lk) ini juga tergantung pada

keadaan ujung ujungnya, apakah sendi, jepit, bebas, dan sebagainya.

2. 1. 5 Angka Kelangsingan ( λbatas )

λbatas adalah batas angka kelangsingan dimana Euler tidak lagi berlaku

(berarti memasuki daerah plastis). Euler hanya berlaku di daerah elastis.

P

kr

=

( 2. 1 )

Dimana :

Lk = panjang tekuk

E = modulus elastisitas

I = momen inersia terhadap sumbu yang tegak lurus arah tekuk

i = jari jari kelembaman

I = i2 x A ( 2. 4 )

Dimana :

A = luas penampang

Substitusi persamaan ( 2. 4 ) ke dalam persamaan ( 2. 1 ) sehingga

diperoleh :

P

kr

=

( 2. 5 )

Dengan :

σ

kr

=

( 2. 6 )

Sehingga :

P

kr

= σ

cr

x A

( 2. 7 )

Dimana :

σ

kr = tegangan kritis

Dimana :

P

kr

= σ

cr

x A

P

kr

=

Maka didapat :

σ

kr

x A =

Sehingga :

Akibat pengaruh residual strees maka tegangannya menjadi 0,7 σ1, sehingga :

λg = _,!

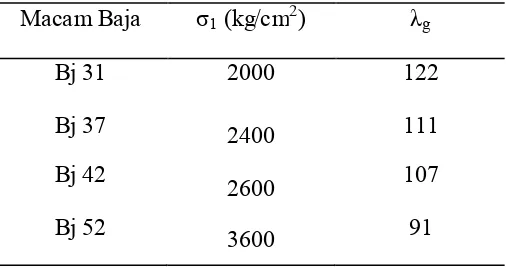
Selanjutnya λg untuk bermacam macam baja dapat dilihat di tabel berikut :

2. 1. 6 Stabilitas dari Struktur Kolom

Masalah kesetimbangan kolom erat kaitannya dengan stabilitas suatu

struktur batang. Konsep stabilitas sering diterangkan dengan menggangap

kesetimbangan dari bola pejal pada beberapa posisi, yaitu sebagai berikut.

1. Kesetimbangan Stabil

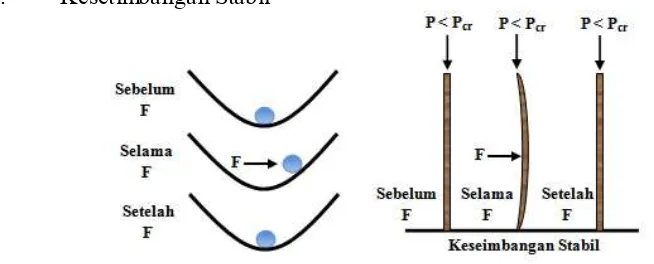
Gambar 2. 2 Kesetimbangan Stabil

Berdasarkan gambar 2. 2 bola pejal berada di permukaan yang cekung.

Kemudian bola pejal berubah posisinya ketika diberikan gaya F. Saat gaya F

hilang, posisi bola pejal kembali seperti semula. Kondisi ini adalah penganalogian

dari suatu kolom bermuatan P < Pkr yang diberikan gaya F tegak lurus sumbu

kolom sehingga mengalami lendutan. Jika gaya F dihilangkan maka kolom akan

kembali ke bentuk linearnya. Kondisi kesetimbangan ini disebut kesetimbangan

stabil (stable equilibrium).

2. Kesetimbangan Netral

Kolom dengan beban P = Pkr dianalogikan dengan bola pejal yang berada

di permukaan datar. Bola pejal tersebut diberi gaya F dan berpindah tempat tanpa

kembali ke tempatnya semula. Berdasarkan anggapan itulah suatu kolom

bermuatan P = Pkr jika diberikan beban sebesar F, maka kolom tersebut akan

mengalami tekuk. Ketika gaya F dilepaskan, kolom tidak akan kembali ke bentuk

linearnya. Kondisi kesetimbangan ini disebut kesetimbangan netral (precarious

equilibrium).

3. Kesetimbangan Tidak Stabil

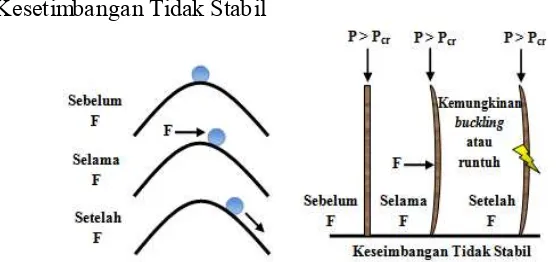
Gambar 2. 4 Kesetimbangan Tidak Stabil

Bola pejal berada pada permukaan yang cembung kemudian diberikan

gaya F maka akan terjadi pergeseran mendadak. Hal ini merupakan penganalogian

untuk kolom dengan P > Pkr. Kolom diberikan gaya F tegak lurus sumbu kolom

kemudian mengalami deformasi. Apabila beban diberikan secara konstan maka

akan berdampak runtuhnya kolom (bucking). Kondisi kesetimbangan ini disebut

dengan kesetimbangan tidak stabil (unstable equilibrium).

Batang tekan harus direncanakan sedemikian rupa sehingga terjamin

stabilitasnya (tidak ada bahaya tekuk). Hal ini harus diperlihatkan dengan

menggunakan persamaan :

Dimana :

Harga ω dapat dicari dari Tabel 2, 3, 4 atau 5 PPBBI ’83 berdasarkan mutu

baja Bj 34 (Fe 310), Bj 37 (Fe 360), Bj 44 (Fe 430) dan Bj 52 (Fe 510).

Harga λ ini dapat ditentukan dengan persamaan :

λ

g

=

_,!

Sifat baja yang terpenting dalam pengunaanya sebagai bahan konstruksi

adalah kekuatannya yang tinggi, dibandingkan dengan bahan lainnya seperti kayu,

dalam tegangan, regangan maupun dalam kompresi sebelum kegagalan, serta sifat

homogenitas yaitu sifat keseragaman yang tinggi.

Baja merupakan bahan campuran besi ( Fe ), 1,7 % Zat arang atau karbon

(C), 1,65 % mangan, 0,6 % silikon ( Si ) dan 0,6% tembaga ( Cu ). Baja

dihasilkan dengan menghaluskan bijih besi dan logam besi tua bersama sama

dengan bahan tambahan pencampur yang sesuai, dalam tungku temperatur tinggi

untuk menghasilkan massa massa besi yang besar, selanjutnya dibesihkan untuk

menghilangkan kelebihan zat arang dan kotoran kotoran lain.

Berdasarkan persentase zat arang yang dikandung, baja dapat

dikategorikan sebagai berikut :

1. Baja dengan persentase zat arang rendah ( low carbon steel )

Yakni lebih kecil dari 0,15 %

Baja untuk bahan struktur termasuk kedalam baja yang persentase zat

arang yang ringan ( mild carbon steel ), semakin tinggi kadar zat arang yang

terkandung didalamnya, maka semakin tinggi nilai tegangan lelehnya. Sifat sifat

bahan struktur yang paling penting dari baja adalah sebagai berikut :

Modulus elastisitas untuk semua baja ( yang secara relatif tidak tergantung

dari kuat leleh ) adalah 28000 sampai 30000 ksi atau 193000 sampai

207000 Mpa. Nilai untuk desain lazimnya diambil sebesar 29000 ksi atau

200000 Mpa.

Berdasarkan Peraturan Perencanaan Bangunan Baja Indonesia ( PPBBI ),

nilai modulus elastisitas baja adalah 2,1 x 106 kg/cm² atau 2,1 x 105 MPa.

2. Modulus Geser ( G )

Modulus geser setip bahan elastis dihitung berdasarkan formula :

/ = 2 (1+ 4)

Dimana : P = perbandingan poisson yang diambil sebesar 0,3 untuk baja.

Dengan menggunakan P = 0,3 maka akan memberikan G = 11000 ksi atau

77000 MPa.

Berdasarkan Peraturan Perencanaan Bangunan Baja Indonesia ( PPBBI ),

nilai modulus geser ( gelincir ) baja adalah 0,81 x 106 kg/cm² atau 0,81 x

105 MPa.

3. Koefisien Ekspansi ( α )

Koefisien ekspansi adalah koefisien pemuaian linier. Koefisien ekspansi

baja diambil sebesar 12 x 106 per oC.

4. Tegangan Leleh ( σ )

Tegangan leleh ditentukan berdasarkan mutu baja.

5. Sifat sifat lain yang penting.

Sifat – sifat ini termasuk massa jenis baja, yang sama dengan 490 pcf atau

atau 76, 975 kN/m³, berat jenis baja umumnya adalah sebesar 7,850 t/m3.

Untuk mengetahui hubungan antara tegangan dan regangan pada baja

dapat dilakukan dengan uji tarik di laboratorium. Sebagian besar percobaan atas

baja akan menghasilkan bentuk hubungan antara tegangan dan regangan seperti

tergambar di bawah ini.

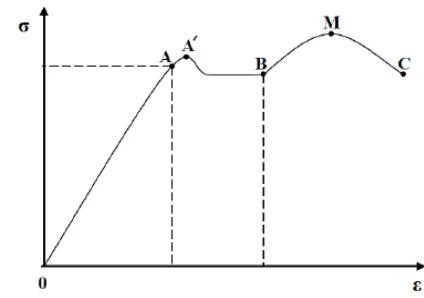
Gambar 2. 5 Hubungan Tegangan Regangan untuk Uji Tarik pada Baja

Lunak

Keterangan gambar :

σ = tegangan baja

ε = regangan baja

A = titik proporsional

A’ = titik batas elastis

B = titik batas plastis

M = titik runtuh

C = titik putus

Dari gambar di atas dapat dilihat bahwa sampai titik A hubungan antara

tegangan dan regangan masih linier atau keadaan masih mengikuti hukum Hooke.

regangan untuk baja lunak memiliki titik leleh atas ( upper yield point ), σy dan

daerah leleh datar. Secara praktis, letak titik leleh atas ini, A’ tidaklah terlalu

berarti sehingga pengaruhnya sering diabaikan. Titik A’ sering juga disebut

sebagai titik batas elastis ( elasticity limit ). Sampai batas ini bila gaya tarik

dikerjakan pada batang baja maka batang tersebut akan berdeformasi. Selanjutnya

bila gaya itu dihilangkan maka batang akan kembali kebentuk semula. Dalam hal

ini batang tidak mengalami deformasi permanen.

Bila beban yang bekerja bertambah, maka akan terjadi pertambahan

regangan tanpa adanya pertambahan tegangan. Sifat pada daerah AB inilah yang

disebut sebagai keadaan plastis. Lokasi titik B, yaitu titik batas plastis tidaklah

pasti tetapi sebagai perkiraan dapat ditentukan yakni terletak pada regangan 0,014.

Daerah BC merupakan daerah strain hardening, dimana pertambahan

regangan akan diikuti dengan sedikit pertambahan tegangan. Disamping itu,

hubungan tegangan dengan regangannya tidak lagi bersifat linier. Kemiringan

garis setelah titik B ini didefenisikan sebagai Ez. Di titik M, yaitu regangan

berkisar antara 20 % dari panjang batang, tegangannya mencapai nilai maksimum

yang disebut sebagai tegangan tarik batas ( ultimate tensile strength ). Akhirnya

bila beban semakin bertambah besar lagi maka titik C batang akan putus.

Tegangan leleh adalah tegangan yang terjadi pada saat baja mulai meleleh.

Dalam kenyataannya, sulit untuk menentukan besarnya tegangan leleh, sebab

perubahan dari elastisitas menjadi plastis seringkali besarnya tidak tetap. Sebagai

sejajar dengan sudut kemiringan modulus elastisitasnya, dari regangan sebesar

0,2 %.

Gambar 2. 6 Penentuan Tegangan Leleh

Dari titik regangannya 0,2 % ditarik garis sejajar dengan garis OB

sehingga memotong grafik tegangan regangan dan memotong sumbu tegangan.

Tegangan yang diperoleh ini disebut dengan tegangan leleh. Tegangan tegangan

leleh dari bermacam macam baja bangunan diperlihatkan pada tabel 2. 2 di bawah

ini :

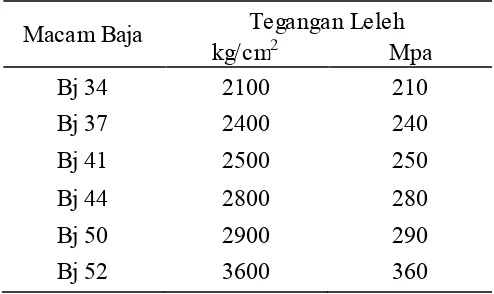
Tabel 2. 2 Harga Tegangan Leleh

Baja memiliki beberapa kelebihan sebagai bahan konstruksi, diantaranya :

1. Nilai kesatuan yang tinggi per satuan berat

Macam Baja Tegangan Leleh kg/cm2 Mpa

Bj 34 2100 210

Bj 37 2400 240

Bj 41 2500 250

Bj 44 2800 280

Bj 50 2900 290

2. Keseragaman bahan dan komposit bahan yang tidak berubah terhadap

waktu

3. Dengan sedikit perawatan akan didapat masa pakai yang tidak terbatas

4. Daktalitas yang tinggi

5. Mudah untuk diadakan pengembangan struktur

Di samping itu baja juga mempunyai kekurangan dalam hal :

1. Kekuatan baja lemah dalam memikul beban tekan

2. Biaya pengadaan anti api yang besar ( fire proofing cost )

3. Dibandingkan dengan kekuatannya kemampuan baja melawan tekuk kecil

4. Nilai kekuatannya akan berkurang, jika dibebani secara berulang /

periodik, hal ini biasanya disebut dengan leleh atau fatigue.

Dengan kemajuan teknologi, perlindungan terhadap karat dan kebakaran

pada baja sudah ditemukan, hingga akibat buruk yang mungkin terjadi bisa

dikurangi/dihindari.

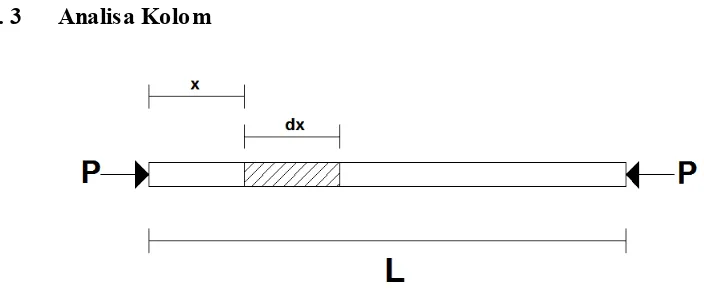
2. 3 Analisa Kolom

Gambar 2. 7 Batang Lurus yang Dibebani Gaya Aksial

Sebuah batang lurus dengan panjang L yang dibebani oleh gaya aksial P

seperti yang diperhatikan pada gambar 2. 5 uraian gaya gaya yang bekerja pada

adalah komponen gaya longitudinal dan transversal pada potongan itu, dan M

adalah momen lentur.

Gambar 2. 8 Potongan Batang Sejauh x dari Tumpuan

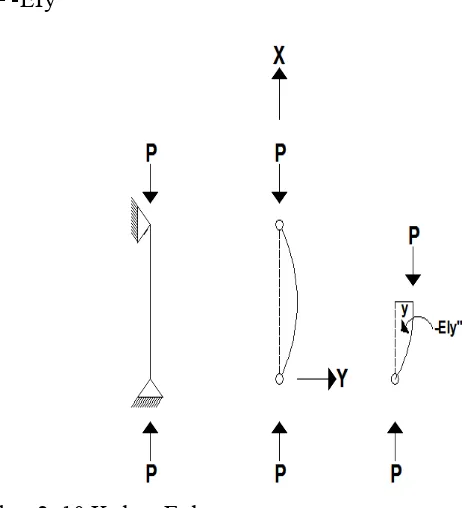
Pengaruh dari adanya rotasi struktur, persamaan kesetimbangan dari

elemen kolom ramping yang terdeformasi diperlihatkan pada gambar 2. 7.

Gambar 2. 9 Kolom Terdeformasi

Untuk deformasi yang kecil, maka dapat diasumsikan bahwa sudut putar β

adalah kecil. Dengan demikian sin β dan cos β secara berurutan dapat dianggap β

dan l. Persamaan kesetimbangan gaya dapat diperoleh dengan menguraikan

masing masing gaya yang bekerja sesuai dengan subu x dan y. Dari uraian gaya

pafa sumbu x diperoleh :

N + ( N + dN ) – Q β + ( Q + dQ ) ( β + dβ ) = 0

NI + QI + βI = 0

Dimana :

NI = dN/dx

QI = dQ/dx

Dari uraian gaya pada sumbu y diperoleh :

geser melintang sangat kecil. Kita biasanya mengambil asumsi bahwa bentuk

kuadratik yang menggambarkan interaksi non linear antara gaya geser yang kecil

dan putaran dapat diabaikan. Dari asumsi yang diambil maka tiga persamaan

kesetimbangan disederhanakan menjadi bentuk berikut :

NI = 0 ( 2. 13 )

diperoleh :

NI= 0

(EIII)II– NyII = 0

Untuk harga EI yang konstan, persamaan menjadi :

NI = 0

EIyIV – N yII = 0

Persamaan ( 2. 14 ) merupakan bentuk kuadrik dalam variabel variabel N

dan Y. Oleh karena itu merupakan persamaan diferensial non linier. Dari

persamaan ( 2. 13 ) terlibat bahwa N konstan sepanjang X dan dari kondisi batas

x=0 dan x=1, kita lihat bahwa N = P. Dengan demikian persamaann ( 2. 14 )

dapat disederhanakan menjadi bentuk lazim dikenal :

EIyIV – PyII = 0 ( 2. 17 )

Persamaan di atas adalah diferensial dari kolom ramping yang mengalami

tekukan. Dari persamaan dapat ditentukan besarnya pada saat struktur akan

runtuh. Misalnya k2 = P/EI dan subtitusikan kedalam persamaan sehingga

diperoleh :

678

6%8 + K 67_6% = 0 ( 2. 19 )

Persamaan umum dari persamaan diferensial adalah :

Dimana : A, B, C, D adalah tetapan tertentu yang dapat ditentukan dengan

menggunakan syarat syarat batas yaitu kondisi batas ujung ujung batang

atau yang disebut dengan boundary condition.

2. 3. 1 Kolom Euler

Rumus kolom Euler diturunkan dengan membuat berbagai anggapan

sebagai berikut :

1. Bahan elastis sehingga memenuhi Hukum Hooke

2. Material homogen sempurna dan isotropis

3. Batang pada mulanya lurus sempurna, prismatis dan beban terpusat

dikerjakan sepanjang sumbu titik berat penampang

4. Penampang batang tidak terpuntir, elemennya tidak dipengaruhi tekuk

setempat dan distorsi lainnya selama melentur

5. Batang bebas dari tegangan residu

6. Ujung ujung batang ditumpu sederhana. Ujung bawah ditumpu pada sendi

yang tidak dapat berpindah, ujung atas ditumpu pada tumpuan yang dapat

berotasi dengan bebas dan bergerak vertical tetapi tidak dapat bergerak

horizontal.

7. Deformasi dari batang cukup kecil sehingga bentuk ( y’ )² dari persamaan

kurva y” / (1 + (y’)2)2/3 dapat diabaikan. Dari sini kurva dapat didekati

dengan y”.

Bahwa batang yang ditekan akan mengalami bentuk yang sedikit

melengkung seperti pada gambar 2. 10. Jika sumbu koordinat diambil seperti

asal adalah :

Mx = EIy” ( 2. 21 )

Gambar 2. 10 Kolom Euler

Dengan menyamakan momen lentur luar P.y, maka diperoleh persamaan :

EIy” + P.y = 0 ( 2. 22 )

Persamaan ( 2. 21 ) adalah persamaan diferensial linear dengan koefisien

konstan dan dapat dirubah menjadi :

y” + k².y = 0 ( 2. 23 )

Dimana :

k² = 9 ( 2. 24 )

Penyelesaian umum persamaan ( 2. 22 )

y = A sin kx + B cos kx ( 2. 25 )

Untuk menentukan besaran konstanta A dan B, maka menggunakan syarat batas :

y = 0 dan x = 1

Dengan memasukkan syarat batas pertama ke dalam persamaan ( 2. 25 )

maka diperoleh :

B = 0

Sehingga diperoleh :

y = A sin kx ( 2. 26 )

Dari syarat batas kedua diperoleh :

A sin kl = 0 ( 2. 27 )

Persamaan ( 2. 27 ) dapat dipenuhi oleh tiga keadaan yaitu :

1. Konstanta A = 0, yaitu tidak ada lendutan ( 2. 28 )

Pada beban yang diberikan oleh persamaan ( 2. 31 ) kolom berada dalam

keadaan kesetimbangan dalam bentuk yang agak bengkok, dimana bentuk

deformasinya diberikan oleh persamaan ( 2. 32 ).

Ragam (mode) tekuk dasar yaitu lendutan dengan lengkungan tunggal

akan diperoleh jika nilai n diambil sama dengan 1, dengan demikian beban kritis

Pkr =

; ( 2. 33 )

Dan persamaan lendutan menjadi :

Y =

sin

%

; ( 2. 34 )

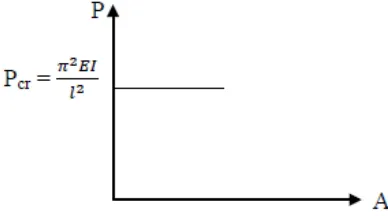
Kelakuan kolom Euler dapat digambarkan secara grafik seperti

pada gambar :

Gambar 2. 11 Grafik Kolom Euler

Dari grafik dapat dilihat bahwa sampai beban Euler dicapai, kolom harus

tetap lurus. Pada beban Euler ada percabangan kesetimbangan yaitu kolom dapat

tetap lurus atau dapat dianggap berubah bentuk dengan amplitude tidak tentu.

Kelakuan ini menunjukkan bahwa keadaan kesetimbangan pada saat beban Euler

merupakan transisi dari kesetimbangan stabil dan tidak stabil.

2. 3. 2 Rumus Kolom Euler untuk Berbagai Pe rletakan

2. 3. 2. 1 Kolom dengan Satu Ujung Terjepit dan yang lainnya Bebas

Tinjau suatu sumbu sumbu koordinat seperti ditunjukkan pada gambar,

dimana kolom dalam kedudukan yang agak melengkung, menghasilkan momen

lentur pada suatu penampang melintang sebesar :

M = P ( δ – y ) ( 2. 35 )

Dan persamaan diferensial M = EI 6 7

EI6 7

6% = P (δ – y ) ( 2. 36 )

Karena ujung atas kolom adalah bebas, maka jelaslah bahwa tekuk pada

kolom akan terjadi pada bidang dengan kekakuan lengkungan terkecil, yang

dianggap merupakan bidang simetris.

Nilai EI yang terkecil ini digunakan dalam persamaan ( 2. 36 ) di atas dan dengan

memakai notasi sebelumnya yaitu :

k² = 9

Kita dapat menuliskan persamaan dalam bentuk :

6 7

6% + k²y = k² δ

Penyelesaian umum dari persamaan ini adalah :

Y = A cos kx + B sin kx + δ

Dimana A dan B adalah konstanta integrasi, yang ditentukan dari syarat syarat

ujung jepit kolom yaitu :

Y = 67

6% = 0 pada x = 0

Syarat syarat ini dipenuhi jika :

A = δ B = 0

Dan persamaan b menjadi :

Y = δ ( 1 – cos kx ) ( 2. 37 )

Sedang syarat pada ujung bebas kolom menghendaki bahwa

Y = δ pada x = 1

Yang memenuhi jika

Persamaan c menghendaki bahwa salah satu δ dan cos kl harus nol. Bila δ = 0,

maka lengkungan tidak ada. Bila cos kl = 0, kita akan memperoleh hubungan

Kl = ( 2n – 1 ) /2 ( 2. 38 )

Dimana n = 1, 2, 3,…… persamaan ini untuk menentukan nilai nilai k

sehubungan dengan bentuk tekukan yang terjadi.

Nilai kl terkecil yang memenuhi persamaan ( 2. 38 ) diperoleh dengan

mengambil n = 1, memberikan nilai beban kritis terkecil yaitu :

Kl = l 9 =

Atau

Pkr =

&;

( 2. 39 )

Besaran kx dalam persamaan ( 2. 37 ) untuk kasus ini berubah ubah dari 0

s/d /2, dan bentuk lengkungan seperti ditunjukkan pada gambar di atas.

Dengan mensubtitusikan n = 2, 3, . . . . ke dalam persamaan ( 2. 38 ), kita peroleh

hubungannya dengan nilai nilai beban kritis sebagai berikut :

Pkr = +

&; Pkr=

* &;

Besaran kx menurut persamaan ( 2. 37 ) dalam hal ini berubah dari 0 s/d

3/2, dari 0 s/d 5/2, . . . , dan hubungannya dengan kurva lengkungan pada gambar

( 2. 37 ) dan gambar ( 2. 38 ). Untuk bentuk kurva lengkungan pada gambar

( 2. 37 ) diperlukan suatu gaya sebesar sembilan kali beban kritis terkecil, dan

keadaan pada gambar ( 2. 38 ), diperlukan gaya sebesar dua puluh lima kali beban

Bentuk bentuk tekukan seperti itu hanya dapat terjadi pada batang yang

sangat ramping, dan dengan memasang penyokong pada titik peralihan untuk

mencegah lengkungan lateral. Sebaliknya bentuk tekukan ini adalah tidak stabil,

dan mempunyai arti praktis yang kecil, sebab struktur telah mengalami suatu

lengkungan yang besar pada saat beban mendekati nilai nilai yang diberikan oleh

persamaan ( 2. 39 ).

Gambar 2. 12 Kurva Lendutan Tekuk Sinusoidal dengan Satu Ujung Terjepit dan

yang Lainnya Bebas

2. 3. 2. 2 Kolom dengan Kedua Ujungnya berupa Sendi

Mint – P.y = 0 ( 2. 40 )

Dari hubungan momen dengan kelengkungan didapat :

Mint = EI 6 7

6% ( 2. 41 )

EIy” – P.y = 0 ( 2. 42 )

EIy” + P.y = 0

y” + 9

?

= 0 ;

9 dimisalkan @2

y” + k2y = 0 ( 2. 43 )

Jawaban umum persamaan diferensial di atas :

Dari syarat batas yang ada, y = 0 pada saat x = 0 dan x = L

Untuk x = 0 ; y = B = 0

Untuk x = L ; y = A sin kl = 0

Karena A ≠ 0 maka sin kl = 0

kl = nπ

@2

= : ( 2. 45 )

Untuk n = 1

P =

Dimana I = inersia pada sumbu lemahnya

Pada suatu kasus kolom dengan kedua ujungnya berupa sendi (gambar 2.

13), tampak dari kesimetrisannya bahwa tiap setengah panjang batang adalah

mirip dengan batang pada gambar 2.13. Karena itu beban kritis pada kasus ini

diperoleh dengan mensubtitusikan l/2 untuk besaran l dalam persamaan, yang

memberikan

Pkr=

& A = ; ( 2. 46 )

Kasus suatu batang dengan kedua ujung berupa sendi, mungkin dianggap

lebih sering dalam prakteknya dari yang lain. Kasus ini disebut “kasus dasar”

Gambar 2. 13 Kolom dengan Kedua Ujungnya berupa Sendi

2. 3. 2. 3 Kolom dengan Kedua Ujungnya Terjepit

Bila kedua ujung kolom berupa jepitan (gambar 2. 12), maka ada momen

momen reaksi yang mencegah ujung ujung kolom dari perputaran selama tekukan

terjadi. Momen momen ujung dan gaya gaya tekan aksial adalah ekivalen dengan

gaya gaya P yang bekerja eksentris seperti ditunjukkan pada gambar. Titik titik

peralihan ditempatkan dimana garis kerja gaya P memotong kurva lengkungan,

sebab pada titik titik ini momen lentur adalah nol.

Titik titik peralihan dan titik tengah bentang membagi batang atas empat bagian

yang sama. Oleh karena itu, beban kritis dalam kasus ini diperoleh dengan

mensubtitusikan l/4 untuk besaran l, yaitu :

EI 6 7

6% + Py = Mo ( 2. 47 )

6 7 6% + k

2

y = BC ( 2. 48 )

dimana, k² = 9

Penyelesaian dari persamaan ini adalah :

y = A sin kx + B cos kx + BC

Dari syarat batas : 67 6% = 0

y = 0 pada x = 0

y = 0 pada x = 0 didapat ;

B = BC

9

, dan A = 0

Sehingga :

y = DE (1−cos@F) ( 2. 50 )

cos kl = 1.0 ( 2. 51 )

kl = 2π

Maka didapat :

Pkr=

&; ( 2. 52 )

2. 3. 2. 4 Kolom dengan Kedua Ujung Terjepit tetapi Salah Satu dapat Bergeser Arah Lateral

Pada gambar 2. 15 tampak bahwa kolom bebas gerak arah lateral pada

ujung atas tetapi dikendalikan sedemikian rupa, sehingga garis singgung pada

kurva elastis tetap tegak. Dengan adanya titik peralihan pada pertengahan bentang

(gambar 2. 13b.), beban kritis didapatkan dengan mensubtitusikan l/2 untuk l

dalam persamaan ( 2. 52 ), dan dengan demikian dalam kasus ini juga berlaku

rumus ( 2. 46 ).

Gambar 2. 15 Kolom dengan Kedua Ujung Terjepit tetapi Salah Satu dapat

Bergeser arah Lateral

2. 3. 2. 5 Kolom dengan Ujung-ujung Terjepit dan Sendi

Kita tinjau suatu penampang mn sejauh x dari sendi, dan dengan

lengkungan sebesar y (gambar), memberikan momen lentur sebesar :

Mx = P.y + H0.x ( 2. 53 )

Dengan demikian persamaan menjadi :

EI 6 7

Gambar 2. 16 Kolom dengan ujung ujung Terjepit dan Sendi

Dan dengan bantuan notasi k² = P/EI, persamaan b dapat dituliskan dalam bentuk:

6 7

6% + k²y =

−

HC

_F

( 2. 55 )

Penyelesaian umum dari persamaan ini adalah :

Y = A cos kx + B sin kx HC

9

F

( 2. 56 )

Dimana A dan B adalah konstanta integrasi, yang ditentukan dari syarat syarat

ujung kolom yaitu :

Y = 0 pada x = 0 dan x = l

dy/dx = 0 pada x = l

Dari syarat ujung y = 0 pada x = 0 diperoleh A = 0. Untuk y = 0 pada x = l

memerlukan :

B = HC ;

9 IJK L; ( 2. 57 )

Sedang untuk dy/dx = 0 pada x = l memberikan :

Untuk memecahkan persamaan dipakai metoda grafis. Kurva kurva pada gambar

menyatakan tg kl sebagai fungsi kl. Kurva kurva ini menyinggung garis tegak kl

=π /2, 3π/2,. . . . pada titik jauh tak terhingga ( secara asimtotis ).

Gambar 2. 17 Kurva kl

Akar akar persamaan ditunjukkan oleh titik perpotongan kurva dengan

garis lurus y = kl. Akar terkecil adalah absis dari koordinat titik A yaitu sebesar :

Kl = 4,493 radian

Yang memberikan nilai beban kritis sebesar

Pkr = ,$+

;

=

( ,M++$) ( 2. 59 )

Dalam setiap kasus yang telah diterangkan diatas, dianggap bahwa kolom

bebas tertekuk dalam suatu arah, maka jelaslah bahwa besaran EI menyatakan

kekakuan lengkung terkecil. Jika kolom dikekang sedemikian rupa, sehingga

tekukan hanya mungkin dalam satu bidang utama saja, maka EI menyatakan

kekakuan lengkung dalam bidang itu.

Dalam pembicaraan sebelumnya juga dianggap bahwa batang sangat

langsing, sehingga tegangan tekan terbesar yang terjadi selama tekukan masih di

rumus rumus beban kritis diatas dapat berlaku. Untuk menentukan batas

pemakaian rumus rumus ini, mari kita tinjau kasus dasar seperti yang telah

disebutkan sebelumnya. Dengan membagi beban kritis dari pers. Dengan luas

penampang melintang A, dan mengambil

r = ( 2. 60 )

Dimana r menyatakan jari jari putaran, besar tegangan tekan kritis adalah

σkr

=

9

=

_A ( 2. 61 )

Tegangan ini hanya tergantung pada besaran E dan rasio kelangsingan l/r.

Sebagai contoh, pada suatu struktur baja, batas proporsional 2100 kg/cm² dan E =

2,1 x 106 kg/cm², maka didapat nilai l/r terkecil dari pers. ( 2. 61 ) sebesar 100.

Karenanya, beban kritis pada kolom dari bahan ini, yang bersendi pada kedua

ujungnya, dapat dihitung dengan pers. ( 2. 46 ), bila diinginkan rasio l/r lebih

besar dari 100.

Jika l/r lebih kecil dari 100, tegangan tekan sudah mencapai batas proporsional

sebelum terjadi tekukan, sehingga pers ( 2. 46 ) tidak berlaku.

Persamaan ( 2. 53 ) dapat dinyatakan secara grafis oleh kurva ACB pada

gambar 2. 16, dimana tegangan kritis digambarkan sebagai fungsi l/r. Kurva

mendekati sumbu mendatar secara asimtot, dan tegangan kritis mendekati nol

dengan bertambahnya rasio kelangsingan. Kurva juga mendekati sumbu tegak

secara asimtot tetapi yang berlaku hanya sepanjang tegangan σcr yang masih

proportiona sebesar 2100 kg/cm². jadi hanya bagian BC dari kurva yang

memenuhi.

Sekarang bandingkan kasus kasus lain yang dinyatakan pada gambarm 2.

16, analog didapat rumus tegangan tegangan kritis sebagai berikut :

σkr = _A σkr= _A σkr= _N,OPPA

Gambar 2. 18 Kurva ACB

Tampak bahwa ketiga persamaan analog dengan persamaan ( 2. 62 ),

dimana panjang l sebenarnya digantikan dengan panjang reduksi L. Dengan

demikian dapat dituliskan secara umum rumus tegangan sebagai berikut :

σkr = _Q ( 2. 62 )

Dimana besaran L = 2l, l/2, atau 0,6991.

2. 4 Panjang Efektif

Kolom dengan kekangan yang besar terhadap rotasi dan translasi ujung

ujungnya (contohnya tumpuan jepit) akan mampu menahan beban yang lebih

besar dibandingkan dengan kolom yang mengalami rotasi serta translasi pada

bagian tumpuan ujungnya (contohnya adalah tumpuan sendi). Selain kondisi

tekan juga tergantung dari panjang efektifnya. Semakin kecil panjang efektif suatu

komponen struktur tekan, maka semakin kecil pula risikonya terhadap masalah

tekuk.

Sejauh ini pembahasan mengenai kekuatan kolom mengasumsikan sendi

dimana tidak ada kekangan rotasional momen. Kekangan momen nol pada ujung

merupakan situasi paling lemah untuk batang tekan yang salah satu ujungnya

tidak dapat bergerak transversal relatif terhadap ujung yang lainnya. Untuk kolom

berujung sendi semacam ini, panjang ekivalen ujung sendi kL merupakan panjang

L sebenarnya, dengan demikian K = 1,0 seperti pada tabel 2. 3. Panjang L

ekivalen berujung sendi disebut panjang efektif.

Untuk kebanyakan situasi nyata, kekangan momen pada ujung ujung yang

ditahan seperti pada tabel 2. 3. Dimana panjang efektif tereduksi dalam banyak

situasi, sangat sulit, atau bahkan tidak mungkin, untuk menilai secara tepat derajat

kekangan momen yang disumbangkan oleh batang batang berdekatan yang

mengikat ke kolom, oleh pondasi setempat dan lapisan tanah dibawahnya dan

interaksi penuh semua batang dalam struktur rangka baja.

Baik apakah derajat ujung ditentukan dengan tepat atau tidak,desainer

harus memahami konsep tentang braced frame (goyangan dicegah dengan sabuk

penyokong) dan unbraced frame (tanpa sabuk penyokong, goyangan tidak

dicegah).

Panjang efektif suatu kolom secara sederhana dapat didefinisikan sebagai

jarak di antara dua titik pada kolom tersebut yang mempunyai momen sama

kelengkungan kolom. Dalam perhitungan kelangsingan komponen struktur tekan

(λ = L/i), panjang komponen struktur yang digunakan harus dikalikan dengan

suatu faktor panjang tekuk k untuk memperoleh panjang efektif dari kolom

tersebut. Besarnya faktor panjang efektif sangat tergantung dari kondisi perletakan

pada ujung ujung komponen struktur tersebut. Prosedur penentuan nilai k

dilakukan dengan analisa tekuk terhadap suatu kolom.

Panjang efektif batang kolom pada suatu portal, bergantung pada jenis

portal yang ditinjau, yaitu portal bergoyang dan portal tidak bergoyang. Portal tak

bergoyang (yang disokong) adalah portal yang kestabilan lateralnya diberikan

oleh penyambung yang memadai ke penopang diagonal ke dinding geser, ke

struktur di dekatnya yang memiliki stabilitas lateral yang memadai, atau ke plat

lantai atau penutup atap yang diikat secara horizontal terhadap dinding atau

dengan system penopang yang sejajar dengan bidang portal. Atau dengan kaya

lain portal tak bergoyang didefenisikan sebagai portal yang tekuk bergoyangnya

dicegah oleh elemen penopang yang tidak termasuk rangka struktural itu sendiri.

Faktor K untuk portal bergoyang adalah 0<K<1.

Sedangkan portal tidak bergoyang (yang tidak disokong) adalah portal

yang kestabilan lateralnya bergantung pada kekakuan lentur balok dan kolom

yang disambung secara kaku. Faktor K untuk portal bergoyang adalah K>1.

Faktor panjang efektif (K) untuk kolom ideal dengan perletakan yang berbeda dapat

2. 5 Metode Beda Hingga 2. 5. 1 Pendahuluan

Metode beda hingga adalah teknik numerik untuk mendapatkan solusi

perkiraan untuk persamaan diferensial. Dalam metode persamaan diferensial

digantikan oleh seperangkat setara persamaan aljabar yang biasanya lebih mudah

untuk memecahkan daripada persamaan diferensial. Dasar dari teknik beda hingga

adalah bahwa turunan dari suatu fungsi pada suatu titik dapat didekati dengan

ekspresi aljabar yang terdiri dari nilai fungsi pada saat itu dan di beberapa titik di

dekatnya. Mengingat fakta ini adalah mungkin untuk mengganti derivatif dalam

persamaan diferensial dengan ekspresi aljabar dan dengan demikian mengubah

persamaan diferensial menjadi persamaan aljabar.

Sebagai aturan, persamaan diferensial menggambarkan perilaku sistem

yang berkelanjutan, sedangkan persamaan aljabar menggambarkan perilaku

sistem parameter yang disamakan. Penggantian fungsi kontinu dalam persamaan

diferensial dengan ekspresi aljabar yang terdiri dari nilai fungsi yang di beberapa

titik diskrit demikian setara dengan mengganti sistem kontinyu dengan satu terdiri

dari sejumlah diskrit poin massa. Metode beda hingga karena itu mirip dengan

metode energi yang baik menyederhanakan solusi dari masalah dengan

mengurangi jumlah derajat kebebasan. Metode energi ini dilakukan dengan

mendekati perilaku sistem, yaitu, dengan asumsi bentuk dibelokkan, sedangkan

teknik beda hingga menyederhanakan sistem itu sendiri.

Secara umum, jika sistem kontinu diganti dengan n titik massa diskrit,

diferensial diganti dengan n simultan persamaan aljabar dalam variabel tersebut.

Karena turunan dari fungsi yang tidak diketahui di titik didekati oleh ekspresi

yang terdiri dari nilai fungsi pada saat itu dan di beberapa titik tetangga, semakin

dekat titik titik yang satu dengan yang lain yang lebih baik adalah perjanjian

antara turunan dan aljabar pendekatan, dan lebih akurat akan menjadi solusi untuk

masalah ini. Namun, karena jumlah poin meningkatkan begitu juga dengan jumlah

persamaan simultan yang harus dipecahkan.

Karena jumlah besar pekerjaan numerik yang terlibat, metode beda hingga

yang sangat cocok untuk digunakan ketika kecepatan tinggi komputer elektronik

tersedia.

Kerugian utama dari metode ini adalah bahwa hal itu memberikan nilai

numerik dari fungsi yang tidak diketahui pada titik titik diskrit bukan ekspresi

analitis yang berlaku untuk seluruh sistem. Jika ekspresi analitis diperlukan, itu

harus diperoleh dengan pas kurva dengan nilai nilai diskrit yang diperoleh dalam

larutan. Kelemahan ini akan lebih parah masalah keseimbangan daripada di

masalah eigenvalue, karena hubungan berlaku umum biasanya dapat diperoleh

untuk beban kritis, sedangkan ekspresi terus menerus untuk fungsi defleksi yang

pernah diperoleh. Terlepas dari kelemahan tersebut, prosedur beda hingga adalah

metode analisis yang sangat berguna di berbagai penerapan perusahaan.

2. 5. 2 Rasio Diferensial

Turunan dari fungsi, pada suatu titik, dapat dinyatakan kurang dalam hal

nilai fungsi pada saat itu dan nilai pada satu atau lebih poin terdekat. Hal seperti

gambar. 2. 19, yang nilainya diketahui pada x = i dan di beberapa titik merata

spasi ke kanan dan ke kiri x = i.

Gambar 2. 19 Rasio Diferensial

Turunan pertama dari f (x) pada titik x dapat didekati dengan

RS

RF ≅ S (F + ∆F) − S (F)∆F

Pada x = i ungkapan ini dapat ditulis dalam bentuk

6V

6% %W

≅ ∆S =

VXYZ- VX

[ ( 2. 63 )

Dimana fi dan f i + h adalah nilai nilai dari fungsi f (x) pada x = i, dan pada x = i +

h, h adalah jarak antara dua titik, dan f i adalah pendekatan dari derivatif df / dx

di x = i. Hal ini jelas bahwa perbedaan antara turunan dan pendekatan yang f

akan menurun sebagai h menurun.

Pendekatan dari df / dx turunan yang diberikan oleh Persamaan. ( 2. 63 )

melibatkan f fungsi pada x = i dan pada titik di sebelah kanan x = i. Oleh karena

itu dikenal sebagai forward difference. Persamaan serupa yang melibatkan fungsi

f di x = i dan pada x = i h adalah

∆S =

VX- VX\Z

Bentuk pendekatan ini dikenal sebagai backward difference. Persamaan ketiga

mungkin melibatkan poin di kedua sisi x = i

∆S =

VXYZ- VX\Z

[ ( 2. 65 )

Hal ini dikenal sebagai diferensial utama. Dari tiga pendekatan, diferensial utama

adalah yang paling akurat untuk diberikan jarak h. Diskusi yang tersisa berurusan

dengan pendekatan derivatif yang lebih tinggi karena itu akan terbatas pada

diferensial utama.

Setelah diferensial pertama telah ditetapkan, diferensial kedua dapat

diperoleh dengan mengambil perbedaan perbedaan pertama. Jika b didefinisikan

sebagai operator perbedaan yang sesuai dengan operator diferensial d / dx, maka

∆ S = ∆(∆S ) =

∆]VXYZ_[- VX\Z^

=

∆VXYZ- ∆V_[ X\Z

Persamaan ( 2. 66 ) memberikan diferensial sentral kedua di titik x = i.

∆

&

_{S = ∆ (∆ S) =}

∆ S

`[

− 2∆ S + ∆ S

-[

ℎ

=

_XY Z\ _XYZY _X

Z - _XYZ\ _XY _X\ZZ ` _X\ _X\ZY _X\ ZZ

[

=

VXY Z- &VXYZ` MVX- &VX\Z` VX\ Z

[8 ( 2. 68 )

Dengan "molekul komputasi" pada gambar 2. 20 memberikan representasi

Gambar 2. 20 Molekul Komputasi untuk Rasio Diferensial

bergambar pers. ( 2. 64 ), ( 2. 65 ), ( 2. 66 ), dan ( 2. 67 ). Ini cara yang sangat

nyaman mewakili rasio perbedaan yang disebabkan oleh Bickley.

2. 6 Perhitungan Beban Kritis dengan Beda Hingga

Dalam tugas akhir ini metode beda hingga akan digunakan untuk

menentukan beban kritis kolom sendi sendi yang ditunjukkan pada

gambar 2. 21(a).

Solusinya mengikuti garis besar umum dari analisis yang sama disampaikan oleh

Salvadori. Persamaan diferensial dan batas kondisi untuk kolom sendi sendi yang

?

′′

+

9

?

Dan

y(0) = y(l) = 0 ( 2. 70 )

Untuk mendapatkan hubungan diferensial yang sesuai, rentang anggota dibagi

menjadi segmen segmen yang sama n panjang h = l / n dan lendutan pada akhir

segmen i dinotasikan dengan yi (gambar 2. 21(b)).

Menurut persamaan. ( 2. 66 ), turunan kedua pada titik i dapat didekati dengan

rasio diferensial

Gambar 2. 21 Kolom Sendi sendi Dibagi Menjadi Segmen yang Sama n

∆ ? =

7XYZ- 7X` 7X\Z

[

( 2. 71 )

di mana yi + 1 dan yi 1 adalah defleksi pada titik titik di kedua sisi titik i.

Jika ( 2. 71 ) digantikan turunan kedua dalam Pers. ( 2. 69 ), diperoleh

?

`[

− 2? + ?

-[

+

9[

? = 0

( 2. 72 )

persamaan diferensial pada titik i.

Persamaan diferensial adalah ekspresi yang tepat dari kondisi

sepanjang anggota tersebut. Sebagai perbandingan, persamaan diferensial

mengungkapkan kondisi keseimbangan hanya kira kira, dan dengan memuaskan

menjadi salah satu upaya untuk menetapkan keseimbangan hanya pada titik x = i.

2. 6. 1 Pendekatan Pertama n = 2

Biarkan anggota yang dibagi menjadi dua bagian yang sama panjang h = l

/ 2, dan membiarkan ujung segmen ini akan ditandai dengan i = 0, 1, dan 2, seperti

ditunjukkan pada gambar 2. 21. Dalam hal ini, perlu untuk menulis persamaan

diferesial hanya pada titik i = 1. Pada dua titik batas, baik defleksi dan lengkung

kurvatur dan memenuhi persamaan.

Gambar 2. 22 Pendekatan dengan n = 2

Tertulis persamaan ( 2. 72 ) di i = 1 memberikan

? − 2?

$

+ ? +

9;_&

?

$

= 0

( 2. 73 )

Dari kondisi batas

y0 = y2 = 0

Jadi :

Seperti khas di masalah tekuk linear, persamaan. ( 2. 74 ) mengarah ke solusi

trivial pada beban apapun, asalkan y1 = 0, dan untuk beban kritis

L

=

d _; ( 2. 75 )

Perbandingan hasil ini dengan solusi yang tepat, 9,87 EI / l2, menunjukkan

pendekatan beda hingga menjadi kesalahan sekitar 19%. Untuk mendapatkan

solusi yang lebih akurat, maka perlu memenuhi persamaan perbedaan pada lebih

dari satu titik interior.

2. 6. 2 Pendekatan Kedua n = 3

Gambar 2. 23 Pendekatan dengan n = 3

Jika anggota tersebut dibagi menjadi tiga segmen yang sama panjang h = l

/ 3, seperti yang ditunjukkan pada gambar 2. 23, akan ada dua titik interior, i = 1

dan 2, dimana persamaan diferensial dapat ditulis.

Tertulis persamaan. ( 2. 72 ) di i = 1 mengarah ke

? − 2?$+ ? + ?$ = 0 ( 2. 76 )

Dan pada i = 2 diperoleh

Dimana

λ = Pl2/9 EI.

Memanfaatkan kondisi batas dan menata kembali perihal, pers. ( 2. 76 )

dan ( 2. 77 ) dapat ditulis dalam bentuk :

( − 2) ?_$+ ? = 0

?$+ ( − 2)? = 0

Persamaan ini linear dan homogen. Dengan demikian mereka memiliki solusi

trivial y1 = y2 = 0 dan solusi trivial yang diperoleh dengan menetapkan penentu

mereka sama dengan nol. Itu adalah,

e − 2_{1 − 2 e = 0}1 ( 2. 78 )

Mengembangkan Persamaan. (2. 78) mengarah ke

− 4 + 3 = 0 ( 2. 79 )

persamaan polinomial yang akar terkecil adalah beban kritis. Akar persamaan

( 2. 79 ) adalah

$= 1, = 3

Dimana

$

=

+ _;

,

=

! _;

Oleh karena itu beban kritis adalah

L

=

+ _; ( 2. 80 )

Solusi ini berbeda dari beban Euler sebesar 9%. Kesalahan 19% yang ada saat

dikurangi menjadi 9% dengan memenuhi persamaan diferensial pada dua titik

interior.

2. 6. 3 Pendekatan Ketiga n = 4

Jika anggota tersebut dibagi menjadi empat bagian yang sama panjang h =

l / 4, seperti yang ditunjukkan pada gambar 2. 23 akan ada tiga poin interior

dimana persamaan diferensial dapat ditulis.

Gambar 2. 24 Pendekatan dengan n = 4

Namun, dengan mempertimbangkan fakta bahwa modus tekuk kolom sendi sendi

simetris, yaitu, y1 = y3, jumlah persamaan yang harus ditulis dikurangi menjadi

dua. Pada i = 1, persamaan. ( 2. 72 ) mengarah ke

? − 2?$+ ? + _$M 9; ?$ = 0 ( 2. 81 )

Dan pada i = 2 diperoleh

Dengan menggunakan kondisi batas dan simetri, persamaan ini dapat ditulis

yang akar terkecil adalah λ = 0,59, karena itu

L

=

+,& _; ( 2. 85 )

Jawaban ini berbeda dari beban Euler sebesar 5%.

Dengan terus meningkatkan derajat kebebasan dan memenuhi persamaan

diferensial pada semakin banyak poin, akurasi dari solusi dapat ditingkatkan ke

tingkat yang diinginkan. Namun, proses ini memerlukan solusi dari sejumlah

besar persamaan simultan. Seperti yang ditunjukkan oleh Salvadori, cara yang

lebih cepat dan lebih sederhana untuk meningkatkan akurasi dari solusi yang

diberikan oleh skema ekstrapolasi Richardson.

Hal ini dapat menunjukkan bahwa kesalahan, e, dari solusi perkiraan kira

kira sebanding dengan kuadrat dari ukuran mesh, h. Demikian

h = iℎ ( 2. 86 )

dimana C adalah konstanta. Jika n1 dan n2 adalah jumlah bagian mana anggota

telah dibagi, dan h1 = l / n1dan h2 = l / n2 adalah ukuran mesh yang sesuai, dan

jika β1 dan β2 adalah perkiraan dari solusi yang tepat, β, diperoleh dengan

h_$= j − j_$= i_lk

$

Dan

h = j − j = i_lk

Eliminasi C antara hubungan ini mengarah ke

j = :" m"- : m

:_"- : ( 2. 87 )

Persamaan ( 2. 87 ) memberikan nilai ekstrapolasi dari solusi memberikan

perkiraan β1 dan β2 mendekati solusi eksak monoton. Hal ini biasanya

memungkinkan terjadinya untuk mendapatkan konvergensi monoton dengan

memilih urutan yang tepat dari n.

Untuk menggambarkan efektivitas skema ekstrapolasi Richardson, hasil

perkiraan yang diperoleh untuk kolom sendi sendi, membiarkan n = 3 dan 4, akan

diganti menjadi persamaan ( 2. 87 ), demikian

j = 9 (9) − 16 (9,4)_{9 − 16} = 9,85

Dimana

L

=

+,d* _; ( 2. 88 )

Solusi ini berbeda dari beban Euler oleh hanya 0,2%.

Setiap solusi perkiraan bersama dengan persentase kesalahan antara itu

dan jawaban yang tepat diberikan dalam tabel 2. 3. Hasil ini menunjukkan bahwa

ekstrapolasi rumus sederhana hanya dengan membagi anggota menjadi jumlah

yang sangat besar dari interval dan dengan memecahkan sejumlah besar

Tabel 2. 3 Ringkasan Solusi Beda Hingga untuk Kolom Sendi sendi

Sumbu utama adalah sumbu yang saling tegak lurus dan akan memberikan

momen inersia, I maksimum dan I minimum pada suatu penampang. Pada

komponen struktur yang mengalami gaya aksial / normal tekan maka

kecendrungannya batang akan tertekuk terhadap sumbu dengan momen inersia

yang paling lemah (minimum). Dengan demikian penentuan sumbu utama dan

momen inersia utama menjadi penting.

Sumbu x dan sumbu y diputar sehingga menjadi sumbu x’ dan sumbu y’

dengan sudut putar sebesar θ. Dengan demikian dapat diperoleh hubungan sebagai

berikut :

x’ = x cos θ + y sin θ

y’ = y cos θ – x sin θ

Ix’ = s ?′ R

Ix’ = s(? cosw − F sin w) R

Ix’ = Ix cos2 θ + Iy sin2 θ – 2 Ixy sin θ cos θ

Iy’ = s F′ R

Iy’ = s(F cosw + ? sin w) R

Iy’ = Iy cos2 θ + Ix sin2 θ – 2 Ixy sin θ cos θ

Ix’y’ = s F′?′ R

Ix’y’ = s(F cosw + ? sin w)(?cosw − F sin w) R Ix’y’ = (Ix – Iy) sin θ cos θ + Ixy (cos2 θ – sin2 θ)

Catatan :

sin 2θ = 2 sin θ cos θ

cos 2θ = cos2 θ – sin2 θ

cos2 θ =

½ + ½ cos 2θ

sin2 θ =

½ ½ cos 2θ

Ix’ = Ix (½ + ½ cos 2θ) + Iy (½ ½ cos 2θ) – Ixy sin 2θ

Ix’ =

½ Ix + ½ Ix cos 2θ + ½ Iy – ½ Iy cos 2θ – Ixy sin 2θ

Dengan cara yang sama dapat ditentukan Iy’ dan Ixy’ sebagai berikut :

Iy’ = % ` 7

−

% - 7 cos 2θ + Ixy sin 2θ ( 2. 90 )

Ix’y’ = % - 7 sin 2θ + Ixy cos 2θ ( 2. 91 )

Dari persamaan ( 2. 89 )

Ix’ = % - 7

=

% - 7 cos 2θ – Ixy sin 2θ ( 2. 92 )

Persamaan ( 2. 92 ) dan persamaan ( 2. 93 ) masing masing dikuadratkan

kemudian dijumlahkan sehingga diperoleh :

xrF

y

₋

%` 7

_{z + rF′?′}

₌

_x

%- 7

_z

_{+ Ixy}2

( 2. 93 )

Persamaan ( 2. 93 ) adalah persamaan lingkaran dengan bentuk (x a)2 + y2 = r2

Gambar 2. 26 Lingkaran dengan Salib Sumbu Ix’ dan Sumbu Ixy’

Dari gambar 2. 25 di atas dapat ditentukan momen inersia maksimum dan momen

inersia minimum

Imaks = OM = OC + CM

Imin = ON = OC – CM

Sehingga :

Imin = % ` 7

−

%- 7

+ rF?

Pada saat terjadi Imaks dan Imin maka Ix’y’ = 0, sehingga dari Persamaan

( 2. 92 ) diperoleh :

% ` 7

sin 2θ + Ixy cos 2θ = 0