5.1 Quantum Mechanics - Mekanika Quantum

(1)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 1

Quantum Mechanics

Model Bohr untuk atom sepertinya berada pada trek yang benar, tapi ….

hanya berlaku untuk atom dengan satu elektron saja… tidak berlaku untuk helium…

tidak memperhitungkan intensitas garis spektrum…

tidak memperhitungkan interaksi antar atom… dan tidak menjelaskan “stationary states.”

5.1 Quantum Mechanics

Pada mekanika Newton, jika anda tahu posisi dan momentum partikel, bersama dgn seluruh gaya yg bekerja padanya, anda dapat memprediksi perilakunya setiap saat.

Tapi kita telah melihat bahwa karena partikel memiliki sifat sebagai gelombang, kita hanya dapat mengukur pendekatan/ perkiraan dimana partikel berada dan mau kemana partikel bergerak. Kita hanya dapat memprediksi probabilitas keberadaanya dikemudian.

Mekanika quantum adalah cara mengekspresikan hukum konservatif mekanika klasik sehingga mencakup dualitas

wave-particle yang telah kita pelajari.

Mekanika quantum mengambil hukum fundamental dari fisika klasik dan memasukan sifat gelombang dari benda (matter).

simbol yang kita gunakan untuk fungsi gelombang adalahΨ

(“si”), yang termasuk time dependence, atauψ, yang hanya

tergantung pada spatial koordinat.

(2)

Mekanika quantum memiliki perhatian terhadap fungsi

gelombangΨ, walaupunΨitu sendiri tidak memiliki

interpretasi fisis.

Magnitude absolute Ψ∗Ψyang dievaluasi pada saat dan tempat

tertentu akan menceritakan kepada kita probabilitas untuk

menemukan sistem yang direpresentasikan denganΨpada

state (xyzt).

Jika sistem yang dijelaskan denganΨeksis,maka *

-dV = 1 .

∞

Ψ Ψ

∫

Yaitu, system eksis dlm beberapa state pd seluru waktu.

Fungsi gelombang seperti inidinormalisasi.

Fungsi gelombang harus “well-behaved”: Ψdan turunannya

hrs kontinyu dan bernilai tunggal dimana saja, dan Ψharus

dapat dinormalisasi.

Ψdapat merepresentasikan partikel tunggal atau seluruh

sistem. Mari kita gunakan kata “partikel” untuk sementar.

Pada satu dimensi, probabilitas untuk menemukan particle

yang direpresentasikan olehΨantara x₁dan x₂adalah

2

1 x

* x Ψ Ψdx .

∫

Mari kita gunakan contoh. MisalkanΨ(x,t) = Ax, dimana A adalah konstanta.

Ψtdk tergantung waktu; shg kita dapat menulisnya hanya sebagai

Ψ(x) [or ψ(x)].

ApakahΨ“well-behaved?”Ψdan turunannya adalah single-value dan continuous, tapi tidak bisa dinormalisasi karena integral dariΨ*Ψ_{“blows” up:}

Ψ Ψ*Ψ_.

Warna merah menyatakan nilai integral. Apa yang akan kita peroleh jika -∞< x < ∞?

Akan tetapi, jika kita batasi partikel ini didalam “box,” makaΨdapat dinormalisasi. Shg untuk contoh fungsi gelombang kita, kita akan gunakanΨ(x) = Ax, for 0 ≤x ≤1, danΨ(x) = 0 dilainnya, dimana A adalah konstata yang harus ditentukan.

Step pertama selalu normalisasiΨ (kecuali jika, Ψsudah dinormalisasi).*

JikaΨ memiliki beberapa “unknown constant,” seperti A (contoh diatas), kita harus normalisasi!

(3)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 9 Untuk menormalisasi, integralkan :

*

limits of integration is the second common mistake.

( )

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 10 2

A 1 =

3 A = 3 .

Kita telah menormalisasiΨ: Ψ(x) = 3 x for 0≤ ≤x 1 .

Tunggu dulu, kita telah sebutkan bahwaΨartinya ada t (waktu) di fungsi gelombang, danψartinya tdk ada t (waktu) difungsi gelombang. Dimanat (waktu)?

Kita dapat menambahkan :

(x, t) = 3 x for 0 x 1 and all t .

Ψ ≤ ≤

That was a lot of work for a stupid little linear function. What good is this?

Good question! Answer: now that we know ψ, in principle we

“know” (i.e., can calculate) everything knowable about the

particle represented by ψ. That’s quite a powerful statement!

OK, berikan kami contoh dari sesuatu yang dapat kita hitung!

Hitung probabilitas dimana pengukuran dapat menemukan

partikel yg direpresentasikan denganψantara x = 0 dan x =

0.5. 2

Apakah hasil ini memberikan sense?* Bagaimana mengeceknya?

(4)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 13 Dibawah ini adalah plot fungsi gelombang. Tetapi ingat, kita tidak mengukur fungsi gelombang. Yang kita ukur adalah sebanding dengan besaran fungsi gelombang dikuadratkan.

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 14 Dibawah ini adalah plot dari kerapatan probabilitas (besar fungsi gelombang kuadrat).

Kita tidak dapat mengatakan probabilitas particle ada di x = 0.5 (Heisenberg), tapi kita dapat mengatakan probabilitas bahwa particle dapat ditemukan didalam area dx berpusat pada x = 0.5.

Daerah merah menyatakan probabilitas particle dapat ditemukan pada 0 ≤x ≤0.5.

Daerah biru merepresentasikan probabilitas particle dapat ditemukan diantara 0.5 ≤x ≤1.0.

Sepertinya daerah merah 1/8 dari total area; daerah biru sekitar 7 kali lebih besar dibanding daerah merah?

Kita peroleh P(0 ≤x ≤0.5) = 1/8. Apa yg akan kita peroleh jika kita hitung P(0.5 ≤x ≤1.0)?

Kita telah mengakui dalam beberapa bab bahwa partikel mempunyai sifat gelombang, dan kita sudah melihat beberapa contoh dari percobaan yang mendukung klaim ini.

5.2 The Wave Equation

Secepatnya, kita harus menghadapi tantangan, dan sampai pada beberapa teori matematika yg serius untuk mendukung klaim ini.

Jika partikel mempunyai sifat gelombang dan dapat dijelaskan oleh suatu fungsi gelombang, harus ada suatu persamaan gelombang untuk partikel. kita harus menemukan fungsi ini.

(5)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 17 Ini adalah bentuk umum dari persamaan gelombang :

.

2 2

2 2 2

y 1 y

=

x v t

∂ ∂

Solusi y(x,t) adalah suatu gelombang yang menjalar dengan kecepatan v melalui ruang (satu dimensi) dan waktu.

(Persamaan 1-dimensional diatas dapat dengan mudah digeneralisasi untuk 3 dimensi.)

What are these things?

∠merepresentasikan turunan parsial. jika F adalah fungsi dari (xyz), maka jika kita lakukan

∠

F/

∠

x, kita menganggap y dan z adalah konstant :

2 2 F 2

If F(xyz) = 9xy + x yz , then = 9y + 2xyz .

x

∂ ∂

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 18 Solusi persamaan gelombang mempunyai bentuk

x

y = F t ± .

v

 

 

 

Tanda - menyatakan gelombang yang yang menjalar ke arah x+, dan tanda + menyatakan gelombang yang yang menjalar ke arah

x-Bentu fungsi yang equivalent adalah y = F ( k x ± ωt ) .

Suatu contoh solusi persamaan gelombang adalah gelombang yang setara dengan partikel bebas:

(Partikel bebas adalah partikel yang tidak dipengaruhi oleh gaya-luar, termasuk yang menimbulkan suatu potensial.)

j ( kx - ωt )

y = A e

= A cos ( kx -

ω

t ) + j A sin ( kx -

ω

t ) .

Jika kita mengambil bagian riil dari y, kita mempunyai pergerakan gelombang dalam suatu dawai diregangkan. (Persamaan di buku Beiser's sedikit berbeda tapi equivalen)

Pada bagian ini kita baru menuliskan suatu bentuk persamaan gelombang yang diperbaiki. Kita mengingatkan diri kita bahwa jika objek dinyatakan sbg gelombang, fungsi gelombangnya harus memenuhi bentuk beberapa persamaan gelombang.

Pada bagian ini kita akan memperkenalkan persamaan Schrödinger, yang anda dapat pikirkan sebagai sebagai pernyataan mekanika kuantum untuk kekekalan energi, dan mungkin merupakan persamaan mekanika kwantum yang paling utama.

5.3 Persamaan Schrödinger: Bentuk Time-Dependent

Mari kita turunkan persamaan Schrödinger.

(6)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 21 Kita mulai dengan conservasi energi:

Dimana potential U merepresentasikan pengaruh alam pada partikel (atau system) yang kita pelajari.

U dapat merepresentasikan pengaruh applied electric fields, charged partikels, gravity, springs, etc.

2

p

E = K + U = + U ,

2m

Misalkan partikel (or system) direpresentasikan dengan fungsi gelombang Ψ(x,t).

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 22 j (kx - ωt) (j/ ) (Px - Et)

Kalikan persamaan konservasi energi dengan Ψ(x,t) :

Jika ini harus merupakan persamaan gelombang, maka hrs memiliki solusi

Selesaikan untuk P2Ψ_{/2m, kita peroleh}

(7)

Selesaikan untuk EΨ,

Masukan apa yg sudah kita peroleh EΨdan P2Ψ_{/2m kedalam}

persamaan konservasi energi maka akan diperoleh

Ini adalah bentuk satu-dimensi time-dependent persamaan Schrödinger; ini akan mudah untuk mengeneralisasi untuk 3 dimensions.

Telah memperdaya kita, karena p betul-betul merepresentasi-kanoperator∂/∂x (ingat, dlm mekanika Newton momentum berhubungan dgn velocity, yg merupakan turunan pertama

dari posisi) dan E merepresentasikanoperator∂/∂t.

2

1

E (x, t) = p (x, t) + U(x, t) (x, t)

2m

Ψ Ψ Ψ

Persamaan kita yg original :

Kita telah “justified” pers. Schrödinger, tapi belum menurunkannya

Persamaan konservasi energi kita yg simple merupakan persamaan differential linear.

Tidak masalah – kita tidak pernah menurunkan hkm Newton. Namun kita membenarkannya, menunjukan hal itu bekerja, dan menggunakannya. Kita percaya karena hkm itu menjelaskan kenyataan.

Hal yang sama berlaku untuk persamaan Schrödinger. Yang mendalilkan prinsip pertama, persamaan ini lahir karena pengamatan atas kenyataan fisik, dan dipercaya karena sukses menjelaskan alam semesta.

Dengan kata lain, “we believe it because it works.”*

2 2

Pers. Schrödinger merupakan pers. differential linier dari fungsi

gelombangΨ.

(8)

Kalau kita tahu kondisi batas untuk partikel dan potential U(x,t), secara prinsip kita dapat menyelesaikan untuk fungsi gelombang pd berbagai t dan x.

Sekali kita punya fungsi gelombang, maka persoalan telah kita selesaikan.

Pada bab ini kita akan menyelesaikan pers. Schrödinger untuk beberapa potential yang simpel.

2 2

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 30 Apa potensial yang paling simple yg dpt anda pikirkan?

Betul: U=0, yaitu potential untuk partikel bebas.

Kita gunakan pers. Schrödinger, dgn U=0, dan solve Ψ.

Atau kita dapat lebih effisien dan mengambil partikel bebasΨ,

masukan ke pres. Schrödinger, dan perhatikan jika kita dapat memperoleh identitas yang ada.

Fungsi gelombang untuk partikel bebas

Ψ

_{= e}

-(j/ ) (Et - Px)h

_.

pres. Schrödinger untuk partikel bebas (U = 0) adalah

(

-(j/ ) (Et - Px)

)

Bagian kiri :

Bagian kanan:

Kita sudah ingat bentuk tsb.

Tapi tentu saja kita perlu mengecek konsistensi pd kasus yg paling simpel sebelum kita menghabiskan waktu untuk pres. Schrödinger.

Ingat—ini versi nonrelativistic.

(9)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 33 5.4 Linearitas dan Superposisi

2 2

Dalam mekanika kwantum, ilmu fisika dan matematik

sepertinya terlibat untuk selamanya. Artinya kita dapat sering memperoleh pengertian yang mendalam dengan melihat pers matematik, tidak terikat pada sistem fisik tertentu

pres. Schrödinger linear dlmΨ. Dengan kata lain, tdk memiliki

istilah independen dariΨ, dan tdk ada istilah melibatkan

“higher powers”Ψatau turunannya.

Hal itu juga berarti fungsi gelombang “behave well.”

Sebagai konsekuensi linearitas, jikaΨ₁danΨ₂adalah solusi

untuk pres. Schrödinger, maka mereka merupakan kombinasi linear

1 1 2 2

= a + a ,

Ψ Ψ Ψ

dimana a₁dan a₂adalah konstanta.

Konsekwensi lebih lanjut adalah fungsi gelombang mematuhi superposisi dan exhibit interference.

Jika sistem direpresentasikan dengan fungsi gelombangΨ=

a₁Ψ₁+ a₂Ψ₂, bagaimana kita menghitung kerapatan

probabilitas untukΨ?

Kita tdk dapat hanya menambahkan probabilitas! Kita tdk

dapat menulis P = a₁P₁+ a₂P₂, dimana P₁= Ψ₁* Ψ

1dan P2 =

Ψ₂*Ψ 2!

Beiser menggunakan hasil ini untuk menunjukan kenapa tembakan electron melalui double slit memperlihatkan effek interference (tdk seperti partikel murni tapi seperti

gelombang).

5.5 Nilai Ekspektasi

Sekali kita “solve” pres. Schrödinger untuk Ψ, kita mengetahui

segalanya tentang partikel yang bisa diketahui di dalam batas yang dikenakan oleh asas ketakpastian.

Telah kita ceritakan bagaimana cara mengkalkulasi kemungkinan menemukan partikel dalam sebuah volume berpusat pada koordinat (x,t) dalam satu dimensi atau (x,y,z,t) dalam tiga dimensi.

(10)

Mari kita mulai dengan contoh.

Misalkan kita ingin menemukan rata-rata dari sekumpulan

bilangan 1,1,1,2,2,3,3,3,3,4,4,4,4,4. Bagaimana kita

menghitung rata-rata?

Jumlahkan bilangan dan bagi dengan jumlah bilangan? Itu bisa dilakukan, tapi bagaimana jika kita punya zillions bilangan. Adakah cara yang lebih baik?

Rata-rata adalah

(

3 ×1 +

) (

2 ×2 +

) (

4 ×3 +

) (

5 ×4

)

3 2 4

+ + +

5 .

Kadang-kadang kita ingin mengkalkulasi nilai rata-rata

beberapa kwantitas terukur. Seperti halnya mekanika kwantum

yang mempunyai cara sendiri menghitung probabilitas,

mekanika kwantum mempunyai cara yang khusus untuk menghitung rata-rata.

Secara umum, rata-rata N_ibilangan memiliki nilai x_iadalah

i i

jika variable x kontinyu, kita ganti “sum” dgn integral.

Dlm mekanika quantum, probabilitas P_iuntuk menemukan

partikel dlm interval dx pada x_iadalah

2

i i

P dx =

Ψ

dx .

PikirkanΨ*Ψ_{seperti N (“how much probability”}⇔_“how

many”).

Dalam QM (mekanika kwantum) karena kita berhadapan dengan kemungkinan, kita menggunakan istilah nilai harapan dibanding nilai rata-rata.

(“expectation value” rather than “average value.”)

i i

memperoleh QM average <x>…

…ganti ini dgnΨ*Ψ…

…ganti ini dgnΨ*Ψdengan ekstra x di dlmnya

…dan ganti ini dgn integral (krn variable kita kontinyu).

Nilaiekspektasi x adalah

*

Di mana kita sudah menggantikan variabel diskrit dgn kontinyu dan penjumlahan menjadi integral.

Nilai ekspektasi adalah ekuivalen mekanika kuantum dari nilai rata-rata.

“like” N

Jika Ψdinormalisasi, integral pada pembagi = 1, dan

*

-x = ∞x dx .

∞ Ψ Ψ

∫

(11)

Posisi, momentum, energi, kinetik energi, etc. secara aktual

adalahoperator, dan urutan bagaimana kita

menggunakannya adalah sangat penting.

Ingat, momentum berhubungan dgn∂/∂x dan

energi berhubungan dengan∂/∂t.

Pendekatan yang benar adalah membuat “Ψ*Ψsandwich”

untuk memperoleh nilai ekspektasi.

*

-x = ∞ x dx

∞Ψ Ψ

∫

Secara umum, nilai ekspektasi suatu kuantitas, termasuk operator adalah

Menggunakan ekspresi operator untuk momentum juga mencegah kita menggunakan

ˆ *ˆ

-p = ∞ p dx

∞Ψ Ψ

∫

Untuk mengklaim cara mengingkari prinsip ketidakpastian

the “hat” reminds us momentum is an operator

Mari kita gunakan fungsi gelombang kita sbg contoh

(x) = 3 x for 0 x 1

ψ ≤ ≤

Refreshing your memory…

Nilai ekspektasi x seperti probabilitas rata-rata menemukan suatu partikel pada mengkoordinir x. yg merupakan titik di

mana kita bisa “balance”ψ*ψ_{plot pada ujung jari.}

Saya akan gerakkan penunjuk laser sepanjang x-axis. Anda katakan “ stop” kapan saja jika anda pikir saya telah mencapai titik di mana area merah akan seimbang pada ujung jari saya.

Mari kita cek apakah matematika setuju dgn keputusan anda.

(12)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 45 5.6 Operators

Seperti yang telah kita bahas ketika melakukan justifikasi pada persamaan Schrödinger's, energi dan momentum adalah operator dalam dunia mekanika kwantum. Kita menggunakan

tanda “topi” (∧) untuk mengidentifikasi operator

ˆp

Konservasi energi menjadi operasi:

ˆ ˆ ˆ

E = K +U.

Dan operator energi kinetik adalah

ˆ 2 2 _.

Seperti yang diperlihatkan Beiser, mendalikan bentuk opertor E dan p sama dengan mendalilkan persamaan Schrödinger.

Bagian ini juga menunjukan kenapa bentuk yang tepat untuk nilai ekspektasi adalah

(

)

*

(

)

-G x, p = ∞ G x, p dx .

∞Ψ Ψ

∫

5.7 Persamaan Schrödinger: Bentuk Steady-State

Dalam satu dimensi (yaitu, Ψhanya fungsi dari x dan t), Ψ

dapat ditulis dalam bentuk

-(jE/ ) t (jp/ ) x -(jE/ ) t

= A e

e

= e

,

Ψ

h h

ψ

h

Dimanaψadalah hanya fungsi posisi (x).

Biasanya, gaya yang bekerja pada objek adalah independen terhadap waktu. Sebagai contoh, gaya tarik gravitasi matahari adalah independen terhadap waktu.

Jika gaya yang bekerja pada objek hanya tergantung pada posisi dan independen terhadap waktu, maka potensial U juga hanya fungsi dari posisi.

Dalam kasus persamaan Schrödinger

2 2

Ini adalah persamaanSchrödinger steady-state dalamsatu

(13)

Beiser, hal 174, menunjukan bagaimana menuliskannya dlm 3 dimensi.

Untuk Fungsi gelombang yang mengikuti persamaan ini, harus mematuhi syarat batas, dan dia beserta derivatif-nya harus terbatas, kontinyu, dan bernilai tunggal

Catat bahwa energi partike terikat secara khas terkuantisasi (hanya memiliki nilai yang diskrit), tetapi variabel lain, seperti posisi, tidak perlu dikuantisasi.

Jika tidak ada fungsi gelombang seperti itu untuk U tertentu, maka sistem tidak bisa ada pada suatu posisi mantap.

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 50 Eigenvalue—energy Endimana persamaan Schrödinger

memiliki solusi.

Eigenfunction— fungsi gelombangψ_nyang merupakan solusi persamaan Schrödinger.

Eigenfunctionψ_nmemiliki hubungan dengan eigenvalue E_n.

Sebenarnya, persamaan eigenvaluememiliki bentuk

ˆ

n n n

Gψ = Gψ .

“G-hat” adalah operator, ψnadalah eigenfunction, adn Gn

adalah eigenvalue.

Schrödinger’s equation is just one example of an eigenvalue equation.

5.8 Particle in a Box

Apa yang akan kita lakukan?

2 2 2

2m

+ (E - U) = 0 .

x

ψ

∂ _ψ

∂ h

PersamaanSchrödinger steady-state dalamsatu dimensi _{OK, mari kita coba bermain dengan persamaan diatas.}

Fisikawan selalu mulai dengan yang paling mudah. Apa sistem yang paling mudah dalam hal ini?

U = 0?

Ya, partikel bebas—tapi kita telah melakukannya. Sistem termudah yang bagaimana dengan “something” happening?

Sistem dengan U = 0 tapi partikel tidak bebas?

Yaitu — partikel dalam box!

2 2 2

2m

+ (E - U) = 0 .

x

ψ

∂ _ψ

(14)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 53 Kita telah bahas “particle dlm box” pd Bab 3.

Tapi pada bab ini kita akan bahas dengan cara MQ”

*So the particle can’t get “over” the wall.

**So the particle can’t pass through the wall.

∞ ∞

Buat box dengan tinggi dan kuat dinding yg tidak terbatas

∞

Next step: solve.

2

Diluar box, ψ= 0 (partikel tdk dapat keluar dari box).

Kita perlu untuk solve

untukψ, di dalam box.

Bagimanakitaselesaikan persamaan diatas?

jikaψ= 0 untuk x < 0 dan x > L, maka jikaψkontinyu, kita harus punya

ψ(0) = 0 danψ(L) = 0 .

Karenaψadalah kontinyu, solusi kita dibatasi oleh kondisiψ(0)

(15)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 57 Bagaimana kita selesaikan persamaan ini?

Cara lama (hard work)?

Lihat di buku? —masih banyak yang harus dikerjakan

Diterka?

Berapa jumlah solusi linear yg independent yg dimiliki persamaan ini?

Jawab : hanya dua. Jika kita terka* dua solusi, masukan ke dalam pers., dan jika terkaan kita betul maka kita telah menyelesaikan pers. diatas tanpa kerja keras.

Pers. ini memiliki 2 solusi linear yg independent. Ada beberapa solusi, semuanya dapat dikonstruksi dari 2 solusi linear yg independent

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 58 Solusi macam apa yang akan anda terka?

Saya akan terka dengan solusi gelombang.

Saya akan terka dengan bentuk komplek exponentials :

+

ψ

= A e

(j p/ ) xh

or

ψ

= A e

- (j p/ ) xh

.

-Ada 2 solusi yg independent. Jika ini adalah solusi persamaan Schrödinger untuk partikel dlm box, maka solusi lainnya harus kombinasi linier dari solusi diatas.

Jika kita ambil selisihψ₊-ψ_-dan gunakan relasi Euler, kita

akan dapatkan fungsi sinus. Jika kita ambil jumlahψ++ψ- kita

akan dapatkan fungsi cosinus.

Bentuk gelombang yg bagaimana yang anda terka?

Fungsi sinus dan cosinus menyatakan dua fungsi linier yg independent, dan karena itu kita dapat menulis solusi sebagai sinus dan cosinus.

Karena kita temukan cara termudah adalah menggunakan sinus dan cosinus, dan karena Beiser juga menggunakan cara yg sama, maka kita akan terka fungsi kita dibuat dari sinus dan cosinus

2mE 2mE

= A sin x + B cos x .

ψ

h h

Ini datang dari p = (2mE)½_{dan dari fakta bahwa kita akan}

mereproduksi bab 3 tentang kuantisasi energi pada perhitungan sekarang.

see note

Note: this trial solution is a linear combination of two linearly independent functions; if it works, we have found both the needed solutions.

Tunggu — (2mE)½_{ini apa dan bagaiman mendapatkannya?}

Kita dapat masukan

Ke dalam 2

dan verifikasi apakan persamaan diatas terpenuhi (yaitu, kita akan mendapatkan suatu identitas). Ini berlaku dengan baik. Silahkan coba sendiri jika tidak percaya.

Ini berarti terkaan kita memberikan kita dua unik kandidat untuk solusi.

Berikutnya, kita perlu menggunakan kondisi batas dan melihat apa yang mereka katakan tentang solusi kita (dan koeffisient A dan B).

ψ = A sin 2mEx + B cos 2mE x .

(16)

BC (Boundary Conditions): ψ(0) = ψ(L) = 0, karena partikel

tidak mungkin ada di dalam infinite potential wall, dan harus kontinyu pada perbatasan.

ψ = A sin 2mEx + B cos 2mE x .

Catat bahwa n = 0 bukan solusi karena fungsi gelombang kita = 0 (“non-particle”).

2mE

L = n , n = 1,2,3,...π

h

Energy level terkuantisasi, sama seperti pada bab 3. Dari persamaan diatas kita dapatkan E :

2 2 2

Ini identik dengan solusi pd bab 3 kecuali kita gunakanħdisini

dan h pd bab 3.

Masukan energy eigenvalues E_ndari persamaan diatas ke

ψ n

n

2mE

= A sin x

h

Kita dapatkan eigenfunctions ψn

n x

= A sin .

L

π

Langkah terakhir adl normalisasi untuk mendapatkan harga A.

* don’t forget appropriate limits!

Menyelesaikan “particle in a box” adalah salah satu dari syarat mahasiswa lulus QM.

Ada beberapa web sites yang memuat “particle in a box” physics.

hyperphysics

Wolfram Research

Physics 252 at Univ. of Virginia

my Mathcad document

Anda harus dapat mengidentifikasi eigenfunctions untuk n=1, 2, 3,

etc.

Anda hrs dapat menghitung probabilitas pada daerah yg berbeda dalam box.

(17)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 65 Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 66 2 2 2

n 2

n

E = , n = 1,2,3, ...

2mL

π h

Jelaskan fenomena dibawah ini

CdSe ZnS

2.3 nm 4.2 nm 4.8 nm 5.5 nm

Larger Band Gap

Smaller Band Gap

Courtesy of Bawendi and Coworkers. 2 2 2

n 2

n

E = , n = 1,2,3, ...

2mL

π h

Dengan menggunakan

Optional advanced material.

2 2 2

j = - + U .

t 2m x

∂Ψ ∂ Ψ _Ψ

∂ ∂

h h

Mari kita mulai dengan time-dependent Schrödinger equation

Dan biarkan U = 0 di dlm box.

2 2 2

j = - .

t 2m x

∂Ψ ∂ Ψ

∂ ∂

h h

Dua kemungkinan solusi*

(j/ ) (px - Et) (j/ ) (-px - Et)

(x, t) = A e

and (x, t) = A e

.

Ψ

h

Ψ

h

(18)

Selesaikan seperti sebelumnya, kita dapatkan fungsi gelombang

Ψ*Ψ_{adalah independent terhadap waktu karena}

-jEt/ jEt/

e

h

e

h

= 1.

Ini mengillustrasikan arti istilah “stationary state.” Distribusi

probabilitasΨ*Ψ_{adalah independent terhadap waktu.}

only difference is that now we explicitly show the time dependence

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 70 E=U

x E

x=0 x=L

L

sumur potential terbatas memiliki panjang L dan tinggi U.

Ada tiga region: I, II, dan III.

I II III

Pada regions I dan III, pers. Schrödingeris

yg dapat kita tuliskan sbg

2

Pada slide berikut kita akan asumsikan E<U shg akan menjadi real.

E=U

Perhatikan partikle dgn E < U. Solusi pd region I dan III adalah

ax -ax ax -ax

Solusi ini adalah real, dan tdk exponential komplex. C, D, F, dan G adalah koefisien yg akan ditentukan lewat syarat batas.

Regions I dan III diperluas ke x = -∞dan x = +∞.

Karena fungsi gelombang harus finite disetiap tempat, koeffisien D dan F harus 0, shg

ψ ax ψ -ax

I= Ce and III= Ge .

Kedua solusi menurun secara eksponensial dengan semakin jauhnya posisi dari dinding batas.

(19)

Persamaan ini memiliki solusi yg sama dgn sebelumnya partikel dlm (infinite) box:

Kecuali sekarang B ≠0 karenaψmemiliki amplitude pd

masing-masing barrier.

-∞ +∞

ax -ax

Ada 5 informasi yg kita inginkan: koeffisien A, B, C, dan G, dan energi E.

Kita punya 5 kondisi: ψkontinyu pd x = 0 dan x = L, ψ′

kontinyu pd x = 0 and x = L, dan normalisasiψ. 5 kondisi ini

memberikan 5 persamaan.

6 persamaan, 5 yg tdk diketahui, sisanya hanya matematik.

Salah satu cara menyelesaikannya adalah dengan menggunakan tool seperti Mathcad.

ψfor n=1

ψfor n=2

ψfor n=3

Notice bagaimana ekor fungsi gelombang memanjang kedalam barrier—ada finite probability untuk menemukan partikel disana.

Ekor fungsi gelombang yg lebih panjang artinya gelombang yg lebih panjang dan krn itu momentum dan energi lebih kecil.

partikel di dlm finite box dapat memiliki energi lebih rendah dibanding partikel di dlm infinite box.

(20)

Ini adalah perbandingan probability density

functions untuk infinite dan finite square wells, n=1, 2, dan 3.

Which probability goes with which well. Why?

Which plot corresponds to n=2? How can you tell?

What is the meaning of the red shaded areas?

Apakah kamu berusaha untuk ceritakan ada suatu kemungkinan menemukan batu bata ini terjepit separuhnya pada suatu dinding tak dapat tembus?

Persisnya tdk seperti itu

ada suatu kemungkinan menemukan batu bata di suatu tempat di dalam dinding yang tak dapat tembus

Efek Terobosan (Tunnel Effect)

Kita menemukan sesuatu yang “aneh” pada partikel dalam sumur terhingga.

Dari hasil perhitungan diperoleh hasil bahwa ada probabilitas partikel berada didalam dinding meskipun dindingnya diharapkan tidak dapat ditembus partikel.

Atau, dari perhitungan kita dapatkan bahwa ada probabilitas partikel berada ditempat yang tidak seharusnya ada.

Ini adalah percobaan yg kita pikirkan. Lemparkan bola pada dinding tembok setinggi 3 m.

Terlalu rendah shg mantul kembali

Cukup tinggi shg melampaui dinding

(21)

Jika E < U akan mantul kembali.

Jika E > U akan melewati.

U

U E

E

Sebenarnya, partikel menembus tetapi penjelasan diatas hanya sekedar gambaran konseptual.

Efek Terobosan (Tunnel Effect)

Bagaimana tentang suatu partikel klasik energi E menumbuk pada suatu penghalang setinggi U?

Bagaimana tentang partikel quantum mekanik berenergi E yg menumbuk penghalang setinggi U?

jika E < U akan dipantulkan kembali.

atau mungkin juga tidak.

U

U E

E

Kita harus bayangkan partikel sbg gelombang ketika melakukan eksperiment ini.

Efek Terobosan (Tunnel Effect)

jika E > U akan melewatinya.

atau mungkin juga tidak.

U

U E

E

E > U?

Efek Terobosan (Tunnel Effect)

U

E E

Mari kita pikirkan hal berikut ini…

Energi kinetik sebelum dan sesudah penghalang adl sama (tdk ada kehilangan energi ketika melewati penghalang), shg momentum dan wavelength juga sama.

Bagaimana dgn panjang gelombang di dlm penghalang?

KE_inside= (E – U) < E = KE_outsideshg KE_insideharus lebih kecil.

maka p_inside< p_outsidedanλ_inside> λ_outside.

Jika E < U makaλinsideadalah imajiner?!

λ₁ λ₂= λ₁

(22)

Jika kamu sedang memakai kacamata, lalu melepaskannya, dan letakan enam inchi atau lebih dari muka anda, dan lihat pada kaca mata.

Anda dapat melihat melalui kaca mata. Jika ada benda yg terang dibelakang anda, anda bisa melihatnya melalui refleksi pada kaca mata.

Seseorang yang berdiri di sebelah lain kacamata anda akan melihat juga objek yang terang melalui kacamata anda.

Beberapa photon melewati kaca mata, yang lainnya direfleksikan. Ada probabilitas transmisi, dan probabilitas refleksi.

Efek Terobosan (Tunnel Effect)

Karena photon adalah gelombang maka hal itu dapat terjadi.

Partikel juga gelombang. Jadi mereka dapat direfleksikan dan di transmikan.

Dalam slide berikut ini kita akan menyelesaikan persamaan Scrödinger untuk mencari partikel quantum yang dapat menerobos penghalang yg tinggi, atau direfleksikan oleh penghalang yang rendah.

Ini adalah diagram potential untuk masalah kita.

Partikel memiliki masa dan energi E, dan penghalang dgn

tinggi U dan panjang L. x

E

Kita harus menyelesaikan persamaan Schrödinger untuk partikel yang memiliki energi E di dalam ketiga region seperti pada gambar diata.

Persamaan Schrödinger di regions I, II, dan III menjadi…

x

Pekerjaan kita adalah menyelesaikan persamaan ini, equations,

sesuai dengan syarat batasψyang ada, dan sesuai dgn kondisi

bahwaψdan turunannya harus kontinyu dan terbatas.

Ketiga persamaan adalah valid baik untuk E > U atau E < U. Kita akan asumsikan E < U ketika kita menyelesaikan

persamaan Schrödinger pada region II.

(23)

Kita mulai dgn mengasumsikan solusi

wave-like untukψdi regions I dan III,

dimana potential U = 0.

Solusi wave-like yang tepat adalah

ψ j k x1 - j k x1 Karena energi kinetik adl sama pd region I dan III. Partikel tdk kehilangan ketika melewati penghalang.

ψ j k x1 - j k x1

Ingatψ_Idanψ_IIIadalah berbentuk

ψ

dimanaψ_I+_{menyatakan gelombang pd region I yg bergerak}

kearah kanan, ψ_I-_{menyatakan gelombang pd region I yg}

bergerak kearah kiri,

dan ψ_III+_{menyatakan gelombang pd region III yg bergerak}

kearah kanan, danψ_III-_{menyatakan gelombang pd region III}

yg bergerak kearah kiri.

Kita asusmsikan gelombang kita bergerak dari kiri ke kanan.

x E

U

0 L

I II III

Jika gelombang kita menembus penghalang, pada region III tdk akan ada yang direfleksikan kembali ke kiri.

Hal ini mengatakan kepada kitaψ_III-_{= 0 shg G = 0.}

Solusi lengkap persoalan ini memerlukan perhitunganψdi

setiap tempat, shg kita akan perluψ_I, ψ_II, danψ_III. Akan tetapi,

sering dalam perhitungan MQ, Solusi lengkap tidak diperlukan. Sekarang kita hanya akan menghitung probabilitas transmisi melalui penghalang.

ψ j k x1 - j k x1

III = F e + G e

Fungsi gelombang partikel (wave) yang menumbuk penghalang:

ψ

I+adalah rapat probabilitas gelombang datang. Pd satu

dimensi, itu adalah rapat probabilitas linier yang memiliki satuan partikel/meter.

Jika v is kecepatan group gelombangψI+, maka jml partikel per

meter2_{perdetik yg menumbuk penghalang dari kiri adalah}

SI+= ψI+* ψI+ v.

Sama dgn diatas, jml partikel per meter2 perdetik yg keluar dari

(24)

Probabilitas transmissi adalah

( ) ( )

Untuk mendapatkan ekspresi T yang bermanfaat, kita perlu

menerapkan kontinuitasψdan turunannya untuk mengeliminasi

A dan F.

Berarti kita perlu melihat persamaan Schrödinger in region II.

Pada region II, persamaan Schrödinger adalah

Solusi pada region II adl: ψII = C ej k x + D e- j k x

′ ′

dimana k = ′ 2m E - U

(

)

.

h

wavenumber adalah k'. Tapi jika E < U, maka k' adalah imajiner.

Apa implikasinya ?

Apa implikasinya ? Jawabnya: damped atau blowing up

exponentials, bukan gelombang, pd region II.

Apakah anda dapat menangkap sense tsb? Ya, jika anda pikirkan.

Dari sini jelas bahwaψ_IIbukan merepresentasikan gelombang

, tapi lebih sebagai damped atau blowing up exponential.

Secara Philosopi, sesorang dapat berargumentasi bahwa karena

ψ_IItdk merepresentasikan gelombang , maka tdk

merepresentasikan partikel yg bergerak, karena itu tdk ada

partikel di region II. TapiψII*ψIImerepresentasikan rapat

probabilitas, shg ada probabilitas untuk menemukan partikel di dlm penghalang.

Mari kita pikirkan tentang perhitungan yg telah kita lakukan.

Kita memiliki ekspresi untuk transmissi, berisi constanta A dan F. Kita perlu mencari konstanta tsb untuk menghitung transmissi.

Kita juga telah menuliskan solusi wavefunction pd region II, tapi hanya mendapatkan konstanta, C dan D. Ini kelihatan belum menolong. Malah membuat lebih rumit krn menambah

konstanta yg harus dicari.

Apa yg dapat kita lakukan, sekarang kita punya solusi di region I, II, dan III, adalah gunakan syarat batas pada kedua sisi.

(25)

sebenarnya ada 5 konstanta yg harus dicari dgn 4 kondisi.

Untuk mendapatkan T hanya memerlukan 4 konstanta. Jika kita ingin menyelesaikan persamaan gelombang kita perlu satu kondisi lagi

A,B C,D F

ψ& ψ′cont. ψ& ψ′cont.

Jika kita ingin mencari solosi persamaan gelombang, kita perlu menerapkan normalisasi, yang akan memberikan kondisi ke lima untuk 5 konstanta, shg sekarang masalah dpt

Ini adalah kondisi batas

Pd bagian kiri (x = 0),

Masukanψ_Idanψ_IIke dalam (2) diperoleh

( ) ( ) ( ) ( )

Sekarang kita gantikan

(26)

Ada masalah: 5 unknown dengan 4 equation. Kita perlu satu lagi equation. Akan tetapi ingat, kita dapat menerapkan normalisasi jika kita memerlukan

Kita hanya tertarik menyelesaikan rasio F*F / A*A. Kita dapat menyelesaikan N equation dlm N+1 unknown coefficien untuk rasio dua coefficien.

A + B = C + D

Bagaimana mendapatkan A/F?

Silahkan coba sendiri.

Jawabannya adalah :

(jk + k L1 2) (jk -k L1 2)

Kita dapat sederhanakan persoalan dgn mengasumsikan penghalang yang tinggi dan lebar.

Tinggi berarti potential penghalang relatif tinggi thd energi

kinetik. Pada kasus ini k₂/k₁>k₁/k₂. (lihat lagi definisi k1 dan

k2.)

Lebar artinya fungsi gelombang betul-betul disusutkan pada

region penghalang antara x=0 dan x=L. artinya k₂L >> 1.

Dengan pendekatan ini, persamaan untuk A/F dapat disederhanakan menjadi

Kita harus mendapatkan complex conjugate A*/F* (hanya ganti j dgn -j ). Transmissi menjadi

2

Kuantitas pada kurung kotak bervariasi “slowly” dibandingkan dengan bagian exponential, dan besarnya disekitar 1, shg kita dapat sederhanakan lagi

(27)

2 -2k L

T = e

k = ₂ 2m U - E

(

)

h

Simpan dlm ingatan bahwa ini hanya berlaku untuk penghalang yg tinggi dan lebar. Jika penghalang tdk tinggi dan lebar, kita harus gunakan ekspresi penuh untuk A/F (kemudian kita kalikan dgn complex conjugate).

Tadi kita sederhanakan bahwa besaran dlm kurung kotak memiliki nilai sekitar 1, namun sebenarnya lebih dekat ke 4. Apakah menggangu?

Iya, tapi 4 lebih dekat ke 1 dibanding ke 10, shg kita anggap bernilai 1.

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 106 “Artinya kita menerima error sampai faktor 10?” Teori apa?

Ini adalah teori yang hebat, jika kita hanya ingin

mengembangkan “feel for the physics”. Tentu saja, dalam “real life” kita harus menggunakan full expression, tanpa pendekatan

Mari kita lihat contoh. Misalkan 1 eV elektron menumbuk penghalang 5 eV dan 0.5 nm lebar.

5 adalah lebih besar dari 1, dan 0.5 nm lebih panjang dibanding panjang gelombang elektron energi rendah. Sehingga kita mungkin dapat menggunakan persamaan transmissi yang disederhanakan.

Pertama-tama, kita cari k₂.

Absolutely not! The square root “messes up” your units. You will be wrong every time!

-10 -1 2

k = 1.00×10 m

What mass do I use here? What is the object?

Electron!

Can I keep energies in eV and use the

T sebaiknya diantara 0 dan 1. Untuk pendekatan ini sebaiknya kecil. Sepertinya pendekatan kita OK.

Dapatkah kita menghitung probabilitas refleksi?

(28)

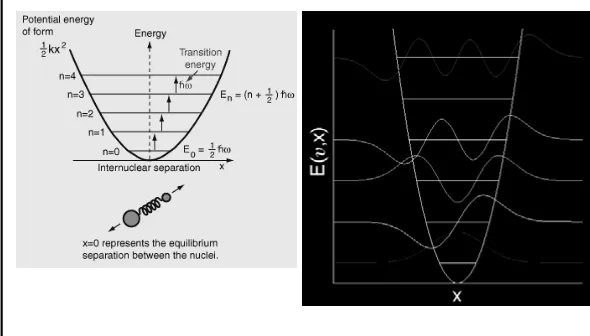
5.11 Harmonic Oscillator

Deret Maclaurin (deret Taylor disekitar origin):

2 2 3 3

Jika F menyatakan gaya balik (restoring) (gaya yang mengembalikan sistem ke asalnya) maka F(0) = 0.

Untuk simpangan yang kecil, seluruh orde yang tinggi (termasuk x2_{, x}3_{, dsb.) cukup kecil, sehingga}

0

Tanda – ada karena F adalah gaya restoring, shg turunannya adalah negatif.

Pada simpangan yang kecil, semua gaya balik(restoring)

mengikuti hukum Hooke:

F(x) = - k x .

Secara klasik, osilator harmonik tunduk pd hukum Hooke.

Satu pers. differential lagi yang harus dicari solusinya! Dari Hukum ke-2 Newton F = ma. diperoleh

2

Solusi dari persamaan differential tadi berbentuk

x = A cos (ωt + φ)

Dimana frekuensi osilasi f

k

Dari Fisika Dasar, potential harmonik osilator adalah

Banyak sistem yang dijelaskan dengan osilator harmonik. Kita lebih baik melihat tinjauan quantum mekanik tentang ini.

Mari kita pikirkan tentang osilator harmonik…

Klasih, seluruh energi diperbolehkan . Menunut QM?

Hanya energi tertentu (kuantisasi)?

Klasik, enrgi = nol diperbolehkan. Menunut QM?

Nonzero, seperti partikel dlm box

Klasik, osillator tdk dapat eksis dlm daerah terlarang. Sebagai contoh osilasi pendulum dgn amplitude A tdk dapat memiliki simpangan > A.

(29)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 113 Mari kita selesaikan persamaan Schrödinger untuk potential osilator harmonik.

maka persamaan Schrödinger menjadi

(

)

Solusi persamaan ini harus mengikuti semua persyaratan yg telah kita diskusikan danψharus dinormalisasi.

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 114 Persamaan dapat diselesaikan hanya untuk hargaαtertentu, yaituα=2n+1 dimana n = 0, 1, 2, 3, ...

Untuk hargaαtersebut diatas, fungsi gelombang memiliki bentuk

Orang biasa mungkin akan melihat persamaan diatas rumit, namun bagi ahli matematika persamaan diatas adalah simpel. Hanya kumpulan angka, fungsi exponential, dan Polynomial Hermite Hn. Polynomial adalah simple. H0(y) = 1, H1(y) = 2y, dan polynomial berikutnya lihat di Table 5.2 buku Beiser.

Yang lebih penting, kita menemukan bahwa pers. gelombang dapat diselesaikan hanya dengan nilai E tertentu (ingat, α= 2E/hf = 2n+1),

Energi E dari osilator harmonika mekanika quantum

terkuantisasi dengan step hf, dan zero point energinya adalah E₀= ½hf.

Dokumen Mathcad yg mengilustrasikan tingkat energi osilator harmonik QM, probabilitas, dan nilai ekspektasi adalad sbb.

Karena scaling yg kita lakukan dlm re-writing persamaan Schrödinger, sulit sekali mengidentifikasi daerah terlarang pada grafik Mathcad. Gantinya silahkan lihat Figures 5.12 dan 5.13, hal. 191 dari buku Beiser, untuk illustrasi bagaimana ekor fungsi gelombang dlm daerah terlarang mengkerut dgn naiknya

(30)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 117 Probability Densities

n = 1 n = 2

OSILATOR HARMONIK

Deret Maclaurin (deret Taylor disekitar origin):

2 2 3 3

2 3

0 0 0

dF x d F x d F

F(x) = F(0) + x + + + . . .

dx 2! dx 3! dx

   

 

   

 

     

Jika F menyatakan gaya balik (restoring) (gaya yang mengembalikan sistem ke asalnya) maka F(0) = 0.

Untuk simpangan yang kecil, seluruh orde yang tinggi (termasuk x2_{, x}3_{, dsb.) cukup kecil, sehingga}

0 dF

F(x) x = - k x . dx

 

≈ _ _

 

Tanda – ada karena F adalah gaya restoring, shg turunannya adalah negatif.

Pada simpangan yang kecil, semua gaya balik(restoring) mengikuti hukum Hooke:

F(x) = - k x .

Secara klasik, osilator harmonik tunduk pd hukum Hooke.

Satu pers. differential lagi yang harus dicari solusinya! Dari Hukum ke-2 Newton F = ma. diperoleh

2 2 d x - k x = m .

dt

2 2 d x

(31)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 121 Solusi dari persamaan differential tadi berbentuk

x = A cos (ωt + φ)

Dimana frekuensi osilasi f

k

Dari Fisika Dasar, potential harmonik osilator adalah

Banyak sistem yang dijelaskan dengan osilator harmonik. Kita lebih baik melihat tinjauan quantum mekanik tentang ini.

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 122 Mari kita pikirkan tentang osilator harmonik…

Klasik, seluruh energi diperbolehkan . Menunut QM?

Hanya energi tertentu (kuantisasi)?

Klasik, energi = nol diperbolehkan. Menunut QM?

Nonzero, seperti partikel dlm box

Klasik, osillator tdk dapat eksis dlm daerah terlarang. Sebagai contoh osilasi pendulum dgn amplitude A tdk dapat memiliki simpangan > A.

Ada kemungkinan menemukan sistem di daerah terlarang

Mari kita selesaikan persamaan Schrödinger untuk potential osilator harmonik.

maka persamaan Schrödinger menjadi

(

)

Solusi persamaan ini harus mengikuti semua persyaratan yg telah kita diskusikan danψharus dinormalisasi.

Persamaan dapat diselesaikan hanya untuk hargaαtertentu, yaituα=2n+1 dimana n = 0, 1, 2, 3, ...

Untuk hargaαtersebut diatas, fungsi gelombang memiliki bentuk

(32)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 125 Yang lebih penting, kita menemukan bahwa pers. gelombang dapat diselesaikan hanya dengan nilai E tertentu (ingat, α= 2E/hf = 2n+1),

n

1

E = n + hf , n = 0,1,2, ...

2

 

 

 

Energi E dari osilator harmonika mekanika quantum

terkuantisasi dengan step hf, dan zero point energinya adalah E0 = ½hf.

Dokumen Mathcad yg mengilustrasikan tingkat energi osilator harmonik QM, probabilitas, dan nilai ekspektasi adalad sbb.

Karena scaling yg kita lakukan dlm re-writing persamaan Schrödinger, sulit sekali mengidentifikasi daerah terlarang pada grafik Mathcad. Gantinya silahkan lihat Figures 5.12 dan 5.13, hal. 191 dari buku Beiser, untuk illustrasi bagaimana ekor fungsi gelombang dlm daerah terlarang mengkerut dgn naiknya

n. _{Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla}

126 Wave Functions

Probability Densities

n = 1 n = 2

(33)

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 129 Figure 5.11, potential yang berbeda untuk sistem yang berbeda menyebabkan tingkat energi yg berbeda

Modifikasi dari Slide Phys107 O. A. Pringle Physics Dept. U. Missouri-Rolla 130 Priview Bab 5

Fungsi Gelombang – probability densities – normalization – expectation values – “good” and “bad”* wave functions – perhitungan probabilitas.

Partikel dlm box – Bagaimana menyelesaikan SE – tingkat energi – kuantisasi – nilai ekspektasi – pengaruh panjang box – perhitungan probabilitas.

Partikel dlm sumur – Bagaimana menyelesaikan SE – tingkat energi – kuantisasi – nilai ekspektasi – pengaruh panjang box – perhitungan probabilitas– bandingkan dgn infinite well –forbidden regions (klasik).

Tunneling – (mencari solusi SE) – probabilitas transmissi – probabilitas refleksi – efek masa partikle dan energi pd probabilitas tunneling – efek tinggi penghalang pada probabilitas tunneling.

Beberapa conyoh aplikasi. Scanning tunneling microscope (STM). Efek Quantum pd IC dengan semakin kecilnya ukuran IC .

Osilator Harmonik – (mencari solusi SE) – tingkat energi – zero point energi – kuantisasi – nilai ekspektasi –