BAB VI. FUNGSI TRANSENDEN

BAB VI. FUNGSI TRANSENDEN

•

Fungsi Logaritma Natural

•

Fungsi Balikan (Invers)

•

Fungsi Eksponen Natural

•

Fungsi Eksponen Umum dan Fungsi Logaritma

Umum

•

Masalah Laju Perubahan Sederhana

•

Fungsi Trigonometri Balikan

•

Turunan Fungsi Trigonometri

Untuk menyajikan persoalan-persoalan yang lebih rumit, kita memerlukan perluasan fungsi-fungsi yang dapat dipakai.

Fungsi Logaritma Natural

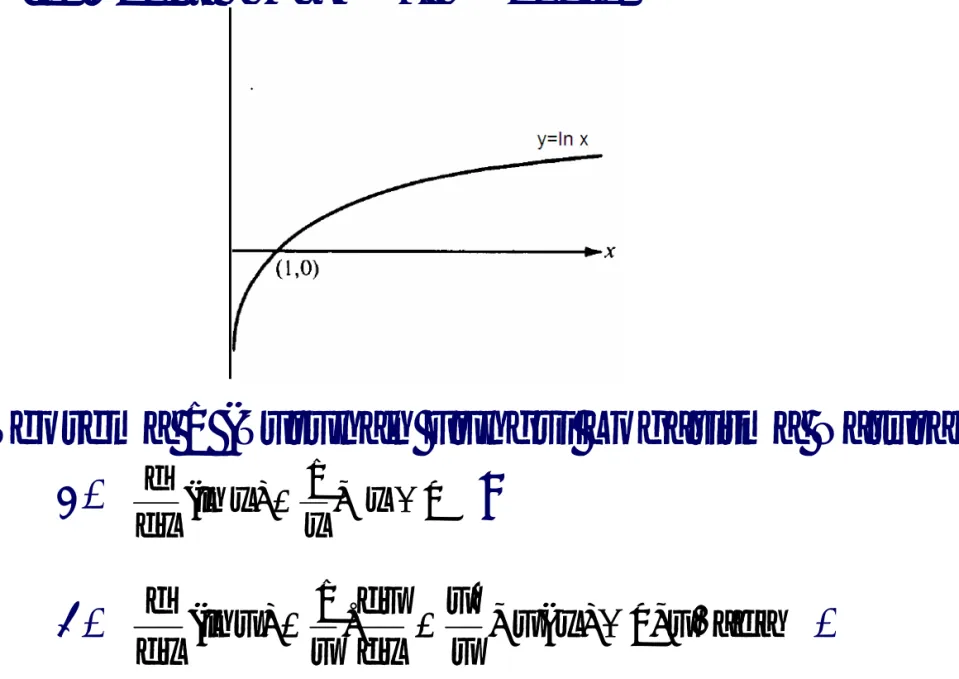
Fungsi Logaritma Natural (disingkat ln), ditulis f(x)=ln

x, didefinisikan sebagai,

Daerah definisi (D

_f

) dan Daerah nilai (R

_f

) fungsi ini

adalah D

_f

= (0,+ ) dan R

_f

= R.

Fungsi ini ada hubungannya dengan fungsi logaritma

∫

> = x x dt t x 1 0 , 1 ln

∞

Grafik dari fungsi f(x)=ln x adalah,

Teorema 1 (Turunan Fungsi Logaritma Natural)

1. ; 2. . 0 , 1 ) (ln = x > x x dx d ada u x u u u dx du u u dx d _′ > ′ = = 1 . , ( ) 0, ) (ln

Teorema 2 (Sifat Logaritma Natural).

Jika a, b > 0 dan r є Q dan r ≠ -1, maka 1. ln 1 = 0;

2. ln a.b = ln a + ln b; 3. ln a/b = ln a – ln b; 4. ln ar _{= r.ln a.}

Contoh 1.

(Menggunakan rumus turunan dan sifat logaritma natural. Selain itu, dapat juga menggunakan Aturan Rantai). Sedangkan D = (-1,1). 1 2 1 1 1 1 ) 1 ln( ) 1 ln( ) 1 1 (ln ₂ − = + − − − = + − − = + − x x x x x x x dx d

Setiap bentuk turunan itu ada rumus integralnya. Akibatnya dari teorema 1, diperoleh

Contoh 2. Hitung .

Jawab. Misalkan u=10-x2_{, du=-2x dx, maka}

Menurut Teorema dasar kalkukus diperoleh,

Agar perhitungan di atas berlaku, 10-x2_{≠0 pada [-1,3].}

. 0 , ln 1 ≠ + =

∫

du u C u u dx x x

∫

− − 3 1 2 10 C x C u du u dx x x + − − = + − = − = −

∫

∫

2 2 ln10 2 1 ln 2 1 1 2 1 10 . 9 ln 2 1 10 ln 2 1 10 3 1 2 3 1 2 ⎥⎦ = ⎤ ⎢⎣ ⎡_{− −} = − ₋ −

∫

x dx x x

Latihan.

A. Tentukan turunan fungsi di bawah ini. 1. f(x) = ln(1/x - 1).

2. y = ln√(x-2)/x2_.

B. Hitung nilai integral berikut. 1. 2. . . 1 1 1 0 2 dx x x

∫

₊+ . tan dxx

∫

Fungsi Balikan (Invers).

Misalkan fungsi y=f(x), dengan x є D_f dan y є R_f. Bila

f dapat dibalik, maka diperoleh fungsi x= f-1_(y). Fungsi f-1 disebut balikan (invers) dari fungsi f. Sebagai contoh, jika y=f(x)=x3_{-1, maka x=f}-1_(y)=

Tidak semua fungsi mempunyai balikan. Sebagai contoh, jika y=f(x)=x2 _{tidak mempunyai balikan,}

kecuali kalau daerah definisinya dibatasi.

Teorema 3. Eksistensi Fungsi Balikan.

Jika fungsi f monoton murni pada daerah definisinya, maka f mempunyai balikan.

. 1 3 _y +

Langkah-langkah mencari inver fungsi y=f(x), 1. Nyatakan x dengan y dari persamaan y=f(x);

2. Nyatakan bentuk dalam y sebagai f-1_{(y)→x= f}-1_(y);

3. Ganti y dengan x dan x dengan y dari x= f-1_(y),

diperoleh y= f-1_(x).

Contoh 3. Tentukan rumus untuk f-1(x) bila

y=f(x)=x/(1-x). Jawab.

Langkah1: y = x/(1-x)↔(1-x).y=x↔x(1+y)=y↔x=y/(1+y);

Langkah2: f-1_{(y) = y/(1+y);}

Bila f mempunyai balikan f-1 _{maka f}-1 _{juga memiliki}

balikan f sehingga diperoleh,

f-1(f(x)) = x dan f(f-1(y)) = y.

Jika f mempunyai balikan, maka

x = f-1(y) ↔ y = f(x).

Catatan. Lambang f-1 _{bukan berari 1/f.}

Grafik fungsi y=f-1(x) adalah

pencerminan grafik y=f(x) terhadap garis y=x. Sebagai

contoh, grafik fungsi y=f-1_(x)=

adalah pencerminan grafik y=f(x)=x3_{-1 terhadap garis y=x.}

3 1 + x 3 +₁ = x y x y = 1 3 − = x y

Teorema 4. (Turunan Fungsi Balikan).

Misalkan f mempunyai turunan dan monoton murni pada I. Jika f ’(x) ≠ 0 untuk suatu x Є I, maka f-1

dapat diturunkan di titik y = f(x) pada daerah nilai f dan berlaku

Rumus tersebut dapat juga ditulis

Contoh 4. Misalkan y=f(x)= x5+ 2x + 1. Maka

(Berdasarkan fakta y=4 sepadan dengan x=1 dan

f’(x)=5x4 _{+ 2} ) . ) ( 1 ) ( ) ( 1 x f y f ′ = ′ − . 1 dx dy dy dx = 7 1 2 5 1 ) 1 ( 1 ) 4 ( ) ( 1 = + = ′ = ′ − f f

Latihan.

Rumuskan f-1_{(x) dari fungsi f(x) berikut,}

1. f(x) = √2x+5 2. f(x) = -x/4 + 5

3. f(x) = (2x-2)/(x+3) 4. f(x) = x3/2_{, x ≥ 0.}

Fungsi Eksponen Natural.

Bilangan e adalah suatu bilangan real yang

merupakan jawaban tunggal dari persamaan ln x = 1. Nilai hampirannya adalah e = 2,71828……….

Fungsi eksponen natural adalah suatu fungsi yang

didefinisikan oleh persamaan f(x) = ex_.

Teorema 5. (Hubungan Fungsi ln dengan exp).

Fungsi f : R → (0,+∞), f(x) = ex _{adalah invers dari}

fungsi g : (0,+∞) → R, g(x) = ln x. Bentuk lain dapat ditulis

Karena antara exp dan ln adalah fungsi-fungsi yang saling invers, maka grafik y = ex _{adalah grafik y = ln x}

yang dicerminkan terhadap garis y = x. (Seperti gambar di samping).

Teorema 6 (Sifat Exponen Natural).

Jika a, b є R, maka 1. e0 _{= 1;}

2. ea_.eb _{= e}a+b_;

3. ea_/eb _{= e}a-b_;

Teorema 7 (Turunan Fungsi Eksponen Natural) 1. ; 2. Contoh 5. 1. 2.

Akibatnya, rumus integral fungsi eksponen natural,

x x e e dx d = ) ( . ' ; ' ) ( e u u ada dx du e e dx d _{u u u} = =

(

ln

)

ln

(

2

)

ln 2 ln

(

2

)

ln 1 ln 2 1 ln 2 2 2 2 x xe x x x x e x x dx d e e dx d _{x x x x x x x x} + = ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₊ = =

(

e x

)

e ( x) ( x)e e ( x x) dx d _{x x x x} sin cos cos sin cos = − + = − u u = +

∫

Contoh 6.

(Misalkan u = -x3_{, sehingga du = -3x}2₎

Latihan.

A. Tentukan turunan fungsi berikut.

1. y = x2 _esin x_{; 2. y = ln (1 - e}x_{)/(1 + e}x_).

B. Hitung nilai integral berikut. 1. ; 2. . ) 3 ( 3 3 3 3 1 2 3 1 2 C e dx x e dx e x −x = −

∫

−x − = −x +

∫

dx x e x

∫

2 1 2 3

∫

x ₋₁ e dx

Fungsi Eksponen Umum

Fungsi eksponen dengan bilangan dasar a>0 dan peubah bebas real x didefinisikan sebagai,

f(x) = ax = ex ln a.

Akibatnya,

ln ax _{= x ln a.}

Teorema 8. (Sifat-sifat eksponen umum).

1. a0 _{= 1, a>0; 5. a}-x _{= 1/a}x_{, a>0, x,yЄR;}

2. a1 _{= a, a>0; 6. (a}x)y _{= a}xy_{, a>0, x,yЄR;}

3. ax_.ay _{= a}x+y_{, a>0, x,yЄR; 7. (ab)}x_{= a}x_.bx_{,a,b>0, yЄR;}

Teorema 9.(Turunan fungsi eksponen Umum).

1. 2.

Akibatnya diperoleh,

Catatan. Bedakan dengan fungsi f(x)=xa_.

; 0 , ln ) (a = a a a > dx d _{x x} . ' ; ' ) ln ( ) (a a a u u ada dx d _{u u} = . 1 , 0 , ln + > ≠ =

∫

C a a a a du a u u

Fungsi Logaritma Umum

Jika a>0 dan , maka fungsi logaritma dengan bilangan dasar a, ditulis

y = f(x) = a log x.

Didefinisikan sebagai invers dari fungsi eksponen dengan

bilangan dasar a, ax_.

Hubungan kedua fungsi ini ditentukan oleh relasi y = a _{log x ↔ x = a}x_.

Teorema 10.(Hubungan logaritma dengan log. Natural)

1. a _{log x = ln x / ln a, a>0,}

2. a _{log e = 1/ln a; ln a = 1/}a _{log e, a>0,}

1 ≠ a ; 1 ≠ a . 1 ≠ a

Teorema 11.(Sifat-sifat Logaritma).

Jika a>0 dan dan x,y>0, maka

1. a_{log x.y =} a_{log x +} a_{log y; 4.} a_{log 1 = 0;}

2. a_{log (x/y) =} a_{log x -} a_{log y; 5.} a_{log a = 1.}

3. a_{log x}y _{= y} a_{log x;}

Teorema 12.(Turunan fungsi Logaritma Umum).

1. 2.

1

≠

a

; 0 , 1 , 0 , log ) log ( = a > a ≠ x > x e x dx d _a a ; ' , 0 , 1 , 0 , ' ). log ( ) log ( a a u u ada u u e u dx d _a a > ≠ > =

Contoh 7.

1. 2. 3.

Latihan.

A. Hitung turunan berikut.

1. 2xy _{= xy}2_{; 2.} 2_{log xy = xy}2_.

B. Hitung Integral berikut. 1. 2.

(

x x

) (

x x

)

( ) ( ) x x x x x x dx d _{ln ln ln} 2 . 2 ln . ln 1 ln 1 . . 2 ln 2 2 ⎟ = + ⎠ ⎞ ⎜ ⎝ ⎛ ₊ =

(

)

( ) ( x) e x x e x dx d x e x dx d tan . log sin . cos log cos . cos log log(cos 3 3 3 3 = = − = − C C du dx x dx x x u u x x = = = + = + ∫ ∫ ∫4 4 (3 ) 4 _ln4_{4 3}4_.ln4 3 3 3 3 1 3 1 2 3 1 2 ; 3 1 ln dx x e x

∫

dx x x e

∫

2 3 log

Masalah Laju Perubahan Sederhana

Misalkan suatu populasi yang besarnya setiap saat

berubah bergantung pada waktu t. Bila laju perubahan populasinya setiap saat sebanding dengan besarnya populasi saat itu, maka masalah yang muncul

dinamakan Masalah Laju Perubahan Sederhana. Untuk menyelesaikan masalah ini, misalkan

P(t) = besarnya populasi pada saat t, maka dP/dt = laju perubahan populasi pada saat t. Karena diketahui dP/dt sebanding P, terdapat konstanta k ≠ 0, sehingga

P’ = dP/dt = kP, k ≠ 0. (*)

Selanjutnya akan diselesaikan persamaan (*). dP/P = k dt, k ≠ 0 dan P > 0

∫ dP/P = ∫ k dt

ln P = kt + C1, C1 konstanta sebarang. P = e kt + C1 _{= C e} kt _{, C > 0.}

Ini berarti, populasinya berubah secara eksponen terhadap t.

Contoh 8. Laju pertumbuhan penduduk suatu kota pada

setiap saat berbanding lurus dengan jumlah penduduknya pada saat itu. Bila jumlah penduduk kota itu bertambah dari 1,2 juta jmenjadi 1,8 juta jiwa dalam kurun waktu 20 tahun, tentukan lamanya waktu yang diperlukan sehingga

penduduk kota itu bertambah dari 1,2 juta menjadi 2,7 juta jiwa.

Contoh 9. Suatu zat radio aktif meluluh dengan laju yang

sebanding dengan banyaknya zat saat itu. Zat tersebut memerlukan waktu 5570 tahun untuk mneyusut menjadi setengahnya. Apabila pada saat awal ada 10 gram,

Fungsi Trigonometri Balikan.

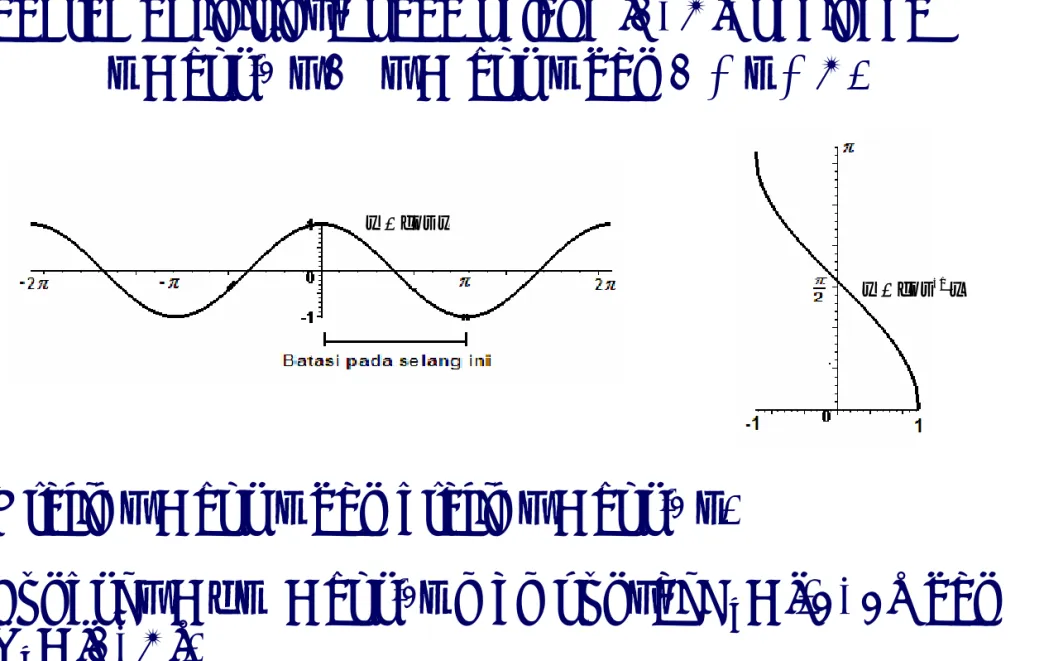
Balikan dari Sinus diperoleh dengan membatasi

daerah definisinya pada selang [-π/2, π/2], sehingga x = sin-1 _{y ↔ y = sin x dan -π/2 ≤ x ≤ π/2.}

Grafik y = sin x dan grafik y = sin-1 _x.

Fungsi y = f(x) = sin-1_{x mempunyai D}

f = [-1, 1] dan

R_f = [-π/2, π/2].

x

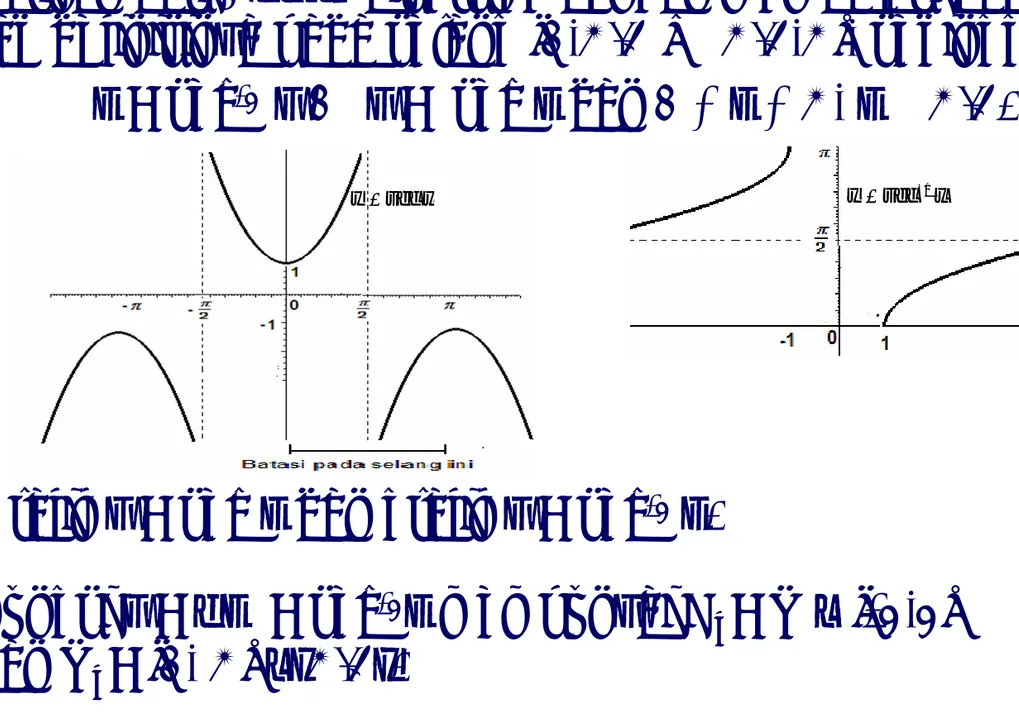
Balikan dari Cosinus diperoleh dengan membatasi daerah definisinya pada selang [0, π], sehingga

x = cos-1 _{y ↔ y = cos x dan 0 ≤ x ≤ π.}

Grafik y = cos x dan grafik y = cos-1 _x.

Fungsi y = f(x) = cos-1_{x mempunyai D}

f = [-1, 1] dan R_f = [0, π]. x y =cos x y =cos−1

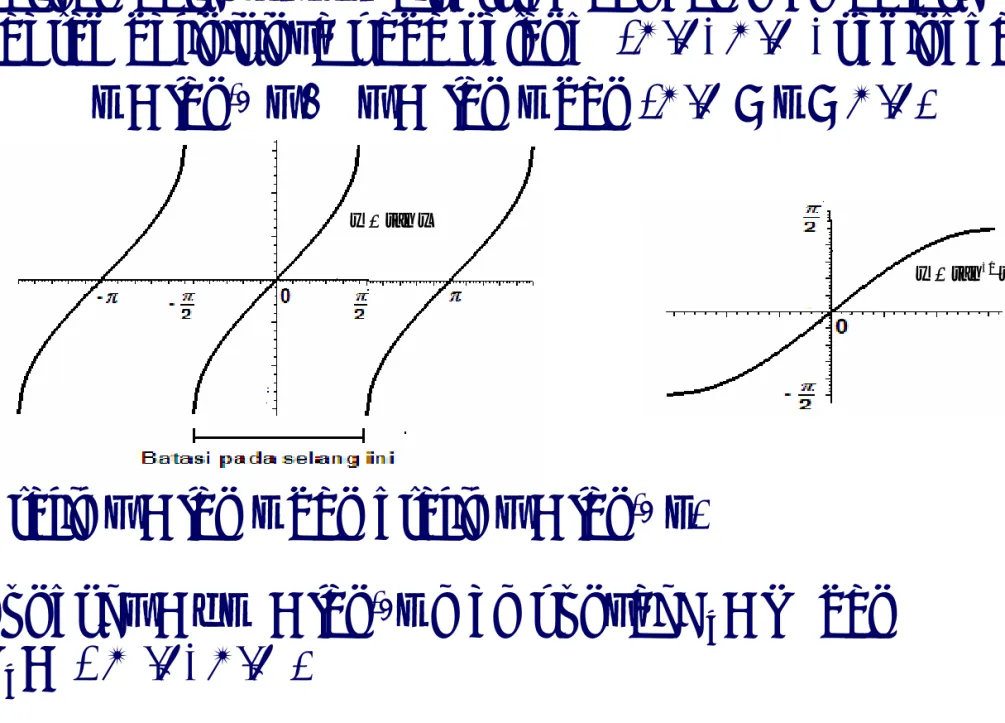
Balikan dari Tangen diperoleh dengan membatasi daerah definisinya pada selang (-π/2, π/2), sehingga

x = tan-1 _{y ↔ y = tan x dan -π/2 < x < π/2.}

Grafik y = tan x dan grafik y = tan-1 _x.

Fungsi y = f(x) = tan-1_{x mempunyai D}

f = R dan R_f = (- π /2, π/2). x y =tan x y =tan−1

Balikan dari Secan diperoleh dengan membatasi dae-rah definisinya pada selang [0,π/2)U (π/2,π], sehingga

x = sec-1 _{y ↔ y = sec x dan 0 ≤ x ≤ π, x ≠ π/2.}

Grafik y = sec x dan grafik y = sec-1 _x.

Fungsi y = f(x) = sec-1_{x mempunyai D}

f = R – [-1,1]

dan R_f = [0, π] –{π/2}.

x

Teorema 13. (Turunan Balikan fungsi Trigonometri) 1. 3.

2. 4.

Akibatnya, diperoleh integral berikut, 1. 2. 3.

(

)

, 1 1; 1 1 sin 2 1 − < < − = − x x x dx d

(

)

, 1 1; 1 1 cos 2 1 − < < − − = − x x x dx d

(

1

)

₂ 1 1 tan x x dx d + = −

(

)

, 1 1 1 sec 2 1 > − = − x x x x dx d

∫

= + − − C x dx x 1 2 sin 1 1

∫

= + + − C x dx x 1 2 tan 1 1

∫

= + − − C x dx x x 1 2 sec 1 1

Contoh 10. 1. 2. ( ) ( ) . 3 8 16 4 2 4 . ) 2 4 ( 1 1 ) 2 4 ( sin 2 2 1 − + − = − − − = − − x x x dx d x x dx d C x dx x dx x + = − = − − ∫ ∫ 1 2 2 ₄ sin 1 1 1 4 1 4 4 1

Fungsi Hiperbolik dan Balikannya.

Fungsi Hiperbolik diperoleh dari campuran fungsi ex

dan fungsi e-x_{. Fungsi sinus hiperbolik, cosinus}

hiperbolik dan empat fungsi hiperbolik lainnya, didefinisikan sebagai berikut.

Berlaku hubungan : cosh2 _{x – sinh}2 _{x = 1}

x x h x x h x x x x x x e e x e e x x x x x sinh 1 csc cosh 1 sec sinh cosh coth cosh sinh tanh ) ( 2 1 cosh ) ( 2 1 sinh = = = = + = − = − −

Teorema 14. (Turunan fungsi hiperbolik) ) sinh( x y = ) cosh( x y = x x h x h dx d x x h x h dx d x h x dx d x h x dx d x x dx d x x dx d coth . csc ) (csc tanh . sec ) (sec csc ) (coth sec ) (tanh sinh ) (cosh cosh ) (sinh 2 2 − = − = − = = = =

Balikan Fungsi Hiperbolik.

Dengan cara membatasi daerah definisi fungsi hiper-bolik pada suatu himpunan tertentu agar fungsinya satu-kesatu, maka dapat didefinisikan balikan fungsi hiperbolik sebagai berikut.

x = sinh-1_{y ↔ y = sinh x} x = cosh-1_{y ↔ y = cosh x, x ≥ 0} x = tanh-1_{y ↔ y = tanh x} x = coth-1_{y ↔ y = coth x, x ≠ 0} x = sech-1_{y ↔ y = sech x, x ≥ 0} x = csch-1_{y ↔ y = csch x}

Karena fungsi hiperbolik dapat dinyatakan sebagai fungsi eksponen, maka balikannya dapat dinyatakan sebagai fungsi logaritma natural.

Teorema 14. (Balikan fungsi hiperbolik dalam logaritma)

1 1 . 1 0 , 1 1 ( ln sec ]. 1 , 1 [ , 1 1 ln coth . 1 1 , 1 1 ln tanh . 1 , 1 ( ln cosh . 1 ( ln sinh 2 2 1 1 1 2 1 2 1 + + ≤ < − + = − ∉ − + = < < − − + = > − + = + + = − − − − − − x x x x x h x x x x x x x x x x x x x x x

Rumus turunan balikan fungsi hiperbolik diperoleh dari rumus turunan fungsi balikan atau dapat juga dari

bentuk logaritma naturalnya. Turunan balikan fungsi hiperbolik dinyatakan oleh rumus berikut.

Teorema 15. (Turunan Balikan fungsi hiperbolik)

Latihan. Buktikan Teorema 13, 14 dan Teorema 15.

. 0 , 1 1 ) (csc . 1 1 , 1 1 ) (sec ]. 1 , 1 [ , 1 1 ) (coth . 1 1 , 1 1 ) (tanh . 1 , 1 1 ) (cosh . 1 1 ) (sinh 2 1 2 1 2 1 2 1 2 1 2 1 ≠ + − = < < − − − = − ∉ − = < < − − = > − = + = − − − − − − x x x x h dx d x x x x h dx d x x x dx d x x x dx d x x x dx d x x dx d

SOAL-SOAL BAB 6. 7.1 no. 3, 6, 7,8, 17, 21. 7.2 no. 8,17, 27. 7.3 no. 3, 6, 17, 19, 22, 31, 32. 7.4 no. 2, 4, 15, 18, 25, 27. 7.5 no. 2, 14. 7.6 no. 2, 5, 26, 35 7.7 no. 5, 7,14, 21, 23, 29, 35, 36. 7.8 no. 1, 9, 12, 22, 23, 25.