BAB II LANDASAN TEORI

Sumber Input Antrian Mekanisme Pelayanan Unit-unit yang

membutuhkan

pelayanan Unit-unit yang_{telah dilayani}

Sistem Antrian (langganan)

BAB II

LANDASAN TEORI

2.1 Definisi Antrian

Teori antrian adalah teori yang menyangkut studi matematis dari antrian-antrian atau baris-baris penungguan (Tjutju, et al., 2004).

Antrian adalah suatu garis tunggu dari nasabah (satuan) yang memerlukan layanan dari satu atau lebih pelayan (fasilitas pelayanan). Studi matematikal dari kejadian atau gejala garis tunggu ini disebut teori antrian (Siagian, 1987).

Proses yang terjadi pada model antrian dapat diperlihatkan pada Gambar 2.1 (Tjutju, et al., 2004).

Kejadian garis tunggu timbul disebabkan oleh kebutuhan akan layanan melebihi kemampuan (kapasitas) pelayanan atau fasilitas layanan, sehingga nasabah yang ada tidak bisa segera mendapat layanan disebabkan kesibukan pelayanan. Dalam kehidupan sehari-hari, kejadian ini sering kita temukan misalnya seperti pada loket bioskop, loket kereta api, loket-loket pada bank, dermaga di pelabuhan, loket jalan tol, pelabuhan udara, telepon jarak jauh, tempat praktek dokter, tempat pembayaran rekening listrik atau telepon dan banyak lagi yang lainnya.

Dalam banyak hal, tambahan fasilitas pelayanan dapat diberikan untuk mengurangi antrian atau untuk mencegah terjadinya antrian. sering timbulnya antrian yang panjang akan mengakibatkan hilangnya langganan atau nasabah.

Jadi masalah yang dihadapi oleh tiap manajer adalah bagaimana mengusahakan keseimbangan antara biaya tunggu (antrian), terhadap biaya mencegah antrian itu sendiri guna memperoleh untung yang maksimum. Suatu analisa dari sistem antrian ini akan dapat memberi jawaban yang memadai secara umum.

2.2 Konsep-Konsep Dasar Teori Antrian 2.2.1 Tujuan

Tujuan dasar model-model antrian adalah untuk meminimumkan jumlah antrian yang terjadi dalam suatu perusahaan agar perusahaan tidak kehilangan pelanggan dikarenakan antrian yang panjang.

2.2.2 Sumber Masukan

Karakteristik yang perlu diketahui dari sumber input ini adalah ukurannya (jumlahnya), yaitu jumlah total unit yang memerlukan pelayanan dari waktu ke waktu atau disebut jumlah total langganan potensial. Ini bisa dianggap terbatas maupun tidak terbatas.

Pola statistik dari penurunan unit-unit yang memerlukan pelayanan ini harus juga ditentukan. Dalam hal ini, asumsi yang biasa digunakan adalah unit-unit ini diturunkan dengan mengikuti proses Poisson, artinya sampai suatu waktu tertentu jumlah unit yang

diturunkan ini mempunyai distribusi Poisson. Ini adalah suatu kasus di mana kedatangan pada sistem antrian terjadi secara random, tetapi dengan tingkat rata-rata tertentu. Asumsi berikutnya adalah bahwa distribusi kemungkinan dari waktu antar kedatangan (inter-arrival time) adalah distribusi eksponensial.

Asumsi lain yang juga harus dispesifikasikan mengenai kelakuan unit-unit (langganan) yang memerlukan pelayanan ini adalah balking, yaitu bahwa unit-unit yang memerlukan pelayanan itu akan menolak memasuki sistem antrian jika antrian itu terlalu panjang.

2.2.3 Sistem Antrian

Sistem antrian adalah suatu proses kelahiran dan kematian dengan suatu populasi yang terdiri dari para pelanggan yang sedang menunggu mendapatkan pelayanan atau yang sedang dilayani. Suatu kelahiran terjadi apabila tiba di suatu fasilitas pelayanan, sedangkan apabila pelanggannya meninggalkan fasilitas tersebut maka terjadi suatu kematian. Keadaan sistem adalah jumlah pelanggan dalam suatu fasilitas pelayanan.

Sistem antrian pada dasarnya dicirikan oleh komponen-komponen berikut ini:

1. Pola kedatangan

Pola kedatangan adalah cara dimana individu-individu dari populasi dimasuki sistem, yang biasanya dicirikan oleh waktu antar kedatangan yaitu waktu antara kedatangan dua pelanggan yang berurutan yang pada suatu fasilitas pelayanan.

Individu-individu mungkin datang dengan tingkat kedatangan yang konstan atau acak.

Distribusi probabilitas poisson adalah salah satu pola kedatangan yang paling sering (umum) bila data kedatangan didistribusikan secara random. Hal ini terjadi karena distribusi poisson menggambarkan jumlah kedatangan per unit waktu bila sejumlah besar variabel-variabel random mempengaruhi tingkat kedatangan.

Bila pola kedatangan individu mengikuti suatu distribusi poisson maka waktu antar kedatangan atau interrival time (yaitu waktu antar kedatangan setiap individu) adalah random dan mengikuti distribusi eksponensial.

2. Pola pelayanan

Pola pelayanan biasanya dicirikan oleh waktu pelayanan (service time) yaitu waktu yang dibutuhkan seorang pelayan untuk melayani para pelanggan. Waktu pelayanan ini dapat bersifat diterministik (diketahui secara pasti) atau berupa suatu variabel acak yang distribusi probabilitasnya dianggap telah diketahui. Juga yang menarik adalah apakah seorang pelanggan hanya dilayani oleh satu pelayan saja, sementara pelanggan ini membutuhkan barisan pelayan. Bila tidak disebutkan secara khusus maka anggapan dasarnya adalah bahwa satu pelayanan saja dapat melayani secara tuntas urusan seorang pelanggan.

Waktu pelayan adalah waktu yang digunakan untuk melayani individu-individu dalam suatu sistem. Waktu ini mungkin konstan atau random. Bila waktu pelayanan mengikuti distribusi eksponensial atau distribusinya acak maka waktu pelayanan akan mengikuti distribusi poisson.

Perbedaan distribusi-distribusi waktu pelayanan dapat diliputi oleh model-model antrian dengan lebih mudah dibandingkan perbedaan distribusi waktu kedatangan.

3. Disiplin antrian

Disiplin antrian menunjukkan pedoman keputusan yang digunakan untuk menyeleksi individu-individu yang memasuki antrian untuk dilayani terlebih dahulu. Aturan-aturan ini didasar pada yang pertama masuk, pertama keluar, yang terakhir masuk, dan seterusnya. Untuk lebih jelasnya berikut ini adalah disebutkan beberapa bentuk disiplin antrian: a. First Come First Served adalah disiplin antrian yang

menerangkan bahwa pelanggan yang datang pertama akan dilayani terlebih dahulu.

b. Last Come First Served adalah disiplin antrian yang menyebutkan bahwa pelanggan yang terakhir datang dalam antrian akan dilayani terlebih dahulu.

c. Service In Random Order adalah pemberian pelayanan didasarkan pada pemilihan secara sembarang atau berdasarkan pada peluang secara acak, tidak penting siapa yang datang terlebih dahulu.

d. Emergency First yaitu pelayanan yang diberikan kepada pelanggan yang menghadapi keadaan darurat yang perlu ditangani secepatnya. Dalam hal ini tentunya tidak melihat siapa yang datang terlebih dahulu atau yang datang belakangan.

4. Kapasitas sistem

Kapasitas sistem adalah jumlah maksimum pelanggan, mencakup yang sedang dilayani dan yang berada dalam antrian, yang ditampung oleh fasilitas pelayanan pada saat yang sama. Banyak sistem antrian yang dapat menampung jumlah individu-individu yang relatif besar, tetapi ada beberapa sistem yang mempunyai kapasitas yang terbatas. Bila kapasitas antrian menjadi faktor pembatas besarnya jumlah individu yang dapat dilayani dalam sistem secara nyata, berarti sistem mempunyai kepanjangan antrian yang terbatas.

2.2.4 Keluar (Exit)

Sesudah seseorang selesai dilayani, dia keluar dari sistem. Sesudah keluar dia mungkin bergabung dengan populasi asal dan mempunyai probabilitas yang sama untuk memasuki sistem kembali, atau dia mungkin bergabung dengan populasi lain yang mempunyai probabilitas lebih kecil dalam hal kebutuhan pelayanan tersebut kembali.

2.3 Struktur Antrian

Dalam struktur antrian dikenal dua istilah yaitu Chanel (Single atau Multiple) dan Phase (Single atau Multiple). Istilah chanel atau saluran menunjukkan jumlah fasilitas pelayanan. Sementara istilah phase adalah jumlah stasiun-stasiun pelayanan, dimana pelanggan harus melaluinya sebelum pelayanan dianggap lengkap. Terdapat empat model struktur antrian dasar yang umum terjadi dalam seluruh sistem antrian, yang selanjutnya akan dijelaskan dalam Gambar 2.2 – Gambar 2.5 (P. Siagian, 1987).

1. Single Chanel – Single Phase

Gambar 2.2 Single Chanel – Single Phase

2. Single Chanel – Multiple Phase

Gambar 2.3 Single Chanel – Multiple Phase

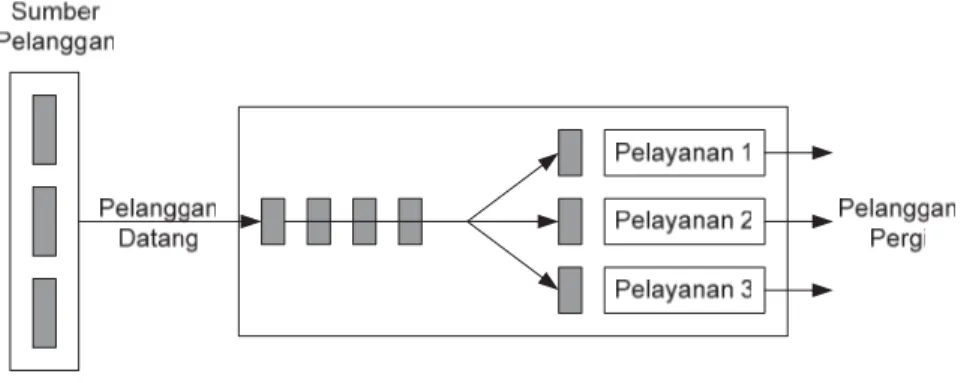
3. Multiple chanel – Single Phase Pelayanan 1 Sumber Pelanggan Pelanggan Datang Pelanggan Pergi Pelayanan 2

Gambar 2.4 Multiple Chanel – Single Phase

4. Multiple Chanel – Multiple Phase Sumber Pelanggan Pelayanan 1 Pelayanan 2 Pelanggan Pergi Antrian 1 Antrian 2

5. Campuran

Struktur campuran ini adalah merupakan campuran dua atau lebih struktur fasilitas service di atas. Struktur ini dipergunakan misalnya oleh toko-toko besar, dimana beberapa pelayanan toko yang melayani pembeli (Multiple Chanel), namun pembayaran hanya pada seorang kasir (Single Chanel). Ada pula yang mempergunakan struktur campuran yang lain, misalnya pelayan/service terhadap pengunjung rumah makan dan sebagainya.

2.4 Proses Kedatangan Konsumen

Untuk dapat menguraikan proses kedatangan konsumen, diambil asumsi-asumsi:

1. Interval waktu antara dua kedatangan yang berurutan saling bebas dan juga merupakan variabel-variabel non negatif dengan distribusi yang identik.

2. Didalam setiap interval waktu tersebut selalu ada peluang untuk datangnya nasabah (pelanggan).

3. Didalam setiap waktu yang kecil, paling banyak ada satu kedatangan.

Atau dengan kata lain sebagai berikut, jika banyaknya kedatangan rata-rata konstan sebesar O, maka didalam selang waktu (0, t + h) akan berlaku:

1. P ada tepat 1 kedatangan dalam interval (t, t + h) = O u h 2. P ada 0 kedatangan dalam interval (t, t + h) = 1 - O u h

3. P ada lebih dari 1 kedatangan dalam interval (t, t + h) = 0 Berdasarkan asumsi tersebut, maka akan dapat ditentukan formulasi matematis untuk proses kedatangan, yaitu dengan terlebih dahulu mendefinisikan bahwa Pn (t) = P ada tepat n kedatangan dengan interval (0, t).

Hal ini akan diperoleh bentuk-bentuk berikut:

P0 (t, t + h) = Kemungkinan ada 0 kedatangan dalam interval (0, t +

h)

= P ada 0 kedatangan dalam (0, t + h)

= P ada 0 kedatangan dalam interval (0, t) dikali dengan P ada 0 kemungkinan dalam interval (t, t + h)

= P0 (t) u (1 - O u h) atau:

P

t

h

h

t

P

t

P

0 0 0

_O

Jika diambil limit untuk h = 0, akan diperoleh:

t

P

t

d

t

dP

0 0

_O

Bila syarat batas P0 (0) = 1, artinya pada t = 0 tidak akan ada

kedatangan, maka diperoleh: P0 (t) = e

-O.t

Dengan cara yang sama akan dapat ditentukan proses kedatangan n konsumen dalam interval waktu (0, t + h), yaitu:

Pn (t, t + h) = Kemungkinan ada n kedatangan dalam interval (0, t + h)

P ada 0 kedatangan dalam interval (t, t + h)

= P ada n (n – 1) kedatangan dalam interval (0, t) dikali dengan

P ada 1 kedatangan dalam interval (t, t + h) = Pn (t) u (1 - Oh) + Pn-1 (t) u O u h atau:

Pn

t

P

t

h

t

Pn

h

t

Pn

1 n

_O

_O

Pn (t) t

Gambar 2.6 Grafik Distribusi Poisson

Jika diambil limit h = 0 maka diperoleh:

t

P

t

Pn

h

t

Pn

d

1 n

O

O

Dimana nilai n = 0, 1, 2, 3, …, n

Bila syarat batas P0 (0) = 1, artinya pada t = 0 akan ada

kedatangan, maka Pn (t) dapat ditentukan mulai dari n = 0 sampai dengan n = 1.

e

t

!

n

t

t

Pn

n

O

O

u

atau

!

x

e

x

P

O

O

x

Bentuk persamaan di atas, menyatakan bahwa besarnya kemungkinan ada n kedatangan di dalam interval waktu (0, t) adalah merupakan distribusi kemungkinan poisson dengan nilai rata-rata (O.t). Grafik distribusi poisson dapat diperlihatkan dalam Gambar 2.6.

2.5 Proses Pelayanan Konsumen

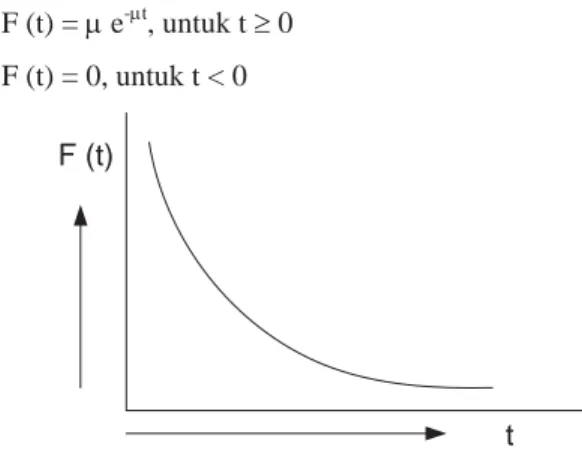
Yang dimaksud dengan waktu pelayanan adalah lamanya waktu yang digunakan untuk melayani konsumen sampai selesai. Bila waktu pelayanan yang diberikan oleh suatu fasilitas pelayanan berdistribusi eksponensial dengan parameter P dimana grafik distribusi eksponensial diperlihatkan pada Gambar 2.7, maka bentuk distribusinya secara matematis adalah:

F (t) = P e-Pt, untuk t t 0 F (t) = 0, untuk t < 0

t F (t)

Gambar 2.7 Grafik Distribusi Eksponensial

Maka:

³

f f

_e

t

1

dy

y

f

t

F

P , untuk t t 0

³

f f

_e

t

1

dy

y

f

t

F

P , untuk t < 0

Harga rata-rata dari distribusi eksponensial, E (t), diperoleh dari:

³

³

f f f 0 t

_dt

e

t

dt

t

f

t

t

F

P

P

Jika persamaan integral ini diturunkan maka:

t 0 0 t

_e

_E

_t

_dx

_e

e

t

t

E

P f

_³

f

_³

_³

P

Apabila notasi Sn mempresentasikan waktu pelayanan yang diberikan kepada konsumen ke-n, maka kemungkinan waktu pelayanan untuk konsumen ke-n adalah:

P(Sn) d t = t – e-P t, untuk t t 0

Dimana 1/P = rata-rata waktu pelayanan, e = konstanta (2.71828)

2.6

Notasi yang Digunakan dalam Model Antrian

Untuk menggambarkan suatu model antrian, maka digunakan notasi yang sesuai dengan notasi G. Kendall (1953) memperkenalkan notasi model antrian pelayanan banyak yang menyebutkan tiga karakteristik antrian, yaitu distribusi kedatangan, distribusi kepergian, dan jumlah saluran pelayanan. Kemudian A. Lee (1966) menambahkan dua karakteristik lainnya yaitu disiplin pelayanan dan jumlah maksimum dalam sistem. Pada akhirnya ditambah lagi dengan satu karakteristik sehingga lengkapnya menjadi:

(a / b / c) : (d / e / f) Dimana:

a = Distribusi kedatangan atau antar kedatangan b = Distribusi kepergian atau distribusi waktu pelayanan

c = Jumlah stasiun pelayanan yang disusun secara paralel dan independen antara satu dengan yang lainnya.

d = Disiplin pelayanan

e = Jumlah maksimum konsumen yang diperbolehkan berada dalam sistem

f = Sumber populasi konsumen

Pada aplikasinya, persoalan notasi-notasi di atas sering digantikan dengan simbol lain, yaitu:

a = Dapat diganti dengan M, yaitu dengan menunjukkan distribusi kedatangan secara poisson atau distribusi antar kedatangan eksponensial.

b = Dapat diganti dengan simbol M, menunjukkan waktu pelayanan berdistribusi eksponensial atau diganti dengan simbol D, menunjukkan waktu pelayanan secara deterministik. Atau notasi b ini dapat diganti pula dengan simbol Ek, artinya waktu pelayanan

mempunyai parameter k (Erlang) atau berdistribusi Gamma. Atau juga diganti dengan simbol GI, yang artinya distribusi waktu pelayanan bersifat General Independent.

c = Dapat diganti dengan bilangan-bilangan positif yang menunjukkan jumlah fasilitas pelayanan.

d = Dapat diganti dengan simbol-simbol seperti FCFS, LCFS, SIRO, GD atau yang lain yang menunjukkan disiplin pelayanan.

e = Dapat diganti dengan N atau a yang menunjukkan jumlah maksimum pelanggan dalam sistem.

f = Dapat diganti dengan N atau a tergantung dari sumber input atau populasi.

2.7 Parameter dan Variabel Sistem Antrian

Untuk menganalisa model antrian digunakan beberapa parameter dan variabel yaitu sebagai berikut: (Tjutju et al, 2004)

N = Jumlah konsumen

Pn(t) = Probabilitas transien-state untuk jumlah n konsumen dalam sistem pada saat t.

Pn = Probabilitas steady-state untuk jumlah n konsumen dalam sistem.

O = Tingkat kedatangan konsumen rata-rata (jumlah rata-rata konsumen yang datang per satuan waktu).

P = Tingkat pelayanan rata-rata (jumlah rata-rata konsumen yang dapat dilayani per satuan waktu).

S = Jumlah fasilitas pelayanan

U = Tingkat kegunaan/waktu sibuk pelayan. Ws = Waktu rata-rata konsumen dalam sistem.

Wq = Waktu rata-rata konsumen menunggu dalam antrian. Ls = Jumlah rata-rata konsumen dalam sistem.

2.8 Definisi Transien dan Steady State

Dalam analisa masalah dengan memakai teori antrian ada beberapa persyaratan yang harus diperhatikan agar hasil analisa yang dibuat benar, maka selain penggunaan karakteristik yang dikemukakan tadi sebagai modelnya, juga perlu diteliti status dari sistem yang akan dianalisa. Sistem antrian yang akan dianalisa harus berada dalam kondisi steady state/status mapan, artinya kondisi dari sistem yang akan dianalisa tidak tergantung dari waktu. Kondisi ini akan tercapai setelah sistem dioperasikan dalam jangka waktu yang cukup lama, selain itu kondisi pada status mapan dapat diketahui jika rata-rata jumlah kedatangan pada interval satuan waktu tertentu lebih kecil dari lamanya waktu pelayanan rata-rata yang diberikan. Kebalikan dari kondisi status mapan adalah kondisi transien, dimana sistem masih dalam kondisi yang transien atau kondisi peralihan menuju ke kondisi yang steady state. Suatu sistem antrian berada dalam kondisi yang transien jika karakteristik operasional (tingkah lakunya) dari sistem masih berubah-ubah sehingga sulit ditentukan arahnya, dan kondisi seperti ini tampak pada saat sistem mulai dioperasikan.

Perlu diketahui bahwa setiap sistem antrian beroperasi sebagai fungsi dari waktu misalnya antrian dengan laju kedatangan O yang lebih tinggi dari pada laju keberangkatan P tidak akan pernah mencapai steady state tanpa bergantung pada waktu yang berlalu, karena ukuran antrian akan meningkat dengan waktu. Dengan keacakannya kondisi transien dansteady state akan bisa berulang-ulang beberapa kali. Untuk itu kita harus memutuskan dalam menganalisa sebuah sistem antrian, apakah akan menganalisa berdasarkan kondisi transien atau steady state. Jalan

lain untuk menganalisa sistem yang tidak memperhatikan kondisi transien dan steady state adalah dengan menggunakan simulasi komputer.

2.9 Model-Model Antrian

Model antrian yang dipakai atau digunakan oleh perusahaan harus sesuai dengan kondisi perusahaan yang bersangkutan, dengan maksud agar tidak terjadi kerancuan atau kesalahan dalam pemecahan persoalan perusahaan (Tjutju et al, 2004).

2.9.1 Model-Model Single Server (S=1)

Seperti yang telah dijelaskan, model-model antrian dapat mempunyai pelayan tunggal, dapat juga mempunyai jumlah pelayan yang banyak. Berikut ini adalah model-model antrian yang digunakan apabila pelayannya hanya ada satu (S=1) dengan disiplin pelayanan tertentu.

2.9.1.1 Input Poisson dan Waktu Pelayanan Eksponensial Model ini adalah kasus khusus dari proses kelahiran-kematian yang mengkombinasikan proses kelahiran murni dengan proses kematian murni. Jadi

O

_n

O

untuk n=0, 1, 2, … Dan

P

_n

P

untuk n=1, 2, ….

Dari solusi steady state (

O

P

) kita peroleh:

P

O

P

O

¸¸

_¹

·

¨¨

©

§

1

1

1

P

1 0 untuk n > 0

n 0 n

P

P

_¸¸

¹

·

¨¨

©

§

P

O

Karena

U

O

P

, maka:

n n

1

P

U

U

untuk n = 0, 1, 2, …

Dengan demikian, maka:

O

P

O

U

U

1

L

_S

P

O

P

O

2 q

L

U

P

O

P

1

1

1

W

_S

P

O

P

O

q

W

2.9.1.2 Input Poisson Dan Waktu Pelayanan Sembarang

Asumsi: waktu pelayanan rata-rata

1

P

dengan varians

V

2. Maka jika

U

O

P

1

, didapat:

U

1

P

₀

U

U

V

O

1

2

L

_q 2 2 2 q S

L

L

U

O

q q

L

W

P

1

W

W

_{S q}

2.9.1.3 Input Poisson dan Waktu Pelayanan Konstan

Pada model ini, waktu pelayanan untuk setiap langganan adalah konstan sehingga

V

2

0

Karena itu:

U

U

1

2

L

_q 2

Demikian juga untuk Ls, Wq, dan Ws. Perhatikan bahwa Lq

dan Wq harganya adalah setengah kali harga Lq dan Wq untuk model

waktu pelayanan eksponensial.

2.9.1.4 Input Poisson dan Waktu Pelayanan Erlang

Fungsi probabilitas kepadatan untuk distribusi Erlang adalah:

K

_t

K 1

_e

K t

!

1

K

K

t

F

P

P

untuk

t

t

0

dimana

P

dan K

adalah parameter-parameter distribusi yang berharga positif. Harga rata-rata dan varians adalah

1

P

dan

1

K

P

2 . Jadi K adalah parameter yang menentukan dispersi dari distribusi. Model ini adalah kasus khusus dari model input poisson dan waktu pelayanan sembarangan, dimana

2 2

₁

_K

_P

P

P

O

O

U

U

P

O

2 ₂ 2 2 q

₂

K

₁

1

₂

_K

K

1

L

P

O

P

O

K

2

K

1

W

_q

P

1

W

W

_{S q}

W

L

_S

O

2.9.1.5 Input Poisson dan Waktu Pelayanan Eksponensial dengan Antrian Terbatas

Pada model ini panjang garis (line length) tidak boleh melebihi sejumlah tertentu (dinyatakan dengan M). Setiap langganan yang datang pada saat antrian sudah penuh, harus meninggalkan sistem tanpa mendapat pelayanan. Jadi, model ini adalah kasus khusus dari proses kelahiran-kematian, dimana:

¯

®

­

t

M

n

jika

,

0

1

M

...,

,

2

,1

,

0

n

jika

,

n

O

O

dan

P

_n

P

untuk n = 1, 2, …. Steady State dicapai sebagai berikut:

1 M 0

1

1

P

U

U

sehingga:

n 1 M n

1

1

P

U

U

U

¸¸

¹

·

¨¨

©

§

untuk n = 0, 1, 2, …, M

1 M 1 M S

1

1

M

1

L

U

U

U

U

Dengan S = 1 maka

L

_q

L

_S

1

P

₀

Di sini tidak perlu

O

P

Ekspektasi waktu menunggu adalah:

O

S S

L

W

,

O

q q

L

W

Dimana:

M

1 M 0 n n 0 n n n

P

1

P

P

_¦

¦

f

O

O

O

O

2.9.2 Model-Model Multiple Server (S>1)

2.9.2.1 Input Poisson dan Waktu Pelayanan Eksponensial Model ini mengasumsikan bahwa kedatangan terjadi menurut input poisson dengan parameter

O

, dan bahwa waktu pelayanan untuk masing-masing unit mempunyai distribusi eksponensial dengan rata-rata

O

1

. Jadi, distribusi waktu pelayanan sama, tanpa memperhatikan pelayanan mana dari sejumlah S pelayan yang melakukan pelayanan untuk unit.

Tingkat pelayanan rata-rata untuk seluruh sistem antrian adalah tingkat rata-rata dimana unit yang sudah dilayani meninggalkan

sistem, dan bergantung pada state sistem

E

_n. Tingkat pelayanan rata-rata per pelayanan yang sibuk adalah

P

, karena itu tingkat pelayanan keseluruhan adalah

P

_n

n

P

jika

n

d

S

. Jika

n

t

S

, berarti semua pelayan sibuk sehingga

P

_n

S

P

. Jadi, model ini adalah kasus khusus dari proses kelahiran-kematian dengan

O

_n

O

(untuk n=0, 1, 2, …) dan

¯

®

­

t

d

d

S

n

jika

,

S

S

n

0

jika

,

n

n

P

P

P

Jika

O

S

P

(tingkat kedatangan rata-rata lebih kecil dari tingkat pelayanan rata-rata maksimum), maka hasil steady state-nya adalah:

¦

¦

f

¸¸

¹

·

¨¨

©

§

1 S 0 n n S S n S n 0

S

!

S

!

n

1

P

P

O

P

O

P

O

¦

1

S 0 n S n 0

S

1

1

!

S

!

n

1

P

P

O

P

O

P

O

dan

°

°

¯

°

°

®

­

t

d

d

P

jika

n

S

S

!

S

S

n

0

jika

P

!

n

P

0 S n n 0 n n

P

O

P

O

Dengan

U

O

S

P

, maka

2 S 0 q

1

!

S

P

L

U

U

P

O

O

q q

L

W

P

1

W

W

_{S q}

P

O

P

O

_¸¸

¹

·

¨¨

©

§

q q S

L

1

W

L

Untuk mendapatkan distribusi kemungkinan dari waktu menunggu, asumsikan bahwa disiplin pelayanannya FCFS. Notasi standar P(>t) digunakan untuk menyatakan probabilitas bahwa suatu kedatangan random harus menunggu dalam antrian (sebelum dilayani) adalah lebih besar dari t. Jelas bahwa penungguan dalam antrian ini terjadi jika ada S atau lebih unit di dalam sistem.

U

P

O

U

P

O

!

_¦

f

_¦

f

1

!

S

P

!

S

P

P

0

P

S 0 0 j j S 0 S n n U P

!

_t

_e

S t1

P

P(>0)

Jika variabel random WS adalah waktu menunggu termasuk

pelayanan dari suatu kedatangan random, maka (untuk t

t

0):

»

»

¼

º

«

«

¬

ª

¸¸

¹

·

¨¨

©

§

!

P

O

U

P

O

P OP P

1

S

e

1

1

!

S

P

1

e

t

W

P

t S 1 S 0 S t

Jika Wq adalah variabel waktu menunggu dalam antrian (tidak

termasuk waktu pelayanan) dari suatu kedatangan random, maka untuk

0

_!

>

@

SP t1 U q q

t

1

P

W

0

e

W

P

Dimana:

S

¦

1 0 n n q

0

P

W

P

Jika

S

1

O

P

0

maka

O

P

P O P

1

S

e

1

t S 1 diganti dengan

P

t

.

2.9.2.2 Input Poisson dan Waktu Pelayanan Eksponensial dengan Antrian Terbatas

Pada model ini panjang garis tidak boleh melebihi sejumlah tertentu M. Jadi, merupakan kasus khusus dari proses kelahiran-kematian, dimana:

¯

®

­

t

M

n

jika

,

0

M

n

0

jika

,

n

O

O

¯

®

­

t

d

d

S

n

jika

,

S

S

n

0

jika

,

n

n

_P

P

P

Jadi:

_{^ `}

°

°

°

°

¯

°°

°

°

®

­

!

d

d

d

M

n

jika

,

0

M

n

S

jika

,

P

S

!

S

M

,

S

min

n

jika

,

P

!

n

P

_{n S 0} n 0 n n

P

O

P

O

Dimana:

^ `

¦

¦

¸¸

¹

·

¨¨

©

§

M 1 S n S n S M , S min 0 n n 0

S

!

S

!

n

1

P

P

O

P

O

P

O

Jika

M

d

S

, biasanya

L

_q

0

dan

¦

M 0 n n S

n

P

L

Jika

M

!

S

, maka

U

>

U

U

U

@

U

P

O

_M

_S

₁

1

1

!

S

P

L

₂ M S M S S 0 q dan

¸

¹

·

¨

©

§

_¦

¦

S1 0 n n q 1 S 0 n n S

n

P

L

S

1

P

L

WS dan Wq dicari dengan cara yang sama seperti pada model

2.9.2.3 Model Sumber Terbatas

Model ini merupakan kasus-kasus dari proses kelahiran-kematian, dimana:

¯

®

­

t

d

M

n

jika

,

0

M

n

jika

,

n

M

n

O

O

¯

®

­

t

d

d

S

n

jika

,

S

S

n

0

jika

,

n

n

_P

P

P

Maka:

°

°

°

¯

°

°

°

®

­

!

d

d

d

d

M

n

jika

0

M

n

S

jika

S

!

S

!

n

M

!

M

P

S

n

0

jika

!

n

!

n

M

!

M

P

P

_{0 n S} n n 0 n

O

P

P

O

Dimana:

¦

¦

M S n n S n 1 S 0 n n 0

S

!

S

!

n

M

!

M

!

n

!

n

M

!

M

1

P

P

O

P

O

n M S n q

n

S

P

L

_¦

¸

¹

·

¨

©

§

_¦

¦

S1 0 n n q 1 S 0 n n S

n

P

L

S

1

P

L

O

L

W

_S ;

O

Q q

L

W

dimana

M

L

O

O

2.9.2.4 Model dengan State dimana Tingkat Pelayanan dan atau Tingkat Kedatangan Bersifat Dependent

Pada model single server, tingkat pelayanan rata-rata untuk kasus ini diperoleh dengan mengalihkan tingkat pelayanan rata-rata “normal”, yaitu tanpa tekanan, dengan nc dimana n adalah langganan dalam sistem dan c adalah “koefisien tekanan”. Jika seluruh pelayan (sejumlah S) sedang sibuk sehingga bekerja dengan tekanan, maka tingkat pelayanan rata-ratanya harus dikalikan dengan (n/S)c karena n/S merupakan jumlah langganan dalam sistem per pelayan. Dengan demikian maka:

°¯

°

®

­

t

d

S

n

jika

S

S

n

S

n

jika

n

1 c 1 n

P

P

P

Jika kemudian diasumsikan bahwa sistem antrian mempunyai input Poisson dengan

O

_n

O

(untuk n = 0, 1, 2, …) dan waktu pelayanan eksponensial dengan

P

_n seperti di atas, maka modelnya akan menjadi kasus khusus yang lain dari proses kelahiran-kematian. Hasil steady state-nya adalah:

°

°

¯

°

°

®

­

t

d

P

jika

n

S

S

S

!

n

!

S

S

n

jika

P

!

n

P

0 S n c 1 c n 1 0 n 1 n

P

O

P

O

Dimana:

_¦

¦

f

»

¼

º

«

¬

ª

S n c n c 1 1 c 1 S 1 S 0 n n 1 0

!

n

S

!

S

S

!

n

1

P

P

O

P

O

Karena itu, maka:

¦

¦

f f

¸¸

¹

·

¨¨

©

§

S n c n c 1 1 c 1 S 0 S n n q

!

n

S

!

S

S

P

P

S

n

L

O

P

¸

¹

·

¨

©

§

_¦

¦

S1 0 n n q 1 S 0 n n S

n

P

L

S

1

P

L

O

q q

L

W

,

O

S S

L

W

Model ini dapat juga digeneralisasi untuk memungkinkan tingkat kedatangan rata-rata “melakukan reaksi” terhadap garis panjang antrian dengan cara yang sama dengan pada model single server, untuk itu ditetapkan:

°¯

°

®

­

t

d

S

n

jika

S

S

n

S

n

jika

n

1 a 1 n

_P

P

P

°¯

°

®

­

t

d

1

S

n

jika

1

n

S

1

S

n

jika

1 b 1 n

O

O

O

Proses kelahiran-kematian dengan parameter-parameter ini menghasilkan Pn, Lq, dan Ls yang sama dengan di atas jika c = a + b. 2.10 Model Keputusan

Analisa teori antrian bukanlah suatu teknis optimasi langsung seperti programa linier atau sejenisnya. Analisa pada teori antrian dipakai untuk mendapatkan harga-harga dari sistem yang dianalisis, misalnya parameter rata-rata jumlah kedatangan pada suatu interval tertentu atau harga parameter rata-rata waktu pelayanan yang diberikan pada setiap konsumen yang membentuk barisan antrian, atau juga parameter waktu menunggu, parameter panjang antrian, dan parameter utilitas fasilitas pelayanan, kedua parameter ini dibandingkan akan menunjukkan kondisi dari sistem yang diambil.

Salah satu pendekatan yang dipakai untuk meningkatkan performansi suatu sistem yaitu untuk mengoptimalkan hasil yang diinginkan, optimasi parameter sistem dapat dilakukan dengan dua cara, pertama model minimasi ongkos dan yang kedua model aspirasi. Model minimasi ongkos dapat dipakai jika ongkos waktu pelayanan dan ongkos waktu menunggu pelayanan ditentukan besarnya. Akan tetapi cara ini umumnya sulit untuk dilakukan karena ongkos waktu menunggu bagi setiap konsumen akan sangat berbeda besarnya, apalagi untuk sistem dengan input yang sangat beraneka ragam. Cara yang kedua dikenal dengan model level aspirasi. Model ini digunakan untuk menentukan nilai optimal sistem. Nilai optimal dalam metode ini didesain secara langsung dari harga-harga parameternya dengan anggapan bahwa

keputusan yang diambil adalah optimal jika memenuhi batas-batas aspirasi yang diharapkan oleh pengambil keputusan atau pertimbangan preferensi tertentu.

2.10.1 Model Ongkos

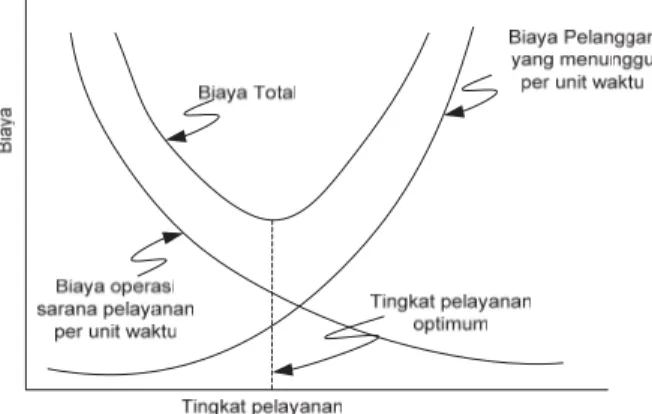
Model-model biaya, seperti diperlihatkan dalam Gambar 2.8, pada dasarnya menyeimbangkan kedua jenis biaya yang bertentangan berikut ini:

1. Biaya menunggu

Biaya menunggu mencakup biaya menganggurnya karyawan, kehilangan penjualan, tingkat persediaan yang berlebihan, kehilangan kontrak dan lain-lain. Biaya menunggu tidak selalu mudah ditentukan, bahkan sangat sulit. Dalam kasus-kasus tertentu seperti bila individu-individu yang menunggu berasal dari sistem interval (misal persediaan) biaya menunggu dapat langsung diukur.

2. Biaya pelayanan

Walaupun biaya menunggu dapat dikurangi dengan cara menambahkan fasilitas pelayanan, tetapi hal ini akan menaikkan biaya persediaan fasilitas pelayanan. Biaya pelayanan dapat mencakup investasi awal dalam peralatan atau fasilitas, biaya pemasangan fasilitas, latihan bagi karyawan dan biaya-biaya variabel seperti gaji karyawan dan pengeluaran tambahan untuk pemeliharaan.

Gambar 2.8 Model Keputusan Ongkos Total

Teori antrian dengan model ongkos dapat juga digunakan untuk menentukan kecepatan pelayanan dan jumlah fasilitas pelayanan yang optimal. Dalam menentukan kecepatan pelayanan dan jumlah fasilitas pelayanan yang optimum diperlukan dua jenis ongkos, yaitu:

1. Ongkos pelayanan tiap pelanggan yang dikaitkan dengan penggunaan fasilitas pelayanan per satuan waktu (C1)

2. Ongkos menunggu pelayanan per satuan waktu per konsumen (C2)

Ada dua model optimum biaya yang digunakan dalam menentukan biaya yang optimal, yaitu (Hamdy A. Taha,1996):

1. Laju Pelayanan Optimum

Menentukan nilai optimum dari tingkat pelayanan, dengan model matematikanya adalah:

O

P

O

P

P

₂ 1

C

C

TC

1 2

C

C

O

O

P

Keterangan:

C1 = Biaya pelanggan yang menunggu per unit waktu

C2 = Biaya operasi sarana pelayanan per unit waktu

TC = Biaya total

P = Tingkat pelayanan rata-rata O = Tingkat kedatangan

Sehingga jumlah ongkos menunggu dan melayani per satuan waktu dengan diketahui bahwa laju pelayanan adalah P sehingga:

^

C

`

C

1

C

2

L

S

T

P

u

P

u

C1u P = ongkos pelayanan per satuan waktu

C2u LS = ongkos menunggu pelanggan 2. Jumlah Pelayanan Optimum

Model ongkos yang akan dikembangkan ialah menyangkut jumlah pelayanan optimal C. Dianggap bahwa O dan P adalah tetap, sehingga:

c

L

C

C

c

c

TC

u

₁

₂

u

_S

Dan LS (c) berlaku untuk sistem dengan pelayanan

ganda. Karena c adalah diskrit maka pendeferensialan tidak mungkin dilakukan. Meskipun demikian jumlah c optimum tetap dapat ditemukan dengan substitusi langsung harga-harga

C secara berturut-turut sampai harga T{(c)} minimum dapat ditentukan.

Untuk membuat prosedur perhitungan lebih efisien, harus ditentukan syarat perlu untuk harga minimum fungsi yang diketahui.

Syarat perlu itu adalah:

^

C

c

1

`

TC

c

T

t

dan

T

^

C

c

1

`

t

TC

c

Dari syarat itu dapat diketahui bahwa:

c

Ls

Ls

C

C

1 c 2 1

_d

dan c 1 2 1

_Ls

_c

_Ls

C

C

t

Dengan demikian hasil akhirnya adalah:

c

Ls

Ls

C

C

Ls

c

Ls

_{c 1} 2 1 1 c

d

d

Ls(c) = ekspektasi jumlah pelanggan dalam sistem

Dimana harga

2 1

C

C

memberikan petunjuk ke arah mana pencarian harga c optimum.

2.10.2 Model Level Aspirasi

Model tingkat aspirasi menyadari kesulitan dalam mengestimasi parameter biaya, dan karena itu model ini didasari oleh analisis yang lebih sederhana. Model ini secara langsung memanfaatkan karakteristik yang terdapat dalam sistem yang bersangkutan dalam memutuskan nilai-nilai “optimal” dari parameter perancangan. Optimalitas di sini dipandang dalam arti memenuhi tingkat aspirasi tertentu yang ditentukan oleh pengambil keputusan. Tingkat aspirasi

didefinisikan sebagai batas atas dari nilai-nilai ukuran yang saling bertentangan, yang ingin diseimbangkan oleh pengambil keputusan tersebut.

Dalam model pelayan berganda dimana kita perlu menentukan jumlah pelayan c yang optimum, dua ukuran yang bertentangan adalah:

1. Waktu menunggu yang diperkirakan dalam sistem Ws.

2. Persentase waktu menganggur para pelayan X.

Kedua ukuran ini mencerminkan aspirasi pelanggan dan pelayan. Anggaplah tingkat aspirasi (batas atas) untuk Ws dan X

diketahui

D

dan

E

. Maka metode tingkat aspirasi dapat diekspresikan secara matematis sebagai berikut:

Tentukan jumlah pelayan sedemikian rupa sehingga

D

d

s

W

dan

X

d

E

Ekspresi untuk Ws diketahui dari analisis model antrian.

Ekspresi untuk X diketahui:

¸

¹

·

¨

©

§

¦

c

n

P

100

1

_c

c

100

X

c 0 n n

U

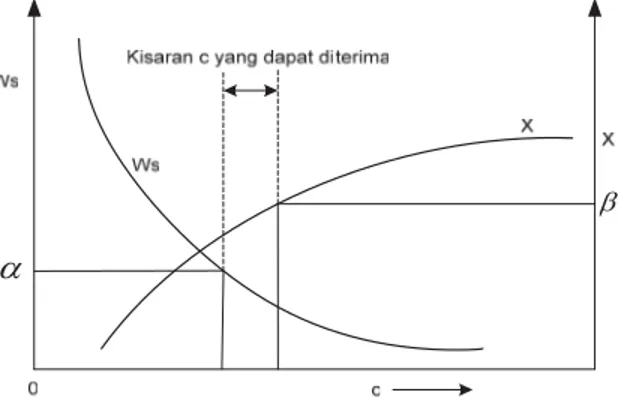
Untuk membatasi dalam mengambil keputusan spesifik dalam kasus metode tingkat aspirasi, kita dapat menghitung kisaran parameter biaya C2 yang dihasilkan dari pemilihan c untuk tingkat aspirasi tertentu

seperti diperlihatkan dalam Gambar 2.9. Kita secara spesifik memilih C2

dan bukan C1, karena biasanya lebih sulit untuk mengestimasi biaya

menunggu dalam kebanyakan model-model antrian. Prosedur yang kami berikan di sini karena itu mengasumsikan bahwa C1, biaya tambahan

yang berkaitan dengan memperoleh satu pelayan baru, dapat diestimasi tanpa banyak kesulitan.

D

E

Gambar 2.9 Model Keputusan Tingkat Aspirasi

2.11 Pengujian Hasil Pengumpulan Data 2.11.1 Uji Keseragaman Data

Selain pengujian kecukupan data, juga dilakukan pengujian keseragaman data, yang tujuannya adalah untuk mengetahui apakah data-data yang diambil sudah seragam atau belum. Yang harus diperhatikan dalam pengujian keseragaman data ini adalah data yang berada di dalam batas-batas kontrol, sehingga dimasukkan dalam perhitungan. Sedangkan data-data yang berada di luar batas kontrol harus dibuang karena berasal dari sistem sebab yang berbeda. Pada perhitungan selanjutnya semua data dalam sub grup ini tidak ikut diperhitungkan. Adapun langkah-langkahnya adalah sebagai berikut (Ronald E. Walpole et al, 1995):

k

X

X

¦

i

Dimana: Xi = harga rata-rata sub grup ke-i k = banyak sub grup yang terbentuk

2. Hitung standar deviasi sebenarnya dari waktu penyelesaian

1

N

X

X

_i 2

¦

V

Dimana: N = jumlah pengamatan pendahuluan

3. Hitung standar deviasi harga rata-rata sub grup

n

X

V

V

Dimana: n = besarnya sub grup

4. Tentukan batas kontrol atas (BKA) dan batas kontrol bawah (BKB) X

2

X

BKA

V

X

2

X

BKB

V

2.11.2 Uji Kecukupan Data

Pengujian ini dilakukan untuk mengetahui apakah data yang sudah terkumpul itu sudah mencukupi maka perlu dilakukan uji kecukupan data. Jika menurut hasil perhitungan pada pengamatan belum

mencukupi maka harus dilakukan pengambilan data kembali. Dalam pengujian ini dilakukan dengan membandingkan antara N’ (N hitung) dengan N (jumlah pengamatan) dengan menggunakan tingkat ketelitian (

D

) sebesar 5% dan tingkat keyakinan (

E

) 95% dengan rumus (Ronald E. Walpole et al, 1995):

2 i 2 i 2 i

X

X

X

N

Z

'

N

»

»

¼

º

«

«

¬

ª

¦

¦

¦

D

Dimana:

N’ = banyaknya pengukuran yang diperlukan untuk suatu tingkat ketelitian dan keyakinan tertentu. Tingkat ketelitian (

D

) sebesar 5% dan tingkat keyakinan (

E

) 95% pengukur membolehkan hasil pengukurannya menyimpang 5% dari rata-rata sebenarnya dan kemungkinan berhasil mendapatkan 95%.

N = jumlah pengamatan pendahuluan yang dilakukan.

Xi = waktu penyelesaian teramati selama pengamatan pendahuluan yang telah dilakukan.

Untuk menentukan nilai dari Z bisa dilakukan interpolasi dan untuk menentukan besarnya nilai dapat dilihat dari tabel statistik.

Apabila N’ lebih kecil atau sama dengan N maka sampel yang diambil telah mencukupi, tetapi apabila N’ lebih besar atau sama dengan N maka sampel yang diambil belum mencukupi, sehingga harus

dilakukan pengumpulan data kembali sampai data benar-benar mencukupi.

2.11.3 Pengujian Bentuk Distribusi

Dalam memecahkan masalah antrian menggunakan teori antrian, salah satu syarat yang harus diketahui adalah bentuk distribusi kedatangan dan waktu pelayanan konsumen. Tujuannya adalah untuk menentukan model antrian yang digunakan, untuk menganalisa bentuk distribusi tes hipotesa “Goodness of Fit”. Sebelum dilakukan pengujian bentuk distribusi, sebaiknya perlu diketahui gambaran data hasil pengamatan dalam bentuk distribusi frekuensi.

Untuk membuat daftar kelas frekuensi dengan panjang kelas yang sama dilakukan sebagai berikut (Ronald E Walpole et al, 1995):

1. Tentukan rentang dengan cara mengurangi data terbesar dengan data terkecil.

2. Tentukan banyak kelas interval yang diperlukan, banyak kelas sering biasanya diambil paling sedikit 5 kelas dan paling banyak 15 kelas, dipilih menurut keperluan. Cara lain untuk menentukan banyak kelas interval adalah dengan menggunakan aturan sturges, yaitu:

Banyak kelas = 1 + (3.3) log n

Dimana n = banyaknya data dan hasil akhir dijadikan bilangan bulat

3. Tentukan panjang kelas interval (p):

kelas

banyak

g

tan

ren

kelas

Panjang

4. Menentukan titik tengah tiap interval kelas.

5. Titik tengah kelas interval ditentukan dengan menjumlahkan batas kelas atas dan batas kelas bawah setiap interval kelas, kemudian dibagi dua atau batas kelas bawah ditambah lebar kelas interval dibagi dua, rumusnya adalah sebagai berikut:

2

BKA

BKB

X

i i ti

Dimana: Xti = nilai tengah kelas ke-i BKBi = batas kelas bawah ke-i BKAi = batas kelas atas ke-i i = 1, 2, 3, …, k

Untuk data yang telah disusun ke dalam daftar distribusi frekuensi maka rata-ratanya dihitung dengan rumus:

¦

¦

¦

i i i

f

Xt

f

X

Dimana:

X

= harga rata-rata

Fi = frekuensi dari kelas ke-i Xti = nilai tengah kelas interval ke-i

2.11.4 Uji Kesesuaian (Goodness of Fit Test)

Uji kesesuaian adalah suatu cara untuk memeriksa apakah suatu himpunan data mentah tertentu sesuai dengan distribusi teoritis tertentu dengan cara membandingkan secara grafik distribusi empiris

kumulatif dengan fungsi kepadatan kumulatif yang bersesuaian dengan distribusi yang bersangkutan. Jika kedua fungsi tersebut tidak memperhatikan deviasi berlebihan maka terdapat kemungkinan yang cukup besar bahwa distribusi teoritis ini sesuai dengan data mentah tersebut.

Uji Chi-Kuadrat

Uji chi-kuadrat berlaku untuk variabel acak diskrit kontinyu yang didasari oleh perbandingan fungsi kepadatan probabilitas, dari pada fungsi kepadatan kumulatif yang pengukuran jumlah deviasi antara fungsi kepadatan empiris dan teoritis.

Langkah-langkah uji chi-kuadrat untuk uji kesesuaian sebagai berikut (Ronald E. Walpole et al, 1995):

¾ Menentukan hipotesa awal H0 melawan Hi

Dimana untuk pengujian distribusi kedatangan:

H0 = distribusi kedatangan pada interval waktu hasil

pengamatan mengikuti distribusi poisson.

Hi = distribusi kedatangan pada interval waktu hasil

pengamatan tidak mengikuti distribusi poisson. ¾ Menentukan tingkat signifikasi/ketelitian tertentu (

D

)

D

ini sebagai simbol dari tipe 1 dalam pengujian hipotesis artinya adalah menolak hipotesis yang seharusnya diterima. Untuk taraf signifikasi ini biasanya digunakan

D

= 0.05 atau

D

= 0.01.

¦

k

1 i i 2 i i 2

e

e

f

F

Dimana:

fi = frekuensi hasil pengamatan pada kelas interval ke-i

ei = frekuensi ekspektasi (harapan) teoritis pada kelas

interval ke-i

k = jumlah kelas interval

N = banyaknya data/jumlah data pengamatan ¾ Membandingkan F2hitung dengan F2tabel:

Pengujian uji chi-kuadrat ini menggunakan derajat kebebasan

v = k – m – 1, dimana:

k = banyaknya kelas interval (sel)

Bila frekuensi amatan dekat dengan frekuensi harapan padanannya, maka nilai F2 akan kecil, menunjukkan kesesuaian yang baik. Bila frekuensi amatan cukup berbeda dengan frekuensi harapan maka nilai F2 akan besar dan kesesuaian jelek. Kesesuaian yang baik akan mendukung permintaan H0, sedangkan kesesuaian yang jelek

mendukung penolakannya. Daerah kritis akan terjadi pada ujung kanan distribusi chi-kuadrat. Untuk taraf keberartian

D

, ditemukan nilai kritis

2

D

F

dari tabel L.5 maka

F

2

!

F

_D2 menyatakan daerah kritis. Patokan keputusan yang diuraikan di sini sebaiknya tidak dipakai kecuali bila tiap frekuensi harapan paling sedikit sebesar 5. Dalam hal kurang dari 5 maka mungkin diperlukan penggabungan sel yang berdampingan yang mengakibatkan pengurangan dalam besarnya derajat kebebasan.