BAB II
TINJAUAN PUSTAKA
2.1. Definisi Torsi
Erwin (2009) berpendapat bahwa torsi adalah puntir yang terjadi pada
batang lurus apabila batang tersebut dibebani momen yang cenderung menghasilkan rotasi terhadap sumbu longitudinal batang. Sebagai contoh dalam
kehidupan sehari-hari yaitu jika seseorang memutar obeng, maka tangannya memberikan torsi ke obeng.
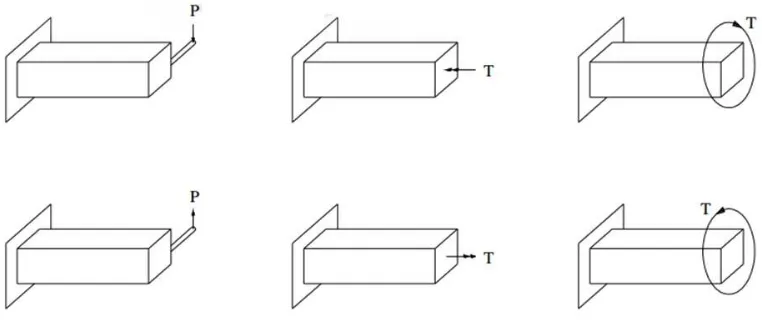
Gambar 2.1 Arah kerja torsi sesuai kaidah tangan kanan dan panah lengkung
Demikian pula halnya dengan komponen struktur suatu bangunan. Jika diperhatikan lebih seksama, sebenarnya balok-balok pada bangunan mengalami torsi akibat beban-beban pada pelat. Demikian pula halnya dengan kolom. Namun
torsi pada kolom kebanyakan diakibatkan oleh gaya-gaya yang arahnya horizontal seperti gaya angin ataupun gempa. Berikut ini beberapa ilustrasi yang
memperlihatkan adanya torsi yang terjadi pada balok dan kolom.
▸ Baca selengkapnya: seorang pekerja pada bangunan menaikkan pasir dengan cara seperti terlihat pada gambar berikut
(2)dari statika, momen kopel merupakan hasil kali dari gaya dan jarak tegak lurus
antara garis kerja gaya. Satuan untuk momen pada USCS adalah ft) dan (lb-in), sedangkan untuk satuan SI adalah (N.m).
Untuk mudahnya, momen kopel sering dinyatakan dengan vektor dalam bentuk panah berkepala ganda. Panah ini berarah tegak lurus bidang yang mengandung kopel, sehingga dalam hal ini kedua panah sejajar dengan sumbu
batang. Arah momen ditunjukkan dengan kaidah tangan kanan untuk vektor momen yaitu dengan menggunakan tangan kanan, empat jari selain jempol dilipat
untuk menunjukkan momen sehingga jempol akan menunjuk arah vektor. Representasi momen yang lain adalah dengan menggunakan panah lengkung yang
mempunyai arah torsi.
Momen yang menghasilkan puntir pada suatu batang disebut momen puntir atau momen torsi. Batang yang menyalurkan daya melalui rotasi disebut
poris atau as (shaft). Dalam tugas akhir ini, shaft yang akan dibahas secara khusus adalah shaft yang dalam bidang teknik struktur bangunan banyak dijumpai yaitu pada balok dan kolom struktur beton bertulang.
2.2. Elastisitas
Elastisitas ialah sifat suatu bahan apabila gaya luar mengakibatkan
perubahan bentuk (deformation) tidak melebihi batas tertentu, maka perubahan bentuk akan hilang setelah gaya dilepas. Hampir semua bahan teknik memiliki sifat elastisitas ini (Erwin,2009).
Dalam pembahasan torsi dalam tugas akhir ini, bahan-bahan akan dianggap bersifat elastis sempurna yaitu benda akan kembali seperti semula secara
2.3. Tegangan
Tegangan didefinisikan sebagai intensitas gaya yang bekerja pada tiap
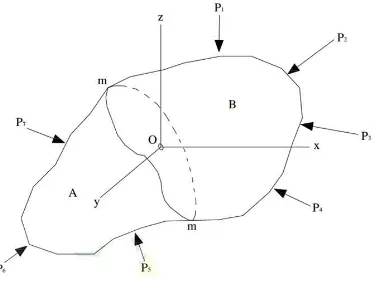
satuan luas bahan. Untuk menjelaskan ini, maka akan ditinjau sebuah benda yang dalam keadaan setimbang seperti terlihat pada Gambar 2.2. Akibat kerja gaya luar
, dan , maka akan terjadi gaya dalam di antara benda. Untuk
mempelajari besar gaya ini pada titik sembarang O, maka benda diandaikan dibagi menjadi dua bagian A dan B oleh penampang mm yang melalui titik O
(Erwin,2009).
Gambar 2.2. Benda Tampang Sembarang yang Dibebani Oleh Gaya-gaya Luar
Kemudian tinjaulah salah satu bagian ini, misalnya A. Bagian ini dapat
dinyatakan dalam keadaan setimbang akibat gaya luar , dan ,
bahan. Oleh karena intensitas distribusi ini, tegangan dapat diperoleh dengan
membagi gaya tarik total P dengan luas potongan penampang A.
Untuk memperoleh besar gaya yang bekerja pada luasan kecil δA,
misalnya dari potongan penampang mm pada titik O, dapat diamati bahwa gaya yang bekerja pada elemen luas ini diakibatkan oleh kerja bahan bagian B terhadap bagian A yang dapat diubah menjadi sebuah resultante δP. Apabila tekanan
diberikan pada luas elemen δA, harga batas δP/ δA akan menghasilkan besar tegangan yang bekerja pada potongan penampang mm pada titik O dan arah batas
resultante δP adalah arah tegangan.
Umumnya arah tegangan ini miring terhadap luas δA tempat gaya bekerja sehingga dapat diuraikan menjadi dua komponen tegangan yaitu tegangan normal
yang tegak lurus terhadap luas dan tegangan geser yang bekerja pada bidang luas δA.
Tegangan normal dinotasikan dengan huruf dan tegangan geser dengan
huruf . Untuk menunjukkan arah bidang dimana tegangan tersebut bekerja,
digunakan subscript terhadap huruf-huruf ini. Tegangan normal menggunakan sebuah subscript yang menunjukkan arah tegangan yang sejajar terhadap sumbu
koordinat tersebut, sedangkan tegangan geser menggunakan dua buah subscript dimana huruf pertama menunjukkan arah normal terhadap bidang yang ditinjau
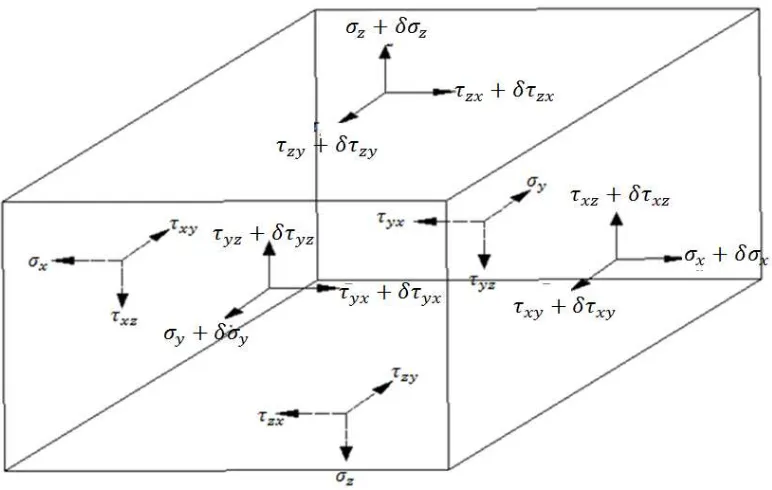
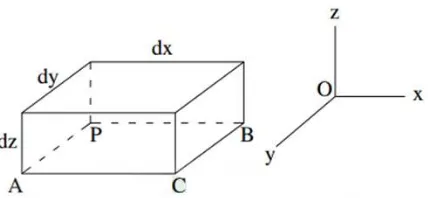
Gambar 2.3. Komponen-komponen Tegangan yang Bekerja pada Kubus Kecil
Untuk menjelaskan tegangan yang bekerja pada keenam sisi elemen ini
diperlukan tiga simbol untuk tegangan normal dan simbol
untuk tegangan geser. Dengan meninjau kesetimbangan elemen secara sederhana, maka jumlah simbol tegangan geser dapat dikurangi
menjadi tiga
.
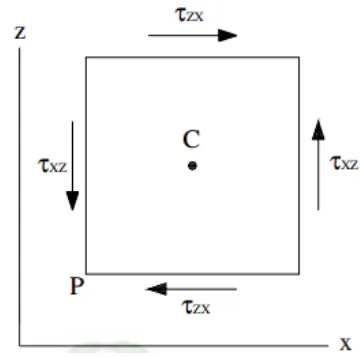
Apabila momen gaya yang bekerja pada elemen terhadap garis yang
melalui titik tengah C dan sejajar sumbu x, maka hanya tegangan permukaan yang diperlihatkan pada Gambar 2.4. yang perlu ditinjau. Gaya benda, seperti berat
elemen, dapat diabaikan karena semakin kecil ukuran elemen, maka gaya benda yang bekerja padanya berkurang sebesar ukuran linier pangkat tiga. Sedangkan gaya permukaan berkurang sebesar ukuran linear kuadrat. Oleh karena itu, untuk
elemen yang sangat kecil, besar gaya benda sangat kecil jika dibandingkan dengan gaya permukaan sehingga dapat dihilangkan ketika menghitung momen.
Dengan cara yang sama, orde momen akibat ketidak-merataan distribusi gaya normal lebih tinggi dibandingkan dengan orde momen akibat gaya geser dan
menjadi nol dalam limit. Juga gaya pada masing-masing sisi dapat ditinjau sebagai luas sisi kali tegangan di tengah. Jika ukuran elemen kecil pada Gambar 2.4. adalah dx, dy, dz, maka momen gaya terhadap P, maka persamaan
kesetimbangan elemen ini adalah :
(2.1)
Dua persamaan lain dapat diperoleh dengan cara yang sama sehingga didapatkan :
(2.2)
Dengan demikian enam besaran
cukup untuk menjelaskan tegangan yang bekerja pada koordinat bidang
Jika kubus pada Gambar 2.3. diberikan suatu komponen gaya per satuan
volume sebesar X, Y, Z pada masing-masing sumbu x, y, dan z maka gambar komponen tegangan dalam Gambar 2.3. akan menjadi seperti pada Gambar 2.5. di
bawah ini.
Gambar 2.5. Komponen-komponen Tegangan yang bekerja pada kubus kecil dimana Gaya Luar per Satuan Volume yang Bekerja
Sesudah dibagi dengan , maka akan didapatkan persamaan
kesetimbangan yaitu:
Persamaan (2.3) ini harus dipenuhi di semua titik di seluruh volume benda.
Tegangan berubah di seluruh volume benda, dan apabila sampai pada permukaan, tegangan-tegangan ini harus sedemikian rupa sehingga setimbang dengan gaya
luar yang bekerja pada permukaan benda (Timoshenko, S., 1958).
2.4. Regangan
Erwin (2009) menyatakan bahwa regangan didefinisikan sebagai suatu perbandingan antara perubahan dimensi suatu bahan dengan dimensi awalnya.
Karena merupakan rasio antara dua panjang, maka regangan ini merupakan besaran tak berdimensi, artinya regangan tidak mempunyai satuan. Dengan
demikian, regangan dinyatakan hanya dengan suatu bilangan, tidak bergantung pada sistem satuan apapun. Harga numerik dari regangan biasanya sangat kecil karena batang yang terbuat dari bahan struktural hanya mengalami perubahan
panjang yang kecil apabila dibebani.
Dalam membahas perubahan bentuk benda elastis, selalu dianggap bahwa benda terkekang sepenuhnya sehingga tidak bisa bergerak sebagai benda kaku
sehingga tidak mungkin ada perpindahan partikel benda tanpa perubahan bentuk benda tersebut.
Pada pembahasan ini yang ditinjau hanya perubahan bentuk yang kecil yang biasa terjadi pada struktur teknik. Perpindahan kecil partikel yang berubah bentuk ini diuraikan ke dalam komponen u, v, w berturut-turut sejajar dengan
Gambar 2.6. Elemen Kecil Berdimensi dx dy dz
Tinjau elemen kecil dx dy dz dari sebuah benda elastis seperti terlihat pada Gambar 2.6. Apabila benda mengalami perubahan bentuk dan u, v, w merupakan komponen perpindahan titik P, perpindahan titik di dekatnya, A, dalam arah x
pada sumbu x adalah orde pertama dalam dx, yaitu u + (δu/δx) dx akibat pertambahan fungsi u sebesar (δu/δx) dx sesuai dengan pertambahan panjang
elemen PA akibat perubahan bentuk adalah (δu/δx) dx. Sedangkan satuan perpanjangan (unit elongation) pada titik P dalam arah x adalah (δu/δx). Dengan cara yang sama, maka diperoleh satuan perpanjangan dalam arah y dan z adalah (δv/δy) dan (δw/δz).
Sekarang tinjaulah pelentingan sudut antara elemen PA dan PB dalam
Gambar 2.7. Apabila u dan v adalah perpindahan titik P dalam arah x dan y, perpindahan titik A dalam arah y dan titik B dalam arah x berturut-turut adalah v + (δv/δx) dx dan u + (δu/δy) dy. Akibat perpindahan ini, maka P’A’ merupakan arah
baru elemen PA yang letaknya miring terhadap arah awal dengan sudut kecil yang ditunjukkan pada gambar, yaitu sama dengan (δv/δx). Dengan cara yang sama arah P’B’ miring terhadap PB dengan sudut kecil (δu/δy). Dari sini dapat dilihat
bahwa sudut awal APB yaitu sudut antara kedua elemen PA dan PB berkurang
sebesar (δv/δx) + (δu/δy). Sudut ini adalah regangan geser (shearing strain) antara bidang xz dan yz. Regangan geser antara bidang xy dan xz dan yx dan yz
dapat diperoleh dengan cara yang sama.
Selanjutnya kita menggunakan huruf untuk satuan perpanjangan dan
huruf y untuk regangan geser. Untuk menunjukkan arah regangan digunakan subscript yang sama terhadap huruf ini sama seperti untuk komponen tegangan.
Kemudian diperoleh dari pembahasan di atas beberapa besaran berikut:
(2.4)
2.5. Hukum Hooke
Hubungan linear antara komponen tegangan dan komponen regangan umumnya dikenal sebagai hukum Hooke. Satuan perpanjangan elemen hingga
batas proporsional diberikan oleh:
(2.5)
dimana E adalah modulus elastisitas dalam tarik (modulus of elasticity in
tension).
Bahan yang digunakan di dalam struktur biasanya memiliki modulus yang sangat besar dibandingkan dengan tegangan izin, dan besar perpanjangannya
sangat kecil. Perpanjangan elemen dalam arah x ini akan diikuti dengan pengecilan pada komponen melintang yaitu
(2.6)
dimana adalah suatu konstanta yang disebut dengan ratio Poisson (Poisson’s Ratio). Untuk sebagian besar bahan, ratio poisson dapat diambil sama dengan
0,25. Untuk struktur baja biasanya diambil sama dengan 0,3.
Apabila elemen di atas mengalami kerja tegangan normal secara
serempak, terbagi rata di sepanjang sisinya, komponen resultante regangan dapat diperoleh dari persamaan (2.5) dan (2.6) yaitu:
[ ( )]
[ ] (2.7)
[ ( )]
Pada persamaan (2.7), hubungan antara perpanjangan dan tegangan
dapat juga digunakan untuk mendefinisikan hubungan antara regangan geser dan
tegangan geser (Timoshenko, S., 1958).
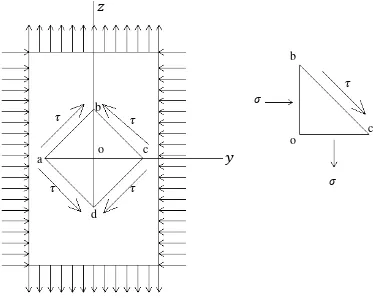
Gambar 2.8. Perubahan Bentuk Segi Empat Parallelogram
Tinjaulah kasus khusus yaitu perubahan bentuk segi empat paralellogram
dimana , , dan . Potonglah sebuah elemen abcd dengan
bidang yang sejajar dengan sumbu x dan terletak 45° terhadap sumbu y dan z (Gambar 2.8). Dengan menjumlah gaya sepanjang dan tegak lurus bc, bahwa
tegangan normal pada sisi elemen ini nol dan tegangan geser pada sisi ini adalah:
⁄ ( ) (2.8)
Kondisi tegangan seperti itu disebut geser murni (pure shear).
Pertambahan panjang elemen tegak Ob sama dengan berkurangnya panjang elemen mendatar Oa dan Oc, dan dengan mengabaikan besaran kecil dari orde
b
a
d
c o
b
o
kedua, kita bisa menyimpulkan bahwa panjang elemen ab dan bc tidak berubah
selama terjadinya perubahan bentuk. Sudut antara sisi ab dan bc berubah dan
besar regangan geser yang bersangkutan bisa diperoleh dari segitiga Obc. Sesudah perubahan bentuk akan didapatkan:
Untuk yang kecil, dan ( ⁄ ) ⁄ , maka :
Maka diperoleh :
Sedangkan jika nilai-nilai , , dan disubstitusikan ke dalam
persamaan (2.7) maka akan diperoleh :
[ ]
[ ]
Maka diperoleh hubungan antara regangan dengan regangan geser :
(2.9)
Hubungan antara regangan dan tegangan geser didefinisikan oleh konstanta E dan
v yaitu:
Jika digunakan notasi :
(2.11)
Maka persamaan (2.10) akan menjadi :
(2.12)
dimana konstanta G didefinisikan oleh persamaan (2.11), dan disebut modulus elastisitas dalam geser (modulus of elasticity in shear) atau modulus kekakuan
(modulus of rigidity).
Apabila tegangan geser bekerja ke semua sisi elemen, seperti terlihat pada
Gambar 2.4, pelentingan sudut antara dua sisi yang berpotongan hanya tergantung kepada komponen tegangan geser yang bersangkutan dan diperoleh (Timoshenko, S., 1958). :
2.6. Analogi Membran Elastis oleh Prandtl (Soap Film Analogy)
Untuk pembahasan analogi membran ini, potonglah suatu bukaan pada potongan melintang dari elemen yang mengalami torsi untuk diselidiki.
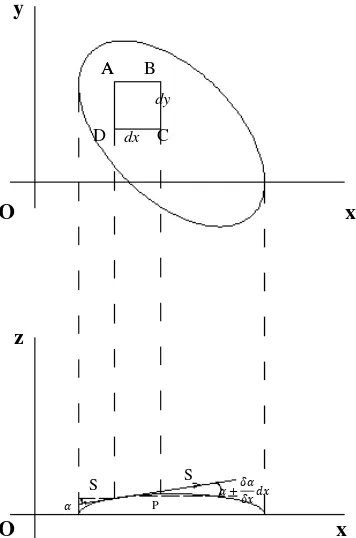
Gambar 2.9. Analogi Selaput Sabun (Soap Film Analogy)
Kemudian tinjaulah suatu elemen membran elastis ABCD dengan dimensi dx dy seperti ditunjukkan pada Gambar 2.9. Dengan menggunakan z sebagai
besaran perpindahan lateral dari membran elastis, p adalah tekanan lateral dalam gaya per satuan luas, dan S sebagai tegangan inisial dalam gaya per satuan panjang, maka gaya vertical murni yang diakibatkan oleh tegangan S yang bekerja
sepanjang sisi AD dan BC dari membran (dengan mengasumsikan perpindahan yang terjadi adalah sangat kecil sehingga nilai sin α ≈ tan α ) berturut-turut adalah
Dengan cara yang sama akan diperoleh gaya vertikal murni yang
diakibatkan oleh tegangan S yang bekerja sepanjang sisi AB dan DC berturut-turut adalah
( )
Jika keempat gaya vertikal di atas dijumlahkan maka akan diperoleh persamaan membran untuk elemen dx dy adalah sebagai berikut
( ) ( )
( ) ( )
(2.13)
Persamaan (2.13) ini dikenal sebagai persamaan Analogi Membran Prandtl. Persamaan ini kemudian akan digunakan untuk menyelesaikan
2.7. Analisis Torsi Pada Tampang Sembarang (Metode Semi-Invers
Saint-Venant)
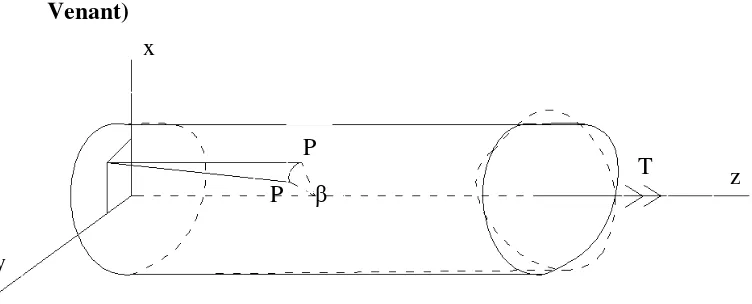
Gambar 2.10. Elemen Torsi dengan Tampang Sembarang
Anggap suatu bahan yang mengalami torsi dengan suatu potongan melintang seragam dari tampang sembarang seperti terlihat pada Gambar 2.10
Tegangan yang didistribusikan pada ujung-ujung yaitu dan akan
menghasilkan torsi sebesar T. Pada umumnya, semua distribusi tegangan pada
ujung potongan akan menghasilkan torsi.
Menurut Saint-Venant, distribusi tegangan pada potongan yang cukup jauh dari ujung bergantung hanya pada besar momen torsi dan tidak tergantung pada
distribusi tegangan pada ujungnya. Oleh karena itu, untuk suatu elemen torsi panjang, distribusi tegangan pada ujung tidak akan mempengaruhi distribusi pada bagian makro dari elemen torsi.
Metode Saint-Venant dimulai dengan suatu perkiraan komponen perpindahan akibat torsi. Perkiraan ini didasarkan pada perubahan geometri yang
terjadi pada elemen torsi yang terdeformasi. Saint-Venant mengasumsikan tiap elemen torsi lurus dengan tampang tetap selalu memiliki suatu sumbu putar yang tegak lurus terhadap potongan melintangnya yang bertindak sebagai poros kaku
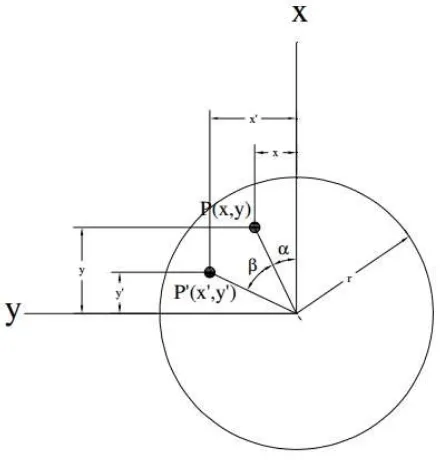
Tinjau suatu titik P dengan koordinat (x, y, z) dari pusat O sebelum
mengalami deformasi. Setelah mengalami deformasi akibat torsi, P bergerak ke P’, P akan berpindah sejauh w sejajar sumbu z karena warping (distorsi ke arah
luar bidang) dari potongan melintang dan berpindah sejauh u dan v sejajar sumbu x dan sumbu y karena rotasi dasar potongan melintang di mana P berada dengan
sudut puntir sebesar β terhadap poros. Sedangkan sudut puntir β ini bervariasi
menurut jarak z dari poros. Dapat dituliskan bahwa dβ/dz sebagai suatu laju
puntiran . Maka pada jarak z dari pusat O, sudut puntir adalah sebesar β = .
Gambar 2.11. Potongan Melintang Suatu Elemen Torsi
Dengan mengacu pada Gambar 2.11., diperoleh :
[ ] [ ]
[ ] [ ]
Untuk perpindahan yang sangat kecil, akan diperoleh nilai-nilai sin β = β dan cos β = 1, maka :
Sedangkan untuk komponen w diambil :
Dimana adalah fungsi warping.
Setelah komponen perpindahan ini diperoleh, maka kita akan mensubstitusikan nilai-nilai u, v, dan w ke dalam persamaan (2.4) dan diperoleh:
Tinjau kembali persamaan (2.3). Untuk komponen yang mengalami torsi
murni, , , , , , , sehingga dari
tergantung pada z dam komponen tegangan harus memenuhi persamaan (2.15.c). Oleh karena itu, diambil persamaan tegangan geser ini menjadi :
Kemudian kedua persamaan diatas disubstitusikan ke persamaan (2.15.c) menjadi :
menunjukkan bahwa persamaan (2.16) yang diambil memenuhi persamaan (2.15.c).
Tinjau kembali persamaan (2.14). jika masing-masing dan
didiferensiasi parsial-kan terhadap y dan x, maka diperoleh :
Jika persamaan (2.17.a) dengan (2.17.b), maka akan diperoleh :
(2.18) Substitusikan hubungan antara regangan geser dengan tegangan geser pada
persamaan (2.4) ke dalam persamaan (2.18), maka akan diperoleh:
Maka didapatkan suatu persamaan yang kemudian akan kita kenal sebagai
persamaan torsi :
Persamaan (2.20) akan digunakan untuk menurunkan fungsi torsi dengan bantuan persamaan analogi membran Prandtl yang telah diturunkan sebelumnya.
Karena permukaan elemen torsi ini bebas dari gaya lateral, maka resultan dari gaya geser τ pada potongan melintang dari elemen torsi pada keliling potongan ini harus berarah tegak lurus terhadap garis normalnya. Kedua
komponen tegangan geser dan yang bekerja pada potongan melintang
dengan sisi-sisi dx, dy, dan dx dapat dinyatakan dengan :
Gambar 2.12 Potongan Melintang Elemen Torsi
Dengan mengacu pada Gambar 2.12
(2.21)
Karena komponen tegangan geser pada arah n sesuai gambar pada keliling elemen
Maka didapat :
Dari penyelesaian ini menunjukkan bahwa nilai konstan di sepanjang keliling S.
Karena tegangan merupakan turunan partial dari , maka nilai kontan ini dapat
dianggap nol.
Dengan menyelesaikan persamaan 2.23.c, maka akan diperoleh hubungan antara momen torsi dengan fungsi torsi. Ambillah salah satu komponen integral dari persamaan (2.23.c). Karena fungsi tegangan tidak bervariasi dalam arah y
untuk sebuah garis setebal dy seperti tampak pada Gambar 2.12. Turunan parsial dapat digantikan dengan suatu turunan total sehingga diperoleh :
∫ ∫ ∫ ∫
| ∫
Mengingat nilai pada tepi-tepi elemen , maka diperoleh :
Langkah yang sama dilakukan untuk komponen lain dari integral pada persamaan
(2.23.c) sehingga diperoleh :
∫ ∫ ∫ ∫
Dengan menjumlahkan kedua komponen ini, maka diperoleh hubungan antara momen torsi dengan fungsi torsi yaitu (Erwin, 2009). :
∫ ∫ ∫ ∫ ∫ ∫ (2.24)
2.9. Torsi pada Tampang Lingkaran
Gambar 2.13 Tampang Lingkaran Selama Diberi Puntir Tetap
Pada gambar 2.13 ukuran dari permukaan tampang lingkaran selama diberi puntir tetap. Diameter dan panjangnya juga tidak berubah dengan catatan bahwa sudut puntirnya kecil.
Cakram seperti Gambar 2.13.b akan mengikuti arah regangan. Ada putaran
pada bagian bawah tampang terhadap bagian atas tampang membentuk sudut ,
dimana adalah besar putaran dari potongan mn terhadap ujung. Elemen persegi
abcd dari pinggir cakram seperti pada Gambar 2.13.b., panjang sisinya tetap sama
disebut dalam keadaan geser murni dan besar dari regangan gesernya didapat
dari segitiga kecil cac’ :
Karena c’c membentuk lengkungan kecil dengan jari-jari d/2 sesuai dengan
perbedaan dalam sudut putaran dari dua tampang yang berdekatan, maka c’c
= (d/2) dan diperoleh
Untuk balok yang berputar karena torsi pada ujungnya, sudut puntirnya sebanding
dengan panjang bentang dan besar tetap. Besarnya sudut puntir persatuan
panjang balok dinotasikan sebagai θ. Lalu, dari persamaan (2.25) didapatkan :
Tegangan geser yang bekerja pada sisi-sisi elemen dan menghasilkan geser pada arah tersebut. Besar tegangan gesernya didapat dari persamaan (2.12) yaitu :
Karena d/2 = r, maka dihasilkan :
Timoshenko (1958) menyatakan bahwa kesetimbangan bagian dari balok diantara bagian bawah dan potongan mn pada Gambar 2.13.a dapat disimpulkan
berlawanan dengan momen torsi . Untuk tiap elemen pada luasan dA pada
Gambar 2.13.c gaya gesernya yaitu . Momen terhadap gaya tersebut adalah
. Maka momen torsinya yaitu
∫ ∫
Dimana Momen inersia polar dari tampang lingkaran dengan
⁄ , maka:
Jika v merupakan sudut puntir maka :
Substitusikan persamaan (2.30) ke persamaan (2.28), sehingga :
Johannes, T. (2014) mengatakan bahwa secara umum, khusus tampang segi empat, persamaan inersia torsinya yaitu :
α
Dimana, α = koefisien untuk mencari J a = tinggi penampang
b = lebar penampang
Untuk mencari tegangan geser akibat torsi pada tampang segi empat, dapat dihitung dengan rumus :
τ
τ τ
Dimana,
β
Keterangan, , β, X = koefisien untuk mencari tegangan geser a = tinggi penampang
b = lebar penampang
Gambar 2.14. Diagram Tegangan Torsi pada Tampang Segi Empat
Tabel 2.1. koefisien α, β, X berdasarkan perbandingan a/b
a/b α β X
1 0,141 4.81 1.000 1.5 0,196 4.33 0.853 2 0,229 4.06 0.796 2.5 0,249 3.88 0.768 3 0,263 3.74 0.753 4 0,281 3.55 0.745 5 0,291 3.43 0.744 6 0,299 3.35 0.743 8 0,307 3.26 0.743 10 0,312 3.20 0.743 - 0,333 3.00 0.743
2.11. Tulangan Torsi pada Beton Bertulang
Batang beton bertulang yang menerima gaya torsi besar akan runtuh secara mendadak jika tidak diberikan tulangan torsi. Penambahan tulangan torsi tidak
mengubah besar torsi yang akan menyebabkan retak tarik diagonal, melainkan mencegah batang tersebut terpisah. Oleh karena itu, tulangan torsi ini akan mampu menahan momen torsi yang cukup besar tanpa runtuh. Pengujian
menunjukkan bahwa tulangan longitudinal dan sengkang tertutup (atau spiral)
perlu dipasang untuk menahan sejumlah retak tarik diagonal yang terjadi pada seluruh permukaan dari batang yang menerima gaya torsi cukup besar (Jack C.
McCormac, 2004).
2.12. Momen Torsi yang Harus Ditinjau dalam Desain Beton Bertulang
Jack C. McCormac (2004) menyatakana bahwa momen torsi dikenal sebagai torsi keseimbangan dan torsi kompatibilitas. Berikut penjelasannya :
Torsi keseimbangan. Untuk struktur statis tertentu, hanya ada satu alur di
mana momen torsi dapat dipindahkan ke tumpuan. Jenis momen torsi ini
disebut torsi keseimbangan atau torsi statis tertentu dan tidak dapat direduksi oleh redistribusi gaya dalam atau oleh rotasi batang.
Torsi kompatibilitas. Momen torsi pada bagian tertentu dari struktur statis
tak tentu dapat direduksi cukup besar jika bagian struktur tersebut retak
akibat torsi dan berotasi. Hasilnya adalah redistribusi gaya dalam struktur. Dalam beberapa bagian dari struktur yang ditinjau memuntir untuk mempertahankan deformasi dari kompatibilitas struktur.
2.13. Tegangan Torsi pada Beton Bertulang
Tegangan torsi ditambahkan pada tegangan geser pada satu sisi dari balok
Gambar 2.15. Tegangan Torsi dan Geser dalam Balok Berongga
Tegangan torsi mendekati pusat balok pejal sangat rendah. Oleh karenanya, balok berongga diasumsikan mempunyai kekuatan torsi yang hampir
sama seperti balok pejal dengan dimensi luar yang sama (Jack C. McCormac, 2004).
Dalam penampang pejal, tegangan geser akibat torsi terkonsentrasi pada “tube” luar dari batang, sebagaimana ditunjukkan dalam Gambar 2.16(a),
sedangkan tegangan geser akibat tersebar sepanjang lebar penampang solid,
sebagaimana ditunjukkan pada Gambar 2.16(b). Akibatnya, kedua jenis tegangan geser akibat geser dan torsi dikombinasikan dengan rumus akar pangkat dua yang ditunjukkan dalam subbab berikutnya.
Setelah retak, ketahanan beton terhadap torsi diasumsikan untuk
diabaikan. Retak torsi cenderung membentuk spiral di sekeliling batang membentuk sudut sekitar 45 dengan sumbu longitudinal batang. Torsi
diasumsikan ditahan oleh rangka batang ruang efektif yang terletak di luar ”tube”
dari batang beton. Rangka ini diperlihatkan pada Gambar 2.17. Tulangan longitudinal di sudut batang dan sengkang transversal tertutup bekerja sebagai batang tarik dalam “rangka” tersebut, sedangkan beton diagonal di antara
sengkang yang bekerja sebagai batang tekan. Beton yang retak masih mampu
memikul tegangan tekan (Jack C. McCormac, 2004).
Gambar 2.17. Rangka Batang Ruang Fiktif
2.14. Tulangan Torsi yang Disyaratkan Peraturan SNI-03-2847-2002
Perencanaan tulangan beton bertulang terhadap torsi didasarkan pada
analogi tube dinding tipis dengan rangka batang ruang di mana beton bagian dalam atau inti diabaikan. Setelah torsi menyebabkan batang retak, ketahanannya
terhadap torsi hampir seluruhnya diberikan oleh sengkang tertutup dan tulangan longitudinal yang terletak dekat permukaan batang. Setelah terjadi retak, beton diasumsikan mempunyai kekuatan torsi yang dapat diabaikan (Jack C.
Dalam SNI-03-2847-2002 subbab 13.6.1.a dinyatakan bahwa pengaruh
torsi dapat diabaikan untuk batang non-pratekan jika :
√
Dimana
= luas yang dibatasi oleh keliling luar penampang beton = keliling luar penampang beton
2.15. Kekuatan Momen Torsi pada Beton Bertulang
Dimensi elemen yang menerima geser dan torsi dibatasi oleh aturan SNI sehingga retak yang tak terlihat tereduksi dan untuk mencegah kehancuran pada permukaan beton yang disebabkan tegangan tekan miring. Hal ini dicapai dengan
persamaan berikut, di mana bagian kiri menggambarkan tegangan geser karena geser dan torsi. Jumlah kedua tegangan ini dalam elemen tertentu tidak boleh
= jarak dari serat tekan terluar ke titik berat tulangan tarik longitudinal,
= momen puntir terfaktor pada penampang
= keliling dari garis pusat tulangan sengkang torsi terluar
= luas daerah yang dibatasi oleh garis pusat tulangan sengkang torsi terluar = kuat geser nominal yang disumbangkan oleh beton
Kuat leleh rencana untuk tulangan puntir non-prategang tidak boleh melebihi 400 Mpa.
2.16. Perencanaan Tulangan Torsi
Peraturan SNI-03-2847-2002 mensyaratkan bahwa luas sengkang yang
digunakan untuk menahan torsi dapat dihitung dengan persamaan berikut:
Dimana
= luas bruto yang dibatasi oleh lintasan aliran geser =
Peraturan SNI-03-2847-2002 mensyaratkan bahwa luas tulangan longitudinal yang digunakan untuk menahan torsi dapat dihitung dengan persamaan berikut:
( )
Dimana
= kuat leleh tulangan torsi longitudinal
2.17. Retak pada Balok Beton Bertulang
Dua teori yang sangat berbeda digunakan untuk menjelaskan kekuatan dari
beton bertulang dalam menahan torsi. Teori yang pertama berdasarkan pada teori skew bending oleh Lessig yang dikembangkan kembali oleh Hsu yang mana
merupakan dasar bagi peraturan perencanaan torsi pada ACI 1971 -1989. Teori ini
lagi ditahan oleh tulangan. Pola keruntuhannya diasumsikan menghasilkan
pembengkokan pada permukaan yang miring dari retakan yang menyebar ke tiga dari empat sisi balok seperti pada Gambar 2.18 dan 2.19 (James G. Macgregor,
1997).
Gambar 2.18. Pola Retak Akibat Torsi Murni
Menurut ACI tentang peraturan distribusi penulangan pada balok dan pelat satu arah yang berdasarkan persamaan Gergely- Lutz yaitu :
√
Dimana
w = lebar retak dengan satuan 0,001 in
= faktor kedalaman; harga rata-rata = 1,20
= ketebalan penutup ke lapis tulangan yang pertama(in)
= tegangan maksimum (ksi) dalam baja pada saat tingkat beban layan
dengan 0,6 untuk dipergunakan jika tidak ada perhitungan yang
tersedia
Gambar 2.19. Teori Skew Bending
2.18. Metode Elemen Hingga
Yerri Susatio (2004) menyatakan bahwa metode elemen hingga adalah metode numerik yang digunakan untuk menyelesaikan permasalahan teknik dan
problem matematis dari suatu gejala fisis. Tipe masalah teknis dan matematis fisis yang dapat diselesaikan dengan metode elemen hingga terbagi dalam dua
kelompok, yaitu kelompok analisa struktur dan kelompok masalah-masalah non struktur. Tipe-tipe permasalahan struktur seperti :
1. Analisa tegangan, meliputi analisa truss dan frame serta masalah-masalah
yang berhubungan dengan tegangan-tegangan yang terkonsentrasi 2. Buckling
3. Analisa getaran
Secara umum langkah-langkah yang dilakukan dalam menggunakan metode elemen hingga dirumuskan sebagai berikut:
1. Pemilihan tipe elemen dan diskritisasi
3. Mencari hubungan strain/displacement dan stress/strain
4. Dapatkan matrik kekakuan dari elemen yang dibuat 5. Gunakan persamaan kesetimbangan {F}=[k]{d}
6. Selesaikan persamaan pada langkah 5, dengan menghitung harga yang belum diketahui
7. Hitung strain dan stress dari tiap elemen
8. Interpretasikan kembali hasil-hasil perhitungan yang diperoleh
2.19. Peranan ANSYS dalam Bidang Engineering
Muhammad Daud Pinem (2013) menyatakan bahwa ANSYS adalah
salah satu perangkat lunak berbasiskan metode elemen hingga yang dipakai untuk menganalisa masalah-masalah rekayasa (engineering). ANSYS dapat berjalan di platform Windows dan Linux. Elemen-elemen yang bisa dieksekusi dengan
ANSYS dalam bidang struktural yaitu : a)Link
Elemen link secara umum dapat dipakai di beberapa jenis permasalahan
struktur yang dimodelkan seperti garis. Salah satunya yaitu batang dan pegas. b)Beam
Elemen beam dapat menyelesaikan permasalahan struktur yang dimodelkan seperti balok. Elemen ini dapat menerima tarik, tekan, dan tekuk.
c) Solid
Elemen solid digunakan untuk permodelan tiga dimensi struktur pejal. Elemen
d)Pipe
Elemen pipe ini memiliki karakter tekuk, tekan, torsi, dan tekuk. e) Shell