FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
0 dari 490
Cari Halaman
Kembali
Layar Penuh
Versi Cetak:
Judul:
Analisis Regresi dengan R
Tahun terbit: 2009
FMIPA-UNEJ
Daftar Isi
Judul ◭◭ ◭ ◮ ◮◮
1 dari 490
Cari Halaman
Kembali
FMIPA-UNEJ
Daftar Isi
Judul ◭◭ ◭ ◮ ◮◮
2 dari 490
Cari Halaman
Kembali
Layar Penuh
Analisis Regresi dengan R
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
3 dari 490
Cari Halaman
Kembali
Layar Penuh
I. M. Tirta, (Prof. Drs. M.Sc., Ph.D.)
itirta.fmipa@unej.ac.id; tirtaimade@gmail.com
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
4 dari 490
Cari Halaman
Kembali
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
5 dari 490
Cari Halaman
Kembali
Layar Penuh
DAFTAR ISI
1 DASAR-DASAR PEMODELAN STOKASTIK 23
1.1 Prinsip Pemodelan . . . 27
1.2 Langkah-langkah Penting Dalam Pemodelan . . . 37
1.2.1 Langkah penting dalam Pemodelan secara Umum 37
1.2.2 Langkah Penting dalam Pemodelan Statistika . . . 39
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
6 dari 490
Cari Halaman
Kembali
Layar Penuh
1.3.1 Metode Kuadrat Terkecil . . . 45
1.3.2 Metode Likelihood Maksimum . . . 47
1.3.3 Mencari Maksimum dengan Metode Numerik . . 48
1.4 Model Linier dan Perkembangannya . . . 52
1.4.1 Model linier klasik . . . 53
1.4.2 Model Linier Tercampur . . . 56
1.4.3 Model Linier Tergeneralisir . . . 60
1.4.4 Model untuk Data Tidak Normal dan Tidak Saling Bebas . . . 64
1.4.5 Pengembangan Lain Model Linier . . . 67
1.5 Model-model Nonlinier . . . 70
1.6 Tinjauan singkat Program Statistika R . . . 71
1.6.1 Aplikasi R untuk Manipulasi Grafik . . . 77
1.6.2 Aplikasi R untuk Model Statistika/ Analisis Regresi 88 1.6.3 RCommnder RGUI untuk analisis dasar . . . 91
1.7 Ringkasan . . . 92
1.8 Bacaan Lebih Lanjut . . . 94
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
7 dari 490
Cari Halaman
Kembali
Layar Penuh
2 ALJABAR MATRIKS UNTUK STATISTIKA 97
2.1 Materi . . . 99
2.2 Defenisi dan Jenis Matriks . . . 100
2.3 Operasi Matriks dan Sifat-sifatnya . . . 105
2.3.1 Operasi uner . . . 105
2.3.2 Operasi biner . . . 106
2.3.3 Determinan dan Invers Matriks . . . 115
2.4 Kebergantungan Linier dan Rank Matriks . . . 118
2.5 Bentuk Kuadrat dan Diferensial Matriks . . . 123
2.6 Aplikasi R untuk Operasi Matriks . . . 134
2.6.1 Mendefinisikan matriks. . . 135
2.6.2 Operasi Matriks dengan R . . . 139
2.7 Bacaan Lebih Lanjut . . . 144
2.8 Ringkasan . . . 145
2.9 Latihan Soal-soal . . . 147
3 MODEL LINIER KLASIK 151 3.1 Bentuk dan Asumsi . . . 154
3.2 Estimasi Parameter . . . 156
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
8 dari 490
Cari Halaman
Kembali
Layar Penuh
3.2.2 Estimasi dengan Metode Likelihood Maksimum . 161
3.3 Uji Inferensial dariβˆj . . . 165
3.3.1 Distribusi βˆj . . . 165
3.3.2 Estimasi selang dari βj . . . 169
3.3.3 Uji Hipotesis . . . 170
3.3.4 Koefisien Determinasi R2 . . . 172
3.4 Penggunaan Matriks untuk Regresi Peubah Ganda . . . . 180
3.4.1 Perluasan hasil untuk Regresi Peubah Ganda . . . 180
3.4.2 Pendekatan Matriks Metode Kuadrat Terkecil . . 183
3.4.3 Pendekatan Matriks untuk Metode Kemungkinan Maksimum . . . 186
3.5 Interval Keyakinan µdan Prediksi Y . . . 191
3.6 Melaporkan Nilai Probabilitas p . . . 194
3.7 Model Linier dengan Variabel Kualitatif . . . 196
3.7.1 Variabel Boneka dengan Model Berkonstanta . . . 197
3.7.2 Variabel Boneka dengan Konstanta tidak Eksplisit 202 3.8 Ilustrasi Model Linier Normal dengan R . . . 206
3.8.1 Simulasi dengan R . . . 206
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
9 dari 490
Cari Halaman
Kembali
Layar Penuh
3.8.3 Model dengan Variabel Kualitatif . . . 218
3.8.4 Analisis dengan Subset . . . 231
3.9 Ringkasan . . . 233
3.10 Bacaan Lebih Lanjut . . . 235
3.11 Latihan Soal- Soal . . . 236
4 DIAGNOSTIK DAN TRANSFORMASI 239 4.1 Asumsi Analisis Regresi Klasik . . . 242
4.2 Memeriksa Sebaran Data melalui Grafik . . . 243
4.3 Pemeriksaan Hubungan Peubah melalui Grafik . . . 248
4.3.1 Diagram pencar data . . . 248
4.3.2 Diagram Pencar Sisa . . . 252
4.3.3 Memeriksa Model Melalui Diagram . . . 253
4.4 Uji Statistika Terkait Asumsi . . . 260
4.5 Memeriksa Model melalui AIC . . . 261
4.6 Transformasi Data. . . 265
4.7 Ringkasan . . . 270
4.8 Bacaan Lebih Lanjut . . . 272
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
10 dari 490
Cari Halaman
Kembali
Layar Penuh
5 MODEL LINIER TERGENERALISIR 275
5.1 Distribusi Keluarga Eksponensial. . . 277
5.1.1 Bentuk umum . . . 277
5.1.2 Nilai-tengah dan Ragam dari a(Y) . . . 278
5.1.3 Beberapa Bentuk Khusus . . . 283
5.2 Konsep Dasar Model Linier Tergeneralisir . . . 292
5.2.1 Sisi lain Model Linier Normal . . . 292
5.2.2 Generalisasi Model Linier Klasik ke Model Linier Tergeneralisir . . . 293
5.3 Estimasi pada Model Linier Tergeneralisir . . . 298
5.3.1 Metode Penduga Kuadrat Terkecil . . . 301
5.3.2 Metode Penduga Likelihood Maksimum . . . 303
5.4 Inferensi pada Model Linier Tergeneralisir . . . 312
5.4.1 Distribusi dari Penduga Likelihood Maksimum . . 314
5.4.2 Kecocokan Model . . . 317
5.5 Model Logit, Probit dan Log-linier. . . 322
5.6 dispersi berlebih . . . 325
5.7 Ilustrasi GLM dengan R . . . 326
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
11 dari 490
Cari Halaman
Kembali
Layar Penuh
5.7.2 Prediksi pada GLM . . . 343
5.8 Ringkasan . . . 345
5.9 Bacaan Lebih Lanjut . . . 347
5.10 Latihan Soal-soal . . . 348
6 MODEL UNTUK RESPON TIDAK SALING BEBAS 349 6.1 Model Marjinal . . . 355
6.2 Quasi-Likelihood dan Generalized Estimating Equations (GEE) . . . 360
6.3 Generalisasi dan Bentuk GEE . . . 363
6.4 Ilustrasi GEE dengan R . . . 368
6.5 Gamma-HGLM dan Model Lainnya . . . 374
6.5.1 Gamma-HGLMs . . . 375
6.5.2 Likelihood Bersama: Model JGIG . . . 378
6.5.3 Estimasi Parameter β dan v. . . 380
6.5.4 Pendugaan parameter dispersi ν dan α . . . 388
6.5.4.1 Prosedur Pendugaan . . . 390
6.5.5 Analisis HGLM dengan R . . . 391
6.6 Bacaan Lebih Lanjut . . . 396
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
12 dari 490
Cari Halaman
Kembali
Layar Penuh
6.8 Latihan Soal-soal . . . 398
GLOSARIUM 399 A BEBERAPA FUNGSI TERKAIT REGRESI 417 A.1 Fungsi dari Paket stats. . . 418
A.2 Fungsi dari Paket cars . . . 419
A.3 Fungsi dari Paket gam . . . 420
A.4 Fungsi dari Paket graphics . . . 421
A.5 Fungsi dari Paket gee . . . 422
A.6 Fungsi dari Paket lme4. . . 423
A.7 Fungsi dari Paket hglm . . . 424
A.8 Fungsi dari Paket glmmML . . . 425
A.9 Skrip Manipulasi Grafik . . . 426
A.10Skrip Membangkitkan Data Regresi dengan Peubah Kelom-pok . . . 428
B DATA UNTUK ILUSTRASI 431 B.1 Data dari Paket actuar . . . 432
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
13 dari 490
Cari Halaman
Kembali
Layar Penuh
B.3 Data dari Paket agricolae . . . 439
B.4 Data dari Paket asuR . . . 441
B.5 Data dari Paket car . . . 443
B.6 Data dari Paket DAAG. . . 446
B.7 Data dari Paket dataset . . . 452
B.8 Data dari Paket demogR . . . 458
B.9 Data dari Paket faraway . . . 459
B.10Data dari Paket gam . . . 466
B.11Data dari Paket ISwR . . . 467
B.12Data dari Paket lmtest . . . 470
B.13Data dari Paket MASS. . . 471
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
14 dari 490
Cari Halaman
Kembali
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
15 dari 490
Cari Halaman
Kembali
Layar Penuh
DAFTAR GAMBAR
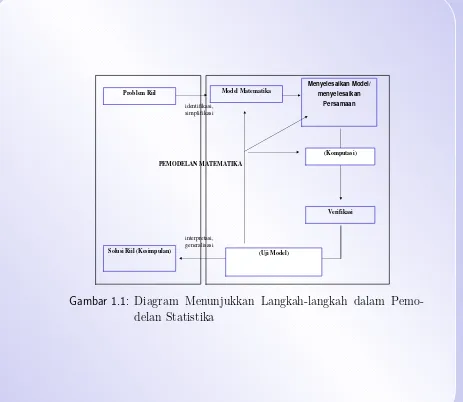
1.1 Diagram Menunjukkan Langkah-langkah dalam
Pemo-delan Statistika . . . 42
1.2 Pembagian dan Perkembangan Model Linear . . . 66
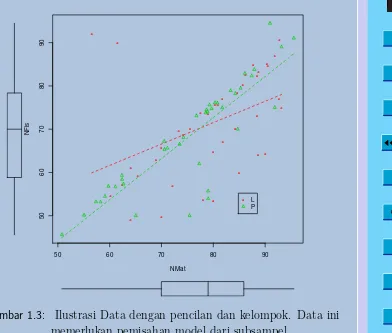
1.3 Ilustrasi Regresi . . . 69
1.4 Contoh Histogram dengan Kurva Densitas . . . 83
1.5 Contoh Diagram Pencar dengan rug dan boxplot. . . . 84
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
16 dari 490
Cari Halaman
Kembali
Layar Penuh
1.7 Contoh Gabungan Grafik dengan Pembagian Layar . . 86
1.8 Contoh Gabungan Grafik dengan pembagian layar . . . 87
3.1 Ilustrasi Garis regresi dan sabuk keyakinan . . . 193
3.2 Sebaran data dengan variabel kualitatif . . . 198
3.3 Garis Regresi sejajar dengan selisih konstanta β2 dan
gradien sama (β1) . . . 201
3.4 Garis Regresi berbeda dengan selisih konstanta β2 dan
selisih gradien β3 . . . 203
3.5 Grafik Penduga ˆβ1 = ˆα dari penarikan sampel 100 kali
masing-masing berukuran 60. Nilai parameter sebe-narnya adalah α= 3. . . 211
3.6 Grafik Penduga ˆβ1 = ˆαdari beberapa penarikan sampel
dengan ukuran mulai 10 sampai dengan 1000. Nilai parameter sebenarnya adalah α = 3. . . 212
3.7 Contoh Histogram dengan Kurva Densitas Data Cars . 216
3.8 Diagram Pencar X dengan Y yang mengandung kelom-pok yang dapat digabung. . . 221
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
17 dari 490
Cari Halaman
Kembali
Layar Penuh
4.1 Grafik Quantile dari Data Berdistribusi Normal (kiri) dan Data Cenderung Tidak Berdistribusi Normal (Kanan)244
4.2 Grafik Sebaran Peluang dari Data Berdistribusi Normal (lebih simetris, warna biru) dan Data Tidak Berdis-tribusi Normal (tidak siumetris, warna merah) . . . 245
4.3 Boxplot respon dengan kelompok . . . 247
4.4 Grafik Pencar Data dengan Hubungan Linear dan Ra-gam Relatif Konstan . . . 249
4.5 Grafik Pencar Data dengan hubungan Linear tetapi Ra-gam Relatif tidak Konstan . . . 250
4.6 Grafik Pencar Data dengan hubungan lebih cenderung nonlinear. . . 251
4.7 Grafik Pencar Data dengan Hubungan Eksponensial . . 252
4.8 Grafik Pencar Sisa Data yang memenuhi syarat ho-moskedastisitas. . . 254
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
18 dari 490
Cari Halaman
Kembali
Layar Penuh
4.10 Grafik Diagnostik dari Objek yang Dihasilkan oleh Fungsi
lm(). Grafik menunjukkan data relatif memenuhi asumsi Model Linier Normal . . . 258
4.11 Grafik Diagnostik dari Objek yang Dihasilkan oleh Fungsi
lm(). Grafik menunjukkan data tidak memenuhi asumsi Model Linier Normal, yang ditandai dengan adanya hu-bungan tidak linier dan pencilan. . . 259
4.12 Sebaran data asli (naik dan membuka ke atas) dan trans-formasi yang bisa dilakukan. Beberapa transtrans-formasi meng-hasilkan sebaran yang mengikuti garis lurus tetapi ragam tidak konstan . . . 266
4.13 Sebaran data asli (naik dan terbuka ke bawah) dan trans-formasi yang bisa dilakukan. Beberapa transtrans-formasi meng-hasilkan sebaran yang mengikuti garis lurus tetapi ragam tidak konstan . . . 268
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
19 dari 490
Cari Halaman
Kembali
Layar Penuh
5.1 Plot Densitas dari sampel dengan berbagai nilai-tengah dengan ukuran sampel 100 . . . 289
5.2 Sebaran Data dengan ukuran sampel 100 dengan dis-tribusi Normal (b) dan Gamma (r) . . . 290
5.3 Respon dengan Fungsi Hubungan Logit dan Probit . . 296
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
20 dari 490
Cari Halaman
Kembali
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
21 dari 490
Cari Halaman
Kembali
Layar Penuh
DAFTAR TABEL
1.1 Tabel jumlah (kg) salak dan anggur dan harga yang dibayar . . . 34
1.2 Fungsi dan paket untuk menggambar grafik R . . . 79
2.1 Fungsi R terkait matriks . . . 134
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
22 dari 490
Cari Halaman
Kembali
Layar Penuh
5.1 Rangkuman Distribusi Anggota Keluarga Eksponensial 288
5.2 Ciri-ciri khas Distribusi Keluarga Eksponensial. . . 291
5.3 Jumlah Sukses(S) dan Gagal dalam Berbagai Kelom-pok Faktor. . . 324
5.4 Distribusi dan Link pada R . . . 329
5.5 Jumlah Kelulusan dalam Berbagai Kelompok Perlakuan 331
5.6 Format Data R Jumlah Kelulusan dan Kegagalan . . . 332
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
23 dari 490
Cari Halaman
Kembali
Layar Penuh
BAB
1
DASAR-DASAR PEMODELAN STOKASTIK
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
24 dari 490
Cari Halaman
Kembali
Layar Penuh
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
25 dari 490
Cari Halaman
Kembali
Layar Penuh
Kompetensi
Pembaca diharapkan memahami hakekat pemodelan dalam bidang statistika serta mempunyai gambaran tentang kedudukan dan perkem-bangan regresi atau model linier dalam uji statistika. Secara lebih khusus diharapkan:
1. dapat menyebutkan hakekat dari pemodelan matematika, khusus-nya pemodelan statistika;
2. dapat menjelaskan langkah-langkah penyusunan model statistika;
3. dapat menjelaskan langkah-langkah mengestimasi parameter da-lam model statistika;
4. dapat menjelaskan perkembangan model statistika penting.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
26 dari 490
Cari Halaman
Kembali
Layar Penuh
Materi
1. Prinsip Pemodelan
2. Langkah-langkah PemodelanStatistika
3. Estimasi Parameter dalam Model Statistika
4. Perkembangan Model Statistika
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
27 dari 490
Cari Halaman
Kembali
Layar Penuh
1.1.
Prinsip Pemodelan
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
28 dari 490
Cari Halaman
Kembali
Layar Penuh
pemodelan matematika.
Definisi 1.1(Prinsip Pemodelan). Model matematika dari suatu
ma-salah adalah rumusan mama-salah dalam bentuk persamaan matematika
Definisi 1.2. Pemodelan matematika adalah proses menerjemahkan
masalah dalam bahasa umum(sehari-hari) ke dalam bahasa atau per-samaan matematika
Sebagai ilustrasi, berikut disampaikan contoh soal penerapan sistim persamaan linier dan langkah- langkah penyelesaian yang di-anjurkan.
Contoh 1.1. Seorang ibu membeli 3 kilogram salak dan 2 kilogram
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
29 dari 490
Cari Halaman
Kembali
Layar Penuh
Untuk menjawab persoalan di atas dianjurkan untuk menem-puh langkah- langkah berikut. Hal ini dimungkinkan hanya dilakukan secara implisit.
1. Kita misalkan bilangan yang ingin dicari (dalam hal ini harga satu kilogram salak dan harga satu kilogram anggur) masing-masing sebagai a dan b. Kita membuat persamaan matema-tika dari persoalan dalam bentuk cerita tadi. Dalam hal ini sebenarnya kita sedang membuat model matematika suatu per-soalan. Untuk soal di atas model matematika yang diperoleh adalah
3a+ 2b = 1700 3a+ 5b = 29000
(1.1)
2. Kita menyelesaikan persamaan matematika di atas dengan teori matematika yang kita miliki. Dengan metodeeleminasidan sub-stitusi balik kita memperoleh a = 3000 danb = 4000.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
30 dari 490
Cari Halaman
Kembali
Layar Penuh
4. Menyimpulkan bahwa harga satu kilogram salak adalah Rp 3000 dan harga satu kilogram anggur adalah Rp 4000.
Jadi harga x kg salak dan y kg anggur adalah
H = 3000x+ 4000y
Jadi dapat dipahami bahwa pemodelan atau menerjemahkan masalah sehari-hari ke persamaan matematika merupakan bagian yang sangat penting dalam menggunakan matematika untuk menyelesaikan persoalan sehari- hari. Pentingnyapemodelandalam matematika juga dinyatakan oleh Prof. J. Neyman, yang dikutip dari Meyer, sebagai berikut:
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
31 dari 490
Cari Halaman
Kembali
Layar Penuh
not a given mathematical model is adequate before some ob-servational data are obtained. In order to check the validity of the model, we must deduce a number of consequences of our model and then compare these predicted results with
observa-tions. [Kapan saja kita menggunakan metematika untuk
mem-pelajari fenomena yang teramati, kita mesti perlu memulai de-ngan membangun suatu model matematika (deterministik atau probabilistik) untuk fenomena tersebut. Sangat penting, mo-del yang dibuat harus menyederhanakan persoalan dan bebe-rapa rincian mesti diabaikan. Keberhasilan model bergantung pada apakah rincian yang diabaikan benar- benar tidak pen-ting dalam pengembangan fenomena yang dipelajari. Biasanya sangat sulit untuk menyatakan dengan pasti, apakah suatu mo-del matematika adalah tepat atau tidak sebelum diperoleh data pengamatan. Dalam rangka memeriksa validitas model, kita harus menurunkan sejumlah konsekuensi (dalil) dari model kita dan membandingkan hasil dugaan teoritis dengan pengamatan] (Meyer [28]).
ko-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
32 dari 490
Cari Halaman
Kembali
Layar Penuh
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
33 dari 490
Cari Halaman
Kembali
Layar Penuh
apakah model yang kita pakai perlu diperbaiki atau tidak. Pada Con-toh 1.1, ada asumsi yang dikenakan dalam persoalan tersebut yaitu pedagang diasumsikan mengenakan harga yang tetap kepada semua pembeli. Ini berarti peubah harga dianggap merupakan peubah tetap yang tidak bersifat acak. Dengan demikian mengambil dua pembeli sudah cukup untuk mementukan atau menghitung harga dua komu-ditas (anggur dan salak).
Persoalan akan menjadi lebih kompleks apabila dalam kenyataan di lapangan pedagang mengenakan harga yang berbeda-beda kepada pembeli dan sangat boleh jadi kenyataan inilah yang banyak terjadi di lapangan, terutama di pasar-pasar tradisional. Dalam kondisi ini ada kemungkinan dari beberapa pembeli diperoleh informasi (data) yang berbeda- beda misalnya dari 10 pembeli diperoleh informasi seperti pada Tabel1.1 yang berupa data fiktif.
meru-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
34 dari 490
Cari Halaman
Kembali
Layar Penuh Tabel 1.1: Tabel jumlah (kg) salak dan anggur dan harga yang dibayar
Nomor Pembeli
Jumlah Kg
Salak (X1)
Jumlah Kg
Anggur (X2)
Jumlah Harga dalam Rupiah (H)
1 2 4 20 500
2 6 3 29 000
3 3 2 17 000
4 4 5 31 500
5 5 6 40 000
6 6 3 30 500
7 3 5 29 000
8 2 2 14 500
9 5 6 39 500
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
35 dari 490
Cari Halaman
Kembali
Layar Penuh
pakan hubungan matematika yang bersifat fungsional murni (misal-nya, y = f(x)). Pemodelan yang kedua, menganggap peubah harga berubah-ubah dengan sebaran tertentu (misalnya, normal). Pemo-delan yang kedua ini disebutpemodelan stokastik(statistika). Hu-bungan yang diperoleh selain mengandung komponen fungsional, juga mengandung adanya galat yang merupakan peubah acak yang berdis-tribusi dengan sebaran tertentu. Jadi hubungan yang diperoleh men-jadi y = f(x, α, β) +e, dengan e adalah peubah acak/ random yang berdistribusi normal, misalnya. Fungsi f dan sebaran e biasanya bergantung kepada suatu konstanta yang belum diketahui yang dise-but parameter. Parameter inilah yang biasanya menjadi fokus ke-pentingan dalam pemodelan statistika. Dalam contoh di atas X1, X2
dan Y disebut variabel/ peubah yang diketahui dari data sedang-kan α dan β adalah parameter (yang akan dicari nilainya). Dengan demikian, persamaan matematika yang sekarang harus diselesaikan adalah
h=β1x1 +β2x2+ǫ.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
36 dari 490
Cari Halaman
Kembali
Layar Penuh
sederhana yang juga menghasilkan model yang paling sederhana ada-lah bahwa ǫi berdistribusi identik dan independen mengikuti sebaran
normal. Model-Statistika Linier membahas berbagai alternatif model serta penyelesaiannya. Dengan prosedur penyelesaian model stokastik, dihasilkan persamaan berupa dugaan harga (ˆh)
ˆ
h= 3001,73x1+ 3968,40x2
dengan 3001,732 disebut penduga β1 atau ˆβ1 yaitu dugaan harga 1 kg
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
37 dari 490
Cari Halaman
Kembali
Layar Penuh
1.2.
Langkah-langkah Penting Dalam Pemodelan
1.2.1.
Langkah penting dalam Pemodelan secara Umum
Dari uraian pada Contoh 1.1 sebenarnya sudah tergambar langkah-langkah yang penting dalam pemodelan secara umum. Langkah- lang-kah tersebut dapat diuraikan secara lebih eksplisit seperti berikut ini.
1. Penentuan model. Langkah ini meliputi:
(a) menentukan/ mengidentifikasi peubah beserta batas semes-tanya;
(b) menentukan jenis dan derajat fungsi yang dibentuk;
Penentuan jenis dan derajat fungsi disesuaikan dengan kondisi, tujuan dan sifat permasalahan yang dihadapi.
2. Menyelesaikan model. Langkah ini meliputi menghitung nilai
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
38 dari 490
Cari Halaman
Kembali
Layar Penuh
3. Melakukan verifikasi. Hasil yang diperoleh dari
penyelesa-ian model sebelum disimpulkan atau diinterpretasikan ke da-lam persoalan nnyata semestinya diverifikasi apakah sudah se-suai dengan model yang digunakan. Langkah ini penting untuk meyakinkan tidak adanya kesalahan perhitungan, kesalahan pe-mrograman (kalau menggunakan komputer), maupun kesalahan konsep matematika yang digunakan dalam menyelesaikan model.
4. Menarik kesimpulan. Selanjutnya hasil yang diperoleh
diin-terpretasikan sesuai dengan persoalan riil yang menjadi dasar pemilihan model.
5. Melakukan uji kecocokan. Karena pada umumnya
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
39 dari 490
Cari Halaman
Kembali
Layar Penuh
mencoba hubungan fungsi yang lebih kompleks.
1.2.2.
Langkah Penting dalam Pemodelan Statistika
Sebenarnya langkah- langkah dalam pemodelan stokastik sudah ter-gambar langkah- langkah yang penting dalam pemodelan secara umum. Namun ada beberapa langkah yang sifatnya khas yang tidak dilakukan dalam pemodelan umum. Sifat khas ini disebabkan karena dalam pemodelan statistika ada parameter yang menjadi kepentingan dan ada komponen galat yang bersifat acak dan memiliki sebaran ter-tentu. Langkah-langkah penting yang harus ditempuh dalam pemo-delan stokastik dapat diuraikan seperti berikut ini.
1. Penentuan model yang meliputi:
(a) menentukan/ mengidentifikasi peubah;
(b) menentukan parameter yang menjadi kepentingan;
(c) menentukan hubungan antara parameter dan peubah serta
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
40 dari 490
Cari Halaman
Kembali
Layar Penuh
Penentuan hubungan serta distribusi ini disesuaikan dengan kon-disi dan sifat permasalahan yang dihadapi.
2. Mengestimasi parameter yang menjadi kepentingan.
Lang-kah ini identik dengan Penyelesaian persamaan matematika yang diperoleh sebagai model matematika dari permasalahan yang di-hadapi. Langkah ini meliputi menghitung nilai estimasi titik
yang ada pada model dengan menggunakan kaidah- kaidah sta-tistika baik secara analitik maupun numerik.
3. Menarik kesimpulan/ melakukan uji inferensi. Dalam
pe-modelan stokastik, karena peubah yang dihadapi adalah peubah yang bersifat random/ acak maka nilai estimasi titik yang yang diperoleh masih harus dilanjutkan dengan perhitugan estimasi interval/selang keyakinan atau dilanjutkan dengan uji signifi-kansi secara statistika:
(a) bagaimana besaran kesalahan dari dugaan yang diperoleh,
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
41 dari 490
Cari Halaman
Kembali
Layar Penuh
(c) apakah hasil yang diperoleh secara statistika signifikan atau tidak.
4. Melakukan uji kecocokan (goodness of fit) atau mengadakan
diagnostik model. Hasil yang diperoleh selain diuji signifikansinya, mestinya juga diuji kecocokannya dengan kondisi riil dilapangan. Melalui langkah diagnostik diperiksa
(a) apakah ada kecocokan atau tidak antara asumsi yang di-lakukan dengan kondisi riil data;
(b) apakah perlu melalukan remidi (mentransformasi data se-hingga kondisi yang disyaratkan oleh model terpenuhi) atau
(c) apakah perlu mencari alternatif model yang lebih cocok.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
42 dari 490
Cari Halaman
Kembali
Layar Penuh Problem Riil
Solusi Riil (Kesimpulan)
Model Matematika
Menyelesaikan Model/
menyelesaikan
Persamaan
PEMODELAN MATEMATIKA
interpretasi, generalisasi identifikasi, simplifikasi
Verifikasi (Komputasi)
(Uji Model)
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
43 dari 490
Cari Halaman
Kembali
Layar Penuh
Dalam hal pengembangan model statistika, para Teorisi sta-tistika, atau statistisi, menurunkan metode umum/ prosedur dalam mengestimasi parameter, menguji dan mendiagnosis, serta meremidi model yang dibuat. Para praktisi berkewajiban menerapkan metode sesuai dengan persyaratan yang ditentukan atau yang dihasilkan oleh para statistisi. Selain itu, tugas para teorisi statistika (statistisi) ada-lah juga membangun berbagai model alternatif, untuk berbagai kon-disi di lapangan. Kemudian, secara deduktif (matematis) menurunkan sifat- sifat dari model tersebut, cara mengestimasi parameter, cara mendiagnosis model serta mengaplikasikan model-model yang ditu-runkan kedalam suatu paket komputer yang ramah (gampang dipakai dan dipahami) sehingga bisa dipakai oleh para praktisi di lapangan. Lebih tegasnya menurut Mendenhall (1979) dikatakan:
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
44 dari 490
Cari Halaman
Kembali
Layar Penuh
proses pengambilan keputusan untuk kondisi tertentu. Bah-kan lebih jauh mereka menyediaBah-kan informasi berkaitan dengan kecocokan dari suatu prosedur pengambilan kepu-tusan] (Mendenhall [26]).
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
45 dari 490
Cari Halaman
Kembali
Layar Penuh
1.3.
Metode Mengestimasi Parameter
Salah satu langkah pokok dalam pemodelan statistika adalah menges-timasi parameter yang menjadi kepentingan. Dalam analisis regresi, ada dua kelompok parameter yang menjadi kepentingan yaitu yang paling penting adalah parameter efek tetap atau parameter regresi βj
(j = 0,1,2, ..., k) tergantung pada dimensinya) dan biasanya diper-lukan juga mengestimasi parameter dispersi (misalnya,σ, tergantung pada model yang dihadapi). Kadang- kadang parameter dispersi ini diasumsikan diketahui. Ada dua metode yang banyak dipakai dalam mengestimasi parameter efek tetap dalam model linier yaitu:
1. metode kuadrat terkecil (least square method) dan
2. metode likelihood maksimum (maximum likelihood method).
1.3.1.
Metode Kuadrat Terkecil
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
46 dari 490
Cari Halaman
Kembali
Layar Penuh
terkecil (least square), menggunakan pendekatan geometris. Secara geometris, garis yang paling mewakili sebaran sampel adalah garis yang mempunyai simpangan minimum, atau error/galat terkecil dari pencaran data. Untuk memudahkan perhitungan, jarak yang aslinya berupa harga mutlak dari error,|ǫi|diganti dengan kuadrat galat
terse-but, yaitu ǫ2 i.
Langkah langkah dalam mengestimasi parameter dari sampel se-banyak n dengan metode kuadrat terkecil adalah:
1. mengubah persamaan model
yi =xiβ+ǫi menjadi ǫi =xiβ−yi;
2. mencari bentuk kuadrat dan jumlah kuadrat dari galat, yaitu
Q=Pni=1ǫ2 i;
3. menghitung penduga parameter dengan mencari minimum dari
Q terhadap βj.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
47 dari 490
Cari Halaman
Kembali
Layar Penuh
maksimum/ minimum, bukan nilai maksimum/ atau minimum fungsi tersebut. Dalam hal ini yang menjadi kepentingan adalah nilai β, bukan nilai Q.
1.3.2.
Metode Likelihood Maksimum
Kalau metode kuadrat terkecil menggunakan pendekatan geometris, maka metode likelihood maksimum menggunakan pendekatan distribusi. Dari data yang dimiliki serta asumsi distribusi yang diberlakukan pada data tersebut kita memperoleh fungsi likelihood dari data tersebut. Jelasnya langkah tersebut dapat diuraikan sebagai berikut.
1. Tentukan likelihood dari data Y1, Y2,· · · , Yn, yang saling bebas
dan mempunyai fungsi kepadatan peluang masing- masing, mi-salnya ψi(θ). Likelihood keseluruhan ini adalah
L(θ) =
n
Y
i=1
ψi(θ)
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
48 dari 490
Cari Halaman
Kembali
Layar Penuh
2. Tentukan maksimum dariL atau log−L terhadap parameterθ.
Dalam kenyataannya, orang lebih seringmencari maksimum dari fungsi log-likelihood, log (L) dari pada L. Hal ini bisa dilakukan karena yang dicari adalah penyelesaian (nilai variabel y yang meye-babkan terjadinya nilaiLmaksimum) bukan nilai maksimumL. Fungsi log adalah fungsi monoton yang tidak mengubah nilai y yangmenye-babkan L maksimum. Selain itu transformasi logaritma juga mem-berikan beberapa keuntunan dalam perhitungan yaitu menghilangkan exponen dan menyederhanakan produk menjadi jumlah.
ℓ(θ) =
n
X
i=1
log (ψ(θ))
1.3.3.
Mencari Maksimum dengan Metode Numerik
Pada umumnya maksimum suatu fungsi tidak bisa diperoleh secara analitik, oleh karenanya diperlukan pendekatan yang disebut metode numerik. Mencari maksimum/ minimum suatu fungsiF pada dasarnya sama dengan mencari nilai nol atau penyelesaian fungsif(θ) =F′(θ) =
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
49 dari 490
Cari Halaman
Kembali
Layar Penuh
likelihood adalah Metode Newton-Raphson yang merupakan metode iteratif. Langkah- langkah pokok dari metode Newton-Raphson ini dapat diuraikan sebagai berikut:
1. menentukan nilai awal b0
2. melakukan iterasi sampai konvergen (sampai kriteria konver-gensi terpenuhi)
b1 =b0−
F′(b
0)
F′′(b
0)
(1.2)
atau
b1 =b0−
f(b0)
f′(b
0)
(1.3)
dengan f =F′.
Apabila peubah atau parameternya berdimensi tinggi, maka fungsi turunan pertamanya berupa vektor (D) sedang turunan keduanya akan berupa matriks yang disebut matriks Hessian (H). Bentuk mul-tivariat dari Newton- Raphson ini adalah
b1 =b0−D(b0)H
−1
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
50 dari 490
Cari Halaman
Kembali
Layar Penuh
Lebih khusus lagi, dalam statistika matriks Hessian ini kadang kadang lebih sederhana jika diganti dengan negatif dari nilai hara-pannya yang disebut matriks informasi dan dinotasikan I =−E[H]. Persamaan iterasi yang menggunakan matriks informasi dikenal de-ngan metode skoring dari Fisher (Fisher’s scoring) yang ditunjukkan oleh persamaan berikut.
b1 =b0+D(b0)I
−1
(b0) (1.5)
Ada tiga hal penting yang harus diperhatikan dalam mengap-likasikan metode numerik (Newton-Raphson maupun skoring dari Fisher) yaitu: (i) algoritma yang dipakai (lengkap atau terpartisi), (ii) nilai awal dan (iii) kriteria konvergensi.
Nilai awal untuk b0 ditentukan sedemikian sehingga pada saat
itu xb0 = y, sedangkan kriteria konvergensi bisa menggunakan max
(|b1−b0|< δ,) untuk δ bilangan positif sangat kecil, misalnya 10−3.
Jika parameter yng diestimasi terdiri atas beberapa unsur, maka ada beberapa cara yang ditempuh dalam mengestimasi dengan menggu-nakan metode Newton-Raphson yaitu seperti berikut ini.
param-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
51 dari 490
Cari Halaman
Kembali
Layar Penuh
eteryang diestimasi sebagai sebuah vektor penduga. Cara ini disebut pendekatan algoritma penuh. Cara ini cocok apabila setiap unsur dari vektor parameter mempunyai sifat-sifat (kon-vergensi) yang relatif sama.
2. Mengelompokkan unsur-unsur parameter yang sejenis. Unsur-unsur sejenis lalu diberlakukan sebagai suatu vektor. Dengan demikian akan diperoleh lebih dari satu vektor parameter. Ma-sing - maMa-sing vektor parameter yang diestimasi dengan cara multivariate, tetapi pendugaan vektor satu dengan lainnya di-lakukan secara selang-seling. Selang seling dapat didi-lakukan pada setiap iterasi (nested), atau setelah masing- masing konvergen pada kondisi tertentu(zig-zag). Algoritma seperti ini disebut al-goritma terpartisi (partitioned algorithm). Pengelompokan bi-asanya dilakukan berdasarkan parameter regresi (β) dan param-eter dispersi (φ) yang biasanya kedua jenis parameter ini mem-punyai sifat-sifat yang berbeda terutama dilihat dari kecepatan konvergensinya.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
52 dari 490
Cari Halaman
Kembali
Layar Penuh
1.4.
Model Linier dan Perkembangannya
Perkembangan pemodelan stokastik, terutama model linier, dapat di-katakan dimulai pada abad ke 19 yang didasari oleh teori matematika yang diletakkan diantaranya oleh Gauss, Boole, Cayley dan Sylvester yang terkait dengan teori invarian dalam aljabar. Teori invarian al-jabar mempelajari bentuk-bentuk kuantitas yang tidak berubah ter-hadap suatu transformasi linier. Teori invarian ini yang mendasari perkembangan teori nilai eigen, vektor eigen, matriks determinan, metode dekomposisi dan masih banyak lagi yang lainnya. Salah satu contoh dalam statistika kita tahu bahwa korelasi dua peubah acak tidak berubah walaupun peubah- peubah tersebut mengalami trans-formasi.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
53 dari 490
Cari Halaman
Kembali
Layar Penuh
perkembngan model linier lebih dititik beratkan dari dua asumsi dasar yaitu distribusi dan independensi galat.
Sebagaimana diuraikan sebelumnya, bahwa pemodelan dimulai dari yang sederhana, yang secara matematis mudah diselesaikan, ke-mudian berkembang ke arah yang lebih realistik. Hal ini dapat di-lakukan, salah satunya dengan menerapkan berbagai asumsi yang ber-beda terhadap distribusi galat dalam model yang digunakan. Prin-sip seperti ini telah berkembang dari model yang paling sederhana (klasik), ke model hirarkis tergeneralisir yang saat ini merupakan pe-modelan yang paling terkini. Dalam sub-bab ini diuraikan secara ringkas perkembangan model linier ditinjau dari segi distribusi dan independensi galatnya.
1.4.1.
Model linier klasik
Pemodelan linier memiliki bentuk umum
yi = p
X
j=0
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
54 dari 490
Cari Halaman
Kembali
Layar Penuh
Untuk i= 1,2, . . . , n dan j = 1,2, . . . , p, atau dalam bentuk matriks
Y =Xβ+ǫ (1.7)
Dalam hal ini (i) ǫ merupakan galat atau error yang diasumsikan merupakan peubah acak yang memenuhi distribusi tertentu, misal-nya normal; (ii) peubah x adalah peubah tetap yang tidak bersifat acak dan (iii)β adalah parameter yang menentukan koefisien dari pe-ubah pepe-ubah tetap tadi. Dalam ilustrasi pada Contoh 1.1. misalnya, dianggap bahwa sebenarnya ada hubungan yang bersifat tetap yang menentukan harga barang di pasar. Namun, selain itu masih ada lagi faktor lain yang bersifat acak yang menyebabkan harga barang tadi dalam kenyataannya dari pembeli ke pembeli mungkin menyimpang dari fungsi hubungan tadi. Dalam pemodelan statistika/ stokastik, ke-dua komponen ini dipisahkan yaitu yang bersifat tetap dan fungsional dinotasikan denganf(x, β), yang bisa disebut sebagai komponen tetap
(fixed), sedangkan komponen lainnya,ǫ, yang bersifat acak disebut
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
55 dari 490
Cari Halaman
Kembali
Layar Penuh
adalah model linier. Sedangkan dari segi komponen acaknya, yang pal-ing sederhana adalah asumsi bahwa galatnya berdistribusi normal dan saling independen antara satu respon dengan respon lainnya. Asumsi ini menghasilkan model linier normal sederhana atau normal linear
models (NLM). Dari kedua hal tersebut lahirlah yang disebut model
normal sederhana atau model linier klasik yang secara formal dapat diuraikan sebagai berikut.
Definisi 1.3 (Bentuk dan Asumsi Model Linier Klasik).
Model:
yi = k
X
j=0
xijβi+ǫi (1.8)
atau untuk keseluruhan respon dapat dituliskan dalam bentuk matriks seperti persamaan (1.7),
Y=Xβ+ǫ
Asumsi: xi bukan peubah acak dan diukur tanpa galat dan ǫi
in-dependen dengan ǫ′
i untuk setiap i 6= i′ dan masing- masing
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
56 dari 490
Cari Halaman
Kembali
Layar Penuh
Berdasarkan asumsi di atas diperoleh bahwa secara keseluruhan
ǫdapat dianggap berdistribusi multivariat normal (MVN) dengan koe-fisen variasi konstan, yang dinotasikan dengan ǫ ∼ M V N(0, σ2I).
Model mensyaratkan bahwa respon ke i dan kei′ adalah saling bebas (independen), yang berarti tidak ada korelasi diantaranya. Beberapa referensi yang membahas model linier normal ini diantaranya adalah Neter et al. [31], Bowerman et al.[3].
1.4.2.
Model Linier Tercampur
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
57 dari 490
Cari Halaman
Kembali
Layar Penuh
sehingga dianggap kurang pas kalau ditangani dengan metode mul-tivariat biasa. Untuk menangani respon-respon semacam ini model linier klasik di atas lalu dikembangkan menjadi model linier tercam-pur atau linear mixed models (LMM). Dalam model ini hubungan antara respon yang satu dengan lainnya dianggap berasal dari pen-garuh suatu peubah yang tidak kentara atau laten (subjek, misalnya). Untuk itu komponen tetap (f(x)) diuraikan lagi menjadi komponen tetap dan komponen efek acak (random effects). Dengan demikian model ini memiliki dua komponen acak yaitu komponen error (ǫ) dan komponen efek acak yang biasanya dinotasikan dengan u. Model ini biasa disebut model linier tercampur (linear mixed model) yang dapat didefinisikan sebagai berikut.
Definisi 1.4 (Bentuk dan Asumsi Model Linier Tercampur).
Model:
Y =Xβ+Zu+ǫ (1.9)
Asumsi: u ∼ M V N(0, σ2
1I) dan ǫ ∼ M V N(0, σ22I). u independen
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
58 dari 490
Cari Halaman
Kembali
Layar Penuh
Sebenarnya ragam u dapat bervariasi sehingga membentuk ma-triks ragam-koragam dari (Y) yang bervariasi juga. Struktur ma-triks ragam-koragam ini dapat dibentuk sesuai kondisi respon yang dihadapi. Bentuk yang paling sederhana di atas menghasilkan matriks ragam-koragam yang disebut matriksuniformataucompound symme-try atau seragam. Dengan menggunakan jumlah peubah acak yang berdistribusai normal dan saling independen bisa diperoleh bahwa bentuk ragam-koragamY, yang identik dengan jenis korelasi uniform, adalah
atau secara umum
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
59 dari 490
Cari Halaman
Kembali
Layar Penuh
Model ini mengasumsikan bahwa korelasi antara pengamatan satu dan lainnya bersifat konstan (uniform). Struktur lain yang juga banyak diterapkan adalahAuto Regresive1 (AR1) atau disebut ragam-koragam dengan korelasi serial yaitu:
V =φ
Model ini mengasumsikan bahwa seiring dengan jarak yang makin jauh, maka korelasi/ hubungan antara respon tersebut semakin kecil. Dalam beberapa paket komputer, yang dimodelkan adalah struktur korelasinya, bukan matriks ragam-koragamnya.
Model linier tercampur sering juga disebut dengan istilah mo-del linier bertingkat (hierarchical linear model). Istilah bertingkat di-gunakan karena model ini biasa juga didefinisikan secara bertingkat seperti berikut ini.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
60 dari 490
Cari Halaman
Kembali
Layar Penuh
1. Ada efek acakuiyang berhubungan dengan strata atau subjek ke
i,untuk i= 1, ...ndimana antara satu efek acak dengan lainnya saling independen dan berdistribusi normal dengan nilai-tengah 0;
2. Kondisional terhadap efek acak ke i , respon-respon di dalam strata ini juga saling independen dan berdistribusi normal de-ngan nilai-tengah dan ragam konstan.
Model linier Campuran banyak diaplikasikan untuk data yang berasal dari pengukuran berulang yang dikenal dengan data
longitu-dinalataurepeated meassurement. Referensi yang bisa dijadikan acuan
untuk mempelajari model linier bertingkat ini diantaranya adalah Bab 4 dari Davidian dan Giltinan [9], Diggle et al. [10], Laird dan Ware [19]. Sedangkan untuk model yang lebih umum yaitu termasuk model-model non-linier dapat dilihat pada Davidian dan Giltinan [9]
1.4.3.
Model Linier Tergeneralisir
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
61 dari 490
Cari Halaman
Kembali
Layar Penuh
dis-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
62 dari 490
Cari Halaman
Kembali
Layar Penuh
tribusi yang sifatnya lebih umum, dimana distribusi- distribusi yang banyak kita kenal (Normal, Gamma, Poisson) termasuk di dalamnya dan merupakan bentuk- bentuk khusus dari distribusi Keluarga Eks-ponensial. Definisi distribusi Keluarga Eksponensial ini akan dibahas pada bab selanjutnya. Kalau kita simak model linier klasik, kita men-emukan beberapa hal yang sifatnya khas dan istimewa yaitu:
1. ada komponen tetap yang disebut prediktor linier ;
2. responyi berdistribusi normal dan saling independen dan
3. nilai-tengah yi adalah µi =Pkj=0xijβj.
Pada model linier tergeneralisir/terampat, hubungan di atas men-galami perubahan atau generalisasi, sebagaimana dalam definisi ber-ikut:
Definisi 1.6 (Asumsi Model Linier Tergeneralisir). Model linier
ter-generalisir adalah model yang mengandung tiga hal yaitu:
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
63 dari 490
Cari Halaman
Kembali
Layar Penuh
2. respon yi berdistribusi secara independen dalam keluarga
eks-ponensial;
3. hubungan antara nilai-tengah dengan prediktor linier ditunjukkan fungsig(.) yang disebut fungsi ’link’ sedemikian sedinggag(µi) =
ηi. Fungsi g() disebut fungsi hubungan (link-function).
Ada fungsi hubungan khusus yang disebut fungsi hubungankanonik
ataunatural yang berkaitan erat dengan distribusi y. Misalnya, jika
distribusinya normal maka g() adalah identitas. Dari hal di atas di-katakan bahwa komponen penting dalam model linier tergeneralisir ada tiga yaitu:
(i) adanya prediktor linier,
(ii) adanya distribusi keluarga eksponensial dan
(iii) adanya fungsi-hubungan.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
64 dari 490
Cari Halaman
Kembali
Layar Penuh
1.4.4.
Model untuk Data Tidak Normal dan Tidak Saling
Bebas
Seiring dengan semakin luasnya penggunaan metode statistika dalam menganalisis data, maka data yang dihadapi ada kemungkinan tidak saja tidak berdistribusi Normal tetapi juga tidak saling bebas. Untuk menganalisis data semacam ini ada tiga kelompok metode yang banyak dipakai untuk menyelesaikan model linier tercampur tergeneralisir.
GLMM . Model ini merupakan kombinasi antara LMM dan GLM. Pada model ini, walau komponen galat tidak harus berdistribusi Normal, tetapi komponen acaknya masih diasumsikan berdis-tribusi Normal dan menggunakan bentuk aditif seperti pada mo-del linier tercampur normal. Momo-del linier ini biasa disebut seba-gai Model linier tercampur tergeneralisir (GLMM =Generalized
Linear Mixed Model)
Mo-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
65 dari 490
Cari Halaman
Kembali
Layar Penuh
del linier ini termasuk model linier yang relatif baru dan masih sedang dikembangkan (lihat misalnya Lee dan Nelder [20] dan Tirta ([37], [39],[38].
GEE Pendekatan yang relatif lebih praktis, Liang & Zeger [21] dan Zeger & Liang [52] memperkenalkan metode yang disebut
dise-but Generalized Estimating Equations (untuk selanjutnya
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
66 dari 490
Cari Halaman
Independen? Dependen
(Multi kolinieritas)?
RKU Seleksi Variabel
R. BERTATAR STEPWISE
Var.Laten? REGRESI
GULUD (RIDGE)
SEM
Pencilan/Outlier?
REGRESI ROBUST
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
67 dari 490
Cari Halaman
Kembali
Layar Penuh
1.4.5.
Pengembangan Lain Model Linier
Selain berkembang akibat variasi asumsi distribusi dari galat, model linier juga berkembang ke arah variasi kondisi peubah bebas atau pe-ubah penjelas X, seperti ditujukkan oleh Gambar 1.2. Asumsi dasar dari peubahX adalah bukan peubah acak (tidak memiliki distribusi) dan merupakan besaran kuantitatif.
Dalam perkembangannya, ada kalanya Xj, j = 0,1,2,3, . . . , p−
1 merupakan peubah acak sedangkan Xj dan Xj′ tidak saling bebas
untuk suatuj 6=j′, dalam kondisi seperti ini, dikatakan terjadi
multi-kolinieritasantara peubah bebasX. Tingginya multikolinieritas dapat
menyebabkan adanya estimasi parameter tidak teliti. Secara matema-tisXj danXj′ yang tidak saling bebas, menunjukkan bahwa salah satu
kolom matriksX merupakan kombinasi linier linier dari kolom-kolom lainnya yang menyebabkanXtidak dalam rank penuh, sehingga invers matriks XTX menjadi tidak terdefinisikan. Ada beberapa prosedur
atau tehnik untuk menangani masalah multikolinieritas, diantaranya adalah regresi Ridge dan Regresi dengan Komponen Utama (RKU) (lihat Neter et al[31]).
sesungguh-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
68 dari 490
Cari Halaman
Kembali
Layar Penuh
nya merupakan sekumpulan dari berapa kelompok data atau sampel sesungguhnya terdiri atas beberapa subsampel. Persoalan yang di-hadapi adalah apakah model (garis regresi) masing- masing kelompok harus berbeda atau dapat digabung dalam satu model yang sama. Dalam hal ini sebagian peubah penjelas Xj akan merupakan peubah
kualitatif, atau merupakan indikator kelompok atau grup dari kelom-pok yang ada pada data, sampel maupun populasi. Analisis model linier yang menangani data semacam ini menggunakan peuban boneka
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
69 dari 490
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
70 dari 490
Cari Halaman
Kembali
Layar Penuh
1.5.
Model-model Nonlinier
Pada model-model yang telah dibicarakan sebelumnya, ada ciri khas hubungan antara parameter dan peubah prediktornya, yaitu adanya kombinasi linier antara peubah prediktor dengan parameter regresinya (yaitu ηi =Ppi=1xijβj. Sementara itu hubungan antara µi dengan ηi
tidak selalu linier (misalnya log, resiprokal dan lain-lain). Ciri-ciri tersebut menyebabkan model yang telah dibicarakan masih termasuk kelompok model linier.
Perkembangan lain dari model statistika tidak mewajibkan ada-nya kombinasi linier (ηi), tetapi mengadopsi bentuk yang lebih luas
yaitu polinomial atau bentuk aditif, η(x) = α+Ppj=1fj(xj).
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
71 dari 490
Cari Halaman
Kembali
Layar Penuh
1.6.
Tinjauan singkat Program Statistika R
Penggunaan piranti lunak komputer dalam analisis regresi hampir tidak bisa ditunda lagi. Selain untuk mempercepat proses perhitun-gan, penggunaan piranti lunak memungkinkan peneliti atau analis data dapat melakukan dengan cepat (i) berbagai alternatif model (baik dilihat dari jenis sebaran, jenis hubungan serta jumlah peu-bah yang dimuat) serta memilih model yang terbaik; (ii) melengkapi hasil analissi data secara numerik dengan visualisasi grafik yang dapat membantu pemahaman dalam menginterpretasi model. Dalam sub-bab ini akan dibahas secara singkat beberapa kemampuan R terkait pemodelan statistika atau analisis regresi, diantaranya:
1. kemampuan umum terkait cara mengaktifkan paket, melihat-dokumentasi paket termasuk contoh penggunaannya;
2. kemampuan manipulasi grafik terkait pemeriksaan asumsi mo-del yang dipergunakan dan visualisasi untuk melengkapi hasil analisis secara numerik;
re-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
72 dari 490
Cari Halaman
Kembali
Layar Penuh
gresi mulai dari yang paling sederhana (regresi klasik) sampai yang sangat kompleks (respon nonnormal dan tidak saling be-bas, hubungan nonlinier).
R adalah piranti lunak utuk analisis data dan penyajian grafik yang berbasis Open Sources. Sebagian besar kemampuan R hanya bisa dimanfaatkan melalio pendekatanCLI (command line interface), yaitu dengan mengirim perintah dalam bentuk kumpulan perintah baris atau skrip. Hanya sebagian kecil kemampuan R yang dapat dimafaatkan melaui menu grafis GUI(graphical user interface) Ada dua cara memanfaatkan R melalui CLI.
1. Menulis perintah langsung pada Rconsole. Untuk pertintah-perintah singkat yang jarang diulang, biasanya langsung ditulis pada layar Rconsole.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
73 dari 490
Cari Halaman
Kembali
Layar Penuh
keseluruhan sesuai kebutuhan. Untuk mengaktifkan editor skrip pada R dapat dilakukan langkah berikut:
(a) Pada menu File pilih New Script atau Open Script
(b) setelah perintah ditulis pada layar editor eksekusinya dapat dilakukan dengan mengaktifkan menu Edit pada Editor, selanjutnya bisa pilih run lines atau run all
Hampir semua paket atau Pustaka R yang terkait dengan ana-lisis data tingkat lanjut (advanced statistical analyses), termasuk re-gresi hanya bisa dimanfaatkan melalui pendekatan perintah baris atau skrip. Hanya sebagian kecil dan yang masih bersifat mendasar yang dapat dimanfaatkan melalui pendekatan menu, misalnya RComman-der (lihat Tirta [43]. Untuk itu, pembaca perlu memahami cara me-manfaatkan R melalui skrip (Untuk dokumentasi lebih detail dapat dilihat pada Tirta [42]). Secara umum ada beberapa perintah pen-ting yang perlu dikuasai untuk dapat memanfaatkan R dengan baik yaitu:(i) cara mengaktifkan paket, (ii) melihat dokumentasi paket, (iii) menjalankan contoh pada paket.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
74 dari 490
Cari Halaman
Kembali
Layar Penuh
yang dikemas dalam bentuk paket. Paket yang dimiliki R belum bisa dimanfaatkan sampai paket itu diaktifkan. Ada dua cara mengaktifkan suatu paket yaitu.
library(nama_paket) require(nama_paket)
Misalnya untuk mengaktifkan paket gee, kita dapat memanggil dengan salah satu cara berikut.
library(gee) require(gee)
Jika dilakukan akan muncul pesan
Loading require package: gee
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
75 dari 490
Cari Halaman
Kembali
Layar Penuh
cara memanggil dokumentasi paket, dengan contoh khusus paket gee.
help(nama_paket) ?nama_paket help(gee) ?gee
Setelah perintah tersebut dijalankan, maka akan muncul doku-mentasi tentang paket gee, diantaranya berisi (i) cara meman-faatkan paket gee,(ii) jenis dan interpretasi keluaran gee, (iii) referensi terkait gee, serta (iv) contoh penggunaan gee.
3. Menjalankan contoh-contoh pada paket. Satu paket R dapat terdiri atas beberapafungsi analisis. untuk menjalankan contoh-contoh fungsi pada paket dapat ditempuh dua cara. (Paket gee secara kebetulanjuga memuat fungsi analissi yang disebut gee).
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
76 dari 490
Cari Halaman
Kembali
Layar Penuh
example(nama_fungsi) example(gee)
(b) Dengan menyalin teks pada contoh; dengan cara ini teks contoh yang ada pada dokumentasi, disalin (copy) lalu ditem-pelkan (paste) pada Rconsole.
4. Menyimpan objek dan memeriksa komponen objek. Hasil perhi-tungan dengan R biasanya disimpan dalam bentuk objek.
Kom-ponen objek dapat dilihat dengan menggunakan perintahnames(nama_objek).
nama_objek<-fungsi names(nama_objek)
Sebagai contoh komponen objek yang dihasilkan oleh analisis model linier dapat ditujnukkan pada tampilan berikut.
lm1<-lm(y~x) names(lm1)
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
77 dari 490
Cari Halaman
Kembali
Layar Penuh
Selanjutnya untuk mencetak sebagian komponen dari objek ber-sangkutan dilakukan dengan perintah
newline print(objek$komponen)).
Berikut adalah perintah dan hasil keluaran yang dilakukan pada objek lm1 di atas.
> print(lm1$coeff) (Intercept) x -3.317963 3.111967
>print(lm1$call) lm(formula = y ~ x)
1.6.1.
Aplikasi R untuk Manipulasi Grafik
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
78 dari 490
Cari Halaman
Kembali
Layar Penuh
diagram pencar sisa), juga bermanfaat dalam memberikan visualisasi model (diagram pencar data yang dilengkapi garis regresi, khususnya untuk dua dimensi). Tabel 1.2 memuat beberapa paket dan fungsi yang terkait dengan penyajian grafik dalam analisis regresi.
Visualisai tentang sebaran data baik terkait sebaran univariat, maupun pencaran bivariat dapat disajikan dalam berbagai cara ( lay-out), misalnya menyisipkan grafik kecil dalam grafik besar, atau
mem-bagi lay out layar. Informasi lebih lengkap dapat dilihat pada Tirta
[42] atau Burns [4]. Berikut adalah beberapa contoh penyajian grafik terkait regresi.
1. Histogram dilengkapi dengan kurva densitas (baik teoritis mau-pun emperik). Grafik ini memberikan gambaran secara intuitif kesesuaian sebaran data dengan sebaran teoritis yang menjadi asumsi (skrip berikut hasilnya terlihat pada Gambar 1.4).
hist(x,freq=FALSE,ylim=c(0,0.45),
main="HISTOGRAM DENGAN KURVA DENSITAS") lines(density(x),lty=4) #densitas emperik
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
79 dari 490
Cari Halaman
Kembali
Layar Penuh Tabel 1.2: Fungsi dan paket untuk menggambar grafik R
Fungsi Paket Penggunaan
barplot() graphics menggambar grafik batang
hist() graphics menggambar histogram
boxplot() graphics menggambar boxplot
plot() graphics menggambar grafik X-Y
pairs() graphics menggambar Matriks Dia-gram Pencar
abline() graphics menggambar garis lurus yang diketahui konstanta dan gradiennya
contour() graphics menggambar kontur
persp() graphics menggambar boxplot
rug() graphics menggambar sebaran data pada sumbu
qq.plot() car menggambar plot per-bandingan kuantil
reg.line() car menggambar garis regresi
pen-FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
80 dari 490
Cari Halaman
Kembali
Layar Penuh
2. Diagram pencar dilengkapi dengan rugplot dan boxplot marjinal (untuk peubah penjelas dan peubah respon). Grafik ini mem-berikan gambaran secara intuitif kesesuaian sebaran data secara univariate (skrip berikut hasilnya terlihat pada Gambar 1.5)
plot(x,y,xlab="X", ylab="Y",col="red",
main="DIAGRAM PENCAR DENGAN RUG & BOXPLOT") abline(lm(y~x),col="blue")
rug(side=1, jitter(x, 5),col="green" ) rug(side=2, jitter(y, 20),col="green" )
par(mar=c(1,2,5,1)) boxplot(y, axes=F)
par(mar=c(5,1,1,2))
boxplot(x, horizontal=T, axes=F)
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
81 dari 490
Cari Halaman
Kembali
Layar Penuh
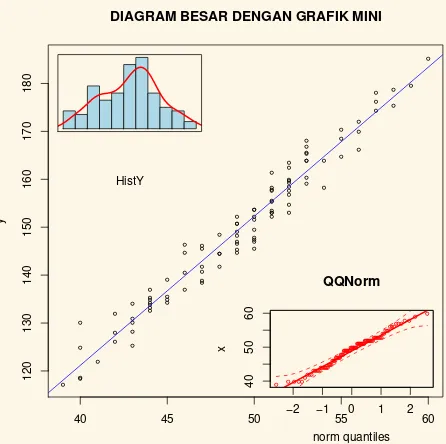
dalam diagram pencar (lihat Gambar 1.6) atau dengan mengatur lay out tampilan grafik seperti Gambar1.7dan Gambar1.8. Berikut adalah skrip untuk Layout c(1,2)-c(2,1), untuk Gambar 1.7, yaitu pertama layar dibagi atas 1 baris dan 2 kolom, selanjutnya layar kolom kedua dibagi menjadi 2 baris 1 kolom.
split.screen(c(1,2))
split.screen(c(2,1), screen = 2) screen(1)
plot(x,y,main="Diagram Pencar (X,Y)") abline(lm(y~x))
screen(3)
hist(y, probability=T, main="Histogram Y")
lines(density(y), col="red", lwd=2) screen(4)
qq.plot(x,main="QQ.norm X")
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
82 dari 490
Cari Halaman
Kembali
Layar Penuh split.screen(c(2,1))
split.screen(c(1,2), screen = 2) screen(1)
plot(x,y,main="Diagram Pencar (X,Y)") abline(lm(y~x))
screen(3)
hist(y, probability=T, main="Histogram Y")
lines(density(y), col="red", lwd=2) screen(4)
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
83 dari 490
Cari Halaman
Kembali
Layar Penuh
HISTOGRAM DENGAN KURVA DENSITAS
x
Density
−3 −2 −1 0 1 2
0.0
0.1
0.2
0.3
0.4
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
84 dari 490
Cari Halaman
DIAGRAM PENCAR DENGAN RUG & BOXPLOT
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
85 dari 490
Cari Halaman
DIAGRAM BESAR DENGAN GRAFIK MINI
x
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
86 dari 490
Cari Halaman
Diagram Pencar (X,Y)
x
y
Histogram Y
y
Frequency
120 140 160 180
0
Diagram Pencar (X,Y)
x
y
Histogram Y
y
Frequency
120 140 160 180
0
Diagram Pencar (X,Y)
x
y
Histogram Y
y
Frequency
120 140 160 180
0
Diagram Pencar (X,Y)
x
y
Histogram Y
y
Frequency
120 140 160 180
0
Diagram Pencar (X,Y)
x
y
Histogram Y
y
Frequency
120 140 160 180
0
Diagram Pencar (X,Y)
x
y
Histogram Y
y
Density
120 140 160 180
0.000
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
87 dari 490
Cari Halaman
Diagram Pencar (X,Y)
x
y
Histogram Y
y
Density
120 140 160 180
0.000
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
88 dari 490
Cari Halaman
Kembali
Layar Penuh
1.6.2.
Aplikasi R untuk Model Statistika/ Analisis Regresi
Analisis regresi menggunakan R tersebar dalam banyak paket, di-antaranya ada yang telah terintegrasi dengan paket minimal R ada pula yang harus diinstal dan dipanggil secara khusus. Berikut ada-lah fungsi-fungsi yang dipakai menganalisis model linier beserta paket yang memuatnya.
Fungsi dan paket untuk model statistika dalam R
Fungsi Paket Penggunaan
lm() stats regresi/model linier dengan respon
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
89 dari 490
Cari Halaman
Kembali
Layar Penuh
glm() stats regresi/model linier dengan respon berdistribusi Keluarga Eksponensial termasuk distribusi Normal denganre-spon masih saling bebas. Paket ini telah terintegrasi dengan R dan su-dah dapat dimanfaatkan melalui menu RCommander
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
90 dari 490
Cari Halaman
Kembali
Layar Penuh
glmmML()glmmML *)
regresi dengan respon berdistribusi Keluarga Eksponensial denganpen-dekatan Likelihood Maksimum
lrm() Design *) Khusus untuk data dengan respon berdistribusi Binomial dan fungsi hu-bungan logit
gee() gee *) regresi dengan dengan respon berdis-tribusi Keluarga Eksponensial dan tidak saling bebas
geese() geepack *)
regresi linier dengan dengan respon berdistribusi Keluarga Eksponensial dan tidak saling bebas. Hampir sama dengan gee(), tetapi memiliki alnatif pemodelan yang lebih luwes ter-masuk pemodelan koragamnya
gam() gam, mgcv
regresi atau model statistika dengan hubungan yang lebih luas termasuk noonlinier dan semiparamerik
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
91 dari 490
Cari Halaman
Kembali
Layar Penuh
*) menunjukkan bahwa paket harus diinstal secara khusus
1.6.3.
RCommnder RGUI untuk analisis dasar
Ada RGUI yang disebut RCommander yang telah menyediakan bebe-rapa analisis regresi mendasar melalui menu grafis, diantaranya:
1. regresi linier klasik sederhana (satu peubah bebas dan satu pe-ubah penjelas);
2. model linier klasik dengan beberapa peubah poenjelas termasuk peubah kualitatif;
3. GLM (model linier terampat/ tergeneralisir).
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
92 dari 490
Cari Halaman
Kembali
Layar Penuh
1.7.
Ringkasan
Hal-hal penting yang perlu dipahami dalam bab ini adalah seperti berikut.
1. Pemodelan stokastik mengandung komponen tetap yang meru-pakan komponen regresi dan komponen kesalahan yang bersifat acak yang memiliki sebaran tertentu;
2. Kepentingan utama dalam analisis model stokastik (analisis re-gresi) adalah mengestimasi koefisien komponen tetap (parameter regresi).
3. Metode yang biasa dipakai untuk mengestimasi koefisien regresi adalah metode kuadrat terkecil dan metode kecenderungan mak-simum.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
93 dari 490
Cari Halaman
Kembali
Layar Penuh
5. Untuk komponen acak yang bersebaran normal dan saling bebas, analisisnya biasa disebut model linier normal.
6. Untuk komponen acak yang tidak bersebaran normal, tetapi masih dalam sebaran keluarga eksponensial dan masih saling bebas, analisisnya biasa disebut model linier tergeneralisir (ter-ampat).
7. Berbagai pendekatan telah dikembangkan untuk komponen acak yang masih bersebaran keluarga eksponensial tetapi tidak saling bebas, diantaranya adalah GEE, GLMM, dan HGLM.
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
94 dari 490
Cari Halaman
Kembali
Layar Penuh
1.8.
Bacaan Lebih Lanjut
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
95 dari 490
Cari Halaman
Kembali
Layar Penuh
1.9.
Latihan
1. Jelaskan apa perbedaan penting antara pemodelan matematika secara umum dan pemodelan statistika.
2. Sebutkan langkah-langkah penting pemodelan statistika.
3. Sebutkan beberapa macam pemodelan statistika linier yang anda kenal dilihat dari asumsi distribusi dan kebergantungannya.
4. Sebutkan beberapa macam pemodelan statistika nonlinier yang anda kenal.
5. Carilah referensi yang terkait dengan pemodelan statistika linier baik di perpustakaan maupun di internet. Sebutkan masing- ma-sing lima referensi yang belum terdaftar dalam Daftar Pustaka dari buku ini.
6. Lakukan eksplorasi pada R
FMIPA-UNEJ
Daftar Isi
Judul
◭◭ ◭ ◮ ◮◮
96 dari 490
Cari Halaman
Kembali
Layar Penuh
(b) buat tampilan jendela grafik dengan berbagaioutline.
(c) buat histogram dengan dilengkapi judul dan kurva sebaran; (d) buat diagram pencar yang dilengkapi dengan marjin
box-plot;
(e) bagaimana menggunakan fungsi lm()};
(f) sebutkan komponen objek yang dihasilkan dari fungsilm(); (g) jalankan contoh analisis regresi dengan glm;
(h) periksa komponen-komponen objek yang dihasilkan oleh fungsi glm.
7. Lakukan eksplorasi pada RCommander:
(a) panggil salah satu data dari pustaka yang ada;
(b) sebutkan grafik yang dapat dibuat melalui menu RCom-mander;.
(c) aktifkan plugin terkait demo/animasi statistika;