THE DIFFERENCE OF STUDENTS MATHEMATICAL REPRESENTATION ABILITY BY USING COOPERATIVE LEARNING MODEL TYPE TEAMS GAMES TOURNAMENT AND CONVENTIONAL LEARNING IN GRADE VIII SMP NEGERI 1 TANJUNG MORAWA ACADEMIC YEAR 2014/2015.

(1)

By :

Mhd.Surya Pohan ID. 4103312020

Bilingual Mathematics Education

THESIS

Submitted to Fulfill the Requirement for Sarjana Pendidikan Degree

MATHEMATICS DEPARTMENT

FACULTY OF MATHEMATICS AND NATURAL SCIENCES

MEDAN STATE UNIVERSITY

(2)

iv

ACKNOWLEDGEMENT

Alhamdulillah, Praise and great attitude to Allah SWT for the mercy and

help to complete this thesis on time. Shalawat and salaam to Prophet Muhammad

SAW, family and his friends. Thesis entitled “The Difference of Student’s Mathematical Representation Ability by Using Cooperative Learning Model Type

Teams Games Tournament and Conventional Learning in Grade VIII SMP Negeri

1 Tanjung Morawa Academic Year 2014/2015” submitted in partial fulfilment of

the requirements for Mathematics Education Bachelor’s Degree Faculty of Mathematics and Natural Science in State University of Medan.

For this chance I want to say thank you to supervisor Prof. Dr. Edi

Syahputra, M.Pd for providing guidance, ideas, motivation and advice. The warm

thanks go to Prof. Dr. Sahat Saragih, M.Pd, Prof. Dr. Pargaulan Siagian, M.Pd,

Mulyono, S.Si, M.Si for guidance, advice and reviewing this thesis also big thanks

to Drs. Sahat Siahan, M.Pd as academic supervisor and then thank you so much

for all my lecturer.

Great thanks are extended to Prof. Dr. Ibnu Hajar, M. Si. as rector of

State University of Medan and employee staff in office of university head, Prof.

Drs. Motlan, M.Sc., Ph.D as Dean Faculty of Mathematics and Natural Sciences

and to coordinator of bilingual Prof. Dr. rer.nat. Binari Manurung, M.Si., Drs.

Syafari, M. Pd. as Chief of Mathematics Department, Zul Amry, M. Si. as Chief

of Mathematics Education Study Program, Drs. Yasifati Hia, M. Si as Secretary of

Mathematics Education, and all of employee staff who have helped the author.

Great thanks are extended to Mr. Elfian Lubis as principal school in

SMP Negeri 1 Tanjung Morawa for providing permit research. The warm thanks

go to Mom Duena as mathematics teacher in SMP Negeri 1 Tanjung Morawa for

providing guidance, advice in the implementation of research.

Special thanks to beloved father Abdul Hasyim Pohan, S.Ag and beloved

mother Maryam Siregar for love, pray, motivation, encouragement and giving

great contribution in terms of material, spiritual to complete study in this

(3)

v

Arwansyah Harahap younger brother Hasmar Pohan are always exemplifies the

best attitude for the sake of personal development author. And then thanks to

beloved nephew Asyifa Arwansyah and Aufa Arwansyah for giving joy and spirit

very deep.

The warm thanks to best friends in Bilingual Mathematics Education

2010, Abdul, Anggi, Dian, Dwi, Elfan, Erlin, Kiki, Falni, Lia, Mila, Maria,

Martyanne, Melin, Nelly, Petra, Riny, Rully, Sartika, Shela, Siti, Wulida, Zulika

for providing spirit, motivation, pray, also support. Also thanks to Retni Triandini,

Mhd Arief, Satria Pratama, Ridho Pahwan Kasio, Julizar Mutaqqin, Agung,

Christine and Helma also everyone who has ever known the author for the spirit

and help to complete this thesis.

The author has given maximum effort to compiling this thesis but the

author is aware that this thesis have many weakness. So that, the author needs

some suggestions, criticism for reader to make this thesis be better. Hopefully this

thesis can be useful for us and become the input for the parties in need.

Medan, 2014

Writer,

(4)

vi

1.2. Problem Identification 9

1.3. Problem Limitation 9

1.4. Problem Formulation 10

1.5. Research Objectives 10

1.6. Research Benefits 10

1.7. Operational Definition 11

CHAPTER II LITERATURE REVIEW 13

2.1. Theoretical Framework 13

2.1.1. Representation 13

2.1.2. Representation in Mathematics 13

2.1.3. Mathematical Representation Ability 15

2.1.4. Cooperative Learning Model 18

2.1.4.1. The Steps of Cooperative Learning Model 20 2.1.4.2. Cooperative Learning Model Type

Teams Games Tournament Model 21 2.1.5. Relationship between Cooperative Learning Model

Type Teams Games Tournament to Student’s

Mathematical Representation Ability 25

2.1.6. Conventional Learning Model 27

2.1.7. The Comparison between Cooperative Learning Model Type Teams Games Tournament and

(5)

2.1.8. Learning Theory Support 30 2.1.8.1. Learning Theory Support by Vygotsky 30 2.1.8.2. Learning Theory Support by Brunner 31

2.2. Conceptual Framework 33

2.3. Action Hypothesis 35

CHAPTER III RESEARCH METHODOLOGY 36

3.1. Location and Time of Research 36

3.2. Population and Sample of Research 36

3.3. Variable of Research 36

3.3.1. Independent Variable 37

3.3.2. Dependent Variable 37

3.6.3. Test of Mathematical Representation Ability of Students 40

3.6.3.1. Validity of Test 43

3.6.3.2. Reliability of Test 45

3.7. Data Analysis Technique 46

3.7.1 Observation Sheet 46

3.7.2 Normalized Gain (N- Gain) 47

3.7.3 Normality Test 48

3.7.4 Homogenous Test 48

3.7.5 Hypotheses Test 49

CHAPTER IV RESULT AND DISCUSSION 51

4.1. Result of Research

4.1.1. The Description of Students’ Mathematical Representation

Ability 51

4.1.2. Analysis of Research Data 56

4.1.2.1. Normality Test 56

4.1.2.2. Homogeneity Test 59

4.1.2.3. Compare Means Test (One Tailed) 61 4.1.2.4. Analysis of Observation Sheet 64

4.2. Discussion of Research 66

(6)

viii

CHAPTER V CONCLUSION AND SUGGESTION 70

5.1 Conclusion 70

5.2 Suggestion 70

REFFERENCE 71

(7)

LIST OF TABLES

Page Table 2.1. Indicator of Mathematical Representation Ability

Table 2.2. The Syntaxes of Cooperative Learning

17 20

Table 2.3. Award Criteria Group 24

Table 2.4. The Comparison Between Cooperative Learning type Teams

Games Tournament and Conventional Learning 24 Table 2.5 The Syntaxes of Conventional Learning

Table 2.6. The Comparison between Cooperative Learning Model Type Teams Games Tournament and Conventional Learning

28

29 Table 3.1 The Blueprint of Mathematical Representation Ability Problem 41 Table 3.2. The Rubric of Mathematical Representation Ability Problem 42

Table 3.3. Classification of Validity Interpretation 44 Table 3.4. Validity Testing of Each Instrument test (Pretest) 44

Table 3.5. Validity Testing of Each Instrument Test (Posttest) 45 Table 3.6. Classification of Reability Interpretation

Table 3.7 Criteria of Observation Sheet Table 3.8. Criteria of Gain Index

Table 4.1 Pretest of Mathematical Representation Ability Table 4.2 Posttest of Mathematical Representation Ability Table 4.3 N-Gain of Mathematical Representation Ability

Table 5.2. The Observation Results of Teacher Activity in Classroom Table 5.3. The Observation Results of Students Activity in Classroom

(8)

ix

LIST OF FIGURES

Page Figure 1.1. Observation Result of Student’s Answer Number One 5

Figure 1.2. Observation Result of Student’s Answer Number Two 5

Figure 1.3. Observation Result of Student’s Answer Number Three 6

Figure 2.1. The Relationship between Internal and External Representation in Developing Child’s Understanding of the Concept of Numeracy

Figure 2.2. Placement of Table Tournament

Figure 2.2. The Relationship between Teams Games Tournament and Student’s Mathematical Representation Ability

Figure 3.1. Procedure of Research

Figure 4.1. The Diagram of Students’ Mathematical Representation Ability (Pretest)

Figure 4.2. The Diagram of Students’ Mathematical Representation Ability (Posttest)

Figure 4.3. The Diagram of Students’ Mathematical Representation Ability (N-Gain)

15 23

26 39 54

55

(9)

LIST OF APPENDICES

Appendix 1 The Blueprint of Mathematical Representation Ability Initial

Test 74

Appendix 2 Initial Test of Mathematical Representation Ability 75

Appendix 3 Alternative Solution of Mathematical Representation Ability 77

Appendix 4 Lesson Plan of Experiment Class ( Meeting 1) 79

Appendix 7 Student Activity Sheet (Meeting 1) 104

Appendix 10 Problem of Games Tournament (Meeting 1) 128

Appendix 13 Lesson Plan of Control Class 1 143

Appendix 16 Blueprint of Research Instrument 155

Appendix 17 Mathematical Representation Ability Test (Pretest) 156

Appendix 18 The Alternative Solution of Mathematical Representation

Ability Test (Pretest) 159

Appendix 19 Mathematical Representation Ability Test (Posttest) 163

Appendix 20 The Alternative Solution of Mathematical Representation

Ability Test (Posttest) 166

Appendix 21 Scoring Guideline of Mathematical Representation Ability

Test

170

Appendix 22 Data Distribution of Experiment Class 172

(10)

xii

Appendix 24 N-Gain Criteria of Experiment Class 174

Appendix 25 N-Gain Criteria of Control Class 175

Appendix 26 Validity Test (Pretest) 176

Appendix 27 Reliability Test (Pretest) 181

Appendix 28 Validity Test (Posttest) 183

Appendix 29 Reliability Test (Posttest) 188

Appendix 30 Normality Test 190

Appendix 31 Homogeneity Test 193

Appendix 32 Hypothesis Test 196

Appendix 33 The Value of r-Product Moment 201

Appendix 34 Table of Critical Value in Kolmogorov – Smirnov Test 202

Appendix 35 The Value of t-Distribution 203

Appendix 36 Research Documentation

Appendix 37 Requirement Letters

204

(11)

CHAPTER I

INTRODUCTION

1.1. Background

Modern era faced by Indonesia at this time requires quality human

resources were able to compete with other countries and have the maximum

advantage. One factor in achieving this is education, so that the quality of

education in Indonesia must have improvement in all aspects. Since according by

Undang-Undang Number 20 Year 2003 about National Education System (in

Trianto, 2009: 1) state that national education serves to develop of ability and

character formation also civilization which dignity in order to educate life of

nation.

Therefore, the education in Indonesia must be increased so that the

function of national education that have been implemented in Undang-Undang

can be done well so that Indonesian education has good quality and able to

compete with other countries. Increasing of education in Indonesia can be done by

improving the educational system, especially of learning strategies in the

classroom so that to create learning process maximally. This situation can be

realized if the educational atmosphere in Indonesia have adequate access such as

the use of learning tools, the quality of teaching and learning models and

strategies are applied.

National education system put mathematics as compulsory subject given

to students from elementary to secondary school. This situation caused since

mathematics as a subject has important rule in countries progress. Santosa, (in

Hudojo, 2005: 25)state that mathematics has important rule on progress countries

namely 60% - 80% while Slameto (2010: 45)state that if the success of country

can be seen from mathematics progress since mathematics as a way to represent

all of science.

Hutagaol (2013) state that mathematics learning objectives at every level

of education is developing mathematical thinking ability of students which this

(12)

2

concept and apply it in various situation. Therefore, the students must be able to

develop their mathematical thinking ability in mathematics learning since the

situation is important to understanding of students in mathematics learning.

In learning mathematics, students must have comperhension, skills, and

knowledge which is this aspects are known and can be done by teachers and

students on learning mathematics in a school. National Council Teacher of

Mathematics or NCTM (in Effendi: 2012) states that the expected goals in

learning mathematics are to set of five process standard that must be owned by

students namely problem solving ability, communication ability, connection

ability, reasoning ability, and representation ability. As stated by Fadillah (2011)

that besides solving problem ability, reasoning, communication, and connection,

entering representation as component of standard process in Principles and

Standards for School Mathematics is very exact since for mathematical thinking

and communicating of mathematical ideas, the students needs to represent on various form of mathematical representation. Moreover can’t be denied that mathematic objects are abstract so that to learn and understanding of abstract

ideas require representation.

Meanwhile, Jones (in Fadillah: 2011) also explain three reason why

representation as a standard process, namely (1) basic ability must be owned of

students to build a concept and mathematical thinking is doing translation on

various representation type smoothly; (2) the teacher should be provide

mathematical ideas through various representation since the situation can provide

enormous influence to students in learning mathematics; and (3) teacher should

provide various exercise to students since the students really need these exercise

to build their representation so that have ability and good understanding of

concept and flexible can be used on provlem solving.

This is consistent with the opinions expressed by Yuniawatika (2011)

said that students can be encouraged to find and create various representations that

could be used as a thinking way in expressing of students' knowledge from

(13)

representation ability as a way to increase and expressing of mathematical

thinking ability of students.

Rahmi (in Hutagaol: 2013) said that diagram, picture, table, chart,

mathematical statement, written text, also combination of all as representation

variety can be used of students in expressing mathematical ideas of students.

Variety of representation like as table, picture, graph, and another symbol are part of mathematics that can’t be separated since mathematical representation as a part of mathematics.

But based on last situation, mathematical representation ability of

students in school less attention since many student who dont understand to

mathematical representation ability. Though mathematical representation ability is

very important in learning mathematics since facilitating the students to represent

problem in form of mathematical visual object which is more interesting.

As stated by Hudiono, (in Fadillah: 2011) is in his research on learning mathematics at Junior High School conclude that the lack of teacher’s knowledge and learning habits of students using conventional learning has not been possible

to develop representation power of students maximally. Accordingly, NCTM (in

Fadillah: 2011) also said that mathematical representation ability of students is

very limited since seen from ability of students in solving mathematical problem

which students tend to see critical elements of mathematical problem that dominated in symbolic representation so don’t pay attention to other representation. As’ari (in Fatayati: 2012) also said that the students did not just

understand abstract ideas contained in mathematics but the abstract idea must be

expressed in different forms of representation and easily understood of students

such as in the form of images, symbols, and words since the representation is one

of alternative forms can be used to solve problems in mathematics.

From problem result which addressed to some students in grade VIII at

SMP Negeri 1 Tanjung Morawa, it was found that the mathematical

representation ability of students is still less, since can be seen from some of

(14)

4

representation to table representation, making the mathematical model from other

representations are given, also solving problems involving mathematical

expressions and the students have not been exact in answering questions using a

written text.

Here are question and student’s answer which are given in order to know the mathematical representation ability of students, namely:

1. A farmer has 4 rectangular land as shown below:

From the picture above, fill in the table below:

2. Known that the price of a shoes pair is twice the price of a sandals pair.

The trader must pray as Rp275.000,00 . Determine the price of 3 pairs of

shoes and 5 pairs of sandals and first determine the mathematical model

from problem above.

(15)

3. Based on these equations, which one the linear equations of two variable?

Give your reason!

The result of student’s answer:

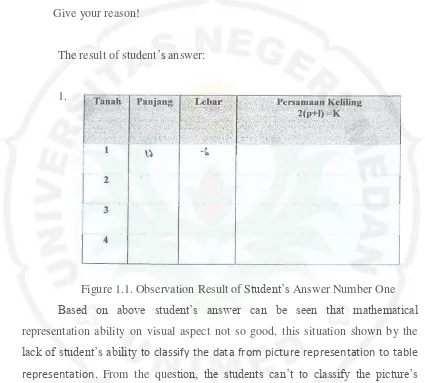
1.

Figure 1.1. Observation Result of Student’s Answer Number One Based on above student’s answer can be seen that mathematical representation ability on visual aspect not so good, this situation shown by the lack of student’s ability to classify the data from picture representation to table representation. From the question, the students can’t to classify the picture’s

information namely length, wide and equation of circumference to the table since lack of students’ visual representation ability.

2.

(16)

6

Based on above student’s answer can be seen that mathematical representation ability on equation or mathematical expression aspects is not satisfactory, this situation shown from student’s answer that student have not been able to make equation, mathematical model, and using mathematical expression.

3.

Figure 1.3. Observation result of student’s answer number three

The purpose given the question number 3 is to expect the students able to

represent their reason or ideas from question representation given into written text, but from above student’s answer can be seen that mathematical representation ability on written text aspect is also not satisfactory since student

have not been able to express the ideas or their reason into written text.

From 31 students who answer the question, can be seen 51.61% of

students have not been able to build of their visual representation in drawing right

triangle exactly, while 86.29% of students also have not been able to build their

mathematical representation ability on equation or mathematical expression

aspects especiallt to make equation, mathematical model from initial

representation is given and 75.81% of students have not been able to represent

their idea or knowledge to written text form.

Based on observation’s result, can be conclude that mathematical representation ability of students still not satisfactory. This situation cause since

lack of their understand about linear equation of one variable and also since they

have not been accustomed to represent something from abstract to concrete.

Maulia, (2009) also state that especially of students at SMP, many of

(17)

representation ability of students and students were never given the opportunity

to express their representation ability.

This is consistent with fact that occur lately where learning used is

conventional learning, which is conventional learning as a learning that provide all learning activity to teachers. Based on observation’s result of mathematics value to one of mathematics teacher at SMP Negeri 1 Tanjung Morawa on May

15th 2014, they use conventional learning but depends on material to be taught.

On the same occasion, teacher also state that mathematics value still not

satisfactory namely only 65% of students in grade VIII at SMP Negeri 1 Tanjung

Morawa whose get mathematics value according to predetermined minimum

criteria (KKM).

Based on information above, can be conclude that mathematical

representation ability is very important abilty for representation power

development especially of students at Junior High School. Accordingly, Piaget (in

Hutagaol: 2013) said that at age of Junior High School strongly encouraged to

provide many opportunities to manipulate and representing concrete objects and

diagrams, where it can be used of student to help them when formulating abstract

concepts.

Therefore, in an effort to maximize of mathematical representation ability

of students in learning activities in the classroom, teacher must be able to plan all

the activities that will be implemented in the classroom as a model, strategy, and

evaluation of planned can help the learning activities process carried out

effectively so that learning goals agreed can be achieved by maximal. Djamarah

dan Zain (2010: 109) states the factors that influence of success of learning goals

are goals, teachers, students, teaching activities, evaluation tools, and atmosphere

evaluation. Brunner (in Hudiono: 2010) state that process of development

representation and cognition development of child can be affected by activities

and environment. Based on this insight, in this research to chose cooperative

(18)

8

Slavin (in Trianto, 2009: 56) state that cooperative learning is learning

model which provide of students to work together in mastering the material by

forming groups of 4 or 5 students. Then Trianto (2009: 58) also state in an effort

to increase student participation and facilitate students with leadership in a group

and provide the opportunity for students to work together is an arrangement of the

cooperative learning model. This can be done on cooperative learning model

Teams Games Tournament.

Cooperative learning model type Teams Games Tournament is learning

model initiated by teacher's explanation of learning material that will be taught

to students. Then learning activities provide practice and concludes with questions

to students in a game form. Accordingly, Teams Games Tournament is a learning

initiated by teacher’s explanation about learning material. While Rusman, (in

Yuliana: 2012) said that Teams Games Tournament is one type of cooperative

learning that puts students in the study group consisted of 5 to 6 students who

have the ability, gender and ethnicity or a different race.

The advantages of cooperative learning type Teams Games Tournament,

namely:

1. Teams Games Tournament model not only make students intelligent

(academically capable high) is more prominent in learning, but the

students are capable academy also less active and have an important

role in group

2. With this learning model, will foster a sense of togetherness and

mutual respect among members of the group.

3. In this learning, making students more enthusiastic about the course.

Because in this learning, the teacher promises a tribute to the best

students or groups.

4. In this learning, the learners become more fun in the class because

(19)

Thus, cooperative learning model type Teams Games Tournament is one

of alternative which is appropriate and effective to develop mathematical

representation ability of students.

Based on the background above, researchers interested in conducting

research entitled: “The difference of Students’ Mathematical Representation Ability by using Cooperative Learning Model Type Teams Games Tournament and Conventional Learning in Grade VIII SMP Negeri 1 Tanjung Morawa Academic Year 2014/2015’’

1.2. Problem Identification

Based on background above, so problem identification in this research

are:

1. Mathematical representation ability of students is still low

2. Students still have difficulty in solving mathematical representation test

3. Mathematics value still not satisfactory namely only 65% of students in grade

VIII at SMP Negeri 1 Tanjung Morawa whose get mathematics value

according to predetermined minimum criteria (KKM).

4. Cooperative learning model type Temas Games Tournament still not

implemented since still using conventional learning.

1.3. Problem Limitation

Since limitation of researcher ability, time and fund so that problem

limitation in this research is The difference of Students’ Mathematical

Representation Ability by using Cooperative Learning Model Type Teams Games

Tournament and Conventional Learning in Grade VIII SMP Negeri 1 Tanjung

(20)

10

1.4. Problem Formulation

Problem formulation in this research is: ”Whether students’ mathematical

representation ability by using cooperative learning model type Teams Games

Tournament better than conventional learning in grade VIII SMP Negeri 1

Tanjung Morawa Academic Year 2014/2015?’’

1.5. Research Objective

Research objective in this research are: To know whether students’

mathematical representation ability by using cooperative learning model type

Teams Games Tournament better than conventional learning in grade VIII SMP

Negeri 1 Tanjung Morawa Academic Year 2014/2015

1.6. Research Benefit

The expected benefits of this research are:

1. For teachers, especially for teachers of mathematics, can be used as a

material consideration and input in choosing one of alternative mathematics

learning models in learning activities at school.

2. For prospective teachers, can be used as considered appropriate to solving

problems and difficulties that often arise in school so that can be a

professional teacher.

3. For students, can be used as referenced and encouragement to improve the

mathematical representation of students in learning mathematics.

4. For researchers, can be used to increase the knowledge and insights of

researchers about problems and difficulties arise in school

5. For schools, can be used as consideration and input to school in improving

the quality of teachers and classroom learning system and improvement of

(21)

1.7. Operational Definitions

To avoid differences of meaning clarity about important terms contained

in this research, it will be noted of operational definition namely:

1. Mathematical representation ability is ability of students to express

mathematical ideas (problem, statement, definition, and soon) into form: (1)

Picture, diagram, graph, or table; (2) Mathematical notation,

numerical/algebra symbol; (3) Written text/ words as interpretation of their

mind

2. Cooperative learning model type teams games tournament is one type of

cooperative learning model that promotes learning in heterogeneous group

as well contain elements of the game and reinforcement. The syntaxes of

cooperative learning model type teams games tournament are:

Phase 1: Presenting learning goals and set

Teacher explain the learning goal and preparing students ready to learn

Phase 2: Present Information (Class Presentation)

Teacher explain the material in a class, usually using direct teaching or

lecture and discussion with teacher as a leading.

Phase 3: Organize students into learning teams (Teams)

Teacher steer students to make the teams by heterogeneous based on based

on pretest value, academic value, gender, ethnic.

Phase 4: Assist team work and study (Teams)

Teacher guide the students when doing students activity sheets

Phase 5: Test on the materials (Games Tournament)

Teacher as a leading when students doing games tournament

Phase 6: Provide recognition (Team Recognize)

Teacher announce the winning teams

3. Conventional learning is a learning where teacher as a learning center in a

class and also in this learning occur two way communication namely

communication from teacher to students. The syntaxes of conventional

(22)

12

Phase 1: Teacher Convey the learning goals to students of the topic will be

taught

Phase 2: Teacher gives explanation of the topic and asking the students if

they did not understand

Phase 3: Teacher gives examples of the problem and asking the students if

they did not understand

(23)

CHAPTER V

CONCLUSION AND SUGGESTION

5.1 Conclusion

Based on the result of research and discussion can be concluded that

students’ mathematical representation ability using cooperative learning model

type teams games tournament better than conventional learning in grade VIII

SMP Negeri 1 Tanjung Morawa.

5.2 Suggestion

Based on the results of research and the above conclusion, then

researcher submits some suggestions, as follows:

1. Cooperative Learning Model Type Teams Games Tournament can be as

consideration to teachers in junior high school to develop students’

mathematical representation ability.

2. For further researcher, result and instrument of this research can be used as

consideration to implement cooperative learning type TGT in different class

level and topic.

(24)

71

REFERENCES

Amit, M., Fried, M. N., (2005), Multiple Representation in 8th Grade Algebra Lesson: Are Learners Relly Getting It, Proceedings of the 29th Conference of the International Group for The Psychology of Mathematics Education, 2, 57-64

Ansari, B., (2009), Komunikasi Matematik, Pena, Banda Aceh

Arikunto, S., (2012), Dasar–Dasar Evaluasi Pendidikan, Rineka Cipta, Jakarta.

, S., (2010), Prosedur Penelitian Suatu Pendekatan Praktik, Rineka Cipta,

Effendi, (2012), Pembelajaran Matematika Dengan Metode Penemuan Terbimbing Untuk Meningkatkan Kemampuan Representasi dan Pemecahan Masalah Matematis Siswa SMP, Jurnal Pendidikan Penelitian, 13(2), 2

Effendi, K., (2012), Pendekatan Kooperatif Tipe TGT (Teams Games Tournament) Untuk Meningkatkan Hasil Belajar Siswa (Kompetensi Dasar Menentukan Sifat – Sifat Bangun Ruang Sederhana) Pada Pembelajaran Matematika Di Kelas IV SD Negeri 02 Tlogosih Kecamatan Kebonagung Kabupaten Demak Semester II Tahun Pelajaran 2011/2012,

Available via:

http://repository.library.uksw.edu/bitstream/handle/123456789/867/T1_292 008115_BAB%20II.pdf?sequence=3 (accessed January 12th 2014)

Fadillah, S., (2011), Penerapan Pembelajran Matematika Dengan Strategi React Untuk Meningkatkan Kemampuan Koneksi dan Representasi Matematik Siswa Sekolah, Jurnal Pendidikan Matematika, 8: 104-110

Fatayati, N., (2012), Pengaruh Metode Pembelajaran Penemuan Terbimbing Terhadap Prestasi Belajar Dan Kemampuan Representasi Matematika Siswa SMK Negeri 1 Godean, Available via: http://eprints.uny.ac.id/9362/2/BAB%201%20-%2005301244060.pdf

(accessed January 9th 2013)

(25)

Handayani, N., (2014), Perbedaan Hasil Belajar Siswa Yang Diajarkan Dengan Pembelajaran Kooperatif Tipe Teams Games Tournament Dan Tipe STAD Pada Materi Aljabar Di Kelas VII SMP PAB- 3 Saentis T.A 2013/2014, Skripsi, FMIPA, Unimed, Medan

Harries, T., and Barmby, P., Representing Multiplication, Procceedings of the British Society for Research into Learning Mathematics, 26(3)

Hudiono, B., (2010), Peran Pembelajaran Diskursus Multi Representasi Terhadap Pengembangan Kemampuan Matematika dan Daya Representasi Pada Siswa SMP, Jurnal Cakrawala Pendidikan, 8(2), 101-203

Hudojo, H., (2005), Pengembangan Kurikulum dan Pembelajaran Matematika, Malang, Universitas Negeri Malang

Hutagol, K., (2013), Pembelajaran Kontekstual Untuk Meningkatkan Kemampuan Representasi Matematis Siswa Sekolah Menengah, Jurnal Ilmiah Program Studi STKIP Siliwangi Bandung Matematika, 2(1), 85-9

Hwang, et al., (2007), Multiple Representation Skills and Creativity Effects on Mathematical Problem Solving using a Multimedia Whiteboard System, Educational Technology & Society, 10(2), 191-212

Kartini, (2009), Peranan Representasi Dalam Pembelajaran Matematika, Prosiding Desember 2009, 361-372

Lie, A., (2010), Mempraktekkan Cooperative Learning di Ruang – Ruang Kelas, Jakarta, Grasindo,

Maulia, S. M., (2009), Pengaruh Prosedur Siklus Belajar 5E dalam Meningkatkan Kemampuan Representasi Matematis Siswa SMP, Available Via: http:// repository.upi.edu

Nasution, N. A., (2014), Perbedaan Hasil Belajar Siswa Yang Diajarkan Dengan Model Pembelajaran Kooperatif Tipe TGT (Teams Games Tournament) Dan STAD (Student Team Achievement Divison) Pada Materi Aritmatika Sosial Di SMP Negeri 21 Medan T.A 2013/2014, Skripsi, FMIPA, Unimed, Medan

Neria, D. & Amit, M., (2004), Students Preference of Non-Algebraic Representation in Mathematical Communication, Proceedings of the 28th Conference of the International Group for the Psychology of Mathematical Education, 3, 409-416

(26)

73

Sagala, F., (2012), Perbedaan Hasil Belajar Siswa Yang Diajarkan Dengan Pembelajaran Kooperatif Tipe TGT Dan Tipe STAD Pada Pokok Bahasan Aljabar Di Kelas VII SMP Negeri 1 Portibi T.A 2011/2012, Skripsi, FMIPA, Unimed, Medan

Sanjaya , W., (2008), Kurikulum Dan Pembelajaran, Jakarta, Kencana

Satrianawati, (2012), Menerapkan Model Pembelajaran Kooperatif Tipe Teams Games Tournaments (TGT) pada Pelajaran Matematika Materi Pokok KPK dan FPB di Kelas VC SD Negeri 03 Baruga Kota Kendari, Jurnal, 14: 6-8

Slameto, (2010), Belajar dan Faktor–Faktor yang Mempengaruhinya, Rineka Cipta, Jakarta.

Slavin, R. E., (2010), Cooperative Learning Teori, Riset, dan Praktik, Nusa Media, Bandung

Sudjana, (2005), Metoda Statistika, Tarsito, Bandung

Suprijono, A., (2010), Cooperative Learning Teori dan Aplikasi Paikem, Pustaka Pelajar, Yogyakarta

Susanti, N., (2013), Penerapan Model Pembelajaran Kooperatif Tipe Team Game Tournament Dalam Pembelajaran Matematika SD, Jurnal,15

Suryana, A., (2012), Kemampuan Berpikir Matematis Tingkat Lanjut (Advanced Mathematical Thinking) Dalam Mata Kuliah Statistika Matematika 1, Prosiding November 2012, 38-48

Sutikno, S.M., (2013), Belajar dan Pembelajaran, Holistica, Lombok

Taylor and Francis, (2001), The Role of Representation(s) in Developing Mathematical Understanding, Theory Into Practice, 40(2), 118-127

Trianto., (2009), Mendesain Model Pembelajaran Inovatif dan Progresif, Jakarta, Kencana Prenada Media Group

Yazid, A., (2012), Pengembangan Perangkat Pembelajaran Matematika Model Kooperatif dengan Strategi TTW (Think-Talk-Write) Pada Materi Volume Bangun Ruang Sisi Datar, Journal of Primary Educational, 1(1): 33-37

Yuliana, (2012), Pengaruh Penerapan TGT Terhadap Hasil Belajar Pada Pembelajaran Matematika Kelas IV SDN 11, Artikel Penelitian, 18

Yuniawatika, (2011), Meningkatkan Kemampuan Representasi Multipel Matematika Siswa SMP Melalui Pembelajaran Dengan Pendekatan