DISTRIBUSI SUHU KEADAAN TAK TUNAK PADA BENDA PADAT KOMPOSIT DUA DIMENSI DENGAN SALAH SATU DARI DUA BAHANNYA BERBANGKIT ENERGI

(1)

DISTRIBUSI SUHU KEADAAN TAK TUNAK

PADA BENDA PADAT KOMPOSIT DUA DIMENSI

DENGAN SALAH SATU DARI DUA BAHANNYA

BERBANGKIT ENERGI

TUGAS AKHIR

Diajukan Untuk Memenuhi Salah Satu Syarat

Memperoleh Gelar Sarjana Teknik Jurusan Teknik Mesin

DISUSUN OLEH :

LISTA KURNIA

NIM : 005214016

PROGRAM STUDI TEKNIK MESIN

JURUSAN TEKNIK MESIN

FAKULTAS TEKNIK

UNIVERSITAS SANATA DHARMA

YOGYAKARTA

(2)

UNSTEADY – STATE TEMPERTURE DISTRIBUTIONS

OF TWO - DIMENSIONAL COMPOSITE SOLID

WITH ENERGY GENERATING

AT ONE OF IT’S TWO MATERIALS

FINAL PROJECT

As Partial Fulfilment of Requirements to Obtain the Sarjana Teknik Degree

In Mechanical Engineering

By:

LISTA KURNIA

NIM : 005214016

MECHANICAL ENGINEERING STUDY PROGRAM

MECHANICAL DEPARTMENT

SANATA DHARMA UNIVERSITY

YOGYAKARTA

(3)

(4)

(5)

HALAMAN PERSEMBAHAN

KUPERSEMBAHKAN TULISAN INI KEPADA :

TUHAN YESUS, MAMAK, BAPAK, MARINA, RIO, MONIKA, DAN DINA.

Perkataan ini deras menembus relung hatiku:

Tuhan takkan terlambat juga takkan lebih cepat. Semuanya itu, Dia jadikan indah pada waktu-Nya.(Pengkhotbah 3:1-15)

Sebab rancanganKu bukanlah rancanganmu dan jalanKu bukanlah jalanmu. Seperti tingginya langit dari bumi demikianlah tingginya jalanKu dari jalanmu dan rancanganKu dari rancanganmu. (Yesaya 55:8-9)

(6)

Pernyataan Keaslian Karya

Saya menyatakan dengan sesungguhnya bahwa tugas akhir ini tidak memuat karya atau bagian karya orang lain kecuali yang telah dinyatakan dalam kutipan dan daftar pustaka sebagaimana layaknya karya ilmiah.

Yogyakarta, Desember 2006

(7)

KATA PENGANTAR

Atas berkat dan karunia dari Allah Bapa di surga maka sudah terlaksana penulis menyelesaikan Tugas Akhir dengan judul Distribusi Suhu Keadaan Tak Tunak Pada Benda Padat Komposit Dua Dimensi Dengan Salah Satu Dari Dua Bahannya Berbangkit Energi.

Tugas Akhir ini merupakan salah satu syarat untuk memperoleh gelar Sarjana pada Jurusan Teknik Mesin Fakultas Teknik Universitas Sanata Dharma Yogyakarta. Pada kesempatan ini penulis mengucapkan terima kasih pada :

1. Tuhan yang telah menyertai dan memberi kekuatan selama penulis menyelesaikan Tugas Akhir.

2. Bapak Ir. PK. Purwadi. M.T. , pembimbing Tugas Akhir, yang telah dengan sabar membimbing dan membantu menyelesaikan Tugas Akhir dari awal hingga akhir. 3. Bapak Ir. YB. Lukiyanto. M.T. , pembimbing akademik, yang juga mendorong

untuk menyelesaikan Tugas Akhir ini.

4. Romo Ir. Gregorius Heliarko, SJ, S.S., B.S.T, M.A., M.Sc., selaku dekan fakultas Teknik.

5. Bapak Yosef Agung Cahyanto, S.T., M.T., selaku ketua jurusan Teknik Mesin. 6. Bapak dosen pengajar yang telah memberikan teori-teori sebagai dasar pembuatan

Tugas Akhir ini.

7. Bapak dan mamak yang selalu memberikan dukungan baik material maupun spiritual dan yang selalu berdoa untuk penulis.

(8)

9. Semua teman-teman, serta semua pihak yang telah memberikan dukungan penuh hingga selesainya Tugas Akhir ini.

10.Mbah kakung, mbah putri dan semua saudara yang telah mendukung dan selalu mendoakan penulis.

Penulis menyadari bahwa dalam penulisan Tugas Akhir ini masih banyak kekurangan sehingga jauh dari sempurna. Dengan demikian kritik dan saran diharapkan penulis guna menyempurnakan tulisan ini.

Akhir kata penulis berharap semoga Tugas Akhir ini dapat berguna dan bermanfaat bagi pembaca.

(9)

ABSTRAK

Penelitian ini bertujuan untuk mengetahui (1) pengaruh perubahan nilai koefisien perpindahan panas konveksi (h) terhadap suhu pada benda komposit pada keadaan tak tunak dengan salah satu bahan berbangkit energi (2) pengaruh perubahan nilai energi pembangkitan (

•

q) terhadap suhu pada benda komposit pada keadaan tak tunak dengan salah satu bahan berbangkit energi (3) pengaruh perubahan bahan terhadap suhu pada benda komposit pada keadaan tak tunak dengan salah satu bahan berbangkit energi. Penelitian dilakukan dengan metode komputasi numerik, dengan memakai metode beda hingga cara eksplisit. Di analisis dalam dua dimensi.

Penelitian dilakukan pada benda padat komposit. Benda uji berbentuk balok dengan lebar 14 cm (0,14 m), tinggi 14 cm (0,14 m) dan panjang 1 m. Kondisi awal benda merata. Suhu awal benda Ti = 100 oC. Penelitian dilakukan dengan

memvariasikan nilai koefisien perpindahan panas konveksi (h), nilai energi pembangkitan (

•

q) dan bahan yang di luar.

Hasil penelitian yang pada kasus ditinjau menunjukkan bahwa semakin besar nilai koefisien perpindahan panas konveksi (h) maka distribusi suhu di dalam benda semakin tinggi (proses pemanasan) dan suhu semakin cepat menyesuaikan dengan lingkungan sekitar. Semakin besar nilai energi pembangkitan (

•

(10)

DAFTAR ISI

Halaman Judul ………... i

Halaman Persetujuan ………. ii

Halaman Pengesahan ………. iii

Halaman Persembahan ………... iv

Pernyataan Keaslian Karya ……… v

Kata Pengantar ………... vi

Abstrak ………... viii

Daftar Isi ……… x

Daftar Gambar ……… xiii

Daftar Tabel ………... xvi

BAB I PENDAHULUAN 1.1. Latar Belakang ………... 1

1.2. Batasan Masalah ……… 2

1.3. Perumusan Masalah ………... 2

1.4. Tujuan ……… 7

1.5. Manfaat ……….. 8

BAB II DASAR TEORI 2.1. Perpindahan Panas ………. 9

2.1.1. Perpindahan Panas Konduksi ……… 9

2.1.2. Perpindahan Panas Konduksi ……….……….. 12

(11)

2.2.1. Beda Maju ………. 22

2.2.2. Beda Mundur ……… 23

2.2.3 Beda Tengah ……….. 24

BAB III PERSAMAAN PADA SETIAP TITIK 3.1. Model Matematika ………. 26

3.2. Persamaan Pada Setiap Titik ………... 28

3.2.1. Kasus 1 ……….. 31

3.2.2. Kasus 2 ……….. 32

3.2.3. Kasus 3 ……….. 34

3.2.4. Kasus 4 ……….. 36

3.2.5. Kasus 5 ……….. 38

3.2.6. Kasus 6 ……….. 40

BAB IV HASIL PERHITUNGAN DAN PEMBAHASAN 4.1. Hasil Perhitungan ………... 42

4.1.1. Distribusi Suhu Pada Benda Dengan h Yang Divariasikan …….. 42

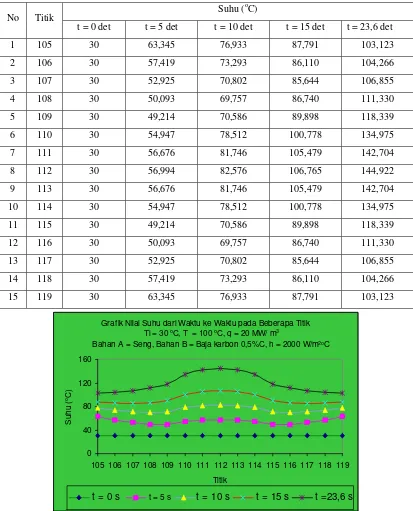
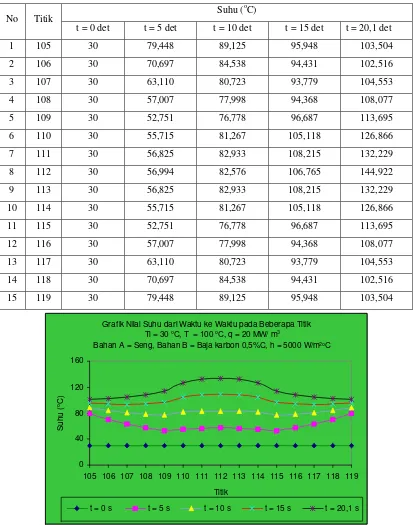
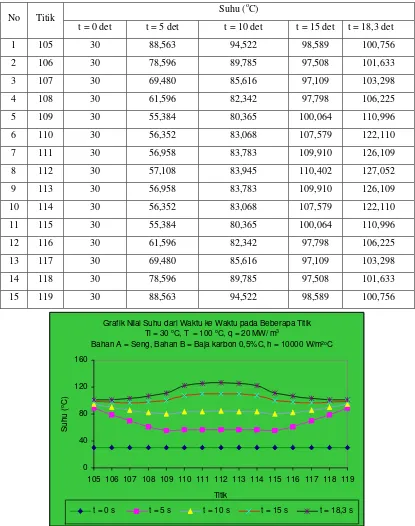
4.1.1.1. Distribusi Suhu Pada Benda Dengan h = 1000 W/m2oC …. 43 4.1.1.2. Distribusi Suhu Pada Benda Dengan h = 2000 W/m2oC …. 46 4.1.1.3. Distribusi Suhu Pada Benda Dengan h = 5000 W/m2oC …. 47 4.1.1.4. Distribusi Suhu Pada Benda Dengan h = 10000 W/m2oC … 48 4.1.1.5. Distribusi Suhu Pada Benda Dengan h = 20000 W/m2oC … 49 4.1.2. Distribusi Suhu Pada Benda Dengan • qYang Divariasikan …….. 51

(12)

4.1.2.2. Distribusi Suhu Pada Benda Dengan

•

q= 50 MW/m3 …….. 52

4.1.2.3. Distribusi Suhu Pada Benda Dengan • q= 75 MW/m3 …….. 53

4.1.2.4. Distribusi Suhu Pada Benda Dengan • q= 100 MW/m3 …… 54

4.1.2.5. Distribusi Suhu Pada Benda Dengan • q= 125 MW/m3 …… 55

4.1.3. Distribusi Suhu Pada Benda Dengan Bahan 1 Divariasikan ……. 58

4.1.3.1. Distribusi Suhu Pada Benda Dengan Bahan Baja Karbon 0,5% C ……… 58

4.1.3.2. Distribusi Suhu Pada Benda Dengan Bahan Nikel ……….. 59

4.1.3.3. Distribusi Suhu Pada Benda Dengan Bahan Seng ………... 60

4.1.3.4. Distribusi Suhu Pada Benda Dengan Bahan Tembaga …… 61

4.1.3.5. Distribusi Suhu Pada Benda Dengan Perak …….………… 62

4.2. Pembahasan ……… 65

4.2.1. Distribusi Suhu Dengan Variasi h ………. 65

4.2.2. Distribusi Suhu Dengan Variasi • q……… 66

4.2.3. Distribusi Suhu Dengan Variasi Bahan Pada Bagian Luar ……... 67

BAB V PENUTUP 5.1. Kesimpulan ……… 69

5.2. Saran ……… 69

DAFTAR PUSTAKA ……… 70

(13)

DAFTAR GAMBAR

1. Gambar 1.1. Benda padat komposit dengan energi pembangkitan pada

benda bagian dalam ……… 3

2. Gambar 2.1. Sketsa yang melukiskan perjanjian tentang tanda untuk aliran panas konduksi ………. 10

3. Gambar 2.2. Perpindahan panas konduksi ………. 10

4. Gambar 2.3. Perubahan konduktivitas termal berbagai zat padat terhadap suhu ……… 11

5. Gambar 2.4. Perubahan konduktivitas termal berbagai zat cair terhadap suhu ……… 11

6. Gambar 2.5. Perubahan konduktivitas termal berbagai zat gas terhadap suhu ……… 12

7. Gambar 2.6. Perpindahan panas konveksi ………. 13

8. Gambar 2.7. Sketsa batas aliran laminar, transisi, dan turbulen pada bidang datar ……… 17

9. Gambar 3.1. Sketsa yang melukiskan koordinat untuk penurunan persamaan konduksi panas umum dalam koordinat Cartesius ……… 27

10.Gambar 3.2. Gambar titik-titik pada benda uji ……… 30

11.Gambar 3.3. Volume kontrol pada kasus 1 ……… 31

(14)

15.Gambar 3.7. Volume kontrol pada kasus 5 ……… 38 16.Gambar 3.8. Volume kontrol pada kasus 6 ……… 40 17.Gambar 4.1. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk h = 1000 W/m2oC ……… 45 18.Gambar 4.2. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk h = 10000 W/m2oC ..……… 48 21.Gambar 4.5. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk h = 20000 W/m2oC ..……… 49 22.Gambar 4.6. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk semua harga h pada saat t = 15 s ……… 50 23.Gambar 4.7. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk

•

q= 20 MW/m3 ………... 52

24.Gambar 4.8. Perjalanan suhu pada beberapa titik yang ditinjau dari

•

q= 50 MW/m3 ………... 53

•

(15)

•

q= 100 MW/m3 ……….. 55

•

q= 125 MW/m3 ……….. 56

waktu ke waktu untuk semua

•

qpada saat t = 7s ………... 57

waktu ke waktu untuk besi ...… 59 30.Gambar 4.14. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk nikel ………... 60 31.Gambar 4.15. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk seng ………….………... 61 32.Gambar 4.16. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk magnesium. …..………... 62 33.Gambar 4.17. Perjalanan suhu pada beberapa titik yang ditinjau dari

waktu ke waktu untuk aluminium . …..………... 63 34.Gambar 4.18. Perjalanan suhu pada beberapa titik yang ditinjau dari

(16)

DAFTAR TABEL

1. Tabel 2.1. Bilangan Nusselt untuk dinding vertikal ………... 14

2. Tabel 2.2. Konstanta persamaan permukaan isotermal ……….. 16

3. Tabel 2.3. Nilai – nilai koefisien perpindahan panas konveksi untuk berbagai keadaan ……… 19

4. Tabel 2.4. Konstanta C dan n untuk perpindahan panas dari silinder ……. 20

5. Tabel 2.5. Konstanta C dan n untuk perpindahan panas dari silinder tak Bundar ……… 20

6. Tabel 4.1. Nilai sifat-sifat logam ……… 41

7. Tabel 4.2. Hasil perhitungan dengan nilai h = 1000 W/m2oC ……… 45

10.Tabel 4.5. Hasil perhitungan dengan nilai h = 10000 W/m2oC ………….. 48

11.Tabel 4.6. Hasil perhitungan dengan nilai h = 20000 W/m2oC …………. 49

12.Tabel 4.7. Hasil perhitungan dengan nilai • q= 20 MW/m3 ……… 51

(17)

18.Tabel 4.13. Hasil perhitungan untuk bagian luar : nikel ……… 59 19.Tabel 4.14. Hasil perhitungan untuk bagian luar : seng ………. 60 20.Tabel 4.15. Hasil perhitungan untuk bagian luar : magnesium ………. 61 21.Tabel 4.16. Hasil perhitungan untuk bagian luar : aluminium ………….. 62 22.Tabel 4.17. perjalanan suhu dari waktu ke waktu pada saat t = 15 detik,

suhu titik di sudut benda mencapai 100oC , komposisi bahan seng –

baja karbon 0,5%C, dan

•

q= 20 MW/m3, Ti = 30oC, T∞= 100oC ……... 65

23.Tabel 4.18. waktu yang diperlukan titik sudut benda mencapai 100oC,

komposisi bahan seng – baja karbon 0,5%C, dan

•

q= 20 MW/m3,

Ti = 30oC, T∞= 100oC ……….……… 66

24.Tabel 4.19. perjalanan suhu dari waktu ke waktu pada saat t = 7 detik, suhu titik di sudut benda mencapai 100oC, komposisi bahan seng –

baja karbon 0,5%C, dan h = 5000 W/m2oC, Ti = 30oC, T∞= 100oC …….. 66

25.Tabel 4.20. waktu yang diperlukan titik sudut benda mencapai 100oC, komposisi bahan seng – baja karbon 0,5%C, dan h = 5000 W/m2oC,

Ti = 30oC, T∞= 100oC ……… 67

26.Tabel 4.21. perjalanan suhu dari waktu ke waktu pada saat t = 15 detik, suhu titik di sudut benda mencapai 100oC, h = 5000W/m2oC, dan

•

q= 20 MW/m3, Ti = 30oC, T∞= 100oC ……….. 68

27.Tabel 4.22. waktu yang diperlukan node sudut benda mencapai 100oC,

h = 5000W/m2oC, dan

•

(18)

BAB I PENDAHULUAN

1.1.Latar Belakang Masalah

Perpindahan panas dapat kita jumpai baik dalam kehidupan sehari-hari atau dalam industri. Pada kehidupan sehari-hari perpindahan panas dapat kita jumpai pada heater, setrika listrik, panci yang dipanaskan, dan lain-lain. Sedangkan pada industri dapat kita jumpai pada pengolahan logam.

Benda berbangkit energi adalah benda yang mampu memberikan atau membangkitkan energi. Contohnya : kawat berarus listrik, elemen pemanas air (heater), elemen setrika listrik, kompor listrik, dan lain-lain.

Di kehidupan sehari-hari sering kita jumpai suatu benda terdiri dari dua atau lebih bahan, contoh kabel terdiri dari kawat dan isolator, heater terdiri dari elemen dan isolator, atau tembok yang terdiri dari batubata dan semen, dan lain-lain.

(19)

1.2.Batasan Masalah

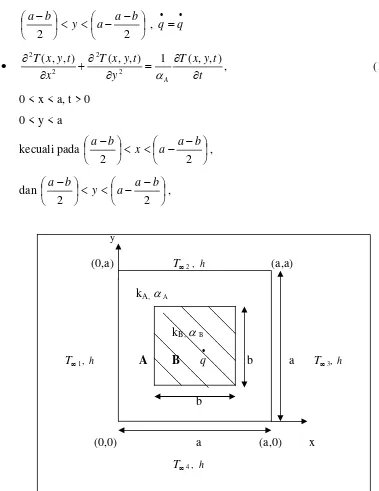
Menghitung dan menganalisa perubahan suhu dari waktu ke waktu pada benda padat komposit 2 dimensi dengan energi pembangkitan pada bahan yang di dalam, keadaan tak tunak. Benda padat komposit tersusun dari dua bahan yang berbeda.

Pada analisis ini diambil beberapa titik tertentu dan titik pusat sebagai wakil untuk dianalisis. Nilai h selama proses berlangsung (pada keadaan tak tunak) dianggap bernilai tetap dan merata. Penyelesaian dilakukan dengan metode komputasi numerik, cara beda hingga dengan metode eksplisit.

1.3.Perumusan Masalah

Benda uji yaitu benda dengan bahan komposit (dua bahan) yang memiliki suhu mula-mula merata T =Ti, kemudian secara tiba-tiba dicelupkan pada fluida yang bergerak yang mempunyai suhu T = T_∞ yang tetap dipertahankan selama proses tak

tunak berlangsung, dengan nilai koefisien perpindahan kalor konveksi h yang nilainya tetap. Energi pembangkitan dihidupkan tepat pada saat benda uji dicelupkan pada fluida (pada bahan yang didalam). Pencarian distribusi suhu dari waktu ke waktu diselesaikan dengan model matematik yang sesuai.

a. Model matematika

•

t t y x T k

q y

t y x T x

t y x T

B

B ∂

∂ = + ∂

∂ + ∂

∂ ( , , ) ( , , ) • 1 ( , , )

2 2 2

2

α , (1.1)

⎟ ⎠ ⎞ ⎜

⎝

⎛ ₋ −

< < ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

2 2

b a a x b a

(20)

⎟ ⎠ ⎞ ⎜

⎝

⎛ ₋ −

< < ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

2 2

b a a y b a

,

• •

=q q

•

t t y x T y

t y x T x

t y x T

A ∂

∂ = ∂

∂ + ∂

∂ ( , , ) ( , , ) 1 ( , , ) 2

2 2

2

α , (1.2)

0 < x < a, t > 0 0 < y < a

kecuali pada ⎟ ⎠ ⎞ ⎜

⎝

⎛ ₋ −

< < ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

2 2

b a a x b a

,

dan ⎟

⎠ ⎞ ⎜

⎝

⎛ −

− < < ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ −

2 2

b a a y b a

,

y

(0,a) T_∞2 , h (a,a)

kA, αA

kB, αB

T_∞1, h A B

•

q b a T_∞3, h

b

(0,0) a (a,0) x T_∞4 , h

Gambar 1.1. Benda padat komposit, dengan ada energi pembangkitan pada benda bagian dalam.

Keterangan :

A : bahan 1, bahan dengan nilai kA, ukuran luar a x a dengan lubang di tengah b x b

(21)

∞

T 1 = T∞2 = T∞3 = T∞4 = T∞ = suhu fluida sekitar benda uji (oC).

h = koefisien perpindahan panas konveksi (W/m2 oC)

kA = αA xρA x cA , koefisien perpindahan panas konduksi bahan 1 (W/moC)

kB = αB xρB x cB , koefisien perpindahan panas konduksi bahan 2 (W/moC)

•

q = energi pembangkitan (W/m3) αA = difusivitas termal bahan 1 (m2/s).

ρA= kerapatan (density) bahan 1(kg/m3)

cA = panas jenis bahan1 (J/kg oC)

αB = difusivitas termal bahan 2 (m2/s).

ρB= kerapatan (density) bahan 2 (kg/m3)

cB = panas jenis bahan 2 (J/kg oC)

b. Kondisi awal

T(x,y,0) = Ti , 0≤ x≤a, 0≤ y≤ a, t = 0 (1.3)

c. Kondisi batas

1. Kondisi batas dinding permukaan samping kiri

⎥ ⎥ ⎥ ⎥ ⎥

⎦ ⎤

⎢ ⎢ ⎢ ⎢ ⎢

⎣ ⎡

∂ ∂ + ∂

∂ +

− −

∂ ∂ −

∂ + =

∞ =

x t y x T A k y

t y x T A k

T t y x T hA y

t y x T A k

y y y

y y

) , , ( 2 )

, , ( 2

) ) , , ( ( )

, , (

2 1

t t y x T V c

∂ ∂

= ( , , )

2

ρ (1.4)

x = 0, 0 < y < a, t > 0

(22)

2. Kondisi batas dinding permukaan atas

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ − ∂ ∂ + − + ∂ ∂ − ∂ + = ∞ = y t y x T A k x t y x T A k t y x T T hA x t y x T A k x x x x x ) , , ( 2 ) , , ( 2 )) , , ( ( ) , , ( 2 2 t t y x T V c ∂ ∂ = ( , , ) 2

ρ (1.5)

y = a, 0 < x < a, t > 0 3. Kondisi batas dinding permukaan samping kanan

⎥ ⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ − ∂ ∂ − − + ∂ ∂ ∂ + = ∞ = x t y x T A k y t y x T A k t y x T T hA y t y x T A k y y y y y ) , , ( 2 ) , , ( 2 )) , , ( ( ) , , ( 2 3 t t y x T V c ∂ ∂ = ( , , ) 2

ρ (1.6)

x = a, 0 < y < a, t > 0

4. Kondisi batas dinding permukaan atas

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ + ∂ ∂ − − − ∂ ∂ ∂ + = ∞ = y t y x T A k x t y x T A k T t y x T hA x t y x T A k x x x x x ) , , ( 2 ) , , ( 2 ) ) , , ( ( ) , , ( 2 4 t t y x T V c ∂ ∂ = ( , , ) 2

ρ (1.7)

y = 0, 0 < y < a, t > 0

5. Kondisi batas sudut kiri atas permukaan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ − ∂ ∂ + − + − − _∞ _∞ y t y x T A k x t y x T A k t y x T T A h T t y x T A h ) , , ( 2 ) , , ( 2 )) , , ( ( 2 ) ) , , ( (

2 1 2

t t y x T V c ∂ ∂ = ( , , ) 4

ρ (1.8)

x = 0, y = a, t > 0

(23)

6. Kondisi batas sudut kanan atas permukaan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ − ∂ ∂ − − + − _∞ ∞ y t y x T A k x t y x T A k t y x T T A h t y x T T A h ) , , ( 2 ) , , ( 2 )) , , ( ( 2 )) , , ( (

2 2 3

t t y x T V c ∂ ∂ = ( , , ) 4

ρ (1.9)

x = a, y = a, t > 0

7. Kondisi batas sudut kanan bawah permukaan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ + ∂ ∂ − − − − _∞ ∞ y t y x T A k x t y x T A k T t y x T A h t y x T T A h ) , , ( 2 ) , , ( 2 ) ) , , ( ( 2 )) , , ( (

2 3 4

t t y x T V c ∂ ∂ = ( , , ) 4

ρ (1.10)

x = a, y = 0, t > 0

8. Kondisi batas sudut kiri bawah permukaan

⎥ ⎥ ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎢ ⎢ ⎣ ⎡ ∂ ∂ + ∂ ∂ + − − − − _∞ _∞ y t y x T A k x t y x T A k T t y x T A h T t y x T A h ) , , ( 2 ) , , ( 2 ) ) , , ( ( 2 ) ) , , ( (

2 4 1

t t y x T V c ∂ ∂ = ( , , ) 4

ρ (1.11)

x = 0, y = 0, t > 0 Keterangan

α = k /ρc , difusivitas termal (m2/s).

ρ = kerapatan (density) (kg/m3)

c = panas jenis (J/kg oC)

h = koefisien perpindahan panas konveksi (W/m2 oC). k = koefisien perpindahan panas konduksi (W/m oC) t = waktu (s)

(24)

Dilakukan variasi pada :

1. Nilai koefisien perpindahan panas konveksi (h).

2. Nilai energi pembangkitan ⎟ ⎠ ⎞ ⎜ ⎝ ⎛•

q .

3. Bahan yang tidak berbangkit energi (bahan yang di luar). Dengan asumsi :

1. Sifat-sifat bahan tetap (ρ,c,k : tetap) atau tidak berubah terhadap perubahan

suhu.

2. Sifat bahan merata, atau tidak merupakan fungsi posisi.

3. Benda dianggap tidak mengalami perubahan bentuk dan volume.

4. Besar energi pembangkitan: q, bersifat merata dan tetap (tidak berubah terhadap waktu) untuk benda di bagian dalam.

5. Benda uji merupakan benda padat komposit dua dimensi.

1.4.Tujuan

Tujuan dari penulisan tugas akhir ini adalah :

1. Mendapatkan pengaruh perubahan nilai koefisien perpindahan panas konveksi (h) terhadap suhu pada benda komposit pada keadaan tak tunak dengan salah satu bahan berbangkit energi.

(25)

3. Mendapatkan pengaruh perubahan bahan terhadap suhu pada benda komposit pada keadaan tak tunak dengan salah satu bahan berbangkit energi.

1.5.Manfaat

Manfaat dari penulisan tugas akhir ini adalah :

1. Mengetahui pengaruh perubahan nilai koefisien perpindahan panas konveksi (h) terhadap suhu pada benda komposit pada keadaan tak tunak.

2. Mengetahui pengaruh perubahan nilai energi pembangkitan (q) terhadap suhu pada benda komposit pada keadaan tak tunak.

3. Mengetahui pengaruh perubahan bahan terhadap suhu pada benda komposit pada keadaan tak tunak.

(26)

BAB II DASAR TEORI

2.1. Perpindahan Panas

Perpindahan panas atau kalor yaitu berpindahnya energi dari satu daerah ke daerah yang lain akibat dari adanya perbedaan suhu antara daerah-daerah tersebut. Panas berpindah dari suhu yang tinggi ke suhu yang lebih rendah. Perpindahan panas ada tiga macam yaitu konduksi, konveksi, dan radiasi.

2.1.1. Perpindahan Panas Konduksi

Hubungan dasar untuk perpindahan panas dengan cara konduksi diusulkan oleh ilmuan Perancis, J.B.J. Fourier,pada tahun 1882. Hubungan ini menyatakan bahwa q yaitu laju aliran panas dengan cara konduksi dalam suatu bahan, sama dengan hasilkali dari tiga buah besaran berikut :

1. k adalah konduktivitas termal bahan.

2. A adalah luas penampang melalui mana panas mengalir dengan cara konduksi, yang harus diukur tegak lurus terhadap arah aliran panas.

3. dT/dx adalah gradien suhu pada penampang tersebut, yaitu laju perubahan suhu T terhadap jarak dalam arah aliran panas x.

(27)

Gambar 2.1. Sketsa yang melukiskan perjanjian tentang tanda untuk aliran panas konduksi

(F. kreith, Prinsip – prinsip perpindahan panas, Halaman: 8)

A k q

T1 T2

∆x

Gambar 2.2. Perpindahan panas konduksi

Dari beberapa hal diatas, dapat ditulis persamaan :

dx dT kA

q=− (2-1) Dengan :

q = laju aliran panas (W)

A = Luas perpindahan panas (m2)

k = konduktivitas termal benda (W/moC)

dx dT

(28)

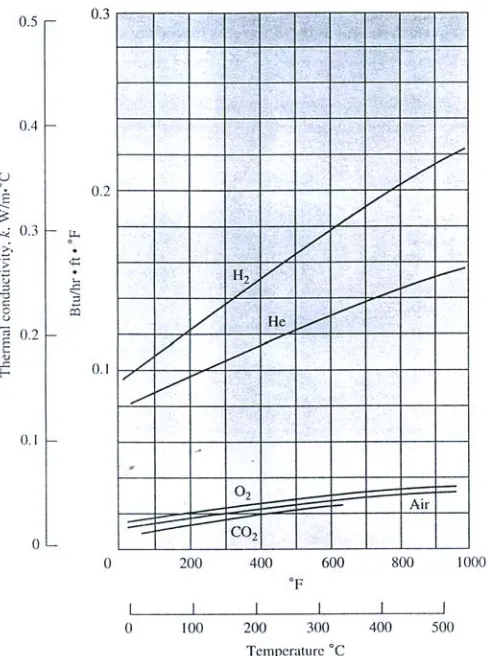
Gambar 2.3. Perubahan konduktivitas termal berbagai zat padat terhadap suhu. (Yunus A. Cengel, Heat Transfer A Practical Approach, Halaman: 105)

(29)

Gambar 2.5. Perubahan konduktivitas termal berbagai zat gas terhadap suhu. (J.P. Holman, Heat Transfer, Halaman: 8)

2.1.2. Perpindahan Panas Konveksi

Hubungan dasar untuk perpindahan panas dengan cara konveksi diusulkan oleh ilmuan Inggris, Isaac Newton, pada tahun 1701. Laju perpindahan panas dengan cara konveksi antara suatu permukaan dan suatu fluida dapat dihitung dengan hubungan :

) ( − _∞ =hAT T

(30)

T_∞ h q

A Tw

Gambar 2.6. Perpindahan panas konveksi Dengan

q = laju aliran panas (W)

A = Luas perpindahan panas (m2)

h = koefisien perpindahan panas konveksi (W/m2oC)

∞

T = suhu benda (oC)

Tw = suhu fluida (oC)

Cara mendapatkan nilai koefisien perpindahan panas konveksi (h)

1. Perpindahan panas konveksi bebas

(31)

Rayleigh number (Ra)

Bilangan Rayleigh dinyatakan dengan persamaan :

Ra = Gr Pr = ( ) Pr 2

3

v T T

gβ _s − _∞ δ

(2.3)

f T

1 =

β dengan

2

∞ + =T T

T s

f

dengan

g = Percepatan gravitasi (9,8 m/s2) δ = Panjang karakteristik (δ = L), m

Ts = Suhu dinding, K

∞

T = Suhu fluida, K

Tf = Suhu film, K

v = Viskositas kinematik, m2/s Pr = Bilangan Prandtl

Gr = Bilangan Grashof Bilangan Nusselt (Nu)

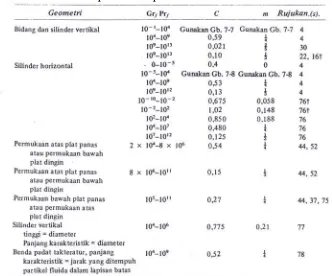
Tabel 2.1. Bilangan Nusselt untuk dinding vertikal: Geometri Panjang

Karakteristik

Ra Nusselt (Nu)

104 s.d

109 Nu = 0,59Ra1/4 104 s.d

109 Nu = 0,1Ra1/3 Ts

L

= δ

Untuk semua

Ra

[

(

)

]

2

27 / 8 16 / 9

6 / 1

Pr / 492 , 0 1

387 , 0 825

, 0

⎥ ⎥ ⎦ ⎤ ⎢

⎢ ⎣ ⎡

+ +

= Ra

Nu

(32)

Dari bilangan Nusselt dapat diperoleh nilai koefisien perpindahan panas konveksi :

k h

Nu = δ atau

δ

k Nu

h= . (2.4)

dengan

h = Koefisien perpindahan panas konveksi, W/m2 oC. δ = Panjang karakteristik, m.

k = Koefisien perpindahan panas konduksi dari fluida, W/m oC.

2. Perpindahan panas konveksi bebas melewati permukaan

Perpindahan panas konveksi bebas melewati permukaan seperti pada permukaan silinder vertikal, silinder horizontal dan bola.

Koefisien perpindahan panas konveksi bebas rata-rata untuk berbagai situasi, dapat dinyatakan sebagai berikut:

Nuf = C (Grf Prf)m (2.5)

Di mana subskrip f menunjukkan bahwa sifat-sifat untuk gugus tak berdimensi dievaluasikan pada suhu film

2

w f

T T

T = ∞ + (2.6)

Perkalian antara angka Grashof dan angka Prandtl disebut angka Rayleigh:

Ra = Gr Pr (2.7)

a. Konveksi bebas melewati silinder vertikal Rumus yang berlaku

Nu1/2 =

(

)

[

₉_/₁₆

]

8/27 6 / 1

Pr / 492 , 0 1

387 , 0 825

, 0

+

(33)

Tabel 2.2. Konstanta persamaan permukaan isotermal

(Sumber: J.P. Holman, Perpindahan Kalor, Halaman: 304) b. Konveksi bebas melewati silinder horisontal

Rumus yang berlaku

Nu1/2 =

(

)

[

]

6 / 1

9 / 16 16 / 9 Pr / 559 , 0 1

Pr 387

, 0 60 , 0

⎪⎭ ⎪ ⎬ ⎫ ⎪⎩

⎪ ⎨ ⎧

+

+ Gr 10-5 < Gr Pr < 1012 (2.9)

c. Konveksi bebas melewati bola Rumus yang berlaku

• bola dengan udara

Nuf = 2 + 0,392 Grf1/4 1 < Grf < 105

Nuf = 2 + 0,43 (Grf Prf)1/4 (2.10)

• bola dengan air

(34)

3. Perpindahan panas konveksi paksa

Proses perpindahan panas konveksi paksa ditandai dengan adanya fluida yang bergerak yang dikarenakan adanya alat bantu. Untuk mencari nilai koefisien perpindahan panas konveksi (h) dapat dicari dari bilangan Nusselt. Bilangan Nusselt yang dipilih harus sesuai dengan kasusnya, karena setiap kasus mempunyai bilangan Nusselt sendiri.

Ada dua bilangan Nusselt yaitu bilangan Nusselt lokal dan bilangan Nusselt rata-rata. Bilangan Nusselt lokal untuk mencari nilai h pada jarak x yang ditinjau. Sedangkan bilangan Nusselt rata-rata untuk menghitung nilai h rata-rata dari x = 0 sampai dengan jarak x yang ditinjau.

Bilangan Nusselt (Nu) untuk bidang datar

Gambar 2.7. Sketsa batas aliran laminar, transisi, dan turbulen pada bidang datar (Yunus A. Cengel, Heat Transfer A Practical Approach, Halaman: 353)

Untuk aliran laminar

(35)

Rex =

µ ρU_∞x

(2.12)

Berlaku persamaan Nusselt Lokal Nu pada jarak x, untuk Pr > 0,6

Nux =

f x k

x h

= (0,332) 3 1 2 1

Pr

Rex (2.13)

Berlaku persamaan Nusselt rata-rata untuk x = 0 sampai dengan x = L

Nu = f k hL

= (0,664) 3 1 2 1

Pr

Re_L (2.14)

Dengan

Re = Bilangan Reynold

ρ = Massa jenis fluida, kg/m3

∞

U = Kecepatan fluida, m/s

Nu = Bilangan Nusselt

µ = Viskositas, m2/s

kf = Koefisien perpindahan panas konduksi fluida, W/m oC

h = Koefisien perpindahan panas konveksi, W/m2 oC Pr = Bilangan Prandtl

L = Panjang dinding, m

Untuk turbulen

Syarat aliran turbulen : 500000 < Re < 107

Berlaku persamaan Nusselt Lokal Nu pada jarak x, untuk 0,6≤Pr ≤60

Nux =

f x k

x h

= (0,0296) 3 1 5 4

Pr

(36)

Berlaku persamaan Nusselt rata-rata untuk x = 0 sampai dengan x = L Nu =

f k hL

= (0,037) 3 1 5 4

Pr

Re_L (2.16)

Untuk kombinasi laminar dan turbulen

Berlaku persamaan Nusselt rata-rata untuk x = 0 sampai dengan x = L

Nu = f k hL

= 3

1 5

4

Pr ) 871 Re 037 , 0

( _L− (2.17)

Dengan syarat 0,6≤Pr ≤60

Tabel 2.3. Nilai-nilai koefisien perpindahan panas konveksi (h) untuk berbagai keadaan.

No Tipe konveksi Nilai kisaran h, W/m2oC Konveksi bebas

• untuk fluida gas 2 –25 1

• untuk fluida cairan 1 – 1000 Konveksi paksa

• untuk fluida gas 25 – 250 2

• untuk fluida cairan 50 – 20.000 Konveksi dengan perubahan fase

3

• untuk proses pendidihan dan pengembunan 2500 – 100.000 (Sumber: Yunus A. Cengel, Heat Transfer A Practical Approach, Halaman: 30) 4. Perpindahan panas konveksi paksa melewati permukaan benda

Perpindahan panas konveksi paksa melewati permukaan seperti pada permukaan silinder dan bola.

a. Perpindahan panas konveksi paksa melewati permukaan silinder

Koefisien perpindahan panas konveksi paksa rata-rata untuk gas dan zat cair, dapat dinyatakan sebagai berikut:

Nu = Pr1/3

n

f

f v

d u C k hd

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛

(37)

Tabel 2.4. Konstanta C dan n untuk Perpindahan panas dari silinder

Redf C n

0,4 - 4 4 – 40 40 – 4000 4000 – 40.000 40.000 – 400.000

0,989 0,911 0,683 0,193 0,0266

0,330 0,385 0,466 0,618 0,805 (Sumber: J.P. Holman, Perpindahan Kalor, Halaman: 268)

2. Perpindahan panas konveksi paksa melewati permukaan silinder tak bundar

Nu = Pr1/3

n

f

f v

d u C k hd

⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ = ∞

(2.19)

Tabel 2.5. Konstanta C dan n untuk Perpindahan panas dari silinder tak bundar

(38)

5. Benda berbangkit energi

Benda berbangkit energi adalah benda yang mampu memberikan/ membangkitkan energi. Contoh benda berbangkit energi yaitu kawat berarus listrik, elemen pemanas air, elemen setrika listrik, reaktor nuklir dan lain-lain.

Besar energi pembangkitan pada alat pemanas dapat dihitung dengan persamaan:

L D

VI v

P q

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ = = •

4

2

π (2.20)

Dengan

•

q = energi pembangkitan (W/m3)

P = Daya alat pemanas (W) v = volume alat pemanas (m3) V = tegangan (volt)

I = arus (A)

D = diameter alat pemanas (m) L = panjang alat pemanas (m)

2.2. Metode Beda Hingga

(39)

pada akurasi dan waktu penyelesaian. Untuk permasalahan ini menggunakan metode beda hingga cara eksplisit.

Pendekatan secara numerik dengan metode beda hingga untuk derivatif suatu fungsi terhadap variable bebasnya menggunakan persamaan dari deret Taylor. Untuk mendapatkan derivatif pertama dari suatu fungsi, pendekatan dilakukan dengan cara pemotongan deret ketiga dan keempat, dan seterusnya dari deret Taylor, yang harganya dapat diabaikan. Pendekatan dapat dilakukan dengan cara beda maju, beda mundur, atau beda tengah.

2.2.1. Beda Maju

Bila fungsi f(x) analitik, maka f(x + ∆x) dapat dinyatakan dengan deret Taylor sebagai berikut :

... !

3 ) ( !

2 ) ( ) ( ) ( )

( ₃

3 3 2

2 2

+ ∂ ∂ ∆ + ∂ ∂ ∆ + ∂ ∂ ∆ + =

∆ +

x f x x

f x x f x x f x x

f (2.21)

atau dapat ditulis,

∑

∞

= ∂

∂ ∆ + ∂ ∂ ∆ + =

∆ +

2 !

) ( )

( ) ( ) (

n

n n n

x f n

x x

f x x f x x

f (2.22)

dari persamaan (2.22) diperoleh,

∑

∞

= ∂

∂ ∆ − ∆

− ∆ + = ∂ ∂

2 !

) ( ) ( ) (

n

n n n

x f n

x x

x f x x f x f

(2.23)

atau dapat ditulis,

) ( 0 ) ( ) (

x x

x f x x f x f

∆ + ∆

− ∆ + = ∂ ∂

(2.24)

atau dapat dinyatakan dalam bentuk,

) ( 0

1

x x

f f x

f i i

i

∆ + ∆

− = ∂

∂ +

(40)

Untuk mendapatkan harga pendekatan turunan kedua dari fungsi f terhadap x, dilakukan langkah-langkah sebagai berikut,

... ! 3 ) ( ! 2 ) ( ) ( ) ( ) ( 3 3 3 2 2 2 + ∂ ∂ ∆ + ∂ ∂ ∆ + ∂ ∂ ∆ + = ∆ + x f x x f x x f x x f x x

f (2.26)

bila f(x + 2∆x) diekspansikan dengan deret Taylor, menghasilkan persamaan berikut,

... ! 3 ) 2 ( ! 2 ) 2 ( ) 2 ( ) ( ) 2 ( 3 3 3 2 2 2 + ∂ ∂ ∆ + ∂ ∂ ∆ + ∂ ∂ ∆ + = ∆ + x f x x f x x f x x f x x

f (2.27)

bila f(x + 2∆x) - 2f(x + ∆x) menghasilkan,

... ) ( ) ( ) ( ) ( 2 ) 2 ( 3 3 3 2 2 2 + ∂ ∂ ∆ + ∂ ∂ ∆ + − = ∆ + − ∆ + x f x x f x x f x x f x x

f (2.28)

dari persamaan (2.18) dapat diperoleh,

) ( 0 ) ( ) ( ) ( 2 ) 2 ( 2 2 2 x x x f x x f x x f x

f ₊ _∆

∆ − ∆ + − ∆ + = ∂ ∂ (2.29)

atau dapat dinyatakan dengan,

) ( 0 ) ( 2 2 1 2 2 2 x x f f f x

f i i i

i ∆ + ∆ − − = ∂ ∂ ₊ ₊ (2.30)

2.2.2. Beda Mundur

Bila fungsi f(x) analitik, maka f(x-∆x) dapat dinyatakan dengan deret Taylor terhadap x sebagai berikut :

... ! 3 ) ( ! 2 ) ( ) ( ) ( ) ( ₃ 3 3 2 2 2 + ∂ ∂ ∆ − ∂ ∂ ∆ + ∂ ∂ ∆ − = ∆ − x f x x f x x f x x f x x

f (2.31)

atau dapat ditulis,

∑

∞ = ∂ ∂ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∆ ± + ∂ ∂ ∆ − = ∆ − 2 ! ) ( ) ( ) ( ) ( n n n n x f n x x f x x f x x

f , (2.32)

(41)

) ( 0 ) ( ) ( x x x x f x f x f ∆ + ∆ ∆ − − = ∂ ∂ (2.33)

atau dapat dinyatakan dalam bentuk,

) ( 0 1 _x x f f x

f i i

i ∆ + ∆ − = ∂ ∂ − (2.34)

Untuk mendapatkan harga pendekatan turunan kedua dari fungsi f terhadap x, dapat dilakukan dengan menggunakan ekspansi deret Taylor fungsi f(x-∆x) dan bila f(x-2∆x).

... ! 3 ) ( ! 2 ) ( ) ( ) ( ) ( 3 3 3 2 2 2 + ∂ ∂ ∆ − ∂ ∂ ∆ + ∂ ∂ ∆ − = ∆ − x f x x f x x f x x f x x

f (2.35)

... ! 3 ) 2 ( ! 2 ) 2 ( ) 2 ( ) ( ) 2 ( ₃ 3 3 2 2 2 + ∂ ∂ ∆ − ∂ ∂ ∆ + ∂ ∂ ∆ − = ∆ − x f x x f x x f x x f x x

f (2.36)

bila f(x-2∆x) - 2f(x-∆x), diperoleh turunan kedua dari fungsi f terhadap x, yang dapat dinyatakan dengan persamaan berikut,

) ( 0 ) ( ) 2 ( ) ( 2 ) ( 2 2 2 x x x x f x x f x f x f ∆ + ∆ ∆ − + ∆ − − = ∂ ∂ (2.37)

) ( 0 ) ( 2 2 2 1 2 2 x x f f f x

f i i i

i ∆ + ∆ + − = ∂ ∂ ₋ ₋ (2.38)

2.2.3. Beda Tengah

Dengan memanfaatkan ekspansi dari fungsi f(x+∆x) dan f(x-∆x), dapat diperoleh turunan pertama f terhadap x dengan cara beda tengah :

∑

∞ = ∂ ∂ ∆ + ∂ ∂ ∆ + = ∆ + 2 ! ) ( ) ( ) ( ) ( n n n n x f n x x f x x f x x

(42)

∑

∞ = ∂ ∂ ⎥ ⎦ ⎤ ⎢ ⎣ ⎡ ∆ ± + ∂ ∂ ∆ − = ∆ − 2 ! ) ( ) ( ) ( ) ( n n n n x f n x x f x x f x x

f (2.40)

bila f(x+∆x) - f(x-∆x), diperoleh,

... ! 3 ) ( 2 2 ) ( ) ( ₃ 3 3 + ∂ ∂ ∆ + ∂ ∂ ∆ = ∆ − − ∆ + x f x x f x x x f x x

f (2.41)

dari persamaan (2.41), didapat, 2 ) ( 0 2 ) ( ) ( x x x x f x x f x

f ₊ _∆

∆ ∆ − − ∆ + = ∂ ∂ (2.42)

atau dapat dinyatakan dalam bentuk, 2 1 1 ) ( 0

2 x x

f f x

f i i

i ∆ + ∆ − = ∂ ∂ + − (2.43)

Untuk mendapatkan harga pendekatan turunan kedua dari fungsi f terhadap x, dapat dilakukan dengan menambahkan persamaan f(x+∆x) dengan f(x-∆x).

... ! 3 ) ( ! 2 ) ( ) ( ) ( ) ( 3 3 3 2 2 2 + ∂ ∂ ∆ + ∂ ∂ ∆ + ∂ ∂ ∆ + = ∆ + x f x x f x x f x x f x x

f (2.44)

... ! 3 ) ( ! 2 ) ( ) ( ) ( ) ( 3 3 3 2 2 2 + ∂ ∂ ∆ − ∂ ∂ ∆ + ∂ ∂ ∆ − = ∆ − x f x x f x x f x x f x x

f (2.45)

bila f(x+∆x) + f(x-∆x), menghasilkan persamaan yang dapat dinyatakan dengan persamaan berikut :

2 2 2 2 ) ( 0 ) ( ) ( ) ( 2 ) 2 ( x x x x f x f x x f x f ∆ + ∆ ∆ − − − ∆ + = ∂ ∂ (2.46)

2 2 1 1 2 2 ) ( 0 ) ( 2 x x f f f x

f i i i

(43)

BAB III

PERSAMAAN PADA SETIAP TITIK

Pada penelitian ini menggunakan metode numerik, dengan memilih metode beda hingga cara eksplisit

3.1. Model Matematika

Untuk mendapatkan model matematika dari persoalan yang sesuai dengan permasalahan didapat dari kesetimbangan energi pada volume kontrol yang dinyatakan sebagai berikut :

Untuk 3 dimensi keadaan tak tunak

Seluruh energi Energi yang Seluruh energi

yang masuk dibangkitkan yang keluar Perubahan ke dalam + di dalam = dari dalam + energi dalam volume kontrol volume kontrol volume kontrol selama∆t selama∆t selama∆t selama∆t

Atau secara aljabar

t T dxdydz c

q q

q dxdydz q

q q

qx y z x dx y dy z dz

∂ ∂ +

+ +

= +

+

+ ) •( ) ( ₊ ₊ ₊ ) ( )

( ρ (3.1)

Energi yang masuk ke dalam volume kontrol

dydz x T k

qx ⎟

⎠ ⎞ ⎜

⎝ ⎛

∂ ∂ − =

dxdz y T k

qy ⎟⎟

⎠ ⎞ ⎜⎜

⎝ ⎛

∂ ∂ −

= (3.2)

dxdy z T k

q_z ⎟

⎠ ⎞ ⎜

⎝ ⎛

(44)

Gambar 3.1. Sketsa yang melukiskan koordinat untuk penurunan persamaan konduksi panas umum dalam koordinat Cartesius

(F. Kreith, Prinsip - Prinsip Perpindahan Panas, Halaman: 78)

Energi yang keluar dari dalam volume kontrol

dydz dx x T k x x T k

q_x _dx _⎥

⎦ ⎤ ⎢

⎣ ⎡

⎟ ⎠ ⎞ ⎜

⎝ ⎛

∂ ∂ − ∂

∂ + ⎟ ⎠ ⎞ ⎜

⎝ ⎛

∂ ∂ − = +

dxdz dy y T k y y T k

q_y _dy _⎥

⎦ ⎤ ⎢

⎣ ⎡

⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

∂ ∂ − ∂

∂ + ⎟⎟ ⎠ ⎞ ⎜⎜

⎝ ⎛

∂ ∂ − =

+ (3.3)

dxdy dz z T k z z T k

q_z _dz _⎥

⎦ ⎤ ⎢

⎣ ⎡

⎟ ⎠ ⎞ ⎜

⎝ ⎛

∂ ∂ − ∂

∂ + ⎟ ⎠ ⎞ ⎜

⎝ ⎛

∂ ∂ − = +

Kurangkan energi yang masuk ke volume kontrol dengan energi yang keluar dari volume kontrol, kita memperoleh

dxdydz x

x T k q

q_x _x _dx

∂ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∂ ∂ ∂ = − ₊

dxdydz y

y T k q

q_y _y _dy

∂ ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

∂ ∂ ∂ =

− ₊ (3.4)

dxdydz z

z T k q

q_z _z _dz

∂ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

(45)

Masukkan rumus-rumus ini ke dalam kesetimbangan energi dan bagilah tiap suku dengan dx dy dz, maka akan diperoleh

t T c q z T z k y T y k x T x k

∂ ∂ = + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∂ ∂ ∂

∂ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛

∂ ∂ ∂

∂ + ⎟ ⎠ ⎞ ⎜ ⎝ ⎛

∂ ∂ ∂

∂ •

ρ (3.5)

jika sistemnya homogen dan panas jenis (specific heat) c serta kerapatan (density) ρ

tidak tergantung pada suhu. Jika k dianggap konstan dan persamaan (3.5) dibagi k, maka persamaannya menjadi

t T k

q z

T y

T x

T

∂ ∂ = + ∂ ∂ + ∂ ∂ + ∂

∂ •

α

1

2 2 2 2 2 2

(3.6)

di mana konstanta α =k/cρ disebut difusivitas termal dengan satuan m2/s.

Untuk kasus 2 dimensi keadaan tak tunak seperti kasus dalam penelitian ini, maka persamaannya adalah

t T k

q y

T x

T

∂ ∂ = + ∂ ∂ + ∂

∂ •

α

1

2 2 2 2

(3.7)

3.2. Persamaan Pada Setiap Titik

Penyelesaian dilakukan metode beda hingga cara eksplisit. Oleh karena itu diperlukan persamaan numerik pada setiap node. Pada kasus yang ditnjau, ada enam persamaan utama :

1. Titik di sudut benda A

(46)

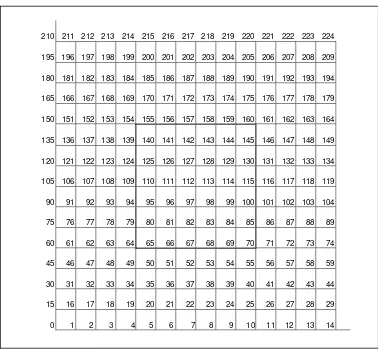
2. Titik di permukaan benda A

Yaitu titik 1 sampai 13, 15, 29, 30, 44, 45, 59, 60, 74, 75, 89, 90, 104, 105, 119, 120, 134, 135, 149, 150, 164, 165, 179, 180, 194, 195, 209 dan 211 sampai 223.

3. Titik di dalam benda A

Yaitu titik 16 sampai 28, 31 sampai 43, 46 sampai 58, 61 sampai 63, 71 sampai 73, 76 sampai 78, 86 sampai 88, 91 sampai 93, 101 sampai 103, 106 sampai 108, 116 sampai 118, 121 sampai 123, 131 sampai 133, 136 sampai 138, 146 sampai 148, 151 sampai 153, 161 sampai 163, 166 sampai 178, 181 sampai 193 dan 196 sampai 208.

4. Titik di sudut antara benda A dengan benda B Yaitu titik 64, 70, 154 dan 160.

5. Titik di permukaan antara benda A dengan benda B

Yaitu titik 65 sampai 69, 79, 85, 94, 100, 109, 115, 124, 130, 139, 145 dan 155 sampai 159.

6. Titik di dalam benda B

(47)

210 211 212 213 214 215 216 217 218 219 220 221 222 223 224

195 196 197 198 199 200 201 202 203 204 205 206 207 208 209

180 181 182 183 184 185 186 187 188 189 190 191 192 193 194

165 166 167 168 169 170 171 172 173 174 175 176 177 178 179

150 151 152 153 154 155 156 157 158 159 160 161 162 163 164

135 136 137 138 139 140 141 142 143 144 145 146 147 148 149

120 121 122 123 124 125 126 127 128 129 130 131 132 133 134

105 106 107 108 109 110 111 112 113 114 115 116 117 118 119

90 91 92 93 94 95 96 97 98 99 100 101 102 103 104

75 76 77 78 79 80 81 82 83 84 85 86 87 88 89

60 61 62 63 64 65 66 67 68 69 70 71 72 73 74

45 46 47 48 49 50 51 52 53 54 55 56 57 58 59

30 31 32 33 34 35 36 37 38 39 40 41 42 43 44

15 16 17 18 19 20 21 22 23 24 25 26 27 28 29

0 1 2 3 4 5 6 7 8 9 10 11

(48)

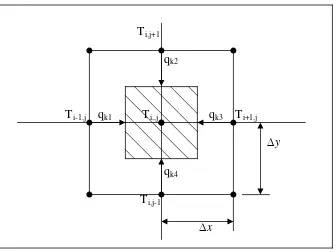
3.2.1. Kasus 1 (Titik di sudut benda A, misal titik 0)

qc2, T∞, h

Ti,j Ti+1,j

T_∞, h qc1 qk1 ∆y

Ti,j-1 qk2

∆x

Gambar 3.3. Volume kontrol pada kasus 1 = volume kontrol

q = energi yang masuk ke volume kontrol [ qc1 + qc2 + qk1 + qk2 ] + [

•

q V ] =

t T cV

∂ ∂

ρ (3.8)

( )

(

)

( )

(

)

( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + − ∞ ∞ y T T x k x T T y k T T x h T T y h n j i n j i n j i n j i n j i n j i , 1 , , , 1 , , 1 2 1 2 1 2 1 2 =

( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + t T T y x c n j i n j i , 1 , 1 2 2

ρ (3.9)

l y x=∆ =

∆

(

)

(

) (

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − = − + − + − + − + − + ∞ ∞ t T T cl T T k T T k T T hl T T

hl inj

n j i n j i n j i n j i n j i n j i n j i , 1 , 2 , 1 , , , 1 , , 4 2 2 2 2 ρ (3.10 )

(

) (

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − = − + − + − + − + ∞ t T T cl T T k T T k T T hl n j i n j i n j i n j i n j i n j i n j i , 1 , 2 , 1 , , , 1 , 4 2 2 ρ (3.11)

Persamaan (3.11) dikali k 4 , maka

(

) (

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − = − + − + − + − + ∞ t T T l k c T T T T T T k

hl inj

n j i n j i n j i n j i n j i n j i , 1 , 2 , 1 , , , 1

, 2 2

4 ρ

(49)

Bila

c k

ρ

α = maka persamaan (3.12) menjadi

(

n

)

j i n j i n j i n j i n j i n j i n j

i T T

t l T T T T T k hl T k hl , 1 , 2 , 1 , , , 1

, 2 2 2 2

4 4 − ∆ = − + − + − + − +

∞ _α (3.13)

2 ) ( x t Fo ∆ ∆

= α , maka diperoleh

(

n

)

j i n j i o n j i n j i n j i n j

i T T

F T T T T k hl T k hl , 1 , , 1 , , 1 , 1 4 2 2 4 4 − = − + + − + − +

∞ (3.14)

n j i n j i n j i o n j i o n j i o n j i o o T T T F T F T F T k hlF T k hlF , 1 , , 1 , , 1

, 2 2 4

4 4 − = − + + − + − +

∞ (3.15)

1 , , , , 1 , , 1 4 4 ) 2 (

2 ₊ + ₋ + _∞ + − n − o _in_j = _in_j+

j i o n j i n j i n j i

o T T

k hlF T F T T k hl T T

F (3.16)

n j i o o n j i n j i o n j i T k hlF F T k hl T T F

T 1, , 1 ,

1 , 4 4 1 ) 2 ( 2 ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ₋ ₋ + + + = ₊ ₋ _∞ + (3.17) Dengan syarat stabilitas

0 4

4

1− − ≥

k hlF

Fo o

) 1 ( 4 1 Bi F_o + ≤

( )

) 1 ( 4 2 Bi x t + ∆ ≤ ∆

α (3.18)

3.2.2. Kasus 2 (Titik di permukaan benda A, misal titik 1)

qc, T∞, h

T_i₋n₁_,_j T_i_,n_j T_in₊₁_,_j

qk3 qk1 ∆y

qk2

Ti,j-1

∆x

(50)

= volume kontrol

q = energi yang masuk ke volume kontrol [qc + qk1 + qk2 + qk3 ] + ⎢⎣⎡ ⎥⎦⎤

2 V q =

t T cV

∂ ∂

ρ (3.19)

( )

(

)

( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + − ∆ + − − ∞ x T T y k y T T x k x T T y k T T x h n j i n j i n j i n j i n j i n j i n j i , , 1 , 1 , , , 1 , 1 2 1 ) ( 1 2 1 ) ( =

( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ ∆ + t T T y x c n j i n j i , 1 , 1 2 ) (

ρ (3.20)

l y x=∆ =

∆

(

) (

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − = − + − + − + − + − − + ∞ t T T cl T T k T T k T T k T T hl n j i n j i n j i n j i n j i n j i n j i n j i n j i , 1 , 2 , , 1 , 1 , , , 1 , 2 ) ( 2 2 ρ (3.21

(

) (

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − = − + − + − + − + − − + ∞ t T T l k c T T T T T T T T k

hl inj

n j i n j i n j i n j i n j i n j i n j i n j i , 1 , 2 , , 1 , 1 , , , 1

, 2 ( )

2 ρ (3.22) Bila c k ρ

(

n

)

j i n j i n j i n j i n j i n j i n j i n j i n j

i T T

t l T T T T T T T k hl T k hl , 1 , 2 , , 1 , 1 , , , 1

, 2 2

2 2 − ∆ = − + − + − + − + − − +

∞ _α (3.23)

2 ) ( x t F_o ∆ ∆

(

n

)

j i n j i o n j i n j i n j i n j i n j

i T T

F T T T T T k hl T k hl , 1 , , , 1 1 , , 1 , 1 4 2 2

2 ₋ ₊ ₊ ₊ ₋ ₌ + ₋

− − +

∞ (3.24)

n j i n j i n j i o n j i o n j i o n j i o n j i o o T T T F T F T F T F T k hlF T k hlF , 1 , , , 1 1 , , 1

, 2 4

2 2 − = − + + + − + − − +

∞ (3.25)

1 , , , , , 1 1 , , 1 2 4 ) 2 2

( ₊ + ₋ + ₋ + _∞ + − − = n+

j i n j i o n j i o n j i n j i n j i n j i

o T T

k hlF T F T T k hl T T T

F (3.26)

n j i o o n j i n j i n j i o n j i T k hlF F T k hl T T T F

T_, 1 ( ₁_, 2 _, ₁ ₁_, 2 ) 1 4 2 ⎟ _, ⎠ ⎞ ⎜ ⎝ ⎛ ₋ ₋ + + + + = ₊ ₋ ₋ _∞ + (3.27) Dengan syarat stabilitas

0 2

4

1− − ≥

k hlF

F o

o ⇒

) 2 ( 2 1 Bi F_o + ≤ ⇒ ) 2 ( 2 ) ( 2 Bi x t + ∆ ≤ ∆

(51)

3.2.3. Kasus 3 (Titik di dalam benda A, misal Titik 17)

Ti,j+1

qk2

Ti-1,j qk1 Ti,,j qk3 Ti+1,j

∆y qk4 Ti,j-1 x ∆ Gambar 3.5. Volume kontrol pada kasus 3

= volume kontrol

q = energi yang masuk ke volume kontrol

[qk1 + qk2 + qk3 + qk4 ] +

[ ]

qV =

t T cV

∂ ∂

ρ (3.29)

( )

( )( )

( )

( )( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ − + + − y T T x k x T T y k y T T x k x T T y k n j i n j i n j i n j i n j i n j i n j i n j

i 1, , , 1 , 1, , , 1 ,

1 1 ) ( 1 1 ) ( =

( )( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ ∆ + t T T y x c n j i n j i , 1 , 1 ) (

ρ (3.30)

l y x=∆ =

∆

(

) (

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − = − + − + − + − + − + + − t T T cl T T k T T k T T k T T k n j i n j i n j i n j i n j i n j i n j i n j i n j i j i , 1 , 2 , 1 , , , 1 , 1 , , .

(52)

(

) (

)

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − = − + − + − + − + − + + − t T T l k c T T T T T T T T n j i n j i n j i n j i n j i n j i n j i n j i n j i n j i , 1 , 2 , 1 , , , 1 , 1 , , ,

1 ( )

ρ (3.32) Bila c k ρ

(

n

)

j i n j i n j i n j i n j i n j i n j i n j i n j i n j

i T T

t l T T T T T T T T , 1 , 2 , 1 , , , 1 , 1 , , , 1 − ∆ = − + − + − + − + − + +

− _α (3.33)

2 ) ( x t F_o ∆ ∆

(

n

)

j i n j i o n j i n j i n j i n j i n j

i T T

F T T

T T

T₋₁_, + _, ₊₁+ ₊₁_, + _, ₋₁−4 _, = 1 _,+1− _, (3.34) n j i n j i n j i o n j i o n j i o n j i o n j i

oT FT FT FT FT T T

F ₋₁_, + _, ₊₁+ ₊₁_, + _, ₋₁ −4 _, = _,+1 − _, (3.35) 1 , , , 1 , , 1 1 , ,

1 ) 4

( ₋ + ₊ + ₊ + ₋ + − = inj+

n j i o n j i n j i n j i n j i n j i

o T T T T T FT T

F (3.36)

(

)

n j i o n j i n j i n j i n j i o n j

i F T T T T F T

T_,+1 = ( ₋₁_, + _,₊₁+ ₊₁_, + _, ₋₁)+ 1−4 _, (3.37) Dengan syarat stabilitas

0 4

1− F_o ≥

4 1 ≤ o F α 4 ) ( x 2 t ≤ ∆

(53)

3.2.4. Kasus 4 (Titik di sudut antara benda A dengan benda B, misal titik 64)

Ti,j+1

k1 qk2

qk3

Ti-1,j qk1 Ti,j Ti+1,j

q qk4 ∆y

qk6 qk5 k2

Ti,j-1

∆x

Gambar 3.6. Volume kontrol pada kasus 4

= volume kontrol

q = energi yang masuk ke volume kontrol

[qk1 + qk2 + qk3 + qk4 + qk5 + qk6 ] + ⎢⎣⎡ ⎥⎦⎤

4 V q =

t T cV

∂ ∂

ρ (3.39)

( )

_⎟⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ⎟ ⎠ ⎞ ⎜ ⎝ ⎛ ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ + ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ ∆ − ∆ − + + + x T T y k x T T y k y T T x k x T T y k n j i n j i n j i n j i n j i n j i n j i n j

i 1, ,

2 , , 1 1 , 1 , 1 , , 1 1 1 2 1 2