SIMULASI NUMERIK KONVEKSI ALAMI PADA SINGLE FIN DAN MULTIPLE FINS DALAM KOTAK 2D DENGAN METODE BEDA HINGGA

(1)

SKRIPSI

Diajukan sebagai salah satu syarat untuk memperoleh gelar

Sarjana Teknik

Oleh :

FERRY ENDHARTA NIM. I1407514

JURUSAN TEKNIK MESIN

FAKULTAS TEKNIK UNIVERSITAS SEBELAS MARET

SURAKARTA

(2)

ii Di susun oleh : Ferry Endharta NIM. I1407514

Dosen Pembimbing I Dosen Pembimbing II

Eko Prasetya Budiana, S.T.M.T. Budi Kristiawan, S.T.M.T. NIP. 197109261999031002 NIP. 197104251999031001

Telah dipertahankan di hadapan dosen tim penguji pada hari Selasa, tanggal 13 Juli 2010.

1. Syamsul Hadi, S.T.M.T.

NIP. 197106151998021002 ………..

2. Purwadi Joko Widodo, S.T.M.Kom

NIP. 197301261997021001 ………..

3. Rendy Adhi Rachmanto, S.T.M.T.

NIP. 197101192000121006 ………..

Mengetahui,

Ketua Jurusan Teknik Mesin Koordinator Tugas Akhir

(3)

iii

Capailah cita–citamu dengan usaha maksimal niscaya akan berhasil. Percayalah Allah akan selalu ada untuk kita, sesulit apapun masalah

yang kita hadapi pasti ada jaln untuk kita

Berbuatlah yang terbaik untuk setiap detiknya Dan tak perlu kau pikirkan esok akan jadi apa

Bila keadaan sudah berada dititik buruk yang paling buruk, rendah yang paling rendah dan sakit yang paling sakit, maka tidak lain yang akan

terjadi adalah menjadi baik.

Persembahan

(4)

iv

Simulasi numerik untuk konveksi alami dalam kotak 2D pada single fin dan multiple fins dilakukan untuk mengetahui fenomena yang terjadi pada pola aliran dan distribusi temperatur di sekitar fin pada kotak 2D. Tulisan ini menguraikan metode untuk penyelesaiaan konveksi alami steady dalam kotak 2D. Metode ini didasarkan pada skema Runge – Kutta untuk diskritisasi waktu dan skema kompak beda hingga orde-4 untuk diskritisasi ruang. Kesulitan pada penyelesaian tekanan diselesaikan dengan metode kompresibilitas tiruan. Metode beda hingga dituliskan dengan bahasa Fortran dan divisualisasikan dengan perangkat lunak Matlab. Hasil dari visualisasi menunjukkan bahwa separasi muncul karena adanya pusaran kecepatan disekitar sirip. Semakin besar angka Rayleigh dengan domain dan panjang sirip yang sama, kerapatan pepindahan panas disekitar dinding akan meningkat. Hasil menunjukkan pada angka Rayleigh 106 dan 107 telah terjadi separasi disekitar sirip.

(5)

v

Numerical simulation for natural convection in 2D cavity with single fin and multiple fins done to know the phenomenon that happened at stream function and distribution of temperature around fin in 2D cavity. This paper present numerical method for solving steady natural convection in 2D cavity. The method is based on Runge-Kutta schemes for temporal discretization and fourh-order compact finite difference schemes for spatial discretization. Difficulty related to the pressure can be overcome by using artificial compressibility method. Finite difference written by Fortran language and visualized by Matlab. Result shown that separation appear caused by vortex in the velocity vector around fin. Increasing of Rayleigh number with same fin length and domain, density of heat transfer around wall will be increase. Result show for Rayleigh number 106 and 107 have happened separation around fin.

(6)

vi

rahmat, hidayah serta kekuatan kepada Penulis, sehingga Penulis dapat melaksanakan penelitian dan menyelesaikan laporan Tugas Akhir dengan judul “Simulasi Numerik Konveksi Alami Pada Single Fin Dan Multiple Fins Dalam Kotak 2D Dengan Metode Beda Hingga”, sebagai salah satu syarat untuk memperoleh gelar Sarjana Teknik di Jurusan Teknik Mesin Fakultas Teknik Universitas Sebelas Maret Surakarta.

Dalam kesempatan ini, Penulis ingin menyampaikan ucapan terima kasih yang sebesar – besarnya kepada semua pihak yang telah memberikan bantuan, doa, dukungan dan semangat, baik moral maupun spiritual kepada :

1. Bapak Dody Ariawan, ST., MT., selaku Ketua Jurusan Teknik Mesin UNS.

2. Bapak Eko Prasetya Budiana, ST.,MT., selaku Pembimbing I tugas akhir, atas bimbingan, nasehat, kesabaran, dan ilmu pengetahuan yang diajarkannya.

3. Bapak Budi Kristiawan, ST.,MT., selaku Pembimbing II tugas akhir , atas bimbingan , nasehat, kesabaran dan ilmu pengetahuan yang diajarkannya. 4. Bapak Purwadi Joko Widodo, S.T.M.Kom, selaku Pembimbing

Akademik.

5. Bapak – bapak dosen dan staf karyawan di lingkungan Teknik Mesin UNS, atas didikan, nasehat, ilmu yang diajarkan dan kerjasamanya.

6. Teman – teman Teknik Mesin transfer angkatan 2007 Teman – teman Teknik Mesin UNS

7. Teman – teman kos Oblong.

8. Dan semua pihak yang telah membantu Penulis dalam menyelesaikan skripsi ini.

(7)

vii

(8)

viii

HALAMAN PENGESAHAN ………. .... ii

MOTTO DAN PERSEMBAHAN……….. ... iii

ABSTRAK………. .. iv

ABSTRACT……… ... v

KATA PENGANTAR……… ... vi

DAFTAR ISI………. ... viii

DAFTAR GAMBAR……… ... x

DAFTAR TABEL ... xii

DAFTAR NOTASI...……….. ... xiii

DAFTAR LAMPIRAN……. ... xv

BAB I PENDAHULUAN ... 1

1.1Latar Belakang Masalah ... 1

1.2Perumusan Masalah ... 2

1.3Batasan Masalah... 2

1.4Tujuan Penelitian ... 2

1.5Manfaat Penelitian ... 2

1.6Sistematika Penulisan ... 3

BAB II LANDASAN TEORI ... 4

2.1Tinjauan Pustaka ... 4

2.2Dasar Teori………. ... 6

2.2.1Sirip……… ... 6

2.2.2Konveksi Alami……… . 7

2.2.2.1 Persamaan Atur Konveksi Alami ... 8

2.2.2.2 Diskritisasi Waktu ... 8

2.2.2.3 Diskritisasi Ruang ... 9

2.2.2.4 Metode Kompresibilitas Tiruan ... 13

(9)

ix

3.3.2 Diskritisasi Persamaan Energi ... 18

3.3.3 Diskritisasi Metode Kompresibilitas Tiruan ... 19

3.4 Diskritisasi Syarat Batas ... 19

3.5 Algoritma Pemrograman ... 24

BAB IV HASIL DAN PEMBAHASAN 4.1 Simulasi Konveksi Alami Sirip Tunggal dan Multiple Sirip . 24 4.2 Validasi Program ... 32

BAB V PENUTUP ... 37

5.1 Kesimpulan ... 37

5.2 Saran ... 37

DAFTAR PUSTAKA ... 38

(10)

x

Gambar 2.3 Beberapa contoh jenis extended surface: (a) sirip longitudinal (memanjang) dengan profil segiempat (b)pipa silindris dengan sirip berprofil segiempat (c) sirip longitudinal dengan profil trapezioda (d) sirip longitudinal dengan profil parabola (e) pipa silindris dengan sirip radial berprofil segiempat (f) pipa silindris dengan sirip radial berprofil trapezoida (g)cylindrical spine (h)truncated conical spine (i) truncated parabolic

spine ... 6

Gambar 2.4 Galat dispersi untuk pendekatan numerik dari turunan Pertama ... 10

Gambar 2.5 Galat disipasi untuk pendekatan numerik dari turunan kedua ... 12

Gambar 3.1 Domain dan syarat batas ... 18

Gambar 4.1 Isothermal pada ra = 106 pada sirip tunggal ... 24

Gambar 4.2 Isothermal pada Ra = 106 pada 2 sirip ... 24

Gambar 4.5 Isothermal pada Ra = 107 pada sirip tunggal ... 25

Gambar 4.9 Stream function pada Ra = 106 pada sirip tunggal ... 27

Gambar 4.10 Stream function pada Ra = 106 pada 2 sirip... 28

Gambar 4.11 Stream function pada Ra = 106 pada 3 sirip... 28

Gambar 4.12 Stream function pada Ra = 106 pada 4 sirip ... 28

Gambar 4.13 Stream function pada Ra = 107 pada sirip tunggal... 29

(11)

xi

Gambar 4.19. Kurva konvergensi untuk Ra=10 sirip tunggal ... 31 Gambar 4.20 Domain dan Syarat Batas penelitian Pranowo dan Tri Iswanto 32 Gambar 4.21 Distribusi temperatur (a) dan stream function (b) yang

dibuat penulis pada Ra = 106 ... 33 Gambar 4.22 Distribusi temperatur (a) dan stream function (b) yang

dibuat penulis pada Ra = 107 ... 33 Gambar 4.23 Distribusi temperatur (a) dan stream function (b) yang

dibuat Pranowo dan Tri Iswanto pada Ra = 106 ... 34 Gambar 4.24 Distribusi temperatur (a) dan stream function (b) yang

dibuat Pranowo dan Tri Iswanto pada Ra = 107 ... 34 Gambar 4.25 Separasi di sekitar sirip yang dibuat penulis ... 36 Gambar 4.26 Separasi di sekitar sirip oleh F. Xu, J.C. Patterson

(12)

xii

turunan pertama ... 10 Tabel 2.3 Perbandingan skema beda hingga dan skema kompak

(13)

xiii bM : koefisien skema Runge-Kutta c : konstanta persamaan konveksi 1-D g : percepatan gravitasi (m/s2)

H : tinggi kotak

HM : variabel untuk skema Runge-Kutta i,j : indek nodal

k : numerical wave number

Lr : variabel referensi untuk panjang kotak nx : jumlah index arah x

ny : jumlah indek arah y Nu : bilangan Nusselt p : tekanan

u : kecepatan arah x v : kecepatan arah y

Vr : variabel referensi untuk kecepatan x,y : koordinat

Pr : bilangan Prandtl Ra : bilangan Rayleigh t : variabel waktu

tr : variabel reverensi untuk waktu

Huruf Yunani

 : koefisien skema kompak  : koefisien ekspansi volumetri  : operator diferensial

(14)

xiv ” : variabel turunan kedua

 : densitas

 : variabel temperatur  : vortisitas

(15)

xv

Lampiran 4. Numerical Wavenumber ... 47

Lampiran 5. Program Konveksi Alami Pada Sirip Tunggal ... 49

Lampiran 6. Program Konveksi Alami Pada 2 Sirip... 62

Lampiran 9. Program Tambahan Untuk Sirip Tunggal ... 120

Lampiran 10. Program Tambahan Untuk 2 Sirip ... 127

(16)

1

Dalam kehidupan sehari – hari sering sekali kita jumpai aplikasi mengenai perpindahan panas,salah satunya adalah perpindahan panas secara konveksi. Perpindahan panas secara konveksi berdasarkan jenis penyebab aliran fluida yang terjadi dikategorikan menjadi dua kategori, yaitu konveksi paksa dan konveksi alami.

Konveksi paksa (forced convection) adalah konveksi dimana aliran fluida yang terjadi disebabkan adanya alat – alat eksternal,seperti fan,pompa,aliran udara atmosfer (angin). Sedangkan konveksi alami (natural convection) adalah konveksi yang terjadi karena fluida yang berubah densitasnya (kerapatannya) disebabkan proses pemanasan dan fluida ini bergerak naik karena adanya gaya apung (bouyancy force).

Untuk meningkatkan perpindahan panas antara permukaan utama dan fluida di sekitarnya biasanya kita menggunakan sirip (fin). Sirip biasa digunakan dalam berbagai macam aplikasi,misalnya pada sistem pendingin ruangan,peralatan elektronik,tubin gas dan sebagainya,dengan udara sebagai media perpindahan panasnya.

Penelitian mengenai fenomena perpindahan panas konveksi alami dengan menggunakan sirip tunggal maupun multiple sirip telah banyak dilakukan baik secara eksperimental maupun secara numerik. Penelitian secara eksperimen untuk mengetahui fenomena yang terjadi pada proses perpindahan panas konveksi alami dengan menggunakan sirip tunggal maupun multiple sirip membutuhkan biaya yang cukup mahal dan proses yang cukup rumit.

(17)

secara numerik konveksi alami pada sirip tunggal dan multiple sirip dalam kotak 2D dengan menggunakan metode beda hingga orde-4.

1.3Batasan Masalah

Dalam penelitian ini masalah dibatasi sebagai berikut :

a. Masalah pada penelitian ini dibatasi pada persoalan konveksi alami pada sirip tunggal dan multiple sirip dalam kotak 2D dengan menyelesaikannya menggunakan metode beda hingga orde-4 untuk memperoleh distribusi temperatur dan pola aliran (stream function).

b. Aliran fluida diasumsikan sebagai aliran fluida tak mampat (incompressible flow).

c. Penelitian dibatasi pada ruang 2 dimensi.

1.4Tujuan Penelitian

Adapun tujuan dari penelitian ini adalah untuk mengetahui fenomena yang terjadi pada aliran dan perpindahan panas konveksi alami pada sirip tunggal dan multiple sirip dalam kotak 2D,meliputi profil aliran fluida dan distribusi temperatur.

1.5Manfaat Penelitian

Manfaat dari penelitian ini :

a. Untuk mengembangkan ilmu pengetahuan, terutama dalam bidang komputasi numerik dan perpindahan panas.

(18)

Sistematika penulisan yang digunakan adalah : BAB I : PENDAHULUAN

Berisi latar belakang masalah, batasan dan perumusan masalah, tujuan dan manfaat penelitian serta sistematika penulisan.

BAB II : LANDASAN TEORI

Berisi tentang tinjauan pustaka, dasar teori perpindahan panas konveksi dan penjelasan mengenai metode beda hingga orde 4. BAB III : PELAKSANAAN PENELITIAN

Berisi tentang alat dan bahan yang digunakan dalam penelitian, cara penelitian, diskritisasi persamaan atur.

BAB IV : HASIL DAN PEMBAHASAN

Berisi hasil penelitian (simulasi) dan pembahasannya. BAB V : PENUTUP

Berisi kesimpulan penelitian dan saran – saran untuk penelitian selanjutnya.

(19)

4

sirip tunggal dan multiple sirip dalam sebuah kotak bujur sangkar dengan pemodelan numerik,dimana dipengaruhi oleh medan listrik, aliran dan temperaturnya. Parameter yang digunakan adalah tegangan, Rayleigh number, ukuran kotak, penyusunan elektroda, jumlah sirip, dan panjang sirip. Dihasilkan bahwa dengan angka Rayleigh yang sama maka koefisien perpindahan panas akan bertambah besar dengan menambah jumlah sirip dan panjang sirip.

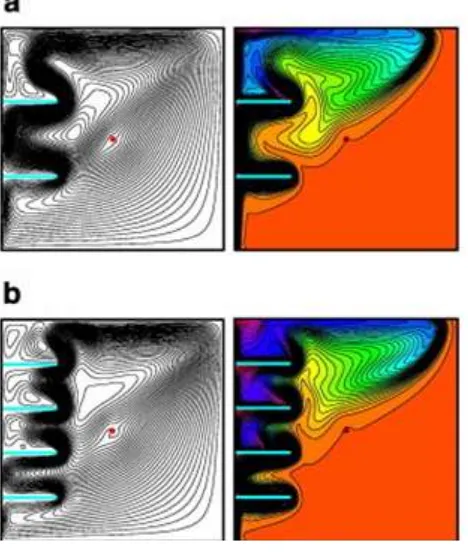
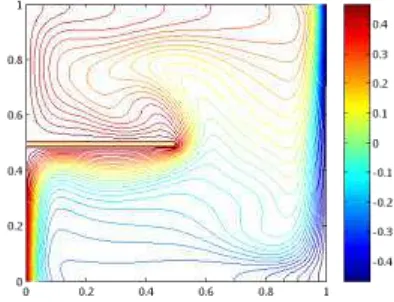
Gambar 2.1. stream function dan isotherm pada Ra = 106

(20)

Gambar2. 2. separasi di sekitar sirip

Wilson dan Demuren(1998) menggunakan skema kompak beda hingga untuk diskritasi ruang dan skema Runge-Kutta untuk diskritasi waktu pada simulasi aliran fluida tak mampat. Pada penelitian ini skema kompak beda hingga digunakan untuk diskritisasi turunan ruang dan skema Runge-Kutta orde-empat untuk diskritasi turunan waktu.

Le Querre (1990) menggunakan algoritma pseudo – spectral Chebsyev untuk meneliti konveksi alami pada kotak 2D dengan dinding bawah di panasi dan dinding atas adiabatic. Dengan metode ini dapat menghilangkan osilasi numeric dan mencapai hasil yang akurat hingga nilai Ra 108.

Pranowo dan Priyo tri Iswanto (1999) menyelesaikan persamaan Navier – Stoke 2 dimensi dengan menggunakan primitive variable pada non staggered grid dengan diskritisasi beda hingga. Hasil simulasi dengan metode ini menunjukkan hasil yang akurat untuk Ra = 106 dan Ra = 107.

(21)

Sirip digunakan dalam banyak alat penukar kalor untuk meningkatkan luasan perpindahan panas. Aplikasi sirip banyak dijumpai dalam sistem pendingin ruangan,peralatan elektronik,turbin gas dan sebagainya, dengan udara merupakan media perpindahan panasnya. Dalam alat penukar panas sirip terbagi dari berbagai macam tipe, mulai dari bentuk yang sederhana, seperti sirip segiempat (rectangular), silindris, annular, tirus (tapered) atau pin, sampai kombinasi dari berbagai geometri yang berbeda telah digunakan. Tipe sirip yang digunakan tergantung dari proses permesinan dan ruang yang tersedia dalam peralatan pembangkit panas yang terlibat dalam proses pendinginan.

Dalam desain dan konstruksi dari berbagai macam peralatan perpindahan panas, bentuk-bentuk sederhana seperti; silinder, batang dan plat biasa diterapkan pada aliran panas antara sumber panas dan penyerap panas (heat source and heat sink). Permukaan-permukaan penyerap panas maupun pembuang panas masing-masing dikenal sebagai permukaan utama (prime surface). Apabila permukaan utama diperluas dengan permukaan tambahan seperti dalam gambar 2.3, maka gabungan antara kedua permukaan tersebut dinamakan permukaan yang diperluas (extended surface). Elemen yang digunakan untuk memperluas permukaan utama dikenal sebagai sirip (sirip).

Gambar 2.3. Beberapa contoh jenis extended surface: (a) sirip longitudinal (memanjang) dengan profil segiempat (b)pipa silindris dengan sirip berprofil segiempat (c) sirip longitudinal dengan profil trapezioda (d) sirip longitudinal dengan profil parabola (e) pipa silindris dengan sirip radial berprofil segiempat (f)

(22)



Konveksi alami adalah perpindahan panas antara suatu permukaan dan fluida yang mengalir diatasnya. Aliran fluida disebabkan oleh adanya perbedaan densitas fluida yang ditimbulkan oleh pemanasan dan pendinginan. Densitas fluida akan berkurang jika fluida mendapat pemanasan sehingga fluida akan mengapung dan daerah yang ditinggalakan akan diisi oleh fluida yang relatif dingin. Fluida yang relatif panas jika mendekati dinding yang relatif dingin densitasnya akan meningkat sehingga akan mengalir turun akibat tarikan gaya grafitasi. Dengan demikian densitas merupakan driving force sirkulasi fluida. Konveksi alami memegang peranan penting dalam rekayasa industri seperi: perancangan alat penukar kalor, perancangan ventilasi, pendinginan transformator, pendinginan kabel bawah tanah dan pendinginan komponen elektronika. Pada penelitian konveksi alami model matematika yang dipakai adalah persamaan kontinyuitas, persamaan Navier-Stokes dan persamaan energi.

2.2.2.1Persamaan Atur Konveksi Alami

Untuk permasalahan 2-D persamaan atur konveksi alami dalam bentuk variabel tak berdimensi adalah sebagai berikut (Le Quere,1990):

(1)

(23)

Kutta orde-4 dari Williamson(Wilson dan Demuren,1998) yang didefinisikan sebagai berikut :

(5)

Tabel 2.1 Koefisien Runge-Kutta orde-4 dari Carpenter dan Kennedy

M aM bM

1 0 0.14965902

2 -0.41789047 0.37921031 3 -1.19215169 0.82295502 4 -1.69778469 0.69945045 5 -1.51418344 0.15305724

2.2.2.3Diskritisasi Ruang

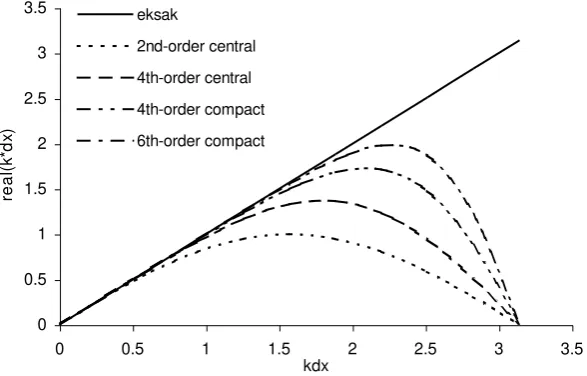
Skema beda-hingga orde-2 untuk turunan pertama memiliki galat dispersi yang besar, sedangkan skema kompak beda hingga memiliki kelebihan yaitu akurasi tinggi, fleksibel dan pengoperasiannya lebih mudah.

a. Turunan pertama.

Bentuk diskritisasi turunan pertama dengan pendekatan skema kompak beda hingga orde-4 dirumuskan oleh Lele(Wilson dan Demuren, 1998). Bentuk persamaannya adalah seperti berikut :

(24)

 

Perbandingan skema ekplisit beda-hingga dan skema kompak beda hingga dari turunan pertama ditunjukkan dalam tabel 2.2. Di sini terlihat bahwa skema kompak beda hingga memiliki grid stensil yang lebih sedikit, koefisien galat pemenggalan berkurang menjadi ¼ untuk orde-4 dari koefisien beda tengah ekplisit untuk orde yang sama.

Tabel 2.2 Perbandingan skema beda hingga dan skema kompak turunan pertama Skema Kesalahan pemenggalan Jumlah stensil

Beda tengah orde-4 _(-4/5!)( 4 ) dianalisa dengan mentransformasi persamaan konveksi 1-D sebagai berikut:

(7)

(8)

Dalam mode Fourier ~(t)eikx maka :

(9)

(10) Sehingga persamaan konveksi 1-D menjadi :

(25)

0

k* adalah numerical wave number.

Numerical wave number untuk skema kompak beda hingga dari turunan pertama dalah :

(15)

Simpangan dari kurva real(k*) terhadap k menunjukkan galat dispersi.

0

Gambar 2.4. Galat dispersi untuk pendekatan numeric dari turunan pertama

Syarat batas diselesaikan dengan skema kompak orde-3 dengan persamaan sebagai berikut :

(26)

 

2



1 1



 

2



2 2



Persamaan skema kompak beda hingga untuk turunan kedua adalah sebagai berikut :

 = koefisien skema kompak beda hingga turunan kedua

Untuk orde-empat, =1/10, a6/5, b=0

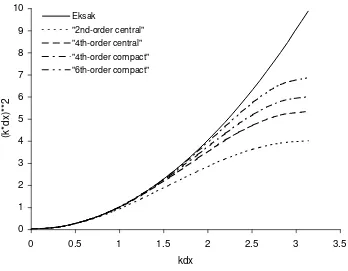
Perbandingan antara skema beda-hingga ekplisit dan skema kompak beda hingga ditunjukkan dalam tabel 2.3. Di sini terlihat bahwa skema kompak beda hingga memiliki stensil lebih sedikit, koefisien galat pemenggalan berkurang menjadi ½ untuk orde-4 dari koefisien beda tengah ekplisit untuk orde yang sama. Tabel 2.3 Perbandingan skema beda hingga dan skema kompak turunan kedua Skema Kesalahan pemenggalan Jumlah stensil

Beda tengah orde-4 (-8/6!)(x)4(6) 5

Kompak orde-4 (-3.6/6!)(x)4(6) 3

Analisa resolusi untuk turunan kedua dari pendekatan numerik skema kompak beda hingga dilakukan dengan cara yang sama dengan analisa turunan pertama. Numerical wave number untuk skema kompak beda hingga dari turunan kedua adalah :

(18)

(27)

 





Gambar 2.5. Galat disipasi untuk pendekatan numerik dari turunan kedua

Galat disipasi dari berbagai skema beda-hingga tampak pada gambar 2.5 dapat diketahui bahwa nilai numerical wavenumber untuk skema kompak lebih mendekati nilai exact wavenumber.

Kondisi batas pada i=1 dan i=N diselesaikan dengan skema kompak orde-3 sebagai berikut :

(19)

dimana, bs =11 dan abs1=13, abs2=-27, abs3=15 dan abs4 =-1 adalah koefisien skema kompak orde-3.

2.2.2.4 Metode Kompresibilitas Tiruan (Artificial Compressibility)

Konsep metode kompresibilitas tiruan adalah menambahkan turunan terhadap waktu pada persamaan kontinyuitas. Bentuk modifikasi persamaan adalah :

(28)

(29)

14

 Intel Pentium Dual CPU E2140 @ 1.6GHz

 Memori 512 MB

b. Perangkat lunak Mikrosoft Fortran Power Station 4.0 c. Perangkat lunak Matlab 6.1 Realease 12

d. Printer Canon iP 1880

3.2Garis Besar penelitian

Penelitian dilakukan dengan cara membuat implementasi program untuk menyelesaikan persamaan momentum, persamaan energi dan persamaan kontinyuitas dengan pendekatan skema kompak orde-empat dan skema Runge-Kutta orde-empat. Program dibuat dalam Bahasa Fortran dan untuk visualisasi hasil program menggunakan perangkat lunak Matlab 6.

Langkah-langkah penelitian yang dilakukan adalah seperti berikut : 1. Mengumpulkan literatur

2. Mempelajari literatur

a. Mempelajari penelitan-penelitian yang pernah dilakukan

b. Mempelajari persamaan atur yang berhubungan dengan permasalahan 3. Merencanakan algoritma program

a. Membuat diskritisasi persamaan atur b. Menyusun bagan alir program

4. Menulis bagan alir dalam bahasa program (Fortran) 5. Menjalankan program

6. Memperbaiki kesalahan pemrograman a. kesalahan penulisan

b. kesalahan algoritma

(30)

ya

tidak 8. Menyusun laporan penelitian

Garis besar penelitian tersebut dapat dibuat diagram alir sebagai berikut :

Mengumpulkan dan Mempelajari literatur - literatur

Membuat diskritisasi persamaan atur Mulai

Membuat algoritma program

Menulis bagan alir dalam bahasa fortran

Menjalankan program

Program benar

Membuat visualisasi dengan Matlab

Analisa hasil

(31)





M

Persamaan atur konveksi alami terdiri dari persamaan kontinuitas, persamaan momentum dan persamaan energi. Model matematika dari persamaan atur konveksi alami terdiri dari persamaan diferensial parsial orde-1 dan orde-2. Agar persamaan atur konveksi alami dapat diaplikasikan dalam bahasa program maka terlebih dahulu dibuat diskritisasi persamaan atur. Diskritisasi waktu dilakukan dengan skema Runge-Kutta orde-4 dan diskritisasi ruang dengan skema kompak beda hingga orde-4. Matrik yang terbentuk dari diskritisasi turunan ruang adalah matrik tridiagonal yang bisa diselesaikan dengan algoritma Thomas.

3.3.1 Diskritisasi persamaan momentum

Diskritisasi persamaan momentum dengan skema Runge-Kutta adalah seperti berikut :

Kecepatan arah x (u)

(21)

(22)

Kecepatan arah y (v)

(23)

(24)

Diskritasi turunan ruang dengan skema kompak orde-4 adalah seperti berikut : Diskritisasi turunan pertama

(25)

(32)



M



Diskritisasi turunan kedua

(31)

(32)

(33)

(34)

3.3.2. Diskritisasi persamaan energi

(35)

(36)

Diskritasi turunan ruang dengan skema kompak orde-4 adalah seperti berikut : Diskritisasi turunan pertama

(37)

(33)

 



iM j



3.3.3. Diskritisasi metode kompresibilitas tiruan.

(41)

(42)

3.4Diskritisasi Syarat Batas

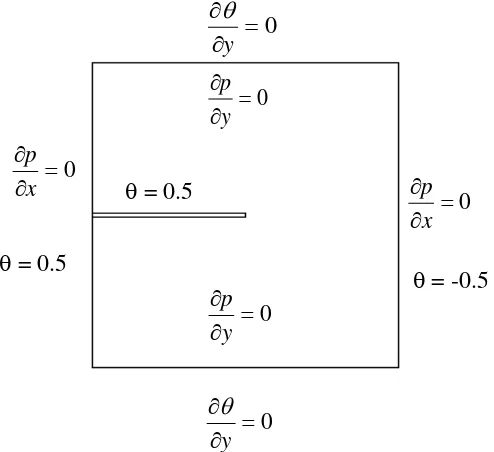
Dalam penelitian ini kasus yang dibahas adalah konveksi alami dalam kotak 2-D dengan dinding bawah dan atas merupakan dinding adiabatis, dinding kiri mendapat pemanasan dan dinding kanan mendapat pendinginan,dengan grid 201 x 201. Pada seluruh dinding kecepatan bernialai nol sedangkan syarat batas tekanan dan temperatur adalah seperti berikut :

Gambar 3.1 Domain dan syarat batas

(34)

(35)

(36)

Untuk j=1 dan j=ny

(69)

(70)

(37)

(81)

(82)

3.5Algoritma Pemrograman

Algoritma pemrograman dari sistem persamaan diatas adalah sebagai berikut :

1. Tentukan kondisi awal (t=0), dan kondisi batas untuk semua variabel (u,v,,p).

2. Hitung turunan pertama dari kecepatan, temperatur dan tekanan

(ux,uy,vx,vy,x,y,px,py) dan turunan kedua dari kecepatan dan

temperatur(uxx,uyy,vxx,vyy,xx,yy) dengan skema kompak orde-empat.

3. Hitung kecepatan(u,v) dengan skema Runge-Kutta orde-empat. 4. Hitung tekanan dengan metode artificial compressibility.

5. Hitung temperatur()dengan skema Runge-Kutta orde-empat.

6. Periksa apakah sudah mencapai batas perhitungan atau belum, jika belum kembali ke langkah 2, jika sudah ke langkah 7.

(38)

Bagan alir program yang akan dibuat adalah sebagai berikut:

MULAI

DATA AWAL

SYARAT BATAS

TENTUKAN

TURUNAN PERTAMA UNTUK u,v,p,

DAN TURUNAN KEDUA UNTUK u,v,

SELESAIKAN PERSAMAAN MOMENTUM UNTUK MEMPEROLEH

Um+1 DAN vm+1

HITUNG TEKANAN pm+1 DENGAN METODE ARTIFICIAL COMPRESSIBILITY

SELESAIKAN PERSAMAAN ENERGI UNTUK MEMPEROLEH

m+1

PERIKSA KONVERGENSI ?

TULIS HASIL

SELESAI Y

(39)

24

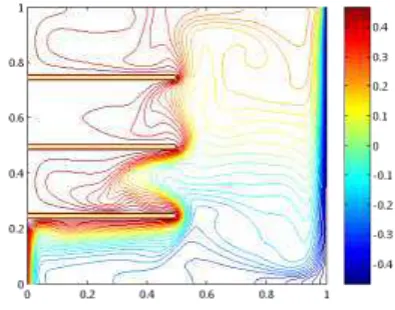
ditampilkan dengan susunan grid sebesar 201 x 201, bilangan Prandtl (Pr) = 0.71 dan langkah waktu dt = 0.0025 serta angka Rayleigh yang digunakan adalah Ra = 106 dan 107. Hasil simulasi disrtibusi temperatur selengkapnya dapat dilihat pada gambar berikut :

Gambar 4.1 isothermal pada Ra = 106 pada sirip tunggal

(40)

Gambar 4.3 isothermal pada Ra = 106 pada 3 sirip

(41)

(42)

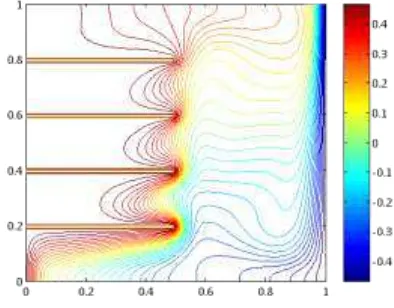
Dari hasil di atas maka dapat kita tinjau secara visual mengenai gambar distribusi temperatur. Dari gambar 4.1 sampai 4.8 dapat dilihat bahwa pergerakan fluida panas akan bergerak keatas karena adanya gaya apung (buoyancy force),hal ini disebabkan karena density yang turun karena temperatur, sedangkan fluida dingin bergerak ke bawah karena density lebih besar dan karena adanya gaya gravitasi. Semakin banyak sirip maka dapat dilihat arah perpindahan panasnya. Distribusi temperatur yang relatif panas dibagian kiri atas akan semakin condong ke kanan dan distribusi temperatur yang relatif dingin pada bagian kiri bawah semakin condong ke kiri. Dengan adanya peningkatan Ra maka akan membuat lapis batas termal di dinding menipis sehingga gradien temperatur di dinding meningkat,hal ini terjadi karena kecepatan fluida yang membawa panas juga meningkat seiring peningkatan Ra.

Pola aliran fuida dapat dilihat pada gambar berikut :

(43)

Gambar 4.10 stream function pada Ra = 106 pada 2 sirip

(44)

Gambar 4.13 stream function pada Ra = 107 pada sirip tunggal

(45)

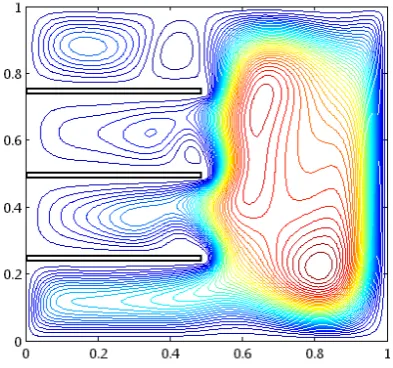
Dari gambar 4.9 sampai gambar 4.16 dapat kita lihat pola stream fungtionnya, dari gambar diatas dapat dilihat bahwa pada Ra = 106 telah muncul separasi, separasi ini timbul akibat adanya suatu gerakan berputar pada vektor kecepatan,untuk lebih jelasnya dapat ditampilkan pada gambar 4.17.

(46)

Kurva Konvergensi

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

Gambar 4.18. Kurva konvergensi untuk Ra=106 sirip tunggal

Gambar 4.19. Kurva konvergensi untuk Ra=107 sirip tunggal

(47)

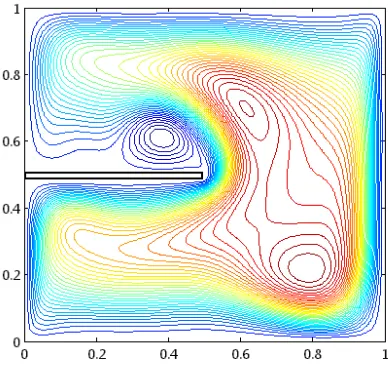
Untuk meguji validitas dari program yang telah dibuat, hasil dari proses simulasi dibandingkan secara visual maupun perhitungan dengan hasil yang telah dilakukan oleh Pranowo dan Tri Iswanto pada domain kotak bujur sangkar 2D dengan aspek rasio 1 :1, dengan kondisi dinding bawah dan atas merupakan dinding adiabatis, dinding kiri mendapat pemanasan dan dinding kanan mendapat pendinginan.

Gambar 4.20. Domain dan Syarat Batas penelitian Pranowo dan Tri Iswanto

Disrtibusi temperatur dan pola aliran hasil penelitian yang dibuat Pranowo dan Tri Iswanto ditunjukkan pada gambar 4.23 dan gambar 4.24 sedangkan distribusi temperatur dan pola aliran hasil penelitian yang dibuat penulis ditunjukkan oleh gambar 4.21 dan 4.22.

 = 0.5  = -0.5

0

  

y



0

  

y



0

  

x p

0

  

y p

0

  

x p

0

(48)

( a ) ( b )

Gambar 4.21. Distribusi temperatur (a) dan stream function (b) yang dibuat penulis pada Ra = 106

( a ) ( b )

(49)

( a ) ( b )

Gambar 4.23. Distribusi temperatur (a) dan stream function (b) yang dibuat Pranowo dan Tri Iswanto pada Ra = 106

Gambar 4.24. Distribusi temperatur (a) dan stream function (b) yang dibuat Pranowo dan Tri Iswanto pada Ra = 107

(50)

Tabel.4.1Hasil Perhitungan dan Perbandingan untuk Ra=106

Sekarang Le Quere Beda (%)

middle 0.0164552 0.016384 0.43

max 0.0169117 0.016811 0.60

X 0.150000 0.1500 0.00

Y 0.550000 0.5470 0.55

umax(1/2,y) 0.0649050 0.064834 0.11

Y 0.850000 0.850 0.00

vmax(x,1/2) 0.220236 0.2206 0.17

X 0.040 0.038 5.26

Nuwall 8.73394 8.8252 1.03

Numiddle 8.82299 8.8244 0.02

Numax 17.1575 17.5343 2.15

Y 0.030 0.039 23.08

Numin 0.98427 0.97948 0.49

Y 1.0 1.0 0.00

Tabel 4.2 Hasil Perhitungan dan Perbandingan untuk Ra=107

sekarang Le Quere Beda (%)

middle 0.00936819 0.00928496 0.90

max 0.00964076 0.00953872 1.07

X 0.0866667 0.086 0.78

Y 0.553333 0.556 0.48

umax(1/2,y) 0.0473129 0.046986 0.70

Y 0.88 0.879 0.11

vmax(x,1/2) 0.221048 0.21118 4.67

X 0.02 0.021 4.76

Nuwall 16.2068 16.523 1.91

Numiddle 16.5638 16.523 0.25

Numax 40.3192 39.3947 2.35

Y 0.00667 0.018 62.94

Numax 1.37516 1.36635 0.64

Y 1.0 1.0 0.00

Dari gambar 4.21 dan 4.22 dapat dilihat bahwa secara visual hasil penelitian ini menunjukkan kesamaan yang baik dengan penelitian dari Pranowo dan Tri Iswanto dan dari tabel 4.1 dan 4.2 hasil perhitungan pada penelitian ini menunjukkan kedekatan yang baik dengan hasil penelitian Le Querre sehingga dengan metode ini dapat diterima sebagai validasi.

(51)

aliran hasil penelitian yang dibuat penulis ditunjukkan oleh gambar 4.25.

Gambar 4.25 Separasi di sekitar sirip yang dibuat penulis

(52)

37

Dari penelitian dan pembahasan yang telah dilakukan, dapat ditarik beberapa kesimpulan yaitu :

a. Hasil penelitian pada domain busur sangkar tanpa sirip mempunyai kedekatan visual yang baik dengan hasil penelitian dari Pranowo dan Tri Iswanto baik pada Ra = 106 maupun pada Ra = 107.

b. Metode yang digunakan untuk kasus konveksi alami pada single fin dan multiple fins dalam kotak 2D mampu mensimulasikan pola aliran dan distribusi temperatur sampai Ra = 107.

c. Separasi timbul karena adanya pusaran pada pola aliran disekitar sirip. d. Separasi muncul pada daerah sekitar sirip saat Ra 106 dan 107.

e. Semakin besar angka Rayleigh maka kerapatan perpindahan panas disekitar dinding akan meningkat.

f. Semakin banyak jumlah sirip maka perpindahan panas akan meningkat. 5.2 Saran

(53)

38

Kasayapanand, N. 2008. A Computational Fluid Dynamics Modeling of Natural Convection in Siripned Enclosure Under Electric Field. Applied Thermal Engineering 29 (2009) 131-141.

Lemos, C.M. FDFlow: a Fortran-77 Solver for 2-D Incompressible Fluid Flow. Computers & Geosciences, Vol. 20 (1994): pp.265-261.

Pranowo dan Priyo Tri Iswanto. 1999. Analisis Numerik Konveksi Alami Dalam Kotak dengan Primitive Variable pada Grid Kolokasi. Makalah Seminar Regional Universitas Sanata Dharma Yogyakarta.

Prijono, Arko. 1985. Prinsip-prinsip Perpindahan Panas, Terjemahan dari Principles Of Heat Transfer Third Edition (Frank Kreith, 1958).

Quere, P.L. 1990. Accurate Solutions to The Square Thermally Driven Cavity at High Rayleigh Number. International Journal of Computers & Fluids, Vol.20, No. 1, hal. 29-41.

Sulistiyono, Aris. 2006. Simulasi Numeric Konveksi Alami Dalam Kotak 3 Dimnsi Dengan Variasi Kemiringan Dengan Metode Beda Hingga.

Wilson, Robert V., and Demuren, Ayodeji O., 1998, Higher-Order Compact Schemes for Numerical Simulation of Incompressible Flows, ICASE Report No. 98-13, NASA Langley Research Center, Hampton.

(54)

NON-DIMENSIONALISASI PERSAMAAN ATUR

Persamaan atur dibuat tanpa dimensi dengan membagi variabel yang ada dengan parameter referensi yang mempunyai dimensi samam (Le Quere,1990), seperti dibawah ini :

Lr

1. Non-dimensionalisasi Persamaan Kontinyuitas

0

Persamaan (L1.1) dimasukkan ke dalam persamaan (L1.2) :

0

Tanda (*) pada persamaan (L1.4) dihilangkan sehingga diperoleh :

(55)



Persamaan (L1.1) dimasukkan kepersamaan (L1.6) :



Persamaan momentum arah y



T

Tr



(56)





3. Non-dimensionalisasi Persamaan Energi















(57)

Skema kompak beda-hingga dapat diturunkan dengan menggunakan formula PADE (Hirsch.1961). Beberapa operator diferensial yang digunakan untuk penurunan skema kompak beda hingga adalah seperti berikut :

 adalah operator beda tengah :

2

 adalah operator beda tengah :



1 1



E adalah operator pergeseran :

1



 i i u

Eu (L2.3)

Hubungan antara operator-operator tersebut adalah seperti berikut :



1



Diskritisasi turunan pertama

(58)

4 4

4 x

Diskritisasi turunan kedua

(59)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

Gambar 1. Kurva konvergensi untuk Ra=106 sirip tunggal

Gambar 2. Kurva konvergensi untuk Ra=107 sirip tunggal

(60)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

Gambar 4. Kurva konvergensi untuk Ra=107 pada 2 sirip

(61)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

-3 -2,5 -2 -1,5 -1 -0,5 0

0 2000 4000 6000 8000 10000 Jumlah Iterasi

Lo

g1

0

(du

/dx

+

dv

/dy

)

(62)

NUMERICAL WAVENUMBER

Untuk mengetahui akurasi berbagai skema beda hingga dapat dilakukan dengan analisa numerical wavwnumber. Perhitungan numerical wavenumber beberapa skema beda hingga dijelaskan di bawah ini.

Sebelumnya kita definisikan variabel  dalam mode Fourier adalah :

 

ikx

 adalah koefisien Fourier darai , i= 1dan k adalah wavenumber.

)

Skema beda tengah orde-dua

(63)

x

Skema kompak beda hingga



1





2 2



(64)

C--- C Program penyelesaian konveksi alami pada sirip tunggal C--- PARAMETER(m=500,n=500)

COMMON/aa1/u(m,n),v(m,n),p(m,n),ux(m,n),uy(m,n), 1 vx(m,n),vy(m,n),px(m,n),py(m,n),

1 uxx(m,n),uyy(m,n),vxx(m,n),vyy(m,n),x(m,n),y(m,n) 1 ,o(m,n),ox(m,n),oy(m,n),oxx(m,n),oyy(m,n)

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 OPEN(8,FILE='C:\matlab6p1\work\temp1') OPEN(7,FILE='C:\matlab6p1\work\pv1') OPEN(4,FILE='C:\matlab6p1\work\temp') OPEN(3,FILE='C:\matlab6p1\work\pv') OPEN(2,FILE='C:\matlab6p1\work\num') OPEN(1,FILE='C:\matlab6p1\work\div') call awal

do k=1,nt ck=0. call rkv do i=1,nx do j=1,ny

ck=ck+abs(ux(i,j)+vy(i,j)) end do

end do if(ck.gt.0) then

WRITE(*,*)k,LOG10(ck/nx/ny) WRITE(1,*)k,LOG10(ck/nx/ny) endif

end do call hasil stop end

C--- C Syarat awal dan syarat batas C--- subroutine awal

PARAMETER(m=500,n=500) CHARACTER mul*2

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 WRITE(*,*)' t= '

(65)

i2=nx j1=1 j2=ny dx=1./200. dy=1./200. dt=0.0025 nt=tt/dt+1 pr=0.71 ra=1000000.

WRITE(*,*)' Dari awal ?' READ(*,'(a)')mul IF(mul.eq.'y')then do i=1,nx

do j=1,ny x(i,j)=(i-1)*dx y(i,j)=(j-1)*dy u(i,j)=0. v(i,j)=0. p(i,j)=0. o(i,j)=0. enddo enddo

do j=1,ny o(1,j)=0.5 o(nx,j)=-0.5 enddo

else do j=1,ny do i=1,nx

READ(7,*)x(i,j),y(i,j),u(i,j),v(i,j),p(i,j) READ(8,*)x(i,j),y(i,j),o(i,j)

end do end do end if

return end

C--- C Penyelesaian persamaan Navier - Stokes C--- subroutine rkv

(66)

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2

DIMENSION h1(m,n,6),h2(m,n,6),s1(m,n,6),s2(m,n,6),a(5),b(5) DATA a(1),a(2),a(3),a(4),a(5)/0.,-0.41789047,-1.19215169, 1 -1.69778469,-1.51418344/

DATA b(1),b(2),b(3),b(4),b(5)/0.14965902,0.37921031,0.82295502, 1 0.69945045,0.15305724/

do i=2,nx-1 do j=2,ny-1 s1(i,j,1)=u(i,j) s2(i,j,1)=v(i,j) end do end do do k=1,5

call derv1(u,ux,uy) call derv1(v,vx,vy) call derv2(u,uxx,uyy) call derv2(v,vxx,vyy) call derp1(p,px,py)

do i=2,nx-1 do j=2,ny-1

h1(i,j,k)=-u(i,j)*ux(i,j)-v(i,j)*uy(i,j)-px(i,j) 1 +(uxx(i,j)+uyy(i,j))*pr/SQRT(ra) h2(i,j,k)=-u(i,j)*vx(i,j)-v(i,j)*vy(i,j)-py(i,j) 1 +(vxx(i,j)+vyy(i,j))*pr/SQRT(ra)+pr*o(i,j) end do

end do

IF(i.le.101.and.j.ge.98.and.j.le.102)then u(i,j)=0.

v(i,j)=0 else

h1(i,j,k)=h1(i,j,k)+a(k)*h1(i,j,k-1) h2(i,j,k)=h2(i,j,k)+a(k)*h2(i,j,k-1) s1(i,j,k+1)=s1(i,j,k)+b(k)*dt*h1(i,j,k) s2(i,j,k+1)=s2(i,j,k)+b(k)*dt*h2(i,j,k) u(i,j)=s1(i,j,k+1)

v(i,j)=s2(i,j,k+1) endif

(67)

c Tekananan dihitung dengan artifisial kompresibiliti c--- do i=2,nx-1

do j=2,ny-1

IF(i.lt.101.and.j.gt.98.and.j.lt.102)then p(i,j)=0

else

p(i,j)=p(i,j)-(ux(i,j)+vy(i,j))*dt*0.5 endif

end do end do

do i=1,nx IF(i.le.101)then j1=1

j2=98 j3=102 j4=ny else j1=1 j2=ny endif

p(i,j1)=(48*p(i,j1+1)-36*p(i,j1+2)+16*p(i,j1+3)-3*p(i,j1+4))/25 p(i,j2)=(48*p(i,j2-1)-36*p(i,j2-2)+16*p(i,j2-3)-3*p(i,j2-4))/25 p(i,j3)=(48*p(i,j3+1)-36*p(i,j3+2)+16*p(i,j3+3)-3*p(i,j3+4))/25 p(i,j4)=(48*p(i,j4-1)-36*p(i,j4-2)+16*p(i,j4-3)-3*p(i,j4-4))/25 end do

i1=1 i2=nx j1=1 j2=ny do j=1,ny

IF(j.ge.98.and.j.le.102)then i1=101

else i1=1 i2=nx endif

p(i1,j)=(48*p(i1+1,j)-36*p(i1+2,j)+16*p(i1+3,j)-3*p(i1+4,j))/25 p(i2,j)=(48*p(i2-1,j)-36*p(i2-2,j)+16*p(i2-3,j)-3*p(i2-4,j))/25 enddo

call rkt

(68)

end

C--- C Penyelesaian persamaan energi C--- subroutine rkt

PARAMETER(m=500,n=500)

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 DIMENSION h(m,n,6),s(m,n,6),a(5),b(5)

DATA a(1),a(2),a(3),a(4),a(5)/0.,-0.41789047,-1.19215169, 1 -1.69778469,-1.51418344/

DATA b(1),b(2),b(3),b(4),b(5)/0.14965902,0.37921031,0.82295502, 1 0.69945045,0.15305724/

do i=2,nx-1 do j=2,ny-1 s(i,j,1)=o(i,j) end do end do do k=1,5

call dero1(o,ox,oy) call derv2(o,oxx,oyy)

IF(i.lt.101.and.j.gt.98.and.j.lt.102)then o(i,j)=0.

else

h(i,j,k)=-u(i,j)*ox(i,j)-v(i,j)*oy(i,j)+

1 (oxx(i,j)+oyy(i,j))/SQRT(ra)+a(k)*h(i,j,k-1) s(i,j,k+1)=s(i,j,k)+b(k)*dt*h(i,j,k)

o(i,j)=s(i,j,k+1) endif

end do end do

(69)

o(i,j4)=(48*o(i,j4-1)-36*o(i,j4-2)+16*o(i,j4-3)-3*o(i,j4-4))/25 else

j1=1 j2=ny

o(i,j1)=(48*o(i,j1+1)-36*o(i,j1+2)+16*o(i,j1+3)-3*o(i,j1+4))/25 o(i,j2)=(48*o(i,j2-1)-36*o(i,j2-2)+16*o(i,j2-3)-3*o(i,j2-4))/25 endif

end do

do j=1,ny

else i1=1 i2=nx endif o(i1,j)=0.5 end do i1=1 i2=nx j1=1 j2=ny do i=1,nx do j=1,ny

endif end do end do end do return end

C---

C Turunan pertama variabel kecepatan C---

subroutine derv1(q,qx,qy)

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 COMMON/aa4/a(500),b(500),c(500),d(500),l1,l2 DIMENSION q(500,500),qx(500,500),qy(500,500) alp=0.25

ak=1.5 do j=1,ny

(70)

i1=1 i2=nx endif

qx(i1,j)=(-3*q(i1+4,j)+16*q(i1+3,j)-36*q(i1+2,j)+48*q(i1+1,j) 1 -25*q(i1,j))/12/dx

qx(i2,j)=(3*q(i2-4,j)-16*q(i2-3,j)+36*q(i2-2,j)-48*q(i2-1,j) 1 +25*q(i2,j))/12/dx

do 10 i=i1+1,i2-1 a(i)=alp

b(i)=1. c(i)=alp

10 d(i)=ak*(q(i+1,j)-q(i-1,j))/2/dx d(i1+1)=d(i1+1)-a(i1+1)*qx(i1,j) a(i1+1)=0.

d(i2-1)=d(i2-1)-c(i2-1)*qx(i2,j) c(i2-1)=0.

l1=i1+2 l2=i2-1 call tridi

do 20 i=i1+1,i2-1 20 qx(i,j)=d(i) enddo

j2=98 j3=102 j4=ny

qy(i,j3)=(-3*q(i,j3+4)+16*q(i,j3+3)-36*q(i,j3+2)+48*q(i,j3+1) 1 -25*q(i,j3))/12/dy

qy(i,j4)=(3*q(i,j4-4)-16*q(i,j4-3)+36*q(i,j4-2)-48*q(i,j4-1) 1 +25*q(i,j4))/12/dy

do 110 j=j3+1,j4-1 a(j)=alp

b(j)=1. c(j)=alp

110 d(j)=ak*(q(i,j+1)-q(i,j-1))/2/dy d(j3+1)=d(j3+1)-a(j3+1)*qy(i,j3) a(j3+1)=0.

d(j4-1)=d(j4-1)-c(j4-1)*qy(i,j4) c(j4-1)=0.

l1=j3+2 l2=j4-1 call tridi

(71)

j2=ny endif

do 11 j=j1+1,j2-1 a(j)=alp

b(j)=1. c(j)=alp

d(j2-1)=d(j2-1)-c(j2-1)*qy(i,j2) c(j2-1)=0.

do 21 j=j1+1,j2-1 21 qy(i,j)=d(j) enddo

return end

C---

C turunan pertama variabel temperatur C---

subroutine dero1(q,qx,qy)

ak=1.5

do j=1,ny

(72)

do 10 i=i1+1,i2-1 a(i)=alp

b(i)=1. c(i)=alp

d(i2-1)=d(i2-1)-c(i2-1)*qx(i2,j) c(i2-1)=0.

j2=98 j3=102 j4=ny qy(i,j1)=0.

qy(i,j4)=0.

do 110 j=j1+1,j2-1 a(j)=alp

b(j)=1. c(j)=alp

d(j2-1)=d(j2-1)-c(j2-1)*qy(i,j2) c(j2-1)=0.

do 210j=j1+1,j2-1 210 qy(i,j)=d(j)

do 111 j=j3+1,j4-1 a(j)=alp

(73)

a(j3+1)=0.

d(j4-1)=d(j4-1)-c(j4-1)*qy(i,j4) c(j4-1)=0.

do 211 j=j3+1,j4-1 211 qy(i,j)=d(j)

else j1=1 j2=ny qy(i,j1)=0. qy(i,j2)=0. do 11 j=j1+1,j2-1 a(j)=alp

b(j)=1. c(j)=alp

d(j2-1)=d(j2-1)-c(j2-1)*qy(i,j2) c(j2-1)=0.

do 21 j=j1+1,j2-1 21 qy(i,j)=d(j) endif enddo

return end

C---

C Turunan pertama variabel tekanan C---

subroutine derp1(q,qx,qy)

ak=1.5 do j=1,ny

(74)

i1=1 i2=nx endif qx(i1,j)=0. qx(i2,j)=0. do 10 i=i1+1,i2-1 a(i)=alp

b(i)=1. c(i)=alp

d(i2-1)=d(i2-1)-c(i2-1)*qx(i2,j) c(i2-1)=0.

j2=98 j3=102 j4=ny qy(i,j3)=0. qy(i,j4)=0.

do 110 j=j3+1,j4-1 a(j)=alp

b(j)=1. c(j)=alp

d(j4-1)=d(j4-1)-c(j4-1)*qy(i,j4) c(j4-1)=0.

do 210 j=j3+1,j4-1 210 qy(i,j)=d(j)

(75)

qy(i,j2)=0. do 11 j=j1+1,j2-1 a(j)=alp

b(j)=1. c(j)=alp

d(j2-1)=d(j2-1)-c(j2-1)*qy(i,j2) c(j2-1)=0.

return end

C---

C Turunan kedua variabel kecepatan dan temperatur C---

subroutine derv2(q,qxx,qyy)

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 COMMON/aa4/a(500),b(500),c(500),d(500),l1,l2 DIMENSION q(500,500),qxx(500,500),qyy(500,500) alp=0.1

ak=1.2

do 10 j=2,ny-1

s1=(13*q(i1,j)-27*q(i1+1,j)+15*q(i1+2,j)-1*q(i1+3,j))/dx/dx s2=(-1*q(i2-3,j)+15*q(i2-2,j)-27*q(i2-1,j)+13*q(i2,j))/dx/dx do 20 i=i1+1,i2-1

a(i)=alp b(i)=1. c(i)=alp

20 d(i)=ak*(q(i+1,j)-2*q(i,j)+q(i-1,j))/dx/dx b(i1+1)=b(i1+1)-11*alp

(76)

do 30 i=i1+1,i2-1 30 qxx(i,j)=d(i)

qxx(i1,j)=s1-11*qxx(i1+1,j) qxx(i2,j)=s2-11*qxx(i2-1,j) 10 continue

do 40 i=1,nx-1 IF(i.le.101)then j1=1

j2=98 j3=102 j4=ny

s3=(13*q(i,j3)-27*q(i,j3+1)+15*q(i,j3+2)-q(i,j3+3))/dy/dy s4=(-q(i,j4-3)+15*q(i,j4-2)-27*q(i,j4-1)+13*q(i,j4))/dy/dy do 51 j=j3+1,j4-1

a(j)=alp b(j)=1. c(j)=alp

51 d(j)=ak*(q(i,j+1)-2*q(i,j)+q(i,j-1))/dy/dy b(j3+1)=b(j3+1)-11*alp

d(j3+1)=d(j3+1)-s3*alp b(j4-1)=b(j4-1)-11*alp d(j4-1)=d(j4-1)-s4*alp l1=j3+2

l2=j4-1 call tridi

do 61 j=j3+1,j4-1 61 qyy(i,j)=d(j)

qyy(i,j3)=s1-11*qyy(i,j3+1) qyy(i,j4)=s2-11*qyy(i,j4-1) else

j1=1 j2=ny endif

s1=(13*q(i,j1)-27*q(i,j1+1)+15*q(i,j1+2)-q(i,j1+3))/dy/dy s2=(-q(i,j2-3)+15*q(i,j2-2)-27*q(i,j2-1)+13*q(i,j2))/dy/dy do 50 j=j1+1,j2-1

a(j)=alp b(j)=1. c(j)=alp

50 d(j)=ak*(q(i,j+1)-2*q(i,j)+q(i,j-1))/dy/dy b(j1+1)=b(j1+1)-11*alp

(77)

l2=j2-1 call tridi

do 60 j=j1+1,j2-1 60 qyy(i,j)=d(j)

qyy(i,j1)=s1-11*qyy(i,j1+1) qyy(i,j2)=s2-11*qyy(i,j2-1) 40 continue

return end

C--- C Algoritma Thomas C--- SUBROUTINE TRIDI parameter (m=500)

COMMON /AA4/A(m),B(m),C(m),D(m),L1,l2 DO 1 I=L1,L2

RT=-A(I)/B(I-1) B(I)=B(I)+RT*C(I-1) 1 D(I)=D(I)+RT*D(I-1) D(L2)=D(L2)/B(L2) DO 2 I=L2-1,L1-1,-1 2 D(I)=(D(I)-C(I)*D(I+1))/B(I) RETURN

END

C--- C Hasil perhitungan C--- subroutine hasil

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 WRITE(2,*)NX

WRITE(2,*)NY do 10 j=1,ny do 10 i=1,nx

WRITE(3,*)x(i,j),y(i,j),u(i,j),v(i,j)!,p(i,j) 10 WRITE(4,*)x(i,j),y(i,j),o(i,j)

(78)

C Program penyelesaian konveksi alami pada 2 sirip C--- PARAMETER(m=500,n=500)

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 OPEN(8,FILE='C:\matlab6p1\work\temp1') OPEN(7,FILE='C:\matlab6p1\work\pv1') OPEN(4,FILE='C:\matlab6p1\work\temp') OPEN(3,FILE='C:\matlab6p1\work\pv') OPEN(2,FILE='C:\matlab6p1\work\num') OPEN(1,FILE='C:\matlab6p1\work\div') call awal

do k=1,nt ck=0. call rkv do i=1,nx do j=1,ny

ck=ck+abs(ux(i,j)+vy(i,j)) end do

end do if(ck.gt.0) then

WRITE(*,*)k,LOG10(ck/nx/ny) WRITE(1,*)k,LOG10(ck/nx/ny) endif

end do call hasil stop end

C--- C Syarat awal dan syarat batas C--- subroutine awal

PARAMETER(m=500,n=500) CHARACTER mul*2

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 WRITE(*,*)' t= '

(79)

j2=ny dx=1./200. dy=1./200. dt=0.0025 nt=tt/dt+1 pr=0.71 ra=10000000.

WRITE(*,*)' Dari awal ?' READ(*,'(a)')mul IF(mul.eq.'y')then do i=1,nx

do j=1,ny x(i,j)=(i-1)*dx y(i,j)=(j-1)*dy u(i,j)=0. v(i,j)=0. p(i,j)=0. o(i,j)=0. enddo enddo

do j=1,ny o(1,j)=0.5 o(nx,j)=-0.5 enddo

else do j=1,ny do i=1,nx

READ(7,*)x(i,j),y(i,j),u(i,j),v(i,j),p(i,j) READ(8,*)x(i,j),y(i,j),o(i,j)

end do end do end if

return end

C---

C Penyelesaian persamaan Navier - Stokes C---

subroutine rkv

(80)

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2

DIMENSION h1(m,n,6),h2(m,n,6),s1(m,n,6),s2(m,n,6),a(5),b(5) DATA a(1),a(2),a(3),a(4),a(5)/0.,-0.41789047,-1.19215169, 1 -1.69778469,-1.51418344/

DATA b(1),b(2),b(3),b(4),b(5)/0.14965902,0.37921031,0.82295502, 1 0.69945045,0.15305724/

do i=2,nx-1 do j=2,ny-1 s1(i,j,1)=u(i,j) s2(i,j,1)=v(i,j) end do end do do k=1,5

call derv1(u,ux,uy) call derv1(v,vx,vy) call derv2(u,uxx,uyy) call derv2(v,vxx,vyy) call derp1(p,px,py)

h1(i,j,k)=-u(i,j)*ux(i,j)-v(i,j)*uy(i,j)-px(i,j) 1 +(uxx(i,j)+uyy(i,j))*pr/SQRT(ra) h2(i,j,k)=-u(i,j)*vx(i,j)-v(i,j)*vy(i,j)-py(i,j) 1 +(vxx(i,j)+vyy(i,j))*pr/SQRT(ra)+pr*o(i,j) end do

end do

IF(i.le.101.and.j.ge.65.and.j.le.69)then u(i,j)=0.

v(i,j)=0

ELSEIF(i.le.101.and.j.ge.131.and.j.le.135)then u(i,j)=0.

v(i,j)=0 else

h1(i,j,k)=h1(i,j,k)+a(k)*h1(i,j,k-1) h2(i,j,k)=h2(i,j,k)+a(k)*h2(i,j,k-1) s1(i,j,k+1)=s1(i,j,k)+b(k)*dt*h1(i,j,k) s2(i,j,k+1)=s2(i,j,k)+b(k)*dt*h2(i,j,k) u(i,j)=s1(i,j,k+1)

v(i,j)=s2(i,j,k+1) endif

(81)

c---

c Tekananan dihitung dengan artifisial kompresibiliti c---

IF(i.lt.101.and.j.gt.65.and.j.lt.69)then p(i,j)=0

ELSEIF(i.lt.101.and.j.gt.131.and.j.lt.135)then p(i,j)=0

else

p(i,j)=p(i,j)-(ux(i,j)+vy(i,j))*dt*0.5 endif

end do end do

j2=65 j3=69 j4=131 j5=135 j6=ny else j1=1 j2=ny endif

p(i,j1)=(48*p(i,j1+1)-36*p(i,j1+2)+16*p(i,j1+3)-3*p(i,j1+4))/25 p(i,j2)=(48*p(i,j2-1)-36*p(i,j2-2)+16*p(i,j2-3)-3*p(i,j2-4))/25 p(i,j3)=(48*p(i,j3+1)-36*p(i,j3+2)+16*p(i,j3+3)-3*p(i,j3+4))/25 p(i,j4)=(48*p(i,j4-1)-36*p(i,j4-2)+16*p(i,j4-3)-3*p(i,j4-4))/25 p(i,j5)=(48*p(i,j5+1)-36*p(i,j5+2)+16*p(i,j5+3)-3*p(i,j5+4))/25 p(i,j6)=(48*p(i,j6-1)-36*p(i,j6-2)+16*p(i,j6-3)-3*p(i,j6-4))/25 end do

i1=1 i2=nx j1=1 j2=ny do j=1,ny

elseif(j.ge.131.and.j.le.135)then i1=101

(82)

p(i1,j)=(48*p(i1+1,j)-36*p(i1+2,j)+16*p(i1+3,j)-3*p(i1+4,j))/25 p(i2,j)=(48*p(i2-1,j)-36*p(i2-2,j)+16*p(i2-3,j)-3*p(i2-4,j))/25 enddo

call rkt

c--- end do

return end

C--- C Penyelesaian persamaan energi C---

subroutine rkt

COMMON/aa2/nx,ny,nt,dx,dy,dt,pr,ra,i1,i2,j1,j2 DIMENSION h(m,n,6),s(m,n,6),a(5),b(5)

DATA a(1),a(2),a(3),a(4),a(5)/0.,-0.41789047,-1.19215169, 1 -1.69778469,-1.51418344/

DATA b(1),b(2),b(3),b(4),b(5)/0.14965902,0.37921031,0.82295502, 1 0.69945045,0.15305724/

do i=2,nx-1 do j=2,ny-1 s(i,j,1)=o(i,j) end do end do do k=1,5

call dero1(o,ox,oy) call derv2(o,oxx,oyy)

ELSEIF(i.lt.101.and.j.gt.131.and.j.lt.135)then o(i,j)=0.

else

h(i,j,k)=-u(i,j)*ox(i,j)-v(i,j)*oy(i,j)+

(83)

end do end do

j2=65 j3=69 j4=131 j5=135 j6=ny

o(i,j1)=(48*o(i,j1+1)-36*o(i,j1+2)+16*o(i,j1+3)-3*o(i,j1+4))/25 o(i,j2)=0.5

o(i,j3)=0.5 o(i,j4)=0.5 o(i,j5)=0.5

o(i,j6)=(48*o(i,j6-1)-36*o(i,j6-2)+16*o(i,j6-3)-3*o(i,j6-4))/25 else

j1=1 j2=ny

o(i,j1)=(48*o(i,j1+1)-36*o(i,j1+2)+16*o(i,j1+3)-3*o(i,j1+4))/25 o(i,j2)=(48*o(i,j2-1)-36*o(i,j2-2)+16*o(i,j2-3)-3*o(i,j2-4))/25 endif

end do

do j=1,ny

else i1=1 i2=nx endif o(i1,j)=0.5 end do i1=1 i2=nx j1=1 j2=ny do i=1,nx do j=1,ny

(84)

end do end do end do return end

C---

C Turunan pertama variabel kecepatan C---

subroutine derv1(q,qx,qy)

ak=1.5

do j=1,ny

qx(i1,j)=(-3*q(i1+4,j)+16*q(i1+3,j)-36*q(i1+2,j)+48*q(i1+1,j) 1 -25*q(i1,j))/12/dx

qx(i2,j)=(3*q(i2-4,j)-16*q(i2-3,j)+36*q(i2-2,j)-48*q(i2-1,j) 1 +25*q(i2,j))/12/dx

do 10 i=i1+1,i2-1 a(i)=alp

b(i)=1. c(i)=alp

d(i2-1)=d(i2-1)-c(i2-1)*qx(i2,j) c(i2-1)=0.

(85)

j2=65 j3=69 j4=131 j5=135 j6=ny

do 110 j=j3+1,j4-1 a(j)=alp

b(j)=1. c(j)=alp

d(j4-1)=d(j4-1)-c(j4-1)*qy(i,j4) c(j4-1)=0.

do 210 j=j3+1,j4-1 210 qy(i,j)=d(j)

do 222 j=j5+1,j6-1 a(j)=alp

b(j)=1. c(j)=alp

d(j6-1)=d(j6-1)-c(j6-1)*qy(i,j6) c(j6-1)=0.

do 322 j=j5+1,j6-1 322 qy(i,j)=d(j)

(86)

do 11 j=j1+1,j2-1 a(j)=alp

b(j)=1. c(j)=alp

d(j2-1)=d(j2-1)-c(j2-1)*qy(i,j2) c(j2-1)=0.

return end

C---

C turunan pertama variabel temperatur C---

subroutine dero1(q,qx,qy)

ak=1.5

do j=1,ny