PENGUJIAN REGRESI ZERO-INFLATED POISSON DALAM MENGATASI OVERDISPERSI PADA REGRESI POISSON
SKRIPSI
MUTIA SARI 150803023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2019
PENGUJIAN REGRESI ZERO-INFLATED POISSON DALAM MENGATASI OVERDISPERSI PADA REGRESI POISSON
SKRIPSI
Diajukan untuk melengkapi tugas dan memenuhi syarat mencapai gelar Sarjana Sains
MUTIA SARI 150803023
DEPARTEMEN MATEMATIKA
FAKULTAS MATEMATIKA DAN ILMU PENGETAHUAN ALAM UNIVERSITAS SUMATERA UTARA
MEDAN 2019
PERNYATAAN ORISINALITAS
PENGUJIAN REGRESI ZERO-INFLATED POISSON DALAM MENGATASI OVERDISPERSI PADA REGRESI POISSON
SKRIPSI
Saya menyatakan bahwa skripsi ini adalah hasil karya sendiri, kecuali beberapa kutipan dan ringkasan yang masing – masing disebutkan sumbernya.
Medan, 04 Juli 2019
Mutia Sari 150803023
i
PENGESAHAN SKRIPSI
Judul : Pengujian Regresi Zero-Inflated Poisson dalam Mengatasi Overdispersi pada Regresi Poisson
Kategori : Skripsi
Nama : Mutia Sari
Nomor Induk Mahasiswa : 150803023
Program Studi : Sarjana Matematika
Departemen : Matematika
Fakultas : MIPA – Universitas Sumatera Utara
Disetujui di Medan, 04 Juli 2019
Ketua Departemen Matematika Pembimbing
Dr. Suyanto, M. Kom Dr. Open Darnius, M.Sc.
NIP. 19590813 198601 1 002 NIP.19641014 199103 1 004
PENGUJIAN REGRESI ZERO-INFLATED POISSON DALAM MENGATASI OVERDISPERSI PADA REGRESI POISSON
ABSTRAK
Analisis regresi linier klasik adalah analisis yang bertujuan mengetahui hubungan antara variabel respons dengan variabel penjelas dengan asumsi data berdistribusi normal, namun pada data terapan seringkali tidak demikian.
Generalized Linear Model (GLM) dikembangkan untuk data berupa kategorikal dan berdistribusi diskrit. Pada penelitian ini data dibangkitkan berdistrubusi poisson sebanyak , dengan rata-rata dan peluang muncul nol . Regresi poisson merupakan GLM untuk data yang berdistribusi poisson dengan asumsi bahwa ( ) ( ), namun asumsi jarang terjadi pada data terapan. Untuk kejadian yang jarang terjadi pada interval tertentu variabel seringkali bernilai nol, sehingga menyebabkan overdispersi ( ( ) ( )). Lambert (1992) memperkenalkan metode untuk mengatasi overdispersi pada regresi poisson yaitu Regresi Zero- Inflated Poisson (ZIP). Pada penelitian ini dilakukan pengujian Regresi ZIP dalam mengatasi overdispersi untuk melihat batas peluang muncul nilai nol sebagai nilai yang menyebabkan overdispersi. Pengujian dilakukan dengan perangkat lunak RStudio ver. 1.1.463.0. Berdasarkan data yang disimulasikan diperoleh bahwa Regrezi ZIP berhenti mengatasi overdispersi pada kondisi dengan peluang dengan rasio dispersi .
Kata kunci : Generalized Linear Model, Overdispersi, Regresi Linier Klasik, Regresi Poisson, Regresi Zero-Inflated Poisson
iii
REGRESSION ZERO-INFLATED POISSON TESTING IN HANDLING OVERDISPERSION ON POISSON REGRESSION
ABSTRACT
The classical linear regression analysis is an analysis aimed at knowing the relationship between the response variables and the explanatory variables assuming the normal distribution data, but in the applied data is often not the case.
Generalized Linear Model (GLM) was developed for data in the form of categorical and discrete distribution. In this study the data was raised which has a poisson distribution by as much as N, with average λ and the odds appearing zero p. Poisson regression is GLM for Poisson-distributed data assuming that Var (X) = E (X), but asusumption is rare in applied data. For rare occurrences of a specified interval X variables are often zero value, thus causing overdispersion (Var (X) > E (X)).
Lambert (1992) introduced a method for overcoming overdispersion in Poisson regression i.e. the Zero-Inflated regression Poisson (ZIP). In this research conducted a ZIP regression test in overcoming overdispersion to see the opportunity limit p appears zero value as the value that causes overdispersion. Testing is done with RStudio ver. 1.1.463.0 software. Based on the simulated data obtained that Regrezi ZIP stopped overcoming overdispersion at the condition n = 500, λ = 0.7 with the odds P = 0.2 with a dispersion ratio of τ = 1.010.
Keywords : Classic Linear Regression Generalized Linear Model, Overdispersi, Regresi Poisson, Regresi Zero-Inflated Poisson
PENGHARGAAN
Puji syukur penulis ucapkan kehadirat Allah SWT. atas limpahan rahmat serta karunia-Nya sehingga penulis dapat menyelesaikan skripsi yang berjudul “Pengujian Regresi Zero-Inflated Poisson dalam Mengatasi Overdispersi pada Regresi Poisson.”
ini dengan baik. Shalawat dan salam kepada Nabi Muhammad SAW.
Terima kasih penulis sampaikan kepada Dr. Open Darnius, M.Sc selaku dosen pembimbing yang senantiasa membimbing dan mengarahkan penulis sehingga skripsi ini dapat terselesaikan. Selanjutnya penulis sampaikan terima kasih kepada Ibu Dr. Elly Rosmaini, M.Si dan Ibu Dra. Laurentina Pangaribuan, MS selaku dosen penguji penulis yang telah memberi masukan sehingga skripsi ini dapat diselesaikan dengan baik. Bapak Dr. Kerista Sebayang, M.S selaku Dekan FMIPA-USU, Bapak Dr. Suyanto, M.Kom selaku Ketua Departemen Matematika FMIPA-USU, serta seluruh pegawai FMIPA USU yang terlah membantu penulis dalam penyelesaian skripsi ini.
Penulis mengucapkan terima kasih kepada Kedua orang tua, Bapak Sugiono, Ibu Lisdiana, adik M. Abdi Nugraha dan Fazira Maharani serta seluruh saudara yang selama ini selalu memberian motivasi dan doa kepada penulis. Sahabat seperjuangan penulis Sahabat Muslimah (Mirda, Fitri, Afni, Wiwik, Aini, Dilla, Anggi, Tina, Sani, Sundari), Tivani Jakohaka (Eva, Olni, Yeni) serta Tim Asisten Laboratorium S1 Matematika USU. Rekan organisasi penulis Ukmi Al-Falak FMIPA USU, IMKubik FMIPA USU, Ukmi Ad-Dakwah USU sebagai wadah belajar dan menambah pengalaman selama berkuliah USU serta Akhwati di Lingkaran Cahaya, Al Marwah, Hurun „in dan Huriyah juga kepada kakak Fatimah Marwa Nst, S.Si dan kakak Nana Indiyani, S.Si yang telah memberi semangat dan motivasi kepada penulis.
Semoga segala bentuk bantuan yang telah diberikan kepada penulis, mendapatkan balasan yang lebih baik dari Allah SWT. Penulis memohon maaf apabila terdapat kesalahan dalam skripsi ini. Semoga skripsi ini dapat bermanfaat bagi pembaca.
Medan, 04 Juli 2019 Mutia Sari
v DAFTAR ISI
Halaman
PENGESAHAN LAPORAN TUGAS AKHIR i
ABSTRAK ii
ABSTRACT iii
PENGHARGAAN iv
DAFTAR ISI v
DAFTAR TABEL vii
DAFTAR GAMBAR viii
DAFTAR LAMPIRAN ix
BAB 1 PENDAHULUAN
1.1 Latar Belakang 1
1.2 Perumusan Masalah 2
1.3 Batasan Masalah 2
1.4 Tujuan Penelitian 2
1.5 Manfaat Penelitian 3
BAB 2 TINJAUAN PUSTAKA
2.1 Distribusi Binomial 4
2.2 Distribusi Poisson 4
2.3 Distribusi Normal 7
2.3.1 Definisi Distribusi Normal 7
2.3.2 Definisi Distribusi Normal Standar 8
2.4 Regresi Poisson 9
2.4.1 Model Regresi Poisson 9
2.4.2 Penaksiran Parameter Regresi Poisson 10
2.5 Overdispersi 10
2.6 Model Regresi Zero-Inflated Poisson 11 2.7 Uji Khi-Kuadrat pada Regresi Poisson dan ZIP 13
2.8 Uji Pearson Khi-Kuadrat pada Regresi Poisson dan ZIP
14
2.9 Uji Wald pada Regresi Poisson dan ZIP 14
BAB 3 METODE PENELITIAN
3.1 Metodologi Penelitian Kepustakaan 16
3.2 Data 16
3.3 Analisis Data 16
BAB 4 HASIL DAN PEMBAHASAN
4.1 Tahapan Simulasi 18
4.2 Kajian Simulasi Eksplorasi Variabel Y 20
4.3 Uji Khi-Kuadrat 21
4.4 Overdispersi pada Regresi Poisson dan ZIP 23
4.5 Model Regresi Poisson 27
4.6 Model Regresi ZIP 28
4.7 Uji Wald 28
BAB 5 KESIMPULAN DAN SARAN
5.1 Kesimpulan 29
5.2 Saran 29
DAFTAR PUSTAKA 30
LAMPIRAN 31
vii
DAFTAR TABEL
Nomor
Tabel Judul Halaman
4.1 Persentase uji khi-kuadrat terhadap kombinasi 22 4.2 Rasio dispersi terhadap regresi poisson dan ZIP 24 4.3 Rasio disperse dengan 25
DAFTAR GAMBAR
Nomor
Gambar Judul Halaman
2.1 Fungsi peluang distribusi normal 8
2.2 Fungsi peluang distribusi normal dengan
8
4.1 Histogram terhadap variabel pada ,
dengan 20
4.2 Histogram terhadap variabel pada ,
dengan 21
ix
DAFTAR LAMPIRAN
Nomor
Lampiran Judul Halaman
1. Data Variabel dan dengan
31
2. Source program R 32
3. Output pendugaan model regresi poisson dan ZIP untuk
36
4. Output uji wald pada regresi poisson dan ZIP untuk
37
BAB 1 PENDAHULUAN
1.1 Latar Belakang
Analisis Regresi dalam statistika merupakan salah satu metode yang dapat digunakan untuk mengetahui hubungan sebab-akibat antar variabel. Analisis regresi klasik mempunyai syarat bahwa data berdistribusi normal. Analisis ini bertujuan untuk mengetahui arah hubungan antara variabel penjelas dengan variabel respons sekaligus untuk memprediksi nilai dari variabel respons apabila nilai variabel penjelasnya mengalami kenaikan atau penurunan. Dalam praktek di lapangan, data yang ditemukan seringkali tidak memenuhi asumsi yang diisyaratkan regresi linier klasik. Untuk mengatasi hal tersebut dikembangkan Generalized Linear Model (GLM). GLM digunakan sebagai perluasan model regresi umum untuk variabel respons yang berupa data kategorikal dan berdistribusi diskrit (Agresti, 2007).
Variabel respons yang digunakan pada penelitian ini adalah berdistribusi poisson. Distribusi poisson adalah distribusi probabilitas diskrit yang menyatakan peluang jumlah peristiwa yang terjadi pada periode waktu tertentu dengan rata-rata kejadian yang diketahui dan terjadi dalam waktu yang saling bebas.
Sehingga untuk pembentukan model regresinya dapat digunakan regresi poisson yang merupakan salah satu kasus spesial dari Generalized Linear Model (GLM).
Analisis regresi poisson menunjukkan hubungan antara variabel penjelas dengan variabel respons yang menyebar poisson. Karakteristik variabel respons dari sebaran poisson yaitu rataan dan variansnya bernilai sama atau equdispersi. Namun pada data terapan, variabel respons memiliki keragaman yang besar, dengan kata lain sering terjadi penyimpangan berupa overdispersi atau underdispersi. Overdispersi yaitu varians lebih besar dari pada nilai rataan, sedangkan underdispersi yaitu varians lebih kecil dari nilai rataan pada variabel respons. Overdispersi dapat terjadi karena adanya heterogenitas pada variabel respons (Agresti, 2007) juga dikarenakan nilai nol yang berlebih (excess zeros).
Lambert (1992) memperkenalkan zero-inflated poisson regression (ZIP regression) sebagai penanganan model untuk yang akan digunakan untuk mengatasi masalah overdispersi pada data dengan keadaan excess zeros. Lambert (1992) juga
2
mengemukakan keunggulan dari regresi ZIP sangat mudah diterapkan pada beberapa bidang seperti pertanian, peternakan, biostatistika, dan industri. Selain itu, model regresi ZIP mudah diinterpretasi penduga parameternya, dan dapat menjelaskan alasan terjadinya overdispersi pada variabel respons.
Pada penelitian sebelumnya (Dewanti et al., 2016) meneliti mengenai perbandingan analisis regresi zero-inflated poisson (ZIP) dan zero-inflated negative binomial (ZINB) yang dapat mengatasi overdispersi karena tidak memiliki asumsi equidispersi seperti pada regresi poisson. Analisis regresi ZIP sudah mampu mengendalikan nilai nol, namun belum sepenuhnya mengendalikan overdispersi, sehingga pada penelitian ini akan dikaji mengenai kemampuan regresi ZIP dalam mengatasi overdispersi pada regresi poisson.
Dari uraian diatas, penulis memberi judul penelitian ini dengan “Pengujian Regresi Zero-Inflated Poisson dalam Mengatasi Overdispersi pada Regresi Poisson”.
1.2 Perumusan Masalah
Rumusan masalah dalam penelitian ini adalah bagaimana kemampuan regresi zero-inflated poisson (ZIP) untuk melihat batas peluang ( ) dalam mengatasi overdispersi dengan simulasi menggunakan bahasa pemrograman R.
1.3 Batasan Masalah
Batasan masalah dalam penelitian ini adalah :
Penelitian ini akan mengkaji kemampuan regresi zero-inflated poisson dalam mengatasi overdispersi pada regresi poisson untuk melihat batas (threshold) probabilitas munculnya nilai nol sebagai nilai yang menyebabkan terjadinya overdispersi dengan data yang disimulasikan secara random dengan seed.
1.4 Tujuan Penelitian
Tujuan dari penelitian ini adalah untuk mengetahui batas kemampuan regresi zero-inflated poisson dari data yang disimulasikan dalam mengatasi overdispersi dari regresi poisson.
3
1.5 Manfaat Penelitian
Manfaat dari penelitian ini adalah dapat mengetahui kemampuan regresi zero- inflated poisson (ZIP) untuk melihat batas peluang ( ) dalam mengatasi overdispersi dengan simulasi menggunakan bahasa pemrograman R.
BAB 2
TINJAUAN PUSTAKA
2.1 Distribusi Binomial
Distribusi binomial digunakan untuk situasi dimana suatu percobaan terdiri dari 2 hasil yakni kejadian yang sukses dan gagal pada sejumlah percobaan.
Sebuah variabel acak dikatakan berdistribusi binomial dengan parameter dan jika berdistribusi diskrit yang memiliki fungsi peluang sebagai berikut:
( | ) . / ( ) ( ) Pada distribusi ini merupakan bilangan bulat positif sebagai jumlah kejadian dan adalah peluang kejadian terjadi dimana .
Ekspektasi dan varians variabel acak untuk distribusi binomial adalah:
( ) ∑ ( )
( )
( ) ∑ ( ) ( )
(2.3)
2.2 Distribusi Poisson
Downing dan Clark (1997) menjelaskan bahwa distribusi poisson merupakan distribusi binomial dengan yang besar dan yang kecil. Diberikan jumlah panggilan telpon pada suatu perusahaan yang diterima dalam satu jam. Apakah jenis distribusi dari ?
Salah satu caranya adalah dengan membuat daftar semua orang yang mungkin akan menelepon (klien, karyawan dan sebagainya). Misalkan ada dari mereka. Mereka tidak akan mungkin menelpon sekaligus dalam waktu yang bersamaan. Cara untuk membuat model situasi tersebut adalah mengatakan bahwa semua orang memiliki probabilitas panggilan yang sama selama jam bersebut.
Dideskripsikan bahwa akan berdistribusi binomial, namun hal tersebut adalah distribusi binomial yang sangat besar. Diketahui bahwa fungsi peluang distribusi binomial adalah:
5
( ) . / ( ) ( ) di mana:
( ) = peluang munculnya kejadian = variabel acak (kejadian yang diamati) = jumlah seluruh kejadian
Maka akan sulit menghitung untuk yang besar.
Diketahui bahwa ekspektasi dari adalah . Biasanya akan menjadi besar dan sangat kecil, tetapi tepat dalam perhitungan. Diberikan bahwa maka,
( )
( ) ( )
( )( ) ( ( ))
( )
( )(( ) )(( ) ) .( ( )) /( ) ( )( ) ( ( ) )( )
Jika sangat kecil, maka diperoleh
( )( ) ( )
⏟
( )
( )
Dengan menyederhakan perhitungan, menurul Hopital Rule maka akan semakin besar dan besar, ( ) . / mendekati , sehingga diperoleh rumus
( )
( )
Rumus tersebut merupakan fungsi peluang untuk distribusi poisson. adalah variabel acak berdistribusi poisson dengan parameter .
Contoh kasus yang termasuk dalam distribusi poisson:
1. Jumlah novas di galaksi dalam satu decade tertentu.
2. Jumlah film dengan keuntungan lebih dari 25 juta dollar dalam setahun.
3. Jumlah siswa Ph.D yang tidak menyelesaikan disertasi tepat waktu dalam setahun.
6
Ekspektasi variabel acak untuk distribusi poisson adalah:
( ) ∑
∑
∑
( )
andaikan , maka ( ) ∑
∑
Varians dapat dicari dengan cara sebagai berikut:
( ) ∑
∑( )
∑
Jumlah kedua samadengan , seperti yang ditunjukkan sebelumnya. Sekarang:
∑( )
∑( )
∑
( )
andaikan , maka ∑
( )
∑
Jumlah peluang samadengan 1. Sehingga
( ) ( )
( ) ( ) ( )
Sehingga variansnya adalah . Distribusi poisson memiliki sifat yang sangat unik yaitu ekspektasi samadengan varians.
7
2.3 Distribusi Normal
2.3.1 Definisi Distribusi Normal
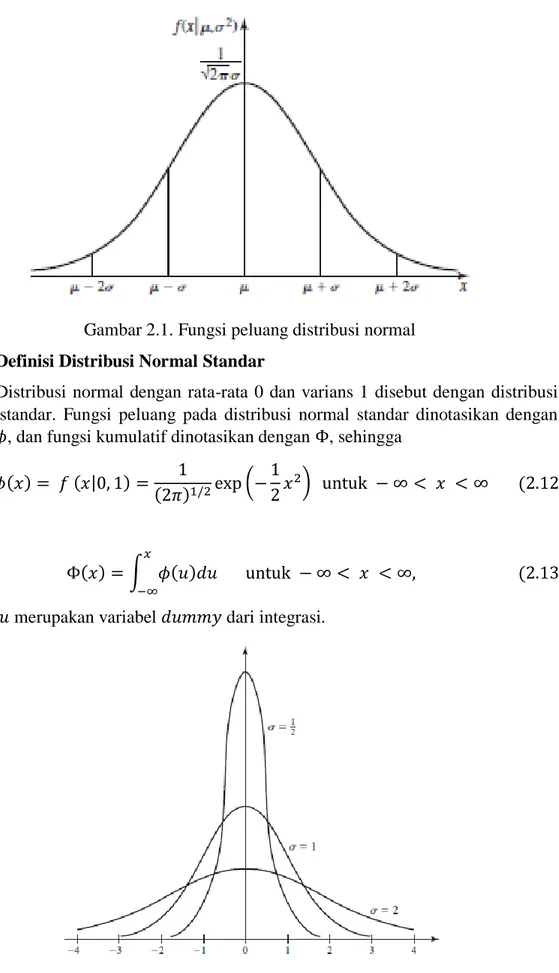
Suatu variabel acak memiliki distribusi peluang dengan rata-rata dan varians ( dan ) jika berdistribusi kontinu dengan fungsi peluang:
( | )
( ) [ .
/ ] ( )
Bukti:
Jelas bahwa persamaan ( ) adalah non-negatif, akan ditunjukkan bahwa,
∫ ( | )
( )
Jika dimisalkan ( ) , maka
∫ ( | )
∫
( ) ( )
Kemudian diandaikan
∫ ( )
( ) Selanjutnya akan ditunjukkan ( ) .
Menurut persamaan ( ), maka diperoleh ∫ ( )
∫ ( )
∫ ∫ [ ( )]
Ubah variabel integral dan menjadi koordinat polar dan dengan memisalkan dan Maka,
∫ ∫ ( ) ( ) Integral dalam dapat dibentuk dengan mensubstitusikan dengan sehingga integral dalamnya adalah
∫ ( )
Dan integral luarnya adalah Sehingga, ( ) dan persamaan ( ) terpenuhi.
8
Gambar 2.1. Fungsi peluang distribusi normal 2.3.2 Definisi Distribusi Normal Standar
Distribusi normal dengan rata-rata 0 dan varians 1 disebut dengan distribusi normal standar. Fungsi peluang pada distribusi normal standar dinotasikan dengan simbol , dan fungsi kumulatif dinotasikan dengan , sehingga
( ) ( | )
( ) ( ) ( ) dan
( ) ∫ ( )
( ) dimana merupakan variabel dari integrasi.
Gambar 2.2. Fungsi peluang distribusi normal dengan
9
2.4 Regresi Poisson
Regresi poisson merupakan analisis regresi yang biasanya digunakan untuk data dengan respons berupa variabel diskrit tetapi tidak biner. Dalam hal ini respons data tersebut berdistribusi poisson dengan parameter . Hal yang sangat penting untuk dicatat bahwa parameter ini sangat bergantung pada beberapa unit tertentu atau periode dari waktu, jarak, luas area, volume, dan sebagainya. Distribusi ini kemudian digunakan untuk memodelkan suatu peristiwa yang keberadaannya relatif jarang atau langka untuk terjadi pada satuan unit tertentu. Regresi poisson memiliki beberapa asumsi sebagai berikut (Pateta, 2005):
1. Variabel respons berupa data diskrit.
2. Distribusi bersyarat dari variabel respons mengikuti distribusi poisson.
3. Nilai rata-rata akan sama dengan variansinya, ( ) ( )
2.4.1 Model Regresi Poisson
Pada model regresi poisson, fungsi penghubung yang digunakan adalah fungsi penghubung log karena fungsi log menjamin bahwa nilai variabel yang diharapkan dari variabel responsnya akan bernilai non-negatif.
( ) ( ) dimana:
= jumlah variabel respons = jumlah amatan
= konstanta
= koefisien regresi variabel penjelas ke-
= variabel penjelas ke- , amatan ke- = kesalahan pada perkiraan
Persamaan di atas dapat pula dituliskan sebagai:
( ) ( ) ( )
10
2.4.2 Penaksiran Parameter Regresi Poisson
Untuk menaksir parameter digunakan metode Maximum Likelihood Estimation (MLE). Prinsip dari metode ini adalah mencari taksiran maksimum likelihood dari parameter, yaitu taksiran dari parameter yang memaksimumkan fungsi likelihood. Berikut adalah turunan pertama dari fungsi likelihood berdasarkan persamaan :
( ) ∏ ( )
∏ { ( ) }
∏ {[ ( ( ∑ ))] ( ∑ ) }
Untuk mempermudah perhitungan dalam memperoleh taksiran maksimum likelihood dari parameter, digunakan bentuk logaritma dari fungsi likelihood pada persamaan di atas sebagai berikut:
( ) ∑ {
( ∑
)
( ∑
) ( ) }
∑* ( ) +
dengan parameter mean , | - ( ).
2.5 Overdispersi
Menurut McCullagh dan Nelder (1989), regresi poisson dikatakan mengandung overdispersi apabila nilai variansnya lebih besar dari nilai rata-ratanya.
Overdispersi memiliki dampak yang sama dengan pelanggaran asumsi jika pada data
11
diskrit terjadi overdispersi namun tetap digunakan regresi poisson, dugaan dari parameter koefisien regresinya tetap konsisten namun tidak efisien. Hal ini berdampak pada nilai standar error yang menjadi under estimate, sehingga kesimpulannya menjadi tidak valid. Fenomena overdispersi dapat dituliskan ( ) ( ). Hubungan parameter dispersi ( ) dengan varians dan rata-rata dalam regresi Poisson adalah:
( )
( ) Perhitungan nilai dispersi dengan menggunakan adalah:
( )
2.6 Model Regresi Zero-Inflated Poisson (ZIP)
Model regresi ZIP adalah model campuran yang sederhana untuk data diskrit dengan banyak peristiwa nol (Lambert, 1992). Jika merupakan variabel acak bebas yang berdistribusi ZIP, maka nilai nol yang terdapat pada observasi diduga telah terjadi dengan dua cara yang sesuai dengan keadaan (state) yang terpisah. Keadaan pertama disebut dengan zero state dengan probabilitas dan keadaan kedua disebut dengan poisson state dengan probabilitas. Kedua keadaan memberikan distribusi campuran dua komponen. Fungsi peluang dari model regresi ZIP adalah:
Untuk setiap pengamatan yang saling bebas dan {
( ) ( ) maka :
( ) {
( ) ( )
( ) Dengan parameter ( ) dan ( ) yang memenuhi :
( ) dan ( ) Dimana logit ( ) .( )/,
dan adalah parameter regresi yang akan ditaksir, sedangkan adalah matriks variabel yang memuat himpunan-himpunan yang berbeda dari faktor eksperimen
12
yang berhubungan dengan peluang pada zero state dan rata-rata poisson pada poisson state.
Variabel-variabel yang mempengaruhi mean poisson pada poisson state bisa sama dan bisa juga berbeda dengan variabel yang mempengaruhi peluang pada zero state. Pada saat variabel yang mempengaruhi mean poisson pada poisson state dan zero state sama serta setiap parameter ( dan ) bukan merupakan fungsi dari yang lainnya, maka pemodelan regresi ZIP dilakukan sebanyak dua kali sesuai dengan banyaknya parameter pada regresi poisson. Pada kasus lain, dimana variabel yang mempengaruhi kedua state berbeda, atau peluang dari zero state tidak bergantung pada variabel, sehingga matriks yang berhubungan dengan zero state tersebut merupakan matriks kolom yang elemen-elemennya adalah 1, maka regresi ZIP hanya dimodelkan satu kali atau sama seperti memodelkan regresi poisson.
Jika variabel yang mempengaruhi dan sama, serta merupakan fungsi dari atau sebaliknya, maka jumlah parameter yang akan ditaksir dapat dikurangi, dengan asumsi bahwa fungsi tersebut diketahui sebanyak suatu konstanta yang mendekati setengah dari jumlah parameter yang dibutuhkan untuk regresi ZIP dan secara nyata dapat mempercepat perhitungannya.
Tetapi, dalam banyak aplikasi hanya terdapat sedikit informasi awal tentang bagaimana berhubungan dengan . Sehingga untuk menaksir parameternya digunakan fungsi penghubung:
( ) dan ( )
dimana nilai sebenarnya dari parameter yang tidak diketahui, mengakibatkan ( )
Dalam persamaan generalized linear models, ( ) dan ( ) adalah link function atau transformasi yang umumnya digunakan untuk melinierkan mean dari poisson dan peluang sukses pada bernoulli. Model kemudian akan dituliskan sebagai ( ).
Link function logit untuk parameter akan simetrik disekitar nilai 0,5. Dua link function asymetric yang sering digunakan adalah log-log link yang didefinisikan sebagai :
( ( ) ) ekuivalen dengan ( )
13
dan complementary log-log link yng didefinisikan sebagai : ( ( ) ) atau ( ).
2.7 Uji Khi-Kuadrat pada Regresi Poisson dan ZIP
Cameron dan Trivedi (1998) menyatakan bahwa masalah utama dari overdispersi terdapat pada model dengan variabel respons diskrit. Penyebab dari overdispersi yang sering terjadi adalah peluang nilai nol yang berlebih pada variabel respons. Kajian overdispersi ini membutuhkan identifikasi dengan melakukan uji khi-kuadrat terhadap peluang muncunya nilai nol pada variabel respons.
Ricci (2005) menyatakan bahwa uji khi-kuadrat digunakan untuk menguji kecocokan sekumpulan data terhadap peluang sebaran tertentu. Uji khi-kuadrat digunakan untuk menguji kecocokan sekumpulan data terhadap peluang sebaran poisson dan ZIP. Pada uji khi-kuadrat frekukensi aktual dalam kategori dibandingkan dengan frekuensi yang secara teoritis diharapkan terjadi, jika data mengikuti peluang sebaran poisson dan ZIP. Hipotesis dari uji khi-kuadrat yaitu
dan ( )
dengan adalah peluang amatan untuk setiap kategori ke dan adalah peluang sebaran poisson. Hipotesis nol menjelaskan bahwa terdapat kecocokan antara peluang amatan dengan peluang sebaran poisson, ataupun sebaliknya untuk interpretasi pada Kemudian, statistik uji khi-kuadrat merupakan selisih antara frekuensi yang diamati dengan frekuensi teoritis terhadap frekuensi teoritis dari peluang sebaran poisson dan ZIP.
∑( )
( ) Dengan adalah fungsi massa peluang dari sebaran poisson dan ZIP, adalah frekuensi yang diamati untuk setiap kategori ke , adalah ukuran contoh, dan adalah jumlah kategori. Di bawah kondisi benar, statistik uji pada persamaan tersebut akan mendekati sebaran dengan derajat bebas ( ), dan adalah jumlah parameter diduga oleh data contoh atau ̂ ̅ sehingga penduga parameternya berjumlah . Dengan demikian keputusannya adalah menolak pada , jika ( ). Penolakan pada berarti bahwa tidak terdapat kecocokan antara peluang amatan dengan peluang sebaran poisson atau variabel respons tidak menyebar poisson atau tidak menyebar ZIP.
14
2.8 Uji Pearson Khi-Kuadrat pada Regresi Poisson dan ZIP
Cameron dan Trivedi (1998) menyatakan bahwa uji pearson khi-kuadrat sering digunakan dalam mengukur kebaikan model regresi poisson dan ZIP.
Pengujian ini dilakukan dengan hipotesis yaitu jika rasio menghasilkan nilai lebih dari satu, maka model tersebut mengalami overdispersi pada hipotesis alternatif ( ). Hipotesis pada uji pearson khi-kuadrat adalah
dan ( )
nilai statistik uji pearson khi-kuadrat dapat didefinisikan sebagai ∑( ( ))
( )
( )
dengan rasio dispersi
( )
dengan adalah nilai aktual pada amatan ke dari variabel respons, ( ) dan ( ) adalah nilai dugaan rataan dan ragam dari regresi poisson dan ZIP. adalah banyaknya amatan pada variabel respons, dan adalah banyaknya parameter regresi poisson dan ZIP. Di bawah kondisi benar, statistik uji akan mendekati sebaran dengan derajat bebas ( ) sehingga keputusannya adalah menolak pada , jika ( ). Pengidentifikasian adanya keragaman data pada variabel respons ( ) terhadap regresi poisson dan ZIP dengan menggunakan kriteria rasio yang didapat dari nilai statisik uji pearson khi-kuadrat terhadap derajat bebas dari regresi poisson dan ZIP.
2.9 Uji Wald pada Regresi Poisson dan ZIP
Agresti (2007) menyatakan bahwa uji wald digunakan untuk mengetahui variabel penjelas yang berpengaruh terhadap variabel respons. Uji wald diterapkan pada model regresi poisson dan ZIP. Hipotesis untuk menguji signifikansi dari koefisien parameter regresi poisson dan ZIP, misalkan , adalah
dan ( )
15
Selang kepercayaan pada uji wald untuk yaitu ̂ ( ̂), dengan statistik uji yang digunakan pada persamaan tersebut adalah
̂
( ̂) ( )
Statistik uji wald pada mendekati sebaran normal baku ketika . Keadaan ini setara dengan yang mendekati sebaran khi-kuadrat dengan derajat bebas , sehingga statistik uji wald yang digunakan yaitu
[ ̂
( ̂)] ( )
dengan ̂ adalah koefisien penduga parameter dan ( ̂) adalah penduga galat baku dari penduga koefisien parameter parameter yang diperoleh dari matriks penduga ragam peragam ̂ .
Statistik uji akan mendekati sebaran dengan derajat bebas di bawah kondisi benar, sehingga keputusannya adalah menolak pada , jika
. Penolakan pada berarti bahwa variabel penjelas ke , untuk suatu tertentu ( ), memiliki pengaruh yang signifikan terhadap variabel respons.
BAB 3
METODE PENELITIAN
3.1 Metode Penelitian Kepustakaan
Metode ini penulis lakukan melalui membaca serta mengambil data-data dari buku-buku, artikel-artikel atau jurnal-jurnal yang mendukung untuk memenuhi landasan teori dalam analisis yang dilakukan.
3.2 Data
Data yang digunakan dalam penelitian ini adalah data simulasi. Data simulasi dibangkitkan berdasarkan karakteristik data. Data simulasi berguna untuk mendapatkan penduga koefisien parameter regresi poisson dan ZIP. Data akan disimulasikan menggunakan bahasa pemrograman R.
3.3 Analisis Data
Analisis data merupakan hal yang dilakukan penulis pada penelitian ini.
Analisis data dilakukan agar data dapat diolah serta bermanfaat untuk memecahkan masalah yang akan diamati. Tahapan analisis yang akan dilakukan yaitu, yaitu:
1. Membangkitkan data variabel respons berdasarkan karakteristik data, kemudian membangkitkan variabel penjelas.
2. Melakukan uji overdispersi pada data.
3. Mengamati kemampuan regresi ZIP dalam mengatasi overdispersi pada regresi poisson.
a. Membangkitkan variabel yang menyebar Poisson ( ), sebanyak dengan peluang nol .
b. Membangkitkan variabel yang menyebar Normal Standar ( ), sebanyak .
c. Data simulasi pada variabel dan dibangkitkan dengan perangkat lunak program RStudio ver. 1.1.463.0 dan akan diulang sebanyak kali dengan kondisi simulasi yang diamati.
17
4. Melakukan analisis regresi poisson dan ZIP untuk mendapatkan penduga koefisien parameter regresi.
5. Membentuk model regresi poisson dan regresi ZIP dari data simulasi.
BAB 4
HASIL DAN PEMBAHASAN
Pengujian regresi zero-inflated poisson dalam mengatasi overdispersi pada regresi poison dilihat dari batas peluang munculnya nol sebagai nilai yang menyebabkan terjadinya overdispersi. Pengujian yang dilakukan akan dilakukan dengan simulasi menggunakan bahasa pemrograman R.
4.1 Tahapan Simulasi
Tahapan simulasi yang dilakukan pada penelitian ini adalah:
a. Membangkitkan data variabel respons yang berdistribusi poisson dengan dan peluang muncul nol sebanyak .
b. Membangkitkan variabel penjelas yang berdistribusi normal standar.
c. Menguji kecocokan data mengikuti sebaran poisson menggunakan uji khi- kuadrat:
1. Mencatat nilai beserta frekuensinya.
2. Menghitung banyaknya nilai .
3. Menghitung peluang setiap amatan dengan fungsi peluang:
( ) 4. Hitung statistik uji khi-kuadrat:
∑( )
5. Lakukan pengujian apakah . 6. Hitung persentase yang memenuhi pengujian.
d. Menguji kecocokan data mengikuti sebaran ZIP menggunakan uji khi-kuadrat:
1. Mencatat nilai beserta frekuensinya.
2. Menghitung banyaknya nilai .
3. Menghitung peluang setiap amatan dengan fungsi peluang:
19
( ) {
( ) ( )
4. Hitung statistik uji khi-kuadrat:
∑( )
5. Lakukan pengujian apakah . 6. Hitung persentase yang memenuhi pengujian.
e. Bentuk model regresi poisson.
f. Catat nilai koefisien pada regresi poisson.
g. Bentuk model regresi ZIP.
h. Catat nilai koefisien pada regresi ZIP.
i. Hitung rasio dispersi pada regresi poisson:
1. Hitung nilai poisson:
( ) 2. Hitung statistik uji pearson khi-kuadrat:
∑( ( )) ( )
3. Hitung rasio dispersi:
( ) ( ) j. Hitung rasio dispersi pada regresi poisson:
1. Hitung nilai ZIP untuk data diskrit:
( ) 2. Hitung nilai ZIP untuk zero-inflation:
( ) ( ) 3. Hitung ( ) dan ( ):
( ) ( ) ( ) ( ) (
) ( ( )) 4. Hitung statistik uji pearson khi-kuadrat:
20
∑( ( )) ( )
5. Hitung rasio dispersi:
( ) ( )
k. Lakukan uji wald pada regresi poisson dan zip untuk melihat hubungan antara variabel respons dengan variabel penjelas.
4.2 Kajian Simulasi Eksplorasi Variabel
Variabel merupakan variabel respons yang berisi data dengan sebaran poisson. Data dari variabel respons dibangkitkan dengan beberapa kondisi.untuk nilai sebanyak dan dengan peluang muncul nilai 0 . Berdasarkan simulasi yang dilakukan ditunjukkan bahwa nilai berpengaruh terhadap . Eksplorasi terhadap variabel akan ditunjukan melalui histogram yang bertujuan untuk mengetahui kondisi sebaran poisson dan ZIP pada variabel .
Pada histogram 4.1 diambil nilai sebagai sampel, dikarenakan nilai tersebut digunakan dalam sebagian besar data terapan pada analisis regresi poisson dan ZIP. Nilai yang akan ditunjukkan adalah dan 10 mewakili yang bernilai kecil dan besar dengan peluang muncul nol yang diambil adalah .
Gambar 4.1. Histogram terhadap variabel pada , dengan
21
Histogram pada Gambar 4.1. menunjukkan bahwa ketika variabel bernilai dengan dan , maka indikasi data masih menyebar poisson. Histogram pada menunjukkan bahwa rataan variabel berada di sekitar nilai . Pada saat variabel memiliki , maka rataan mengalami perubahan menjadi nilai kurang dari yaitu . Pada kondisi nilai p dari sampai , terjadi perubahan nilai yang signifikan, artinya semakin besar nilai , maka nilai menuju nol. Nilai dan dan pada variabel mengindikasikan peluang nol berlebih. Kondisi ini sesuai dengan peningkatan frekuensi nilai nol di setiap yang disimulasikan.
Gambar 4.2. Histogram terhadap variabel pada , dengan
Histogram pada Gambar 4.2. menunjukkan bahwa variabel dengan di setiap p yang disimulasikan, maka diindikasikan menyebar ZIP. Histogram pada menunjukkan bahwa rataan variabel berada di sekitar nilai 10. Variabel memiliki banyak nilai nol yang berlebih pada kondisi terjadi , dan sehingga bentuk sebaran data yang terjadi posisi nilai nol terpisah dengan nilai lainnya yang berada di sekitar nilai 10. Kondisi perubahan nilai p yang disimulasikan pada menunjukkan hasil yang sama dengan kondisi . Hasil indikasi histogram akan diuji menggunakan khi-kuadrat, yang menunjukkan bahwa kondisi dari penyebab overdispersi dan sebaran poisson pada variabel dikarenakan excess zero atau nilai nol yang berlebih.
22
4.3 Uji Khi-Kuadrat
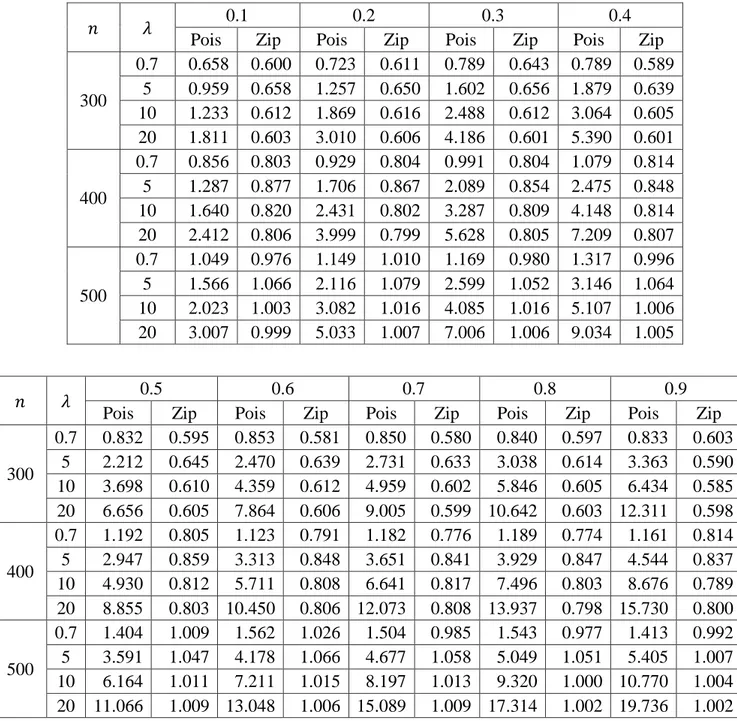
Hasil uji khi-kuadrat dengan α sebesar 0.05 untuk sebaran poisson dan ZIP terhadap kombinasi dari λ, n, p ditunjukan pada Tabel 4.1. Uji khi-kuadrat untuk sebaran poisson menunjukkan bahwa semakin besar λ, n, dan p yang disimulasikan, maka akan semakin kecil persentase sebaran poisson pada variabel . Hasil dari uji khi-kuadrat untuk sebaran poisson berbanding terbalik dengan semakin besarnya λ, n, dan p yang disimulasikan. Uji khi-kuadrat untuk sebaran ZIP menunjukkan bahwa regresi ZIP mampu mengatasi overdispersi yang disebabkan p berlebih pada variabel Kondisi ini ditunjukkan dengan semakin besar nilai λ, maka persentase sebaran poisson mencapai 0% sedangkan persentase sebaran ZIP mencapai kisaran 60%
sampai 80%.
Kejadian overdispersi yang disebabkan peluang nol berlebih pada variabel sangat berpengaruh terhadap nilai λ yang berlaku di setiap n. Hasil eksplorasi pada variabel memberikan indikasi yang sesuai dengan hasil uji khi-kuadrat untuk sebaran poisson dan ZIP. Nilai λ=0.7 yang menghasilkan persentase nol berlebih yang paling kecil dan sebagian besar menyebar poisson. Nilai λ yang dimulai dari 5 sampai λ=20 di setiap p dan n yang disimulasikan menunjukkan bahwa peluang nol berlebih mencapai 100 % dan variabel tidak menyebar poisson, melainkan menyebar ZIP.
Tabel 4.1. Persentase uji khi-kuadrat terhadap kombinasi
0.1 0.2 0.3 0.4
Pois Zip Pois Zip Pois Zip Pois Zip
300
0.7 76.4 85.6 20.8 87.2 0.4 86.6 0 86.6
5 0 85.4 0 85.4 0 86.2 0 85.6
10 0 82.6 0 82.2 0 83 0 80.4
20 0 77.8 0 77 0 76.8 0 76
400
0.7 70.2 86 9 86.6 0 87.4 0 88.4
5 0 86.4 0 87.2 0 86 0 85.4
10 0 82.6 0 83.4 0 82 0 82.2
20 0 76.8 0 77.2 0 77 0 77
500
0.7 70 84.8 5.2 86.6 0 87.2 0 86.6
5 0 86.2 0 86 0 85.8 0 86.6
10 0 81.8 0 81.8 0 82.4 0 83
20 0 77.4 0 78.6 0 75.6 0 77.8
23
4.4 Overdispersi pada Regresi Poisson dan ZIP
Eksplorasi dan pengujian terhadap variabel menunjukkan bahwa adanya indikasi peluang nol berlebih, sehingga dilakukan uji khi-kuadrat untuk mengetahui apakah data memiliki sebaran poisson atau ZIP. Hasil simulasi terhadap kombinasi λ dan disetiap yang disimulasikan menunjukkan bahwa ketika variabel memiliki dan yang semakin besar, maka terjadi overdispersi. Pengujian pada variabel menyatakan bahwa kondisi overdispersi berpengaruh terhadap perubahan sebaran poisson menjadi sebaran ZIP. Uji khi-kuadrat untuk sebaran ZIP menunjukan bahwa regresi ZIP mampu mengatasi overdispersi yang disebabkan nilai nol berlebih pada variabel . Selanjutnya, regresi poisson dan ZIP diukur kebaikan modelnya berdasarkan pengujian overdispersi di setiap kombinasi , dan yang disimulasikan.
Kondisi overdipersi pada setiap kombinasi , dan yang disimulasikan pada regresi Poisson dan ZIP dapat diketahui berdasarkan rasio dan uji pearson khi-kuadrat pada . Rasio menunjukkan nilai dari hasil statistik uji pearson khi-kuadrat terhadap derajat bebas ( ). Nilai dari derajat bebas regresi poisson dan ZIP berbeda, karena pada regresi Poisson menggunakan , yaitu penduga parameter dan . Regresi ZIP menggunakan berdasarkan model diskrit untuk dan model zero-inflation untuk yaitu dan , serta dan .
0.5 0.6 0.7 0.8 0.9
Pois Zip Pois Zip Pois Zip Pois Zip Pois Zip
300
0.7 0 83.8 0 84 0 83.8 0 84 0 82.4
5 0 85.4 0 85.2 0 85.8 0 83.6 0 83 10 0 80.6 0 79.8 0 79.4 0 77.6 0 75 20 0 76 0 72.6 0 72.6 0 69.6 0 66.8
400
0.7 0 87.8 0 84.8 0 84.4 0 83.2 0 84.2 5 0 86.8 0 85.6 0 85.2 0 85.8 0 83.6 10 0 82.2 0 80.4 0 79.8 0 79.6 0 77.2 20 0 78 0 77.4 0 72.6 0 70.8 0 68.2
500
0.7 0 87.8 0 88.2 0 83.8 0 83.6 0 84.4 5 0 84.8 0 86.8 0 85.4 0 85.2 0 83.8 10 0 81.4 0 82.2 0 80.6 0 79.8 0 78.2
20 0 77 0 78 0 76 0 73 0 71.6
24
Tabel 4.2. Rasio dispersi terhadap regresi Poisson dan ZIP
0.1 0.2 0.3 0.4
Pois Zip Pois Zip Pois Zip Pois Zip
300
0.7 0.658 0.600 0.723 0.611 0.789 0.643 0.789 0.589 5 0.959 0.658 1.257 0.650 1.602 0.656 1.879 0.639 10 1.233 0.612 1.869 0.616 2.488 0.612 3.064 0.605 20 1.811 0.603 3.010 0.606 4.186 0.601 5.390 0.601
400
0.7 0.856 0.803 0.929 0.804 0.991 0.804 1.079 0.814 5 1.287 0.877 1.706 0.867 2.089 0.854 2.475 0.848 10 1.640 0.820 2.431 0.802 3.287 0.809 4.148 0.814 20 2.412 0.806 3.999 0.799 5.628 0.805 7.209 0.807
500
0.7 1.049 0.976 1.149 1.010 1.169 0.980 1.317 0.996 5 1.566 1.066 2.116 1.079 2.599 1.052 3.146 1.064 10 2.023 1.003 3.082 1.016 4.085 1.016 5.107 1.006 20 3.007 0.999 5.033 1.007 7.006 1.006 9.034 1.005
0.5 0.6 0.7 0.8 0.9
Pois Zip Pois Zip Pois Zip Pois Zip Pois Zip
300
0.7 0.832 0.595 0.853 0.581 0.850 0.580 0.840 0.597 0.833 0.603 5 2.212 0.645 2.470 0.639 2.731 0.633 3.038 0.614 3.363 0.590 10 3.698 0.610 4.359 0.612 4.959 0.602 5.846 0.605 6.434 0.585 20 6.656 0.605 7.864 0.606 9.005 0.599 10.642 0.603 12.311 0.598
400
0.7 1.192 0.805 1.123 0.791 1.182 0.776 1.189 0.774 1.161 0.814 5 2.947 0.859 3.313 0.848 3.651 0.841 3.929 0.847 4.544 0.837 10 4.930 0.812 5.711 0.808 6.641 0.817 7.496 0.803 8.676 0.789 20 8.855 0.803 10.450 0.806 12.073 0.808 13.937 0.798 15.730 0.800
500
0.7 1.404 1.009 1.562 1.026 1.504 0.985 1.543 0.977 1.413 0.992 5 3.591 1.047 4.178 1.066 4.677 1.058 5.049 1.051 5.405 1.007 10 6.164 1.011 7.211 1.015 8.197 1.013 9.320 1.000 10.770 1.004 20 11.066 1.009 13.048 1.006 15.089 1.009 17.314 1.002 19.736 1.002
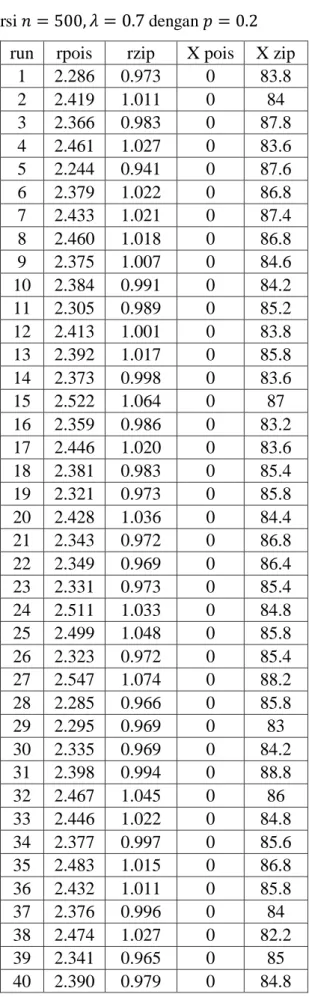
Berdasarkan Tabel 4.2 diketahui bahwa batas kemampuan regresi ZIP dalam mengatasi overdispersi berada pada kondisi pada peluang dengan rasio dispersi Pada Tabel 4.2 ditunjukkan bahwa regresi ZIP berhenti mengatasi overdispersi pada saat , namun pada saatn nilai rasio dispersi , berdasarkan uji pearson khi-kuadrat pada kondisi ini tidak terjadi overdispersi. Sehingga pada saat dilakukan simulasi secara random tanpa menggunakan fungsi set.seed sebanyak 100 kali simulasi.
25
Tabel 4.3. Rasio dispersi dengan run rpois rzip X pois X zip
1 2.286 0.973 0 83.8 2 2.419 1.011 0 84 3 2.366 0.983 0 87.8 4 2.461 1.027 0 83.6 5 2.244 0.941 0 87.6 6 2.379 1.022 0 86.8 7 2.433 1.021 0 87.4 8 2.460 1.018 0 86.8 9 2.375 1.007 0 84.6 10 2.384 0.991 0 84.2 11 2.305 0.989 0 85.2 12 2.413 1.001 0 83.8 13 2.392 1.017 0 85.8 14 2.373 0.998 0 83.6 15 2.522 1.064 0 87 16 2.359 0.986 0 83.2 17 2.446 1.020 0 83.6 18 2.381 0.983 0 85.4 19 2.321 0.973 0 85.8 20 2.428 1.036 0 84.4 21 2.343 0.972 0 86.8 22 2.349 0.969 0 86.4 23 2.331 0.973 0 85.4 24 2.511 1.033 0 84.8 25 2.499 1.048 0 85.8 26 2.323 0.972 0 85.4 27 2.547 1.074 0 88.2 28 2.285 0.966 0 85.8 29 2.295 0.969 0 83 30 2.335 0.969 0 84.2 31 2.398 0.994 0 88.8 32 2.467 1.045 0 86 33 2.446 1.022 0 84.8 34 2.377 0.997 0 85.6 35 2.483 1.015 0 86.8 36 2.432 1.011 0 85.8 37 2.376 0.996 0 84 38 2.474 1.027 0 82.2 39 2.341 0.965 0 85 40 2.390 0.979 0 84.8
26
run rpois rzip X pois X zip 41 2.303 0.976 0 83.4 42 2.319 0.982 0 84.4 43 2.484 1.060 0 84.4 44 2.339 0.975 0 85.4 45 2.335 0.962 0 84.2 46 2.483 1.033 0 82.8 47 2.427 1.027 0 86.4 48 2.555 1.052 0 83.4 49 2.383 1.001 0 85.2 50 2.357 0.981 0 86.2 51 2.341 1.007 0 86.2 52 2.461 1.023 0 88.6 53 2.452 1.036 0 86.2 54 2.409 0.998 0 85.4 55 2.460 1.041 0 87.8 56 2.517 1.063 0 85.8 57 2.603 1.067 0 86.6 58 2.532 1.051 0 85.2 59 2.567 1.070 0 84.6 60 2.569 1.074 0 85 61 2.281 0.936 0 87.4 62 2.281 0.969 0 88.2 63 2.358 1.010 0 86.2 64 2.375 1.004 0 83.8 65 2.446 1.016 0 88.4 66 2.254 0.954 0 88.4 67 2.376 0.985 0 81.6 68 2.469 1.039 0 88 69 2.493 1.056 0 86.6 70 2.345 0.974 0 84.8 71 2.387 1.002 0 84.4 72 2.457 1.013 0 86 73 2.405 1.012 0 84.6 74 2.434 1.027 0 85.8 75 2.493 1.029 0 81.6 76 2.446 1.027 0 84.2 77 2.460 1.009 0 85.6 78 2.433 1.005 0 83.4 79 2.400 1.014 0 83.2 80 2.338 0.968 0 85.2
27
run rpois rzip X pois X zip 81 2.417 0.991 0 86.2 81 2.417 0.991 0 86.2 82 2.280 0.977 0 85.2 83 2.515 1.057 0 86.2 84 2.317 0.993 0 86 85 2.390 0.975 0 86 86 2.334 0.968 0 84.4 87 2.432 1.019 0 85.2 88 2.476 1.024 0 87 89 2.337 0.980 0 87.2 90 2.456 1.047 0 84.8 91 2.480 1.035 0 83.6 92 2.453 1.028 0 87.8 93 2.430 1.025 0 88.6 94 2.445 1.023 0 83.4 95 2.408 1.024 0 84.4 96 2.375 0.979 0 85.2 97 2.405 1.009 0 86.2 98 2.304 0.970 0 85.2 99 2.402 1.001 0 83.6 100 2.425 1.025 0 85.8
Berdasarkan hasil simulasi 100 kali run untuk kondisi tersebut maka diperoleh persentase mengalami overdispersi sebesar 59% sehinggga dapat ditarik kesimpulan bahwa regresi zero-inflated poisson mengatasi overdispersi pada kondisi kondisi pada peluang .
4.5 Model Regresi Poisson
Analisis regresi Poisson digunakan untuk mengevaluasi hubungan antara variabel dengan variabel yang menyebar Poisson. Pendugaan model regresi Poisson pada variabel dengan saat kondisi adalah sebagai berikut:
( )
Interpretasi dari model regresi poisson untuk variabel yang signifikan terhadap variabel Y, yaitu setiap kenaikan pada variabel , maka akan menyebabkan penurunan pada variabel .
28
4.6 Model Regresi ZIP
Analisis regresi ZIP merupakan analisis yang mengevaluasi hubungan antara variabel dengan variabel yang menyebar ZIP. Sebaran ZIP diakibatkan oleh meningkatnya nilai nol pada sebaran poisson. Model pada regresi ZIP terdiri dari dua komponen model yaitu model data diskrit untuk dan model zero-inflation untuk . Model regresi ZIP variabel dengan saat kondisi adalah sebagai berikut:
Model data diskrit untuk
( ) Model zero-inflation untuk
( ) ( ) Sehingga penduga pada regresi ZIP adalah
̂ ( )
Interpretasi dari model diskrit untuk pada regresi ZIP yang signifikan terhadap variabel , yaitu setiap kenaikan variabel , maka akan menyebabkan penurunan jumlah kejadian variabel sebesar . Interpretasi dari model zero-inflation untuk p pada regresi ZIP yang signifikan terhadap variabel Y, yaitu setiap kenaikan variabel , maka resiko terjadinya kejadian meningkat sebesar
kali.
4.7 Uji Wald
Statistik uji wald akan mendekati sebaran dengan derajat bebas 1, sehingga keputusannya adalah menerima pada sebesar 0.05, jika dengan nilai dari . Penolakan pada variabel terhadap variabel mengartikan bahwa variabel tidak memiliki pengaruh yang signifikan terhadap dengan sebesar 0.05. Penerimaan terjadi pada regresi poisson dan ZIP.
BAB 5
KESIMPULAN DAN SARAN
5.1 Kesimpulan
Kajian overdispersi terhadap data simulasi dari kombinasi yang disimulasikan menunjukkan bahwa semakin besar nilai dan maka pada uji khi-kuadrat menghasilkan persentase sebaran poisson yang semakin kecil. Hasil simulasi menunjukkan bahwa regresi ZIP berhenti mengatasi overdispersi pada kondisi dengan . Uji Wald yang dilakukan pada data simulasi menunjukkan bahwa tidak ada pengaruh antara variabel yang berdistribusi poisson dengan variabel yang berdistribusi normal standar.
5.2 Saran
Simulasi pada data untuk mendapatkan variabel dan yang dilakukan dengan menggunakan seed sehingga data yang dibangkitkan tidak berubah, pada penelitian selanjutnya dapat dilakukan untuk data yang teracak atau random.
30
DAFTAR PUSTAKA
Agresti A. 2007. An Introduction to Categorical Data Analysis, Second Edition. New Jersey: John Wiley and Sons, Inc.
Cameron CA dan Trivedi PK. 1998. Regression Analysis of Count Data. Cambridge:
Cambridge University Pr.
Degroot MH dan Schervish MJ. 2012. Probability and Statistics Fourth Edition.
Boston: Pearson Education Inc.
Dewani NPP, Susilawati M, Srinadi IGAM, 2016. Perbandingan Regresi Zero- Inflated Poisson (ZIP) dan Regresi Zero-Inflated Negatif Binomial (ZINB) pada Data Overdispersion (Studi Kasus: Angka Kematian Ibu di Provinsi Bali).
E-Jurnal Matematika, 5 (4): 133-138.
Downing D dan Clark J. Statistics The Easy Way, Third Edition. New York: Barron‟s Educational Series, Inc.
McCullagh, P dan Nelder, JA. 1989.Generalized Linear Models: 2nd Edition.
London: Chapman and Hall.
Nur IM, Yuniarti D, Hayati MN, 2016. Penerapan Generalized Poisson Regression I untuk Mengatasi Overdispersi pada Regresi Poisson (Studi Kasus: Pemodelan Jumlah Kasus Kanker Serviks di Provinsi Kalimantan Timur). Jurnal Eksponensial. 7(1): 59-77.
Lambert D, 1992. Zero-Inflated Poisson Regression, with an Application to Deffects in Manufacturing. Technometrics, 34 (1): 1-14.
Lestari A, Purhadi, Ratna M, 2009. Pemodelan Regresi Zero-Inflated Poisson (Aplikasi pada Data Pekerja Seks Komersial di Klinik Reproduksi Putat Surabaya). Phytagoras, 5(2): 57-72.
Pateta, M. 2005. Fitting Poisson Regression Models Using the Genmod Procedure.
USA: SAS Institute Inc.
Rahayu LP. 2014. Kajian Overdispersi pada Regreasi Poisson dan Zero-Inflated Poisson untuk Beberapa Karakteristik Data [tesis]. Bogor: Institut Pertanian Bogor, Sekolah Pascasarjana.
Ricci V. 2005. Fitting distributions with R. USA: Free Software Foundation.
31
Lampiran 1. Data Variabel dan dengan
[1] -1.28207650 -0.81445416 -1.95695262 0.87130563 0.93946989 [6] 0.57674410 0.14446259 -0.27836960 1.02286695 -0.49201495 [11] -1.41910472 0.47893532 -0.41237008 -0.31007487 -1.54257424 [16] -0.43892808 0.41738214 0.56409776 -0.16054492 0.65673413 [21] -1.19968499 1.30880588 -0.21724199 -0.60324900 0.44654149 [26] 1.10534217 -0.80032527 0.80921276 1.25807414 0.13236731 [31] 1.49837669 0.75740440 -0.46810822 -0.82259298 -0.53195267 [36] -1.09152178 0.01720101 1.26841749 0.84336270 -1.75099430 [41] 0.56602989 0.64157216 -1.52357105 0.92338586 -1.61932492 [46] 1.91800756 -2.33841766 0.16536387 0.66793775 -0.34419980 [51] -0.96075279 -0.20963187 2.38131340 0.05287049 -1.42489978 [56] -0.02436916 -0.44230933 0.41611330 -0.92931855 0.92098105 [61] 1.50830156 -2.69063094 -0.45802457 0.40039043 -1.17921027 [66] 0.87067901 1.33020779 0.41025009 0.34322868 0.26938348 [71] -0.45143733 -0.01863246 0.06664027 -1.24036871 0.34889646 [76] 1.22891327 0.30132621 -2.46389336 -1.05668841 2.41888678 [81] 0.99367120 -1.14264536 -0.41158143 -0.08688385 -1.05898633 [86] 1.21628961 -0.81287982 -0.95253561 0.17275146 -1.35873197 [91] 0.10560289 -1.71103324 1.39670927 0.35717074 -2.16817654 [96] -1.49688998 -1.39080713 -0.91254826 -0.07066951 -0.43710136
[1] 0 0 26 24 18 20 0 23 0 0 0 0 23 0 0 21 0 0 0 0 28 0 0 [24] 0 20 0 0 0 0 0 0 21 0 0 0 0 22 15 0 0 0 19 0 0 0 0 [47] 21 0 0 0 0 0 24 27 0 0 0 0 0 0 0 23 0 18 0 0 0 0 0 [70] 0 28 0 17 25 0 19 0 0 0 0 0 0 0 0 16 0 23 0 16 0 0 19 [93] 25 0 20 23 16 0 0 0
32
Lampiran 2. Source Code Program R require(pscl)
require(vcd) require(lmtest) require(stats) seed<-1:500 n <-300
lambda <- 0.7 pi <- 0.1
chisquare <- NULL chisq.hit <- NULL chisq.tabel <- NULL keputusan <- NULL chisquare1 <- NULL chisq.hit1 <- NULL chisq.tabel1 <- NULL keputusan1 <- NULL
for (i in 1:length(seed)) { set.seed(seed[i])
y<- function(n, lambda, p=0.0) {
if(p>1.0 || p <0) stop("p must be in (0,1)") n.p <- ceiling(p*n)
n.pois <- n-n.p
sample( c( rpois(n.pois, lambda), rep(0,n.p) ) )
}
yi<-y(n, lambda, p=pi)
#menghitung uji khi-kuadrat untuk sebaran POISSON nl1 <- table(yi)
amatan1 <- as.numeric(names(nl1)) a1 <- length(amatan1)
pl1 <- rep(0,length(nl1)) r1 <- 0
for(m1 in amatan1) {
r1 <- r1+1
pl1[r1] <- (exp(-lambda)*lambda^m1)/factorial(m1)
33
}
npl1 <- n*pl1
chisquare1 <- (nl1 - npl1)^2/npl1 chisq.hit1[i] <- sum(chisquare1) chisq.tabel1[i] <- qchisq(0.95,a-1)
ifelse(chisq.hit1[i] < chisq.tabel1[i], keputusan1[i]
<- 1, keputusan1[i] <- 0)
persentase1 <- (sum(keputusan1)/length(keputusan1))*100 b1<-
cbind(chisq.hit1=chisq.hit1[i],panjang.amatan1=a1,chisq.t abel1=chisq.tabel1,
keputusan1=keputusan1) }
for (i in 1:length(seed)) { set.seed(seed[i])
y<- function(n, lambda, p=0.0) {
if(p>1.0 || p <0) stop("p must be in (0,1)") n.p <- ceiling(p*n)
n.pois <- n-n.p
sample( c( rpois(n.pois, lambda), rep(0,n.p) ) ) }
yi<-y(n, lambda, p=pi) xi <- rnorm(n)
#menghitung uji khi-kuadrat untuk sebaran ZIP nl <- table(yi)
amatan <- as.numeric(names(nl)) a <- length(amatan)
pl <- rep(0,length(nl)) r <- 0
for(m in amatan) {
r <- r+1
if(m==0){pl[r] <- (pi + (1-pi)*exp(-lambda))}
else {pl[r] <- ((1-pi)*exp(-
lambda)*lambda^m/factorial(m))}
}
npl <- n*pl
chisquare <- (nl - npl)^2/npl chisq.hit[i] <- sum(chisquare)
34
chisq.tabel[i] <- qchisq(0.95,a-2)
ifelse(chisq.hit[i] < chisq.tabel[i], keputusan[i] <- 1, keputusan[i] <- 0)
persentase <- (sum(keputusan)/length(keputusan))*100 b<-
cbind(chisq.hit=chisq.hit[i],panjang.amatan=a,chisq.tabel
=chisq.tabel,
keputusan=keputusan) }
B=length(seed) p0<-numeric(B) p1<-numeric(B) bd0<-numeric(B) bd1<-numeric(B) gd0<-numeric(B) gd1<-numeric(B) pvalgf<-NULL score.y<-NULL
lambdapois <- matrix(NA,nrow(hasil),ncol(hasil))
chipois.temp <-
matrix(NA,nrow=nrow(hasil),ncol=ncol(hasil)) lambdazip <- matrix(NA,nrow(hasil),ncol(hasil)) wi.zip<- matrix(NA,nrow(hasil),ncol(hasil)) mu.zip <-matrix(NA,nrow(hasil),ncol(hasil)) var.zip <-matrix(NA,nrow(hasil),ncol(hasil)) chizip.temp <-matrix(NA,nrow(hasil),ncol(hasil)) chi.pois<-NULL
rasio.chipois<-NULL chi.zip<-NULL
rasio.chizip<-NULL for(i in 1:B)
{
modelp<-glm(formula = yi ~ xi, family = poisson()) hasilp<-summary(modelp)
dugap<-hasilp$coefficients koefp<-dugap[,1]
secoefp<-dugap[,2]
pvalp<-dugap[,4]
zip<-zeroinfl(yi~xi|xi,dist="poisson",link="logit") mc<-coef(zip, model='count')
mz<-coef(zip, model='zero') hasilzip<-summary(zip)
35
koef<-hasilzip$coefficients modcount<-koef$count
modzero<-koef$zero p0[i]<-koefp[1]
p1[i]<-koefp[2]
bd0[i]<-mc[1]
bd1[i]<-mc[2]
gd0[i]<-mz[1]
gd1[i]<-mz[2]
#Pearson khi-kuadrat untuk regresi Poisson k <- 2
lambdapois<-exp(p0[i]+p1[i]*xi)
chipois.temp<-((yi-lambdapois)^2)/lambdapois chi.pois<-sum(chipois.temp)
db.pois<-nrow(hasil)-k
rasio.chipois<-chi.pois/db.pois
#Pearson khi-kuadrat untuk regresi ZIP q <- 4
lambdazip<-exp(bd0[i]+bd1[i]*xi)
wi.zip<-exp(gd0[i]+gd1[i]*xi)/(1+exp(gd0[i]+gd1[i]*xi)) mu.zip<-(1-wi.zip)*lambdazip
var.zip<-mu.zip+((wi.zip/(1-wi.zip))*(mu.zip^2)) chizip.temp<-((yi-mu.zip)^2)/var.zip
chi.zip<-sum(chizip.temp) db.zip<-nrow(hasil)-q
rasio.chizip<-chi.zip/db.zip }
rasio.chipois rasio.chizip
#Khi-Kuadrat for Poisson persentase1
#Khi-Kuadrat for ZIP persentase
waldtest(modelp) waldtest(zip)
36
Lampiran 3. Output pendugaan model regresi poisson dan ZIP untuk
Poisson
Call: glm(formula = yi ~ xi, family = poisson()) Coefficients:
(Intercept) xi 1.8209 -0.1627
Degrees of Freedom: 99 Total (i.e. Null); 98 Residual
Null Deviance: 1559
Residual Deviance: 1540 AIC: 1691 ZIP
Call:
zeroinfl(formula = yi ~ xi | xi, dist = "poisson", link
= "logit")
Count model coefficients (poisson with log link):
(Intercept) xi 3.05452 -0.01945
Zero-inflation model coefficients (binomial with logit l ink):
(Intercept) xi 0.8807 0.1975
37
Lampiran 4. Output uji wald pada regresi poisson dan ZIP untuk
Wald test POISSON Model 1: yi ~ xi Model 2: yi ~ 1
Res.Df Df F Pr(>F) 1 98 2 99 -1 19.398 2.711e-05 ***
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Wald test ZIP
Model 1: yi ~ xi | xi Model 2: yi ~ 1
Res.Df Df Chisq Pr(>Chisq) 1 96 2 98 -2 1.2809 0.5271