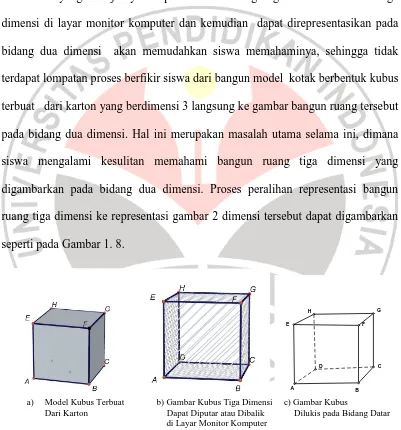
PENINGKATAN KEMAMPUAN SPASIAL DAN DISPOSISI MATEMATIS SISWA SMP DENGAN PENDEKATAN PMRI PADA PEMBELAJARAN GEOMETRI BERBANTUAN KOMPUTER.
Teks penuh
Gambar



Dokumen terkait
Sesuai dengan ketentuan Pasal 12 ayat (1) Undang-Undang Nomor 40 Tahun 2007 tentang Perseroan Terbatas menyatakan perbuatan hukum yang berkaitan dengan kepemilikan saham
Permintaan yang melebihi kapasitas akan membuat produk yang dibuat tidak akan.. selesai pada waktu yang telah disepakati, sehingga perusahaan
Terlebih tanggung jawab sosial merupakan kebaikan untuk perusahaan itu sendiri, karena hal ini tidak hanya meningkatkan reputasi perusahaan, menjalin hubungan yang baik
Desain penelitian yang digunakan merupakan penelitian deskriptif melalui metode ini peneliti ingin mengidentifikasi kualitas hidup lansia yang tinggal di PSTW
Dengan demikian aplikasi ini bisa melakukan pemrosesan nilai dengan cepat, dan memiliki pengarsipan yang baik serta bisa menghasilkan laporan seperti yang
Analisis laporan keuangan ini sangatlah penting untuk mengetahui tingkat likuiditas, solvabilitas dan rentabilitas agar perusahaan dapat melakukan tindakan tindakan atau
Berdasarkan evaluasi terhadap perhitungan PPh Pasal 21 atas karyawan pada tahun 2006 yang dipotong oleh PT Loka Mampang Indah Realty hanya sebagian kecil yang telah sesuai dengan
“Pengaruh Kepemimpinan, Komitmen Organisasi dan Motivasi Terhadap Kinerja Karyawan Bagian Penyadapan Perkebunan Nusantara IX (Persero) Balong Beji Kalitelo Kabupaten