1 . Himpunan penyelesaian adalah {(x, y, z)}. Nilai dari y + z adalah.... A . 5 B . 3 C . 2 D . -4 E . -5 Kunci : C Penyelesaian : 3x + y = 5 y 2z = 7 -3x + 2z = 12 2x + 2z = 10 x = 2 x + z = 5 2 + z = 5 z = 3 3x + y = 5 3 . 2 + y = 5 y = -1 Jadi y + z = -1 + 3 = 2
2 . Nilai dari adalah...
A . 30.900 B . 30.500 C . 16.250 D . 15.450 E . 15.250 Kunci : E Penyelesaian : 5 + 10....+ 500 = Sn1 Sn1 - Sn2 = 25.250 - 10.000 = 15.250
3 . Jumlah suku pertama dari deret aritmatika dinyatakan dengan Sn = n2 + 2n
beda dari deret itu adalah ... A . 3
B . 2 C . 1
D . -2 E . -3
Kunci : B Penyelesaian : U1 = S1 U1 = 1² + 2 = 3 U1 + U2 = S2 3 + U2 = 2² + 2 . 2 = 4 + 4 = 8 U2 = 8 - 5 = 3 b = U2 - U1 = 5 - 3 = 2
4 . Masing-masing kotak A dan B berisi 12 buah lampu pijar. Setelah diperiksa, ternyata pada kotak A terdapat 2 lampu rusak dan pada kotak B terdapat 1 lampu rusak. Dari
masing-masing kotak diambil 1 lampu pijar secara acak. Peluang terambilnya sebuah lampu pijar rusak adalah ...
A . B . C . D . E . Kunci : D Penyelesaian :
5 . Diketahui matriks A = , dan B = .
Matriks X yang memenuhi kesamaan AX = Bt (Bt = transpose B) adalah ... A . B . C . D . E . Kunci : D Penyelesaian :
6 . Diketahui f(x) = x - 4.
Nilai dari f(x2) - ( f(x)2 + 3 f(x) ) untuk x = -2 adalah .... A . -54 B . -36 C . -18 D . 6 E . 18 Kunci : C Penyelesaian : f(x) = x - 4 f(x2) - ( f(x)2 + 3 f(x) ) = (x² - 4) - ((x - 4)² + 3 (x - 4)) = (x² - 4) - (x² - 8x + 16 + 3x - 12) = x² - 4 - x² + 8x - 16 - 3x + 12 = 5x - 8 x = 2 5x - 8 = 5(-2) - 8 = -18
7 . Fungsi f : R R dan g : R R dinyatakan oleh f(x) = x + 2 dan (g f) (x) = 2x2 + 4x + 1, maka g(2x) = ... A . 2x2 + 4x + 1 B . 2x2 - 12x + 1 C . 8x2 - 8x + 1 D . 8x2 + 8x + 1 E . 4x2 - 8x + 1 Kunci : C Penyelesaian : (g f) (x) = 2x2 + 4x + 1 g (x + 2) = 2x2 + 4x + 1 g(x + 2) = 2((x + 2)² - 4x - 4)) + 4(x + 2) - 8 + 1 = 2((x + 2)² - 4(x + 2) + 8 - 4)) + 4(x + 2) - 8 + 1 = 2((x + 2)² - 4(x + 2) + 4)) + 4(x + 2) - 7 = 2(x + 2)² - 8(x + 2) + 8 + 4(x + 2) - 7 = 2(x + 2)² - 4(x + 2) + 1 g(x) = 2x² - 4x + 1 Jadi g(2x) = 2(2x)² - 4(2x) + 1 = 8x² - 8x + 1 8 . Nilai adalah ... A . B . C . D . E . Kunci : A Penyelesaian :
9 . Nilai adalah ... A . -3 B . C . -D . E . Kunci : A Penyelesaian :
10 . Penyelesaian persamaan adalah dan
Nilai adalah ... A . -6 B . -3 C . 1 D . 3 E . 6 Kunci : A Penyelesaian : 2x² + 5x - 3 = 6x + 9 2x² - x - 12 = 0 . = = -6
11 . Penyelesaian persamaan adalah p dan q.
A . 2 B . 3/2 C . 1/2 D . -3/2 E . -5/2 Kunci : B Penyelesaian : x² + 4x + 4 = 3x² -x + 6 0 = 2x² - 5x + 2 0 = (2x - 1) (x - 2) x = = q x = 2 = p p - q = 2 - = 3/2
12 . Himpunan penyelesaian dari adalah ...
A . {x|x < -2 atau x > 5} B . {x|x < -2 atau x > 3} C . {x|x < -2 atau x > 2} D . {x|x < -2 x <3} E . {x|x < -3 x <5} Kunci : B Penyelesaian : 8 + 2x - x² < x + 2 0 <x² - x - 6 x² - x - 6 > 0 (x - 3)(x + 2) > 0 x = - 2 x = 3 Penyelesaian : x < -2 dan x > 3 HP : { x|x < -2 atau x > 3; x R }
13 . Suatu suku banyak P(x) dibagi oleh (x²-1) sisanya (12x - 3) dan jika dibagi oleh (x - 2) sisanya 1.
Sisa pembagian suku banyak oleh (x² - 3x + 2) adalah ... A . 12x - 23 B . -12x + 1 C . -10x + 1 D . 24x + 1 E . 24x - 27 Kunci : A Penyelesaian : P(x) : (x² - 1) sisa (12x - 23) P(x) : (x + 1) (x - 1) sisa (12x - 23)
Berarti : P(1) = 12 - 23 = -11 P(-1) = -12 - 23 = -35 P(x) : (x - 2) sisa 1 Berarti P(2) = 1 P(x) = (x² - 3x + 2) . H(x) + sisa P(x) = (x - 1) (x - 2) . H(x) + ax + b Untuk x = 1 : P(1) = a + b = -11 Untuk x = 2 : P(2) = 2a + b = 1 -a = - 12 a = 12 a + b = -11 12 + b = -11 b = -23
Jadi sisa pembagian oleh (x² - 3x + 2) adalah = ax + b = 12x - 23 14 . Salah satu persamaan x4 + px3 + 7x² - 3x - 10 = 0 adalah 1.
Jumlah akar-akar persamaan tersebut adalah ... A . -10 B . -7 C . -5 D . 3 E . 5 Kunci : C Penyelesaian :
x4 + px3 + 7x² - 3x - 10 = 0 salah satu akarnya 1, maka : 1 + p + 7 - 3 - 10 = 0 p = 5
x1 + x2 + x3 + x4 = - b/a = -p = -5
15 . Dari segi tiga PQR, ditentukan pada sisi PQ = 7 cm, PR = 4 cm, dan QR = 5 cm. Nilai tg sudut PQR adalah ...
A . B . C . D . E . Kunci : D Penyelesaian : r² = p² + q² 2pq cos 49 = 25 + 16 - 2 . 5 . 4 cos 49 = 41 - 40 cos 40 cos = 41 - 49 = -8 cos = -
tg =
16 . Segi tiga ABC berada di dalam lingkaran dimana AB memotong pusat lingkaran, panjang BC = 30 cm. sin A = . Jari-jari lingkaran tersebut adalah ...
A . B . C . D . E . Kunci : D Penyelesaian : Jari-jari lingkaran = . AB = . =
A . B . -C . D . E . Kunci : B Penyelesaian : 18 .
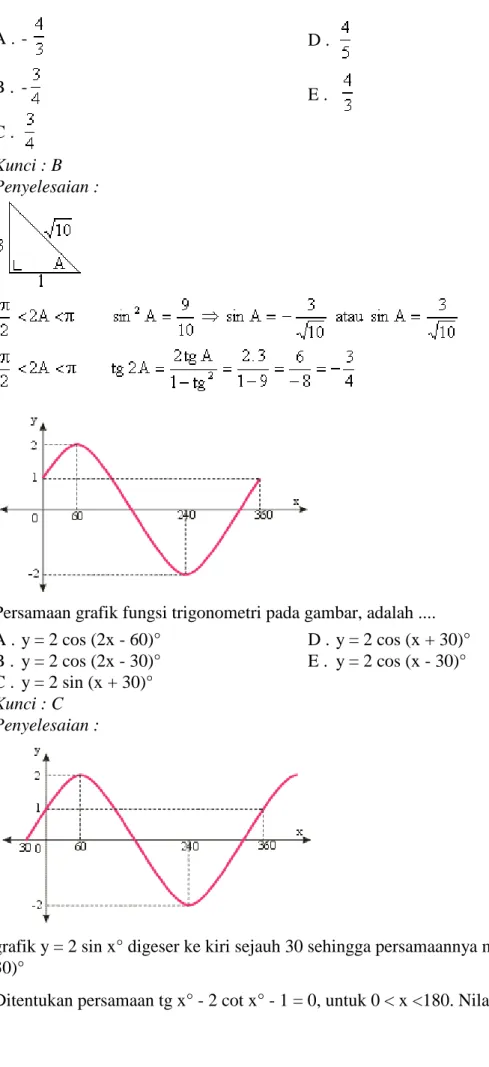
Persamaan grafik fungsi trigonometri pada gambar, adalah .... A . y = 2 cos (2x - 60)° B . y = 2 cos (2x - 30)° C . y = 2 sin (x + 30)° D . y = 2 cos (x + 30)° E . y = 2 cos (x - 30)° Kunci : C Penyelesaian :
grafik y = 2 sin x° digeser ke kiri sejauh 30 sehingga persamaannya menjadi y = 2 sin (x + 30)°
A . B . C . D . E . Kunci : B Penyelesaian : tg x° - 2 cot x° - 1 = 0 tg x° - - 1 = 0 tg²x - 2 - tg x = 0 (tg x - 2) (tg x + 1) = 0
tg x = 2 (nilai tg tidak lebih dari 1) tg x = -1
x = 135°
sin x = sin 135° =
20 . Himpunan penyelesaian dari sin 2x° > , untuk 0 x < 180 adalah ... A . { x | 15 < x < 75 } B . { x | 0 < x < 15 } C . { x | 30 < x < 150 } D . { x | x < 15 atau x > 75 } E . { x | x < 30 atau x > 150 } Kunci : A Penyelesaian : sin 2x° > sin 2x° > sin 30° 2x = 30 + K . 360 x = 15 + K . 180 x = 15 2x = 180 - 30 + K . 360 x = 75 + K . 180 x = 75 15 < x < 75
21 . Diketahui kurva dengan persamaan y = x² + px + q, p dan q konstanta. Garis y = -3x + 5 menyinggung kurva di titik dengan absis 1. adalah ....
A . 5 B . 3 C . -2 D . -3 E . -5 Kunci : E Penyelesaian : Persamaan kurva : y = x² + px + q Titik singgung : (1, 2) Gradien : m = y'
-3 = 2x + p -3 = 2 + p p = -5
22 . Turunan pertama fungsi adalah F' (x) = ....
A . B . C . D . E . Kunci : A Penyelesaian :
23 . Fungsi F(x) = (x - 1) (x² + 7x - 29) naik pada interval adalah .... A . -6 < x < 2 B . -2 < x < 6 C . x < 2 atau x > 6 D . x < -6 atau x > 2 E . x < 2 atau x > 6 Kunci : D Penyelesaian : F(x) = (x - 1) (x² + 7x - 29) Misalkan : u = x - 1, u' = 1 v = x² + 7x - 29, v' = 2x + 7 F'(x) = u'v + uv' = 1(x² + 7x - 29) + (x - 1)(2x + 7) = x² + 7x - 29 + 2x² + 7x - 2x - 7 = 3x² + 12x -36 = x² + 4x - 12 (x + 6) (x - 2) = 0 x < -6 atau x > 2
24 . Fungsi F(x) = x³ + px² + 9x - 18 mempunyai nilai stasioner x = 3. Nilai p adalah .... A . -6 B . -4 C . -3 D . 4 E . 6 Kunci : A Penyelesaian : Syarat stasioner : F'(x) = 0 3x² + 2px + 9 = 0
6p = -36 p = -6
25 . Luas daerah yang dibatasi oleh kurva y = x² + 2x - 3, sumbu X, dan garis x = 2 adalah .... A . 5 B . 4 C . 2 D . 2 E . 13 Kunci : E Penyelesaian : y = x² + 2x -3 (x + 3) (x - 1)
Lihat gambar di bawah ini :
L1 + L2 = 10 + 2 = 13
26 . Turunan pertama dari F(x) = sin³ (5 - 4x) adalah F' (x) = .... A . 12 sin³ (5 - 4x) cos (5 - 4x) B . 6 sin (5 - 4x) cos (10 - 8x) C . -3 sin² (5 - 4x) cos (5 - 4x) D . -6 sin (5-4x) sin (10 - 8x) E . -12 sin² (5-4x) sin (10 -8x) Kunci : D
Penyelesaian : F(x) = sin³ (5 - 4x)
F'(x) = 3 (-4) sin² (5 - 4x) cos (5 - 4x)
= -6 sin (5 - 4x) 2 sin (5 - 4x) cos (5 - 4x) = -6 sin (5 - 4x) sin (10 - 8x) 27 . Nilai = ... A . B . C . D . E . Kunci : B Penyelesaian : 28 . Hasil dari A . B . C . D . E . Kunci : E Penyelesaian :
A . B . C . D . E . Kunci : B Penyelesaian :
30 . Diketahui ABC dengan A(4, -1, 2), B(-2, 3, 4), dan C(7, 1, 3). Kordinat titik berat ABC tersebut adalah ...
A . (4, 1, 3) B . (5, 1, 3) C . (3, 1, 3) D . E . Kunci : C Penyelesaian :
31 . Diketahui panjang vektor pada vektor adalah 8. Nilai p = ....
A . -4 B . -3 C . 3 D . 4 E . 6 Kunci : C Penyelesaian : 64(p² + 16) = (8p + 16)² p² + 16 = (p + 2)² p² + 16 = p² + 4p + 4 4p = 12 p = 3
32 . Lingkaran x + y + 2px + 6y + 4 = 0 mempunyai jari-jari 3 dan menyinggung sumbu x. Pusat lingkaran tersebut adalah ...
A . (-2, 3) B . (2, -3) C . (2, 3) D . (3, -2) E . (-3, 2) Kunci : A Penyelesaian : x + y + 2px + 6y + 4 = 0 r = 3 9 = p² + 9 - 4 p² = 4 p = 2 Persamaan lingkaran : x + y + 4x + 6y + 4 = 0 Pusat lingkaran = (- A, B) = (- . 4, . 6) = (-2, 3)
33 . Persamaan garis singgung pada elips adalah ....
A . x + 2y - 4 = 0 B . x + 2y + 4 = 0 C . 3x + 6y - 1 = 0 D . 3x + 6y + 1 = 0 E . x - 2y - 12 = 0 Kunci : A Penyelesaian :
34 . Parabola melalui titik (3, 5), mempunyai direktris x = 1 dan sumbu simetri y = 3. Persamaannya adalah ... A . (y - 2)² = 4(x - 3) B . (y + 2)² = 4(x - 3) C . (y +3)² = 4(x + 2) D . (y - 3)² = 4(x + 2) E . (y - 3)² = 4(x - 2) Kunci : E Penyelesaian :
p = a - 1 (y - 3)² = 4p (x - a) (y - 3)² = 4(a - 1) (x - a) Melalui (3, 5) : (5 - 3)² = 4(a - 1) (3 - a) 4 = 4(3a - a² - 3 + a) 1 = -a² + 4a - 3 a² - 4a + 4 = 0 (a - 2)² = 0 a = 2 p = a - 1 = 2 - 1 = 1 Jadi persamaannya (y - 3)² = 4 (x - 2)
35 . Garis dengan persamaan y = 2x + 3 dicerminkan terhadap sumbu X kemudian diputar dengan R (0, 90°).
Persamaan bayangannya adalah ... A . x - 2y - 3 = 0 B . x + 2y - 3 = 0 C . 2x - y - 3 = 0 D . 2x + y - 3 = 0 E . 2x + y + 3 = 0 Kunci : A Penyelesaian : y = 2x + 3 x' = y y' = x
Persamaan bayangan adalah x = 2y + 3 x - 2y - 3 = 0 36 .
Perhatikan gambar kubus ABCD.EFGH. Jarak titik C dan bidang AFH = ... A . 5 B . 2 C . 4 D . 4 E . 5 Kunci : A Penyelesaian :
SRC=akar3.gif>
37 .
Perhatikan gambar kubus ABCD.EFGH. Panjang proyeksi AH pada bidang BDFH adalah ... A . 8 B . 8 C . D . 4 E . 4 Kunci : C Penyelesaian :
38 .
Bidang empat ABCD, pada gambar dengan AD tegak lurus alas, BC = 2 . Sudut antara bidang BCD dan BCA adalah , maka tan = ...
A . B . C . D . 2 E . 2 Kunci : E Penyelesaian : BP = DP = 39 .
Perhatikan gambar kubus ABCD.EFGH. Jarak titik C dan bidang AFH adalah ... A . 2 cm B . 2 cm C . 4 cm D . 4 cm E . 5 cm Kunci : D Penyelesaian :
Jarak titik C ke bidang AFH = CC' CC' = CE
= . 6 = 4
40 . Akar persamaan x² + (a + 2)x + (a + 3) = 0 adalah p dan q.
Nilai minimum dari p² + q² - pq dicapai untuk a sama dengan ... A . -1 B . -C . D . 1 E . 5 Kunci : B Penyelesaian : y = p² + q² - pq = (p + q)² - 2pq - pq = (p + q)² - 3pq = {-(a + 2)² - 3(a + 3)} = a² + 4a + 4 - 3a - 9 = a² + a - 5 Y min dicapai untuk a :