ANALISIS KESALAHAN MAHASISWA DALAM MENYE

(1)

Prosiding Seminar Nasional Matematika dan Pembelajarannya. Jurusan Matematika, FMIPA UM. 25 November 2017

ANALISIS KESALAHAN MAHASISWA DALAM

MENYELESAIKAN MASALAH PROGRAM LINEAR

DITINJAU DARI STRUKTUR BERPIKIRNYA

Dewi Sih Wilujeng

1)

_{, Subanji}

2)

_{, Swasono Rahardjo}

3)

123)

_{Universitas Negeri Malang}

dewwisihw@gmail.com

Abstrak

Penelitian ini bertujuan untuk mendeskripsikan kesalahan mahasiswa dalam menyelesaikan masalah program linear. Penelitian ini menggunakan pendekatan kualitatif dan jenis penelitian yang dilakukan adalah deskriptif. Subjek penelitian ini adalah tiga mahasiswa jurusan matematika Universitas Negeri Malang yang masing-masing berkemampuan tinggi, sedang, dan rendah. Hasil penelitian menunjukkan bahwa kesalahan mahasiswa berkemampuan tinggi yaitu comprehension sedangkan kesalahan mahasiswa berkemampuan sedang dan rendah meliputi comprehension, transformation, process skills dan encoding. Meskipun jenis kesalahan antara kemampuan sedang dan rendah sama berdasarkan prosedur Newman namun ditinjau dari struktur berpikirnya terlihat jelas bahwa mahasiswa dengan kemampuan rendah struktur berpikirnya lebih tidak lengkap dibandingkan dengan mahasiswa kemampuan sedang.

Kata kunci: Analisis Kesalahan, Masalah Program Linear, Struktur Berpikir

PENDAHULUAN

Proses berpikir siswa dalam mengonstruk dan memecahkan masalah matematika menghasilkan suatu struktur berpikir (Subanji,2016). Dalam proses belajar matematika, konstruksi struktur berpikir siswa belum tentu sesuai dengan harapan (konsep ilmiahnya). Hal tersebut dapat terjadi karena siswa melakukan kesalahan dalam mengonstruk konsep dan menyelesaikan masalah matematika. Telah banyak penelitian yang mengkaji terkait kesalahan siswa dalam matematika (Santoso, dkk, 2017; Yusof, dkk, 2015; Flagg, 2014; Egodawatte, 2011; Subanji,2011). Subanji (2016) menyatakan bahwa kesalahan yang dilakukan siswa dalam menyelesaikan masalah matematika dapat diakibatkan dari pembelajaran yang kurang bermakna.

Kesalahan dalam menyelesaikan masalah matematika juga dapat dialami oleh mahasiswa (El-Khateeb, 2016; Blanco&Garrote, 2007). Berdasarkan pengamatan dan wawancara dengan pengajar materi program linear, diketahui bahwa masih ada mahasiswa semester V yang melakukan kesalahan dalam menyelesaikan masalah program linear dengan menggunakan metode grafik. Program linear merupakan salah satu konsep yang dapat digunakan seseorang untuk menyelesaikan masalah dunia nyata (khususnya ekonomi dan bisnis) untuk mengoptimumkan (maksimum atau minimum) suatu fungsi tujuan pada sistem persamaan atau pertidaksamaan (Tan,2008). Penting bagi mahasiswa untuk dapat menerapkan konsep tersebut dengan benar, sehingga perlu untuk dikaji dan dianlisis kesalahan-kesalahan yang mereka lakukan dalam menyelesaikan masalah program linear.

(2)

dan simbol). Selanjutnya adalah tahapan Pemahaman (comprehension) mahasiswa diminta un-tuk menjelaskan maksud atau isi soal (Pemahaman kebahasaan dari masalah). Tahapan Trans-formasi (transformation),mahasiswa diminta untuk memilih prosedur atau operasi matematika yang sesuai (Transformasi dari pemahaman kebahasaan ke dalam interpretasi matematika). Ta-hapan Ketrampilan Proses (process skill), mahasiswa diminta untuk menunjukkan prosedur per-hitungan matematika secara tepat (Menjalankan Proses Matematis). Tahapan terakhir adalah pe-nulisan kesimpulan (encoding), mahasiswa diminta untuk merepresentasikan jawaban akhir se-cara tepat. Pada penelitian ini, analisis kesalahan ditinjau dari struktur berpikir mahasiswa dalam menyelesaikan masalah program linear. Melalui proses berpikir dalam menyelesaikan masalah program linear maka dapat digambarkan suatu struktur berpikir mahasiswa. Apabila struktur berpikirnya tidak sesuai dengan struktur masalah maka hal tersebut menandakan maha-siswa melakukan kesalahan.

METODE

Penelitian ini menggunakan pendekatan kualitatif dan jenis penelitian deskriptif. Subjek penelitian ini adalah tiga mahasiswa jurusan matematika Universitas Negeri Malang yang masing-masing berkemampuan tinggi, sedang, dan rendah dan memiliki struktur berpikir yang tidak sesuai dengan struktur masalah. Prosedur pengumpulan data dalam penelitian ini dilakukan melalui dua tahap. Pertama, seluruh mahasiswa dalam satu kelas diberikan soal tes program linear. Berdasarkan hasil tes tersebut, mahasiswa dikelompokkan berdasarkan kemampuan akademiknya (skor tes) selanjutnya dipilih tiga mahasiswa yang masing-masing berkemampuan tinggi, sedang, dan rendah dengan jawaban salah. Kedua, setelah didapatkan subjek kemudian dilakukan wawancara. Peneliti mengembangkan instrumen yang akan digunakan saat pengambilan data. Instrumen penelitian yang digunakan meliputi soal tes dan pedoman wawancara. Soal tes diadaptasi dari soal di buku College Mathematics for the Managerial, Life, and Social Sciences (Tan,2008). Selain itu peneliti juga mengembangkan diagram struktur masalah yang sesuai dengan soal tes. Pedoman wawancara digunakan untuk menggali informasi struktur berpikir subjek. Analisis data penelitian ini terdiri dari tiga langkah. Pertama, kondensasi data, yaitu berdasarkan hasil tes mahasiswa dikelompokkan berdasarkan tingkat kemampuan akademiknya kemudian dipilih mahasiswa masing-masing satu mahasiswa dengan jawaban salah dari setiap kategori yang selanjutnya akan diwawancarai secara mendalam. Kedua, penyajian data, yaitu berdasarkan hasil tes dan wawancara diperoleh gambaran struktur berpikirnya dalam menyelesaiakan masalah program linear yang selanjutnya disajikan dalam bentuk diagram dan tabel. Ketiga, penarikan kesimpulan, yaitu peneliti menarik kesimpulan berdasarkan data hasil kondensasi dan penyejian data terkait kesalahan mahasiswa dalam menyelesaikan masalah program linear ditinjau dari struktur berpikirnya.

HASIL DAN PEMBAHASAN

Soal tes masalah program linear yang diberikan berupa soal uraian. Dalam penelitian ini mahasiswa menyelesaiakan masalah program linear dengan menggunakan metode grafik. Berikut Gambar 1 merupakan soal tes yang diberikan.

(3)

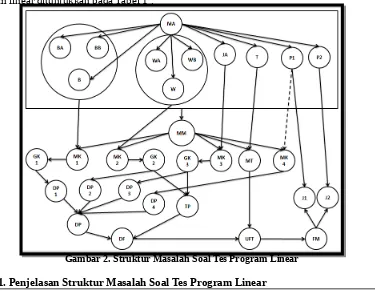
Struktur masalah soal tersebut ditunjukkan oleh Gambar 2 dan penjelasan struktur masalah program linear ditunjukkan pada Tabel 1 .

Gambar 2. Struktur Masalah Soal Tes Program Linear

Tabel 1. Penjelasan Struktur Masalah Soal Tes Program Linear

Kode Keterangan Prosedur

Newman

MA Membaca dan mengerti maksud dari setiap kata dan simbol Reading BA Memahami bahwa untuk memproduksi pot jenis A memerlukan 3 gr besi cair

Comprehensio n BB Memahami bahwa untuk memproduksi pot jenis B memerlukan 4 gr besi cair

B Memahami bahwa besi cair yang tersedia adalah 1000 gr

WA Memahami bahwa untuk memproduksi pot jenis A memerlukan waktu 6 menit WB Memahami bahwa untuk memproduksi pot jenis B memerlukan waktu 3 menit

W Memahami bahwa lama waktu yang tersedia adalah 20 jam atau 1200 menit JA Memahami bahwa pot jenis A diproduksi minimal sebanyak 150 pot per hari

T Memahami bahwa keuntungan satu pot jenis A sebesar Rp 200 dan dan pot B sebesar Rp 150

P1 Memahami pertanyaan soal yaitu banyak pot yang sebaiknya diproduksi untuk memaksimalkan keuntungan

P2 Memahami pertanyaan soal yaitu menentukan keuntungan maksimal yang diperoleh

MM Memodelkan permasalahan secara matematika dengan Memisalkan x adalah banyak pot A yang diproduksi y adalah banyak pot B yang diproduksi MK1 Memodelkan Kendala/konstrain 1 yaitu 3x+4y ≤1000 MK2 Memodelkan Kendala/ konstrain 2 yaitu

6 x

+

3 y ≤

1200

MK3 Memodelkan Kendala/ konstrain 3 yaitu x ≥150

MK4 Memodelkan Kendala/ konstrain 4 yaitu

x ≥

0

dan

y ≥

0

MT Memodelkan Fungsi tujuan 200x+150y (maksimumkan)

GK1 Menggambar grafik dari kendala 1 dengan fungsi

3 x

+

4 y

=

1000

Transformatio n GK2 Menggambar grafik dari kendala 2 dengan fungsi 6x+3y=1200

(4)

Kode Keterangan Prosedur Newman

DP3 Menentukan daerah penyelesaian dari kendala 3 DP4 Menentukan daerah penyelesaian dari kendala 4

DP Menentukan daerah penyelesaian dari kendala 1, 2, 3 dan 4 DF Diperoleh daerah feasible

TP Menentukan titik potong persamaan garis 6x+3y=1200 dan

x

=

150

Dan diperoleh x = 150, y =100 Process Skills

UFT Menentukan nilai fungsi tujuan dengan ketiga titik pojok pada daerah feasible FM Mendapatkan nilai fungsi maksimal yang berada pada titik (150,100)

J1 Menuliskan bahwa perusahaan memproduksi pot A sebanyak 150 unit dan pot

B sebanyak 100 unit untuk memperoleh keuntungan maksimal _Encoding J2 Menuliskan bahwa perusahaan akan memperoleh keuntungan maksimum

sebesar Rp 45000

Berikut Gambar 3. hasil tes penyelesaian masalah program linear mahasiswa berkemampuan tinggi (ST)

Gambar 3. Hasil Tes Program Linear ST

Berdasarkan Gambar 3 diketahui bahwa ST dapat memodelkan semua permasalahan secara lengkap dan tepat namun ST tidak menuliskan pemisalahan dari variabel x dan y yang ia gunakan. ST dapat menggambarkan grafik dan menentukan daerah feasible dari permasalahan tersebut. ST juga dapat menentukan nilai fungsi maksimal dari ketiga titik pojok pada daerah

(5)

Gambar 4. Struktur Berpikir ST dalam Menyelesaikan Masalah Program Linear

Gambar 4 merupakan struktur berpikir ST berdasarkan hasil tes yang ditunjukkan pada Gambar 3. Berdasarkan Gambar 4 diketahui bahwa struktur berpikir ST hampir lengkap. Skema yang belum muncul adalah penulisan pemisalan variabel x dan y yang ia gunakan.

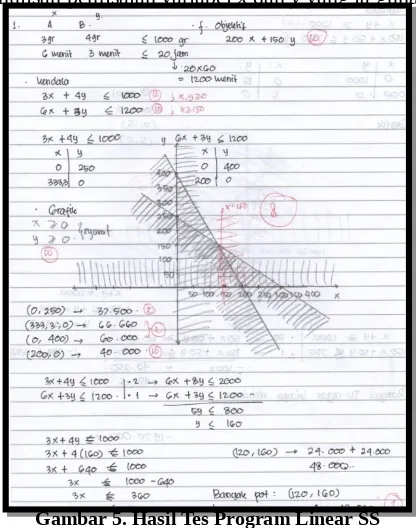
Gambar 5. Hasil Tes Program Linear SS

Gambar 5 merupakan hasil pekerjaan SS dalam mengerjakan masalah program linear. Berdasarkan gambar tersebut dapat terlihat bahwa SS melakukan kesalahan sebagai berikut. SS tidak memahami maksud dari kalimat “pot jenis A diproduksi minimal sebanyak 150 pot per hari” sehingga ia kesulitan dalam memodelkan permasalahan tersebut. SS dapat

menggambarkan grafik dengan benar berdasarkan pemodelan kendala yang ia tuliskan. Karena SS tidak memodelkan kendala 4 sehingga ia menjadi salah dalam menentukan daerah feasible

(6)

mengakibatkan SS tidak dapat menjawab dengan benar permasalahan program linear tersebut.

Gambar 6. Struktur Berpikir SS dalam Menyelesaikan Masalah Program Linear

(7)

Gambar 7. Hasil Tes SR

Gambar 7 merupakan hasil pekerjaan SR dalam mengerjakan masalah program linear. Berdasarkan gambar tersebut nampak bahwa SR melakukan kesalahan di awal pekerjaannya. SR salah dalam memisalkan variabel x dan y. SR memaknai variabel sebagai suatu benda yaitu pot. Padahal seharusnya ia memahami bahwa variabel merupakan simbol yang mewakili himpunan semestanya yaitu bilangan real. Variabel x dan y yang digunakan dalam masalah ini mewakili banyaknya pot A dan pot B . Seperti halnya dengan SS, SR juga tidak memahami maksud dari kalimat “pot jenis A diproduksi minimal sebanyak 150 pot per hari” dan tidak memahami bahwa banyaknya pot yang diproduksi perusahaan tersebut tidak mungkin bernilai negatif (kendala 4 dan 5). Akibatnya SR tidak dapat memodelkan kendala 3,4, dan 5. Meskipun SR telah memodelkan dengan benar kendala 1 dan 2 namun ia tidak menggambarkan grafik dan menentukan daerah penyelesaian dari kendala tersebut. SR hanya mengingat bahwa ia pasti harus menentukan titik potong, sehingga dengan percaya diri SR menentukan titik potong dari persamaan garis dari kendala 1 dan 2. Padahal SR seharusnya menggambarkan grafik dari setiap kendala pada masalah dan menentukan daerah feasible kemudian menentukan semua titik pojok pada daerah feasible. Pemahaman SR yang tidak lengkap terhadap masalah mngakibatkan ia salah dalam tahapan pengerjaan selanjutnya (penentuan titik potong, nilai fungsi tujuan dengan ketiga titik pojoj serta penarikan kesimpulan). Namun berdasarkan hasil tes terlihat bahwa SR sebenarnya sudah dapat melakukan prosedur penentuan titik potong dengan tepat.

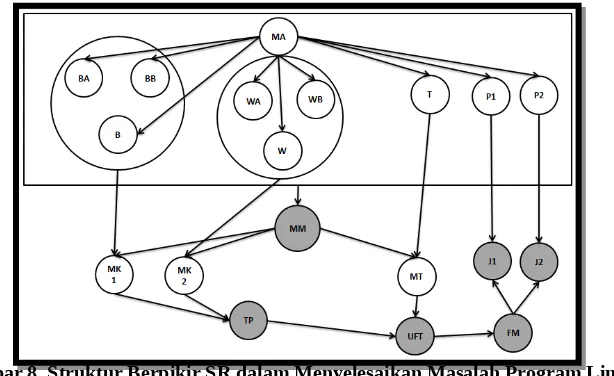
Gambar 8. Struktur Berpikir SR dalam Menyelesaikan Masalah Program Linear

Gambar 8 merupakan struktur berpikir SR dalam mengerjakan masalah program linear yang didasarkan pada hasil pekerjaannya pada Gambar 7. Berdasarkan Gambar 8 dan struktur masalah soal tes (Gambar 2) terlihat bahwa masih banyak skema pada struktur berpikir SR yang masih belum muncul dan terdapat beberapa yang masih mengalami kesalahan.

Berikut tabel 2 menjelaskan perbedaan kesalahan yang dialami ketiga subjek berdasarkan stuktur berpikir dan tahapan analisis kesalahan Newman.

Tabel 2. Penjelasan Struktur Berpikir ST,SS, dan SR dalam Menyelesaikan Masalah Program Linear

MA MA MA Membaca dan mengerti maksud dari setiap kata dan simbol Reading BA BA BA Memahami bahwa untuk memproduksi pot jenis A

memerlukan 3 gr besi cair Comprehension

(8)

Kode

ST KodeSS KodeSR Keterangan ProsedurNewman

WA WA WA Memahami bahwa untuk memproduksi pot jenis A memerlukan waktu 6 menit

WB WB WB Memahami bahwa untuk memproduksi pot jenis B memerlukan waktu 3 menit

W W W Memahami bahwa lama waktu yang tersedia adalah 20 jam atau 1200 menit

JA JA JA Memahami bahwa pot jenis A diproduksi minimal sebanyak 150 pot per hari

T T T Memahami bahwa keuntungan satu pot jenis A sebesar Rp 200 dan dan pot B sebesar Rp 150

P1 P1 P1 Memahami pertanyaan soal yaitu banyak pot yang sebaiknya diproduksi untuk memaksimalkan keuntungan P2 P2 P2 Memahami pertanyaan soal yaitu menentukan keuntungan

maksimal yang diperoleh

MM MM MM Memodelkan permasalahan secara matematika dengan Memisalkan x adalah banyak pot A yang diproduksi y adalah banyak pot B yang diproduksi MK1 MK1 MK1 Memodelkan Kendala/konstrain 1 yaitu

3x+4y ≤1000

MK2 MK2 MK2 Memodelkan Kendala/ konstrain 2 yaitu 6x+3y ≤1200

MK3 MK3 MK3 Memodelkan Kendala/ konstrain 3 yaitu

x ≥

150

MK4 MK4 MK4 Memodelkan Kendala/ konstrain 4 yaitu x ≥0 dan

y ≥

0

MT MT MT Memodelkan Fungsi tujuan 200x+150y (maksimumkan)

GK1 GK1 GK1 Menggambar grafik dari kendala 1 dengan fungsi

3 x

+

4 y

=

1000

Transformation GK2 GK2 GK2 Menggambar grafik dari kendala 2 dengan fungsi

6 x

+

3 y

=

1200

GK3 GK3 GK3 Menggambar grafik dari kendala 3 dengan fungsi

x

=

150

DP1 DP1 DP1 Menentukan daerah penyelesaian dari kendala 1 DP2 DP2 DP2 Menentukan daerah penyelesaian dari kendala 2 DP3 DP3 DP3 Menentukan daerah penyelesaian dari kendala 3 DP4 DP4 DP4 Menentukan daerah penyelesaian dari kendala 4

DP DP DP Menentukan daerah penyelesaian dari kendala 1, 2, 3 dan 4 DF DF DF Diperoleh daerah feasible

TP TP TP Menentukan titik potong persamaan garis

6 x

+

3 y

=

1200

dan

x

=

150

Dan diperoleh x = 150, y =100

Process Skills UFT UFT UFT Menentukan nilai fungsi tujuan dengan ketiga titik pojok

pada daerah feasible

FM FM FM Mendapatkan nilai fungsi maksimal yang berada pada titik (150,100)

J1 J1 J1 Menuliskan bahwa perusahaan memproduksi pot A sebanyak 150 unit dan pot B sebanyak 100 unit untuk

memperoleh keuntungan maksimal Encoding

(9)

Berdasarkan Tabel 2 terlihat perbedaan kesalahan yang dialami ketiga subjek. ST hanya tidak menuliskan (belum memunculkan skema) pemisalan variabel yang ia gunakan sehingga ia men-galami kesalahan pada saat comprehension. Dibandingkan dengan ST, struktur berpikir SS terli-hat masih banyak skema yang belum muncul dan mengalami kesalahan. SS mengalami kesala-han pada semua prosedur Newman kecuali reading. Berdasarkan prosedur Newman, SR men-galami kesalahan yang sama seperti SS. Hal ini didukung oleh Egodawatte (2011:100) yang me-nemukan bahwa siswa mengalami kesulitan menuliskan soal cerita ke dalam ekspresi aljabar dengan benar. Selanjutnya Flagg (2014:137) menyatakan ketika siswa dapat memahami maksud soal,tetapi mereka tidak memahami konsep matematika. Hal ini yang menyebabkan ketidak-mampuan seseorang mengubah soal ke dalam kalimat matematika. Ditinjau dari struktur berpikirnya, dapat terlihat struktur berpikir SR jauh lebih tidak lengkap dibandingkan dengan SS.

Secara keseluruhan mahasiswa sudah dapat menuliskan kendala ke dalam bentuk kali-mat kali-matekali-matika dengan benar. Namun masih ada mahasiswa yang tidak dapat memahami mak-sud dari kendala “pot jenis A diproduksi minimal sebanyak 150 pot per hari” ataupun tidak da-pat mengubah kendala tersebut ke dalam kalimat matematika sehingga pada hasil pengerjaan-nya mereka seoalah mengabaikan kendala tersebut. Hal ini juga didukung oleh temuan White (1995) yaitu siswa kesulitan dalam mengekspresikan kendala pada masalah program linear.

KESIMPULAN DAN SARAN

Berdasarkan pemaparan pada hasil penelitian dan pembahasan diperoleh kesimpulan sebagai berikut: Kesalahan mahasiswa berkemampuan tinggi ditinjau dari struktur berpikirnya dan prosedur Newman yaitu comprehension. Terdapat skema yang tidak muncul yaitu memisalkan variabel yang ia gunakan. Kesalahan mahasiswa berkemampuan sedang meliputi 1)

comprehension, yaitu tidak memahami pernyataan “pot jenis A diproduksi minimal sebanyak 150 pot per hari” sehingga ia tidak dapat memodelkan pernyataan tersebut, 2)transformation, yaitu tidak menggambarkan grafik dan daerah penyelesaian dari kendala 3 serta salah dalam menentukan daerah feasible, 3)process skills, yaitu salah dalam menentukan titik potong dari dua garis serta salah dalam menentukan nilai fungsi maksimalnya, dan 4)encoding, yaitu kesalahan dalam menyatakan jawaban yang sesuai dengan pertanyaan soal. Sementara itu, kesalahan mahasiswa berkemampuan rendah meliputi 1) comprehension, yaitu salah dalam memisalkan variabel, tidak memahami pernyataan “pot jenis A diproduksi minimal sebanyak 150 pot per hari” sehingga ia tidak dapat memodelkan pernyataan tersebut dan tidak memahami bahwa perusahaan tersebut pasti memproduksi kedua jenis pot, 2)transformation, yaitu tidak menggambarkan grafik dari semua kendala, 3)process skills, yaitu salah dalam menentukan titik potong dari dua garis serta salah dalam menentukan nilai fungsi tujuan dengan ketiga titik pojok pada daerah feasible, dan 4) encoding, yaitu kesalahan dalam menyatakan jawaban yang sesuai dengan pertanyaan soal. Berdasarkan simpulan tersebut, maka saran yang direkomendasi adalah sebaiknya pendidik harus lebih memperhatikan pada struktur bahasa, pemahaman soal, dan pemodelan matematika. Sehingga mahasiswa tidak hanya ditekankan pada proses menghitungnya saja.

DAFTAR RUJUKAN

Blanco, L J & Garrote, M.2007. Difficulties in Learning Inequalities in Students of the First Year of Pre-University Education in Spain. Eurasia Journal of Mathematics, Science & Technology Education. 3(3): 221-229

Egodawatte, G.2011. Secondary School Students’ Misconceptions in Algebra. Tesis tidak diterbitkan. Toronto: University of Toronto

(10)

Flagg, V L. 2014. Newman’s Error Analysis and Mathematical Language: Diagnosing Mathematical Errors on Word Problems Made by 4th Graders who Attend a Low Ses School. Disertasi tidak diterbitkan. Macon, GA :Mercer University

Santoso, D. A., Farid, A., & Ulum, B. 2017. Error Analysis Of Students Working About Word Problem Of Linear Program With NEA Procedure. Journal of Physics: Conference Series, (online) 855(1):012043,( http://iopscience.iop.org/article/10.1088/1742-6596/855/1/012043/pdf), diakses 3 November 2017

Subanji. 2011. Teori Berpikir Pseudo Penalaran Kovariasional. Malang: UM PRESS Subanji. 2016. Teori Defragmentasi Struktur Berpikir Dalam Mengonstruksi Konsep dan

Pemecahan Masalah. Malang: UM PRESS

Tan, S.T. 2008. College Mathematics for the Managerial, Life, and Social Sciences. Australia: Thomson.

White, A L. 2005. Active Mathematics In Classrooms: Finding Out Why Children Make Mistakes- And Then Doing Something to Help Them. Square One: Primary Journal of the Mathematical Association of New South Wales, (Online),

ANALISIS KESALAHAN MAHASISWA DALAM MENYE