GEOMETRI
TERJEMAHAN BUKU “THE CONCEPTUAL ROOTS OF
MATHEMATIC” CHAPTER 2 GEOMETRY
Oleh :
DWI WINARNI (S851202016)
HAFIDH JAUHARI (S851202025)
SRI UTOMO BUDI (S851202046)
WAHYU ASTUTI BUDI (S851202054)
PROGRAM STUDI PENDIDIKAN MATEMATIKA PROGRAM PASCA SARJANA
UNIVERSITAS SEBELAS MARET SURAKARTA
Geometri
2.1 Euclid
2.2 Kelima Postulat 2.3 Geometri Non-Euclide
2.4 Geometry Formal dan Geometri Fisika 2.5 Kendala Konseptual
2.6 Geometri yang mana? 2.7 Teori Grup
2.8 Geometri Pythagoras mempunyai metrik yang lebih baik 2.9 Desargues
2.10 Kesimpulan
2.1 Euclid
Jika bukan Logisme, lalu apa ?
dari sudut pandang formalis, kita mungkin bertanya-tanya apakah ini adalah hal yang Euclid lakukan ?
Di luar logika formal, pendekatan aksiomatik semangat Euclid jauh lebih dalam dibanding Hilbert. Fisikawan sering menggunakan dalam mekanika Newton, Teori Relativitas Khusus Teori Relativitas Umum, atau mekanika kuantum, dalam hal aksioma, yang terpenting asumsi teori yang bersangkutan, tetapi mengambil banyak lagi untuk diberikan. Ini adalah prosedur yang sempurna tidak hanya untuk memperkenalkan subjek untukanak sekolah, tetapi juga untuk mengidentifikasi bagi para profesional. Untuk sebagian besar, dalam mengidentifikasi atau menjelaskan geometri Euclidean kebutuhan kita adalah membedakan ciri khas dari geometri yang dari orang lain cukup mungkin digunakan sebagai gantinya. Bahwa mendefinisikan setiap baris perintah dan kontinu tidak normal dipertanyakan, dan hanya mengacaukan komunikasi untuk mengantisipasi pertanyaan sehingga tidak ada lagi pertanyaan yang muncul. Singkatnya tidak hanya cerdas, namun perlunya komunikasi. Sejumlah penjelasan sering tidak beralasan, tetapi obfuscatory. Euclid tidak harus dikritik karena kurangnya ketelitian, tapi dipuji karena rasa relevansinya.
2.2 Kelima Postulat
Program Plato adalah prematur. Tapi geometri axiomatized,adalah program yang sedang dilakukan oleh Eudoxus dan Euclid, sehingga berhasil menurunkan semua dari lima aksioma atau postulat yang dalam bahasa Yunani (aitemata), bersama dengan beberapa pengertian umum,(Koinai ennoiai), murni yang bersifat logis, misalnya
bahwa jika a sama dengan b dan c adalah sama dengan b, maka a sama dengan c. Lima postulat Euclid adalah sebagai berikut:
1. Garis lurus dapat digambar dari (sembarang ) titik sampai sembarang titik lainnya.
2. Ujung garis lurus dapat dilanjutkan terus sebagai garis lurus
3. Lingkaran dapat digambar dari sembarang titik pusat dan dengan jari-jari berbeda.
5. Apabila garis lurus terpotong menjadi dua garis lurus, menyudut di sisi dalam pada kedua garis pada sisi yang sama daripada dua sudut yang sejajar, jika diteruskan sampai ke (titik) tak terhingga, akan berpotongan pada sisi dimana sudutnya lebih kecil dibandingkan sudut yang terbentuk dari dua garis.
Ini umumnya diambil untuk mengekspresikan kebenaran. Hal ini agak mengejutkan, dalam tiga postulat yang pertama tidak benar-benar proposisi sama sekali, tapi instruksi yang diwujudkan dalam infinitif, dan terakhir terlalu kompleks menjadi jelas-tidak ada manusia yang terbatas bisa melihat hal itu benar,karena tidak ada manusia yang terbatas dapat melihat jauh tanpa batas untuk memastikan bahwa dua baris sebenarnya tidak memenuhi dalam setiap kasus. Banyak formulasi lain yang telah ditunjukkan dalam kelima postulat , baik dalam dunia modern maupun kuno. dengan harapan mereka menjadi jelas lebih mandiri. Di antara mereka kita harus perhatikan:
a) Melalui sebuah titik yang bukan pada garis lurus yang diberikan, hanya satu garis saja yang dapat ditarik dan tak pernah bertemu garis yang diberikan Playfair
b) Jumlah sudut sebuah segitiga sama dengan dua sudut siku-siku
c) Mengingat angka, angka lain adalah mungkin yang mirip dengan angka yang diberikan dan setiap ukuran apa pun. (Wallis)
d) Ada dua segitiga yang tidak sama dengan sudut yang sama. (Saccheri dan mungkin juga Plato)
e) Dalam segitiga siku-siku, kuadrat sisi miring sama dengan jumlah kuadrat di dua sisi lainnya. (Pythagoras)
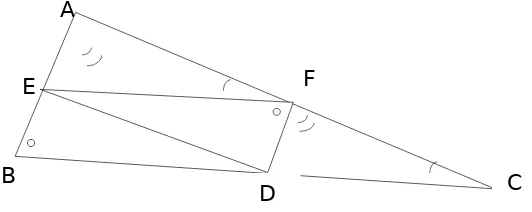
Aksioma Wallis '(c), kita dapat membuktikan bahwa jumlah dari sudut segitiga sama dengan dua sudut yang lain, seperti pada Gambar 2.2.1.
Argumen lain, ditampilkan pada Gambar 2.2.2, menunjukkan bahwa Teorema 'Pythagoras dibuktikan melalui segitiga serupa.
Kita mungkin bertanya, atas nama generasi anak sekolah yang memiliki temuan dengan "kincir angin" bukti Euclid dari proposisi-nya 1.47, mengapa Euclid lebih banyak disukai karena banyak bukti nya lebih rumit. Jawabannya terletak pada asumsi terakhir dalam bukti diberikan pada Gambar 2.2.2, dan akibat adanya besaran dapat dibandingkan kesulitan hal itu sebagai konsekuensi dari teorema Pythagoras.
Argumen Meno menunjukkan bahwa diagonal persegi memiliki panjang √2. √2 adalah salah satu penemuan pengikut Pythagoras
Gambar 2.2.1menunjukkan Bukti dari Wallis: Perhatikan segitiga ABC ∆AFE ≈∆ABC dan setengah ukuran linier. Selanjutnya
AF
AB=ACAE=BCFE=12
Sehingga : AF = FB dan AE = EC. BD = DC, dan karena FE = BD = DC.
Kemudian (argumen beberapa ditinggalkan di sini) ∆CED ≈ ∆CAB, sehingga ED = (1/2) AB = FB.
Jadi dalam ∆EFD dan ∆BDF ,EF = BD, DE = FB, dan FD adalah umum. Jadi ∆EFD = ∆BDF, dan ∆DEF = ∆FBD.
F
B E
A
.
Tapi
∠
BCA
=
∠
FEA dan
∠
CBA
=
∠
CEA
dan
∠
ABC
=
∠
FBD
Jadi
∠
ABC
+
∠
BCA
+
∠
CBA
=
180
0, tidak dapat dinyatakan sebagai rasio dua nilai , dengan pendekatan segitiga serupa, dinyatakan bahwa perbandingan sisi dalam segitiga adalah sama. Euclid , dalam teorinya tentang proporsi, hampir diantisipasi oleh Dedekind 's definisi bilangan real, tapi dalam eksposisi geometris nya secara teknis lebih rumit tetapi secara konseptual kurang pendekatan segitiga.
Sebuah pernyataan dalam Gorgias menunjukkan bahwa Plato memikirkan tentang segitiga serupa dalam dasar geometri. Dalam Gorgias 508a5-7 ia membedakan "Geometris" dari kesetaraan "aritmetika", yang pertama secara proporsional, sedangkan yang terakhir adalah kesetaraan yang ketat. Aristoteles mengambil perbedaan dalam Nicomachean Ethics, dan Politik, dan membuat dasar penafsiran tentang distributif
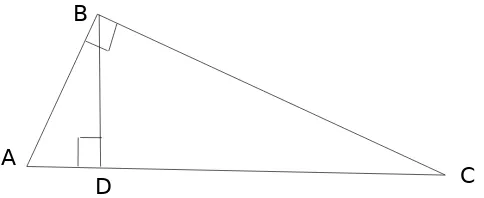
Gambar 2.2.2 Bukti Pythagoras dengan Segitiga serupa: Lihat ∆ABC siku-siku di B. Tarik garis tegak lurus dari B keAC pada D. Kemudian ∆ADB ≈∆ABC dan ∆BDC≈ ∆ABC.
Jadi
AD AB=ACAB
(AD + DC) AC =. AB2 + BC2.
DC BC=BCAC
AC2 = AB2 + BC2
Jadi (AD + DC) AC = AB2 + BC2 dan AC2 = AB2 + BC2
(Kami mengasumsikan bahwa jumlah sudut dalam ∆ = 180 °, danADAB )
D B
A
Plato dan Aristoteles melihat bahwa ada universilitas tentang konsep keadilan.dan keadilan memerlukan perlakuan yang sama,serta menghindari implikasi. Plato menganjurkan untuk memperlakukan perlakuan yang sama,namun juga memperlakukan kasus yang berbeda.Geometri Kesetaraan dimunculkan oleh Plato dan Aristoteles untuk menyatukan prinsip dasar dimana harus ada kesamaan dari semua perbedaan yang ada,dengan membenahi dari keadaan yang sebenarnya . Setiap orang harus diberikan bagian mereka, kata Aristoteles, tapi harus adil dan sebanding dengan kondisi yang ada(Axia)dengan jasa mereka, dan ini tergantung pada keadaan. Inilah perbedaan dari argumen egalitarian fifthcentury Athena, dan memiliki konsekuensi penting bagi politik berpikir dalam dunia kuno.
Bukti dari teorema Pythagoras adalah puncak dari buku pertama Euclid , dan kami telah menunjukkan bagaimana hal itu dapat dibuktikan bukan hanya dari kelima postulat Euclid sendiri tetapi dari proposisi Wallis tentang segitiga serupa. Itu wajar untuk dipertanyakan apakah itu pada gilirannya dapat dibuktikan dari teorema Pythagoras 'diambil sebagai kebenaran. Bahkan itu bisa. Hal ini paling mudah untuk menunjukkan aksioma Saccheri itu (d), bahwa, diberikan Proposisi Pythagoras, harus ada dua segitiga yang samabentuk tetapi ukuran yang berbeda.
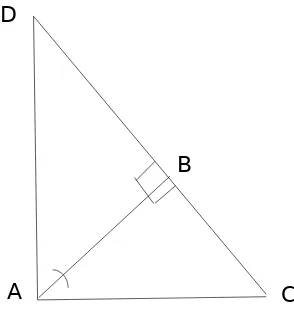
Gambar 2.2.3 Bukti Saccheri dari Pythagoras:
siku siku dan BA=CB, D pada perpanjanganCB se hingga BD=CB
B
A D
.
Selanjutnya ∆ABC = ∆ABD, maka AD = AC dan
∠
BDA
=
∠
BCA
, dan,∆ABC = ∆DBA,
∠
BAC
=
∠
ADB
. Menurut Pythagoras : AC2 = BA2 + CB2= 2CB2
AD2 = BA2 + BD2
= 2BD2 = 2CB2
AC2 + AD2 = 4CB2 = CD2.
Jadi
∠
CAD
adalah sudut yang siku-siku, dan ∆ABC≈∆CAD2.3 Geometri Non-Euclid
Geometri hiperbolik pertama kali ditemukan oleh Bolyai, seorang Hungaria, dan juga oleh Lobachevsky sendiri, seorang Rusia, pada awal abad 19. Alih-alih dari titik yang tidak berada di sebuah garis yang sudah ada dan hanya satu garis yang dapat ditarik berjajar pada garis tersebut seperti dalil Playfair, mereka berdalil bahwa dari sebuah titik tanpa garis lebih dari satu yang tak terbatas jumlahnya, garis-garis dapat ditarik secara parallel pada garis yang sudah ada. Kemudian di abad 19, Riemann mengubah dalil kesejajaran tersebut dengan cara yang berbeda, bahwa tidak hanya satu garis paralel yang dapat ditarik. Hal ini tentunya memerlukan beberapa modifikasi aksioma lain, akan tapi modifikasi tersebut menghasilkan geometri non-euclid lain yang konsisten yaitu geometri ‘eliptik.’
kesejajaran garis bujur sebenarnya tidak sejajar/parallel sama sekali sebab bukan merupakan garis lurus tapi lebih kepada lingkaran).
Jika kita menganggap oktan jeruk atau lingkar segitiga permukaan bumi ditandai dengan garis meridian Greenwich, Ekuator dan Garis bujur barat 90°, maka akan terlihat mempunyai sudut yang tepat di tiap puncak, sehingga jumlah sudutnya bertambah menjadi tiga sudut yang tepat 270° alih-alih hanya dua sudut yang tepat 180°. Segitiga yang lebih kecil akan memiliki jumlah sudut mendekati 180° yang akan terpelihara saat segitiganya mengecil. Jika kita tahu seberapa besar sudut-sudutnya, tentu saja kita dapat mengetahui sisi-sisi pastinya. Hanya segitiga-segitiga lingkar (poligon) yang tiap sudutnya 90° lah yang sisi-sisinya seperempat dari keliling lingkaran besar. Hal ini menjelaskan tesis Wallis-Saccheri bahwa dalam Geometri Non-Euclid tidak ada segitiga yang sama dengan ukuran yang berbeda. Terlihat dengan mudah pada kasus oktan tersebut bahwa dalil Pythagoras jauh dari benar, dalam hal ini h = a = b.
Dengan cara yang sama, keliling lingkaran yang ditarik pada permukaan bola kurang dari 2πr. Jika Kutub Utara diambil sebagai pusat dan beradius seperempat lingkaran besar, Equator yang panjangnya bukan 2π × ((1/4) × (lingkaran besar)) tapi hanya (lingkaran besar) harus ditarik, dan rasio keliling pada jari-jari lingkaran ini bukan 2π tapi 4. Permukaan bola mempunyai lengkungan positif, jadi jika dua bidang ortogonal memotong satu sama lain di sepanjang garis yang tegak lurus terhadap permukaan, tiap bidang memotong permukaan dalam kurva yang sisi cekungnya berada dalam arah yang sama seperti yang lainnya. Sehingga hasil yang menegaskan lengkungan permukaan tersebut adalah positif dimana pun sisi cekung menghadap.
Geometri eliptik
Tidak ada kesejajaran (disimbolkan E0)
lebih dari 180° (disimbolkan >)
h2>a2+b2 (disimbolkan P<)
Keliling ¿2π r2 (disimbolkan O<)
Permukaan bidang bola
Kurva/lengkungan positif (disimbolkan C+)
Tabel 2.3.1
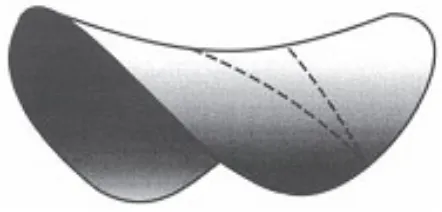
Permukaan dengan lengkungan negatif lebih sulit untuk digambarkan. Permukaan pelana atau puncak pegunungan adalah contohnya. Pada permukaan seperti itu, keliling lingkaran lebih dari 2π kali jari-jari, sehubungan dengan kuadrat sisi miring yang lebih besar daripada jumlah kuadrat dua sisi lainnya. Cukup sulit untuk melihat bahwa jumlah sudut pada sebuah segitiga kurang dari 180°, tapi bila kita mempertimbangkan betapa sangat kecilnya perbedaan pada jalan setapak di puncak gunung dapat membawa ke tujuan yang berbeda-beda, kita dapat memahami bahwa segitiga dapat mempunyai sudut-sudut bertambah kurang dari 180°. Jika bentuk segitiga ini dibawa ke batasnya akan muncul area minimum sebuah segitiga. Hal ini sekali lagi menunjukkan betapa dalil Wallis-Saccheri gagal untuk geometri Non-Euclid. Hal ini juga menarik perhatian kita ke bentuk lain geometri Non-Euclid.
Gambar 2.3.1 Pelana yang menunjukkan segitiga dengan sudut-sudut mendekati nol, tapi masih mencakup area penting
Geometri Non-Euclid masih tetap asing. Kita dapat memahami dan menggambarkannya pada tingkat tertentu, tapi ada hal-hal yang tidak lazim dan mungkin tidak ramah bahkan setelah bersentuhan sekian lamanya. Tapi, bukan berarti geometri ini tidak konsisten, bahkan fakta menunjukkan kekonsistenannya. Memang mudah mengatakan sebuah geometri itu konsisten, tapi sulit untuk membuktikannya. Saccheri menyimpulkan bahwa sistem yang ia telaah sangat tidak masuk akal untuk menjadi tidak konsisten, dan siapa yang membuktikan ia salah? Felix Klein akhirnya membuktikannya dengan alat ‘bukti relativitas konsistensi’ yang mana telah menjadi hal penting dalam dasar-dasar matematika. Klein membuat model geometri hiperbolik dalam geometri Euclid. Ia mempertimbangkan bagian dari bidang Euclidean yaitu bagian dalam lingkaran yang diberikan dan menggambarkan kembali bagian dalam lingkaran tersebut dengan cara tertentu. Ia menunjukkan bahwa aksioma geometri hiperbolik sangat meyakinkan dalam deskripsi baru tersebut. Klein kemudian berkata bahwa jika memang tidak konsisten maka akan ada inkonsistensi yang saling berhubungan pada bidang Euclid dan geometrinya akan menjadi tidak konsisten juga. Jadi kenyataan berbalik, geometri hiperbolik adalah konsisten sehubungan dengan geometri Euclid.
satunya adalah sebuah aksioma atau yang mengikuti dari satu atau lebih garis-garis sebelumnya dari simpulan. Sehingga garis-garis terakhir membentuk A Λ ¬A.
Sekarang mari kita pikirkan urutan-bukti ini bukan sebagai rangkaian perumusan yang seimbang tentang titik dan garis dalam geometri eliptik, tapi sebagai perumusan imbang tentang titik-titik dan lingkaran besar dalam sub ruang dua dimensi dari geometri tiga dimensi Euclid (ditunjukkan oleh sisi kanan tabel). Apa yang sebelumnya adalah aksioma dalam interpretasi eliptik sekarang menjadi dalil sebenarnya dan dapat dibuktikan dari aksioma geometri tiga dimensi Euclid yang (ditunjukkan oleh garis-garis tambahan di atas rangkaian-bukti pada sisi kanan). Sehingga, kita dapat memenuhi urutan-bukti tersebut untuk membuktikannya dari aksioma geometri tiga dimensi Euclid
Geometri hiperbolik
Bolyai, Lobachevsky
Lebih dari satu kesejajaran/paralel (disimbolkan E+)
kurang dari 180° (disimbolkan <)
h2>a2+b2 (disimbolkan P>)
Keliling ¿2πr2 (disimbolkan O>)
Permukaan pelana atau puncak pegunungan
Kurva/lengkungan negatif (disimbolkan C)
Tabel 2.3.2
Bila bukti dalam geometri eliptik berakhir pada perumusan A Λ ¬A, bukti dalam geometri tiga dimensi Euclid akan berakhir pada perumusan A’ Λ ¬A’, yang sebenarnya A Λ ¬A juga, sehingga geometri tiga dimensi Euclid akan menjadi tidak konsisten juga. Jadi, bila geometri tiga dimensi Euclid tidak konsisten maka geometri eliptik juga tidak konsisten, sebaliknya jika geometri tiga dimensi Euclid konsisten maka geometri eliptik juga konsisten.
Geometri bidang eliptik
……extra
……extra
……extra
A Λ ¬A
Diterjemahkan
Diterjemahkan
Diterjemahkan
Diterjemahkan
Diterjemahkan
………..
………..
………..
………..
A’ Λ ¬A’
Tabel 2.3.3
Geometri Non-Euclid telah mempertahankan kekonsistenannya. Dan dengan ketiadaan inkonsitensi mutlak, para ahli matematika telah dibuat bekerja keras untuk memberikan alasan/dasar, dan mengeluarkan mereka dari alasan-alasan.
2.4 Geometri Formal dan Geometri Fisika
Bila bukan Pembuktian Sendiri, lalu apa?
Mungkin saja Formalisme
Bila kita menganggap geometri hanya sebagai sebuah sistem formal yang simpulan-simpulannya mengikuti premis-premis atau aksioma-aksioma, kita tidak akan terlalu khawatir tentang arti kata atau interpretasi istilah-istilah geometri. Yang dipikirkan hanyalah hal-hal yang bersifat sintaksis yang diberikan melalui aturan-aturan penyimpulan dan aksioma. Dengan demikian dapat dikatakan bahwa aksioma Euclid teorema Pyhtagoras yang telah diberikan seperti berikut ini;
Euclid ├ Pythagoras
Ini hanyalah turunan formal dalam logika urutan-pertama dan dapat dengan setara dinyatakan oleh teorema deduksi
├ Euclid Pythagoras
(1) Klub melaksanakan acara makan siang secara berkala dan dihadiri hanya oleh anggota
(2) Setiap anggota klub harus bertemu dengan setiap anggota paling sedikit satu kali dan tidak boleh lebih dari sekali pada satu acara makan siang klub
(3) Daftar anggota klub yang dipilih oleh Sekretaris untuk menghadiri dua acara makan siang tidak pernah seluruhnya berbeda, paling tidak satu anggota berada di keduanya.
(4) Ketua, Bendahara dan Sekretaris adalah anggota klub yang hadir di makan siang yang pertama kali dan paling sedikit tiga anggota klub hadir pada makan siang selanjutnya. Aturan-aturan tersebut terlihat jelas tapi pada pengujian lebih lanjut terkesan mencurigakan, terutama dalam konteks pembahasan geometri, dan memang begitu adanya. Ada aksioma sudut yang luas dari geometri proyektif yang dapat dihitung dengan ‘anggota’ yang melakukan tugas sebagai sebuah titik, ‘makan siang’ untuk sebuah garis serta ‘menghadiri’ untuk kejadian suatu bentuk. Secara formal, jika kita berkonsentrasi pada stuktur sintaksis dari sistim yang secara implisit ditegaskan dengan aksioma-aksioma ini dan tidak mempertimbangkan interpretasinya atau isi substansinya, maka tidak akan ada bedanya antara aksioma geometri proyektif tersebut dan aturan klub makan siang. Dengan begitu, studi ini dapat disebut geometri sistim formal, tentu saja dengan cara yang sama dapat disebut lunchologi (ilmu makan siang), dan dengan mengingat kritik Plato bilakah lunchologi adalah ilmu yang cukup berharga untuk dipelajari oleh orang dewasa. Karakteristik geometri formal telah gagal untuk menangkap apa sebenarnya geometri itu. Klub makan siang tidak ada kaitannya dengan (geometrein) yaitu pengukuran bumi/alam/bentuk.
Jika bukan Formalisme, lalu apa?
Mungkin Empirisme Formal (atau Protagoreanisme)
mempertimbangkan aksioma geometri tapi juga aksioma yang berhubungan dengan interpretasi fisika. Interpretasi fisika standar ini seperti sinar tipis (garis tipis yang memanjang dari sebuah titik yang tak terbatas dalam satu arah) yang dinyatakan sebagai sebagai garis lurus.
Alih-alih mengutarakan dalil aksioma geometri Euclid, kita harus memikirkan hubungan aksioma-aksioma tersebut dengan interpretasi fisika and menanyakan apakah kenyataannya benar. Riemann menanyakan pertanyaan ini dan bukannya mempertimbangkan usulan Pythagoras, yang disingkat Pyth, tapi ╞╞apakah sudut segitiganya bertambah hingga 180°. Ia mengukur sudut-sudut tersebut di puncak tiga pegunungan yang jauh terpisah, serta menemukan bahwa menurut batasan-batasan ketepatan pengamatan, sudut-sudut tersebut ada. Dengan ini, geometri dapat dianggap sebagai ilmu pengetahuan empiris dan dapat diuji dengan cara yang sama dengan setiap teori fisika yang ada, sejauh ini sudah benar. Protagoras diberlakukan kembali.
Poincare mengembangkan argumen ini untuk mendapatkan kesimpulan yang berlawanan. Karena tesis yang diperlakukan untuk pengujian empiris ini bukan hanya kumpulan aksioma Euclid tapi juga hubungan aksioma tersebut dengan interpretasi fisika tertentu, kita dapat selalu berpegang pada aksioma Euclid, sehingga kita dapat membuat penyesuaian yang cocok terhadap interpretasinya. Garis-garis tipis yang memanjang dari sebuah titik yang sudah ada diperbolehkan untuk tidak menyatakan garis-garis lurus. Bahkan jika kemudian sudut segitiga yang sudah diukur itu tidak bertambah hingga 180°, kebenaran geometri Euclid diragukan.
geometri dan lainnya. Hempel menegaskan bahwa alasan/dasar tersebut ada. Ia berpendapat bahwa kita harus mempertimbangkan tidak hanya pada kesederhanaan geometri tapi juga gabungan geometri dan interpretasi fisikanya. Jika ada dua interpretasi fisika PhysInt1 and PhysInt2, maka kadang Euclid +
PhysInt1 lebih rumit daripada Riemann + PhysInt2, sehingga kita memiliki alasan rasional untuk kebelakangnya, walaupun yang sebelumnya mungkin lebih konsisten dengan fakta observasinya. Hempel menyarankan agar kita memilih kombinasi yang paling baik, yaitu yang paling sederhana, dari gabungan aksioma geometris dan interpretasi fisika. Apabila kita berfikir tentang interpretasi fisika yang berbeda PhysInt1, PhysInt2, PhysInt3, interpretasi semantik aksioma dan teorema geometri yang berbeda harus digunakan, yang dinyatakan dengan I=.
Jadi kita punya PhysInt1 ╞ Pyth
dimana Pyth adalah usulan/dalil Pythagoras, tapi PhysInt2 ╞ ¬ Pyth
dan PhysInt3 ╞ ¬ Pyth,
sehingga walaupun ada interpretasi, katakan saja PhysInt1, yang mana Pyth adalah benar, namun demikian kita lebih memikirkan interpretasi yang lain, contohnya PhysInt2, yang mana Pyth adalah salah. Jika misalnya PhysInt2 adalah satu bahwa garis lurus dianggap menjadi garis tipis yang memanjang dari sebuah titik, maka meskipun percobaan Riemann memperkuat tesis =, bahwa sudut-sudut segitiga bertambah jadi 180° dengan batasan ketepatan yang tersedia pada zamannya. Teori yang telah diperkuat oleh observasi sekarang telah ada, berdasarkan pada segitiga-segitiga, ditetapkan dengan garis-garis tipis pada titik, yang mempunyai sudut-sudut yang bertambah hingga lebih dari 180°.
Jadi PhysInt2 ╞ ¬ =,
dan, dengan cara yang sama, PhysInt3 ╞ ¬Pyth.
fisika rumit yang menafsirkan garis-garis dengan cara —PhysInt1—bahwa
PhysInt1 ╞ Pyth tapi harus membayar harga atas seluruh hipotesis ad hoc dan sejumlah asumsi yang tak masuk akal.
2.5 Kendala Konseptual
Ekposisi Hempel jelas indah, argumennya memiliki banyak hal yang menyakinkan, dan kesimpulannya telah diterima secara luas, sehingga merupakan ortodoksi saat ini. Meskipun demikian argumennya terbuka terhadap kritik. Meskipun ia sepenuhnya benar dalam bersikeras, sebagaimana terhadap Poincaré, bahwa kita perlu mempertimbangkan bukan hanya geometri secara sendiri tetapi kombinasi geometri dengan interpretasi, yang berkonsentrasi terlalu eksklusif pada interpretasi fisik, dan tidak mempertimbangkan kendala lain yang beroperasi. Pertama terdapat perbedaan yang nyata antara geometri dan fisika yang menimbulkan beberapa tekanan konseptual yang harus diakui. Kedua, ada hubungan antara beberapa konsep dasar geometri dan konsep-konsep lain di luar geometri yang sangat membatasi berbagai kemungkinan interpretasi.
Ada pembagian kerja antara geometri dan fisika. Fisika terkait dengan sebab dan akibat, dan berusaha untuk memberikan penjelasan fenomena dalam hal hukum alam. Tidak ada bagian dari fungsi geometri untuk melakukan ini, tapi untuk memberikan skema acuan dan deskripsi yang memungkinkan proposisi tentang dunia yang akan dirumuskan dan dibahas, dan untuk menemukan hubungan antara perbedaan proposisi semacam ini. Memang seperti fungsi, geometri tunduk pada berbagai persyaratan. Jadi inefficacy penyebab ruang dan waktu berikut dari yang geometri tidak sendiri terlibat dalam memberikan penjelasan kausal, dan pada gilirannya memaksakan kondisi homogenitas dan isotropi yang konsekuensi geometris.
bicara tentang, materi itu geometri atau bukan, fisika atau bukan yang merupakan kendala yang konseptual.
Titik dan garis tidak hanya sekedar implisit didefinisikan oleh aksioma namun juga ada definisi lain yang terkait. Mari kita amati secara sistematis. - Pertama. beberapa perbedaan mereological dan kategoris:
i. sebuah titik tidak memiliki bagian (Pythagoras)
ii. sebuah titik memiliki posisi tapi bukan besaran, sedangkan
iii. Sebuah garis lurus memiliki bagian
a) garis lurus memiliki posisi dan arah
b) garis lurus memiliki panjang namun tidak mimiliki luas
- Kedua, memiliki perbedaan topologi antara titik dan garis (tidak selalu lurus):
i. sebuah titik tidak dapat memiliki batas, namun dapat sebagai batas
ii. sebuah garis dapat memiliki titik sebagai batas, dan dapat menjadi batas permukaan
iii. permukaan dapat memiliki garis sebagai batas, dan dapat menjadi batas dari volume.
Lebih umum, ada sejumlah definisi yang mungkin dari garis lurus. - Ketiga. Sebuah garis lurus:
i. adalah jarak terpendek antara dua titik
ii. adalah panjang tak berluas
iii. adalah bagian dari sinar cahaya
iv. terlihat lurus
v. tidak memiliki belokan
vi. terletak merata pada dirinya sendiri
vii. adalah sumbu rotasi pada dimensi 3
viii. adalah persimpangan dari dua bangun datar
ix. adalah bahwa yang tengah akhir sampul
dalam Topologi antara lain pemahaman tentang garis lurus. Garis lurus memiliki beberapa pemahaman /konsep:
Menurut ilmu geodesi dan teori relativitas garis lurus adalah jarak terpendek antara dua titik.
Dua garis benar benar lurus jika keduanya akan cocok pas bersama sama dalam satu posisi. Ini sesuai definisi Euclid.
Dalam bahasa modern garis lurus adalah yang memiliki simetri translasi bersama, sebagai sumbu rotasi.
Dari beberapa pemahaman kiranya masuk akal dalam mendefinisiskan garis lurus tetap konseptual pada kurva satu dimensi yang kontinu, tak terbatas, simetri dan rotasinya tak terbatas.
2.6. Geometri Yang Mana?
Jika penjelasan murni formalis dan empiris geometri ditolak, kita dihadapkan sekali lagi dengan pertanyaan "geometri mana yang sebaiknya kita pilih?". Sebagai formalis, kita tidak bisa mengatakan bahwa semua geometri setara, sehingga selama semua geometri konsisten ataupun tidak, kita tetap harus membuat pilihan. Kita harus mengakui bahwa sebagai kaum formalis, kita bebas untuk membuat pilihan yang kita inginkan, dan bahwa kebanyakan yang dapat dipelajari dari studi, geometri dianggap semata-mata sebagai suatu sistem formal. Seperti yang empirisis lakukan, kita tidak bisa membiarkan seluruh pengalaman indrawi memutuskan antara formal yang berbeda sistem, meskipun putusan pengalaman indrawi memberikan geometri plus interpretasi adalah berat, dan tanpa modifikasi kita tidak bisa terus mempertahankan geometri bersama dengan interpretasi yang berkembang dalam menghadapi bukti-bukti empiris. Oleh karena itu, kita harus bertanya pada diri kita sendiri, bagaimana kita harus memilih geometri, dengan mempertimbangkan bahwa ada banyak geometri yang konsisten untuk dipilih.
Tak satu pun dari geometri ini yang meyakinkan dan tidak satupun dari mereka yang tidak konsisten. Namun, dimungkinkan bahwa salah satu dari mereka mungkin yang paling cocok untuk beberapa tujuan tertentu. Akan tetapi, kita dapat memberikan bimbingan rasional untuk pengguna umum pada kekuatan dari beberapa fitur yang tercantum dalam tabel, dan menyimpulkan bahwa Geometri Euclidean adalah Best Buy (Yang Bagus Dibeli) dan ini untuk beberapa alasan.
dalam perumusan Saccheri-Wallis, yang pada dasarnya memberi geometri Euclidean memiliki dua kemungkinan gambaran bentuk yang sama tetapi ukuran yang berbeda.
Pertimbangan yang sama berlaku dengan jumlah paralel. Geometri Euclidean memiliki tepat satu atau lebih spesifik daripada geometri hiperbolik, yang memiliki tak terhingga banyaknya, meskipun dalam kasus ini tidak lebih spesifik daripada geometri elliptik yang telah ada. Tetapi yang terakhir terdapat kecacatan ketika digunakan untuk membangun sistem referensi. Di permukaan bumi, garis bujur berpotongan di kutub: 10 ° E dan 90° N adalah sama dengan 10 ° W dan 90°N.. Kami ingin ada sebuah korespondensi satu-satu antara titik-titik dalam ruang dan set koordinat. Jika ini menjadi begitu, kita perlu "paralelisme topologi", adalah bahwa garis-garis (tidak selalu lurus) didefinisikan oleh semua koordinat kecuali satu yang konstan harus selalu ada dan tidak pernah berpotongan. Sejauh argumen kita ini berjalan, ini tidak harus garis lurus, kita dapat memiliki koordinat lengkung dan tidak menuntut paralelisme geometris. Tetapi penggunaan garis lurus dalam geometri eliptik dikesampingkan, dan penggunaan garis lurus paralel Euclidean sangat disarankan.
2.7 Teori Grup
geometri yang tidak terpengaruh oleh grup translasi, rotasi dan refleksi, yang karena itu disebut grup Euclidean. Grup Euclidean menuntun kita bahwa geometri Euclidean pada satu presentasi, bersama grup Lorentz membawa kita ke Teori Khusus Relativity. Sebuah skeptis tentang keutamaan geometri Euclidean mungkin mengizinkan kewajaran pendekatan grup teoritis, tetapi muncul pertanyaan penting:
“Apa yang begitu baik tentang Grup Euclidean?”
tertentu akan dibedakan dari grup Euclidean. Walaupun hanya ada satu jenis operator rotasi di sekitar beberapa pusat rotasi-itu adalah salah satu variabel parameter radius rotasi sedangkan grup Euclidean, meskipun memiliki dua macam operator berkelanjutan, tidak memiliki parameter lebih lanjut untuk menentukan. Ada jarak antara satu jenis kesederhanaan dan lainnya, tapi kita bisa berpendapat baik secara abstrak bahwa grup Euclidean adalah grup paling sederhana yang melindungi gerakan rigid, dan sebagai masalah praktek bahwa dalam hal translasi dan rotasi sederhana yang menafsirkan gerakan bahan benda di sekitar kita. Kita bisa salah. Bisa jadi bahwa apa yang kita anggap sebagai translasi yang benar-benar rotasi sekitar pusat rotasi sangat jauh. Tapi kami menganggap mereka, tentu cukup, seperti translasi, dan sekali lagi kita membedakan translasi dari rotasi, kami berkomitmen untuk grup Euclidean, dan sehingga juga berlaku untuk geometri Euclidean.
2.8. Geometri Pythagoras mempunyai Metrik yang lebih baik
Dalil Pythagoras, kita perhatikan, dapat mengambil sebagai aksioma bukan sebuah Teorema yang harus dibuktikan, dan dalam banyak hal adalah lebihkarakteristik fitur dari geometri yang
dihasilkan dari rumit Euclidpostulat paralel. Dan kita bisa berdebat
untuk geometri Pythagoraspada nilai proposisi karakteristiknya, P =, menjadi
lebih baik dari proposisi karakteristik, P< dan P>, dari hiperbolikberbentuk bulat panjang dan geometri masing-masing. Untuk P = adalah masuk akalsederhana aturan untuk menentukan ukuran keseluruhan untuk pemisahan mencakuplebih dari satu dimensi.
peduli dengan menetapkan metrik.Meskipun geometri berkembang
sejak Mesir menggunakannya untukmengukur bidang tanah sepanjang Sungai Nil, dan telah lebihbersangkutan dengan bentuk dibandingkan dengan ukuran absolut, hanya diPythagoras geometri bahwa keduanya berbeda, dan di dalamnyaukuran relatif tetap penting. Beberapa geometri geometri-proyektif,misalnya-tidak memperhitungkan ukuran, tapi kebanyakan, dan sejauh
sebagai geometri diterapkan, seperti dalam menata lapangan tenis, itu Adalah penting bahwa nomor harus dialihkan ke segmen lurus garis dan kurva. Hebat matematika sering mendefinisikan metrik pada ruang sebagai fungsi d dari produk Cartesian ruang dengan dirinya menjadi nonnegatif yang bilangan real.
tunduk pada empat kondisi:
(i) d (x, y) = 0 jika dan hanya jika x = y (ii) d (x, y)> 0
(iii) d (x, y) = d (y, x)
(iv) d (x, z) ≥ d (x, y) + d (y, z).
Kita secara alami mungkin bertanya mengapa kondisi ini harus dikenakan pada fungsi metrik. (i) mengungkapkan pikiran bahwa titik tidak memiliki
panjang (besar) 20 dan bahwa setiap dua titik berbeda mendefinisikan lurus garis dan ruas garis itu memiliki panjang. (ii) mengungkapkan berpikir bahwa titik adalah batas minimal dari line.21 (iii) menyatakan mengira bahwa panjang adalah isotropik. (iv) adalah segitiga yang disebut ketidakadilan, dan menetapkan bahwa jarak antara dua titik tidak bisa lebih dari jumlah jarak antara masing-masing dan beberapa titik ketiga, tetapi mungkin kurang. Ini menetapkan sebuah batas atas untuk besaran komposit,
fungsi dari (x - y) 2 atau (x - y) 4, atau (x - y) 6, dll ..., dan jika kita ingin mengambil kasus n-dimensi, maka aditif yang paling alami, selalu non-negatif, fungsi simetris adalah
d = (x1 - y1) 2 + (x2 - y2) 2 + ... + (xn - yn) 2.
Dari tiga geometri yang ditawarkan, karena itu kita harus memilih
salah satu yang memiliki P =, yaitu geometri Euclid, di mana saja teorema Pythagoras berlaku, dan menghasilkan sebuah persamaan yang tepat antara persegi pada sisi miring dan jumlah dari kuadrat pada dua sisi lain dari sebuah segitiga siku-siku. Sudut yang tepat bukan hanya sudut tertentu, tetapi
mengekspresikan kemerdekaan dari dimensi yang berbeda. Bahasa Yunani untuk 'persegi panjang' adalah (orthogonios), dari mana 'ortogonal' kata
datang. Orthogonality sering menyatakan kemerdekaan, terutama dalam analisis Fourier, dimana komponen periodik dari fungsi yang berbeda yang diwakili oleh berbeda dimensi, dan teorema Parseval menyatakan di Hilbert spasi analog dekat teorema Pythagoras. Dalam mekanika kuantum, seperti yang kita bergerak dari mekanika gelombang Schrödinger untuk itu Heisenberg representasi matriks, kami menetapkan toko besar dengan matriks diagonal pada yang produk dari dua vektor keluar sebagai jumlah kuadrat, sehingga lagi membayar upeti kepada eminensia pra-dari Pythagoras memerintah. (Tapi kita harus mencatat bahwa analogi ini tidak tepat. Dalam kuantum mekanik kita berurusan dengan matriks Hermitian, yang beroperasi pada kompleks vektor dan konjugasi mereka, namun analogi ini dekat cukup untuk menjadi sugestif.)
Dengan cara yang sedikit berbeda, geometri Euclidean memfasilitasi penggunaan aturan jajaran genjang untuk peracikan perpindahan di berbeda arah, dan
karenanya, kecepatan percepatan dan gaya juga. Namun, jika dalam geometri eliptik saya mulai karena berada di Kutub Utara, pergi 1/4 x (lingkaran besar) Selatan, putar 90 ° dan pergi 1/4 × (a lingkaran besar) Timur, putar 90 ° dan pergi 1/4 x (lingkaran besar) Utara, putar
90 ° dan pergi 1/4 x (lingkaran besar) Selatan, aku tidak akan berakhir di mana Saya mulai. Urutan di mana saya melakukan perpindahan tidak komutatif,
Jelas bahwa argumen ini, seperti yang dari dua sebelumnya bagian, bukan
deduktif. Tidak ada inkonsistensi dalam seandainya bahwa fungsi jarak diberikan oleh
atau oleh
atau ..., atau dalam memiliki bentuk tergantung pada ukuran, maupun dalam tidak memiliki topologi paralel. Jelas juga bahwa argumen ini tidak induktif. Sama, mereka tidak hanya menyebarkan sebuah sewenang-wenang konvensi. Mereka adalah argumen rasional, meskipun tidak deduktif bukan yang induktif. Hal ini rasional untuk mencari kesederhanaan yang lebih besar, lebih besar umum dan penyatuan yang lebih besar, dan ini argumen menarik
pertimbangan-pertimbangan.
2.9 Desargues
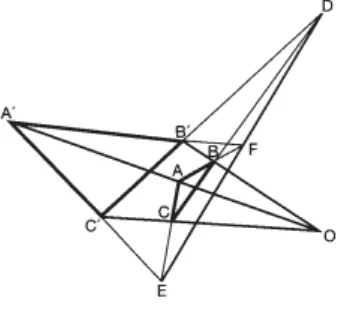
Kami telah menemukan sejumlah cara yang berbeda di mana aksioma geometri yang dapat dibenarkan. Ada satu satu lebih lanjut yang tidak bisa disebut bantuan dari aksioma Euclid, tetapi tersedia untuk pesawat projective geometri, dan sangat penting di tempat lain dalam matematika. Dalam pesawat, yang dua dimensi, geometri proyektif "Desargues ' Teorema "bukan sebuah teorema tetapi harus didalilkan sebagai tambahan aksioma. Desargues 'Teorema menyatakan bahwa jika dua segitiga yang terpusat
perspektif, mereka secara aksial perspektif, yaitu, jika AA ', BB', 'CC yang bersamaan (di O), maka jika D adalah pada SM dan 'B'C, dan E adalah pada CA dan C'A ', dan F adalah pada BA dan B'A', D, E dan F adalah collinear. Teorema Desargues 'bukan teorema dalam dua dimensi. Sana adalah
mudah terbukti dengan memperhatikan pesawat yang berbeda pada baris yang bersangkutan harus masuk Teorema Desargues 'demikian menawarkan suatu kriteria lebih lanjut dari matematika kebenaran. Jika kita menganggap bahwa yang lain aksioma pesawat proyektif geometri adalah P1, P2, P3, P4, dan teorema
Desargues 'adalah D5,
kemudian P1, P2, P3, P4¬├ D5
tapi P1, P2, P3, P4, P6, P7, P8? D5
dimana P1, P2, P3, P4, P6, P7, P8 adalah generalisasi alamiah dari P1, P2, P3, P4.
Gambar 2.9.1 Teorema Desargue, jika AA, BB', CC 'adalah konkuren (di O), maka jika D adalah pada SM dan 'B'C, dan E adalah pada CA dan C'A ', dan F
adalah pada BA dan B'A', D, E dan F adalah collinear.
Tidak semua generalisasi adalah generalisasi alam, tapi jelas 3-dimensi geometri proyektif adalah generalisasi alami 2-dimensi projective geometri, dan fakta bahwa 'Desargues
2.10 Kesimpulan
Yang kami? survei geometri menghasilkan gambaran yang lebih kompleks dari baik formalis atau empiris telah seharusnya. Kamipilihan geometri dan interpretas i geometris istilah tidak sewenang-wenang, tetapi dipandu oleh enam berbagai jenis pertimbangan:
1. Ada hubungan konseptual antara geometris dan lainnya
konsep yang membatasi penerapan istilah-istilah seperti 'titik', 'line', atau 'pesawat, dan membawa kita untuk mengadopsi beberapa proposisisebagai benar dan untuk menolak orang lain sebagai palsu.
2. Sebagai antara satu geometri dan lain, lebih rasional untuk memilih yang pertama adalah yang lebih spesifik. Geometri Euclid adalah lebih spesifik dari baik geometri hiperbolik atau elips karena
2.9.2 Gambar Teorema Desargue dalam tiga dimensi ternyata sepenuhnya pada persimpangan dari berbagai bidang: karena 'BB dan 'CC berpotongan di O, garis-garis BB'O dan CC'O adalah coplanar, dan titik B, B ', O, C, C' semua co-planar, dan sehingga BB 'dan CC' harus berpotongan, di D. Lalu D
adalah co-planar dengan B, B ', C, C', dan begitu juga di setiap pesawat yang mencakup SM, dan sebagainya di ABC, dan ada di setiap pesawat
yang mencakup 'B'C, dan sehingga dalam A'B'C '. Dengan alasan yang sama persis, karena 'CC dan 'AA berpotongan di O,
adalah co-planar dengan C, C ', A, A' dan begitu juga di setiap pesawat yang mencakup CA, sehingga dalam ABC, dan ada di setiap pesawat yang mencakup 'C'A, sehingga dalam A'B'C '. Sekali lagi, dengan penalaran persis sama, karena AA 'dan 'BB berpotongan di O, garis-garis AA'O dan BB'O adalah co-planar, sehingga titik A, A ', O, B, B' semua co-co-planar, dan jadi 'AA dan 'BB harus berpotongan, di F, katakanlah. Maka F adalah co-planar dengan A, A ', B, B' dan begitu juga di setiap pesawat yang mencakup BA, sehingga dalam ABC, dan ada di setiap pesawat yang mencakup A'B ', sehingga dalam
A'B'C '. Jadi D, E dan F adalah semua baik ABC dan 'A'B'C dan sehingga di garis umum untuk dua pesawat.
(a) kelengkungan adalah persis nol, sedangkan mereka adalah baik setiap konstan negatif nomor (hiperbolik) atau positif konstan nomor (elips); (b) sudut segitiga dalam geometri Euclidean menambahkan hingga persis 180 ° sedangkan dalam geometri hiperbolik itu hanyalah kurang dari, dan dalam geometri elips itu hanyalah lebih dari 180 °.
(C) persegi pada sisi miring adalah persis sama dengan jumlah dari kotak pada dua sisi lain dari sebuah segitiga siku-siku,
sedangkan pada geometri lain, sekali lagi, hanya ada sebuah pertidaksamaan, tidak kesetaraan sebuah;
(D) rasio dari keliling lingkaran adalah persis di 2p Geometri Euclidean, tetapi hanya 2p> di hiperbolik, dan <2p di berbentuk bulat panjang, geometri.
3. Sebaliknya, geometri Euclid adalah lebih fleksibel daripada hiperbolik dan geometri berbentuk bulat panjang, dalam ukuran angka tidak ditentukan dengan bentuk mereka, dan tidak ada unit tetap panjang atau daerah dalam Euclidean geometri. Geometri Euclid adalah skala-invarian dan metrically
amorf. Dalam memilih geometri Euclidean, kita tidak melakukan diri pilihan lain, yang dengan demikian dibiarkan terbuka. Geometri Euclidean dengan demikian menyediakan cocok back-kain untuk fisika atau skema jelas lain, dalam hal ini tidak menduduki lebih dulu jawaban yang mereka dapat berikan kepada
mengakomodasi berbagai schemata jelas lain, maka geometri Euclidean adalah yang menonjol setidaknya kita dapat memiliki. Tetapi untuk menerima pilihan ini adalah memilih peran tertentu untuk geometri, dan bukan diajukan
di geometrodynamics, di mana skema penjelasan tunggal yang terintegrasi adalah sought.23
4. Kita bisa melihat geometri tidak axiomatically tetapi kelompok-secara teoritis; dalam hal bahwa kelompok Euclidean dipilih sebagai yang paling dasar,
sebanyak seperti yang dihasilkan oleh non-sepele yang paling sederhana diskrit kelompok, kelompok siklik sederhana terus menerus dan berkesinambungan sederhana seri kelompok. Ada alasan epistemologis dan praktis baik mengapa berkomunikasi agen yang menempati lokasi yang berbeda dalam ruang pada satu waktu harus melampirkan pentingnya untuk fitur yang invarian dalam kelompok Euclidean transformasi.
5. Sebuah kebutuhan metrik untuk memenuhi beberapa kondisi jika ingin menjadi koheren. Jika ada lebih dari satu dimensi, beberapa simetris
fungsi yang dibutuhkan untuk menambahkan jarak dalam arah yang independen. Aturan Pythagoras adalah yang paling sederhana yang memenuhi kondisi. 6. Sebuah geometri, atau bahkan setiap teori matematika, mungkin
tertanam dalam teori lain yang merupakan generalisasi alami