cakul
fi5080
by
khbasar;
sem1
2010-2011
Bab 5
Bilangan dan Fungsi Kompleks
Pada BAB ini dibahas mengenai konsep-konsep bilangan dan variabel kom-pleks serta penggunaannya dalam penyelesaian persoalan fisika.
5.1
Bagian Real dan Imajiner
Bilangan kompleks terdiri dari dua bagian yaitu bagian real dan bagian ima-jiner. Misalnya bilangan kompleks yang dinyatakan dengan 5+3imaka angka 5 merupakan bagian real sedangkan angka 3 disebut bagian imajiner dari bi-langan kompleks tersebut. Dalam penulisan bibi-langan kompleks i = √−1 atau i2 = −1. Perlu diperhatikan bahwa bagian imajiner suatu bilangan
kompleks bukanlah imajiner.
Bilangan kompleks dapat dinyatakan sebagai pasangan antara bagian real dan bagian imajinernya. Jadi misalnya 5 + 3idapat dituliskan sebagai (5,3).
5.2
Bidang Kompleks
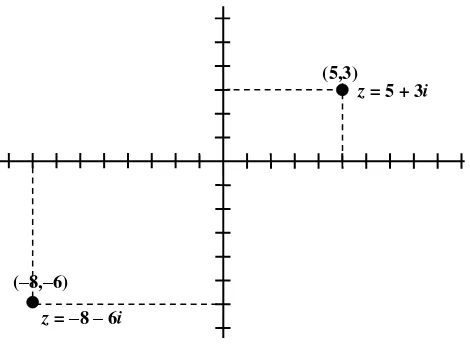
Karena bilangan kompleks biasa dituliskan dalam bentuk pasangan bilang-an sebagaimbilang-ana pasbilang-angbilang-an titik dalam sistem koordinat xy, maka sebuah bilangan kompleks dapat juga digambarkan sebagai titik dalam bidang kom-pleks. Bidang kompleks sering disebut diagram Argand. Sumbu mendatar (sumbu x) menggambarkan bagian real sedangkan sumbu tegak (sumbu y) menggambarkan bagian imajiner sebagaimana ditunjukkan dalam Gambar 5.1. Ini mirip dengan representasi titik dalam sistem koordinat kartesian.
Sebagaimana diketahui bahwa suatu titik dalam bidang xy juga dapat dinyatakan dalam ungkapan polar, maka bilangan kompleks juga dapat di-repesentasikan dalam bentuk polar yaitu (r, θ). Hubungan antara x dan y
z = 5 + 3i (5,3)
z = −−−−8 −−−− 6i
(−−−−8,−−−−6)
Gambar 5.1: Bidang kompleks.
dengan r danθ adalah
x=rcosθ y=rsinθ
Jadi suatu bilangan kompleksz dapat dinyatakan dalam representasi
z=x+iy=r(cosθ+isinθ) =reiθ (5.1)
r dinamakan modulus atau nilai mutlak dariz danθ(dalam radian) disebut sudut dari z.
5.3
Aljabar Kompleks
Menjadikan bentuk
x
+
iy
Setiap bilangan kompleks dapat dinyatakan dalam bentukx+iy.
Contoh 1
cakul
5.3 Aljabar Kompleks 95
Contoh 2
Konjugat kompleks (
Complex conjugate
)
Konjugat dari suatu bilangan kompleks z = x+iy dinyatakan dengan ¯z =
x−iy. Konjugat dari suatu bilangan kompleks diperoleh dengan mengalikan bagian imajinernya dengan −1.
Contoh
Nilai mutlak (modulus) dari suatu bilangan kompleks z = x+ iy meng-gambarkan jarak titik yang direpresentasikan dengan (x, y) dengan pusat koordinat di bidang kompleks. Dengan demikian dinyatakan dalam bentuk
|z|=r =px2+y2=√zz¯ (5.2)
Persamaan Kompleks
Contoh
Tentukan x dany jika (x+iy)2= 2i
(x+iy)2=x2+i2xy−y2= 2i
Dengan demikian diperoleh hubungan
x2−y2= 0 =⇒ y=±x
2xy = 2
Selanjutnya diperoleh
2x2= 2 atau −2x2 = 2
Karenaxharus real makax2tidak mungkin negatif, dengan demikian didapat
x2 = 1 dan y = x. Sehingga solusi persamaan tersebut adalah x = y = 1
ataux =y=−1.
5.4
Fungsi Eksponensial dan Trigonometri
Karena z=x+iy, maka dapat dituliskan bentuk berikut
ez=ex+iy=exeiy=ex(cos y+isin y) (5.3) Sedangkan telah ditunjukkan sebelumnya dalam persamaan 5.1 bahwa bi-langan kompleks dapat direpresentasikan dalam bentuk eksponensial (yang disebut sebagai rumus Euler) yaitu
eiθ= cosθ+isinθ (5.4) Dengan menggunakan rumus Euler tersebut dapat diperoleh bentuk
e−iθ
= cosθ−isinθ (5.5) Bila persamaan 5.4 dan persamaan 5.5 dijumlahkan maka akan diperoleh ungkapan untuk cosθ, sedangkan bila persamaan 5.4 dikurangi dengan per-samaan 5.5 maka akan dapat diperoleh ungkapan untuk sinθsebagai berikut
sinθ= e
iθ−e−iθ
2i
cosθ= e
iθ+e−iθ
2
cakul
5.5 Fungsi Hiperbolik 97
5.5
Fungsi Hiperbolik
Dengan menggunakan rumusan Euler, maka dapat pula diperoleh ungkapan yang lebih umum untuk bilangan kompleksz, yaitu
sinz= e
Tinjau suatu bilangan kompleks yang murni imajinerz =iy, maka dapat dinyatakan
Persamaan 5.8 memberikan definisi tentang fungsi sinus hiperbolik (sinh) dan cosinus hiperbolik (cosh), yang secara umum dituliskan dalam bentuk
sinhz= e
Beberapa fungsi hiperbolik lainnya dapat diperoleh sebagaimana fungsi tri-gonometri biasa, yaitu
tanhz= sinhz
Dari persamaan 5.8 dapat juga dituliskan bahwa
siniy=isinhy
cosiy= coshy (5.11)
5.6
Logaritma
Misalkan suatu bilangan kompleksz danwdi mana hubungannya dinyatak-an dengdinyatak-an z = ew yang berarti w = lnz. Kemudian jika z = reiθ, maka
diperoleh
Contoh 1
Tentukanlah ln(−1).
Dalam ungkapan koordinat polar sebagaimana yang telah dibahas sebelum-nya, z = −1 dapat dinyatakan dengan bentuk eksponensial dengan r = 1 danθ=π,−π,3π,−3π, . . .sehingga
ln(−1) = ln(1) +iθ= 0 +i(π±2nπ) =iπ,−iπ,3iπ, . . . Contoh 2
Tentukan ln(1 +i).
Dengan menggunakan ungkapan dalam koordinat polar dapat diperoleh bah-wa untuk z= 1 +iberarti r=√2 dan θ=π/4±2nπ. Dengan demikian
ln(1 +i) = ln(√2) +iπ
4 ±2nπ
5.7
Penggunaan Bilangan Kompleks dalam
Per-soalan Fisika
Berikut ini diberikan beberapa contoh penggunaan bilangan kompleks dalam persoalan fisika.
Kinematika
Sebagaimana sistem koordinat kartesian dua dimensi, bidang kompleks da-pat digunakan untuk mendeskripsikan gerak suatu benda. Jikazmenyatakan posisi suatu benda, maka jika posisinya berubah tiap saat maka dapat di-nyatakan bahwa z(t).
Misalkan posisi benda tiap saat dinyatakan dengan z= 5eiωt di mana ω
suatu konstanta. Tentukan laju, besar percepatan dan deskripsi gerak benda tersebut.
Laju gerak benda adalah
v = dz
dt = d dt5e
iωt= 5iωeiωt =iωz
Percepatan gerak benda adalah
a= dv
dt = d dt(5iωe
iωt) =
cakul
fi5080
by
khbasar;
sem1
2010-2011
5.7 Penggunaan Bilangan Kompleks dalam Persoalan Fisika 99
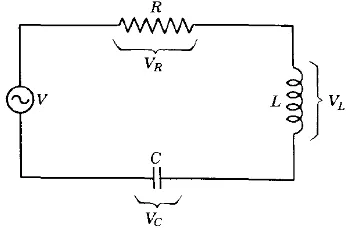
Gambar 5.2: Rangkaian seri RLC dengan sumber tegangan bolak-balik.
Terlihat dari percepatan gerak benda, bahwa percepatan gerak benda sama dengan suatu konstanta dikalikan dengan posisi benda dan hal ini menya-takan suatu gerak harmonik.
Rangkaian AC
Dalam rangkaian arus bolak-balik dengan komponenR(resistor),L (induk-tor) dan C (kapasitor), sebagaimana ditunjukkan dalam gambar 5.2, mi-salnya arus total yang mengalir pada rangkaian dinyatakan dengan bentuk fungsi harmonik I =I0sinωt. JikaVR adalah beda tegangan pada kaki-kaki
resistor R dan I adalah kuat arus yang mengalir pada hambatan tersebut, maka berdasarkan hukum Ohm dapat dinyatakan
VR=IR (5.13)
sedangkan hubungan antara tegangan pada induktor L dengan kuat arus dinyatakan dengan
VL =L
dI
dt (5.14)
dan tegangan pada kapasitor dinyatakan dengan
dVC
dt = I
C =⇒ VC =
1
C
Z
Bentuk arus setiap saat tersebut bila dinyatakan dengan bilangan kompleks
Tegangan total jika ketiga komponen tersusun seri adalah
V =VR+VL+VC=RI+iωLI +
dinamakan sebagai impedansi (kompleks)
pada rangkaian RLC seri.
Hambatan efektif pada komponen induktor dinamakan reaktansi induktif
XL yaitu
XL =
VL
I =iωL (5.20)
sedangkan hambatan efektif pada komponen kapasitor dinamakan reaktansi kapasitifXC yaitu
XC =
Pada rangkaian RLC seri, impedansi (kompleks) dapat diperoleh dengan konsep yang sama dengan susunan seri tiga hambatan (resistor) yang masing-masing dinyatakan dengan R1 = R, R2 = XL = iωL dan R3 = XC =
−i/(ωC) sehingga hambatan total (yaitu impedansi total) diperoleh seba-gaimana telah diungkapkan di atas yaitu
Z =R1+R2+R3
Selanjutnya dapat diperoleh besar impedansi sebagaimana nilai absolut dari
cakul
5.7 Penggunaan Bilangan Kompleks dalam Persoalan Fisika101
Suatu kondisi di mana Z sepenuhnya real (berarti bagian imajinernya sama dengan nol) dinamakan kondisi resonansi.
Demikian pula halnya jika ketiga komponen (resistor, induktor dan kapa-sitor) disusun paralel, maka impedansi totalnya dapat diperoleh sebagaima-na sususebagaima-nan paralel tiga buah hambatan yaituR1 =R,R2 =XL =iωLdan
Pada rangkaian yang terdiri dari hambatan R yang tersusun seri dengan induktor L kemudian keduanya diparalel dengan kapasitor C, sebagaimana ditunjukkan dalam gambar 5.3, tentukanlah impedansi rangkaian tersebut.
Impedansi total rangkaian tersebut adalah
Gambar 5.3: Gambar susunan komponen untuk contoh.
di manaZ1 =R+iωL danZ2=−
i
ωC. Dengan demikian
Ztotal=
5.8
Fungsi Kompleks
Fungsi dengan variabel kompleks dinyatakan misalnya dalam bentuk f(z) dengan z adalah bilangan kompleks. Secara umum fungsi dengan variabel kompleks mempunyai bagian real dan imajiner yang juga merupakan fungsi. Misalkan f(z) =z2, karena z=x+iy maka
cakul
fi5080
by
khbasar;
sem1
2010-2011
5.9 Fungsi Analitik 103
kompleks f(z) = u(x, y) +i v(x, y). Dengan demikian untuk fungsi kom-pleks di atas yang dinyatakan denganf(z) =z2, makau(x, y) =x2−y2 dan
v(x, y) = 2xy.
Contoh
Tentukan bagian real dan bagian imajiner fungsi kompleks f(z) = z
z2+ 1
dengan z=x+iy.
f(z) = x+iy (x+iy)2+ 1 =
x+iy
(x2−y2+ 1) +i2xy
=
x+iy
(x2−y2+ 1) +i2xy
(x2−y2+ 1)−i2xy
(x2−y2+ 1)−i2xy
= x
3−y3+x+ 2xy2
(x2−y2+ 1)2−4x2y2 +i
−x2y−y3+y
(x2−y2+ 1)2−4x2y2
Dengan demikian bagian real dan imajinernya adalah
u(x, y) = x
3−y3+x+ 2xy2
(x2−y2+ 1)2−4x2y2
v(x, y) = −x
2y−y3+y
(x2−y2+ 1)2−4x2y2
5.9
Fungsi Analitik
Suatu fungsif(z) dikatakan analitik dalam suatu daerah pada bidang kom-pleks bila fungsi tersebut mempunyai turunan yang tunggal (unik) pada se-tiap titik dalam daerah tersebut. Jika f(z) analitik di titik z = a berarti bahwa f(z) mempunyai turunan pada setiap titik dalam lingkaran kecil di sekitarz=a. Fungsi yang tidak memenuhi batasan tersebut disebut sebagai fungsi non-analitik.
Beberapa definisi berkaitan dengan fungsi analitik:
• Titik regular (regular point) dari fungsif(z) adalah titik di mana f(z) bersifat analitik
• Titik singular (singular point atau singularity) dari fungsif(z) adalah titik di mana f(z) tak analitik
Teorema I
Jika suatu fungsi kompleksf(z) =u(x, y) +iv(x, y) merupakan suatu fungsi analitik dalam suatu daerah, maka dalam daerah itu berlaku
∂u ∂x =
∂v
∂y, dan ∂v ∂x =−
∂u
∂y (5.25)
Teorema ini disebut juga kondisi Cauchy-Riemann untuk menentukan apa-kah suatu fungsi merupakan fungsi analitik atau bukan.
Contoh 1
Misalkan f(z) =y+ix. Apakahf(z) merupakan fungsi analitik?
Dalam hal iniu=y danv =x, sehingga∂u/∂x= 0, ∂v/∂y= 0, ∂v/∂y = 1 dan ∂u/∂y = 1. Karena tidak memenuhi kondisi Cauchy-Riemann, maka fungsif(z) tersebut bukanlah fungsi analitik.
Contoh 2
Misalkan f(z) =x+iy. Apakahf(z) merupakan fungsi analitik?
Karena
∂u ∂x = 1 =
∂v
∂y dan
∂v
∂x = 0 =− ∂u ∂y
maka berartif(z) adalah fungsi analitik.
Teorema II
Jika u(x, y) dan v(x, y) dan turunan parsialnya terhadap x dan y kontinyu serta memenuhi syarat Cauchy-Riemann dalam daerah tersebut maka f(z) analitik pada semua titik dalam daerah tersebut.
Teorema III
Perhatikan gambar 5.4. Jika f(z) adalah fungsi analitik dalam daerah ter-tentu (R) maka f(z) mempunyai turunan orde berapapun pada titik-titik dalam daerah tersebut danf(z) dapat diekspansikan sebagai deret Taylor di sekitar titik z0 dalam daerah tersebut. Deret pangkat tersebut konvergen di
dalam daerah berbentuk lingkaran C yang berpusat di z0 hingga mencapai
titik singular terdekat (disebut sebagai daerah lingkaran konvergensi atau
cakul
fi5080
by
khbasar;
sem1
2010-2011
5.9 Fungsi Analitik 105
z0
titik singular
R
C
Gambar 5.4: Daerah untuk penjelasan Teorema III.
Contoh
Tentukanlah daerah lingkaran konvergensi (disk of convergence) dari fungsi kompleksf(z) = ln(1−z).
Fungsi f(z) = ln(1−z) dapat diekspansikan dalam bentuk deret pangkat di sekitar z= 0 (uraian Maclaurin), yaitu
ln(1−z) =−z−z
2
2 −
z3
3 −
z4
4 −. . .
Kemudian untuk memperoleh titik singular dari fungsi tersebut adalah titik di mana fungsif(z) tersebut tidak mempunyai turunan. Dalam hal ini titik singular yang dimaksud adalah z = 1. Dengan demikian daerah lingkaran konvergensi dari fungsi tersebut adalah lingkaran berpusat di pusat koordinat dengan jari-jari 1.
Teorema IV
Jika f(z) = u+iv merupakan fungsi analitik dalam suatu daerah, maka u
danv memenuhi persamaan Laplace (∇2u= 0 dan ∇2v = 0) dalam daerah
tersebut (artinya u dan v merupakan fungsi harmonik). Fungsi sembarang
u (atau v) yang memenuhi persamaan Laplace dalam suatu daerah adalah bagian real atau imajiner dari suatu fungsi analitik f(z).
Contoh
Suatu fungsiu(x, y) =x2−y2adalah bagian real dari fungsi kompleksz.
Karena
∇2u= ∂
2u
∂x2 +
∂2u
∂y2 = 2−2 = 0
maka berarti u(x, y) memenuhi persamaan Laplace atau dalam kata lain
u(x, y) adalah fungsi harmonik.
Kemudian dengan menggunakan persamaan Cauchy-Riemann dapat dipero-leh
∂v ∂y =
∂u ∂x = 2x
Maka dengan mengintegralkan terhadap y dapat diperoleh bentuk fungsi
v(x, y), yaitu
v(x, y) =
Z
2x dy= 2xy+g(x)
dengang(x) adalah fungsi dalam xyang merupakan konstanta integrasi. Se-lanjutnya dengan menggunakan kembali syarat Cauchy-Riemann maka dapat diperoleh
∂v ∂x =
∂
∂x(2xy+g(x)) = 2y+g ′
(x) =−∂u∂y = 2y
sehingga berartig′
(x) = 0 atau g= const.
Jadi diperoleh bentuk fungsi v(x, y) = 2xy+ const. Dengan demikian dipe-roleh bentuk fungsi kompleksz adalah
f(z) =u+iv=x2−y2+ 2ixy+ const =z2+ const
5.10
Integral Kontur
Selain keempat teorema yang berkaitan dengan pengertian dan batasan fung-si analitik, terdapat pula beberapa teorema lainnya yang berkaitan dengan penggunaan fungsi kompleks.
Teorema V: Teorema Cauchy
Misalkan C adalah suatu kurva tertutup sederhana dengan lengkungan yang halus kecuali beberapa titik tertentu yang jumlahnya terbatas, maka jika f(z) adalah fungsi analitik di dalam C dapat dinyatakan dengan
I
sekeliling C
f(z)dz = 0 (5.26)
cakul
fi5080
by
khbasar;
sem1
2010-2011
5.10 Integral Kontur 107
Teorema VI: Perumusan Integral Cauchy
Jikaf(z) adalah fungsi analitik pada dan di dalam suatu kurva sederhana C, maka nilaif(z) di suatu titikz=ayang berada di dalam kurva C adalah
f(a) = 1 2πi
I f(z)
z−adz (5.27)
Contoh 1
Hitunglah integral
I
C
sinz
2z−πdz,
dengan C adalah lingkaran pada bidang kompleks dengan |z|= 2 Integral tersebut dapat dituliskan menjadi
I
C
sinz
2z−πdz =
1 2
I
C
sinz z−π/2dz
Kurva C yang digunakan adalah berbentuk lingkaran berjari-jari 2 dalam bidang kompleks. Bentukf(z) adalahf(z) = sinz, dengana=π/2. Karena
f(z) = sinz berartif(z) bersifat analitik di dalam kurva C, sehingga dapat digunakan Teorema VI. Maka diperoleh
1 2
I
C
sinz
z−π/2dz=πisin(π/2) =πi
Contoh 2
Hitunglah integral
I
C
sinz
2z−πdz,
dengan C adalah lingkaran pada bidang kompleks dengan |z|= 1 Integral tersebut dapat dituliskan menjadi
I
C
sinz
2z−πdz =
1 2
I
C
Karena C adalah lingkaran berjari-jari 1 dan menggunakanf(z) = sinz/(z−
π/2), maka berartif(z) adalah fungsi analitik dalam kurva C, sehingga bila menggunakan Teorema V (Teorema Cauchy) dapat dinyatakan:
1
z−ln 2, titik singularnya adalah pada z = ln2. Karena titik singular tersebut berada di dalam daerah yang dibatasi oleh kurva C, maka dapat digunakan rumusan integral Cauchy
f(a) = 1
Dengan demikian diperoleh
I
C
e3z
z−ln 2dz = 2πie
3 ln 2= 16πi
Teorema VII: Teorema Laurent
Misalkan C1 dan C2 adalah dua buah lingkaran yang pusatnya pada titik
z0 dan f(z) adalah suatu fungsi analitik dalam daerah R di antara kedua
lingkaran tersebut maka f(z) dapat diuraikan menjadi bentuk deret yang konvergen dalam R, yaitu
f(z) =a0+a1(z−z0) +a2(z−z0)2+· · ·+
dengan koefisienan dan bn adalah
cakul
5.11 Teorema Residu dan Aplikasinya 109
dengan C adalah adalah sembarang kurva tertutup sederhana yang mengeli-lingi z0 dan terletak pada daerah R.
Beberapa pengertian yang terkait dengan teorema Laurent ini:
• Jika semua koefisien b sama dengan nol maka f(z) bersifat analitik padaz =z0 danz0 disebut sebagai titik regular.
• Jika bn= 0 tapi kemudian nilai b setelahbn sama dengan 0 maka f(z)
dikatakan mempunyai kutub orde n pada z = z0. Jika n = 1 maka
f(z) mempunyai kutub sederhana (simple pole).
• Jika terdapat takhingga banyaknya koefisienbyang tidak sama dengan nol makaf(z) dikatakan mempunyai essential singularity pada z=z0
• Koefisienb1 dari
1
Karena deret ini tidak mempunyai koefisien b (semua bn = 0) maka deret
tersebut analitik pada z = 0. Karena b1 = 0 maka berarti residu dari ez
padaz= 0 adalah sama dengan 0.
Misalkan sebuah deret e
z Bagian utama deret tersebut adalah 1
z3 +
sebut mempunyai kutub orde 3 sedangkan residu dari e
z
5.11
Teorema Residu dan Aplikasinya
Teorema residu sangat berguna untuk menghitung integral. Teorema residu dinyatakan dalam bentuk
I
C
f(z)dz = 2πi×(jumlah residu darif(z) di dalam C) (5.30)
Metode Penentuan Residu
Yang menjadi penting adalah bagaimana cara menemukan residu? Ada be-berapa cara penentuan residu suatu fungsi kompleks sebagaimana yang akan diuraikan berikut ini.
• Deret Laurent
Sebagaimana yang telah diuraikan sebelumnya, uraian deret Taylor da-ri suatu fungsi dapat digunakan untuk menentukan nilai residu fungsi tersebut di suatu titik z=z0.
Contoh
Suatu fungsi kompleksf(z) =ez/(z−1). Tentukan residu darif(z) di
z= 1.
Bila fungsi ez diekspansikan dalam deret pangkat (z − 1) maka
di-peroleh
ez
z−1 =
e ez−1 z−1 =
e z−1
1 + (z−1) + (z−1)
2
2! +. . .
= e
z−1+e+. . .
Karena residu pada z = 1 diperoleh dari koefisien 1
z−1 maka berarti
R(1) =e.
• Kutub tunggal (Simple Pole)
Jika fungsi kompleks f(z) mempunyai kutub sederhana pada z = z0
maka residu pada titik tersebut dapat diperoleh dengan mengalikan
f(z) dengan (z−z0) kemudian hitung nilainya pada z=z0.
Perumusannya secara umum dapat dituliskan sebagai berikut:
R(z0) = lim
z→z0
(z−z0)f(z) (5.31)
Contoh
HitunglahR(−12) danR(5) untuk fungsi kompleks yang dinyatakan
de-nganf(z) = z
(2z+ 1)(5−z).
Untuk menghitung residu di titik z =−1
2, maka fungsi f(z) tersebut
dikalikan dengan (z+ 12), diperoleh
z+1 2
f(z) =
z+1 2
z
(2z+ 1)(5−z) =
z
cakul
fi5080
by
khbasar;
sem1
2010-2011
5.11 Teorema Residu dan Aplikasinya 111
Kemudian hitung nilainya dengan mensubstitusiz=−1
2, diperoleh
R(−12) =
−1 2
2(5 +12) =− 1 22
Cara yang sama juga dilakukan untuk menghitung residu di titikz= 5
(z−5)f(z) = (z−5) z
(2z+ 1)(5−z) =−
z
2z+ 1
R(5) =− z 2z+ 1
z=5=−
5 11
• Kutub ganda (Multiple Poles)
Jika f(z) mempunyai kutub dengan orde n, maka dapat digunakan langkah sebagai berikut untuk memperoleh nilai residu pada z = z0:
kalikan f(z) dengan (z−z0)m, di manam adalah bilangan bulat yang
lebih besar atau sama dengan orde n, kemudian differensialkan hasil-nya m−1 kali, lalu dibagi dengan (m−1)! dan hitung hasil akhirnya dengan mensubstitusi z=z0.
Contoh
Tentukan residu dari f(z) = (zsinz)/(z−π)3 di titikz=π.
Gunakan m = 3 untuk mengeliminasi penyebut, artinya kalikan f(z) dengan (z−π)3 sehingga diperoleh
(z−π)3f(z) = (z−π)3 zsinz
(z−π)3 =zsinz
kemudian differensialkan 2 kali dan selanjutnya dibagi dengan 2! se-hingga diperoleh
R(π) = 1 2!
d2
dz2(zsinz)
z=π=
1
2[−zsinz+ 2 cosz]z=π =−1
Teorema Residu untuk menghitung integral
Sebagaimana telah disinggung sebelumnya bahwa teorema residu dapat digu-nakan untuk menghitung integral tertentu. Berikut ini beberapa contohnya.
Contoh 1
Hitunglah integral
I =
Z 2π
0
dθ
Jika digunakan variabel baru yaituz=eiθ, makadz =ieiθdθ ataudθ = 1
2 . Sedangkan batas integral dalam variabel
θ yaitu dari θ = 0 hingga θ = 2π akan berubah menjadi lingkaran satuan dalam bidang kompleks dengan|z|= 1 dan arahnya berlawanan dengan arah jarum jam. Dengan demikian integral tersebut dapat dinyatakan sebagai in-tegral kontur.
Dengan variabel yang baru tersebut integral yang dimaksud dapat dituliskan kembali dalam bentuk
I =
dengan C adalah kurva yang berupa lingkaran berjejari 1 dan berpusat di titik pusat koordinat pada bidang kompleks. Terlihat bahwa integran (yaitu fungsi yang diintegralkan) berbentuk f(z) = 1
(2z+ 1)(z+ 2) yang berarti mempunyai kutub pada z =−1
2 dan pada z=−2. Karena kurva C adalah
berupa lingkaran berjejari 1, maka berarti dari kedua kutub tersebut hanya kutub z = −1
2 saja yang berada di dalam daerah yang dibatasi kurva C,
sedangkan kutub z=−2 berada di luar daerah yang dibatasi oleh kurva C. Residu dari f(z) pada z = −12 dapat dihitung menggunakan metode kutub
sederhana (simple pole) yaitu
R(−1
Selanjutnya dengan menggunakan teorema residu dapat diperoleh bahwa
cakul
5.11 Teorema Residu dan Aplikasinya 113
Untuk menghitung integral I tersebut, tinjau integral kontur berbentuk
I
C
dz
1 +z2
dengan C adalah kurva tertutup setengah lingkaran pada bidang kompleks (kuadran 1 dan kuadran 2) dengan jejari sembarang ρ > 1. Integran pada integral kontur tersebut berbentuk f(z) = 1
1 +z2 =
1
(z−i)(z+i). Berarti
f(z) mempunyai kutub padaz=idan pada z=−i. Di antara kedua kutub ini hanya kutub pada z = i saja yang berada dalam daerah yang dibatasi oleh kurca tertutup C (ingat bahwa C berbentuk setengah lingkaran pada kuadran 1 dan 2). Kemudian nilai residu f(z) pada z = i dapat diperoleh menggunakan metode kutub sederhana (simple pole) yaitu
R(i) = lim
Dengan demikian dari teorema residu diperoleh
I
C
dz
1 +z2 = 2πiR(i) =π
Integral kontur dengan lintasan berupa kurva C tersebut dapat dinyatakan sebagai integral garis (integral lintasan) dengan lintasan pertama berupa ga-ris lurus sepanjang sumbu datar (sumbux) dari −ρhingga +ρdan lintasan kedua berupa lintasan setengah lingkaran yang dinyatakan dengan persama-an z=ρeiθ dengan θdari 0 hingga π:
Telah dihitung sebelumnya bahwa integral kontur yang dimaksud hasilnya adalahπdan hasil ini tidak bergantung pada berapapun nilaiρyang digunak-an. Perhatikan bahwa asalkan kurva C yang digunakan dalam penghitungan integral kontur adalah setengah lingkaran pada kuadaran 1 dan 2, maka ber-dasarkan teorema residu nilai integralnya tetap sama. Artinya bila diambil
ρ→ ∞, maka dapat dituliskan kembali
Maka diperoleh hasil integral yang dimaksud yaitu
Tinjau suatu integral kontur yang berbentuk
I
C
eizdz
1 +z2
dengan C adalah kurva tertutup setengah lingkaran pada bidang kompleks (kuadran 1 dan kuadran 2) dengan jejari sembarang ρ > 1 sebagaimana padaContoh 2. Integran pada integral kontur tersebut mempunyai bentuk
f(z) = e
iz
1 +z2 yang berarti terdapat dua kutub padaz=idanz =−i. Nilai
residu di dalam kurva C adalah
R(i) = lim
Selanjutnya dengan teorema residu dapat dihitung integral kontur yang di-maksud yaitu
Sedangkan integral kontur tersebut dapat dituliskan dalam dua integral lin-tasan sesuai dengan kurva tertutup C yang digunakan (lihat kembaliContoh 2 di atas)
Dengan demikian diperoleh bahwa
cakul
fi5080
by
khbasar;
sem1
2010-2011
5.11 Teorema Residu dan Aplikasinya 115
Kemudian bila diambil bagian real dari kedua ruas tersebut maka dapat dinyatakan
Re
Z +∞
−∞ eix
1 +x2dx
= Rehπ
e
i
Z +∞
−∞
cosx
1 +x2dx=
π e
Selanjutnya karena fungsi cosx
1 +x2 adalah fungsi genap, maka integral dari
−∞hingga +∞ sama dengan dua kali integral dari 0 hingga +∞, sehingga diperoleh
Z +∞
0
cosx
1 +x2dx=
1 2
Z +∞
−∞
cosx
1 +x2dx=
π