Pengolahan Citra di Ranah Frekuensi

Pengolahan Citra di Ranah Frekuensi

Iwan Setyawan

Dept. Electronic Engineering, Satya Wacana Christian University

Pendahuluan

• Sama seperti pada ranah spatial, pengolahan citra pada ranah

frekuensi juga dapat digunakan untuk tujuan enhancement atau restorasi.

• Pada bagian ini akan dibahas bagaimana merepresentasikan

serta mengolah citra dalam ranah frekuensi.

• Alat utama yang akan digunakan pada bagian ini adalah

transformasi Fourier.

• Pembahasan transformasi Fourier pada bagian ini dibatasi pada

Transformasi Fourier: Intro

• Secara umum, transformasi Fourier digunakan untuk

menguraikan (decompose) sebuah sinyal menjadi komponen-komponen berupa gelombang sinusoida.

• Dalam konteks PCD, output transformasi Fourier adalah

representasi citra dalam ranah frekuensi.

• Dalam ranah frekuensi (ranah Fourier), setiap titik

Transformasi Fourier: Why?

• Transformasi Fourier memungkinkan dilakukannya beberapa hal

yang tidak dapat dilakukan pada ranah spatial.

• Banyak operasi dapat dilakukan dengan lebih cepat dalam ranah

Fourier dibandingkan dalam ranah spatial.

• Filtering dalam ranah Fourier jauh lebih efisien dibanding filtering

dalam ranah spatial, terutama untuk filter-filter besar.

• Dengan transformasi Fourier, kita dapat memproses

frekuensi-frekuensi spesifik. Dengan demikian, proses low- dan high-pass filtering dapat dilakukan dengan lebih presisi.

Transformasi Fourier: Basic Ideas (1)

• Sebuah fungsi periodik (atau fungsi non-periodik yang luasan

dibawah kurva fungsinya berhingga) dapat direpresentasikan sebagai jumlahan fungsi sinus dan cosinus dengan berbagai amplitudo dan frekuensi.

• Ada fungsi-fungsi yang tersusun oleh jumlah komponen yang

berhingga, ada fungsi-fungsi yang tersusun oleh jumlah komponen yang tidak berhingga.

Transformasi Fourier: Basic Ideas (3)

Transformasi Fourier: Kontinu (1)

• Transformasi Fourier dari sebuah fungsi kontinu 1-D f(x)

didefinisikan sebagai berikut:

F(u) =

∫ _∞

−∞ f(x)e

−j2πux_{dx (1)}

• Inverse transformasi Fourier didefinisikan sebagai berikut:

f(x) =

∫ _∞

−∞F(u)e

Transformasi Fourier: Kontinu (2)

• Dalam dua dimensi, pasangan persamaan tadi dapat ditulis

sebagai berikut: F(u, v) = ∫ _∞ −∞ ∫ _∞ −∞ f(x, y)e −j2π(ux+vy) dxdy (3) f(x, y) = ∫ _∞ −∞ ∫ _∞ −∞F(u, v)e j2π(ux+vy)_{dudv (4)}

Transformasi Fourier: DFT 1-D (1)

• Discrete Fourier Transform (DFT) sebuah fungsi diskret 1-D, f(x), x =1, 2, . . . , M−1 adalah F(u) = _M1 M−1

∑

x=0 f(x)e−j2πux/M untuk u=0, 1, 2, . . . , M−1 (5)

• IDFT didefinisikan sebagai berikut:

f(x) = M−1

∑

u=0 F(u)e−j2πux/M −

Transformasi Fourier: DFT 1-D (2)

• Faktor _M1 kadang-kadang dituliskan bukan pada persamaan

transformasi Fourier tapi pada persamaan inverse-nya.

• Kadang-kadang, kedua persamaan dikalikan dengan faktor _√1

M.

• Penghitungan DFT dilakukan sebagai berikut:

1 Set u=0

2 Lakukan summing untuk semua nilai x

3 Jika u<M, set u=u+1 dan kembali ke step 2. Jika u=M, proses

selesai.

• Proses ini membutuhkan kira-kira M2_{buah penjumlahan &}

Transformasi Fourier: DFT 1-D (3)

• Proses penghitungan IDFT mirip dengan prosedur diatas.

• Salah satu sifat paling penting DFT dalam PCD adalah bahwa

semua citra memiliki DFT dan IDFT.

• Sifat diatas dikarenakan pasangan DFT dan IDFT pasti ada asal

f(x)memiliki nilai berhingga. Semua citra digital dapat

Transformasi Fourier: DFT 1-D (4)

• Konsep ranah frekuensi diperoleh dari rumus Euler sebagai

berikut:

ejθ =cosθ+j sinθ (7)

• Dengan mensubstitusikan persamaan ini ke Persamaan (5) (dan

karena cos(−θ) =cosθ), diperoleh

F(u) = _M1

M−1

∑

x=0

f(x)[cos 2πux/M−j sin 2πux/M] (8)

• Ranah F(u)disebut dengan ranah frekuensi dan masing-masing

Transformasi Fourier: DFT 1-D (5)

• Karena F(u)adalah bilangan kompleks, maka sering dituliskan:

F(u) =|F(u)|ejϕ(u) (9) dengan magnitude (spektrum) transformasi Fourier didefinisikan sebagai:

|F(u)| = [ℜ2(u) +ℑ2(u)]1/2 (10) dan sudut fase transformasi didefinisikan sebagai:

ϕ(u) =tan−1 [ ℑ(u) ℜ(u) ] (11)

Transformasi Fourier: DFT 1-D (6)

• Besaran lain yang banyak digunakan adalah power spectrum,

yang didefinisikan sebagai berikut:

P(u) =|F(u)|2 (12)

Transformasi Fourier: DFT 2-D (1)

• DFT dari sebuah citra f(x, y)dengan ukuran M×N adalah

F(u, v) = 1 MN M−1

∑

x=0 N−1

∑

y=0 f(x, y)e−j2π(ux/M+vy/N) (13)

• IDFT 2-D didefinisikan sebagai berikut

f(x, y) = M−1

∑

u=0 N−1

∑

v=0 F(u, v)ej2π(ux/M+vy/N) (14)

Transformasi Fourier: DFT 2-D (2)

• Definisi magnitude, fase dan power spectrum DFT 2-D adalah

|F(u, v)| = [ℜ2(u, v) +ℑ2(u, v)]1/2 (15) ϕ(u, v) =tan−1 [ ℑ(u, v) ℜ(u, v) ] (16) P(u, v) =|F(u, v)|2 =ℜ2(u, v) +ℑ2(u, v) (17)

Transformasi Fourier: DFT 2-D (3)

• Biasanya, citra yang akan ditransformasikan dikalikan lebih

dahulu dengan(−1)x+y, karena

F[f(x, y)(−1)x+y] =F(u−M/2, v−N/2) (18)

• Persamaan ini menunjukkan bahwa titik awal transformasi

Fourier (yaitu, F(0, 0)) berada pada titik u= M/2 dan v= N/2.

• Agar koordinat hasil shifting ini tetap integer, M dan N harus

Transformasi Fourier: DFT 2-D (4)

• Nilai transformasi Fourier pada titik(u, v) = (0, 0)adalah

F(0, 0) = 1 MN M−1

∑

x=0 N−1

∑

y=0 f(x, y) (19)

• Dengan kata lain, jika f(x, y)adalah sebuah citra, nilai F(0, 0)

adalah nilai rata-rata nilai gray-level citra. Komponen ini disebut komponen DC.

• Jika f(x, y)real, maka F(u, v)conjugate symmetric, atau

F(u, v) =F∗(−u,−v) (20) Dari sini diperoleh bahwa

Transformasi Fourier: DFT 2-D (5)

Transformasi Fourier: DFT 2-D (6)

Transformasi Fourier: DFT 2-D (7)

Transformasi Fourier: DFT 2-D (9)

Konsep Frekuensi pada Citra Digital (1)

• Konsep “frekuensi” pada citra digital berkaitan dengan banyaknya

perubahan nilai pixel per derajat sudut pandang.

• Konsep “magnitude” pada citra digital berkaitan dengan besarnya

perubahan tersebut.

• Pada citra, besarnya frekuensi bergantung pada banyak hal, salah

satunya pada jarak antara sensor/mata dengan citra tersebut: Suatu daerah yang dianggap “high-frequency” pada jarak jauh bisa menjadi “low-frequency” pada jarak dekat.

Konsep Frekuensi pada Citra Digital (2)

• Daerah low-frequency kadang disebut daerah dengan energi

rendah dan daerah high-frequency disebut daerah dengan energi tinggi (misalnya pada bidang kompresi citra).

• Human Visual System (HVS) memiliki kepekaan yang lebih tinggi

terhadap daerah low-frequency dibandingkan terhadap daerah high-fequency (yaitu, manusia lebih peka terhadap

perubahan/gangguan yang terjadi pada daerah low-frequency dibanding high-frequency).

Filtering dalam ranah frekuensi: Intro (1)

• Pada umumnya, tidak mudah membuat hubungan bagian-bagian

tertentu dari suatu citra dengan hasil transformasinya.

• Meskipun demikian, dapat ditarik beberapa hubungan umum

antara komponen frekuensi dengan karakteristik spatial citra.

• Contohnya, kita dapat menghubungkan frekuensi dalam ranah

Fourier dengan pola perubahan perubahan luminance pada citra:

• Titik tengah spektrum menunjukkan nilai rata-rata luminance citra.

• Titik-titik yang jauh dari titik tengah spektrum menunjukkan daerah-daerah dengan perubahan level luminance yang besar, seperti edge, noise, dll.

Filtering dalam ranah frekuensi: Intro (2)

Filtering dalam ranah frekuensi: Basics (1)

Secara umum, proses filtering dalam ranah frekuensi adalah sebagai berikut: 1 Hitung f′(x, y) = f(x, y)(−1)x+y 2 Hitung F(u, v) =F[f′(x, y)] 3 Hitung G(u, v) =F(u, v)H(u, v). 4 Hitung ˆg(x, y) =F−1[G(u, v)] 5 Hitung g′(x, y) =ℜ[ˆg(x, y)] 6 Hitung g(x, y) =g′(x, y)(−1)x+y

Filtering dalam ranah frekuensi: Basics (2)

• Pada langkah ke-3, H(u, v)disebut filter karena berfungsi

menekan frekuensi-frekuensi tertentu dan meloloskan sisanya.

• Perkalian pada langkah ke-3 dilakukan per elemen

(masing-masing elemen F(u, v)dikalikan dengan masing-masing

elemen H(u, v)).

• Pada umumnya F(u, v)adalah besaran kompleks sedangkan

H(u, v)adalah besaran real. Dalam hal ini nilai H(u, v)dikalikan dengan bagian real dan imajiner F(u, v).

• Filter seperti diatas disebut dengan filter zero-phase-shift, karena

Filtering dalam ranah frekuensi: Basics (3)

• Hasil operasi IDFT pada umumnya kompleks. Tetapi dalam kasus

ini jika f(x, y)real, seharusnya ˆg(x, y)juga real (yaitu, semua komponen imajinernya 0).

• Pada prakteknya, ˆg(x, y)biasanya masih memiliki komponen

imajiner yang dihasilkan akibat error komputasi (round-off, dll). Oleh karena itu, perlu dilakukan langkah ke-5.

• Perkalian dengan(−1)x+ydilakukan untuk menghilangkan

Filtering dalam ranah frekuensi: Basics (4)

Filtering dalam ranah frekuensi: Basics (5)

• Misalkan kita hendak mem-filter suatu citra sedemikian sehingga

nilai rata-rata gray-level citra tersebut 0.

• Karena dalam ranah frekuensi F(0, 0)merupakan nilai rata-rata

gray-level citra, dengan membuat F(0, 0) =0 kita dapat membuat

sebuah citra yang nilai rata-rata gray-levelnya 0.

• Filter yang dapat digunakan untuk melakukan hal ini adalah

H(u, v) =

{

0 jika(u, v) = (M/2, N/2)

1 otherwise (22)

Filtering dalam ranah frekuensi: Basics (6)

Filtering dalam ranah frekuensi: Basics (7)

• Filter-filter spatial yang telah dibahas pada bab sebelumnya dapat

dikaitkan langsung dengan filter sejenis pada ranah frekuensi.

• Kaitan utama antara ranah spatial dan frekuensi diberikan oleh

teorema konvolusi.

• Proses konvolusi sudah dijelaskan pada pembahasan filter ranah

Filtering dalam ranah frekuensi: Basics (8)

• Hasil paling penting teorema konvolusi dalam hal ini adalah

hubungan:

h(x, y)⇔ H(u, v) (23)

• Persamaan diatas menyatakan bahwa filter spatial h(x, y)dan

filter ranah frekuensi H(u, v)adalah pasangan transformasi

Fourier.

• Dengan kata lain, jika kita memiliki sebuah filter dalam ranah

frekuensi, kita dapat memperoleh filter ranah spatial dengan cara mencari inverse transformasi Fourier-nya.

Filtering dalam ranah frekuensi: Basics (9)

• Pembuatan filter spatial secara langsung dari H(u, v)tidak efisien

karena masalah ukuran.

• Pada prakteknya hasil inverse transformasi Fourier digunakan

sebagai guideline (“prototipe”) pembuatan filter spatial dengan ukuran yang lebih kecil tapi dengan sifat yang hampir sama.

• Karena transformasi Fourier adalah sebuah proses linear,

Filtering dalam ranah frekuensi: Basics (10)

• Sebagai contoh, misalkan sebuah filter Gaussian (1-D) pada ranah

frekuensi, yaitu

H(u) =Ae−u2/2σ2 (24)

• Inverse transformasi Persamaan (24) (dengan kata lain, filter

spatial yang ekuivalen) adalah sebagai berikut

h(x) =√2πσAe−2π2σ2x2 (25)

Filtering dalam ranah frekuensi: Basics (11)

Filtering dalam ranah frekuensi: Basics (12)

Beberapa hal yang dapat diamati dari Gambar 12 adalah:

• Filter H(u)adalah sebuah low-pass filter.

• Bentuk filter h(x)dapat digunakan sebagai dasar pembuatan

kernel filter spatial yang lebih kecil.

• Kedua filter memiliki koefisien yang semuanya positif. Jadi dalam

ranah spatial kita dapat membuat kernel LPF dengan koefisien yang semuanya positif.

Filtering dalam ranah frekuensi: Basics (13)

• Contoh lain filter pada ranah frekuensi adalah sebuah high-pass

filter sebagai berikut

H(u) =Ae−u2/2σ12−_Be−u2/2σ22 (26)

Dalam persamaan ini A ≥B danσ1 >σ2.

• Filter spatial yang ekuivalen dengan filter ini adalah

h(x) =√2πσ1Ae−2π

2_σ2

1x2−√2πσ₂Be−2π2σ22x2 (27)

Filtering dalam ranah frekuensi: Basics (14)

Filtering dalam ranah frekuensi: Basics (15)

• Pada Gambar 13 dapat diamati bahwa bentuk filter spatial yang

dihasilkan dariF−1_{[H(u)]mirip dengan filter spatial yang sudah}

dibicarakan pada bab yang lalu.

• Dari kedua contoh ini dapat dilihat bahwa pengembangan filter

dapat dilakukan dalam ranah frekuensi karena lebih “intuitif”.

• Setelah filter dalam ranah frekuensi diperoleh, penerapan

filtering dapat dilakukan dalam ranah spatial seperti pada bab sebelumnya.

Smoothing Frequency Domain Filters: Intro

• Seperti sudah dibahas sebelumnya, perubahan gray-level yang

tajam (misalnya pada edge atau noise) memberi kontribusi pada komponen frekuensi tinggi spektrum Fourier suatu citra.

• Jadi efek smoothing atau blurring dapat diperoleh dengan

menekan komponen frekuensi tinggi (dalam range tertentu) transformasi Fourier suatu citra.

• Dalam bagian ini akan dibahas 3 jenis filter smoothing yaitu filter

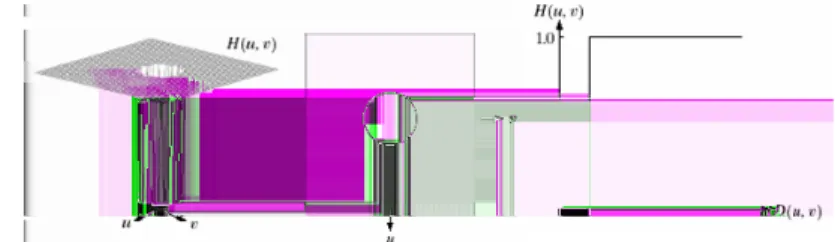
Smoothing Frequency Domain Filters: ILPF (1)

• LPF paling sederhana adalah filter yang membuang semua

komponen frekuensi tinggi yang jaraknya dari titik pusat

transformasi lebih dari suatu jarak tertentu, D0.

• Filter ini disebut LPF ideal (ILPF) 2-D, yang diberikan oleh

persamaan H(u, v) = { 1 jika D(u, v)≤ D0 0 jika D(u, v) >D0 (28)

• Dengan asumsi bahwa transformasi Fourier “centered”, untuk

sebuah citra berukuran M×N kita peroleh hubungan

Smoothing Frequency Domain Filters: ILPF (2)

Smoothing Frequency Domain Filters: ILPF (3)

• Filter ini merupakan filter ideal karena semua frekuensi dalam

lingkaran dengan radius D0diloloskan sementara semua

frekuensi diluar lingkaran tersebut dihilangkan.

• Pada sebuah LPF ideal, titik perubahan antara H(u, v) =1 dan

H(u, v) =0 disebut dengan frekuensi cutoff.

• Transisi yang sedemikian tajam tidak dapat direalisasikan dengan

komponen elektronik, tetapi dapat diterapkan menggunakan komputer.

Smoothing Frequency Domain Filters: ILPF (4)

• Semakin kecil radius D0, semakin sedikit frekuensi yang

diloloskan sehingga citra output akan semakin blur.

• Salah satu cara menentukan frekuensi cutoff adalah dengan

menghitung seberapa besar energi citra yang akan dipertahankan.

• Jumlah total energi suatu citra dihitung dengan menjumlahkan

nilai semua komponen power spectrum untuk tiap titik(u, v),

yaitu PT = M−1

∑

u=0 N−1

∑

v=0 P(u, v) (30)

Smoothing Frequency Domain Filters: ILPF (5)

• Sebuah lingkaran dengan radius r dari titik pusat spektrum

transformasi Fourier akan mengandungα persen energi citra,

atau α=100 [

∑

u

∑

v P(u, v)/PT ] (31)

• Sebagai contoh, gambar berikut menunjukkan spektrum sebuah

citra berukuran 500×500 pixel.

• Masing-masing lingkaran memiliki radius 5, 15, 30, 80 dan 230.

• Masing-masing lingkaran tersebut mencakup 92%, 94.6%, 96.4%,

Smoothing Frequency Domain Filters: ILPF (6)

Smoothing Frequency Domain Filters: ILPF (7)

Smoothing Frequency Domain Filters: ILPF (8)

Smoothing Frequency Domain Filters: ILPF (9)

Smoothing Frequency Domain Filters: ILPF (10)

• Hasil filtering dengan D0=5 bisa dikatakan tidak banyak

berguna. Dari sini dapat dilihat bahwa informasi detail citra terdapat dalam 8% energi citra yang dihilangkan.

• Citra yang difilter dengan D0=15, 30 dan 80 memiliki ciri khas

berupa “ringing”. Hal ini adalah konsekuensi penggunaan filter ideal. Fenomena ini makin berkurang jika semakin banyak energi citra yang dilalukan.

• Citra yang difilter dengan D0=230 hampir identik dengan citra

asli. Hal ini menunjukkan bahwa 0.5% energi yang dibuang tidak banyak mengandung informasi edge.

Smoothing Frequency Domain Filters: ILPF (11)

Fenomena blurring dan ringing dapat dijelaskan sebagai berikut:

• Dalam ranah frekuensi dan spatial, hubungan antara citra input

dan output masing-masing adalah:

G(u, v) =H(u, v)F(u, v) (32)

g(x, y) =h(x, y)∗f(x, y) (33)

Smoothing Frequency Domain Filters: ILPF (12)

Smoothing Frequency Domain Filters: ILPF (13)

• Dari gambar terlihat bahwa filter h(x, y)memiliki ciri khas berupa

komponen utama pada titik pusat dan lingkaran-lingkaran konsentris disekeliling komponen utama.

• Komponen utama menyebabkan efek blurring, sedangkan

lingkaran-lingkaran konsentris mengakibatkan efek ringing.

• Dapat dilihat pula bahwa filter h(x, y)memiliki komponen negatif,

Smoothing Frequency Domain Filters: ILPF (14)

• Hasil yang lebih ekstrim ditunjukkan pada contoh berikut.

Misalkan citra input, f(x, y)adalah citra yang berisi 5 buah “impulse”.

• Hasil filtering citra ini menunjukkan dengan jelas efek blurring

serta efek ringing yang terjadi.

• Hasil dalam contoh ini dapat digunakan untuk menjelaskan efek

ringing dan blurring pada citra yang lebih kompleks, yaitu dengan menganggap masing-masing pixel sebagai impulse-impulse.

Smoothing Frequency Domain Filters: ILPF (15)

Figure 20: Citra asli (kiri), hasil filtering (tengah), cross-section hasil filtering (kanan)

Smoothing Frequency Domain Filters: BLPF (1)

• Sebuah BLPF orde n dengan frekuensi cutoff pada jarak D0dari

titik asal didefinisikan sebagai berikut:

H(u, v) = 1

1+ [D(u, v)/D0]2n

(34)

• Berbeda dengan ILPF, BPLF tidak memiliki transisi yang tajam

pada frekuensi cutoff.

• Dalam kasus seperti ini, biasanya frekuensi cutoff didefinisikan

sebagai titik tempat nilai H(u, v)turun sampai level tertentu dibandingkan nilai maksimumnya.

Smoothing Frequency Domain Filters: BLPF (2)

Smoothing Frequency Domain Filters: BLPF (3)

• Contoh hasil filtering menggunakan BLPF dapat dilihat pada

gambar berikut.

• Perhatikan bahwa dalam gambar berikut tidak teramati adanya

efek ringing.

• Hal ini disebabkan karena transisi yang tidak tajam pada

Smoothing Frequency Domain Filters: BLPF (4)

Smoothing Frequency Domain Filters: BLPF (5)

Smoothing Frequency Domain Filters: BLPF (6)

Smoothing Frequency Domain Filters: BLPF (7)

• BLPF orde 1 tidak memiliki efek ringing. BLPF orde 2 sudah

memiliki efek ringing, tetapi pada umumnya tidak teramati.

• Fenomena ringing semakin parah jika orde BLPF semakin tinggi.

• BLPF dengan orde 20 sudah memiliki efek ringing yang mirip

dengan ILPF.

• Pada umumnya, digunakan BLPF orde 2 sebagai kompromi

antara efektifitas filter dan fenomena ringing.

• Plot BLPF dengan berbagai orde ditunjukkan pada gambar

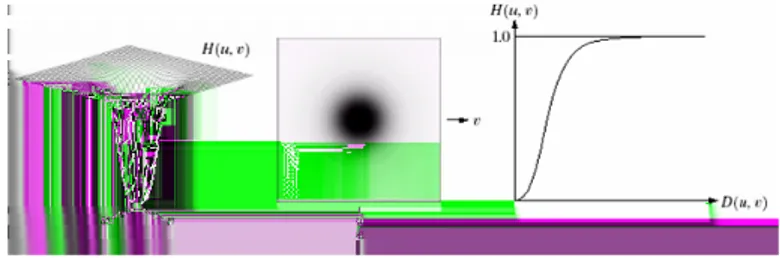
Smoothing Frequency Domain Filters: GLPF (1)

• Sebuah GLPF 2-D diberikan oleh hubungan

H(u, v) =e−D2(u,v)/2σ2 (35)

• Dalam Persamaan (35),σ adalah ukuran “spread” kurva Gaussian.

Jika kita definisikanσ =D0maka dapat dituliskan

H(u, v) =e−D2(u,v)/2D20 (36)

• Dalam persamaan (36), D0adalah frekuensi cutoff. Jika

D(u, v) =D0, magnitude filter memiliki nilai 0.607 kali nilai

Smoothing Frequency Domain Filters: GLPF (2)

• Seperti telah disebutkan di depan, filter spatial

h(x, y) =F−1H(u, v)dalam kasus ini juga berupa kurva Gaussian.

• Dari sini dapat disimpulkan bahwa implementasi GLPF tidak akan

menimbulkan fenomena ringing.

Smoothing Frequency Domain Filters: GLPF (3)

Smoothing Frequency Domain Filters: GLPF (4)

• Gambar-gambar berikut menunjukkan contoh output GLPF.

• Dari gambar-gambar ini terlihat bahwa efek smoothing GLPF

tidak sebaik BLPF untuk nilai frekuensi cutoff yang sama. (Dengan kata lain, GLPF tidak terlalu “selektif”).

• Meskipun demikian, GLPF memiliki keunggulan karena terdapat

jaminan tidak munculnya ringing. Hal ini sangat penting pada aplikasi-aplikasi yang tidak mengijinkan adanya artifact dalam bentuk apapun.

Smoothing Frequency Domain Filters: GLPF (5)

Smoothing Frequency Domain Filters: GLPF (6)

Smoothing Frequency Domain Filters: GLPF (7)

Sharpening Frequency Domain Filters: Intro (1)

• Operasi sharpening dalam ranah frekuensi merupakan kebalikan

operasi smoothing/blurring.

• Operasi sharpening dilakukan dengan menekan

komponen-komponen frekuensi rendah dan meloloskan komponen frekuensi tinggi.

• Jadi secara umum sebuah HPF dapat diperoleh dengan

menggunakan hubungan

Hhp(u, v) =1−Hl p(u, v) (37)

• Pada bagian ini akan dibahas HPF ideal (IHPF), Butterworth

Sharpening Frequency Domain Filters: Intro (2)

Sharpening Frequency Domain Filters: Intro (3)

Sharpening Frequency Domain Filters: Intro (4)

Sharpening Frequency Domain Filters: Intro (5)

• Sama seperti pada LPF ranah frekuensi, representasi spatial HPF

diatas dapat diperoleh dengan menghitungF−1_{[H(u, v)].}

• Bentuk representasi masing-masing filter dalam ranah spatial

Sharpening Frequency Domain Filters: IHPF (1)

• HPF ideal 2-D didefinisikan sebagai berikut:

H(u, v) =

{

0 jika D(u, v)≤ D0

1 jika D(u, v) >D0

(38)

• Sama seperti ILPF, IHPF juga tidak dapat direalisasikan secara

fisik.

• Kinerja IHPF ditunjukkan pada gambar berikut. Sama seperti ILPF,

IHPF juga menunjukkan fenomena ringing yang parah untuk nilai

Sharpening Frequency Domain Filters: IHPF (2)

Sharpening Frequency Domain Filters: BHPF (1)

• Fungsi alih sebuah BHPF dengan orde n dan freqkuensi cutoff D0

adalah

H(u, v) = 1

1+ [D0/D(u, v)]2n

(39)

• Kinerja BHPF orde 2 ditunjukkan pada gambar berikut. Terlihat

Sharpening Frequency Domain Filters: BHPF (2)

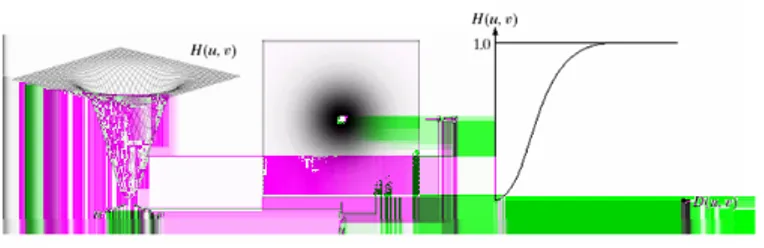
Sharpening Frequency Domain Filters: GHPF (1)

• Fungsi alih GHPF dengan frekuensi cutoff D0adalah

H(u, v) =1−e−D2(u,v)/2D02 (40)

• Kinerja GHPF ditunjukkan pada gambar berikut. Dari gambar

terlihat bahwa hasil filtering GHPF lebih halus dibandingkan kedua filter sebelumnya.

• GHPF dapat juga dibuat berdasarkan selisih 2 buah GLPF.

Pendekatan ini memungkinkan pengaturan yang lebih baik terhadap bentuk filter.

• Akan tetapi, biasanya GHPF diterapkan menggunakan Persamaan

Sharpening Frequency Domain Filters: GHPF (2)

Laplacian in the Frequency Domain (1)

• Dapat dibuktikan bahwa

F [ dnf(x) dxn ] = (ju)nF(u) (41)

• Oleh karena itu, dapat diturunkan

F [ ∂2_{f(x, y)} ∂x2 + ∂2_{f(x, y)} ∂y2 ] = (ju)2F(u, v) + (jv)2F(u, v) =−(u2+v2)F(u, v) (42)

Laplacian in the Frequency Domain (2)

• Atau dengan kata lain

F[∇2_{f(x, y)] =−(u}2_+v2_{)F(u, v) (43)}

• Persamaan (43) menyatakan bahwa Laplacian dapat

diimplementasikan dalam ranah frekuensi menggunakan filter

H(u, v) =−(u2+v2) (44)

• Jika transformasi Fourier “centered”, maka Persamaan (44)

menjadi

Laplacian in the Frequency Domain (3)

• Output filter Laplacian, dalam ranah spatial, diperoleh dengan

menghitung

∇2_{f(x, y) =F}−1_{{−[(u−M/2)}2_{+ (v−N/2)}2_{]F(u, v)} (46)}

• Sama seperti dalam ranah spatial, citra yang sudah dipertajam

menggunakan filter Laplacian dapat diperoleh dengan menghitung

Laplacian in the Frequency Domain (4)

• Operasi diatas dapat juga dilakukan dengan kernel tunggal

sebagai berikut

Unsharp Masking & High-boost Filtering (1)

• Sama seperti dalam ranah spatial, filter unsharp masking dan

high-boost diperoleh masing-masing dengan menghitung

fus(x, y) = f(x, y)− fl p(x, y) (49) fhb(x, y) =A f(x, y)− fl p(x, y) (50)

• Dalam ranah frekuensi, operasi unsharp masking dapat dilakukan

menggunakan filter komposit sebagai berikut

Hus(u, v) =1−Hl p(u, v) (51)

Unsharp Masking & High-boost Filtering (2)

• Sedangkan operasi high-boost filtering dapat dilakukan dengan

filter komposit sebagai berikut

Hhb(u, b) = (A−1) +Hhp(u, v) (52)

dengan Hhp(u, v)merepresentasikan sebuah filter high-pass.

• Secara umum, kinerja filter unsharp masking dan high-boost

pada ranah frekuensi setara dengan filter-filter pada ranah spatial.

High-Frequency Emphasis Filter

• Filter ini akan menonjolkan (accentuate) kontribusi komponen

frekuensi tinggi pada image enhancement.

• Hal ini dapat dicapai menggunakan filter sebagai berikut

Hh f e(u, v) =a+bHhp(u, v) (53)

dengan a≥0 dan b>a.

• Nilai-nilai a dan b yang sering digunakan masing-masing masing

antara 0.25 sampai 0.5 dan antara 1.5 sampai 2.0.

• Dapat dilihat bahwa filter ini sama dengan filter high-boost jika

Frequency Domain Denoising Filters: Intro

• Proses denoising dapat juga dilakukan di ranah frekuensi.

• Noise yang cocok ditangani di ranah frekuensi adalah noise yang

bersifat periodik.

• Dalam bab ini akan dibahas filter-filter ranah frekuensi yang

dapat digunakan untuk menghilangkan noise periodik, yaitu filter band-reject (BRF), band-pass (BPF) dan notch.

Frequency Domain Denoising Filters: BRF (1)

• Filter band-reject menghilangkan atau menekan satu pita

frekuensi disekeliling titik pusat transformasi Fourier.

• Sebuah filter band-reject ideal didefinisikan sebagai berikut:

H(u, v) =      1 jika D(u, v) <D0−W₂ 0 jika D0− W₂ ≤ D(u, v)≤ D0+W₂ 1 jika D(u, v) >D0+W₂ (54)

Frequency Domain Denoising Filters: BRF (2)

• Sebuah filter band-reject Butterworth orde-n didefinisikan

sebagai berikut: H(u, v) = 1 1+ [ D(u,v)W D2_(u,v)−D2 0 ]2n (55)

• Sebuah filter band-reject Gaussian didefinisikan sebagai berikut:

H(u, v) =1−e− 1 2 [ D2(u,v)−D2₀ D(u,v)W ]2 (56)

Frequency Domain Denoising Filters: BRF (3)

Figure 38: Plot BRF ideal (kiri), Butterworth orde 1 (tengah) dan Gaussian (kanan)

Frequency Domain Denoising Filters: BRF (4)

• BRF tepat digunakan untuk menghilangkan noise jika letak

komponen noise dalam ranah Fourier kurang lebih diketahui.

• Dalam contoh berikut, sebuah citra mengalami degradasi karena

noise sinusoidal. Komponen noise ini tampak jelas dalam spektrum Fourier.

• Untuk menghilangkan noise tersebut, dirancang sebuah filter

band-reject Butterworth orde 4 dengan pilihan radius dan lebar pita sedemikian sehingga semua titik spektrum noise tersebut dapat terlingkupi.

Frequency Domain Denoising Filters: BRF (5)

Frequency Domain Denoising Filters: BRF (6)

Frequency Domain Denoising Filters: BPF (1)

• Sebuah filter band-pass melakukan operasi yang berlawanan

dengan filter band-reject.

• Filter band-pass Hbp(u, v)dapat dibuat berdasarkan sebuah filter

band-reject Hbr(u, v)dengan hubungan

Hbp =1−Hbr(u, v) (57)

• Penggunaan BPF secara langsung terhadap suatu citra tidak

lazim karena hal ini pada umumnya akan menyebabkan hilangnya terlalu banyak detail citra.

• Biasanya, BPF digunakan untuk mengisolasi sinyal derau agar

Frequency Domain Denoising Filters: BPF (2)

Figure 41: Hasil filtering citra dengan noise sinusodal, menunjukkan bentuk sinyal noise tanpa “gangguan” isi citra.

Frequency Domain Denoising Filters: Notch (1)

• Sebuah filter notch menekan (atau melalukan) frekuensi yang

berada pada suatu lingkup tertentu disekeliling sebuah frekuensi tengah.

• Karena sifat simetri transformasi Fourier, filter notch harus

muncul sebagai pasangan yang simetris terhadap titik pusat transformasi (jumlah pasangan sembarang).

• Perkecualian dari aturan diatas adalah jika frekuensi tengah ada

pada titik pusat transformasi.

• Plot filter notch ideal, Butterworth dan Gaussian ditunjukkan

Frequency Domain Denoising Filters: Notch (2)

Frequency Domain Denoising Filters: Notch (3)

• Fungsi alih sebuah filter notch-reject dengan radius D0dan

frekuensi tengah pada(u0, v0)dan(−u0,−v0)adalah

H(u, v) = { 0 jika D1(u, v)≤D0atau D2≤ D0 1 lainnya (58) dengan D1(u, v) = [ (u−M/2−u0)2+ (v−N/2−v0)2 ]1/2 (59) dan [ − 2 ₋ 2]1/2

Frequency Domain Denoising Filters: Notch (4)

• Fungsi alih suatu filter notch-reject Butterworth orde n adalah

sebagai berikut: H(u, v) = 1 1+ [ D2 0 D1(u,v)D2(u,v) ]2 (61)

• Fungsi alih sebuah filter notch-reject Gaussian adalah sebagai

berikut: H(u, v) =1−e− 1 2 [ D1(u,v)_D2(u,v) D2₀ ] (62)

Frequency Domain Denoising Filters: Notch (5)

• Sama seperti pada pembahasan yang lalu, sebuah filter notch

untuk melalukan (pass) frekuensi tertentu dapat dibuat dengan berdasarkan filter notch-reject menggunakan hubungan

Hnp(u, v) =1−Hnr(u, v) (63)

• Jika u0 =v0 =0 sebuah filter notch-pass menjadi HPF.

• Contoh penggunaan filter notch ditunjukkan pada

Frequency Domain Denoising Filters: Notch (6)

Frequency Domain Denoising Filters: Notch (7)

Figure 44: Spektrum citra (kiri); spektrum sebuah notch-pass filter yang ditumpangkan pada spektrum citra (kanan)

Frequency Domain Denoising Filters: Notch (8)

Figure 45: Derau yang telah dipisahkan dari citra (kiri); hasil notch-reject filtering (kanan)