seperti yang telah diuraikan di atas adalah pekerjaan rumit. Semakin rumit bentuk fungsinya, semakin rumit pula masalah yang dihadapi. Untuk itu berikut ini diberikan suatu rangkaian rumus-rumus menghitung limit di suatu titik dengan cara sederhana. Kita mulai dengan teorema berikut: (bukti teorema diserahkan kepada pembaca).
Teorema 3.2.1 (Ketunggalan limit fungsi)
Jika limxa f(x) L dan limxa f(x)M maka L = M Teorema 3.2.2
(i) Jika m dan n konstanta, maka limxa (mxn)man (ii) Teorema akibat: limxa a a
(iii) Teorema akibat, jika m suatu konstanta maka limxa mm (iv) limxaxa
(v) limxa x a,a0 (vi) lim1 1, 0
a x a a x
Teorema 3.2.3 (Operasi pada limit fungsi)
Misalkan f dan g adalah fungsi-fungsi yang terdefinisi pada selang buka I yang memuat a kecuali mungkin pada a sendiri dan misalkan limit f dan g di a ada, jika
M x f a x ( ) lim dan g x N a x ( ) lim , maka:
(i) limxa (f(x)g(x))limxa f(x)limxa g(x)M N (ii) limxa (f(x)g(x))limxa f(x)limxa g(x)M N (iii)
lim
xa(
f
(
x
)
g
(
x
))
lim
xaf
(
x
)
lim
xag
(
x
)
MN
(iv) , lim ( ) 0 ) ( lim ) ( lim ) ( ) ( lim N asalkan g x M x g x f x g x f a x a x a x a x (v) n n a x n a x f(x) lim f(x) M
lim , dengan n bilangan positif dan lim f(x) a
x >0
(vi) Teorema akibat limxa (kf(x))klimxa f(x)kM k = konstanta. Teorema 3.2.4
Misalkan Pn(x) dan Pm(x) adalah polinom-polinom (suku banyak) dengan:
Pn(x) = cnxn + cn-1xn-1 + cn-2xn-2 + ……+ c1x + c0 dan
Pm(x) = cmxm + cm-1xm-1 + cm-2xm-2 + ……+ c1x + c0
cn, cn-1, cn-2, …c0 dan cm, cm-1, cm-2, …c0 adalah konstanta yang merupakan kosefisien-koefisien polinom, maka
Limit Fungsi dan Kontinuitas (i) limxa Pn(x)Pn(a) ;a (ii) ; ( ) 0 ) ( ) ( ) ( ) ( lim P a a P a P x P x P m m n m n a x Teorema :
Limit nilai mutlak fungsi : jika suatu fungsi mempunyai limit disuatu titik, maka nilai mutlak fungsinya mempunyai limit dititik itu, tetapi kebalikannya tidak berlaku.
Sifat-sifat : jika limxa f(x)L maka limxa f(x) L
Contoh 6:
Hitung limit fungsi berikut:
1. xlim x2 3 3.
lim
(
23
4
)
2 1
x
x
x 2. 3 5 2 3 lim 2 3 1 x x x x 4. 3 21
sin
sin
lim
x
x
x
Penyelesaian:1. xlim2 x3 xlim2 (x.x.x) xlim2 x.xlim2 x.xlim2 x = (-2)(-2)(-2) = -8 2. ) 3 ( lim 5 2 3 lim 3 5 2 3 lim 1 2 3 1 2 3 1 x x x x x x x x x ( 1) 3 5 ) 1 ( 2 ) 1 ( 3 3 2 0 2 0 2 5 2 3 3.
lim
(
3
4
)
lim
lim
3
lim
4
2 1 2 1 2 1 2 1 2 2
x
x
xx
x
x
x
x
lim lim 3lim12 42 1 2 1 x x x x x x 4 23 4 2 3 4 1 4. 3 2 3 2
1
sin
sin
lim
sin
1
sin
lim
x
x
x
x
x x 3 1 3 3 2 22
1
1
1
1
sin
1
lim
sin
lim
x
x
x x Contoh 7:Hitung limit fungsi berikut dengan menggunakan rumus-rumus limit: 1. lim 3 3 a x a x a x 4. x x x 2 4 lim 4 2. 2 6 5 lim 2 2 x x x x 5. 2 2 1 1 lim 2 x x x 3. 1 3 2 2 lim 3 2 1 x x x x x
lim ( 2 1 2) a ax x a x 2 2 3 2 1 ) . ( 1 a a a a a 2. lim ( 3) 1 ) 2 ( ) 3 )( 2 ( lim 2 6 5 lim 2 2 2 2 x x x x x x x x x x 3. ) 1 2 2 )( 1 ( ) 2 )( 1 ( lim 1 3 2 2 lim 2 1 3 2 1 x x x x x x x x x x x 2 2 1 1 2 1 ) 1 2 2 ( ) 2 ( lim 2 1 x x x x 4. lim 2 4 ) 2 ( ) 2 )( 2 ( lim 2 4 lim 4 4 4 x x x x x x x x x 5. 2 2 2 lim 2 2 1 ) 1 ( lim 2 2 x x x x x x x 4 1 2 1 lim ) 2 ( 2 ) 2 ( lim 2 2 x x x x x x
3.3 Limit Kiri dan Limit Kanan (Limit Sepihak)
Sebelum kita membahas konsep “Limit kiri” dan “limit kanan”, perhatikan dengan seksama fungsi f beserta grafik pada contoh berikut :
Contoh : 0 , 1 0 , 1 | | ) ( x x x x x f
fungsi f ini terdefenisi pada semua bilangan real kecuali di x = 0 jadi Df = R – {0}.
Sebagaimana halnya pada contoh 2 maka pada contoh ini kita amati perilaku fungsi f(x) =| xx| disekitar x = 0. Bilamana x cukup dekat ke 0, maka f(x) tidak mendekati suatu nilai tertentu, sehingga kita katakan
| | lim ) ( lim 0 0 x x x f x x tidak ada .
Akan tetapi, bilamana x mendekati 0 dari arah kanan (dari arah nilai-nilai x yang besar dari 0), maka f(x) akan mendekati 1. dalam hal ini kita katakan bahwa fungsi x mempunyai “limit kanan” di 0 dengan nilai limit kanan 1, ditulis
1 | | lim ) ( lim 0 0 x x x f x x
Demikian juga bilamana x mendekati 0 dari arah kiri (dari arah nilai-nilai x yang lebih kecil 0), maka f(x) akan mendekati bilangan -1. Dalam hal ini kita katakan bahwa fungsi f mempunyai “limit kiri” di 0 dengan nilai limit kirinya -1, ditulis
1 | | lim ) ( lim 0 0 x x x f x x
Dari kenyataan ini kita defenisikan limit kanan dan limit kiri sebagai berikut : 2 -2 -1 1 0 y x Gambar grafik f(x) = | | x x
Limit Fungsi dan Kontinuitas
Definisi 3.3.1: (Definisi Limit Kanan)
Misalkan f sebuah fungsi paling sedikit terdefinisi pada selang terbuka (a,b), maka limit kanan f dititik a ditulis sebagai:
L x f
a
xlim ( ) atau ( f(x) L bila x a+) jika > 0 terdapat bilangan > 0 sedemikian sehingga
0< x - a < f(x) - L <
perhatikan bahwa 0< x–a < mengakibatkan x > a yang berarti x terletak disebelah kanan a Definisi 3.3.2: (Definisi Limit Kiri)
Misalkan f sebuah fungsi paling sedikit terdefinisi pada selang terbuka (c,a), maka limit kiri f dititik a ditulis sebagai:
L x f
a
xlim ( ) atau ( f(x) L bila x a-) jika > 0 terdapat bilangan > 0 sedemikian sehingga
0< a – x < f(x) - L <
perhatikan bahwa 0< a–x < mengakibatkan x < a yang berarti x terletak disebelah kiri a
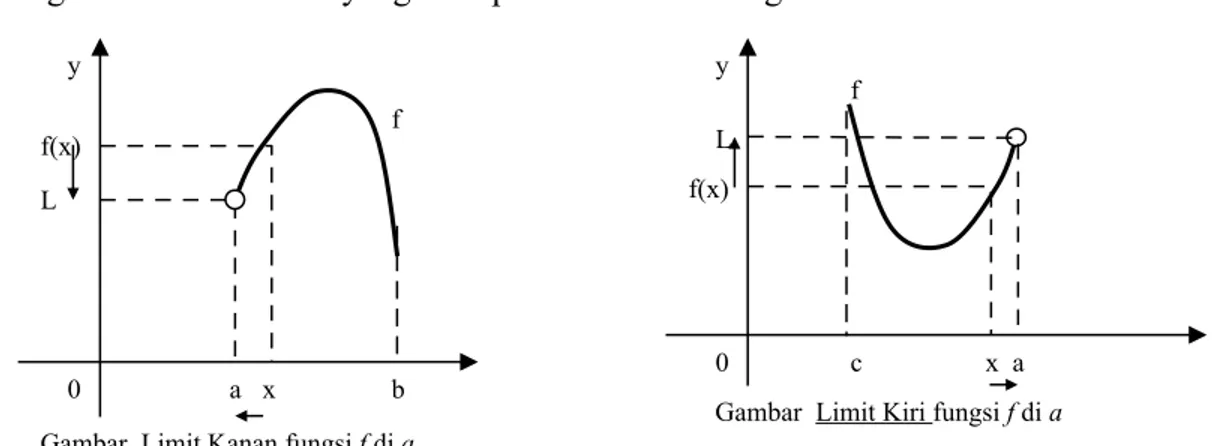
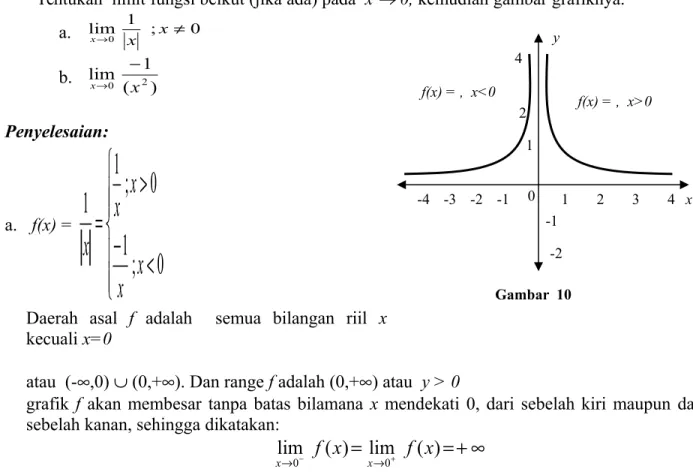
Perhatikan gambar dibawah ini yang memperlihatkan situasi geometri untuk limit kanan dan limit kiri
Bandingkan kedua defenisi ini dengan defenisi limit fungsi f di a. L
x f
a
x ( )
lim jika > 0 , > 0 sehingga 0 < | x – a | < | f(x) – L | <
Bila x a+ , maka x > a. Akibatnya x – a > 0, sehingga
| x – a | = x – a, yang bila digantikan pada defenisi limit akan menghasilkan defenisi limit kanan. Demikian juga
bila x a- , maka x < a. Akibatnya x – a < 0, sehingga
| x – a | = a – x, yang bila digantikan pada defenisi limit akan menghasilkan defenisi limit kiri.
Catatan : f b a x f(x) L y 0
Gambar Limit Kanan fungsi f di a
y 0 x f(x) a c L f
3. Jika fungsi f terdefenisi pada selang terbuka (c,d) maka
) ( lim f x
c
x ditulis limxc f(x), dan xlimd f(x) ditulis limxd f(x) Berdasarkan catatan nomor 3, maka dapat dipahami bahwa :
limx0 x 0
karena f terdefinisi pada Df = [ 0, ) yang berarti f terdefenisi pada interval buka (0,), sehingga menurut catatan no.3 :
) ( lim
0 f x
x ditulis limx0 f(x) = 0
hubungan antara limit fungsi disatu titik dengan limit kiri dan limit kanannya dititik itu diberikan dalam teorema berikut :
Teorema 3.3.3.a L x f x f x f a x a x a x ( ) lim ( )lim ( ) lim Catatan :
Teorema ini menyatakan bahwa limit kiri dan limit kanan fungsi f di a dapat dihitung dengan cara menghitung limit fungsinya di a, asalkan limit fungsi tersebut ada.
Teorema 3.3.3.b Jika ada. dak ti ) ( lim maka dengan ) ( lim dan ) ( lim 1 2 1 2 x f L L L x f L x f a x a x a x Contoh 1. a. Diberikan fungsi
2
;
;
1
1
)(
2
x
x
x
xf
Tunjukkan bahwa limx1 f(x) tidak ada, dan gambar grafiknya.
Penyelesaian: f(x) =
1
;
2
1
;
2x
x
x
Untuk menghitung limit kiri dari f digunakan persamaan 1 ; ) ( 2 x x x f 1 0 1 2 -1 x y y = x2 y = 2 Gambar 6
Limit Fungsi dan Kontinuitas
(domain dari f di sebelah kiri dari 1). Sebaliknya untuk menghitung limit kanan dari f digunakan persamaan f(x)2 ; x1. Sehingga
1
lim
)
(
lim
2 1 1
f
x
xx
x sedangkan 2 2 lim ) ( lim 1 1 x x f xkarena limit kiri tidak sama dengan limit kanan maka disimpulkan bahwa limx1 f(x) tidak ada. Contoh 2: Diberikan fungsi f(x) =
1
;
2
1
1
;
1
;
1
2
2 2x
x
x
x
x
x
x
a. Gambar grafik fb. Tentukan limx1 f(x) , jika ada c. Tentukan limx1 f(x) , jika ada
Penyelesaian:
a. Grafik fungsi f diatur oleh 3 persamaan yaitu : y = 2x + 1, pada selang [1,+)
y = -x2 , pada selang [-1,1)
y = x2 + 2x,, pada selang (-,-1)
sehingga grafik f merupakan gabungan dari tiga kurva diatas (gambar 7)
b. Dengan menggunakan definisi limit, dapat ditunjukkan bahwa pada titik a = -1 maka:
Limit kiri : x
lim
1f
(
x
)
xlim
1x
2
2
x
(
1
)
2
2
(
1
)
1
danLimit kanan : x
lim
1f
(
x
)
xlim
1(
x
2)
(
1
)
2
1
karena limit kiri sama dengan limit kanan maka disimpulkan bahwa xlim1 f(x) 1
c. Pada titik a = 1 , maka
Limit kiri :
lim
(
)
lim
2(
1
)
21
1
1
f
x
xx
x dan
Limit kanan : limx1 f(x) xlim1 (2x1)3
karena limit kiri tidak sama dengan limit kanan maka disimpulkan bahwa ) ( lim 1 f x x tidak ada. Contoh 3: 1 0 1 2 -1 y f(x) 3 -1 -2 x Gambar 7
Perhatikan bahwa grafik fungsi f adalah sebuah lengkungan yang tidak terputus pada selang (-3,1) ; [1,3) ; [3,6); (6,9].
Dari grafik di atas mudah diketahui bahwa :
7 ) ( lim 3 f x x xlim3 f(x) 5 1 ) ( lim 1 f x x xlim6 f(x) 4 4 ) ( lim 1 f x x xlim6 f(x) 4 3 ) ( lim 3 f x x xlim9 f(x) 5
Perhatikan bahwa, dititik x = -3, hanya ada limit kanan dan f(-3) tidak terdefinisi sedangkan dititik x = 9, hanya ada limit kiri dan f(9)= 5 ( terdefinisi)
Dan dititik x = 1, limx1 f(x) limx1 f(x) sehingga limx1 f(x) tidak ada demikian juga dititik
x=3, xlim3 f(x) xlim3 f(x) sehingga limx3 f(x) tidak ada Dan dititik x=6, xlim6 f(x) xlim6 f(x) 4 sehingga
limx6 f(x)4 dan f(6) = 8 Catatan:
Nilai fungsi disuatu titik tidak mempengaruhi penentuan limit di titik tersebut.
3.4
Limit Tak Hingga Dan Limit Di Tak Hingga
3.4.1. LIMIT TAK HINGGA
Definisi 3.4.1.1:
Misalkan f suatu fungsi yang terdefinisi pada selang terbuka yang memuat a, kecuali mungkin pada a sendiri, maka:
x 1 2 3 4 5 6 7 8 9 1 2 3 4 5 6 7 -1 -2 -3 0 Gambar 8
Limit Fungsi dan Kontinuitas
(i) Limit f(x) dikatakan “membesar tanpa batas” (+) bilamana x mendekati a, ditulis sebagai: ( ) lim f x a x jika M > 0, > 0 sedemikian sehingga
M x f a x ( ) 0
(ii) Limit f(x) dikatakan “mengecil tanpa batas” (-) bilamana x mendekati a, ditulis
sebagai: ( ) lim f x a x jika M>0, >0 sedemikian sehingga
M x f a x ( ) 0
Sebagai illustrasi perhatikan contoh-contoh berikut:
Contoh 1:
Selidiki perilaku fungsi f(x) =
x
1
disekitar 0; (x 0) Perhatikan nilai-nilai fungsi f bilamana x dibuat dekat ke 0; (x 0) Tabel 3.4.1.1 x 2 1 10 1 10000 1 1000000 1 … 0 … 1000000 1 10000 1 10 1 2 1 f(x) 2 10 10000 1000000 … ? … -100000 0 -10000 -10 -2 Dari tabel 3.4.1.1 terlihat bahwa :
Nilai f(x) akan semakin membesar tanpa batas, bilaman x semakin dekat ke 0 dari arah kanan , dalam hal ini dikatakan
( ) lim 0 f x x
Nilai f(x) akan semakin mengecil tanpa batas, bilaman x semakin dekat ke 0 dari arah kiri , dalam hal ini dikatakan
( ) lim 0 f x x
Jadi limit kanan f(x) dan limit kiri f(x) pada x =0 dikatakan tidak ada.
Catatan : Lambang - dan + bukan bilangan.
Terlihat bahwa tidak ada bilangan tertentu yang bisa didekati f(x) manakala x dibuat mendekati 0.
Jadi x 1 lim tidak ada. 1 0 1 2 3 x -1 -2 -3 -4 -1 -2 -4 2 y f(x) = , x>0 f(x) = , x<0 Gambar 9
b. lim ( 12) 0 x x Penyelesaian: a. f(x) =
0
;
1
0
;
1
1
x
x
x
x
x
Daerah asal f adalah semua bilangan riil x kecuali x=0
atau (-,0) (0,+). Dan range f adalah (0,+) atau y > 0
grafik f akan membesar tanpa batas bilamana x mendekati 0, dari sebelah kiri maupun dari sebelah kanan, sehingga dikatakan:
( ) lim ( ) lim 0 0 f x x f x x
Meskipun dalam hal ini limit kiri dan limit kanannya sama-sama menuju , akan tetapi
bukan suatu bilangan, maka dikatakan:
x x x ; 1 lim
0 (membesar tanpa batas atau tidak ada.)
b. g(x) = 2 1
x
Perhatikan bahwa nilai f(x) akan mengecil tanpa batas bilamana x semakin dekat ke nol, baik dari kiri maupun dari kanan, maka kita katakan ( ) 1 lim 2 0 x x (tidak ada) 1 0 1 2 3 4 -1 -2 -3 -4 -1 -2 2 4 f(x) = , x>0 f(x) = , x<0 x Gambar 10 1 0 1 2 3 x -1 -2 -3 y -1 -2 -4 f(x) = , x>0 f(x) = , x<0 Gambar 11