BAB II
LANDASAN TEORI
1.1 Loyalitas Pelanggan
Menurut Griffin (2002:4) “loyalty is defined as non random purchase expressed
over time by some decision making unit”. Berdasarkan defenisi tersebut dapat
dijelaskan bahwa loyalitas lebih mengacu pada wujud perilaku dari unit-unit pengambilan keputusan untuk melakukan pembelian secara terus menerus terhadap barang dan jasa suatu perusahaan yang dipilih (Ratih, 2005:129).
Dengan meningkatkan loyalitas konsumen maka akan memberikan manfaat bagi perusahaan, setidaknya dalam beberapa hal berikut:
1. Menurunkan biaya pemasaran, bahwa biaya untuk menarik pelanggan baru jauh lebih besar bila dibandingkan dengan mempertahankan pelanggan yang ada.
2. Menurunkan biaya transaksi, seperti biaya negosiasi kontrak, pemrosesan pesanan, pembuatuan account baru dan biaya lain-lain.
3. Menurunkan biaya turn over konsumen, karena tingkat kehilangan konsumen rendah.
4. Menaikkan penjualan yang akan memperbesar pangsa pasar perusahaan. 5. Word of mouth yang bertambah, dengan asumsi bahwa pelanggan yang setia
berarti puas terhadap produk yang ditawarkan.
6. Menurunkan biaya kegagalan, seperti biaya penggantian atas produk yang rusak.
1.2 Kuesioner
Kuesioner merupakan suatu daftar pertanyaan yang akan ditanyakan kepada responden (obyek penelitian) terdiri dari baris-baris dan kolom-kolom untuk diisi dengan jawaban-jawaban yang ditanyakan. Tujuan kuesioner adalah memperoleh informasi yang relevan dengan tujuan survei, memperoleh informasi dengan tingkat keandalan dan tingkat keabsahan setinggi mungkin (Rangkuti, 1997).
Dengan melakukan penyebaran kuesioner untuk mengukur persepsi responden digunakan Skala Likert. Skala Likert adalah suatu skala psikometrik yang umum digunakan dalam kuesioner, dimana tingkat ukuran ordinal yang banyak digunakan dalam penelitian sosial terutama mengukur pendapat, sikap atau persepsi seseorang. Skala ini meminta responden menunjukkan tingkat persetujuan atau ketidaksetujuannya terhadap serangkaian pernyataan tentang suatu obyek mulai dari “sangat setuju” sampai dengan “sangat tidak setuju”. Pertanyaan dalam kuesioner dibuat dengan menggunakan skala 1 -5 untuk mewakili pendapat dari responden.
Tabel 2.1 Penilaian Jawaban Kuesioner Penilaian Informasi Skor Jawaban Responden
Sangat Setuju 5
Setuju 4
Ragu-ragu 3
Tidak Setuju 2
Sangat Tidak Setuju 1
1.3 Method of Successive Interval (MSI)
Method of successive interval adalah metode penskalaan untuk menaikkan skala
pengukuran ordinal ke skala pengukuran interval. Melakukan manipulasi data dengan cara menaikkan skala ordinal menjadi skala interval bertujuan untuk tidak melanggar kelaziman (data interval/ratio), juga untuk mengubah syarat distribusi normal agar dapat dipenuhi ketika menggunakan statistika parametrik. Sehingga
transformasi menggunakan model ini tidak perlu melakukan uji normalitas (http://dwikurniawan13.wordpress.com).
Langkah-langkah method of successive interval dapat dilakukan dengan cara sebagai berikut:
1. Perhatikan nilai jawaban dari setiap pertanyaan dalam kuesioner.
2. Untuk setiap pertanyaan tersebut, lakukan perhitungan banyak responden yang menjawab skor 1, 2, 3, 4, 5 = frekuensi (f).
3. Setiap frekuensi dibagi dengan banyak n responden dan hasil adalah proporsi (p).
4. Kemudian hitung proporsi kumulatif (pk).
5. Dengan menggunakan tabel normal, hitung nilai distribusi normal (Z) untuk setiap proporsi kumulatif yang diperoleh.
𝐹(𝑍) = 1 √2𝜋𝑒
(−𝑍2 )2
, −∞ < 𝑍 < +∞ 6. Tentukan nilai densitas normal (fd) yang sesuai dengan nilai Z. 7. Tentukan nilai interval (scale value) untuk setiap skor jawaban.
8. Sesuaikan nilai skala ordinal ke interval, yaitu scale value (SV) yang nilainya terkecil (harga negatif yang terbesar) diubah menjadi sama dengan jawaban responden yang terkecil melalui transformasi berikut:
Transformed Scale Value : SV = – (Min data – Min SV)
1.4 Uji Validitas dan Reliabilitas 2.4.1 Uji Validitas
Validitas menunjukkan sejauh mana alat ukur yang telah disusun dapat digunakan untuk mengukur apa yang hendak diukur secara tepat. Alat ukur yang mampu mengukur apa yang ingin di ukur secara tepat disebut valid, berarti memiliki validitas tinggi. Sebaliknya alat ukur yang tidak valid berarti memiliki validitas rendah. Untuk menguji validitas alat ukur, dihitung korelasi antara masing-masing
pernyataan dengan skor total dengan menggunakan rumus teknik korelasi Pearson
Product Moment ( Situmorang, 2007).
Uji hipotesa:
H0 : Item/variabel tidak valid
H1 : Item/variabel valid
𝑟𝑥𝑦 =
𝑛 ∑ 𝑋𝑌 − (∑ 𝑋)(∑ 𝑌)
√[{𝑛 ∑ 𝑋2− (∑ 𝑋)2}{𝑛 ∑ 𝑌2− (∑ 𝑌)2}]
Keterangan: 𝑟𝑥𝑦 = Koefisien korelasi
𝑋 = Skor responden untuk tiap item
𝑌 = Total skor tiap responden dari seluruh item n = Jumlah responden
Dasar pengambilan keputusan:
a) Jika rhitung > r0,05(n –2) dan positif, maka H0 ditolak H1 diterima atau
item/variabel tersebut valid.
b) Jika rhitung < r0,05(n –2) dan negatif, maka H0 diterima H1 ditolak atau
item/variabel tersebut tidak valid.
c) Jika rhitung > r0,05(n –2) dan negatif, maka H0 diterima H1 ditolak atau
item/variabel tersebut tidak valid.
2.4.2 Uji Reliabilitas
Reliabilitas adalah indeks yang menunjukkann sejauh mana suatu alat ukur dapat dipercaya atau dapat diandalkan. Bila suatu alat ukur dipakai dua kali untuk mengukur gejala yang sama dan hasil pengukuran yang diperoleh relatif konsisten, maka alat ukur tersebut reliabel. Untuk menghitung reliabilitas alat ukur digunakan rumus Cronbach’s Alpha (α) (Situmorang, 2007).
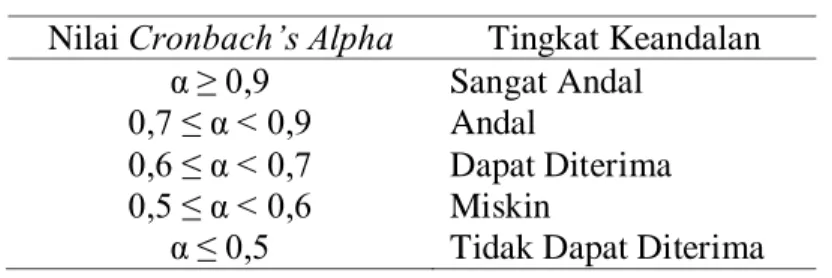
Nilai tingkat keandalan Cronbach’s Alpha dapat ditunjukkan pada tabel berikut ini:
Tabel 2.2 Tingkat Keandalan Cronbach’s Alpha Nilai Cronbach’s Alpha Tingkat Keandalan
α ≥ 0,9 0,7 ≤ α < 0,9 0,6 ≤ α < 0,7 0,5 ≤ α < 0,6 α ≤ 0,5 Sangat Andal Andal Dapat Diterima Miskin
Tidak Dapat Diterima Uji hipotesa:
H0 : Variabel tidak reliabel
H1 : Variabel reliabel
𝛼 = ( 𝑘
𝑘 − 1) (1 − ∑ 𝑆𝑖2
𝑆𝑡2 )
Keterangan: ∑𝑆𝑖2 = Jumlah varians skor tiap-tiap item 𝑆𝑖2 =∑ 𝑋𝑖
2−(∑ 𝑋𝑖) 𝑛
𝑛
𝑋𝑖 = Skor responden item i (i = 1, 2, 3, ..., n)
n = Jumlah Responden 𝑆𝑡2 = Varians total
k = Jumlah item
Dasar pengambilan keputusan:
a) Jika nilai α ≥ 0,6, maka H0 ditolak H1 diterima atau variabel reliabel.
b) Jika nilai α < 0,6, maka H0 diterima H1 ditolak atau variabel tidak reliabel.
1.5 Uji Multikolinearitas
Multikolinearitas berarti antara variabel bebas yang satu dengan variabel bebas yang lain dalam model regresi saling berkorelasi linear. Biasanya, korelasinya mendekati sempurna atau sempurna (koefisien korelasinya tinggi atau bahkan
satu). Adanya multikolinearitas dalam regresi dapat diketahui dengan menganalisis koefisien korelasi antara variabel bebas (Hasan, 2002).
𝑋1 𝑋2 … 𝑋𝑘 𝑋1 𝑋2 ⋮ 𝑋𝑛 ( 𝑟11 𝑟21 ⋮ 𝑟𝑛1 𝑟12 𝑟22 ⋮ 𝑟𝑛2 … … … 𝑟1𝑘 𝑟2𝑘 ⋮ 𝑟𝑛𝑘 ) Uji hipotesa:
H0 : Tidak terdapat multikolinearitas antar variabel bebas
H1 : Terdapat multikolinearitas antar variabel bebas
𝑟𝑛𝑘 = ∑(𝑋𝑛− 𝑋̅𝑛)(𝑋𝑘− 𝑋̅𝑘) √∑(𝑋𝑛− 𝑋̅𝑛)2∑(𝑋
𝑘− 𝑋̅𝑘)2
Keterangan: 𝑟𝑛𝑘 = koefisien korelasi antara 𝑋𝑛 dan 𝑋𝑘 𝑋𝑛 = Skor responden untuk 𝑋𝑛
𝑋𝑘 = Skor responden untuk 𝑋𝑘
Dasar pengambilan keputusan:
a) Jika nilai 𝑟𝑛𝑘 < 0,5, maka H0 diterima H1 ditolak atau tidak terdapat
multikolinearitas antar variabel bebas.
b) Jika nilai 𝑟𝑛𝑘 > 0,5, maka H0 ditolak H1 diterima atau terdapat
multikolinearitas antar variabel bebas.
1.6 Uji Heterokedastisitas
Heterokedastisitas berarti variasi (varians) variabel tidak sama untuk semua pengamatan. Pada heterokedastisitas, kesalahan yang terjadi tidak random (acak) tetapi menunjukkan hubungan yang sistematis sesuai dengan besarnya satu atau lebih variabel bebas. Adanya heterokedastisitas dalam regresi dapat diketahui dengan menggunakan uji koefisien korelasi Spearman (Hasan, 2002).
Uji hipotesa:
H0 : Tidak terdapat heterokedastisitas
H1 : Terdapat heterokedastisitas
𝑟𝑠 = 1 − 6 ( ∑ 𝑑
2
𝑛3− 𝑛)
Keterangan: d = Selisih antara rangking variabel dan ranking nilai mutlak error (|𝑒|)
n = Jumlah sampel
Apabila nilai-nilai dari tiap variabel (X dan Y) ada yang sama maka lebih dahulu dicari nilai tengah urutan nilai-nilai yang sama tersebut. Rumus 𝑟𝑠 menjadi: 𝑟𝑠 = ∑ 𝑟𝑥2+ ∑ 𝑟𝑦2− ∑ 𝑑2 2√∑ 𝑟𝑥2. ∑ 𝑟𝑦2 𝑟𝑥2 = 𝑛3− 𝑛 𝑛 − ∑ 𝑡𝑥3− 𝑡 𝑥 𝑛 𝑟𝑦2= 𝑛3− 𝑛 𝑛 − ∑ 𝑡𝑦3− 𝑡 𝑦 𝑛
Keterangan: 𝑡𝑥 = Jumlah variabel X yang urutannya sama 𝑡𝑦 = Jumlah variabel Y yang urutannya sama
Pengujian hipotesis dilakukan dengan menggunakan distribusi t. 𝑡0=
𝑟𝑠√𝑛 − 2
√1 − 𝑟𝑠
Dasar pengambilan keputusan:
a) Jika 𝑡0≤ 𝑡𝛼(𝑛−2), maka H0 diterima H1 ditolak atau tidak terdapat
heterokedastisitas.
b) Jika 𝑡0> 𝑡𝛼(𝑛−2), maka H0 ditolak H1 diterima atau terdapat
1.7 Uji Autokorelasi
Autokorelasi berarti terdapatnya korelasi antar anggota sampel atau data pengamatan yang diurutkan berdasarkan waktu, sehingga munculnya suatu datum dipengaruhi oleh datum sebelumnya. Autokorelasi muncul pada regresi yang menggunakan data berskala (time series). Adanya autokorelasi dalam regresi dapat diketahui dengan menggunakan uji Durbin-Watson (Hasan, 2002).
Uji hipotesa:
H0 : Tidak terdapat autokorelasi
H1 : Terdapat autokorelasi 𝑑 =∑ (𝑒𝑡− 𝑒𝑡−1) 2 𝑡=𝑁 𝑡=2 ∑𝑡=𝑁𝑡=1𝑒𝑡2
Keterangan: 𝑒𝑡 = nilai residu periode t
𝑒𝑡−1 = nilai residu periode t-1
Dasar pengambilan keputusan:
a) Jika 0 < d < dL, maka terjadi autokorelasi positif
b) Jika dL ≤ d ≤ dU atau (4 – dU) ≤ d ≤ (4 – dL), maka hasil tidak dapat disimpulkan
c) Jika 4 – dL < 0, maka terjadi autokorelasi negatif d) Jika dU < d < (4 – dU), maka tidak terjadi autokorelasi
1.8 Analisis Regresi Linier
Analisis regresi berkenaan dengan studi ketergantungan dari suatu variabel yang disebut variabel tidak bebas (dependent variable), pada satu atau lebih variabel yaitu variabel yang menerangkan, dengan tujuan untuk memperkirakan dan atau meramalkan nilai rata-rata dari variabel tidak bebas apabila nilai variabel yang
menerangkan sudah diketahui. Variabel yang menerangkan sering disebut variabel bebas (independent variable) atau explanatory variable (Supranto, 2005:36).
1.9 Analisis Regresi Linier Ganda
Regresi linear berganda adalah regresi di mana variabel terikatnya (Y) dihubungkan/dijelaskan lebih dari satu variabel, mungkin dua, tiga dan seterusnya variabel bebas (𝑋1, 𝑋2, 𝑋3, … , 𝑋𝑘) namun masih menunjukkan diagram hubungan yang linier (Hasan, 2002).
Bentuk umum persamaan regresi linier berganda: 𝑌𝑖 = 𝑏0+ 𝑏1𝑋1𝑖 + 𝑏2𝑋2𝑖+ ⋯ + 𝑏𝑘𝑋𝑖𝑘+ 𝜀𝑖
keterangan: 𝑌𝑖 = Variabel tak bebas
𝑋𝑖𝑘 = Variabel bebas ke-k dan pengamatan ke-i
k = 1, 2, 3, ..., j i = 1, 2, 3, ..., n
b0 = konstanta yang merupakan intersep (titik potong) antara garis
dengan sumbu tegak Y
bk = Parameter atau koefisien regresi yang akan ditaksir 𝜀𝑖 = Suatu bagian kesalahan taksiran untuk pengamatan ke-i
Bentuk data yang akan diolah dari hasil pengamatan adalah sebagai berikut:
Tabel 2.3 Bentuk Pengolahan Data No Observasi Variabel Tak Bebas (Y) Variabel Bebas 𝑋1 𝑋2 𝑋3 … 𝑋𝑘 1 𝑌1 𝑋11 𝑋12 𝑋13 … 𝑋1𝑘 2 𝑌2 𝑋21 𝑋22 𝑋23 … 𝑋2𝑘 3 𝑌3 𝑋31 𝑋32 𝑋33 … 𝑋3𝑘 ⋮ ⋮ ⋮ ⋮ ⋮ … ⋮ n 𝑌𝑛 𝑋𝑛1 𝑋𝑛2 𝑋𝑛3 … 𝑋𝑛𝑘
Untuk memperkirakan parameter b0, b1, b2, ..., bk ditentukan dengan
menggunakan metode kuadrat terkecil biasa, sehingga ∑𝜀𝑖2 = minimum (terkecil). Hal ini diperoleh dengan jalan menurunkan secara parsial terhadap b0, b1, b2, ..., bk
dan samakan dengan nol (Supranto, 2005).
Dirumuskan sebagai berikut: ∑ 𝜀𝑖2= 𝑛 𝑖=1 ∑(𝑌𝑖− 𝑌̂𝑖) 2 𝑛 𝑖=1 ∑ 𝜀𝑖2 𝑛 𝑖=1 = ∑(𝑌𝑖− 𝑏0− 𝑏1𝑋𝑖1− 𝑏2𝑋𝑖2− ⋯ − 𝑏𝑘𝑋𝑖𝑘)2 𝑛 𝑖=1
Mencari turunan parsial untuk b0, b1, b2, ..., bk dan samakan dengan nol.
𝜕 ∑𝑛 𝜀𝑖2 𝑖=1 𝜕𝑏0 = 2 ∑(𝑌𝑖− 𝑏0− 𝑏1𝑋𝑖1− 𝑏2𝑋𝑖2− ⋯ − 𝑏𝑘𝑋𝑖𝑘)(−1) = 0 𝑛 𝑖=1 𝜕 ∑𝑛 𝜀𝑖2 𝑖=1 𝜕𝑏1 = 2 ∑(𝑌𝑖− 𝑏0− 𝑏1𝑋𝑖1− 𝑏2𝑋𝑖2− ⋯ − 𝑏𝑘𝑋𝑖𝑘)(−𝑋𝑖1) = 0 𝑛 𝑖=1 ⋮ 𝜕 ∑𝑛 𝜀𝑖2 𝑖=1 𝜕𝑏𝑘 = 2 ∑(𝑌𝑖− 𝑏0− 𝑏1𝑋𝑖1− 𝑏2𝑋𝑖2− ⋯ − 𝑏𝑘𝑋𝑖𝑘)(−𝑋𝑖𝑘) = 0 𝑛 𝑖=1
Sehingga diperoleh persamaan normal sebagai berikut: 𝑛𝑏0+ 𝑏1∑ 𝑋𝑖1 𝑛 𝑖=1 + 𝑏2∑ 𝑋𝑖2 𝑛 𝑖=1 + ⋯ + 𝑏𝑘∑ 𝑋𝑖𝑘 𝑛 𝑖=1 = ∑ 𝑌𝑖 𝑛 𝑖=1 𝑏0∑ 𝑋𝑖1 𝑛 𝑖=1 + 𝑏1∑ 𝑋𝑖12 𝑛 𝑖=1 + 𝑏2∑ 𝑋𝑖1𝑋𝑖2 𝑛 𝑖=1 + ⋯ + 𝑏𝑘∑ 𝑋𝑖1𝑋𝑖𝑘 𝑛 𝑖=1 = ∑ 𝑋𝑖1𝑌𝑖 𝑛 𝑖=1 ⋮ 𝑏0∑ 𝑋𝑖1 𝑛 𝑖=1 + 𝑏1∑ 𝑋𝑖1𝑋𝑖𝑘 𝑛 𝑖=1 + 𝑏2∑ 𝑋𝑖1𝑋𝑖2 𝑛 𝑖=1 + ⋯ + 𝑏𝑘∑ 𝑋𝑖𝑘2 𝑛 𝑖=1 = ∑ 𝑋𝑖𝑘𝑌𝑖 𝑛 𝑖=1 ⋯ ⋯ (1)
1.10 Model Regresi Linier Dengan Pendekatan Matriks
Seperti pada persamaan (1) akan lebih sederhana dengan menggunakan matriks 𝑌 = 𝑋𝑏 + 𝜀 Dimana: 𝑌 = [ 𝑌1 𝑌2 ⋮ 𝑌𝑛 ] , 𝑋 = [ 1 𝑋11 1 𝑋21 𝑋12 𝑋22 … 𝑋1𝑘 … 𝑋2𝑘 ⋮ ⋮ 1 𝑋𝑛1 ⋮ 𝑋𝑛2 … ⋮ … 𝑋𝑛𝑘 ] , 𝑏 = [ 𝑏0 𝑏1 ⋮ 𝑏𝑘 ] , 𝜀 = [ 𝑒1 𝑒2 ⋮ 𝑒𝑛 ]
Maka untuk mendapatkan penaksiran kuadrat terkecil bagi b yang minimum
∑𝑛 𝜀𝑖2= 𝜀′𝜀
𝑖=1 = (𝑌 − 𝑋𝑏)′(𝑌 − 𝑋𝑏)
= (𝑌′𝑌 − 𝑌′𝑋𝑏 − 𝑏′𝑋′𝑌′ + 𝑏′𝑋′𝑋𝑏) ⋯ ⋯ (2)
Berdasarkan sifat dari transpose matriks yaitu (𝑋𝑏)′ = 𝑏′𝑋′ dan karena 𝑏′𝑋′𝑌 adalah suatu skalar (bilangan nyata = real number) maka sama dengan transposenya 𝑌′𝑋𝑏.
Sehingga persamaan (2) menjadi: ∑ 𝜀𝑖2= 𝑌′𝑌 − 𝑏′𝑋′𝑌 − 𝑏′𝑋′𝑌 + 𝑏′𝑋′𝑋𝑏 𝑛 𝑖=1 ∑ 𝜀𝑖2= 𝑌′𝑌 − 2𝑏′𝑋′𝑌 + 𝑏′𝑋′𝑋𝑏 𝑛 𝑖=1
Dengan penurunan terhadap 𝑏′ secara parsial: 𝜕 ∑𝑛 𝜀𝑖2
𝑖=1
𝜕𝑏′ = −2𝑋′𝑌 + 2𝑋′𝑋𝑏
Kemudian disamakan dengan nol, maka diperoleh (𝑋′𝑋)𝑏 = 𝑋′𝑌 (persamaan normal) ...(3) 𝑏 = (𝑋′𝑋)−1𝑋′𝑌 , dengan syarat ada invers
Bentuk penulisan persamaan (3) dalam matriks adalah: [ 𝑛 ∑ 𝑋𝑖1 ∑ 𝑋𝑖1 ∑ 𝑋𝑖12 ∑ 𝑋∑ 𝑋𝑖2 𝑖1𝑋𝑖2 … ∑ 𝑋𝑖𝑘 … ∑ 𝑋𝑖1𝑋𝑖𝑘 ∑ 𝑋𝑖2 ∑ 𝑋𝑖1𝑋𝑖2 ∑ 𝑋𝑖22 … ∑ 𝑋𝑖2𝑋𝑖𝑘 ⋮ ⋮ ∑ 𝑋𝑖𝑘 ∑ 𝑋𝑖1𝑋𝑖𝑘 ⋮ ∑ 𝑋𝑖2𝑋𝑖𝑘 ⋮ … ∑ 𝑋𝑖𝑘2 ][ 𝑏0 𝑏1 𝑏2 ⋮ 𝑏𝑘] = [ 1 1 𝑋11 𝑋12 1 𝑋13 … 1 … 𝑋1𝑘 𝑋21 𝑋22 𝑋23 … 𝑋2𝑘 ⋮ ⋮ 𝑋𝑛1 𝑋𝑛2 ⋮ 𝑋𝑛3 ⋮ … 𝑋𝑛𝑘][ ∑ 𝑌1 ∑ 𝑌2 ∑ 𝑌3 ⋮ ∑ 𝑌𝑛] ....(4)
Koefisien regresi b0, b1, b2, ..., bk adalah:
[ 𝑏0 𝑏1 𝑏2 ⋮ 𝑏𝑘] = [ 𝑛 ∑ 𝑋1 ∑ 𝑋1 ∑ 𝑋12 ∑ 𝑋∑ 𝑋2 1𝑋2 … ∑ 𝑋𝑘 … ∑ 𝑋1𝑋𝑘 ∑ 𝑋2 ∑ 𝑋1𝑋2 ∑ 𝑋22 … ∑ 𝑋2𝑋𝑘 ⋮ ⋮ ∑ 𝑋𝑘 ∑ 𝑋1𝑋𝑘 ⋮ ∑ 𝑋2𝑋𝑘 ⋮ … ∑ 𝑋𝑘2 ] −1 [ ∑ 𝑌1 ∑ 𝑋1𝑌2 ∑ 𝑋2𝑌3 ⋮ ∑ 𝑋𝑘𝑌𝑛] ...(5)
1.11 Metode Regresi Stepwise Forward
Metode forward adalah langkah maju dimana memasukkan variabel bebas 𝑋𝑖 satu demi satu menurut urutan besar pengaruhnya terhadap model, dan berhenti bila semua yang memenuhi syarat telah masuk. Urutan penyisipannya ditentukan dengan menggunakan koefisien korelasi sebagai ukuran perlunya variabel bebas 𝑋𝑖 yang masih di luar persamaan untuk dimasukkan ke dalam persamaan, dan tidak dipersoalkan apakah korelasi positif atau negatif karena yang diperhatikan hanyalah eratnya hubungan antara variabel bebas 𝑋𝑖 dengan 𝑌 sedangkan arah hubungan tidak menjadi persoalan (Sembiring, 1995).
2.11.1 Membentuk Matriks Koefisien Korelasi
Koefisien korelasi yang dicari adalah koefisien korelasi linier sederhana antara Y dengan Xi (Sembiring, 1995): 𝑟𝑦𝑥𝑖 = ∑(𝑋𝑖𝑗 − 𝑋̅ )(𝑌𝑖 𝑗 − 𝑌̅) √∑(𝑋𝑖𝑗 − 𝑋̅ )𝑖 2∑(𝑌𝑗 − 𝑌̅)2 Dengan: 𝑌̅ =∑ 𝑌𝑗 𝑛 , j = 1, 2, 3, ..., n 𝑋̅ =𝑖 ∑ 𝑋𝑖𝑗 𝑛 , i = 1, 2, 3, ..., k
Bentuk matriks koefisien korelasi linier sederhana antara Y dan Xi:
𝑟 = [ 𝑟𝑦𝑥1 𝑟𝑦𝑥2 ⋮ 𝑟𝑦𝑥𝑘 ]
2.11.2 Membentuk Regresi Pertama (Regresi Linier Sederhana)
Variabel pertama yang diregresikan adalah variabel yang mempunyai harga mutlak koefisien korelasi yang terbesar antara Y dengan Xi, misalkan Xh. Dari
variabel ini dibuat persamaan regresi linier 𝑌 = 𝑏0+ 𝑏ℎ𝑋ℎ
𝑋 = [ 1 1 𝑋ℎ1 𝑋ℎ2 ⋮ 1 ⋮ 𝑋ℎ𝑛 ] (𝑋′𝑋)−1= [ 𝑛 ∑ 𝑋ℎ ∑ 𝑋ℎ ∑ 𝑋ℎ2] −1 𝑌 = [ 𝑌1 𝑌2 ⋮ 𝑌𝑛 ] 𝑋′𝑌 = [ ∑ 𝑌 ∑ 𝑋ℎ𝑌] 𝛽 = (𝑋′𝑋)−1. 𝑋′𝑌 = [𝑏0 𝑏1]
Perhitungan untuk membuat anava sebagai berikut: SSR = 𝛽′𝑋′𝑌 −(𝑌′𝐽𝑌) 𝑛 = ∑ (𝛽𝑖∑ 𝑋𝑖𝑌) − (∑ 𝑌)2 𝑛 SST = 𝑌′𝑌 −(𝑌′𝐽𝑌) 𝑛 = ∑ 𝑌2− (∑ 𝑌)2 𝑛
Dimana: SSR = Sum Square Regresion (Jumlah Kuadrat Regresi) SST = Sum Square Total (Jumlah Kuadrat Total)
𝐽 = [ 1 1 1 1 … 1… 1 1 1 … 1 ⋮ ⋮ 1 1 … ⋮… 1] n x n
J = Matriks berordo n x n dengan semua nilai adalah 1 SSE = SST – SSR
MSR =p−1SSR MSE = SSE
n−p
SSE = Sum Square Error (Jumlah Kuadrat Kesalahan) MSE = Mean Square Error (Rata-Rata Kuadrat Kesalahan)
Sehingga didapat harga standart error dari b, dengan rumus 𝑆2(𝛽) = 𝑀𝑆𝐸(𝑋′𝑋)−1 𝑆(𝑏
0) = √𝑆2(𝑏0)
Tabel 2.4 Analisa Variansi Untuk Uji Keberartian Regresi Sumber Variansi df SS MS Fhitung
Regresi (𝑿𝒉) p -1 SSR MSR
MSR/MSE
Residu n - p SSE MSE
Total SST
Uji Hipotesa:
H0 : Regresi antara Y dengan Xh tidak signifikan
H1 : Regresi antara Y dengan Xh signifikan
Keputusan:
Bila Fhitung < F(p - 1 ; n - p ; 0,5) maka terima H0
2.11.3 Seleksi Variabel Kedua Diregresikan
Cara menyeleksi variabel yang kedua diregresikan adalah memilih parsial korelasi variabel sisa yang terbesar. Untuk menghitung harga masing-masing korelasi parsial dengan rumus (Sudjana, 2005):
𝑟𝑦𝑥ℎ𝑥𝑘 =
𝑟𝑦𝑥ℎ− 𝑟𝑦𝑥𝑘 𝑟𝑥ℎ𝑥𝑘 √(1 − 𝑟𝑦𝑥2𝑘)(1 − 𝑟
𝑥2ℎ𝑥𝑘)
Keterangan: 𝑋𝑘 merupakan variabel sisa
2.11.4 Membentuk Regresi Kedua (Regresi Linier Ganda)
Dengan memilih korelasi parsial variabel sisa terbesar untuk variabel tersebut masuk dalam regresi, persamaan regresi kedua dibuat 𝑌 = 𝑏0+ 𝑏ℎ𝑋ℎ+ 𝑏𝑘𝑋𝑘 dengan cara sebagai berikut:
𝑋 = [ 1 1 𝑋ℎ1 𝑋ℎ2 𝑋𝑋𝑘1𝑘1 ⋮ 1 ⋮ 𝑋ℎ𝑛 𝑋⋮𝑘𝑛 ] (𝑋′𝑋)−1= [ 𝑛 ∑ 𝑋ℎ ∑ 𝑋𝑘 ∑ 𝑋ℎ ∑ 𝑋ℎ2 ∑ 𝑋ℎ𝑋𝑘 ∑ 𝑋𝑘 ∑ 𝑋ℎ𝑋𝑘 ∑ 𝑋𝑘2 ] −1 𝑌 = [ 𝑌1 𝑌2 ⋮ 𝑌𝑛 ] 𝑋′𝑌 = [∑ 𝑋∑ 𝑌 ℎ𝑌 ∑ 𝑋𝑘𝑌 ] 𝛽 = (𝑋′𝑋)−1. 𝑋′𝑌 = [𝑏𝑏0 ℎ 𝑏𝑘 ]
Uji keberartian regresi dengan tabel anava sama dengan langkah kedua yaitu dengan menggunakan tabel 2.3. Selanjutnya diperiksa apakah koefisien regresi bk signifikan, dengan hipotesa:
H0 : bk = 0
H1 : bk ≠ 0
Fhitung= (𝑆(𝑏𝑏𝑘
𝑘))
Keputusan:
a) Bila Fhitung < F(1 ; n - p ; 0,05), terima H0 artinya bk dianggap sama dengan nol,
maka proses diberhentikan dan persamaan yang terbaik 𝑌 = 𝑏0+ 𝑏ℎ𝑋ℎ.
b) Bila Fhitung ≥ F(1 ; n - p ; 0,05), tolak H0 artinya bk dianggap tidak sama dengan
nol, maka variabel 𝑋𝑘 tetap di dalam penduga.
2.11.5 Seleksi Variabel Ketiga Diregresikan
Dipilih kembali harga korelasi parsial variabel sisa terbesar. Menghitung harga masing-masing parsial korelasi variabel sisa dengan rumus (Sudjana, 2005):
𝑟𝑦𝑥ℎ𝑥𝑘𝑥𝑙 =
𝑟𝑦𝑥ℎ𝑥𝑘− 𝑟𝑦𝑥𝑙𝑥𝑘 𝑟𝑥ℎ𝑥𝑘𝑥𝑙
√(1 − 𝑟𝑦𝑥2𝑙𝑥𝑘)(1 − 𝑟 𝑥ℎ𝑥𝑘𝑥𝑙
2 )
Keterangan: 𝑋𝑙 merupakan variabel sisa
2.11.6 Membentuk Persamaan Regresi Ketiga
Dengan memilih korelasi parsial terbesar, persamaan regresi dibuat 𝑌 = 𝑏0+ 𝑏ℎ𝑋ℎ+ 𝑏𝑘𝑋𝑘+ 𝑏𝑙𝑋𝑙, dengan cara sebagai berikut:
𝑋 = [ 1 𝑋ℎ1 1 𝑋ℎ2 𝑋𝑘1 𝑋𝑙1 𝑋𝑘2 𝑋𝑙2 ⋮ ⋮ 1 𝑋ℎ𝑛 ⋮ ⋮ 𝑋𝑘𝑛 𝑋𝑙𝑛 ] 𝑌 = [ 𝑌1 𝑌2 ⋮ 𝑌𝑛 ] (𝑋′𝑋)−1= [ 𝑛 ∑ 𝑋ℎ ∑ 𝑋ℎ ∑ 𝑋ℎ2 ∑ 𝑋𝑘 ∑ 𝑋𝑙 ∑ 𝑋ℎ𝑋𝑘 ∑ 𝑋ℎ𝑋𝑙 ∑ 𝑋𝑘 ∑ 𝑋ℎ𝑋𝑘 ∑ 𝑋𝑙 ∑ 𝑋ℎ𝑋𝑙 ∑ 𝑋𝑘2 ∑ 𝑋 𝑘𝑋𝑙 ∑ 𝑋𝑘𝑋𝑙 ∑ 𝑋𝑙2 ] −1 𝑋′𝑌 = [ ∑ 𝑌 ∑ 𝑋ℎ𝑌 ∑ 𝑋𝑘𝑌 ∑ 𝑋𝑙𝑌]
2.11.7 Pembentukan Persamaan Penduga
Persamaan penduga 𝑌̂ = 𝑏0+ 𝑏𝑖𝑋𝑖 dimana Xi adalah semua variabel X yang masuk
kedalam penduga (faktor penduga) dan bi adalah koefisien regresi untuk Xi.
2.11.8 Pertimbangan Terhadap Penduga
Sebagai pembahasan suatu penduga, untuk menanggapi kecocokan penduga yang diperoleh ada dua hal yang dipertimbangkan yakni:
a. Pertimbangan berdasarkan R2
Koefisien determinasi ganda (R2) mengukur tingkat ketepatan/kecocokan (goodness of fit) dari regresi linier ganda. Suatu penduga sangat baik digunakan apabila persentase variabel yang dijelaskan sangat besar atau bila R2 → 1
b. Analisa residu
Suatu regresi adalah berarti dan model regresinya cocok (sesuai berdasarkan nilai observasi) apabila asumsi dibawah ini dipenuhi:
𝑒𝑗 ≈ N(0, 𝜎2) berarti residu (ej) mengikuti distribusi normal dengan mean (e) =
0 dan varian (σ2) = konstanta
Asumsi ini dibuktikan dengan analisis residu. Untuk langkah ini pertama dihitung residu (sisa) dari penduga, yaitu selisih dari respon observasi terhadap hasil keluaran oleh penduga berdasarkan prediktor observasi.
Tabel 2.5 Analisa Residu
No. Observasi Respon Penduga Residu 1 2 3 ⋮ n 𝑌1 𝑌2 𝑌3 ⋮ 𝑌𝑛 𝑌̂1 𝑌̂2 𝑌̂3 ⋮ 𝑌̂𝑛 𝑌1− 𝑌̂1 𝑌2− 𝑌̂2 𝑌3− 𝑌̂3 ⋮ 𝑌𝑛− 𝑌̂𝑛 Jumlah - - ∑ 𝑒𝑗 Rata-rata - - ∑ 𝑒𝑗 𝑛 Asumsi
a. Rata-rata residu sama dengan nol (𝑒̅ = 0) b. Varian (ej) = Varian (ek) = 𝜎2
Keadaan ini dibuktikan dengan uji statistika dengan menggunakan uji korelasi Rank Spearman (Spearman’s Rank Correlation Test), ditunjukkan dengan tabel berikut:
Tabel 2.6 Rank Spearman No. Observasi Penduga (Yj) Residu (𝒆𝒋) Rank (Y) Rank (e) 𝐝(𝒓𝒚− 𝒓𝒆) 𝐝 𝟐 1 2 3 ⋮ N 𝑌1 𝑌2 𝑌3 ⋮ 𝑌𝑛 𝑒1 𝑒2 𝑒3 ⋮ 𝑒𝑛 𝑟𝑦1 𝑟𝑦2 𝑟𝑦3 ⋮ 𝑟𝑦𝑛 𝑟𝑒1 𝑟𝑒2 𝑟𝑒3 ⋮ 𝑟𝑒𝑛 d1 d2 d3 ⋮ d𝑛 d12 d22 d32 ⋮ d𝑛2 Jumlah - - - ∑ d𝑗2 Uji Hipotesa: H0 : Varian (𝑒𝑗) = Varian (𝑒𝑘) = 𝜎2 H1 : Varian (𝑒𝑗) ≠ Varian (𝑒𝑘) ≠ 𝜎2
Koefisien korelasi Rank Spearman (rs): 𝑟𝑠= 1 − 6 (
∑ 𝑑𝑗2 𝑛(𝑛2− 1))
Dimana: 𝑑𝑗 = Perbedaan rank yang diberikan oleh dua karakter yang berbeda
n = jumlah responden
Untuk sampel besar (n > 10) diuji dengan menggunakan Uji t dengan rumus:
t0=𝑟𝑠√n − 2 √1 − 𝑟𝑠2
Keputusan:
a) Jika 𝑡0≤ 𝑡𝛼(𝑛−2), maka H0 diterima
b) Jika 𝑡0> 𝑡𝛼(𝑛−2), maka H0 ditolak
Bila H0 diterima maka varian (𝑒𝑗) = varian (𝑒𝑘) = 𝜎2 atau varian seluruh