MA6081 Topik dalam Statistika III. Bagian II : Ukuran risiko imbal hasil dan. model keuangan agregat. Prediksi volatilitas dan imbal hasil

(1)

MA6081 Topik dalam Statistika III Bagian II : Ukuran risiko imbal hasil

dan model keuangan

agregat

Prediksi volatilitas dan imbal hasil

Prediksi volatilitas Prediksi imbal hasil

Ukuran risiko VaR dan ES

MA6081 Topik dalam Statistika III

Bagian II : Ukuran risiko imbal hasil dan

(2)

dan model keuangan

agregat

Prediksi volatilitas

Prediksi imbal hasil

Prediksi volatilitas

Pada model imbal hasil, sejauh ini prediksi yang telah dilakukan adalah prediksi volatilitas (volatility forecasting). Kegiatan ini melibatkan (i) jenis volatilitas dan/atau (ii) penaksiran parameter model yang dapat dilakukan dengan beberapa metode. Perhatikan bahwa penaksiran parameter model volatilitas laten akan jauh berbeda dengan model terobservasi.

(3)

dan model keuangan

agregat

Ukuran risiko VaR dan ES Prediksi volatilitas pertama dikatakan sebagai prediksi empiris;

prediksi kedua disebut prediksi teoretis. Prediksi volatilitas berperan penting pada prediksi imbal hasil.

(4)

dan model keuangan

agregat

Prediksi imbal hasil

Prediksi imbal hasil memanfaatkan ekspektasi bersyarat imbal hasil dan/atau prediksi volatilitas. Secara teoretis, prediksi imbal hasil bernilai nol. Akibatnya diperlukan prediksi imbal hasil kuadrat untuk mendapatkan prediksi imbal hasil.

(5)

dan model keuangan

agregat

Ukuran risiko VaR dan ES Perhatikan model imbal hasil:

Rt =σtεt

Apakah prediktor terbaik untuk imbal hasil? Apakah peran volatilitas? Apakah prediksi titik atau selang yang digunakan pada prediksi imbal hasil/volatilitas? Apakah yang anda ketahui tentang martingale?

(6)

dan model keuangan

agregat

Ukuran risiko VaR dan ES Prediksi imbal hasil dan/volatilitas dapat menggunakan ukuran

(7)

dan model keuangan

agregat

Prediksi volatilitas Prediksi imbal hasil Ukuran risiko VaR dan ES

Konsep risiko

Risiko adalah kerugian akibat kegiatan keuangan/finansial (termasuk perbankan) dan asuransi. Risiko/kerugian adalah akibat (yang tidak menyenangkan) dari suatu tindakan.

(8)

dan model keuangan

agregat

Value-at-Risk (VaR)

Value-at-Risk (VaR) adalah nilai risiko atau kerugian terbesar yang mungkin terjadi dalam rentang batas tolerasi kerugian yang telah ditentukan.

(9)

dan model keuangan

agregat

(10)

dan model keuangan

agregat

Suppose that{Yt}is a sequence of random losses representing

asset returns with probability distribution determined by the parameter vectorθ. The available loss data areY₁, . . . ,Yn. We

aim at forecasting V@Rαn+1;θsuch that it has (conditional)

coverage probability equal toαi.e.

Pθ Yn+1≤V@Rαn+1;θ

Fn

=α, ∀θ,

(11)

dan model keuangan

agregat

In other words, provided that the inverse of (conditional) distribution function ofYn+1exists,

V@Rαn+1;θ =F

−1

(12)

MA6081 Topik dalam Statistika III

Bagian III : Value at-Risk dan Model

Agregat

Value-at-Risk Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi

Model Agregat

Risiko

I Risiko (risk) merupakan ketidakpastian akan terjadinya peristiwa yang dapat menyebabkan kerugian (loss). I _{Untuk menghindari kerugian tersebut, risiko perlu}

dikuantifikasi (melalui peubah acak) dan diukur (menggunakan ukuran risiko).

I Ukuran risiko,%, adalah fungsi yang memetakan koleksi risiko-risiko acak,X, ke himpunan semua bilangan riil,R, atau%:X →_R.

(13)

Agregat

Value-at-Risk Definisi VaR

VaR dari Model Stokastik Prediksi dan Akurasi

Model Agregat

Value-at-Risk: Definisi

I Salah satu ukuran risiko yang sering digunakan adalah Value-at-Risk (VaR).

I VaR dapat didefinisikan sebagai nilai kerugian maksimum yang dapat ditoleransi pada tingkat kepercayaan tertentu. I Pada tingkat kepercayaan sebesar 1−α, VaR dari risiko

acakXdirumuskan sebagai

VaR1−α(X) =inf{x:FX(x)≥1−α}, (1) denganα∈(0,1).

(14)

Agregat

Model Agregat

I Jika invers dari fungsi distribusiFX ada, maka

VaR1−α(X) =FX−1(1−α). (2) I Artinya, VaR pada dasarnya merupakan kuantil-(1−α)

(15)

Agregat

Model Agregat

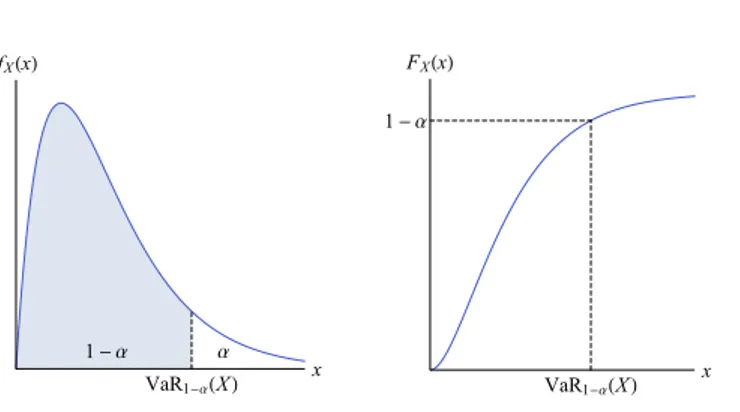
Ilustrasi VaR

1-α α VaR1-α(X) x fX(x) VaR1-α(X) x 1-α FX(x)

(16)

Agregat

Model Agregat

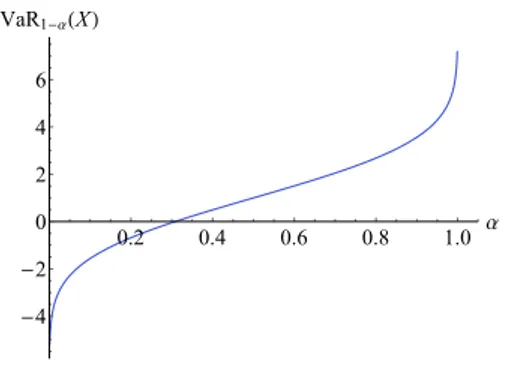
Contoh: VaR dari Risiko Acak Normal

Misalkan risiko acakXberdistribusi normal dengan parameter (µ, σ2), maka VaR1−α(X)adalah nilaiXyang memenuhi

1−α=P X≤VaR1−α(X) =P X−µ σ ≤ VaR1−α(X)−µ σ = Φ VaR1−α(X)−µ σ . Diperoleh VaR1−α(X) =µ+ Φ−1(1−α)σ. (3)

(17)

Agregat

Model Agregat 0.2 0.4 0.6 0.8 1.0 α -4 -2 0 2 4 6 VaR1-α(X)

(18)

Agregat

Model Agregat

Secara umum, jika distribusi dariXsimetris, makaF_X−1(1−α) memuat mean dan variansi/deviasi standar dariX, dan

VaR1−α(X)dapat dinyatakan sebagai

(19)

Agregat

Model Agregat

(20)

Agregat

Model Agregat

(21)

Agregat

Value-at-Risk

Definisi VaR

VaR dari Model Stokastik

Prediksi dan Akurasi

Model Agregat

VaR dari Model Stokastik

I Pada pemodelan statistika, risiko acak dapat

direpresentasikan sebagai proses stokastik{Xt :t≥0} yang seringkali menyatakan imbal hasil dari harga aset. I Jika diberikan himpunan data/informasi sampai waktun,

Fn={Xt :t≤n}, VaR dapat dipandang sebagai nilai prediksi dari risiko di waktun+1,Xbn+1, pada tingkat kepercayaan tertentu.

(22)

Agregat

Value-at-Risk

Definisi VaR

Model Agregat

I Pada tingkat kepercayaan 1−α, VaR dirumuskan sebagai VaR1−α(Xn+1|Fn) =inf{x:FXn+1|Fn(x)≥1−α}

atau

VaR1−α(Xn+1|Fn) =F−_X1

(23)

Agregat

Value-at-Risk

Definisi VaR

Model Agregat

VaR dari Model Stokastik untuk Imbal Hasil

I Didefinisikan imbal hasil

Xt =−ln Pt Pt−1 ,

denganPt adalah harga aset pada waktut.

I Misalkan model stokastik untuk imbal hasil tersebut adalah

Xt=σtεt,

denganεtadalah inovasi yang mempunyai distribusi standar tertentu.

(24)

Agregat

Value-at-Risk

Definisi VaR

Model Agregat

I VaR dari model imbal hasil tersebut adalah VaR1−α(Xn+1|Fn) =σn+1Fε−1(1−α),

denganF_ε−1(1−α)adalah kuantil-(1−α)dari distribusi inovasiεt.

I Hal ini menunjukkan bahwa volatilitas merupakan komponen utama dari ukuran risiko (VaR).

(25)

Agregat

Value-at-Risk

Definisi VaR

Model Agregat

I Perhatikan bahwa volatilitasσn+1dapat bersifat konstan (homoskedastis) maupun dinamis (heteroskedastis). I _{Untuk model heteroskedastis:}

ARCH(1):σn+1 = p a0+a1Xn2 GARCH(1,1):σn+1 = p a₀+a₁X2 n+b1σn2 I Untuk model homoskedastis, dapat dipandang

(26)

Agregat

Value-at-Risk

Definisi VaR

Model Agregat

Bagaimana dengan ukuran risiko dari model stokastik untuk imbal hasil Xt =ln Pt Pt−1 ?

(27)

Agregat

Value-at-Risk

Definisi VaR VaR dari Model Stokastik

Prediksi dan Akurasi Model Agregat

Prediksi VaR

I _{Distribusi (bersyarat) dari risiko acak seringkali} bergantung pada suatu parameterθ.

I Akibatnya, VaR dari risiko acak tersebut merupakan fungsi dariθdan dapat ditulis VaR1−α(Xn+1|Fn;θ). I Dalam praktiknya, parameterθharus ditaksir dari data.

Taksiran untukθditulisθb.

I Dengan menyubstitusi parameterθpada formula VaR dengan taksiranθb, diperoleh prediksi VaRestimative

d

(28)

Agregat

Value-at-Risk

Keakuratan Prediksi VaR

I Untuk mengetahui keakuratan prediksi VaR, salah satu indikator yang dapat digunakan adalah peluang cakupan, yang didefinisikan sebagai

PC=PXn+1 ≤VaRd₁−α(Xn+1|Fn;θb) Fn;θ .

I Prediksi VaR dikatakan akurat jika nilai PC mendekati tingkat kepercayaan yang diberikan, atau PC≈1−α.

(29)

Agregat

Value-at-Risk

I Seringkali peluang cakupan sulit dihitung atau tidak diketahui, sehingga nilainya perlu ditaksir/diaproksimasi. I Misalkan{xn+1,k :k=1,2...,M}adalah realisasi sampel

acak dariXn+1. I Jika didefinisikan Ik= ( 1, xn+1,k≤VaRd₁−α(Xn+1|Fn;θb), 0, xn+1,k>VaR1d −α(Xn+1|Fn;θb), (5)

maka{Ik :k=1,2, ...,M}diharapkan merupakan

realisasi sampel acak dari distribusi Bernoulli dengan parameter 1−α, sehingga

PC≈1−α≈

PM

k=1Ik

(30)

Agregat

Value-at-Risk

Contoh

Dengan menggunakan data Bitcoin selama periode 1-1-2016 hingga 31-12-2018, berikut ini adalah prediksi VaR dari imbal hasil Bitcoin dengan asumsi (1) volatilitas konstan dan (2) volatilitas dinamis melalui model ARCH(1,1).

Tabel 1:Taksiran parameter dari model imbal hasil Bitcoin beserta prediksi VaR dan taksiran peluang cakupannya (dalam tanda kurung)

Asumsi 1 Asumsi 2 Parameter a0 0.0022 0.0018 a1 - 0.1413 Tingkat Kepercayaan 0.95 0.0765 (0.9362) 0.0709 (0.9402) 0.97 0.0874 (0.9588) 0.0811 (0.9608) 0.99 0.1082 (0.9815) 0.1003 (0.9849)

(31)

Agregat

Value-at-Risk

Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi Model Agregat

Model Agregat

I MisalkanX₁,X₂, ...,XNadalah risiko-risiko acak yang dapat saling bergantung.

I Risiko-risiko acak tersebut dapat dijumlahkan menjadi

SN =X1+X2+· · ·+XN yang disebut risiko agregat.

I IndeksNdapat bersifat deterministik (konstanta) maupun probabilistik (peubah acak).

(32)

Agregat

Value-at-Risk

Contoh: Agregat dari Risiko Acak Normal

UntukN =2, misalkanX1,X2berdistribusi normal bivariat dengan parameterθ= (µ1, µ2, σ12, σ22, ρ). Fungsi peluang bersamanya adalah fX1,X2(x1,x2) = 1 2πσ1σ2 p 1−ρ2 exp −q 2 dengan q= 1 1−ρ2 " x1−µ1 σ1 2 −2ρ x1−µ1 σ1 x2−µ2 σ2 + x2−µ2 σ2 2# ,

yang artinyaX1 ∼N(µ1, σ12)danX2∼N(µ2, σ22)dengan korelasi Corr(X₁,X₂) =ρ.

(33)

Agregat

Value-at-Risk

Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi Model Agregat Dapat ditunjukkan bahwaS₂=X₁+X₂berdistribusi normal

dengan mean µS2 =E(S2) =E(X₁+X₂) =E(X₁) +E(X₂) =µ1+µ2 dan variansi σ2_S₂ =Var(S2) =Var(X₁+X₂)

=Var(X1) +Var(X2) +2Cov(X1,X2) =σ₁2+σ2₂+2ρσ1σ2.

(34)

Agregat

Value-at-Risk

Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi Model Agregat Akibatnya, VaR dari risiko agregatS2dapat dituliskan sebagai

VaR1−α(S2) =µS2+ Φ −1₍₁₋_α₎_σ S2 = (µ1+µ2) + Φ−1(1−α) q σ₁2+σ2₂+2ρσ1σ2

(35)

Agregat

Value-at-Risk

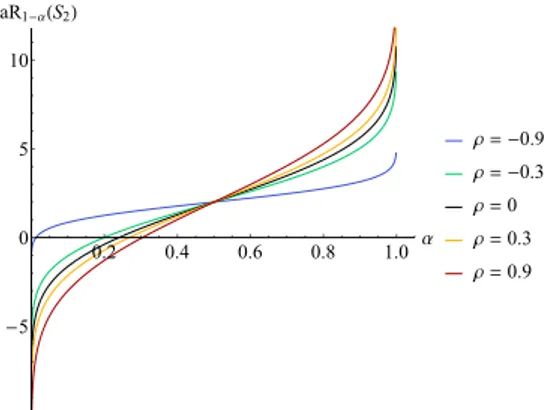
Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi Model Agregat 0.2 0.4 0.6 0.8 1.0 α -5 0 5 10 VaR1-α(S2) ρ= -0.9 ρ= -0.3 ρ=0 ρ=0.3 ρ=0.9

Gambar 3:VaR agregat dari risiko acak normal bivariat dengan

µ1=µ2=1 danσ2

(36)

Agregat

Value-at-Risk

Agregat dari Model Stokastik Imbal Hasil

I Didefinisikan imbal hasil dari harga aset I dan aset II sbb:

X_tI =−ln PI_t PI_t₋₁ , XII_t =−ln PII_t PII_t₋₁ .

I Misalkan model stokastik untuk masing-masing imbal hasil adalah X_tI =σtIε I t, X II t =σ II t ε II t ,

(37)

Agregat

Value-at-Risk

Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi Model Agregat I JikaεIt danεIIt berdistribusi normal bivariat standar dengan

korelasiρ, makaX_tI|FI

t−1danXtII|FtII−1berdistribusi normal bivariat dengan parameter

θ= 0,0,(σIt)2,(σ II t )2, ρ .

(38)

Agregat

Value-at-Risk

Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi Model Agregat I MisalkanSt =XtI+XtII, maka distribusi bersyarat dariSt,

diberikanF_tI₋,II₁, adalah normal dengan mean 0 dan variansi (σ_tI)2+ (σII_t )2+2ρσI_tσ_tII.

I Dengan demikian, VaR dari model agregat tersebut adalah

VaR1−α(Sn+1|FI ,II n ) = Φ −1 (1−α) q (σI n+1)2+ (σnII+1)2+2ρσIn+1σIIn+1.

(39)

Agregat

Value-at-Risk

Definisi VaR VaR dari Model Stokastik Prediksi dan Akurasi Model Agregat Contoh?