Pokok Bahasan pengolahan dan analisis

Pokok Bahasan :

REGRESI LINIER

SEDERHANA

Macam-macam Model Regresi

Model Regresi

Sederhana Berganda

Linier _{Non Linier Linier Non Linier} 1 peubah penjelas _{> 1 peubah penjelas}

Reciprocal Log Multiplikatif

ƒ

Sederhana

ƒ

Linier

ƒ Hubungannya linier

ƒ

Non Linier

ƒ Polinom

ƒ Multiplikatif

ƒ Eksponensial

ƒ Reciprocal

Contoh :

Macam-macam Model Regresi

Model Regresi Linier Sederhana

(yang hubungannya linier

ordo

x=1

)

ƒ Linier dalam parameter

ƒ Sederhana = banyaknya peubah bebas/penjelas hanya satu

ƒ Hubungan antara X dan Y dinyatakan dalam fungsi linier/ordo 1

ƒ Perubahan Y diasumsikan karena adanya perubahan X

ƒ Model populasi regresi linier sederhana yang hubungannya linier

(selanjutnya cukup sebut “regresi linier sederhana”) :

Dengan :

β0 dan β1 adalah parameter regresi

ε adalah sisaan/galat/eror (peubah acak) Y adalah peubah tak bebas (peubah acak)

X adalah peubah bebas yang nilainya diketahui

ε

x

β

β

Asumsi

Model Regresi Linier

ƒ

Bentuk hubungannya linear (Y merupakan

fungsi linier

dari X, plus sisaan yang acak)

ƒ

Sisaan

ε

_i

adalah peubah acak yang bebas thdp nilai x

ƒ

Sisaan merupakan peubah acak yang menyebar

Normal

dengan rataan 0 dan memiliki ragam konstan,

σ

2

(sifat ragam yang konstan/homogen ini disebut homoscedasticity)

ƒ

Sisaan

ε

_i

, tidak berkorelasi satu dengan yang lainnya,

sehingga atau

n)

,

1,

(i

untuk

σ

]

E[

ε

dan

0

]

E[

ε

_i

=

_i2

=

2

=

K

j

i

,

0

]

ε

ε

X

β

β

Y

=

₀

+

₁

+

Komponen linier (fix)

Interpretasi Parameter Model

Regresi Linier Sederhana

X

β

β0 + 1

σ

2

Model Regresi Linier Sederhana (populasi) :

Intersep Y populasi

Koefisien kemiringan populasi

Sisaan/ galat Peubah tak

bebas/

Peubah respon

Peubah bebas/ Peubah penjelas

Komponen acak

(lanjutan)

Sisaan/galat untuk x_i

Y

Nilai

pengamatan Y untuk X_i

Nilai

harapan/rataan Y untuk x_i

Interpretasi Parameter Model

Regresi Linier Sederhana

i

1

0

i

b

b

x

yˆ

=

+

Dugaan persamaan garis regresi linier sederhana

Dugaan Persamaan Garis

Regresi Linier Sederhana

Dugaan bagi intersep

β

₀

Dugaan bagi kemiringan garis regresi

β

₁

Nilai dugaan y pada

pengamatan ke - i

Nilai x pada pengamatan ke - i

Galat individu e_i mempunyai rataan sebesar nol

)

)

ˆ

(

_{i i i 0 1 i}

i

y

-

y

y

-

(b

b

x

ƒ

b

₀

adalah nilai dugaan rataan y

ketika x bernilai nol

(

jika x = 0 dalam

selang pengamatan

)

ƒ

b

₁

adalah nilai dugaan perubahan

rataan y (nilai harapan Y) jika x

berubah satu satuan

Menduga Persamaan Regresi

ƒ

Menduga persamaan regresi linier sederhana

= menduga parameter-parameter regresi

β

₀

dan

β

₁

:

ƒ

Penduga parameter yang dihasilkan harus

merupakan

penduga yang baik

Metode Kuadrat Terkecil

ƒ

b

₀

dan b

₁

adalah dugaan bagi parameter regresi

β

₀

dan

β

₁

yang didapat

salah satunya

dengan cara

meminimumkan jumlah kuadrat galat (JKG).

Galat/sisaan = selisih antara y dan

Æ

Metode

Kuadrat Terkecil (MKT) :

2

Teknik kalkulus digunakan untuk mendapatkan nilai b_o dan b₁ sedemikian hingga meminimumkan JKG

Menduga Persamaan Regresi

ƒ

Penduga bagi koefisien kemiringan garis

β

₁

ialah:

Koefisien Korelasi Pearson

Metode Kuadrat Terkecil

Asumsi Metode Kuadrat Terkecil (MKT)

Agar penduga bagi parameter regresi yang

didapatkan dengan menggunakan MKT merupakan

penduga yang baik

maka sisaan/galat harus

memenuhi kondisi Gauss-Markov berikut ini :

bebas

ticity

homoscedas

homogen

sisaan

ragam

sisaan

taan

Kondisi Gauss - Markov

(lanjutan)

Contoh

Regresi Linier Sederhana

ƒ

Sebuah agen real-estate ingin mengetahui

hubungan antara harga jual sebuah rumah

dengan luas lantainya (diukur dalam m2)

10 buah rumah diambil secara acak sebagai contoh

ƒ

Peubah tak bebas (Y) = harga rumah (juta rupiah)

Data contoh Harga Rumah

Harga Rumah (Rp.juta) (Y) Luas Lantai (m2) (X)

245 1400

312 1600

279 1700

308 1875

199 1100

219 1550

405 2350

324 2450

319 1425

255 1700

Contoh Regresi Linier Sederhana

Luas Lantai

Scatterplot of Harga Rumah vs Luas Lantai

Tebaran Harga Rumah vs Luas Lantai

Contoh Regresi Linier Sederhana

(lanjutan)

Model Regresi-nya

ε

β

β

+

+

=

x

Y

_{0 1}

Persamaan Garis Regresi-nya

x

Y

=

β

₀

+

β

₁

Diduga dengan :

x

b

b

FILM :

MEMBUAT TEBARAN

“HARGA RUMAH” vs ”LUAS LANTAI” MENGGUNAKAN MINITAB

Klik di sini

Data contoh Harga Rumah

Harga Rumah (Rp.juta) (Y)

Luas Lantai (m2) (X)

245 1400

312 1600

279 1700

308 1875

199 1100

219 1550

405 2350

324 2450

319 1425

255 1700

Contoh Regresi Linier Sederhana

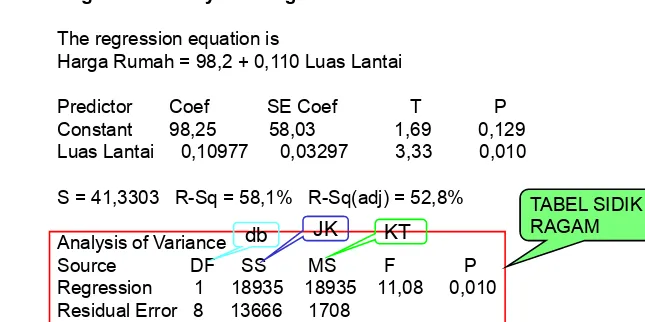
Regression Analysis: Harga Rumah versus Luas Lantai

The regression equation is

Harga Rumah = 98,2 + 0,110 Luas Lantai

Predictor Coef SE Coef T P

Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

S = 41,3303 R-Sq = 58,1% R-Sq(adj) = 52,8%

Contoh Regresi Linier Sederhana

(lanjutan)

MENDUGA PARAMETER REGRESI : OUTPUT MINITAB

Dugaan Persamaan Garis Regresi-nya

b

0

b

Klik di sini

Data contoh Harga Rumah

Harga Rumah (Rp.juta) (Y)

Luas Lantai (m2) (X)

245 1400

312 1600

279 1700

308 1875

199 1100

219 1550

405 2350

324 2450

319 1425

255 1700

Contoh Regresi Linier Sederhana

(lanjutan)

FILM :

0

0 500 1000 1500 2000 2500 3000

Luas Lantai (m2)

H

Tampilan Grafik

ƒ

Model Harga Rumah: scatter plot dan

garis regresi

+

=

Kemiringan = 0.10977

Intersep = 98.248

Contoh Regresi Linier Sederhana

Klik di sini

Data contoh Harga Rumah

Harga Rumah (Rp.juta) (Y)

Luas Lantai (m2) (X)

245 1400

312 1600

279 1700

308 1875

199 1100

219 1550

405 2350

324 2450

319 1425

255 1700

FILM :

MEMBUAT TEBARAN ANTARA

“HARGA RUMAH”

dengan

“LUAS LANTAI”

& GARIS REGRESI-nya

MENGGUNAKAN MINITAB

Contoh Regresi Linier Sederhana

Interpretasi Intersep b

₀

ƒ

b

₀

adalah nilai dugaan bagi nilai rataan

Y ketika X bernilai nol (

jika X = 0 di

dalam selang pengamatan

)

ƒ Dalam hal ini tidak ada rumah yang memiliki luas lantai=0,

jadi b₀ = 98.24833 hanya mengindikasikan bahwa : untuk

luas lantai yang berada dalam selang pengamatan, Rp 98.248.330,- adalah bagian harga rumah yang tidak diterangkan oleh luas lantai

lantai)

(luas

0.10977

98.24833

rumah

harga

=

+

Contoh Regresi Linier Sederhana

Interpretasi koefisien kemiringan, b

₁

ƒ

b

₁

mengukur dugaan perubahan rataan

nilai Y jika X berubah satu satuan

ƒ

Dalam hal ini b

₁

= .10977 menggambarkan

bahwa setiap penambahan satu m

2

_{luas lantai}

rataan harga rumah akan naik sebesar 0,10977

juta rupiah

lantai)

(luas

0.10977

98.24833

rumah

harga

=

+

Contoh Regresi Linier Sederhana

Apakah b

₀

dan b

₁

yang didapat

merupakan penduga yang baik ?

ƒ

Pertanyaan di atas = pertanyaan bahwa: “apakah

sisaan

yang dihasilkan oleh

dugaan persamaan

garis regresi

nya menghasilkan sisaan yang

memenuhi kondisi

Gauss-Markov

?”

ƒ

Untuk sementara ini kita yakini saja dulu bahwa

sisaan yang dihasilkan memenuhi kondisi tersebut

PENGURAIAN

KERAGAMAN TOTAL

Sumber Keragaman Regresi

x

y

X

y

_i

JKT =

∑

(

y

_i

-

y

)

2

JKG =

∑

(

y

_i

-

∧

y

_i

)

2

JKR =

∑

(

y

∧

_i

–

y

)

2

_{_}

_

_

y

∧

Y

y

_

y

∧

_i

Sumber Keragaman Regresi

Sumber Keragaman Regresi

ƒ

Untuk suatu nilai x

_i

keragaman nilai pengamatan y

_i

disebabkan oleh :

ƒ

Menyimpangnya nilai amatan y

_i

terhadap dugaan nilai

harapannya

ƒ

beragam

Æ

menghasilkan dugaan garis

regresi yang beragam

Æ

memiliki rataan

Menyimpangnya suatu dugaan garis regresi terhadap

rataannya menyebabkan beragamnya data.

Mengukur Keragaman

ƒ

Total Keragaman disebabkan oleh dua bagian ini :

JKG

JKR

JKT

=

+

Jumlah Kuadrat Total

Jumlah Kuadrat Regresi

Jumlah Kuadrat Galat/Sisaan

∑

−

=

2

i

y

)

(y

JKT

JKR

=

∑

(

yˆ

_i

−

y

)

2

JKG

=

∑

(y

_i

−

yˆ

_i

)

2

dengan:

= nilai rata-rata peubah tak bebas Y

y_i = nilai pengamatan ke-i peubah tak bebas Y

i = nilai dugaan y untuk suatu nilai xi

yˆ

y

ƒ

JKT = Jumlah Kuadrat Total

ƒ

Mengukur keragaman nilai y

_i

di sekitar nilai

rataannya y

ƒ

JKR = Jumlah Kuadrat Regresi

ƒ

Menjelaskan keragaman karena adanya hubungan

linier antara x dan y

ƒ

JKS = jumlah Kuadrat Sisa

ƒ

Menjelaskan keragaman yang disebabkan oleh

faktor-faktor selain faktor hubungan linier x dan y

(lanjutan)

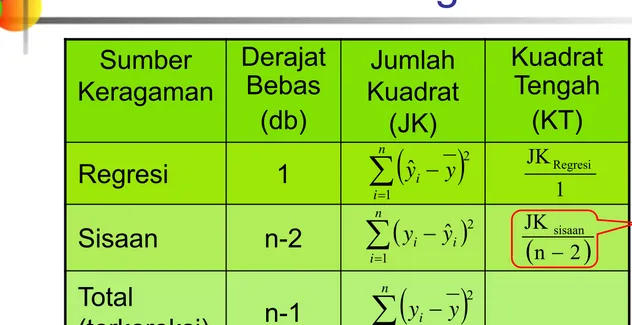
Derajat Bebas Jumlah Kuadrat

ƒ

Ukuran keragaman adalah

ragam

ƒ

Derajat bebas bagi

ƒ

Derajat bebas bagi

(db)

bebas

derajat

(JK)

Kuadrat

Jumlah

Ragam

=

2

-n

JK

_Sisaan

=

1

JK

0

b

|

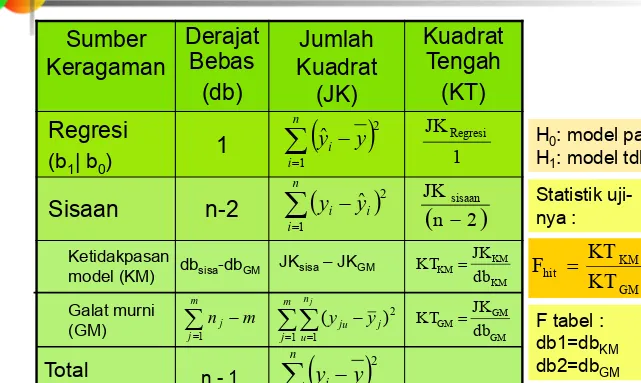
Tabel Sidik Ragam

Sumber

Keragaman

Derajat

Bebas

(db)

Jumlah

Kuadrat

(JK)

Kuadrat

Tengah

(KT)

Regresi

1

Sisaan

n-2

Total

(terkoreksi)

n-1

( )

JK_Regresi

(

n 2

)

JK _sisaan

−

Pada analisis regresi ini tentunya diharapkan JK regresi lebih besar dari JK sisaan Æ sehingga dapat dikatakan bahwa keragaman nilai y

S2_,

Regression Analysis: Harga Rumah versus Luas Lantai

The regression equation is

Harga Rumah = 98,2 + 0,110 Luas Lantai

Predictor Coef SE Coef T P Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

S = 41,3303 R-Sq = 58,1% R-Sq(adj) = 52,8%

Analysis of Variance

Source DF SS MS F P Regression 1 18935 18935 11,08 0,010 Residual Error 8 13666 1708

Total 9 32600

Tabel Sidik Ragam

OUTPUT MINITAB

db JK KT

TABEL SIDIK RAGAM

Penduga bagi Ragam Sisaan/galat

ƒ

Penduga bagi ragam eror/sisaan dari model populasi

adalah :

ƒ

Dibagi dengan n – 2 bukan dengan n – 1 karena model

regresi linier sederhana menggunakan 2 penduga

parameter yaitu, b

₀

dan b

₁

, bukan satu.

adalah

penduga simpangan baku

2

Dengan asumsi bahwa

modelnya pas/cocok

2

s

Regression Analysis: Harga Rumah versus Luas Lantai

The regression equation is

Harga Rumah = 98,2 + 0,110 Luas Lantai

Predictor Coef SE Coef T P Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

S = 41,3303 R-Sq = 58,1% R-Sq(adj) = 52,8%

Analysis of Variance

Source DF SS MS F P Regression 1 18935 18935 11,08 0,010 Residual Error 8 13666 1708

Total 9 32600

e

s

Penduga bagi Ragam Sisaan/galat

OUTPUT MINITAB

Dugaan Ragam Sisaan = s2

(JIKA MODELNYA PAS)

Perbandingan Simpangan Baku

Y

Y

X

X

kecil

s

_e

s

_e

besar

Pengujian Hipotesis

Terhadap

Slope dan Intersep

0

β

1 0

β

β

Diperlukan asumsi bahwa ε_i menyebar Normal

Ragam Koefisien Kemiringan Garis

Regresi (b

₁

)

ƒ

Ragam dari koefisien kemiringan garis regresi

(b

₁

) diduga sbb :

= dugaan simpangan baku kemiringan garis regresi = dugaan ragam x

Membandingkan Simpangan Baku

Koefisien Kemiringan Garis Regresi (b

₁

)

Y

X

Y

X

kecil

1 b

S

S

b₁

besar

mengukur keragaman koefisien kemiringan garis

regresi dari berbagai contoh (set data) yang mungkin.

1

b

Regression Analysis: Harga Rumah versus Luas Lantai

The regression equation is

Harga Rumah = 98,2 + 0,110 Luas Lantai

Predictor Coef SE Coef T P

Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

S = 41,3303 R-Sq = 58,1% R-Sq(adj) = 52,8%

Contoh Regresi Linier Sederhana

(lanjutan)

SIMPANGAN BAKU b1 : OUTPUT MINITAB

Inferensia Koefisien Kemiringan Garis

Regresi (b

₁

): Uji t

Pada

model regresi linier sederhana

:

Uji t untuk koefisien kemiringan garis regresi populasi (β₁)

ƒ Apakah ada hubungan linier antara X dan Y? ƒ Hipotesis Nol dan hipotesis tandingan

H₀: β₁ = 0 (tidak ada hubungan linier antara X dan Y) H₁: β₁ ≠ 0 (ada hubungan linier antara X dan Y)

ƒ Uji Statistik

1

b 1 1

s

β

b

t

=

−

2

n

d.b.

=

−

dengan:

b₁ = koefisien kemiringan regresi

β1 = kemiringan yg dihipotesiskan

Harga Rumah (Rp.juta)

(y)

Luas Lantai (m2)

(x) 245 1400 312 1600 279 1700 308 1875 199 1100 219 1550 405 2350 324 2450 319 1425 255 1700

lantai)

(luas

0.1098

98.25

rumah

harga

=

+

Dugaan persamaan garis regresi:

Koefisien kemiringan garis pada

model ini adalah 0.1098

Meskipun demikian, “apakah luas

lantai mempengaruhi harga jual?”

Contoh Inferensia

Contoh Inferensia

Koefisien Kemiringan Garis (b

₁

): uji t

H

₀

:

β

₁

= 0

H

₁

:

β

₁

≠

0

b

₁

s

b1

3.32938

0.03297

0

0.10977

s

β

b

t

1

b 1

1

−

=

−

=

=

Predictor Coef SE Coef T P

Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010 OUTPUT MINITAB

Apakah luas lantai mempe-ngaruhi harga jual (secara linier)?

Contoh Inferensia

Koefisien Kemiringan Garis (b

₁

): uji t

H

₀

:

β

₁

= 0

H

₁

:

β

₁

≠

0

Statistik Uji-nya : t = 3.329

Cukup bukti untuk mengatakan

bahwa luas lantai

output MINITAB :

s

b1

t

b

₁

Keputusan :

Tolak H

₀

Kesimpulan :

Tolak H₀ Tolak H₀

α/2=.025

-t

Terima H₀

0

α/2=.025

d.b. = 10-2 = 8

t_8,.025 = 2.3060

(lanjutan)

t

Predictor Coef SE Coef T P

Contoh Inferensia

Koefisien Kemiringan Garis (b

₁

): uji t

H

₀

:

β

₁

= 0

H

₁

:

β

₁

≠

0

Nilai peluang P =

0.01039

Cukup bukti untuk mengatakan

bahwa luas lantai

mempengaruhi harga rumah

P-value <

α

jadi

Tolak H

₀

Keputusan:

Kesimpulan:

(lanjutan)

Ini adalah uji dua arah,

jadi p-valuenya adalah

output MINITAB :

Predictor Coef SE Coef T P

Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

P(t > 3.329)+P(t < -3.329)

= 0.01039

(db. 8)

Ragam Intersep Garis Regresi (b

₀

)

ƒ

Ragam dari intersep garis regresi (b

₀

) diduga

sbb :

= dugaan simpangan baku intersep garis regresi

= akar KTG = akar Kuadrat Tengah Galat = dugaan

Inferensia Intersep Garis Regresi (b

₀

): uji

t

Pada

model regresi linier sederhana

:

Uji t untuk intersep garis regresi populasi (β₀)

ƒ Apakah ada nilai Y yang tidak dapat dijelaskan oleh x? ƒ Hipotesis Nol dan hipotesis tandingan

H₀: β₀ = 0 (semua nilai Y dapat dijelaskan oleh x)

H₁: β₀ ≠ 0 (ada nilai Y yg tidak dapat dijelaskan oleh x)

ƒ Statistik uji

0

b 0 0

s

β

b

t

=

−

1

d.b.

=

dengan:

b₀ = intersep garis regresi

β0 = intersep yg dihipotesiskan

Harga Rumah (Rp. Juta)

(y)

Luas Lantai (m2)

(x) 245 1400 312 1600 279 1700 308 1875 199 1100 219 1550 405 2350 324 2450 319 1425 255 1700

lantai)

(luas

0.1098

98.25

rumah

harga

=

+

Dugaan persamaan garis regresi:

Intersep garis pada model ini adalah 98.25 Apakah ada bagian harga rumah yang tidak dapat dijelaskan oleh luas lantai? Apakah ada bagian harga rumah yang tidak dipengaruhi oleh luas lantai?

Contoh Inferensia

Contoh Inferensia

Intersep Garis Regresi (b

₀

): uji-t

H

₀

:

β

₀

= 0

H

₁

:

β

₀

≠

0

0

b

s

b

₀

1.69296

58.03348

0

98.24833

s

β

b

t

0

b 0

0

−

=

−

=

=

output MINITAB :

Predictor Coef SE Coef T P

Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

(lanjutan)

Contoh Inferensia

Intersep Garis Regresi (b

₀

): uji-t

H

₀

:

β

₀

= 0

H

₁

:

β

₀

≠

0

Statistik uji: t

_hit

= 1.69296

Tidak cukup bukti untuk

mengatakan bahwa : ada harga

0

b

s

_t

b

₀

Keputusan:

Kesimpulan :

Tolak H₀ Tolak H₀

α/2=.025

-t

Terima H₀

0

α/2=.025

d.b. = 1

t_{1, .025} = 12,706

(lanjutan)

t

output MINITAB :

Predictor Coef SE Coef T P

Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

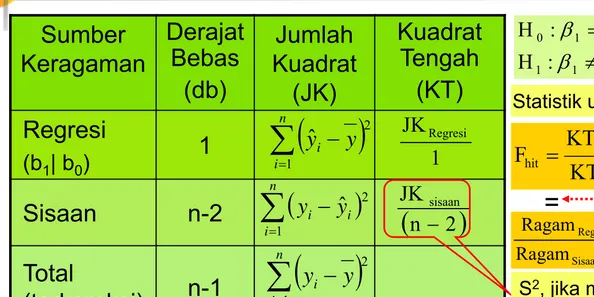
Uji F bagi parameter regresi :

Tabel Sidik Ragam

Sumber

Keragaman

Derajat

Bebas

(db)

Jumlah

Kuadrat

(JK)

Kuadrat

Tengah

(KT)

Regresi

(b₁| b₀)

1

Sisaan

n-2

Total

(terkoreksi)

n-1

( )

JK_Regresi

(

n 2

)

JK _sisaan

−

Statistik uji F tersebut memiliki derajat bebas db1=1 dan db2=n-2

Jika F_hit <1 Æ KT_Regresi < KT_Sisaan ÆRagam Regresi < Ragam Sisaan Æ pengaruh regresi tdk nyata Æ pengaruh x tdk nyata Æ b1 = 0 (tdk perlu tabel)

S2_{, jika}

mo-delnya pas

Statistik uji-nya :

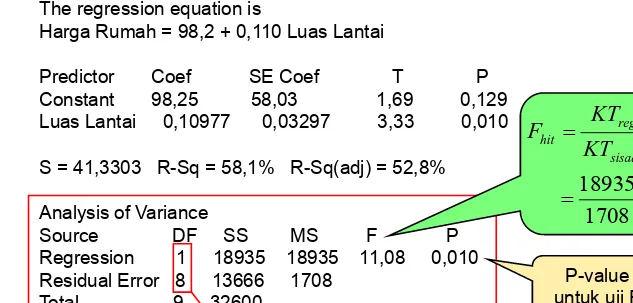
Regression Analysis: Harga Rumah versus Luas Lantai

The regression equation is

Harga Rumah = 98,2 + 0,110 Luas Lantai

Predictor Coef SE Coef T P Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

S = 41,3303 R-Sq = 58,1% R-Sq(adj) = 52,8%

Analysis of Variance

Source DF SS MS F P Regression 1 18935 18935 11,08 0,010 Residual Error 8 13666 1708

OUTPUT MINITAB

Contoh Uji F bagi parameter regresi :

Tabel Sidik Ragam

(lanjutan)

P-value untuk uji F

1708

18935

=

=

sisaan reg hit

Statistik Uji:

Keputusan:

Kesimpulan:

Tolak H

₀

dg

α

= 0.05

Cukup bukti bahwa luas lantai

mempengaruhi harga rumah

0

α = .05

F = 5.32

Tolak H₀ terima

H

Uji F bagi parameter regresi :

Tabel Sidik Ragam

Jika model yang kita pilih di awal ternyata tidak pas

1.

Bolehkah kita menggunakan KT sisaan sebagai

penduga bagi ragam sisaan ?

2. Masih relevankah kita melakukan uji F ?

Agar uji F pada tabel Sidik Ragam dapat digunakan, maka

model yang dipilih harus pas.

Æ

uji

lack of fit

atau periksa

pola sisaannya

Æ

akan dibahas pada sub pokok bahasan

“ Kualitas Fitted Model “ Untuk sementara anggaplah model

yang kita pilih pas.

Perbandingan Tabel Sidik Ragam

Terkoreksi dan Tidak Terkoreksi

Sumber Keragaman

Derajat

Bebas (db) _{Kuadrat (JK)}Jumlah

Kuadrat Tengah (KT)

Regresi

(b₁| b₀) 1

Sisaan n - 2

Total

(terkoreksi) n - 1

( )

JK_Regresi

(

n 2

)

JK _sisaan

−

Regresi (b₀,b₁) 2

Sisaan n - 2

Total n

0

Tidak bisa mem-berikan jawaban apkh x berpe-ngaruh/tidak

Kualitas Fitted Model

•

Apakah model regresi sudah cukup pas mewakili data?

Tebaran

titik amatan / scatter plot

Mana di antara gambar–gam-bar ini yang mo-delnya cukup pas/sesuai ?

a.

_b.

c.

_d.

x

x x

x y

y y

y

Perlu diuji

Tebaran titik amatan / scatter plot

Mana di antara gambar–gam-bar ini yang mo-delnya cukup baik untuk peramalan?

a.

_b.

c.

_d.

y

y y

y

x _x

Perlu suatu be-saran yang dapat mengukur jauh /dekatnya titik pengamatan

Koefisien Determinasi, R

2

ƒ Koefisien determinasi mengukur proporsi keragaman atau variasi

total di sekitar nilai tengah (Y) yang dapat dijelaskan oleh garis regresi

Æ secara grafis mengukur jauh/dekatnya titik pengamatan thdp garis regresi

Koefisien Determinasi, R

2

(lanjutan)

Regression Analysis: Harga Rumah versus Luas Lantai

The regression equation is

Harga Rumah = 98,2 + 0,110 Luas Lantai

Predictor Coef SE Coef T P Constant 98,25 58,03 1,69 0,129 Luas Lantai 0,10977 0,03297 3,33 0,010

S = 41,3303 R-Sq = 58,1% R-Sq(adj) = 52,8%

Analysis of Variance

Source DF SS MS F P Regression 1 18935 18935 11,08 0,010 Residual Error 8 13666 1708

Total 9 32600

5808

,

0

32600

18935

2

=

=

R

OUTPUT MINITAB

Analisis Korelasi

ƒ

Analisis korelasi

digunakan untuk mengukur

kekuatan hubungan (hubungan linier) antara

dua peubah

ƒ

Korelasi hanya khusus untuk kekuatan hubungan

ƒ

Mengukur arah hubungan

Analisis Korelasi

ƒ

Koefisien korelasi populasi

dinotasikan dengan

ρ

(huruf Greek rho)

ƒ

Koefisien korelasi contoh

adalah :

y

Koefisien korelasi Pearson

Pada Model Regresi Linier Sederhana yg hub.nya linier :

ƒ

Untuk melakukan tes bahwa tidak ada

hubungan linier, Hipotesis nol nya :

Statistik ujinya mengikuti sebaran t Student

dengan derajad bebas (n – 2 )

Uji Hipotesis untuk Korelasi

0

ρ

:

H

₀

=

)

r

(1

2)

(n

r

t

2

−

−

=

H

₀

:

ρ

≥

0

H

₁

:

ρ

< 0

H

₀

:

ρ ≤

0

H

₁

:

ρ

> 0

H

₀

:

ρ

= 0

H

₁

:

ρ ≠

0

Kaidah Keputusan

α

α

/2

α

/2

α

-t

_α

t

_α

-t

_α/2

t

_α/2

tolak H₀ jika t < -t_{n-2, α} Tolak H₀ jika t > t_{n-2, α} Tolak H₀ jika t < -t_{n-2, α/2} atau t > t_{n-2, α/2}

2)

(n

r

−

Uji Hipotesis untuk Korelasi

Correlations: Harga Rumah; Luas Lantai

Pearson correlation of Harga Rumah and Luas

Lantai = 0,762

P-Value = 0,010

OUTPUT MINITAB

Uji Hipotesis untuk Korelasi

P-value < 0,025

Æ

Tolak H

₀

Æ

ρ ≠

0

FILM : MENDUGA

KOEFISIEN KORELASI PEARSON dengan

MENGGUNAKAN MINITAB

Data contoh Harga Rumah

Harga Rumah (Rp.juta) (Y)

Luas Lantai (m2) (X)

245 1400

312 1600

279 1700

308 1875

199 1100

219 1550

405 2350

324 2450

319 1425

Correlations: Harga Rumah; Luas Lantai

Pearson correlation of Harga Rumah and Luas Lantai = 0,762

P-Value = 0,010

r

XY

APLIKASI DENGAN MINITAB

DUGAAN BAGI KOEFISIEN KORELASI

r

2

_{= 1}

Interpretasi beberapa nilai r

2

Y

X

Y

X

r

2

= 1

r

2

= 1 dapat diinterpretasikan

sbb. :

Adanya hubungan linier

yang tepat antara X dan Y:

100% keragaman Y

Interpretasi beberapa nilai r

2

Y

X

Y

0 < r

2

_{< 1 dapat}

diinterpretasi-kan sbb. :

Adanya hubungan linier yang

lemah antara X dan Y:

Interpretasi beberapa nilai r

2

Tidak ada hubungan linier

antara X dan Y:

Nilai Y tidak bergantung pada

nilai X. (Tidak ada keragaman

Y yang dapat diterangkan

oleh keragaman X)

Y

X

r

2

_{= 0}

r

2

_{= 0 dapat diinterpretasikan}

Korelasi dan Koefisien

Determinasi R

2

ƒ Koefisien determinasi, R2_{, untuk regresi linier sederhana}

yang hubungannya linier (ordo X = 1) sama dengan koefisien korelasi kuadrat

ƒ Korelasi antara amatan Y_i dengan nilai dugaannya untuk sembarang regresi linier dengan berapapun banyaknya peubah bebas

2 / 1 2 1

xy

R

(tanda

b

)(

R

)

r

=

=

2 xy 2

r

R

=

^ i

Y

R

r

^

Y

Berbagai Kondisi yg Menggambarkan

Perbedaan antara R

2

dan r

_XY

C1

Scatterplot of Y2 vs C1

C1

Scatterplot of Y1 vs C1

Correlations: X1; Y1

Pearson correlation of X1 and Y1 = 1,000 P-Value = *

Correlations: X2; Y2

Pearson correlation of X2 and Y2 = 0,000 P-Value = 1,000

The regression equation is Y1 = 2,00 + 3,00 X1

S = 0 R-Sq = 100,0% R-Sq(adj) = 100,0%

The regression equation is

Y2 = 4,000 + 0,00 X2 + 1,000 X2**2

S = 0 R-Sq = 100,0% R-Sq(adj) = 100,0%

r

_XY

Fitted Line Plot

R2 _{= 1}

r = 0

Berbagai Kondisi yg Menggambarkan

Perbedaan antara R

2

dan r

_XY

X1

Scatterplot of Y3 vs X1

The regression equation is Y3 = 1,27 + 3,10 X1

S = 1,53396 R-Sq = 97,7%

Correlations: Y3; X1

Pearson correlation of Y3 and X1 = 0,988 R2 _{= 97,7%}

r = 0,988

The regression equation is Y4 = 2,07 + 3,01 X1

Scatterplot of Y4 vs X1

R2 _{= 88,7%}

r = 0,942

Correlations: Y4; X1

Pearson correlation of Y4 and X1 = 0,942

(lanjutan)

Berbagai Kondisi yg Menggambarkan

Perbedaan antara b

₁

dan r

_XY

X1

Scatterplot of C7 vs X1

The regression equation is C7 = 37,7 - 3,38 X1

S = 6,09048 R-Sq = 76,0% R-Sq(adj) = 73,0%

Correlations: C7; X1

Pearson correlation of C7 and X1 = -0,872

The regression equation is Y6 = 3,50 + 0,116 X1

S = 0,275434 R-Sq = 64,8% R-Sq(adj) = 60,4%

X1

Scatterplot of Y6 vs X1

Correlations: Y6; X1

Berbagai Kondisi yg Menggambarkan

Perbedaan antara b

₁

dan r

_{XY (lanjutan)}

X

Scatterplot of Y vs X

The regression equation is Y = 1,06 + 4,67 X

S = 2,06491 R-Sq = 53,3% R-Sq(adj) = 52,1%

Analysis of Variance

Source DF SS MS F P

Scatterplot of Y1 vs X1

The regression equation is Y1 = 3,99 + 0,00914 X1 S = 0,0077338 R-Sq = 93,5% R-Sq(adj) = 92,7%

Analysis of Variance

Source DF SS MS F P Regression 1 0,0068911 0,00689 115,21 0,000 Resd Error 8 0,0004785 0,00005

Pearson correlation of X1 and Y1 = 0,967 R2 _{= 93,5%}

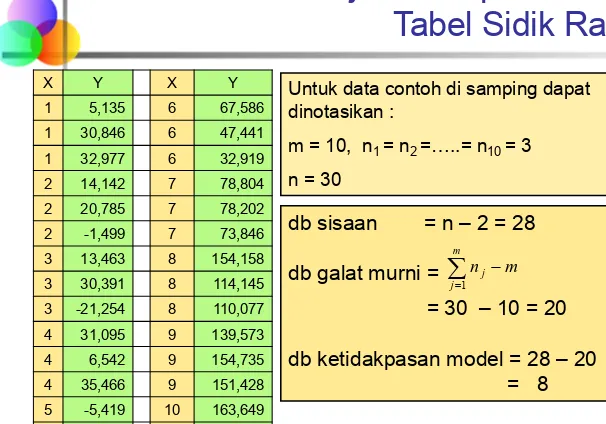
Uji Ketidakpasan Model

ƒ

Harus ada ulangan pengamatan y

_i

pada nilai x

_i

yang sama. Mis. :

Untuk data contoh di samping dapat dinotasikan :

Uji ketidakpasan model :

Tabel Sidik Ragam

Sumber

Keragaman

Derajat

Bebas

(db)

Jumlah

Kuadrat

(JK)

Kuadrat

Tengah

(KT)

Regresi

(b₁| b₀)

1

Sisaan

n-2

Total JK_Regresi

(

n 2

)

JK _sisaan

− Statistik uji-nya :

GM

Ketidakpasan model (KM)

X Y X Y 1 5,135 6 67,586 1 30,846 6 47,441 1 32,977 6 32,919 2 14,142 7 78,804 2 20,785 7 78,202 2 -1,499 7 73,846 3 13,463 8 154,158 3 30,391 8 114,145 3 -21,254 8 110,077 4 31,095 9 139,573 4 6,542 9 154,735 4 35,466 9 151,428 5 -5,419 10 163,649 5 59,32 10 189,114 5 73,178 10 214,504

Contoh : Uji ketidakpasan model

Tabel Sidik Ragam

Untuk data contoh di samping dapat dinotasikan :

m = 10, n₁ = n₂ =…..= n₁₀ = 3

n = 30

db sisaan = n – 2 = 28 db galat murni =

= 30 – 10 = 20 db ketidakpasan model = 28 – 20

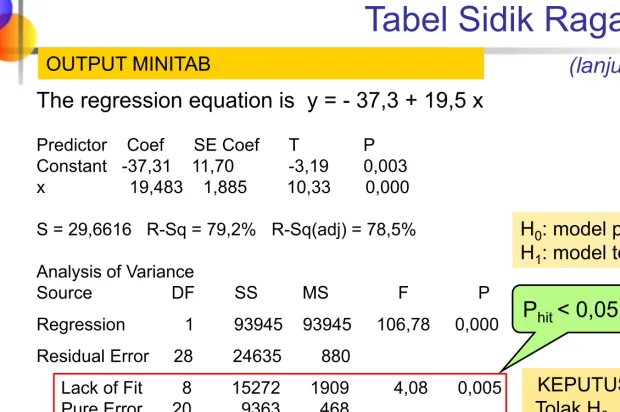
The regression equation is y = - 37,3 + 19,5 x

Predictor Coef SE Coef T P Constant -37,31 11,70 -3,19 0,003 x 19,483 1,885 10,33 0,000

S = 29,6616 R-Sq = 79,2% R-Sq(adj) = 78,5%

Analysis of Variance

Source DF SS MS F P Regression 1 93945 93945 106,78 0,000 Residual Error 28 24635 880

Lack of Fit 8 15272 1909 4,08 0,005 Pure Error 20 9363 468

Total 29 118580

P_hit < 0,05

KEPUTUSAN : Tolak H₀

KESIMPULAN: H₀: model pas H₁: model tdk pas

Contoh : Uji ketidakpasan model

Tabel Sidik Ragam

(lanjutan)

ƒ

Pada contoh tersebut meskipun P-value untuk

pengaruh linier x dan regresi sangat kecil (0,000…)

namun kita tidak memperhatikan hal ini terlebih dahulu.

Kita perhatikan uji ketidakpasan modelnya dulu,

Æ

disimpulkan bahwa model tidak pas.

ƒ

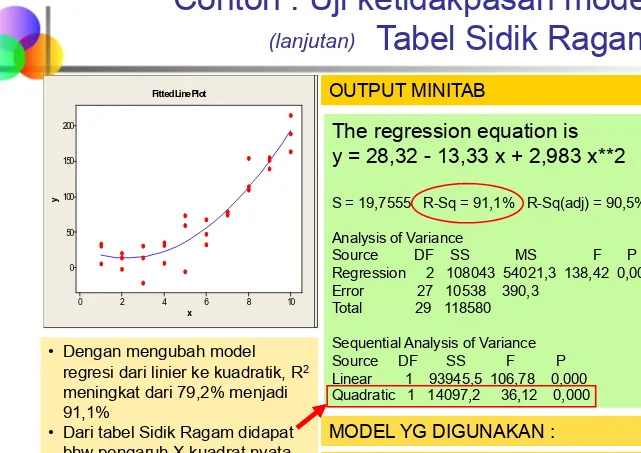
Selanjutnya kita periksa pola tebaran datanya.

x

y

10 8

6 4

2 0

200 150 100 50 0

Scatterplot of y vs x

Pada tebaran data-nya

ter-lihat adanya pola kuadratik

Æ

model yang digunakan

diubah menjadi :

ε

x

β

x

β

β

x

Scatterplot of y vs x

The regression equation is

y = 28,32 - 13,33 x + 2,983 x**2

S = 19,7555 R-Sq = 91,1% R-Sq(adj) = 90,5% Analysis of Variance

Source DF SS MS F P Regression 2 108043 54021,3 138,42 0,00 Error 27 10538 390,3

Total 29 118580

Sequential Analysis of Variance Source DF SS F P

Fitted Line Plot

Contoh : Uji ketidakpasan model

Tabel Sidik Ragam

(lanjutan)

• Dengan mengubah model

regresi dari linier ke kuadratik, R2

meningkat dari 79,2% menjadi 91,1%

• Dari tabel Sidik Ragam didapat bhw pengaruh X kuadrat nyata

OUTPUT MINITAB

FILM :

MENGUJI

KETIDAKPASAN MODEL

dengan

MENGGUNAKAN MINITAB

Klik di sini

X Y X Y 1 5,135 6 67,586 1 30,846 6 47,441 1 32,977 6 32,919 2 14,142 7 78,804 2 20,785 7 78,202 2 -1,499 7 73,846 3 13,463 8 154,158 3 30,391 8 114,145 3 -21,254 8 110,077 4 31,095 9 139,573 4 6,542 9 154,735 4 35,466 9 151,428 5 -5,419 10 163,649 5 59,32 10 189,114 5 73,178 10 214,504

Langkah-langkah

Pemilihan Model yang Pas

1.

Tentukan model, dapatkan dugaan persamaan garis regresinya,

susun tabel Sidik Ragam, jangan dulu melakukan uji F untuk

regresi keseluruhan

2.

Lakukan uji ketidakpasan model.

Jika tidak ada ulangan, cek secara eksploratif : plot sisaan-nya

(akan dijelaskan pada pokok bahasan: Diagnosa Model).

Jika

nyata

: lanjut ke langkah 3

Jika

tidak nyata

: gunakan KT sisaan s

2

_{sebagai dugaan bagi}

Rag(Y) =

σ

2

_{, lakukan uji F secara keseluruhan, hitung R}

2

_,

perik-sa asumsi untuk MKT melalui plot siperik-saan (Diagnoperik-sa Model)

Selang Kepercayaan

bagi koefisien kemiringan

b

₁

Selang kepercayaan bagi koefisien

kemiringan adalah :

Output Excel untuk contoh kasus harga rumah:

Pada tingkat kepercayaan 95%, selang kepercayaan

bagi koefisien kemiringan garis adalah (0.0337, 0.1858)

1

1 1 1 n 2,α/2 b

b

α/2 2, n

1

t

s

β

b

t

s

b

−

₋

<

<

+

₋

Coefficients Standard Error t Stat P-value Lower 95% Upper 95%

Intercept 98.24833 58.03348 1.69296 0.12892 -35.57720 232.07386 Luas Lantai 0.10977 0.03297 3.32938 0.01039 0.03374 0.18580

Selama satuan peubah tak bebas (harga rumah) dalam juta rupiah, kita percaya 95% bahwa rata-rata pengaruh penambahan harga rumah

berada antara Rp. 0,03374 juta sampai dengan Rp.0,18580 juta setiap penambahan satu m2 _{luas lantai}

Coefficients Standard Error t Stat P-value Lower 95% Upper 95%

Intercept 98.24833 58.03348 1.69296 0.12892 -35.57720 232.07386 Luas Lantai 0.10977 0.03297 3.32938 0.01039 0.03374 0.18580

Selang kepercayaan 95% ini tidak memuat angka 0.

Kesimpulan : Ada hubungan linier yang nyata antara harga rumah

dengan luas lantai dengan tingkat nyata sebesar 95%

Selang Kepercayaan

bagi koefisien kemiringan

b

₁

Peramalan

ƒ

Dugaan persamaan garis regresi dapat

digunakan untuk memprediksi/meramal nilai

Y jika x diketahui (

hati-hati hanya untuk x

yang berada dalam selang pengamatan

)

ƒ

Untuk suatu nilai, x

_n+1

, nilai prediksi bagi Y

adalah

1

n

1

0

1

n

b

b

x

317.85

0)

0.1098(200

98.25

lantai)

(luas

0.1098

98.25

rumah

harga

=

+

=

+

=

Berapa kira-kira harga rumah yang luas lantainya

2000 m

2

_{! (2000 bukan titik pengamatan, namun}

masih dalam selang pengamatan).

Æ

interpolasi

Prediksi harga rumah dengan luas lantai

2000 m

2

_{adalah Rp 317,85 juta}

0

0 500 1000 1500 2000 2500 3000

Ha

Selang data yang relevan

ƒ

Ketika menggunakan garis regresi sebagai alat

untuk memprediksi, x yang boleh digunakan adalah

x yang nilainya dalam selang pengamatan

Selang yang relevan

Sangat riskan untuk melakukan

Selang kepercayaan rataan

respon dan dugaan individu

Y

y_i = b₀ + b₁ x_i Selang

kepercayaan bagi rataan Y, untuk x_i

Selang kepercaya-an bagi nilai peng-amatan y

,

untuk x

Selang Kepercayaan bagi nilai harapan

Y, untuk suatu X

Selang kepercayaan bagi

dugaan nilai harapan/rataan y

jika diketahui x

_n+1

Perhatikan bahwa rumus tersebut mengandung

Selang Kepercayaan bagi

individu Y, untuk suatu nilai x

Dugaan bagi Nilai Tengah/Rataan:

Contoh harga rumah

Dapatkan selang kepercayaan 95% bagi rataan

harga rumah dengan luas lantai 2.000 m2

harga rumah y

∧

_i

= 317,85 (Rp. juta)

Selang kepercayaan bagi E(Y

_n+1

|X

_n+1

)

37.12

Selang kepercayaan 95% bagi rataan harga rumah

354.900.000,-Predicted Values for New Observations New

Obs Fit SE Fit 95% CI 95% PI 1 317,8 16,1 (280,7; 354,9) (215,5; 420,1) Values of Predictors for New Observations

New Luas Obs Lantai

1 2000

OUTPUT MINITAB

Dugaan bagi Nilai Tengah/Rataan:

Contoh harga rumah

Selang Kepercayaan 95% bagi dugaan nilai tengah/Rataan untuk suatu nilai x tertentu yg tidak ada pada pengamatan, namun masih dalam selang

Æ

Dugaan Nilai Tengah untuk x = 2000

Dugaan bagi individu/respon:

contoh harga rumah

Dapatkan selang kepercayaan 95% bagi respon individu

harga rumah untuk rumah dengan luas lantai 2.000 m2

y

∧

_i

= 317,85 (Rp. juta)

Selang kepercayaan bagi individu y

_n+1

102.28

Selang kepercayaan 95% bagi harga rumah dengan luas lantai 2000m2 ialah dari Rp 215.500.000,- sampai Rp 420.070.000,-.

OUTPUT MINITAB

Predicted Values for New Observations New

Obs Fit SE Fit 95% CI 95% PI 1 317,8 16,1 (280,7; 354,9) (215,5; 420,1) Values of Predictors for New Observations

New Luas Obs Lantai

1 2000

Dugaan bagi individu/respon:

contoh harga rumah

(lanjutan)

FILM :

MENGHITUNG

SELANG KEPERCAYAAN BAGI

RAMALAN NILAI TENGAH

&

RAMALAN NILAI INDIVIDU

dengan

MENGGUNAKAN MINITAB

Klik di sini

Data contoh Harga Rumah

Harga Rumah (Rp.juta) (Y)

Luas Lantai (m2) (X)

245 1400

312 1600

279 1700

308 1875

199 1100

219 1550

405 2350

324 2450

319 1425