TWO NEW REFINED SHEAR DISPLACEMENT MODELS FOR FUNCTIONALLY GRADED SANDWICH PLATES

(1)

Manajemen dan Rekayasa Struktur C-75

TWO NEW REFINED SHEAR DISPLACEMENT MODELS

FOR FUNCTIONALLY GRADED SANDWICH PLATES

ADDA BEDIA El Abbas(1) , MERDACI Slimane(1), ZIDI Mohamed(1), HEBALI Habib(1), BACHIR BOUIADJRA Rabbab(2), TOUNSI Abdelouahed(1), BENYOUCEF Samir(1),

BOURADA Mohamed

1. INTRODUCTION

(1)

(1) Laboratoire des Matériaux et Hydrologie, Université de Sidi Bel Abbes, BP 89 Cité Ben M’hidi 22000 Sidi Bel Abbes, Algérie.

[email protected]

(2) Université de Sciences et Technologie d’Oran (USTO), Algérie.

Abstract— Two refined displacement models, RSDT1 and RSDT2, are developed for a bending analysis of functionally graded sandwich plates. Unlike any other theory, the number of unknown functions involved is only four, as against five in case of other shear deformation theories. The developed models are variationally consistent, have strong similarity with classical plate theory in many aspects, doe not require shear correction factor, and give rise to transverse shear stress variation such that the transverse shear stresses vary parabolically across the thickness satisfying shear stress free surface conditions. The accuracy of the analysis presented is demonstrated by comparing the results with solutions derived from other higher-order models. The functionally graded layers are assumed to have isotropic, two-constituent material distribution through the thickness, and the modulus of elasticity, Poisson’s ratio of the faces, and thermal expansion coefficients are assumed to vary according to a power law distribution in terms of the volume fractions of the constituents. The core layer is still homogeneous and made of an isotropic ceramic material. Numerical results for deflections and stresses of functionally graded metal–ceramic plates are investigated. It can be concluded that the proposed models are accurate and simple in solving the bending behavior of functionally graded plates.

Keywords— functionally graded plates, shear deformation, higher-order theories

In recent decades, a new class of plates/shells made up of functionally graded materials (FGM), in which the material properties continuously vary through the thickness has become popular in various engineering applications. Because of the feature of continuously distributed material properties in FGM plates/shells, some drawbacks of conventional multilayered composite

(2)

numerical modeling for the analysis of this class of FGM plates and shells has attracted considerable attention from researchers [1 – 7].

x x, y, and z coordinate directions, respectively, and u0, v0, and w0 displacements.

However, in thick and moderately thick plates, the transverse shear strains have to be taken into account. There are numerous plate theories that include these strains. The first-order shear deformation plate theory (FSDPT), which is known as the Mindlin plate theory [8 – 10], considers the displacement field as linear variations of midplane displacements:

, v(x,y,z)=v0+zθy,

In this theory, the relation between the resultant shear forces and the shear strains depends on shear correction factors [11 – 13]. This theory is also used for FGM plates as is described by Sladek et al. [14].

Some other plate theories, e.g., higher-order shear deformation theories (HSDT), which include the effect of transverse shear strains, are reported in the literature.

Higher-order theories based on series

expansions were developed by Donnel

[15], Reissner [16], and Lo et al. [17, 18]

and were modified by Levinson [19],

Murthy [20], and Reddy [21]. The

displacement field in these theories is

x

Reddy [21, 22] put forward a parabolic shear deformation plate theory (PSDPT) which considers not only the transverse shear strains, but also their parabolic variation across the plate thickness. As a result, there is no need to use shear correction coefficients in computing the shear stresses. In this theory,

x

Touratier [23] used sinusoidal shear deformation plate theory (SSDPT) for describing the parabolic distribution of transverse shear strains across the plate thickness and took the displacement field in the form

Soldatos [24] employed hyperbolic shear deformation plate theory (HSDPT) for this purpose:

x

Karama et al. [25] used an exponential

shear deformation plate theory (ESDPT):

(3)

Manajemen dan Rekayasa Struktur C-77 ( )

x h z ze x w z u z y x

u 0 2 / 2θ

0 ) , ,

( + −

∂ ∂ −

= ,

( )

y h z ze y w z v z y x

v 0 2 / 2θ

0 ) , ,

( + −

∂ ∂ −

= ,

) , ( ) , ,

(x y z w0 x y

w =

Ferreira et al. [26] assumed the

displacement field in the form

x

h z x

w z u z y x

u π θ

     + ∂ ∂ −

= sin

) , ,

( 0 0 ,

y h

z y

w z v z y x

v π θ

     + ∂ ∂ −

= sin

) , ,

( 0 0 ,

) , ( ) , ,

(x y z w0 x y

w =

The description of various plate theories is

given in Table 1. There are also many

comparison studies on the behavior of

transverse shear stresses in composite

plates [27 – 31].

In this study, two new displacement

models for an analysis of simply supported

FGM sandwich plates are proposed. The

plates are made of an isotropic material with material properties varying in the thickness

direction only. Analytical solutions for

bending deflections of FGM plates are

obtained. The governing equations are

derived from the principle of minimum total

potential energy. Numerical results for

displacements and stresses are presented for a metal–ceramic FG plate. To make the study reasonable, displacements and stresses are given for different homogenization schemes and exponents in the power-law that describes the variation of the constituents.

2. PROBLEM FORMULATION

Consider the case of a uniform thickness, rectangular FGM sandwich plate composed of three microscopically heterogeneous layers as shown in Fig. 1. The top and bottom faces of the plate are at z=±h/2, and the edges of the plate are parallel to axes x and y.

The sandwich plate is composed of three elastic layers, namely, ‘‘Layer 1’’, ‘‘Layer 2’’, and ‘‘Layer 3’’ from bottom to top of the plate (Fig. 2). The vertical ordinates of the bottom, the two interfaces, and the top are denoted by

2 /

1 h

h =− , h₂, h₃, h₄ =h/2, respectively.

Two homogenization techniques are used to find the effective properties at each point in FGM layer. The rule of mixtures is the conventional and simple technique which is widely used in composite materials. In this technique, the effective property of FGM can be approximated based on an assumption that a composite property is the volume weighted average of the properties of the constituents. Another widely used approach for characterization of the material gradation is the micromechanics technique. In this technique, the effective elastic moduli of an FGM are determined from the volume fractions and shapes of the constituents. The Mori–Tanaka method [32] and self-consistent method [33] are two popular schemes of micromechanics technique.

Recently, Chehel Amirani et al. [34] studied the free vibration of sandwich beam with FG core and they showed that there is insignificant difference between the results obtained by these two techniques (micromechanics technique and the rule of mixtures technique). Hence, in the following sections, the rule of mixtures technique is used for its simplicity. The volume fraction of the FGMs is assumed to obey a power-law function along the thickness direction:

(4)

k

h h

h z

V _

  

 

− − =

1 2

1 )

1

( _,

] , [h₁ h₂

z∈

1 ) 2 ( ₌

V , z∈[h₂,h₃]

k

h h

h z

V _

  

 

− − =

4 3

4 )

3

( _,

] , [h₃ h₄

z∈

where (n)

V , (n=1,2,3) denotes the volume fraction function of layer n; k is the volume

fraction index (0≤k≤+∞), which indicates the material variation profile through the thickness. The effective material properties, like Young’s modulusE, Poisson’s ratioν, and thermal expansion coefficient α then can be expressed by the rule of mixture [31, 35] as

(

)

( )

2 1 2 ) (

)

( n

n

V P P P z

P = + −

where (n)

P is the effective material property of FGM of layer n. P₂ and P₁ denote the property

of the bottom and top faces of layer 1 (h1≤z≤h2), respectively, and vice versa for

layer 3 (h₃ ≤z≤h₄) depending on the volume fraction (n)

V (n=1,2,3). For simplicity, Poisson’s ratio of plate is assumed to be constant in this study for that the effect of Poisson’s ratio on the deformation is much less than that of Young’s modulus [36].

2.1.present refined shear deformation theory

Unlike the other theories, the number of unknown functions involved in the present refined shear deformation theory is only four, as against five in case of other shear deformation theories [21 – 26]. The theory presented is variationally consistent, does not require a shear correction factor, and gives rise to transverse shear stress variation such that the transverse shear stresses vary parabolically

across the thickness, satisfying shear stress free surface conditions.

2.1.1. Assumptions of the present plate theory Assumptions of the present plate theory are as follows:

(i) The displacements are small in comparison with the plate thickness and, therefore, strains involved are infinitesimal.

(ii) The transverse displacement w includes two components of bending w_b, and shear

s

w . These components are functions of coordinates x, y only.

) , ( ) , ( ) , ,

(x y z w x y w x y

w = _b + _s

(iii) The transverse normal stress σ_z is negligible

in comparison with in-plane stressesσxand

y

σ .

(iv) The displacements u in x-direction and v in y

-direction consist of extension, bending, and shear components.

s b u

u u

U= ₀+ + , V =v₀+v_b+v_s

The bending components u_b and v_b are assumed to

be similar to the displacements given by the classical plate theory. Therefore, the expr ession for

b

u and v_b can be given as

x w z

u_b b

∂ ∂ −

= ,

y w z

v_b b

∂ ∂ − =

The shear components u_s and v_s give rise, in conjunction with w_s, to the parabolic variations of shear strains γ_xz, γ_yz and hence to shear

stresses τ_xz, τ_yz through the thickness of the

plate in such a way that shear stresses τ_xz, τ_yz

are zero at the top and bottom faces of the plate. Consequently, the expression for u_s and

s

v can be given as

(9b) (9a)

(9b)

(9c)

(10)

(11)

(12)

(13)

(5)

2.1.2. Displacement Field and Constitutive Equations

In the present analysis, displacement field models satisfying the condition of zero transverse shear stresses on the top and bottom surface of the plate are considered. Based on the assumptions made in preceding section, the displacement field can be obtained using Eqs. (11) – (14) as

RSDT1 and RSDT2



The strains associated with the displacements in Eq. (15) are

For elastic and isotropic FGMs, the constitutive relations can be written as:

)

components, respectively. Using the material properties defined in Eq. (10), stiffness coefficients, Q_ij, can be expressed as

,

2.1.3. Equilibrium Equations

The equilibrium equations are derived by

using the virtual work principle, which can

be written for the plate as

[ ] 0

Substituting Eqs. (17) and (18) into Eq. (20) and integrating through the thickness of the plate, Eq (20) can be rewritten as

(6)

Manajemen dan Rekayasa Struktur C-80 coordinates of the nth layer.

The governing equations of equilibrium can be derived from Eq. (21) by integrating the displacement gradients by parts and setting the coefficients δ u₀, δ v₀, δ w_b and δ w_s zero separately. Thus one can obtain the equilibrium equations associated with the present shear deformation theory,

0

Using Eq. (18) in Eq. (22), the stress resultants of a sandwich plate made up of three layers can be related to the total strains by



defined as

( zz f z zf z f z) dz

Substituting from Eq. (24) into Eq. (23), we obtain the following equation

(7)

differential operators:

j

3. NUMERICAL PROCEDURE

Rectangular plates are generally classified in accordance with the type of support used. We are here concerned with the exact solution of Eqs. (27) for a simply supported FGM plate. The following boundary conditions are imposed at the side edges:

0

To solve this problem, Navier presented the external force in the form of a double trigonometric series:

∑∑

∞ sinusoidally distributed load, we have

1

= =n

m , and q₁₁=q₀

where q₀ represents the intensity of the load at

the plate center.

Following the Navier solution procedure, we assume the following solution form for (u0,v0,wb,ws) that satisfies the boundary

conditions,

,

parameters to be determined using Eqs. (27). One obtains the following operator equation,

[ ]

K

{ } { }

∆ = P,

4. NUMERICAL RESULTS

(8)

In this study, two new shear deformation

theories for FGM sandwich plates are

considered, and comparisons are made

with solutions obtained using other shear

deformation theories available in the

literature. Symmetric and non-symmetric

sandwich plates are examined. Note that the core of the plate is fully ceramic while the bottom and top surfaces of the plate are metal-rich.

In the following, we note that several kinds of sandwich plates are used:

• The (1-0-1) FGM sandwich plate: The plate is symmetric and made of only two equal-thickness FGM layers, i.e. there is no core layer. Thus, h1 =h2 =0.

• The (1-1-1) FGM sandwich plate: Here the plate is symmetric and made of three equal thickness layers. In this case, we have,

6 /

1 h

h =− , h2 =h/6.

• The (1-2-1) FGM sandwich plate: The plate is symmetric and we have: h1=−h/4,

4 / 2 h

h = .

• The (2-1-2) FGM sandwich plate: Here the plate is also symmetric and the thickness of the core is half the face thickness. In this case, we have, h1 =−h/10, h2 =h/10.

• The (2-2-1) FGM sandwich plate: In this case the plate is not symmetric and the core thickness is the same as one face while it is twice the other. Thus,

10 /

1 h

h =− , h2 =3h/10.

The FG plate is taken to be made of aluminum and alumina with the following material properties:

• Metal (Aluminium, Al): 9 10 70×

=

M

E

N/m2;ν =0.3.

• Ceramic (Alumina, Al2O3): EC =380×109; N/m2;ν =0.3.

The various non-dimensional parameters used are

• center deflection 

     =

2 , 2 10

0 2

0 a b

w q a

hE

w ,

• axial stress 

  

  =

2 , 2 , 2 10

0 2

2

h b a q a

h

x

x σ

σ ,

• shear stress 

    

= ,0

2 , 0

0

b aq

h

xz xz τ

τ ,

• thickness coordinate z=z/h.

where the reference value is taken as E0= 1

GPa. We also take the shear correction factor K = 5/6 in FSDPT. Numerical results are presented in Tables 2 – 5 using different plate theories. Additional results are plotted in Figs. 3 to 5 using the present new shear deformation theory (RSDT1). It is assumed, unless otherwise stated, thata/h=10and a/b=1.

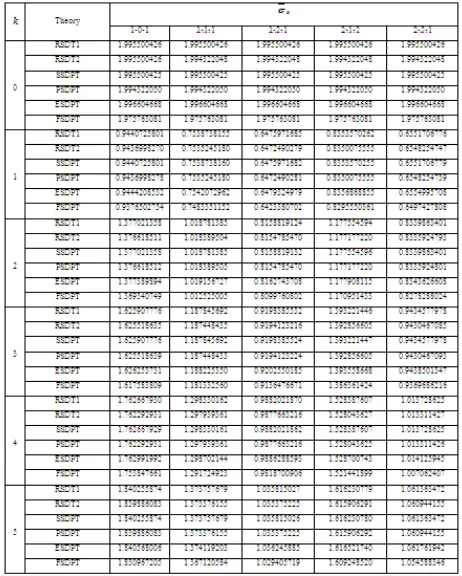
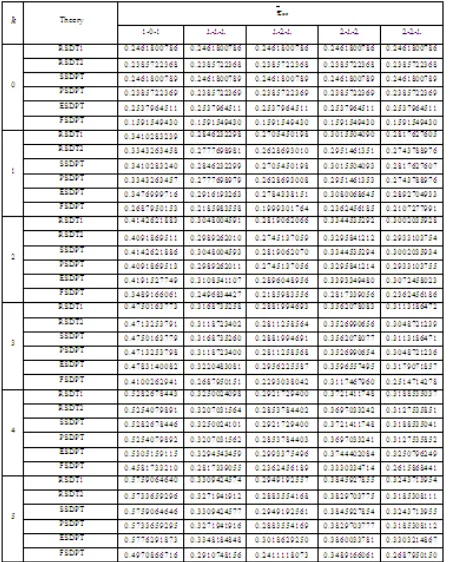
Table 2 contains the dimensionless center deflection w for an FG sandwich plate subjected to a sinusoidally distributed load. The deflections are considered for k= 0, 1, 2, 3, 4, and 5 and different types of sandwich plates. Table 2 shows that the effect of shear deformation is to increase the deflection. The difference between the shear deformation theories is insignificant for fully ceramic plates (k =0). It can be observed that the results obtained by the present refined theories RSDT1 and RSDT2 are identical to those of sinusoidal shear deformation plate theory (SSDPT) and parabolic shear deformation plate theory (PSDPT), respectively.

(9)

aspect ratio a/b increases and this irrespective

of the type of the sandwich plate.

Table 4 lists values of axial stress σx for k= 0, 1, 2, 3, 4, and 5 and different types of sandwich plates. All theories (RSDT1, RSDT2, PSDPT, SSDPT, ESDPT and FSDPT) give the same axial stress σx for a fully ceramic plate (k= 0). In general, the axial stress increases with the volume fraction exponent k. However, the fully ceramic plates (k= 0) give the largest

axial stresses. It is to be noted that the CPT yields identical axial stresses as the FSDPT and so Table 4 lacks the results of CPT.

Table 5 shows similar results of transverse shear stress τxz for a FGM sandwich plate subjected to a sinusoidally distributed load. The results show that the transverse shear stresses as per the FSDPT may be indistinguishable. As the volume fraction exponent increases for FG plates, the shear stress will increase and the fully ceramic plates give the smallest shear stresses.

It can be observed that the results obtained by the present two models RSDT1 and RSDT2 are identical to those of the sinusoidal shear deformation plate theory (SSDPT) and the parabolic shear deformation plate theory (PSDPT), respectively. In general, the fully ceramic plates give the smallest deflections and shear stresses and the largest axial stresses. As the volume fraction exponent increases for FGM sandwich plates, the deflection, axial stress and shear stress will increase.

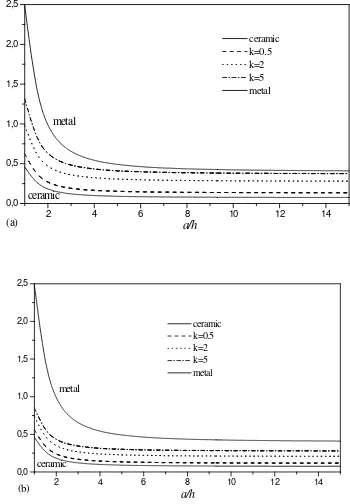
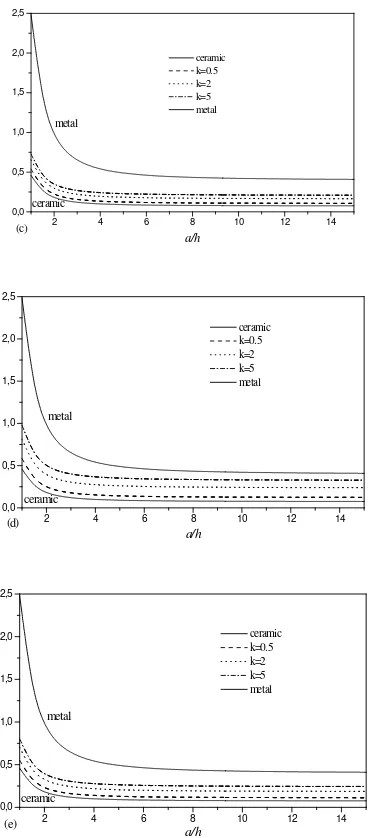
Fig. 3 shows the variation of the center deflection with side-to-thickness ratio for different types of FGM sandwich plates. The FGM plate deflection is between those of plates made of ceramic (Al2O3) and metal (Al). It can

be observed that, deflection of metal rich FGM plate is more when compared to ceramic rich plate. This can be accounted to the Young’s modulus of ceramic (Al2O3;

Fig 4 contains the plots of the axial stress

380 GPa) being

high when compared to that of metal (Al; 70 GPa).

x

σ

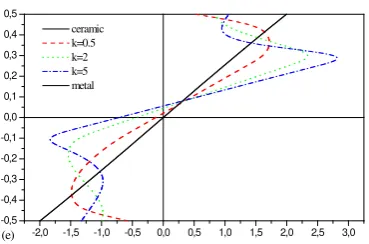
through-the-thickness of the FGM sandwich plates. The stresses are tensile above the mid-plane and compressive below the mid-mid-plane except for the nonsymmetric (2-2-1) FGM plate. The axial stress is continuous through the plate thickness. The results demonstrate a nonlinear variation of the axial stress through the plate thickness for FGM plates. It is important to observe that the maximum stress depends on the value of the volume fraction exponent kand the kind of the sandwich plate.

In Fig. 5 we have plotted the through-the-thickness distributions of the transverse shear stress τxz: The maximum value occurs at a point on the mid-plane of the plate and its magnitude for a FG plate is larger than that for a homogeneous (ceramic or metal) plate. Because of the non-symmetry of the (2-2-1) FGM plate, the maximum value of the transverse shear stress, τxz (Fig. 5d), occurs as discussed before at a point on the mid-plane of the plate.

It is important to observe that the stresses (Figs. 4 and 5) for a fully ceramic plate are the same as that for a fully metal plate. This is because the plate for these two cases is fully homogeneous and the stresses do not depend on the modulus of elasticity.

5. CONCLUSION

(10)

and results were compared with previous other shear deformation theories. The developed theories give parabolic distribution of the transverse shear strains, and satisfy the zero traction boundary conditions on the surfaces of the plate without using shear correction factors. The accuracy and efficiency of the present theories has been demonstrated for static behavior of symmetric and non-symmetric functionally graded sandwich plates. All comparison studies demonstrated that the deflections and stresses obtained using the present two new shear deformation theories (with four unknowns) and other higher shear deformation theories such as PSDPT and SSDPT (with five unknowns) are almost identical. The extension of the present theory is also envisaged for general boundary conditions and plates of a more general shape. In conclusion, it can be said that the proposed theories RSDT1 and RSDT2 are accurate and simple in solving the static behaviors of symmetric and non-symmetric FGM sandwich plates.

REFERENCES

1. C.P. Wu, H.Y. Li, “An RMVT-based third-order shear deformation theory of multilayered functionally graded material plates.” Composite Structures, (2010).

2. M. Şimşek, “Fundamental frequency analysis of functionally graded beams by using different higher-order beam theories,” Nuclear Engineering and Design., 240, 697–705 (2010).

3. J. Ying, C.F. Lü, C. W. Lim, “3D thermoelasticity solutions for functionally graded thick plates,” J. Zhejiang Univ Sci A., 10(3), 327 – 336 (2009).

4. C. F. Lü, C. W. Lim, and W. Q. Chen, “Exact solutions for free vibrations of functionally graded thick plates on elastic foundations,” Mechanics of Advanced Materials and Structures. 16, 576 – 584 (2009).

5. C. F. Lü, C. W. Lim, and W. Q. Chen, “Semi-analytical analysis for multi-directional functionally graded plates: 3-D elasticity solutions,” Int. J. Numer. Meth. Engng, 79, 25–44 (2009).

6. C.P. Wu, S.E. Huang, “Three-dimensional solutions of functionally graded piezothermo-elastic shells and plates using a modified Pagano method.” Comput Mater Continua, 12, 251–82 (2009).

7. S.S.Vel and R.C. Batra, “Three-dimensional exact solution for the vibration of functionally graded rectangular plates,” J. Sound Vib., 272, 703–730 (2004).

8. E. Reissner, “The effect of transverse shear deformation on the bending of elastic plates,” J. Appl. Mech., 12, 69-77 (1945).

9. R. D. Mindlin, “Influence of rotatory inertia and shear on flexural motions of isotropic elastic plates,” J. Appl. Mech.,

18, 31-38 (1951).

10. E. Reissner, “On the theory of bending of elastic plates,” J. Math. Phys., 23, 184-191 (1944).

11. Y. Nath and K. K. Shukla, “Non-linear transient analysis of moderately thick laminated composite plates,” J. Sound Vibrat., 247, No. 3, 509-526 (2001). 12. S. Hui-Shen, “Nonlinear bending of

(11)

13. T. Kant and K. Swaminathan, “Analytical solutions for the static analysis of laminated composite and sandwich plates based on a higher order refined theory,” Compos. Struct., 56, 329-344 (2002).

14. J. Sladek, V. Sladek, Ch. Hellmich and J. Eberhardsteiner, “Analysis of thick functionally graded plates by local integral equation method” Commun. Numer. Meth. Engng, 23, 733–754 (2007).

15. L. H. Donnel, “A theory for thick

plates,” in: Proc. Second U.S. Nat.

Congr. Appl. Mech., ASME Publ.

Univ. Michigan, Michigan (1955), pp.

369-373.

16. E. Reissner, “On the derivation of boundary conditions for plate theory,” in: Proc. Roy. Soc. London, 276, Ser. A, No. 1364, 178-186 (1963).

17. K. H. Lo, R. M. Christensen, and E. M. Wu, “A higher-order theory of plate deformation. Pt. 1: Homogeneous plates,” ASME J. Appl. Mech., 44, 663-668 (1977).

18. K. H. Lo, R. M. Christensen, and E. M. Wu, “A higher-order theory of plate deformation. Pt. 2: Laminated plates,” ASME J. Appl. Mech., 44, 669-676 (1977).

19. M. Levinson, “An accurate simple

theory of the statics and dynamics of

elastic plates,” Mech. Res.

Commun., No. 7, 343-350 (1980).

20. M. V. V. Murthy, An Improved

Transverse Shear Deformation

Theory for Laminated Anisotropic

Plates, NASA Techn. Paper (1981),

pp. 1-37.

21. J. N. Reddy, “A simple higher order theory for laminated composite plates,” J. Appl. Mech., 51, 745-752 (1984). 22. J. N. Reddy, “A refined nonlinear

theory of plates with transverse shear deformation,” Int. J. Solids Struct., 20,

No. 9, 881-896 (1984).

23. M. Touratier, “An efficient standard plate theory,” Int. J. Eng. Sci., 29, No. 8, 901-916 (1991).

24. K. P. Soldatos, “A transverse shear deformation theory for homogenous monoclinic plates,” Acta Mech., 94, Nos. 3-4, 1995-2200 (1992).

25. M. Karama, K. S. Afaq, and S. Mistou, “Mechanical behaviour of laminated composite beam by new multi-layered laminated composite structures model with transverse shear stress continuity,” Int. J. Solids Struct., 40, No. 6, 1525-1546 (2003).

26. A. J. M. Ferreira, C. M. C. Roque, and R. M. N. Jorge, “Analysis of composite plates by trigonometric shear deformation theory and multiquadrics,” Comput. Struct., 83, 225-2237 (2005). 27. A. Idlbi, M. Karama, and M. Touratier,

“Comparison of various laminated plate theories,” Compos. Struct., 37, No. 2, 173-184 (1997).

28. H. Altenbach, “Theories for laminated and sandwich plates,” Mech. Compos. Mater., 34, No. 3, 243-252 (1998). 29. J. N. Reddy and C. M. Wang, “An

(12)

30. M.A. Benatta, I. Mechab, A. Tounsi, E.A. Adda Bedia, “Static analysis of functionally graded short beams including warping and shear deformation effects,“ Comput ational Materials Science, 44, 765–773 (2008). 31. B.O. Sallai, A. Tounsi, I. Mechab, B.M.

Bachir, M. Meradjah, E.A. Adda, “A theoretical analysis of flexional bending of Al/Al2O3 S-FGM thick beams,“ Computational Materials Science, 44, 1344–1350 (2009).

32. T. Mori, K. Tanaka, “Average stress in matrix and average elastic energy of materials with misfitting inclusions.” Acta Metall. 21, 571–574 (1973).

33. R. Hill, “A self-consistent mechanics of composite materials.” J Mech Phys Solids. 13, 213–222 (1965).

34. M. Chehel Amirani, S.M.R. Khalili, N. Nemati, “Free vibration analysis of sandwich beam with FG core using the element free Galerkin method.” Composite Structures. 90, 373–379 (2009).

35. S. Chi, and Y. Chung, “Mechanical behavior of functionally graded material plates under transverse load - Part I: Analysis.” Int. J. Sol. Struc. 43, 3657– 3674 (2006).

36. F. Delale, F. Erdogan F, “The crack problem for a nonhomogeneous plane.” Journal of Applied Mechanics 50, 609 (1983)

Figure. 1: Geometry of rectangular FGM sandwich plate with uniform thickness in rectangular Cartesian coordinates.

Figure. 2: The material variation along the thickness of the FGM sandwich plate

2 4 6 8 10 12 14

0,0 0,5 1,0 1,5 2,0 2,5

(a) ceramic

metal

ceramic k=0.5 k=2 k=5 metal

a/h

2 4 6 8 10 12 14

0,0 0,5 1,0 1,5 2,0 2,5

(b) ceramic

metal

(13)

2 4 6 8 10 12 14

0,0 0,5 1,0 1,5 2,0 2,5

ceramic metal

(c)

a/h

2 4 6 8 10 12 14

0,0 0,5 1,0 1,5 2,0 2,5

(d) ceramic

metal

a/h

2 4 6 8 10 12 14

0,0 0,5 1,0 1,5 2,0 2,5

ceramic metal

(e)

a/h

Figure. 3: Dimensionless center deflection (w) as a function of side-to-thickness ratio (a/h) of an FGM sandwich plate for various values of k and different types of sandwich plates. (a) The (1-0-1) FGM sandwich plate. (b) The (1-1-1) FGM sandwich plate. (c) The (1-2-1) FGM sandwich plate. (d) The (2-1-2) FGM sandwich plate, (e) The (2-2-1) FGM sandwich plate.

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0

(a)

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

-2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 (c)

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 (d)

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

-2,5 -2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5

(b)

(14)

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

-2,0 -1,5 -1,0 -0,5 0,0 0,5 1,0 1,5 2,0 2,5 3,0

(e)

Figure. 4: Variation of axial stress σx through the plate thickness for various values of k and different types of sandwich plates: (a) The (1-0-1) FGM sandwich plate. (b) The (1-1-(1-0-1) FGM sandwich plate. (c) The (1-2-1) FGM sandwich plate. (d) The (2-1-2) FGM sandwich plate, (e) The (2-2-1) FGM sandwich plate.

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35 0,40 0,45

(a)

ceramic k=1 k=2 metal

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35

(b)

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

0,00 0,05 0,10 0,15 0,20 0,25 0,30

(c)

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35

(d)

-0,5 -0,4 -0,3 -0,2 -0,1 0,0 0,1 0,2 0,3 0,4 0,5

0,00 0,05 0,10 0,15 0,20 0,25 0,30 0,35

(e)

Figure. 5: Variation of transverse shear stress xz

τ through the plate thickness for various values of k and different types of sandwich plates: (a) The (1-0-1) FGM sandwich plate. (b) The (1-1-1) FGM sandwich plate. (c) The (1-2-1) FGM sandwich plate. (d) The (2-1-2) FGM sandwich plate, (e) The (2-2-1) FGM sandwich plate.

Table 1 Displacement models.

Model Theory Unknown function

CPT Classical plate theory 3 FSDPT First shear deformation plate

theory [8 – 10]

5 PSDPT Parabolic shear deformation

plate theory [21, 22]

5 SSDPT Sinusoidal shear deformation

plate theory [23]

5 HSDPT Hyperbolic shear deformation

plate theory [24]

5 ESDPT Exponential shear

deformation plate theory [25]