BAB II KAJIAN TEORI. operasi penjumlahan dan operasi perkalian mempunyai sifat-sifat. 1. R merupakan grup komutatif terhadap operasi penjumlahan.

BAB II KAJIAN TEORI

A. Sistem Bilangan Real

Definisi II.A.1

Sistem bilangan real R merupakan suatu sistem aljabar yang terhadap operasi penjumlahan dan operasi perkalian mempunyai sifat-sifat sebagai berikut:

1. R merupakan grup komutatif terhadap operasi penjumlahan.

2. R -{0} merupakan grup komutatif terhadap operasi perkalian.

3. Untuk setiap x,y,zR berlaku x.(yz) x.yx.z.

(Darmawijaya, 2006:19)

Definisi II.A.2

Jika x suatu bilangan real, nilai mutlak (absolute value) x yang dituliskan dengan x didefinisikan sebagai berikut.

Sifat-sifat nilai mutlak pada R adalah:

1. x 0 untuk setiap xR, x 0 jika dan hanya jika x = 0

2. x  x untuk setiap xR 0 untuk  x x  x x untuk x0

3. xy  x y untuk setiap x,yR, dan 4. , y x y x  y0 5. Untuk a0 berlaku: a. x aaxa b. x axa atau xa

6. x2 x2 dan x  x2 untuk setiap xR

7. x  y x2  y2

8. xy  x yuntuk setiap x,yR.(Ketaksamaan Segitiga)

Akibat dari sifat-sifat nilai mutlak di atas adalah:

y x y x y x      untuk setiap x,yR B. Himpunan Definisi II.B.1

Setiap benda disebut objek (object). Beberapa objek atau sekelompok objek, karena suatu sebab, membentuk suatu kesatuan yang biasa disebut himpunan (set). Objek-objek yang membentuk

suatu himpunan disebut element atau anggota (member) himpunan tersebut.

(Darmawijaya, 2006:1)

Definisi II.B.2

Jika I suatu himpunan tertentu dan untuk setiap iI terdapat himpunan X , maka keluarga (family) atau koleksi (collection)_i adalah himpunan yang anggota-anggotanya merupakan himpunan dan ditulis singkat dengan

 

X_i atau



X_i:iI



.

(Darmawijaya, 2006:6)

Definisi II.B.3

Jika A dan B masing-masing dua himpunan yang tak kosong



A dan B



maka himpunan yang didefinisikan dengan :

 



x y x A y B



B

A  , :  & 

disebut himpunan hasil kali kartesius (Cartesian product) himpunan A dengan B.

(Darmawijaya, 2006:6)

1. Himpunan Terbatas

Definisi II.B.1.1

Jika pada suatu himpunan S telah didefinisikan suatu urutan, maka S dinamakan himpunan terurut.

Diberikan himpunan terurut S dan AS. Himpunan A dikatakan terbatas ke atas jika terdapat suatu pS, sehingga untuk semua

A

x berlaku x p. Jadi, p disebut batas atas himpunan A. Jika terdapat suatu qS dan untuk semua xA berlaku xq, maka A dikatakan terbatas ke bawah. Jadi, q disebut batas bawah himpunan A.

(Soemantri, 2000:1.3)

Definisi II.B.1.2

Jika S suatu himpunan terurut, dan AS. Himpunan A terbatas ke atas dan terdapat pS yang memenuhi sifat-sifat berikut:

a. p merupakan batas atas A, dan b. jika u < p maka u bukan batas atas A

maka p disebut batas atas terkecil atau supremum himpunan A, dan diberikan notasi psupA.

(Soemantri, 2000:1.4)

Definisi II.B.1.3

Batas bawah terbesar atau infimum dari suatu himpunan A yang terbatas ke bawah, didefinisikan sebagai qS dengan sifat bahwa q merupakan batas bawah A dan jika v > q maka v bukan batas bawah A. Untuk batas bawah terbesar himpunan A diberikan notasi qinf A.

2. Himpunan Bilangan Real

Definisi II.B.2

Himpunan bilangan real (himpunan bagian di dalam R) yang penulisannya khusus antara lain adalah himpunan-himpunan sebagai berikut. Jika a,bR dan ab, didefinisikan

a.

 

a,b 



xR:a xb



disebut selang tertutup (closed interval)

b.

  

a,b  xR:a xb



disebut selang terbuka (open interval)

c.



a,b

 

 xR:a xb



disebut selang tertutup di kiri atau selang terbuka di kanan

d.



a,b







xR:a xb



disebut selang tertutup di kanan atau selang terbuka di kiri

(Darmawijaya, 2006:46-47)

C. Fungsi

Definisi II.C

Diberikan A,BR, fungsi f :AB adalah suatu aturan yang mengaitkan setiap unsur xA dengan tepat satu unsur yB. Unsur y yang berkaitan dengan unsur x ini diberi lambang y = f(x) yang dinamakan aturan

fungsi. Lambang y = f(x), xA menyatakan sebuah fungsi dengan aturan y = f(x) yang terdefinisi pada himpuan A. Selanjutnya x dinamakan peubah bebas dan y peubah tak bebas yang nilainya bergantung dari x.

Apabila terdapat suatu fungsi y = f(x), maka daerah asal (domain) fungsi f adalah himpunan A, ditulis AD_f , dan daerah nilai fungsi f adalah himpunan R_f 



f(x):xAD_f



. Unsur f(x)Bdinamakan nilai fungsi di x. Jika yang diketahui hanya y = f(x), maka domain dan daerah nilai (range) fungsi f adalah D_f 



xR: f(x)R



dan R_f 



f(x)R:xD_f



.

(Martono, 1999:29)

1. Fungsi Komposisi

Definisi II.C.1

Jika fungsi f dengan domain D_f di A dan range R_f di B dan jika fungsi g dengan domain D_g di B dan range R_g di C.

Gambar 1.1 Diagram Panah Fungsi f(x) R R f x f(x) f R f D f R R f R f D x f(x)

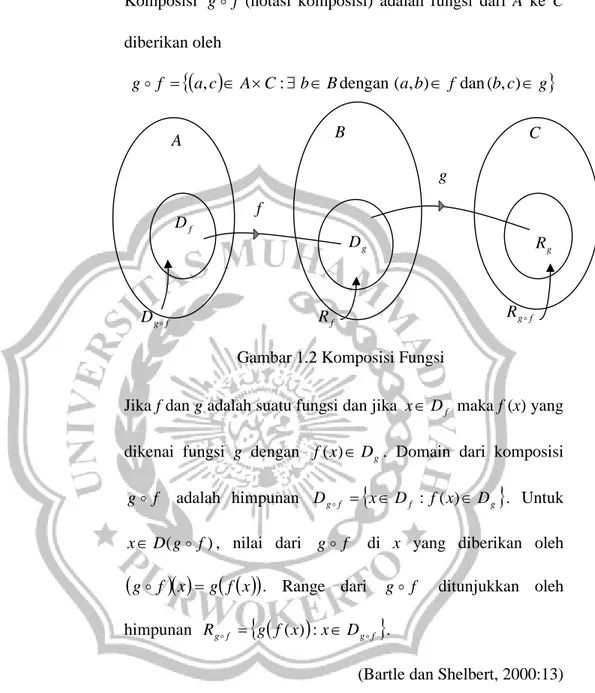
Komposisi g  f (notasi komposisi) adalah fungsi dari A ke C diberikan oleh

 



a c A C b B ab f b c g



f g  ,   :  dengan ( , ) dan( , )

Jika f dan g adalah suatu fungsi dan jika xD_f maka f (x) yang dikenai fungsi g dengan f(x)D_g. Domain dari komposisi

f

g  adalah himpunan D_gf 



xD_f : f(x)D_g



. Untuk )

(g f D

x  , nilai dari g  f di x yang diberikan oleh



g f

 

x g



f

 

x



. Range dari g  f ditunjukkan oleh himpunan R_gf 



g



f(x)



:xD_gf



.

(Bartle dan Shelbert, 2000:13)

2. Fungsi Invers

Definisi II.C.2.1

Jika fungsi f dengan domain D di A dan range_f R_f di B maka fungsi f dikatakan injektif (satu-satu) jika dan hanya jika

Gambar 1.2 Komposisi Fungsi f f g D _ g B C g D A f D f R g R f g R _

a. f(a) f(a') maka aa'

b. a, a'D_f dan aa' maka f(a) f(a')

(Bartle dan Shelbert, 2000:15)

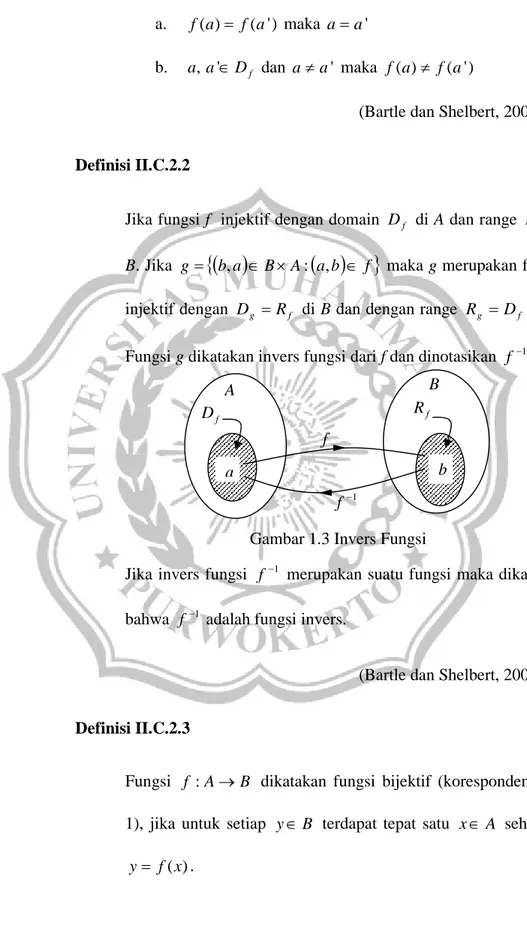
Definisi II.C.2.2

Jika fungsi f injektif dengan domain D_f di A dan range R_f di B. Jika g



 

b,a BA:

 

a,b  f



maka g merupakan fungsi injektif dengan D_g R_f di B dan dengan range R_g D_f di A. Fungsi g dikatakan invers fungsi dari f dan dinotasikan f1.

Jika invers fungsi f1 merupakan suatu fungsi maka dikatakan bahwa f1 adalah fungsi invers.

(Bartle dan Shelbert, 2000:15)

Definisi II.C.2.3

Fungsi f :AB dikatakan fungsi bijektif (korespondensi 1– 1), jika untuk setiap yB terdapat tepat satu xA sehingga

) (x f

y  .

Gambar 1.3 Invers Fungsi

1  f f D a b f R f A B

Definisi II.C.2.4

Jika fungsi f :AB merupakan fungsi bijektif maka kebalikan fungsi f :AB yaitu g:BA pasti merupakan fungsi invers dari f .

3. Jenis Fungsi

a. Fungsi Eksponen

Bentuk umum fungsi eksponen adalah sebagai berikut:

x

a x

f( ) dengan a = bilangan pokok



a0 dan a1



dan x = pangkat



xR



_.

(Varberg, dkk, 2010)

b. Fungsi Transenden

Fungsi transenden terdiri dari fungsi-fungsi sebagai berikut:

1) Fungsi logaritma didefinisikan sebagai berikut: fungsi ,

log )

(x x

f a a0, a1, dan x0

2) Fungsi logaritma alami dapat dituliskan f(x)lnx, x0

3) Invers dari ln disebut fungsi eksponen alami dan dinyatakan exp ( e pangkat). Jadi, xexpyey lnx y, x0 4) Fungsi invers trigonometri

a) 2 2 , sin sin 1        x x y y x b) 2 0 , cos cos 1    



  x x y y x c) 2 2 , tan tan 1        x x y y x d) 2 dan 0 , sec sec1    







  x x x y y x (Varberg, dkk, 2010:357-359) 4. Fungsi Terbatas Definisi II.C.4

Fungsi f dikatakan terbatas jika terdapat M > 0 sehingga M

x

f( )  untuk xD_f.

(Martono, 1999:38)

Contoh:

a. Fungsi f(x)cos x terbatas karena f(x)  cos x 1 untuk

f

D x 

b. Fungsi f(x) x1 tidak terbatas pada interval

 

0, karena tidak ada M 0 sehingga f(x)  x 1M

D. Limit 1. Limit Fungsi di R Definisi II.D.1.1 L x f c x ( )

lim berarti bahwa untuk setiap  0, terdapat  0

yang berpadanan sedemikian rupa sehingga untuk 0 xc  berlaku f(x)L  ; yakni, 0 xc   f(x)L 

(Varberg, dkk, 2010:62)

Definisi II.D.1.2

Diberikan fungsi f yang terdefinisi pada interval (c,b). Limit kanan fungsi f di c adalah L (ditulis f x L

c xlim ( ) atau L x f( ) bila xc) jika  0,  0          c x f(x) L

0 dan jika diberikan fungsi f yang

terdefinisi pada interval (a,c) dengan limit kiri fungsi f di c adalah L (ditulis f x L

c

xlim ( ) atau f(x)L bila

 c x ) jika 0   ,  0  0 xc   f(x)L  (Martono, 1999:53) Contoh: Diberikan fungsi

Tentukan (jika ada):

9 , 2 3   x x  ) (x f 9 , 3 9 2    x x x

a. lim ( ) 9 f x x b. lim ( ) 9 x f x c. lim ( ) 9 f x x Penyelesaian: a. 6 2 3 lim ) ( lim 9 9    _  _  x x f x x b.











lim



3



6 3 3 3 lim 3 9 lim ) ( lim 9 9 9 9           _{  }  _{  }  _x x x x x x x f x x x x

c. Karena limit kanan sama dengan limit kiri maka nilai limitnya ada dan lim ( ) 6

9 

 f x

x

Sifat-Sifat Limit Fungsi:

Jika n bilangan bulat positif, k konstanta, serta f dan g adalah fungsi-fungsi yang mempunyai limit di c, dengan f x L

c x ( ) lim dan M x g c x ( ) lim maka a. k k c x  lim b. x c c x  lim c. Jika



f x g x



L M c x ( ) ( )   lim d.



f x g x



L M c x ( ) ( )   lim

e.



f x g x



L M c x ( ). ( ) . lim   f. , 0 ) ( ) ( lim _        _M M L x g x f c x g. k f x k L c x ( ) . lim   (Leithold, 1991:99) Teorema II.D.1.3 Jika f x L c x ( ) lim , maka f x L c x ( )  lim (Martono, 1999:54) Bukti: Jika f x L c x ( )

lim , maka lim f(x) L lim f(x)

c x c x    . Diketahui f x L c x ( ) lim maka f x L c x ( ) 

lim . Teorema ini

dibuktikan dengan menggunakan definisi limit dimana L

x f

c x ( )

lim berarti bahwa untuk setiap  0, maka harus dibuktikan terdapat  0 sehingga

jika 0 xc  maka f(x) L  Diketahui bahwa f x L

c x ( )

lim , maka dari definisi limit diperoleh

bahwa untuk  0 terdapat ₁ 0 sehingga

Misalkan  adalah lebih kecil dari₁, maka  ₁. Karena itu jika 0 xc  maka f(x)L 

karena f(x) L  f(x)L dan f(x)L  maka sesuai dengan sifat ketaksamaan segitiga diperoleh

     L f x L x f( ) ( ) . 2. Limit Fungsi di R2 Definisi II.D.2

Fungsi f adalah fungsi dua variabel dengan domain D maka dapat dikatakan bahwa limit dari f(x,y) L dan ditulis

L y x f b a y x,lim)( , ) ( , )

( , jika untuk setiap  0 terdapat  0

sedemikian sehingga f(x,y)L  bilamana (x,y)D dan     ( , ) ( , ) 0 x y a b dengan



 

2



2 ) , ( ) , (x y  a b  xa  yb .

(Purcell dan Varberg, 1999:238)

3. Limit Fungsi di Rn

Definisi II.D.3

Definisi yang telah diungkapkan untuk limit fungsi di R dan di

2

R tersebut sedemikian sehingga dapat diperluas untuk fungsi tiga peubah (atau lebih). Secara umum, jika z f(x₁,x₂,...,x_n) adalah fungsi n-variabel dengan domain D maka dapat dikatakan

bahwa limit dari f(x₁,x₂,...,x_n)L dan ditulis L x x x f _n x x x x x x n o o no   ( , ,..., ) lim _{1 2} ) ,..., , ( ) ,..., , (1 2 1 2 , jika untuk  0, 0

sedemikian sehingga f(x₁,x₂,...,x_n)L  bilamana D

x x

x , ,..., _n)

( _{1 2} dan 0 (x₁,x₂,...,x_n)(x_1o,x_2o,...,x_no)  . (Purcell dan Varberg, 1999:239)

E. Kekontinuan

1. Kekontinuan Fungsi di R

Definisi II.E.1.1

Kekontinuan fungsi di satu titik dapat didefinisikan sebagai berikut dimisalkan f terdefinisi pada suatu interval terbuka yang mengandung c. Dikatakan bahwa f kontinu di c jika

) ( ) ( lim f x f c c

x  . Jadi, fungsi f dikatakan kontinu di titik c jika

memenuhi syarat sebagai berikut : a. f(c) ada; b. lim f(x) c x ada; c. lim f(x) f(c) c x 

Jika satu atau lebih dari ketiga syarat ini tidak dipenuhi di c, maka fungsi f dikatakan tidak kontinu di c.

Definisi II.E.1.2

Fungsi f terdefinisi pada interval (a,c) maka fungsi f dikatakan kontinu kanan di c jika lim f(x) f(c)

c

x 

.

Fungsi f terdefinisi pada interval (c,b) maka fungsi f dikatakan kontinu kiri di c jika lim f(x) f(c)

c

x 

.

(Martono, 1999:59)

Definisi II.E.1.3

Fungsi f dikatakan kontinu pada interval terbuka (a,b) jika f kontinu di setiap titik (a,b). Fungsi f kontinu pada interval tertutup [a,b] jika kontinu pada interval terbuka (a,b), kontinu kanan di a, dan kontinu kiri di b.

(Martono, 1999:61)

2. Kekontinuan Fungsi di R2

Definisi II.E.2.1

Fungsi f(x,y) dikatakan kontinu di titik (a,b)D, DR2 jika ) , ( ) , ( lim ) , ( ) ,

(xyab f x y  f a b . Fungsi f dikatakan kontinu pada

domain D jika f kontinu di setiap titik (a,b) dalam D.

Definisi II.E.2.2

Fungsi f(x,y) dikatakan kontinu pada suatu himpunan S, jika f(x,y) kontinu di setiap titik pada himpunan S.

(Purcell dan Varberg, 1999:239)

3. Kekontinuan Fungsi di Rn

Definisi II.E.3

Secara umum, jika fungsi z f(x₁,x₂,...,x_n) dikatakan kontinu di titik (x_1o,x_2o,...,x_no)D, _D _Rn _jika ) ,..., , ( ) ,..., , ( lim _{1 2 1 2} ) ,..., , ( ) ,..., , (1 2 1 2 no o o n x x x x x x n o o no f x x x f x x x   . Fungsi f

dikatakan kontinu pada domain D jika f kontinu di setiap titik ) ,..., , (x_1o x_2o x_no dalam D. F. Turunan 1. Turunan Fungsi di R Definisi II.F.1.1

Jika f fungsi dari [a,b] ke R dan c[ ba, ] maka L disebut diferensial atau turunan f di c jika  0, 0 sehingga untuk x[ ba, ] dengan 0 xc  berlaku

Gambar 1.4 Himpunan S S

A

 B

     L c x c f x f( ) ( )

. Jadi, L merupakan turunan dari f di c jika

L c x c f x f c x     ) ( ) ( lim .

(Bartle and Sherbert, 2000:158)

Fungsi f dikatakan mempunyai turunan (diferensiable) di c atau )

( ' c

f ada, jika f'_(c) f'_(c) dan f'(c) f_'(c) f_'(c) dengan c x c f x f c f c x    _   ) ( ) ( lim ) ( ' dan c x c f x f c f c x    _   ) ( ) ( lim ) ( ' Contoh:

Selidiki apakah terdiferensial di

2 

x . Jika ya, tentukan f'(2)!

Penyelesaian:





2 1 2 . 3 2 2 5 3 lim 2 ) 2 ( ) ( lim ) 2 ( ' 2 2 2           _{ }    x x x x x f x f f x x



















2



lim3 3 ) 2 )( 2 ( 3 lim 2 4 4 3 lim 2 12 12 3 lim 2 14 7 2 5 3 lim 2 7 2 2 5 3 lim 2 2 2 2 2 2 2 2 2 2 2 2 2 2                                       x x x x x x x x x x x x x x x x x x x x x x x





2 1 2 . 3 1 3 lim 2 ) 2 ( ) ( lim ) 2 ( ' 2 2         _{ }    x x x f x f f x x 2 , 1 3x x  ) (x f 2 , 2 2 5 3 2 _    x x x x

3 3 lim 2 ) 2 ( 3 lim 2 6 3 lim 2 7 1 3 lim 2 2 2 2                     x x x x x x x x x x

Jadi, f terdiferensial x = 2 dan f'(2)3

Teorema II.F.1.2

Jika fungsi f terdiferensial di c maka fungsi f kontinu di c

(Varberg, dkk, 2010:102)

Bukti:

f terdiferensial di c artinya f' c( ) ada

c x c f x f c f c x      ) ( ) ( lim ) ( ' ) ( ) ( ) ( ) (x f x f c f c f   

Untuk xc 0 x c maka diperoleh

) ( ) ( ) ( ) ( f c c x c x c f x f x f      ) ( . ) ( ) ( ) ( x c f c c x c f x f x f       Untuk xc maka       _{ }       . ( ) ) ( ) ( lim ) ( lim x c f c c x c f x f x f c x c x ) ( lim lim . ) ( ) ( lim ) ( lim x c f c c x c f x f x f c x c x c x c x          ) ( ) ( lim 0 . ) ( ' c f c f c f c x     Karena    ( ) ( ) lim f c f c c x f kontinu di c.

Akibatnya:

Jika fungsi f tidak kontinu di c maka f tidak terdiferensial di c.

a. Sifat–Sifat Turunan:

1) f(x)k, k konstan  f'(x)0

2) f(x) x  f'(x)1

3) _f(x)_xn _f'(x)_{n x}n1

Jika u' x( ) dan v' x( ) ada maka:

4) f(x)u(x)v(x) f'(x)u'(x)v'(x) 5) f(x)c.u(x) f'(x)c.u'(x), dengan c konstan 6) f(x)u(x).v(x) f'(x)u'(x).v(x)u(x).v'(x) 7)





2 ) ( ) ( ' . ) ( ) ( . ) ( ' ) ( ' ) ( ) ( ) ( x v x v x u x v x u x f x v x u x f     (Leithold, 1991:199)

b. Turunan Fungsi Komposisi

Jika y f(u) dengan ug(x) dan fungsi g(x) kontinu pada domainnya, maka menurut definisi (aturan rantai) dapat dituliskan sebagi berikut:

dx du du dy dx dy . 

Jika y f(u) dengan ug(v) dan vh(x) maka: dx dv dv du du dy dx dy y'  . .

(Purcell dan Varberg, 1993:138-139)

c. Turunan Fungsi Trigonometri

1) f(x)sinx f'(x)cosx

2) f(x)cosx f'(x)sinx

3) f(x)tanx f'(x)sec2x

4) f(x)cot x f'(x)csc2x

5) f(x)sec x f'(x)secx.tanx

6) f(x)csc x f'(x)csc x.cotx

(Varberg,dkk, 2010:114-116)

d. Turunan Fungsi Invers Trigonometri

Jika xsiny maka y sin1x

1) 2 1 1 1 ) ( ' sin ) ( x x f x x f      2) 2 1 1 1 ) ( ' cos ) ( x x f x x f      

3) 1 ₂ 1 1 ) ( ' tan ) ( x x f x x f      4) 1 ₂ 1 1 ) ( ' cot ) ( x x f x x f       5) 1 1 ) ( ' sec ) ( 2 1       x x x f x x f 6) 1 1 ) ( ' csc ) ( 2 1       x x x f x x f

e. Turunan Fungsi Logaritma dan Eksponensial

1) Turunan fungsi logaritma ini dapat dituliskan sebagai

berikut: f₍x₎ a_logx _maka

a x x f ln 1 . 1 ) ( ' 

2) Turunan fungsi logaritma alami dapat dituliskan sebagai

berikut: f(x)lnx maka

x x f'( )1

3) Turunan fungsi eksponensial dapat dituliskan sebagai berikut: f(x)ax maka f'(x)ax.lna

4) Turunan fungsi eksponensial alami dapat dituliskan sebagai berikut: f(x)ex maka f'(x)ex

f. Turunan Fungsi pada Suatu Interval

Definisi II.F.1.f

Jika fungsi y f(x) terdefinisi pada selang I. Turunan fungsi f pada selang I, ditulis f' x( ), adalah suatu fungsi yang aturannya di setiap xI ditentukan oleh

h x f h x f x f h ) ( ) ( lim ) ( ' 0   

 , limit ini ada.

Catatan:

1) Lambang lain untuk turunan adalah

) ( , ), ( , , ' f x D y D f x dx d dx dy y _{x x} . Lambang dx dy dikenal

sebagai notasi Leibniz.

2) Jika I adalah selang tertutup [a,b], maka f' a( ) berarti )

( ' a

f _ sedangkan f' b( ) berarti f' b_( ).

(Martono, 1999:89)

g. Turunan Tingkat Tinggi

Definisi II.F.1.g

Pendiferensialan mengambil sebuah fungsi f dan menghasilkan sebuah fungsi baru f . ' Jika f' dideferensialkan, masih menghasilkan fungsi lain, dinyatakan oleh fungsi f '' (dibaca “f double aksen”) dan disebut turunan

kedua dari f. Dan jika f '' masih dapat diturunkan lagi maka yang demikian menghasilkan f''', yang disebut turunan ketiga, dan seterusnya.

(Purcell dan Varberg, 1993:141)

2. Turunan Fungsi di n

R

Definisi II.F.2.1

Fungsi f adalah suatu fungsi dua peubah x dan y. Jika y dianggap sebagai suatu konstanta, misalnya y y₀, maka f(x,y₀) menjadi fungsi satu peubah x. Turunan fungsi f di xx₀ disebut turunan parsial f terhadap x di f(x₀,y₀) dan dinyatakan sebagai

) , (x₀ y₀ f_x . Jadi, x y x f y x x f y x f x x _       ) , ( ) , ( lim ) , ( 0 0 0 0 0 0 0

Demikian pula, turunan parsial f terhadap y di (x₀,y₀) dinyatakan oleh f_y(x₀,y₀) dan dituliskan sebagai

y y x f y y x f y x f y y _       ) , ( ) , ( lim ) , ( 0 0 0 0 0 0 0

Rumus tersebut mencari f_x(x,y) dan f_y(x,y) dengan menggunakan aturan baku untuk turunan; kemudian mensubstitusikan xx₀ dan y y₀

Contoh:

Carilah f_x(1,2) dan f_y(1,2) jika f(x,y)x2y3y3

Penyelesaian: 4 2 . 1 . 2 ) 2 , 1 ( 0 2 ) , (    _x   x x y xy f f 37 2 . 9 1 ) 2 , 1 ( 9 ) , (  2 2  2 2 y y x y x y f f Catatan:

Jika z f(x,y), dapat dituliskan

x y x f x z y x f_x       ( , ) ) , ( y y x f y z y x f_y       ( , ) ) , ( ) , ( 0 0 0 0 ) , ( y x x x z y x f    ) , ( 0 0 0 0 ) , ( y x y y z y x f    Definisi II.F.2.2

(Turunan Parsial Tingkat Tinggi) Secara umum, karena turunan parsial suatu fungsi x dan y adalah fungsi lain dari dua peubah yang sama, turunan tersebut dapat diturunkan secara parsial terhadap x atau y untuk memperoleh empat buah turunan parsial kedua fungsi f yaitu:

a. ₂ 2 x f x f x f_xx               , b. ₂ 2 y f y f y f_yy               ,

c.

 

x y f x f y f f_{xy x y}                 2 , dan d.

 

y x f y f x f f x y yx _{ }               2 . Contoh:

Carilah keempat turunan parsial dari ( , ) sin x3y2 y x y x f _       ! Penyelesaian: 2 2 3 cos 1 ) , ( x y y x y y x f_{x }       y x y x y x y x f_y 3 2 cos 2 ) , ( _        2 2sin 6 1 ) , ( xy y x y y x f_{xx }        3 4 2 3cos sin 2 2 ) , ( x y x y x y x y x y x f_{yy }              y x y x y x y x y y x f_xy( , ) 1₂ cos ₃ sin _6 2               y x y x y x y x y y x f_yx( , ) 1₂cos ₃sin _6 2              

Definisi II.F.2.3

Untuk turunan parsial tingkat tiga dan lebih tinggi didefinisikan dengan cara yang sama dan ditulis dengan cara yang sama. Jadi, jika f suatu fungsi dua peubah x dan y, turunan-parsial ketiga f yang diperoleh dengan menurunkan f secara parsial, pertamakali terhadap x dan kemudian dua kali terhadap y, akan ditunjukkan oleh xyy f x y f x y f y                 2 3 2

(Purcell dan Varberg, 1999:235)

Definisi II.F.2.4

Secara umum, jika f adalah suatu fungsi n peubah yaitu

n

x x

x₁, ₂,..., . Jika x ,...,₂ x_n dibuat konstan, misalnya

no o

n x x

x

x₂,...,  ₂ ,..., , maka f(x₁,x_2o,...,x_no) menjadi fungsi satu peubah x₁. Turunanya di x₁ x_1o disebut turunan parsial f terhadap x₁ di (x_1o,x_2o,...,x_no) dan dinyatakan sebagai

) ,..., , ( _{1 2} 1 o o no x x x x f atau 1 2 1, ,..., ) ( x x x x f _n   . Jadi, 1 2 1 2 1 1 0 2 1 ) ,..., , ( ) ,..., , ( lim ) ,..., , ( 1 1 x x x x f x x x x f x x x f o o no o o no x no o o x _      

Demikian pula, turunan parsial f terhadap x di₂ (x_1o,x_2o,...,x_no) dan dinyatakan sebagai ( ₁ , ₂ ,..., )

2 o o no x x x x f atau 2 2 1, ,..., ) ( x x x x f _n  

dan dituliskan sebagai

2 2 1 2 2 1 0 2 1 ) ,..., , ( ) ,..., , ( lim ) ,..., , ( 2 2 x x x x f x x x x f x x x f o o no o o no x no o o x _      

Turunan parsial terhadap x₃,x₄,...,x_n didefinisikan dengan cara yang sama. Jadi, untuk turunan turunan parsial f terhadap x di_n

) ,..., ,

(x_1o x_2o x_no dan dinyatakan sebagai f_x (x_1o,x_2o,...,x_no)

n atau n n x x x x f   ( ₁, ₂,..., )

dan dituliskan sebagai

n no o o n no o o x no o o x x x x x f x x x x f x x x f n n        ) ,..., , ( ) ,..., , ( lim ) ,..., , ( 1 2 1 2 0 2 1 Definisi II.F.2.5

Jika fungsi w adalah fungsi yang teriferensialkan pada n variabel yaitu u₁,u₂,...,u_n dimana u adalah fungsi dari n variabel yaitu_i

n

x x

x₁, ₂,..., maka untuk w f(u₁,u₂,...,u_n) diperoleh:

n n n n n x u u w x u u w x u u w x w x u u w x u u w x u u w x w x u u w x u u w x u u w x w                                                       ... . . . ... ... 2 1 2 2 2 2 2 1 1 2 1 1 2 2 1 1 1 1

G. Integral

1. Integral Tak-Tentu (Anti-Turunan)

Definisi II.G.1.1

Suatu fungsi F disebut suatu anti-turunan f pada interval I jika )

( ) (

' x f x

F  pada I, yakni jika F'(x) f(x) untuk semua x dalam I.

(Varberg, dkk, 2010:196)

Teorema II.G.1.2

Jika n bilangan rasional dengan n1, maka c n x dx x n n    



1₁

(Purcell dan Varberg, 1993:233)

Bukti: Misal: _f(x)_xn _dan 1 ) ( 1    n x x F n diperoleh



f(x)dxF(x)c dibuktikan c x F dx x f  



( ) ( )

maka akan ditunjukkan

) ( ) ) ( ( x f dx c x F d  _





) ( ) 1 ( 1 1 1 ) ) ( ( 1 x f n x n x n dx c n x d dx c x F d n n n             _    

berarti



f(x)dxF(x)c atau c n x dx x n n    



1₁ . Untuk n0 diperoleh xndx x dx x cxc   







0 ₀01₁ Jadi,



dxxc

Dari hasil di atas maka dapat dianalogikan untuk integral pada fungsi trigonometri adalah sebagai berikut

a.



sinx dxcosxc b.



cosx dxsinxc c.



sec2x dxtanxc d.



csc2x dxcotxc e.



secx tanxdxsecxc f.



cscx cotxdxcscxc

(Martono, 1999:170)

Teorema II.G.1.3

Jika fungsi f dan g mempunyai anti turunan (integral tak-tentu) dari k suatu konstanta maka:

b.





f(x)g(x)



dx



f(x)dx



g(x)dx

(Purcell dan Varberg, 1993:235)

Bukti:

a.



k f(x)dxk



f(x)dx

f mempunyai anti-turunan misal F + c,

jika



f(x)dxF(x)c artinya ( ( ) ) f(x) dx c x F d  _ misalkan H(x)k F(x) maka





) ( ) ( ) ( ) ( ' k f x dx c x F d k dx x F d k x H     b.





f(x)g(x)



dx



f(x)dx



g(x)dx Jika f(x)g(x) mempunyai anti-turunan misal

) ( ) (x G x

F 

maka dapat dituliskan





f(x)g(x)



dxF(x)G(x) dimana f mempunyai anti-turunan misal F dan g mempunyai anti-turunan misal G jika



f(x)dxF(x)c artinya ( ( ) ) f(x) dx c x F d  _ dan

jika



g(x)dxG(x)c artinya ( ( ) ) g(x) dx c x G d  _ maka



f x g x



dx F x G x



f x dx



g x dx



( ) ( )  ( ) ( ) ( )  ( ) Teorema II.G.1.4

Jika g suatu fungsi yang dapat didiferensialkan, dan jika daerah nilai dari g adalah suatu selang I dimana ada sebuah fungsi f yang didefinisikan pada I dan bahwa F merupakan anti turunan dari f pada I, maka



f



g(x)





g'(x)dx



F(g(x))c (Leithold, 1991:396) Bukti: )) ( ( )) ( ( ' g x f g x F 

dan menurut aturan rantai untuk pendiferensialan



F(g(x))



F'(g(x))



g'(x)



dx d _ diperoleh



F(g(x))



F'(g(x))



g'(x)



f(g(x))



g'(x)



dx d _{ } kesimpulanya



g x dx



F g x c x g f  



( ( )) '( ) ( ( ))

Teorema II.G.1.5

Jika g suatu fungsi yang dapat didiferensialkan dan n suatu bilangan rasional dengan n1, maka









c n x g dx x g x g n n _   



( ) '( ) ( )₁ 1

(Purcell dan Varberg, 1993:236)

Bukti:

Jika ug(x) adalah suatu fungsi yang dapat didiferensialkan dan n suatu bilangan rasional dengan n1, maka

dx du u dx n u d n n . 1 1         

atau dalam cara penulisan fungsional,

) ( ' . )) ( ( )) ( ( . )) ( ( 1 )) ( ( 1 x g x g dx x g d x g dx n x g d n n n           Teorema II.G.1.6

(Integral Parsial) Jika f dan g fungsi-fungsi yang dapat terdiferensial pada interval I, maka



udvuv



vdu

Bukti :

Jika F(x) f(x).g(x) dengan u  f(x) dan vg(x) maka

 

 

 

du v v u dv u du v dv u v u dx v dx du dx dx dv u dx v u dx v u dx v u dx v u v u v u v u x g x f x g x f x F





















                 ' ' ' ' ' ' ' ) ( ) ( ' ) ( ' ) ( ) ( ' 2. Integral Tentu

a. Integral pada Fungsi Satu Variabel

Definisi II.G.2.a.1

Sebuah fungsi f yang didefinisikan pada selang tertutup [a,b]. Himpunan P



ax₀,x₁,x₂,...,x_n b



dengan

b x x

x x

a ₀ ₁ ₂... _n  adalah partisi pada [a,b]. Partisi P membagi interval [a,b] menjadi n selang bagian yaitu



x0,x1

 

, x1,x2

 

,..., xn1,xn



dengan panjang selang bagian ke-i

1    x_i x_i x_i , i = 1, 2, 3, ..., n dan



i n



P maksx_i; 1,2,...,

disebut norma (norm) partisi P sehingga dapat dibentuk jumlah Riemann fungsi f yang terkait dengan partisi P yaitu



   n i i i x x f f P S 1 ) ( ) , ( .

Suatu jumlah Riemann ditafsirkan sebagai sebuah jumlah aljabar dari luas-luas



3

 

4

    

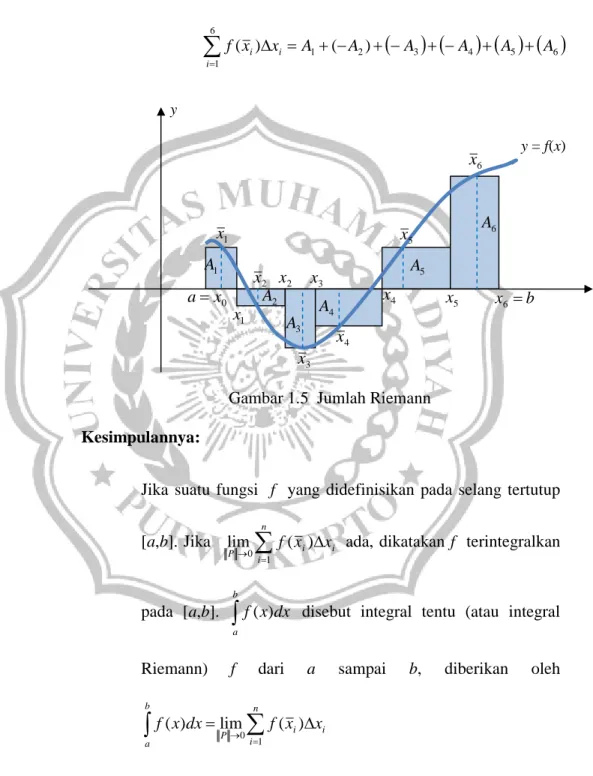
5 6 2 1 6 1 ) ( ) (x x A A A A A A f i i i          



 Kesimpulannya:

Jika suatu fungsi f yang didefinisikan pada selang tertutup

[a,b]. Jika



   n i i i P f x x 1 0 ( )

lim ada, dikatakan f terintegralkan

pada [a,b].



b a

dx x

f( ) disebut integral tentu (atau integral

Riemann) f dari a sampai b, diberikan oleh





  _  n i i i P b a x x f dx x f 1 0 ( ) lim ) (

(Purcell dan Varberg, 1993) y y = f(x) 1 A y 6 A y 4 A y 5 A y 3 A y 2 A y 0 x a y x1 2 x x₃ 4 x x₅ x₆b 1 x 2 x 3 x 4 x 5 x 6 x x

Definisi II.G.2.a.2

Jika f R[ ba, ], fungsi F:[a,b]R dengan rumus

0 ) (a  F dan 



x a f x

F( ) untuk setiap x( ba, ] disebut

primitif (primitive) Riemann fungsi f pada [a,b]

Catatan:

Beberapa penulis merumuskan primitif fungsi f R[ ba, ]

tersebut sebagai berikut  



x a f a F x F( ) ( ) .

Hal ini berarti



f F(a)F(a)0

a a

.

(Darmawijaya, 2006:207)

Teorema II.G.2.a.3

Jika fungsi f dapat diintegralkan pada selang tertutup [a,b], [a,c], dan [c,b] maka







 b c c a b a dx x f dx x f dx x f( ) ( ) ( ) dengan acb. (Leithold, 1991:438-439)

Bukti:

Dimisalkan P suatu partisi dari [a,b]. Dibentuk partisi P dari' [a,b] dengan cara sebagai berikut:

Jika c satu titik dari partisi P, maka P tepat sama dengan P.' Karena itu selang-selang bagian dari partisi P , sama seperti' selang-selang bagian dari P, kecuali selang bagian [x_i1,x_i] dari P yang dibagi menjadi dua selang bagian [x_i1,c] dan

] ,

[c x_i . Jika P' adalah norm dari P dan jika' P adalah norm dari P, maka P'  P.

Jika di dalam partisi P selang [a,c] dibagi menjadi r selang' bagian dan [c,b] dibagi menjadi (n – r) selang bagian, maka bagian dari partisi P' dari a ke c memberikan jumlah Riemann dalam bentuk



   r i i i x x f f P S 1 ) ( ) , ' (

dan bagian lain dari partisi P , dari c ke b, memberikan' jumlah Riemann dalam bentuk



    n r i i i x x f f P S 1 ) ( ) , ' (

dengan menggunakan definisi dari integral tertentu dan sifat-sifat notasi sigma, didapatkan













                     _{  }    n r i i i P r i i i P n r i i i r i i i P n i i i P b a x x f x x f x x f x x f x x f dx x f 1 0 1 0 1 1 0 1 0 ) ( lim ) ( lim ) ( ) ( lim ) ( lim ) (

Karena 0 P'  P , P 0 dapat digantikan oleh 0 '  P menghasilkan







  _    _{ }  n r i i i P r i i i P b a x x f x x f dx x f 1 0 ' 1 0 ' ( ) lim ( ) lim ) (

dengan menerapkan definisi integral tertentu pada ruas kanan persamaan di atas diperoleh







 b c c a b a dx x f dx x f dx x f( ) ( ) ( ) Teorema II.G.2.a.4

(Teorema Dasar Kalkulus). Jika suatu fungsi f kontinu pada selang tertutup [a,b] dan misalkan F suatu fungsi sedemikian sehingga F’(x) = f(x) dan untuk semua x di dalam [a,b] maka



b   a a F b F dx x f( ) ( ) ( ) (Leithold, 1991:452)

Bukti :

Jika f kontinu pada semua titik di dalam [a,b], F’(x) = f(x), maka dapat dituliskan bahwa



 x a dt t f x F( ) ()

dengan mengambil x = b dan x = a, maka diperoleh

c dx x f b F b a  



( ) ) ( dan F a f x dx c a a  



( ) ) ( dapat disimpulkan  







a a b a dx x f dx x f a F b F( ) ( ) ( ) ( ) dengan definisi



( ) 0 a a dx x f maka



  b a dx x f a F b F( ) ( ) ( ) Contoh: Hitunglah



_        1 0 3 3 4 4x dx x . Penyelesaian:



7 3 1 0 1 7 3 7 3 4 3 4 1₀ 7 1 0 3 3 4               



x x dx x x

b. Integral Lipat-Dua Atas Daerah Persegi Panjang

Definisi II.G.2.b.1

Tetapkan D berupa suatu persegi panjang dengan sisi-sisi

sejajar sumbu-sumbu koordinat yakni



x y a x b c y d



D ( , ):   ,   . Bentuk suatu partisi P dari D dengan menggunakan garis-garis sejajar sumbu x dan sumbu y dan membagi D menjadi beberapa persegi panjang kecil, semuanya n buah, yang ditunjukkan dengan

. ,..., 3 , 2 , 1 ,k n

D_k  Tetapkan x_kdan y_k adalah panjang sisi-sisi D_k dan A_k x_ky_k adalah luasnya. Pada D ,_k diambil sebuah titik



x ,_k y_k



dan bentuk jumlahan







  n k k k k y A x f 1 , Gambar 1.6 Daerah D



 

x,y:axb,c yd



z



x ,k yk



c d a b k D c D x y

yang berpadanan (jika f(x,y)0) dengan jumlah volume dari n kotak. Dengan membuat partisi semakin halus sehingga semua D menjadi lebih kecil dan akan menuju ke_k konsep yang diinginkan serta dengan ketentuan tambahan bahwa norma dari partisi P yang dinyatakan oleh P adalah panjang diagonal terpanjang dari setiap persegi panjang bagian dalam partisi.

(Purcell dan Varberg, 1999:283)

Definisi II.G.2.b.2

Jika f suatu fungsi dua variabel yang kontinu dan terdefinisi pada persegi panjang D. Jika







   n k k k k P f x y A 1 0 , lim Gambar 1.7 Permukaan z f(x,y) ( P e r m u k a a n ) c d a b z y x Dk c D ) , (x y f z k k k y A x f   ( , ) Volume

ada, maka f terintegral pada D. Nilai limit ini disebut integral ganda-dua dari f pada D dan diberikan oleh:





_



    D n k k k k P f x ,y A f(x,y)dA lim 1 0 (Neswan, 2011:3)

Sifat-Sifat Integral Lipat-Dua:

Jika f(x,y),g(x,y) kontinu dan kR maka:

1) Integral lipat-dua adalah linear; yaitu:

a)







D D dA y x f k dA y x kf( , ) ( , ) b)

















D D D dA y x g dA y x f dA y x g y x f( , ) ( , ) ( , ) ( , )

2) Integral lipat-dua adalah aditif pada persegi panjang dimana D1D2D maka







  2 1 ) , ( ) , ( ) , ( D D D dA y x f dA y x f dA y x f

3) Sifat perbandingan berlaku jika f(x,y)g(x,y) untuk semua (x,y) di bidang D, maka





 D D dA y x g dA y x f( , ) ( , ) (Neswan, 2011:5)

c. Integral Lipat-Dua Atas Daerah Bukan Persegi Panjang

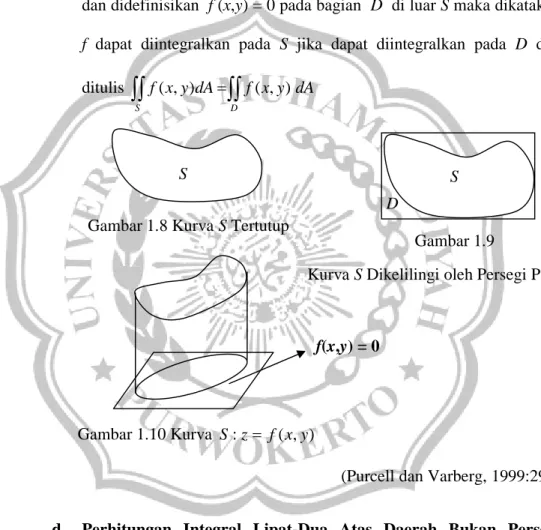
Jika kurva S tertutup dan terbatas di bidang (Gambar 1.8). Kelilingi S oleh suatu persegi panjang D dengan sisinya sejajar sumbu-sumbu koordinat (Gambar 1.9). Jika f (x,y) terdefinisi pada S dan didefinisikan f (x,y) = 0 pada bagian D di luar S maka dikatakan f dapat diintegralkan pada S jika dapat diintegralkan pada D dan ditulis







D S dA y x f dA y x f( , ) ( , )

(Purcell dan Varberg, 1999:295)

d. Perhitungan Integral Lipat-Dua Atas Daerah Bukan Persegi Panjang

Himpunan dengan batas-batas melengkung dapat menjadi sangat rumit. Untuk itu cukup menganalisis apa yang disebut himpunan x sederhana dan himpunan y sederhana. Suatu himpunan y Gambar 1.10 Kurva S:z f(x,y)

f(x,y) = 0

S

Gambar 1.8 Kurva S Tertutup

Gambar 1.9

Kurva S Dikelilingi oleh Persegi Panjang D S

sederhana (Gambar 1.11) jika terdapat fungsi-fungsi kontinu g₁(x) dan g₂(x) pada [a,b] sedemikian sehingga



(x,y):a x b,g₁(x) y g₂(x)



S    

Suatu himpunan S adalah x sederhana (Gambar 1.12) jika terdapat fungsi yang kontinu h₁(y) dan h₂(y) pada [c,d] sederhana sehingga



x y h y x h y c y d



S ( , ): ₁( )  ₂( ),  

Jika akan menghitung integral lipat-dua dari suatu fungsi f(x,y) atau suatu himpunan S dengan y sederhana. Kita lingkungi S dalam suatu persegi panjang D (Gambar 1.13) dan f(x,y) = 0 di luar S, maka





 D S dA y x f dA y x f( , ) ( , ) , dapat dituliskan

 

 





                           b x a x x g y x g y b x a x d y c y D S dx dy y x f dx dy y x f dA y x f dA y x f ) ( ) ( 2 1 ) , ( ) , ( ) , ( ) , ( yg₂(x) ) ( 1 x g y y S D a b x 0 x d c

Gambar 1.12 Kurva x Sederhana S ) ( 1 y h x xh₂(y) d c 0 y x a b ) ( 2 x g y ) ( 1 x g y y x 0 S

Secara ringkas

 



_       b a x g x g S dx dy y x f dA y x f ) ( ) ( 2 1 ) , ( ) , (

Untuk integral sebelah kanan, x dipertahankan tetap; jadi pengintegralan itu adalah sepanjang garis tebal (Gambar 1.13). Pengintegralan ini menghasilkan A(x) diintegralkan mulai dari a sampai b. Jika himpunan S adalah x sederhana (Gambar 1.13), penalaran serupa menuju rumus

 



_       d d y h y h S dy dx y x f dA y x f ) ( ) ( 2 1 ) , ( ) , (

(Purcell dan Varberg, 1999:296)

e. Integral Lipat-Dua pada Koordinat Kutub

Kurva-kurva tertentu pada bidang, seperti lingkaran, kardioid, dan mawar, lebih mudah diuraikan dalam bentuk koordinat polar daripada dalam koordinat Cartesius (persegi panjang). Jadi, integral ganda dua atas daerah yang di lingkungi oleh kurva-kurva yang demikian lebih mudah dihitung dengan menggunakan koordinat kutub. Jika D mempunyai bentuk yang diperlihatkan pada Gambar 1.14, yang merupakan suatu persegi panjang kutub. Jika z = f(x,y) menentukan suatu permukaan atas D dan jika f adalah fungsi yang kontinu dan tak-negatif. Maka volume V dari benda pejal di bawah

permukaan ini dan di atas D (Gambar 1.15) diberikan oleh



 D dA y x f V ( , ) ... (1)

Dalam koordinat kutub, suatu persegi panjang kutub D berbentuk D



 

r, :arb, 



dengan a0 dan

 

 2 sehingga persamaan permukaannya dapat dituliskan sebagai ) , ( ) sin , cos ( ) , (x y f r  r  F r f z  

Partisi D dibagi kedalam persegi panjang kutub yang lebih kecil

n

D D

D₁, ₂,..., dengan menggunakan suatu kisi kutub dan jika r_k dan

k



 menunjukkan ukuran kepingan D_k yang khas, seperti diperlihatkan pada Gambar 1.16. Luas A(D_k) diberikan oleh

k k k k r r D A( )      Sumbu kutub D   b r a r

Gambar 1.14 Persegi Panjang Kutub

Gambar 1.15 Kurva z f(x,y)F

 

r, D z y x z = f(x,y) = F(r,) D Dk k   k r 

dengan r adalah radius rata-rata_k D . Jadi,_k k k k n k k k r r r F V 



   1 ) , (

Jika diambil limit untuk norma (norm) dari partisi mendekati nol, maka diperoleh volume yang sebenarnya. Limit ini adalah suatu integral ganda-dua.







 D D d dr r r r f d dr r r F V ( ,)  ( cos, sin) ... (2)

Jadi, dari (1) dan (2) diperoleh dua rumus untuk V yaitu:





 D D d dr r r r f dA y x f( , ) ( cos, sin) 

(Purcell dan Varberg, 1999:305)

f. Teorema Fubini

Jika f(x,y) kontinu pada persegi panjang D:a xb,cyd,

maka f x y dA f x y dy dx f x y dx dy d y c y b x a x b x a x d y c y D

 

 



                       ( , ) ( , ) ) , ( (Neswan, 2011:7)

Akibatnya, untuk integral lipat-dua atas daerah bukan persegi panjang berlaku:

1) Jika D



(x,y):axb,g₁(x)yg₂(x)



. g₁ dan g₂

kontinu pada[a,b], maka

 



    x b a x x g y x g y D dx dy y x f dA y x f ) ( ) ( 2 1 ) , ( ) , ( 2) Jika D



(x,y):h1(y)xh2(y),cyd,



. h1 dan h2 kontinu pada[ dc, ], maka

 



     d y c y y h x y h x D dy dx y x f dA y x f ) ( ) ( 2 1 ) , ( ) , (

Dapat disimpulkan bahwa

 

 



          d y c y y h x y h x b x a x x g y x g y D dy dx y x f dx dy y x f dA y x f ) ( ) ( ) ( ) ( 2 1 2 1 ) , ( ) , ( ) , ( (Neswan, 2011:12)