G. Minimum Lokal dan Global
Berikut diberikan definisi minimum local (relatif) dan minimum global (mutlak) dari fungsi dua variabel.
Definisi.
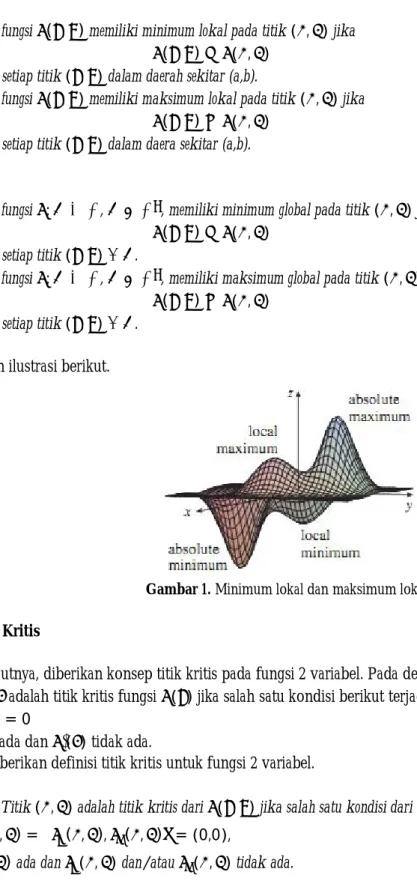
(i) Suatu fungsi ( , ) memiliki minimum lokal pada titik ( , ) jika ( , ) ≥ ( , )
untuk setiap titik ( , ) dalam daerah sekitar (a,b).
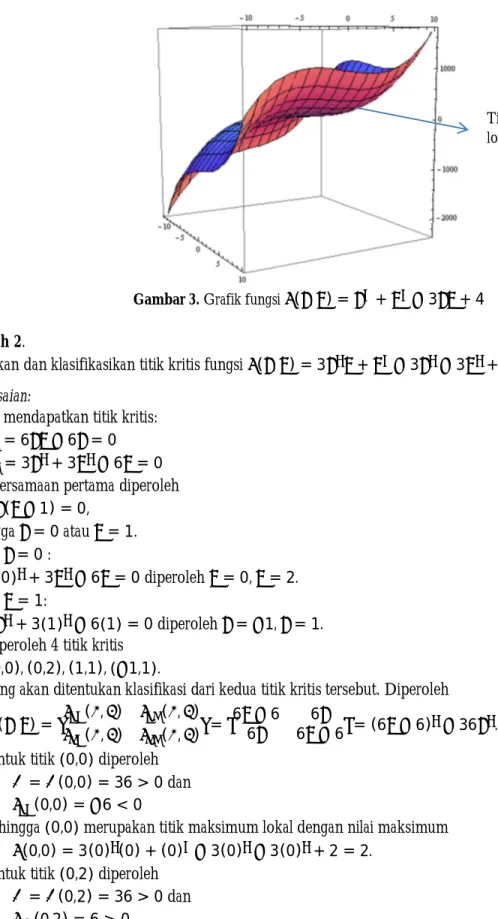
(ii) Suatu fungsi ( , ) memiliki maksimum lokal pada titik ( , ) jika ( , ) ≤ ( , )
untuk setiap titik ( , ) dalam daera sekitar (a,b).
Definisi.
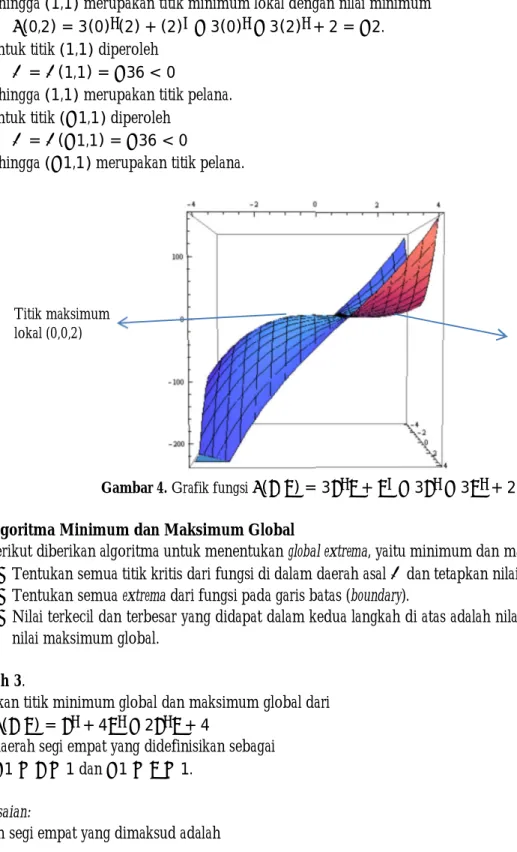
(iii) Suatu fungsi : → ℝ, ⊆ ℝ , memiliki minimum global pada titik ( , ) jika ( , ) ≥ ( , )
untuk setiap titik ( , ) ∈ .
(iv) Suatu fungsi : → ℝ, ⊆ ℝ , memiliki maksimum global pada titik ( , ) jika ( , ) ≤ ( , )
untuk setiap titik ( , ) ∈ . Perhatikan ilustrasi berikut.
Gambar 1. Minimum lokal dan maksimum lokal H. Titik Kritis
Selanjutnya, diberikan konsep titik kritis pada fungsi 2 variabel. Pada definisi titik kritis untuk 1 variabel, titik = adalah titik kritis fungsi ( ) jika salah satu kondisi berikut terjadi, yaitu
a. ( ) = 0
b. ( ) ada dan ′( ) tidak ada.
Berikut diberikan definisi titik kritis untuk fungsi 2 variabel.
Definisi. Titik ( , ) adalah titik kritis dari ( , ) jika salah satu kondisi dari dua syarat berikut berlaku, (i) ∇ ( , ) = ( , ), ( , ) = (0,0),
(ii) ( , ) ada dan ( , ) dan/atau ( , ) tidak ada.
1. Jika > 0 dan ( , ) > 0 maka didapat mínimum lokal pada ( , ).
2. Jika > 0 dan ( , ) < 0 maka didapat maksimum lokal pada ( , ).
3. Jika < 0 maka titik ( , ) adalah titik pelana (saddle point).
4. Jika = 0 maka titik ( , ) mungkin mínimum lokal, maksimum lokal atau titik pelana.
Gambar 2. Klasifikasi titik kritis untuk fungsi satu variabel
Contoh 1.
Tentukan dan klasifikasikan titik kritis fungsi ( , ) = + − 3 + 4.
Penyelesaian:
Untuk mendapatkan titik kritis:
= 3 − 3 = 0
= 3 − 3 = 0
Dari kedua persamaan di atas (dengan substitusi) diperoleh 3 ( − 1) = 0,
sehingga = 0 atau = 1. Untuk = 0 diperoleh = 0, sedangkan untuk = 1 diperoleh = 1. Jadi diperoleh 2 titik kritis (0,0) dan (1,1).
Sekarang akan ditentukan klasifikasi dari kedua titik kritis tersebut. Diperoleh
( , ) = ( , ) ( , )
( , ) ( , ) = 6 −3
−3 6 = 36 − 9.
a. Untuk titik (0,0) diperoleh
= (0,0) = −9 < 0,
sehingga (0,0) merupakan titik pelana.
b. Untuk titik (1,1) diperoleh
= (1,1) = 27 > 0 dan (1,1) = 6 > 0
sehingga (1,1) merupakan titik minimum lokal dengan nilai minimum (1,1) = (1) + (1) − 3(1)(1) + 4 = 3.
Gambar 3. Grafik fungsi ( , ) = + − 3 + 4
Contoh 2.
Tentukan dan klasifikasikan titik kritis fungsi ( , ) = 3 + − 3 − 3 + 2.
Penyelesaian:
Untuk mendapatkan titik kritis:
= 6 − 6 = 0
= 3 + 3 − 6 = 0 Dari persamaan pertama diperoleh
6 ( − 1) = 0,
Sehingga = 0 atau = 1.
Untuk = 0 :
3(0) + 3 − 6 = 0 diperoleh = 0, = 2.
Untuk = 1:
3 + 3(1) − 6(1) = 0 diperoleh = −1, = 1.
Jadi diperoleh 4 titik kritis (0,0), (0,2), (1,1), (−1,1).
Sekarang akan ditentukan klasifikasi dari kedua titik kritis tersebut. Diperoleh
( , ) = ( , ) ( , )
( , ) ( , ) = 6 − 6 6
6 6 − 6 = (6 − 6) − 36 . a. Untuk titik (0,0) diperoleh
= (0,0) = 36 > 0 dan (0,0) = −6 < 0
sehingga (0,0) merupakan titik maksimum lokal dengan nilai maksimum (0,0) = 3(0) (0) + (0) − 3(0) − 3(0) + 2 = 2.
b. Untuk titik (0,2) diperoleh
= (0,2) = 36 > 0 dan (0,2) = 6 > 0
Titik minimum lokal (1,1,3)
d. Untuk titik (−1,1) diperoleh
= (−1,1) = −36 < 0
sehingga (−1,1) merupakan titik pelana.
Gambar 4. Grafik fungsi ( , ) = 3 + − 3 − 3 + 2 I. Algoritma Minimum dan Maksimum Global
Berikut diberikan algoritma untuk menentukan global extrema, yaitu minimum dan maksimum global.
1. Tentukan semua titik kritis dari fungsi di dalam daerah asal dan tetapkan nilai fungsinya.
2. Tentukan semua extrema dari fungsi pada garis batas (boundary).
3. Nilai terkecil dan terbesar yang didapat dalam kedua langkah di atas adalah nilai minimum global dan nilai maksimum global.
Contoh 3.
Tentukan titik minimum global dan maksimum global dari
( , ) = + 4 − 2 + 4
pada daerah segi empat yang didefinisikan sebagai
−1 ≤ ≤ 1 dan −1 ≤ ≤ 1.
Penyelesaian:
Daerah segi empat yang dimaksud adalah
Titik minimum lokal (0,2,-2) Titik maksimum
lokal (0,0,2)
Gambar 5. Daerah segi empat
Garis batas segi empat tersebut adalah Sisi kanan : = 1, −1 ≤ ≤ 1 Sisi kiri : = −1, −1 ≤ ≤ 1 Sisi atas : = 1, −1 ≤ ≤ 1 Sisi bawah : = −1, −1 ≤ ≤ 1
1. Menentukan semua titik kritis dari fungsi di dalam daerah asal dan tetapkan nilai fungsinya.
= 2 − 4 = 0 (1)
= 8 − 2 = 0. (2)
Dari persamaan (2) diperoleh
= ,
sehingga dari (1) diperoleh
2 − 4 = 0
⟺ (2 − ) = 0
= 0 atau = ±√2 = ±1.414...
Karena daerah asal terbatas pada −1 ≤ ≤ 1, sehingga yang memenuhi adalah = 0, sedangkan
= ±√2 tidak memenuhi. Diperoleh
= = = 0.
Dalam hal ini, diperoleh titik kritis tunggal, yaitu (0,0),
dengan nilai fungsi (0,0) = 4.
2. Menentukan semua extrema dari fungsi pada garis batas (boundary).
(i) Garis batas kanan: = 1, −1 ≤ ≤ 1 Didefinisikan fungsi
( ) = (1, ) = 1 + 4 − 2(1 ) + 4 = 4 − 2 + 5.
Kemudian mencari titik kritis ( ) pada range −1 ≤ ≤ 1.
( ) = 0 ⟺ 8 − 2 = 0
⇔ = .
(ii) Garis batas kiri: = −1, −1 ≤ ≤ 1 Didefinisikan fungsi
( ) = (−1, ) = 4 − 2 + 5
Diperoleh fungsi yang sama seperti pada (i), sehingga diperoleh titik kritis
= .
Nilai pada titik-titik ujung = −1, = 1 dan titik kritis = adalah (−1) = 11, (1) = 7, = = 4.75.
Karena ( ) = (−1, ), maka
(−1, −1) = 11, (−1,1) = 7, −1, = 4.75.
(iii) Garis batas atas: = 1, −1 ≤ ≤ 1 Didefinisikan fungsi
ℎ( ) = ( , 1) = + 4(1 ) − 2 (1) + 4 = − + 8 Kemudian mencari titik kritis ℎ( ) pada range −1 ≤ ≤ 1.
ℎ ( ) = 0 ⟺ −2 = 0
⇔ = 0.
Nilai ℎ pada titik-titik ujung = −1, = 1 dan titik kritis = 0 adalah ℎ(−1) = 7, ℎ(1) = 7, ℎ(0) = 8.
Karena ℎ( ) = ( , 1), maka
(−1,1) = 7, (1,1) = 7, (0,1) = 8.
(iv) Garis batas bawah: = −1, −1 ≤ ≤ 1 Didefinisikan fungsi
ℎ( ) = ( , −1) = 3 + 8
Kemudian mencari titik kritis ℎ( ) pada range −1 ≤ ≤ 1.
ℎ ( ) = 0 ⟺ 6 = 0
⇔ = 0.
Nilai ℎ pada titik-titik ujung = −1, = 1 dan titik kritis = 0 adalah ℎ(−1) = 11, ℎ(1) = 11, ℎ(0) = 8.
Karena ℎ( ) = ( , −1), maka
(−1, −1) = 11, (1, −1) = 11, (0, −1) = 8.
Dari proses di atas diperoleh
(0,0) = 4 (1, −1) = 11 (1,1) = 7
1, = 4.75 (−1,1) = 7 (−1, −1) = 11
−1, = 4.75 (0,1) = 8 (0, −1) = 8
3. Jadi, titik minimum global pada (0,0) dengan nilai minimum 4 dan titik maksimum global pada (1,1) dan (−1,1) dengan nilai maksimum 11.
Contoh 4.
Tentukan titik minimum global dan maksimum global dari ( , ) = 2 − + 6
pada daerah lingkaran dengan radius 4, yaitu + ≤ 16.
Penyelesaian:
1. Menentukan semua titik kritis dari fungsi di dalam daerah di dalam lingkaran dan tetapkan nilai fungsinya.
= 4 = 0 (1)
= −2 + 6 = 0.
Diperoleh = 0 dan = 3. Sehingga titik kritis fungsi adalah (0,3),
dengan nilai fungsi (0,3) = 9.
2. Menentukan semua extrema dari fungsi pada garis batas (boundary) berbentuk lingkaran + = 16.
Karena = 16 − , sehingga diperoleh
( ) = 2(16 − ) − + 6 = −3 + 6 + 32.
Kemudian mencari titik kritis ( ) pada range −4 ≤ ≤ 4.
( ) = 0 ⇔ −6 + = 0 ⇔ = 1.
Nilai pada titik-titik ujung = −4, = 4 dan titik kritis = 1 adalah (−4) = −40, (4) = 8, (1) = 35.
Karena = 16 − , sehingga diperoleh
= −4: = 16 − 16 = 0 → = 0
= 4 ∶ = 16 − 16 = 0 → = 0
= 1 ∶ = 16 − 1 = 15 → = ±√15 Dikembalikan ke fungsi ( , ) diperoleh
(0, −4) = −40 (0,4) = 8
√15, 1 = 35
−√15, 1 = 35.
3. Jadi, titik minimum global pada (0, −4) dengan nilai minimum −40 dan titik maksimum global pada (√15, 1) dan (−√15, 1) dengan nilai maksimum 35.
a. ( , ) = + + + 4, = {( , )|| | ≤ 1, | | ≤ 1}
b. ( , ) = 4 + 6 − − , = {( , )|0 ≤ ≤ 4,0 ≤ ≤ 5}.
Kemudian tunjukkan grafik dengan menggunakan Software Mathematica.