KRIPTOGRAFI KURVA ELIPTIK (Elliptic Curve CryptographyIECC)

BAB

111

KRIPTOGRAFI KURVA ELIPTIK

(Elliptic Curve CryptographyIECC)

3.1 Skema Penyandian Kunci Publik

Misalkan { E : e e X } adalah himpunan dari transformasi penyandianlenkripsi, dan misalkan {Dd: de%} adalah himpunan dari transformasi pengupasan sandiidekripsi dimana X ad& mang kunci. Misalkan beberapa pasangan transformasi enkripsildekripsi (E,, Dd) dan misalkan setiap pasangan mempunyai syarat bahwa dengan mengetahui E, adalah secara komputasional tidak mungkidayak jika diberikan sebuah siferteks acak c 6

e,

untuk memperoleh m E JU sehingga E,(m)=c. Syarat ini menyatakan bahwa jika diberikan e maka hal ini tidak mungkin untuk menentukan kunci dekripsi d-nya. (Tentunya e dan d menjelaskan fungsi-fungsi enkripsi dan dekripsi) E, diperlihatkan sebagai suatu fungsi hapdoor one-way (adalah fungsi one-way f:

X+Y dengan syarat tambahan yang diberikan beberapa informasi ekstra (disebut

informasi frupdoor), ini menjadi tidak mungkin untuk mendapatkan suatu x E X sehinggaflx) 7, jika diberikan beberapa y E ImV)) dengan d menjadi informasi t r u p h r untuk menghitung fungsi invers dan karena itu memenuhi dekripsi.

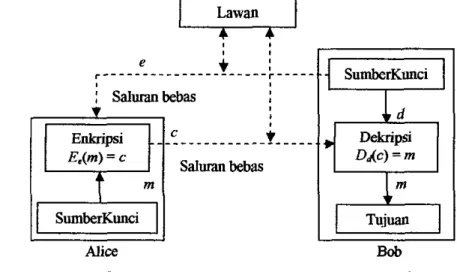
Di bawah asumsi ini, misalkan komunikasi dua kelompok antara Alice dan Bob diilustrasikan dalam Gambar 3. Bob memilih pasangan kunci (e,

4.

Bob mengirimkan kunci enkripsi e (disebut kunci publik) ke Alice melalui beberapa

saluran tetapi kunci delcripsi (kunci pribadi) d tetap dijaga kerahasiaan dan keamanannya. Alice kemudian mengirimkan sebuah pesan m ke Bob dengan mengaplikasikan transformasi enkripsi yang ditentukan oleh kunci publik Bob untuk mendapatkan c=E,(m). Bob mendekripsi siferteks c dengan mengaplikasikan transfonnasi invers Dd secara unik yang ditentukan oleh d.

Karena kunci enkripsi e tidak perlu dijaga kerahasiaannya, kunci ini dibuat umum. Beberapa entitas dapat mengirimkan berita yang disandi setelah itu ke Bob

Penyandian kunci publik mengasumsikan bahwa pengetahuan tentang kunci publik e tidak memberikan komputasi untuk kunci pribadi d. Dengan kata lain, penyandian ini mengasumsikan keberadaan fungsi-fungsi trapdoor one-way.

I/

SnmberKnnci

I

I

Alice

Gambar 3. Enkripsi dengan tekoik kunci pnblik

Berikut ini akan dibahas tentang salah satu contoh skema penyandian kunci publik, yaitu ECC.

3.2 Kriptografi Kurva Eliptik (ECC)

ECC dapat digunakan untuk beberapa keperluan seperti skema enkripsi (contohnya ElGamal ECC), tanda tangan digital (contohnya ECDSA) dan protokol pertukaran kunci (contohnya Diffie-Hielman ECC). Dalam penulisan tesis ini, dibahas tentang algoritme penandaan dijitel ElGamal berbasis ECC dan hal-hal yang diperlukan atau berkaitan dengan algoritme tersebut. Kemudian dibuat program yang merupakan implementasi dari ECC.

Definisi 48 (Koblitz, 1994) Definisi Kurva Eliptik

1. Misalkan K adalah lapangan dengan karakteristik it 2 , 3 . Misalkan

2

+ m

+

b, (a, b E K ) dengan

4d

+

27b2 # 0, merupakan polinomial pangkat tiga yang

tidak mempunyai akar perkalian (multiple root). Kurva eliptik K adalah himpunan titik (x, y) dengan x, y E K yang memenuhi persamaan

,?=i'+mc+b

...

(1) disertai dengan sebuah elemen tunggal, yaitu

0

(titik infinity).

Lapangan K dapat berupa lapangan R (lapangan bilangan real), lapangan Q

(lapangan bilangan rasional), lapangan C (lapangan bilangan kompleks) atau K dapat berupa lapangan berhingga F, dengan q = pr, p adalah suatu bilangan prima dan F, memiliki q elemen.

2. Jika K adalah lapangan yang memiliki karakteristik 2, maka kurva eliptik pada K adalah himpunan titik (x, y) yang memenuhi persamaan:

y + c y = ? + m + b atau $ + x y = . ? + d + b

...

(2) ditambah dengan O sebagai titik infniv.

3. Jika K adalah lapangan yang berkarakteristik 3, maka kurva eliptik pHda K adalah himpunan titik (x, y) yang memenuhi persamaan:

$ = ? + d + b x + c

...

(3) ditambah dengan O sebagai titik inzniq.

Setiap k ~ eliptik akan berbentuk simetris terhadap sumbu x atau garis ~ a @. Karena untuk setiap nilai XGR, terdapat sepasang nilai y e R yang memenuhi

persamaan (I), yaitu y,,, =

4 2

+a+ b

.

Kurva eliptik juga dapat dipandang sebagai suatu himpunan yang terdiri dari titik-titik (x, y) yang memenuhi persamaan (1). Himpunan tersebut dinotasikan dengan E(a, b). Untuk setiap nilai a dan b yang berbeda, dihasilkan himpunan E(a, b) yang berbeda pula.

3.2.1 Order Grup

Kurva eliptik pada lapangan berhingga Z, dengan q = pr dan p adalah suatu bilangan prima, dinotasikan dengan E(Zq) dan juga memenuhi persyaratan

4d

+

27b2 t 0. Titik-titik pada E(&) membentuk suatu grup modulo q.

Jumlah maksimun titik yang terdapat pada suatu kurva eliptik (Z,) dengan q = pr adalah 29 + 1, yaitu 29 pasangan (x, y), dimana x, y E

Z,

yang

memenuhi persamaan kuwa eliptik ditambah dengan sebuah elemen identitas, yaitu C). Jumlah titik pada E(Z,) dinotasikan dengan #E(&), disebut order dari E atas

&.

3.2.2 Penentuan Titik pada K u w a Eliptik

Penentuan titik pada kurva eliptik E(Zp) dengan persamaan

9

= x3

+

a x + b, secara sederhana dapat dijelaskan sebagai berikut:

Untuk setiap x dengan 0 5 x i p , hitung nilai

.?

+

ax + b. Setiap hasil yang didapat diperiksa apakah hasil tersebut mempunyai akar kuadrat modulo p. Jika tidak, maka tidak ada titik dengan nilai x pada E(Zp). Demikian juga untuk sebaliknya, jika ada, maka akan ada dua nilai y yang memenuhi persamaan tersebut (kecuali nilai y tunggal, yaitu 0). Titik (x, y) tersebut merupakan titik pada kunra-kwa eliptik

E(G)

dengan persamaan$ =

2

+

ax

+

b.

Order dari suatu titik P G E adalah bilangan bulat positif terkecil k,

sehingga

kP

= B dan titik P disebut titik hingga Gnitepoint). Jika tidak ada intejer

positif yang memenuhinya, maka order titik tersebut dikatakan tidak berhingga (infinite).

3.2.3 Struktur Grup Kurva Eliptik secara Geometri

Akan dibuktikan bahwa k u ~ a eliptik merupakan suatu grup, yaitu sebagai berikut:

a. Misal diberikan P = (-2.5,-1.369)~ E(R'), Q=(-0.5,1.837)~ E(R') ,

dan P

+

+Q , maka P

+

Q =R merupakan garis yang memotong kurva eliptik tepat di satu titik, sebut -R. Titik -R diiefleksikan dengan sumbu x ke titik R seperti terlihat pada Gambar 4. Dari sini jelas P+Q=R tertutup terhadap

penjumlahan dalam E(F).

I I

b. Kedua, akan dibuktikan (P+Q)+R=P+(Q+R) memenuhi sifat asosiatif. Misal diberikan titik P=(-2.5, -1.369) E E(R2), Q=(-0.5, 1.837) E E(R'), dan R = (-2,-&) E E ( R ' ) . Dengan demikian akan dilakukan sebanyak dua

tahap. Tahap pertama menyelesaikan operasi sisi sebelah kiri yaitu kerjakan

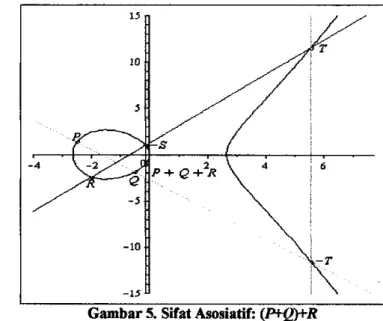
(P+Q). Seperti terlihat pada Gambar 5, (P+Q)=T.

I -- I

Gambar 5. S i Asosiatik (P+e)tR

Kemudian tambahkan titik R yang diperoleh dengan titik T dengan menghubungkan kedua titik tersebut akan diperoleh perpotongan dengan k ~eliptik tepat di satu titik, sebut ~ a -S. Titik -S direfleksikan dengan sumbu x diperoleh titik S yang merupakan hasil terakhir dari penjumlahan.

J Gambar 6. Sifat Asosiatik Pl(QtK)

Demikian pula dengan tahap kedua yaitu menyelesaikan operasi sisi sebelah kanan. Yang dilakukan sama seperti pada tahap pertama, bedanya yang dilakukan pertama kali adalah Q+R. Hasil tahapan ini dapat dilihat pada Gambar 6.

c. Ketiga akan dibuktikan mempunyai identitas. Misal penambahan titik

P i - 2 , -6) E E(R 2 , dan -P merupakan garis vertikal yang tidak memotong kurva eliptik dititik ketiga, maka titik P dan -P tidak dapat ditambahkan seperti penambahan titik P dan Q yang berbeda. Hal ini menyebabkan kurva eliptik meliputi point at infinity dengan definisi P+(-P)=U.

Sebagai hasil dari persamaan ini P+U=P berada dalam grup dan U disebut identitas penjumlahan.

d. Dari pembuktian ketiga dari grup di atas secara otomatis sudah terbukti kuma eliptik ini mempunyai invers dari titik P yaitu -P. Dari keempat bukti di atas dapat disimpulkan bahwa E ( R ~ ) memenuhi grup kurva eliptik. Apakah memenuhi grup komutatif! Dari pembuktian pertama jelas E(R') terbukti memenuhi grup komutatif Jadi dapat dibuktikan bahwa kurva eliptik memenuhi sifat-sifat grup.

3.3 Aritmatika Kurva Eliptik

Mekanisme kriptograti yang didasarkan pada kuma eliptik tergantung pada aritmatika yang melibatkan titik-titik pada kuma. Kurva eliptik didefinisikan pada operasi-operasi lapangan. Operasi-operasi kurva yang efisien juga sangat penting untuk hasilnya.

Ada dua lapangan berhingga yang sering digunakan dalam kriptografi kuwa eliptik, yaitu lapangan berhingga prima

(Z,)

dan lapangan karakteristik 2 (F 2"').

Lapangan berhingga Zp lebih efektif untuk implementasi soflware kriptografi kurva eliptik. Sedangkan lapangan berhingga F zrn lebih efektif untuk hardware yang sistem kerjanya berdasarkan algoritme kriptograii kurva eliptik.

Kuwa eliptik E(a, 6 ) atas

Z p

me~pEtkan himpunan penyelesaian dari persamaan (I), termasuk titik khusus 6. a, b 6

Zp

adalah konstanta, sehingga memenuhi 4a3

+

27b2 # 0 . Domain x dan y adalah

F,.

Kuwa eliptik E(a, b) atas

Z,

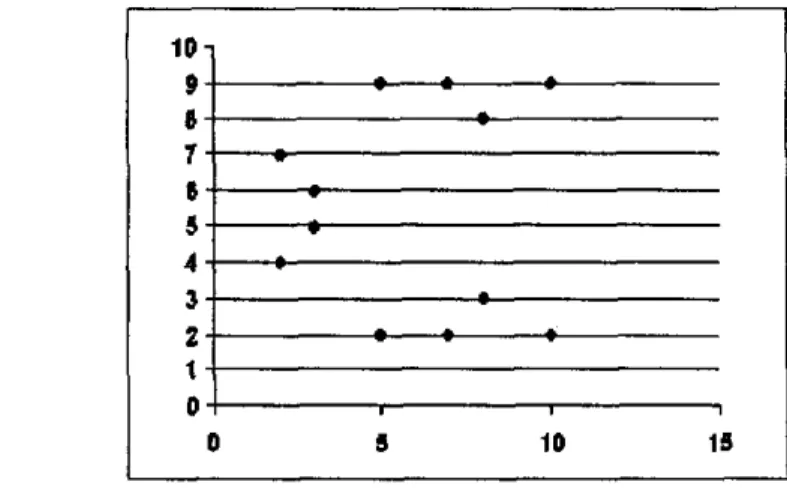
tidak memiliki representasi geometrik yang berbentuk kuwa seperti kuwa eliptik dalam R. Tetapi dapat digambarkan titik- titik kuwa eliptik yang merupakan elemen grup eliptik E(a, b) atas Zp , seperti yang terlihat pada Gambar 8 berikut ini.

Gambar 7. Smlterpbt dari Gmp Eliptik Ell(l, 1)

Kurva Eliptik atas Lapangan Berhingga Fp atau

&,

Teknis dasar kurva eliptik dalam grup Zp dimana p adalah bilangan prima yang lebih besar dari 3. Selanjutnya k u ~ a eliptik secara umum didefinisikan sebagai lapangan berhingga. Sebuah kurva eliptik E atas

Zp

didefinisikan dalam persamaan: y2 = x3 +ax

+

b

,

dimana a, b E Zp dan 4a3

+

27b2 # 0 , dan sebuah titik tertentu 6 (titik infinity). Himpunan E(Zp) = Ep(qb) adalah semua titik (x, y) dimana x, y E

Zp.

Diberikan satu titik

P

= (x, y,), dimana xp adalah koordinat x

pada P dan yp adalah koordiiat y pada P.

Operasi penjumlahan

+

dapat didefinisikan pada himpunan E(Zp) sehingga (E(Zp), +) membentuk grup abelian dengan 6 sebagai identitasnya. Operasi ini

digunakan untuk meng~nstruk~kan ECC. Operasi penjumlahan pada E(Z,,) adalah sebagai berikut:

ii. Jika P = (x, y ) E E(Zp), maka (x, y ) + (x, -y) = 8 , (titik (1, -y) E E(Zp) dinotasikan -P dan disebut negatif P);

y' = r ' - 6 x + 6

Gambar 8. Operasi peujumlahan identitas

iii. Misal P = ( X I , y ~ ) E E(Zp) dan Q = (x2, y2) E E(Zp), dimana P f i Q, maka P + Q = ( x 3 , y 3 ) , dimana x,=a2-x,-x,; y 3 = ~ ( x , - x 3 ) - y l ; dan

a=-

y2 - ' I (lihat Gambar 4). x2 -x, Bukti: ~ : = x , ~ + m c , + b ... 1) Persamaan kuwa : 2 3 y2 = x , + q + b

...

2)

Persamaan 3) dan 1 ) dikurangkan dan dibagi ( 3 -x,), maka diperoleh t j y , Z - y 1 2 = ( ~ 3 - x , 3 ) + ( x 3 - ~ l ) a

2 2

persamaan: o y3 -yi = ( ~ , 2 + x , x ~ + ~ ~ ) + a

x3 -%

Persamaan 3) dan 2) dikurangkan dan dibagi ( x , -x2), maka diperoleh persamaan 5).

Dari persamaan 4) dan 5) diperoleh:

Dan dari pemisalan bahwa A =

-"

, maka diperoleh:

x3 - %

" ( ~ 3 -X,)A=-y, -Y,

C1 y

(

x 3y ...

Contoh:

Misalkan tit& P(3,lO) dan Q(9,7) dalam &3(l,l), maka P+Q=R(xfiy~), dengan XR d a n y ~ diperoleh dengan menghitung nilai ;1 terlebih dahulu.

YQ-YP -

_--

7-10 -3 -1

1 = (mod 23) = -(mod 23) = -(mod 23) = -2-'(mod 23)

x -x, _Q 9-3 6 2

A = 1 1, kemudian dapat dihitung nilai XR d a n y ~ , yaitu:

yR = A(xp - xR)- yp = 1 l(3-17)-lO(rnod23) = -164(mod23) = -3(mod23) y, = 20. Jadi P + Q = R ( ~ f i y ~ ) = R(17,20).m

iv. Misal P = (XI, y,) E E(Z,). P

+

P

= 2P = (x3, y3), dirnana

3 4 + a x 3 = a 2 - 2 % ;

y3=a(T-5)-yl;

d m a =

2Yl Operasi ini disebut doubling suatu titik.

Bukti:

Misalkan P = (XI, yl) E E(Zp) dan 2P = (x3, y3) E E(Zp) Misal A = -Y3 - Yl ...

x3 - XI

6 )

Dari 6 ) diperoleh:

Dari persamaan k ~ y Z ~= x3 a

+

m

+

6 diturunkan terhadap x diperoleh:

a. Doubling titik

P

jika

yP

= 0

Garis tangen akan selalu vertikal jika yP-0 dan tidak memotong EC pada titik lainnya. Dengan definisi 2P-0 untuk titik P, maka

3P=2P+P=B+P=P,

4P=0, 5P=P, dan seterusnya.

= x 3 + s - 7

Gambar 9. Operasi hubling jika y P = 0

Perkaiian pada k U ~ a eliptik dinotasikan sebagai nP adalah didefinisikan sebagai operasi penjumlahan P sebanyak n kali jika n

positif atau penjumlahan (-P) sebanyak

1

n

1

jika n negatif dengan n

b. Doubling titik P jika

yP+

0

9 n r 3 - I 1 + 5

Gambar 10. Operasi doubling jika yP # 0

Contoh: Misalkan titk P(x,,y,) = P(3,lO) E E,(l, l), sehinggaperkalian

skalar 2P = P+P dihitung dengan cara berikut ini. 3x:+a 3.3'+1

A = - - _{(mod 23) = -(mod} 5 _{23) = 4-I (mod 23) = 6.}

2Y I 2.10 20

x,

= 2

- 2 3 =36-6(mod23)=7.

y, = A(xl -x,)- y1 = 6(3 -7)-lO(mod23) = -34mod23 = 12 Jadi, 2P = (x3, y3) = (7, 12).

Banyaknya titik dalam grup eliptikE,(a, b) dinotasikan dengan #E dan berada

padainterval [ p + l - 2 f i , p + l + 2 f i ] .

Contoh perhitungan dalam menentukan elemen-elemen grup eliptik Ep(a,b) atas Z,. Betdasarkan Definisi 43, persamaan kurva eliptik adalah2 =

2

+

+

+ b. Misalkan

o=l, b=6 clan p.11, persamaan kurva eliptik menjadi

9

=

2

+ x

+

6

(mod1 1) ,sehingga 4a'+27b2= 4. 13+27.6' = 976 (mod 11) = 8 # (mod 1 I). Selanjutnya dicari elemen-elemen grup eliptik Eii(1,6) atas ZII, dengan Z11={0,1,2,3,4,5,6,7,8,9,10}.

Sebelum menentukan elemen-elemen E11(l,6), terlebih dahulu mencari residu kuadrat modulo 1 1 (ell) sesuai dengan Definisi 19.

1 S

I

bukan

1

2 5 (2.4) dau (2.7) 4 S bukan 5 4 (5.2) ch~ (5.9) 6 S bukan 7 4 (7.2) dm1 (7.9) 8 9 (8.3) dau (8.5)

Berdasarkan Tabel 4, himpunan Qll adalah Q11={0,1,3,4,5,9). Kemudian menentukan elemen grup eliptik E11(1,6) yang merupakan himpunan penyelesaian dari p e r m a a n $=2+x+6 (mod 1 I ) , untuk XE Zll d a n g ~ QII.

Berdasarkan Tabel 5, untuk x=2, diperoleh $=z2+2+6 (mod 11) = 5 sehingga

dipeloleh nilai y = 4 dan y = 7. Berdasarkan Tabel 4, 42 (mod 11)=5 dan 72 (mod 1 I)+. Perhitungan untuk nilai x dan y yang lain, dilakukan dengan cara yang sama. Dengan demikian diperoleh elemen grup eliptik modulo 11 atas Zll, yaitu:

9

10 I ya

I

(10.2) dam (10.9)

3.4 Parameter Domain Kurva Eliptik

Dalam subbab ini, dibahas tentang parameter-parameter domain kuwa eliptik atas

Z,.

Sebelum mengimplementasikan kriptografi kuwa eliptik, terlebih dahulu dipersiapkan infrastmktur yang dibutuhkan oleh sistem kriptografi tersebut. Infiastruktur yang dimaksud adalah parameter-parameter domain kuwa eliptik sehingga seluruh pengguna sistem dapat mengetahui beberapa parameter yang akan digunakan bersama. Parameter ini bersifat umum dan boleh diketahui oleh setiap pengguna dalam sistem tersebut.

Definisi 49 (Certiwm, 2001) Parameter-parameter domain kuwa eliptik atas Z, didefinisikan sebagai six-tuple D = ( p , a, b,

P,

n , h ).

p : bilangan prima

a , b : koefisien persamaan k u ~ a eliptikg=2 +ax +b (modp), a , b ~ Z, P : titik dasar (basic point), yaitu elemen pembangun grup eliptik Ep(a, b). n : order dari

P,

yaitu bilangan bulat positip terkecil3

nP

= 0.

h : kofaktor h=#E(Zp)ln, #E adalah jumlah titik dalam grup eliptik E,,(a, 6). Kekuatan kriptograf~ kuwa eliptik tergantung dari pemilihan parameter- parameter domain yang digunakan. Pemilihan parameter ini dilakukan sedemikian sehingga dapat terhindar dari serangan-serangan terhadap kekuatan algoritme kriptografi kuwa eliptik. Parameter-parameter tersebut ditentukan secara random menggunakan program yang dibuat sendii oleh penulis.

Pembaca yang ingin memperoleh parameter-parameter domain kuwa eliptik tanpa mencarinya terlebih dahulu, dapat menggunakan parameter-parameter yang diiekomendasikan oleh Certicom Research. Rekomendasi parameter-parameter domain kurva eliptik untuk berbagai ukuran kunci, dapat dilihat secara lengkap pada Certicom [lo].

3.5 Tingkat Keamanan ECC

Kriptografi ini menggunakan masalah logaritma diskrit pada titik-titik kuwa eliptik, yang disebut dengan Masalah Logaritma Diskret Kuwa Eliptik (MLDKE) sehingga kekuatannya terletak pada kesulitan menghitung k jika diketahui P dan Q, dimana Q =

kP.

Operasi dari skema kriptografi kunci publik melibatkan operasi-operasi aritmatika pada k u ~ a eliptik atas lapangan berhingga yang ditentukan oleh parameter-parameter domain k u ~ a eliptik. Parameter domain ECC atas

Z,

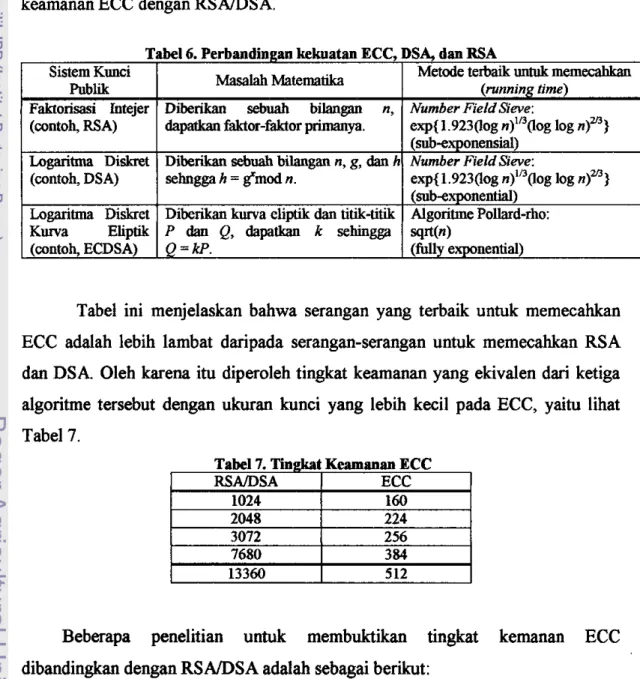
adalah D = (p, a, b, G, n , h ) seperti yang dijelaskan sebelumnya.

Karena parameter keamanan yang utama adalah n, panjang kunci ECC didefinisikan sebagai panjang bit dari n. Sebagai contoh, kurva yang direkomendasikan oleh NIST dijelaskan dengan parameter-parameter yang bisa menghindari semua serangan yang diketahui. Lebih jelasnya dapat dilihat pada tabel berikut ini mengenai serangan-serangan untuk melihat perbandingan tingkat keamanan ECC dengan RSADSA.

(wntoh, RSA) -

I

d a m faktor-faktor

&.

I

exp( 1.9230og n)'"(log log n)*)

I

Tabel 6. Perbandingan kekuatan ECC, DSA, dan RSA

- .

I

(sub-exponen&) Logatitma Diski-et I Diberikan sebuah bilangan n. a, dan h( Number Fieldsieve:

Metode terbaik untnk memecahkan

(running time) Sistem Kunci

Publii

Tabel ini menjelaskan bahwa serangan yang terbaik untuk memecahkan

Faklorisasi Intejer

I

Diberikan sebuah bilangan n, ( NumberFieldSieve:

Masalah Matemafika

( G t o h , DSA) Logaritma Diskret Knrva Eliptik (wntoh, ECDSA)

ECC adalah lebih lambat daripada serangan-serangan untuk memecahkan RSA dan DSA Oleh karena itu diperoleh tingkat keamanan yang ekivalen dari ketiga

-

. -.

sehngga h = g'mod n.

Diberikan kwva eliptik clan titik-titik P dan Q, dapatkan k sehingga

Q=W.

algoritme tersebut dengan ukuran kunci yang lebih kecil pada ECC, yaitu lihat Tabel 7.

exp{1.923(log n)'"(log log n)*} (sub-exponential)

Algoritme Pollard-rho: sqrt(n)

(fully exponential)

Beberapa penelitian untuk membuktikan tingkat kernanan ECC dibandingkan dengan RSA/DSA addah sebagai berikut:

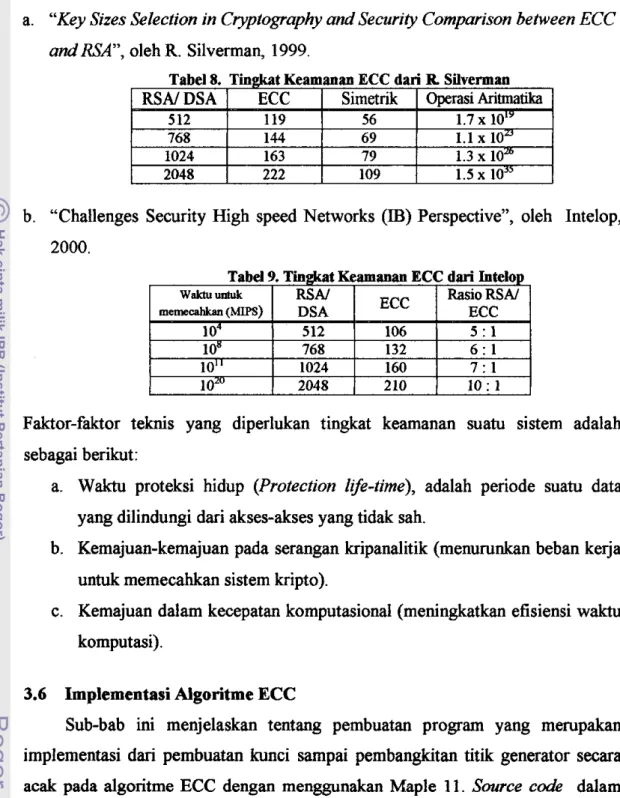
a. "Key Sizes Selection in Cryptography and Security Comparison between ECC and RSA", oleh R. Silverman, 1999.

b. "Challenges Security High speed Networks (El) Perspective", oleh Intelop,

Faktor-faktor teknis yang diperlukan tingkat keamanan suatu sistem adalah sebagai berikut:

a. Waktu proteksi hidup (Protection life-time), adalah periode suatu data yang dilindungi dari akses-akses yang tidak sah.

Tabd 9. Tingkat Keamanan ECC dari Intelop

b. Kemajuan-kemajuan pada serangan kripanalitik (menurunkan beban kerja untuk memecahkan sistem kripto).

c. Kemajuan dalam kecepatan komputasional (meningkatkan efisiensi waktu komputasi).

Walbluoh*

memcshkan (MIPS)

3.6 Implementasi Algoritme ECC

Sub-bab ini menjelaskan tentang pembuatan program yang merupakan implementasi dari pembuatan kunci sampai pembangkitan titik generator secara acak pada algoritme ECC dengan menggunakan Maple 11. Source code dalam Maple 11 terdiri dari deklarasi nama program, variabel-variabel dan tipe data, serta beberapa prosedur, fkngsi-fungsi dan program utama (Iihat Lampiran 3).

RSAI

DSA

Diketahui kuwa eliptik E(a, b) atas Z, merupakan himpunan penyelesaian dari persamaan J? =

2

+

ac

+

b, tennasuk titik khusus 0. a, b E

Z,

adalah

konstanta,

ECC

sehingga memenuhi

4d

+

27b2 $ 0 . Domain x dan y

adalah

F,.

Rasio RSAI

a. Prosedur Pemilihan Prima Aman secara Acak m bit Deklarasi :

-

Deskripsi : Prosedur ini digunakan untuk menghasilkan suatu prima aman p secara acak sepanjang m bit.

b. Fungsi Pemilihan Parameter a dan b pada Kurva Eliptik Deklarasi : ECAcak := proc (p: :posint)

.

Deskripsi : Fungsi ini untuk membangkitkan parameter a dan b (persamaan kurva) dengan b tidak no1 (agar kurva tidak memuat titik [0,0]), secara acak. c. Fungsi Pemilihan Titik Acak pada Kurva Eliptik

Deklarasi : TitikAcak := proc(K::list,p::posint)

Deskripsi : Fungsi ini untuk membangkitkan satu titik secara acak. d. Fungsi Penegatifan Suatu Titik pada Kurva Eliptik

Deklarasi : Neg := proc ( B : :list, P: :posint)

Deskripsi : Fungsi ini untuk menentukan negatif suatu titik. e. Fungsi Pemeriksaan Kesamaan Dua Titik pada Kurva Eliptik

Deklarasi : E q := proc (A: :list, B: :list)

Deskripsi : Fungsi ini untuk memeriksa kesamaan dua titik pada kurva. f. Fungsi Penjumlahan Dua Titik pada Kurva Eliptik

Deklarasi : AdisiTtk:=proc(X: :list,Y: :list,A: :list,P: :posint)

Deskripsi : Fungsi ini untuk menjumlahkan dua titik X dan Y pada kurva eliptik A, dengan unsur identitas [0,0] (titik di tak hingga).

g. Fnngsi Penghitungan Kelipatan Suatu Titik pada Kurva Eliptik Deklarasi : MultiTtk:=proc (A: :list, k: :integer, K: :list,

p::integer)

Deskripsi : Fungsi ini untuk menghitung kelipatan titik sebanyak k kali. h. Fungsi Pemilihan Grup Siklik pada Kurva Eliptik

Deklarasi : GenGrupSiklik:=proc (A: :list, k: :integer, K: :list, p: :integer)