BAB 2 LANDASAN TEORI

BAB 2

LANDASAN TEORI

2.1. Persamaan Integral

Pengintegrasian (integration), bersama dengan pendiferensiasian (differentiation), merupakan konsep matematika yang menjadi jantung dari kalkulus. Berdasarkan Microsoft Encarta Premium 2006 Dictionary Tools, mengintegrasikan (to

integrate) berarti “membawa seluruhnya, bagian per bagian, menjadi sebuah bentuk

utuh; menyatukan; untuk mengindikasikan jumlah total ...” Secara matematik, pengintegrasian dilambangkan dengan:

∫

= b

a f x dx

I ( ) Pers. (2.1)

yang berarti integral dari fungsi f(x) dengan variabel bebas x, dievaluasi berdasarkan batas x = a dan x = b. Fungsi f(x) dalam pers. (2.1) disebut integran (integrand).

Berdasarkan definisi yang diberikan oleh kamus bahasa, “arti” dari pers. (2.1)

adalah nilai total atau penjumlahan (summation) dari f(x) dx dalam jangkauan x = a hingga b. Berdasarkan faktanya, simbol

∫

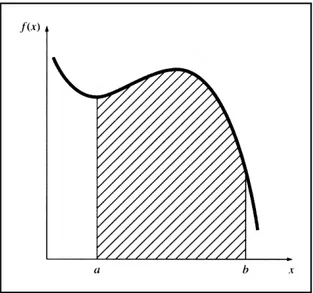
sebenarnya merupakan sebuah huruf kapital S yang diberi sentuhan gaya yang ditujukan untuk menandakan hubungan tertutup antara pengintegrasian dan penjumlahan.

Gambar 2.1 berikut merupakan sebuah penggambaran secara grafik dari konsep tersebut. Untuk fungsi yang terletak di atas sumbu x, integral yang dinyatakan oleh pers. (2.1) mengacu kepada area di bawah kurva f(x) antara x= a dan b.

Gambar 2.1 Penggambaran secara grafik dari integral f(x) antara batas x = a dan b. Integral tersebut ekivalen dengan daerah di bawah kurva

Fungsi yang diintegrasikan akan memiliki satu dari tiga bentuk khusus berikut ini:

• Sebuah fungsi kontinu sederhana, seperti sebuah polinomial, sebuah eksponensial, atau sebuah fungsi trigonometri.

• Sebuah fungsi kontinu yang rumit, yang sulit atau tidak mungkin diintegralkan secara langsung..

• Sebuah fungsi yang ditabulasikan, di mana nilai-nilai dari x dan f(x) diberikan pada sejumlah titik tertentu (diskrit), sebagaimana seringkali terjadi pada kasus dengan data lapangan atau data hasil eksperimen.

Pada kasus pertama, integral dari sebuah fungsi sederhana mungkin dapat dievaluasi secara analitik menggunakan kalkulus. Untuk kasus kedua, solusi analitik seringkali tidak praktis, dan terkadang mustahil, untuk diperoleh. Dalam hal ini, demikian juga dengan kasus ketiga dari data diskrit, metode pendugaan/perkiraan harus

digunakan.

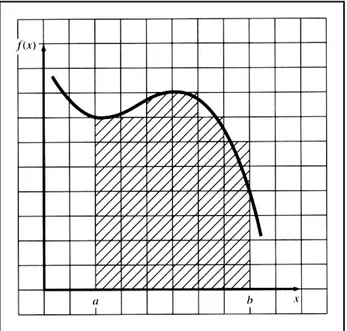
Pendekatan berorientasi visual digunakan untuk mengintegrasikan data tertabulasi dan fungsi yang rumit pada masa sebelum komputer ditemukan. Sebuah pendekatan berdasarkan intuisi yang sederhana adalah dengan menempatkan fungsi tersebut pada sebuah kisi-kisi (grid) (Gambar 2.2) dan menghitung jumlah kotak-kotak yang digunakan sebagai penduga dari daerah tersebut. Jumlah tersebut dikalikan dengan daerah di mana setiap kotak memberikan sebuah perkiraan kasar mengenai daerah total di bawah kurva. Perkiraan ini dapat diperhalus, dengan usaha tambahan, menggunakan sebuah kisi-kisi yang lebih baik.

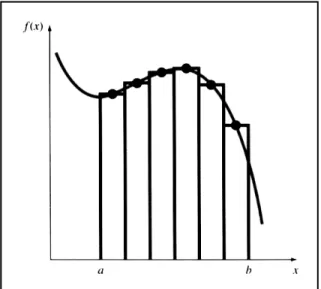
Pendekatan yang masuk akal lainnya adalah dengan membagi daerah tersebut menjadi bagian-bagian berbentuk vertikal, atau strips, dengan tinggi yang setara dengan nilai fungsi pada titik tengah setiap bagian (Gambar 2.3). Daerah dari persegi panjang tersebut dapat kemudian dihitung dan dijumlahkan untuk memperkirakan.jumlah total dari daerah tersebut. Pada pendekatan ini, diasumsikan bahwa nilai pada titik tengah setiap bagian memberikan sebuah pendugaan yang sah dari rata-rata tinggi dari fungsi untuk setiap strip. Sebagaimana dengan metode kisi-kisi, perkiraan yang diperhalus adalah mungkin dengan menggunakan lebih banyak (dan lebih tipis) strips untuk menaksir integral tersebut.

Gambar 2.3 Penggunaan dari persegi panjang atau strips untuk menaksir sebuah integral

2.2. Metode dan Integrasi Numerik

Walaupun pendekatan sederhana yang demikian memiliki sarana untuk pendugaan yang cepat, teknik numerik alternatif juga tersedia untuk tujuan yang sama. Tidak mengejutkan, cara yang paling sederhana dari metode ini mirip dalam hal jiwa dari teknik nonkomputer.

Integrasi numerik atau metode kuadratur (quadrature) tersedia untuk memperoleh integral-integral. Metode-metode ini, yang mana lebih mudah untuk diimplementasikan dibandingkan dengan pendekatan kisi-kisi, sangat mirip jiwanya dengan metode strip. Yaitu, tinggi fungsi dikalikan dengan lebar strip dan dijumlahkan untuk memperkirakan integral tersebut. Bagaimanapun, melalui pemilihan yang cerdas dari faktor pembobot (weighting factor), perkiraan yang dihasilkan dapat dibuat lebih akurat dibandingkan dengan metode strip yang sederhana. Sebagaimana dalam metode

strip sederhana, integrasi numerik menggunakan data pada titik-titik tertentu. Karena

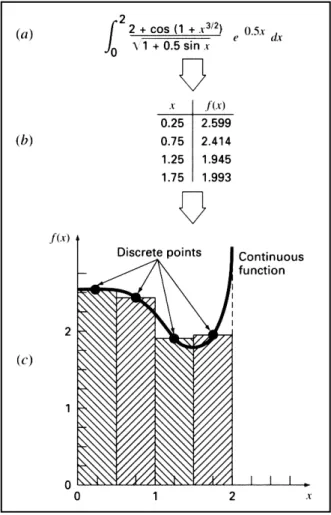
informasi berbentuk tabel sudah berbentuk demikian, maka hal itu dapat cocok dengan banyak dari pendekatan-pendekatan numerik. Sebagaimana ditunjukkan oleh gambar 2.4,

tabel tersebut dapat kemudian dievaluasi dengan sebuah metode numerik.

Gambar 2.4 Aplikasi dari sebuah metode

integrasi numerik: (a) Fungsi kontinu yang rumit. (b). Tabel nilai diskrit dari f(x) yang dihasilkan dari sebuah fungsi. (c). Penggunaan salah satu metode numerik (metode strip) untuk menaksir integral yang berdasarkan kepada titik-titik diskrit. Untuk sebuah fungsi

berbentuk tabel, data sudah dalam bentuk tabel (b); untuk itu, langkah (a) tidak diperlukan

2.3. Integrasi Romberg

Pada subbab 2.1., diketahui bahwa fungsi-fungsi yang akan diintegrasikan secara numerik memiliki dua bentuk yang khas: sebuah tabel berisi nilai-nilai atau sebuah fungsi. Bentuk dari data memiliki pengaruh terhadap pendekatan yang dapat digunakan untuk mengevaluasi integralnya. Untuk informasi berbentuk tabel (yang tidak dibahas dan digunakan dalam skripsi ini), kita dibatasi oleh jumlah dari titik-titik yang diberikan. Berlawanan dengan hal itu, Jika sebuah fungsi tersedia, maka kita dapat menghasilkan sebanyak mungkin nilai dari f(x) yang dibutuhkan untuk mencapai tingkat akurasi yang dapat diterima (seperti gambar 2.4).

Integrasi Romberg merupakan teknik yang digunakan dalam integrasi numerik untuk menganalisis kasus di mana fungsi yang akan diintegrasikan tersedia. Teknik ini memiliki keunggulan untuk menghasilkan nilai-nilai dari fungsi untuk mengembangkan skema yang efisien bagi pengintegrasian secara numerik. Integrasi Romberg didasarkan pada ekstrapolasi Richardson (Richardson’s extrapolation), yang mana merupakan metode untuk mengkombinasikan dua perkiraan integral secara numerik untuk memperoleh nilai ketiga, yang lebih akurat. Integrasi Romberg merupakan algoritma komputasi untuk mengimplementasikan ekstrapolasi Richardson melalui sebuah cara yang sangat efisien. Teknik ini bersifat rekursif dan dapat digunakan untuk menghasilkan sebuah perkiraan integral dalam batas toleransi kesalahan (error

tolerance) yang sudah ditentukan terlebih dahulu.

Integrasi Romberg didasarkan pada aplikasi beturut-turut (rekursif) dari aturan trapesium (trapezoidal rule). Walau bagaimanapun, melalui manipulasi secara

matematik, hasil yang superior dapat dicapai dengan sedikit usaha.

2.3.1. Ekstrapolasi Richardson

Ekstrapolasi Richardson merupakan metode yang menggunakan dua perkiraan dari sebuah integral untuk mengkomputasi pendugaan ketiga, yang lebih akurat.

Perkiraan dan kesalahan (error) yang diasosiasikan dengan aturan trapesium multi-aplikasi (multiple-application trapezoidal rule) dapat digambarkan secara umum sebagai

) ( ) (h E h I I= + Pers. (2.2)

di mana I adalah nilai yang sebenarnya dari integral tersebut, I(h) adalah pendugaan dari sebuah aturan trapesium dengan aplikasi bersegmen n dengan lebar langkahnya h = (b – a)/n, dan E(h) adalah kesalahan pemotongan (truncation error). Jika kita membuat dua perkiraan yang berbeda menggunakan lebar langkah h1 dan h2 dan memiliki nilai yang sebenarnya untuk error-nya,

) ( ) ( ) ( ) (h₁ E h₁ I h₂ E h₂ I + = + Pers. (2.3)

Sekarang ingat bahwa error dari aturan trapesium multi-aplikasi dapat diperkirakan sebagai " 12 ) ( 2 3 f n a b E_a=− − Pers. (2.4)

" 12 2_f h a b E≅− − Pers. (2.5)

Jika diasumsikan bahwa "f adalah konstan, tidak dipengaruhi oleh lebar langkah. Pers. (2.5) dapat digunakan untuk menentukan bahwa rasio dari kedua

error adalah 2 2 2 1 2 1 ) ( ) ( h h h E h E ≅

Pers. (2.6)

Perhitungan ini memiliki efek penting dalam penghilangan bagian "f dari perhitungan. Dengan demikian, hal itu memungkinkan kita untuk menggunakan informasi yang dinyatakan oleh pers. (2.5) tanpa terlebih dahulu mengetahui turunan kedua dari fungsi tersebut. Untuk melakukan hal itu, kita ubah pers. (2.6)

menjadi 2 2 1 2 1) ( ) ( _⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ ≅ h h h E h E Pers. (2.7)

yang mana dapat disubstitusikan ke dalam pers (2.3):

) ( ) ( ) ( ) ( _{2 2} 2 2 1 2 1 I h E h h h h E h I _⎟⎟ ≅ + ⎠ ⎞ ⎜⎜ ⎝ ⎛ + Pers. (2.8)

yang dapat disederhanakan menjadi

2 2 1 2 1 2 ) / ( 1 ) ( ) ( ) ( h h h I h I h E − − ≅ Pers. (2.9)

dalam hal pendugaan integral dan lebar langkahnya. Perkiraan ini dapat disubstitusikan ke dalam ) ( ) (h2 E h2 I I= + Pers. (2.10)

untuk menghasilkan sebuah pendugaan integral yang telah diperbaiki:

)] ( ) ( [ 1 ) / ( 1 ) ( _{2 2 1} 2 1 2 I h I h h h h I I − − + ≅ Pers. (2.11)

Hal ini menunjukkan (Ralston dan Rabinowitz, 1978) bahwa error dari pendugaan ini adalah O(h4). Hasilnya, kita telah mengkombinasikan dua perkiraan aturan trapesium dari O(h2) untuk menghasilkan sebuah penduga yang baru dari O(h4). Untuk kasus khusus di mana intervalnya dibagi dua (h2 = h1/2),

persamaan ini menjadi

)] ( ) ( [ 1 2 1 ) (h2 2 I h2 I h1 I I − − + ≅ Pers. (2.12)

atau, dibentuk menjadi,

) ( 3 1 ) ( 3 4 1 2 I h h I I≅ − Pers. (2.13)

Pers. (2.4) memberikan sebuah cara untuk mengkombinasikan dua aplikasi dari aturan trapesium dengan error O(h2) untuk menghitung penduga ketiga dengan error O(h4). Pendekatan ini adalah sebuah subhimpunan dari sebuah metode yang lebih umum untuk mengkombinasikan integral-integral dari O(h4) pada basis dari tiga penduga aturan trapesium. Kedua penduga tersebut dapat,

dalam perubahannya, dikombinasikan untuk menghasilkan sebuah nilai yang lebih baik dengan O(h6). Untuk kasus khusus di mana penduga trapesium yang asli didasarkan kepada pembagian terus-menerus dari lebar langkah, persamaan yang digunakan untuk keakuratan O(h6) adalah

l m I I I 15 1 15 16 ₋ ≅ Pers. (2.14)

di mana Im dan Il masing-masing adalah penduga yang lebih (more) dan kurang

(less) akurat. Dengan cara yang sama, dua hasil O(h6) dapat dikombinasikan untuk menghitung sebuah integral O(h8) menggunakan

l m I I I 63 1 63 64 ₋ ≅ Pers. (2.15)

2.3.2. Algoritma Integrasi Romberg

Perhatikan bahwa koefisien dari masing-masing persamaan ekstrapolasi (Pers. (2.13), Pers. (2.14), dan Pers. (2.15)) bertambah hingga mendekati satu. Hasilnya, mereka merepresentasikan faktor-faktor pembobot yang, sejalan dengan meningkatnya akurasi, menempatkan bobot yang secara relatif lebih besar pada penduga integral superior. Formulasi-formulasi tersebut dapat diekspresikan dalam bentuk yang umum yang cocok untuk diimplementasikan pada komputer: 1 4 4 1 1 , 1 , 1 1 , − − ≅ − +₋− − k k j k j k k j I I I Pers. (2.16)

akurat, dan Ij,k adalah integral yang diperbaiki. Indeks k menandakan tingkat dari

pengintegrasian, di mana k = 1 mengacu kepada penduga aturan trapesium yang asli, k = 2 mengacu kepada O(h4), k = 3 kepada O(h6), dan seterusnya. Indeks j digunakan untuk membedakan antara penduga yang lebih akurat (j + 1) dan penduga yang kurang akurat (j). Sebagai contoh, untuk k = 2 dan j = 1, pers. 2.16)

menjadi 3 4 _{2,1 1,1} 2 , 1 I I I ≅ − Pers. (2.17)

yang ekivalen dengan pers. (2.13).

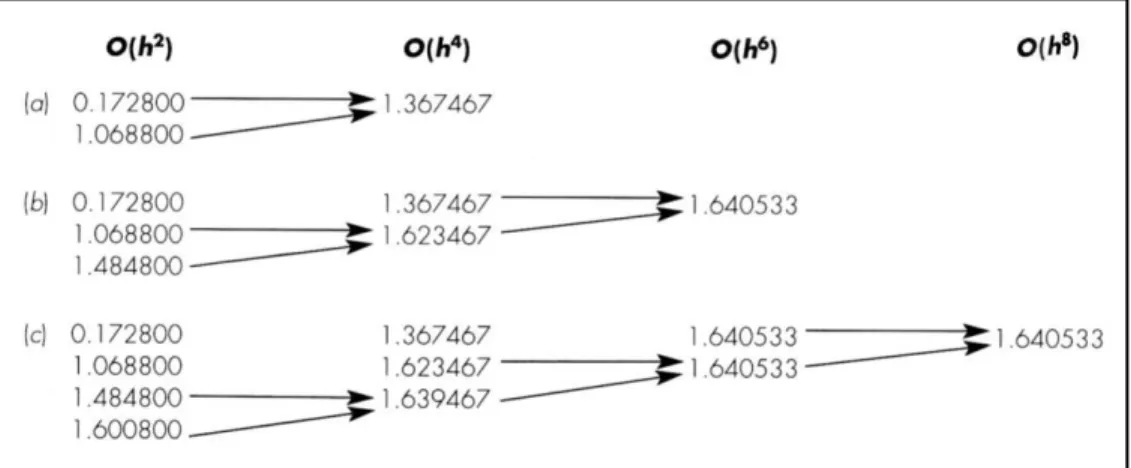
Gambar 2.5 Penggambaran secara grafik dari barisan penduga integral f(x) = 0,2 + 25x –

200x2 _{+ 675x}3 _{– 900x}4 _{+ 400x}5

dari a = 0 hingga b = 0,8, yang dihasilkan menggunakan integrasi Romberg. (a) Iterasi pertama. (b) Iterasi kedua. (c) Iterasi ketiga

Bentuk umum yang direpresentasikan oleh pers. (2.16) merupakan hasil karya Romberg, dan aplikasi sistematik untuk mengevaluasi integralnya dikenal dengan nama Integrasi Romberg. Gambar 2.5 merupakan penggambaran secara grafik dari barisan penduga integral yang dihasilkan menggunakan pendekatan ini. Setiap matriks mengacu kepada sebuah iterasi tunggal. Kolom pertama mengandung evaluasi terhadap aturan trapesium yang menggambarkan Ij,i, di

mana j = 1 adalah untuk sebuah aplikasi bersegmen tunggal (lebar langkahnya adalah b – a), j = 2 adalah untuk sebuah aplikasi dengan segmen dua (lebar langkahnya adalah (b – a)/2), j = 3 adalah untuk sebuah aplikasi bersegmen empat (lebar langkahnya adalah (b – a)/4), dan seterusnya. Kolom matriks lainnya dihasilkan oleh pengaplikasian pers. (2.16) secara sistematis untuk memperoleh penduga yang lebih baik dari suatu integral secara berturut-turut.

Sebagai contoh, iterasi pertama (Gambar 2.5a) melibatkan perhitungan penduga aturan trapesium bersegmen satu dan dua (I1,1 dan I2,1). Pers. (2.16)

kemudian digunakan untuk mencari elemen I1,2 = 1.367467, yang merupakan

sebuah error dari O(h4).

Sekarang, kita harus memeriksa untuk menentukan apakah hasil ini cukup untuk keperluan kita. Sebagaimana dengan metode pendugaan lainnya, sebuah kriteria pengakhiran (termination) atau penghentian (stopping) dibutuhkan untuk menentukan keakuratan dari suatu hasil. Salah satu metode yang dapat digunakan untuk tujuan ini adalah sebagai berikut

% 100 ini saat perkiraan sebelumnya perkiraan ini saat perkiraan a − = ε Pers. (2.18) atau % 100 , 1 1 , 2 , 1 k k k a _I I I − ₋ = ε Pers. (2.19)

sebagaimana telah dilakukan sebelumnya pada proses iterasi lainnya, kita membandingkan penduga yang baru dengan nilai sebelumnya. Ketika pergantian antara nilai yang lama dan baru sebagaimana direpresentasikan oleh ε_a, berada di bawah kriteria error ε_s yang telah ditentukan sebelumnya, maka perhitungan dihentikan. Untuk gambar 2.5a, evaluasi ini menandakan perubahan sebanyak

21,8% terhadap hasil iterasi pertama.

Tugas dari iterasi kedua (Gambar 2.5b) adalah untuk memperoleh penduga

O(h6)—I1,3. Untuk itu, sebuah penduga aturan trapesium tambahan, I3,1 = 1,4848,

ditentukan. Kemudian penduga tersebut dikombinasikan dengan I2,1

menggunakan pers. (2.16) untuk menghasilkan I2.2 = 1,623467. Hasilnya, pada

gilirannya, dikombinasikan dengan I1,2 untuk menghasilkan I1,3 = 1,640533. Pers. (2.17) dapat diaplikasikan untuk menentukan bahwa hasil tersebut merepresentasikan sebuah perubahan sebanyak 1.0% ketika dibandingkan dengan hasil I1,2 sebelumnya.

Iterasi ketiga (Gambar 2.5c) melanjutkan proses tersebut dengan cara yang sama. Pada kasus ini, sebuah penduga trapesium ditambahkan ke dalam kolom pertama, dan kemudian pers. (2.16) diaplikasikan untuk menghitung secara berturut-turut integral yang lebih akurat sepanjang diagonal yang lebih rendah. Setelah hanya tiga kali iterasi, karena mengevaluasi sebuah polinomial berordo lima, hasilnya (I1,4 = 1,640533) adalah tepat.

Integrasi Romberg lebih efisien dibandingkan dengan aturan trapesium dan aturan Simpson (tidak dibahas dalam skripsi ini). Sebagai contoh, untuk

menentukan integral yang ditunjukkan oleh f(x) = 0,2 + 25x – 200x2 + 675x3 –

900x4 + 400x5 dari a = 0 hingga b = 0,8, aturan Simpson 1/3 membutuhkan sebuah aplikasi dengan segmen sebanyak 256 untuk menghasilkan sebuah penduga dari 1,640533. Penaksiran yang lebih baik mustahil dilakukan karena

error yang disebabkan oleh pembulatan angka (di belakang koma). Berlawanan

dengan hal itu, integrasi Romberg mencapai hasil yang tepat (hingga tujuh angka yang signifikan) dengan menggunakan aturan trapesium bersegmen satu, dua, empat, dan delapan; yaitu, dengan pengevaluasian fungsi sebanyak 15 kali saja.

Perlu diingat bahwa integrasi Romberg dirancang untuk kasus di mana fungsi yang akan diintegrasikan sudah diketahui. Hal ini disebabkan karena pengetahuan fungsi tersebut mengijinkan pengevaluasian yang dibutuhkan untuk implementasi pertama dari aturan trapesium.

2.4. Kuadratur Gauss dan Gauss-Legendre

Kuadratur Gauss merupakan pendekatan metode numerik yang digunakan untuk mengatasi kelemahan yang dimiliki oleh persamaan Newton-Cotes, yaitu di mana persamaan Newton-Cotes ini (contoh: aturan trapesium) melakukan pendugaan terhadap suatu integral dengan berdasarkan kepada fungsi bernilai genap. Akibatnya, nilai dasar yang digunakan dalam persamaan ini sudah ditentukan sebelumnya atau bersifat tetap.

Sebagai contoh, seperti pada gambar 2.6, aturan trapesium didasarkan kepada pengambilan daerah pendugaan di bawah garis lurus yang menghubungkan nilai fungsi pada akhir interval integrasi. Rumus yang digunakan untuk menghitung area ini adalah

(

) ( ) ( )

2 b f a f a b I≅ − + Pers. (2.20)

di mana a dan b adalah batas integrasi dan b – a adalah jarak/lebar dari interval integrasi. Karena aturan trapesium harus melewati titik akhir, maka akan muncul kasus-kasus seperti gambar 2.6 di mana rumus tersebut menghasilkan error yang tinggi.

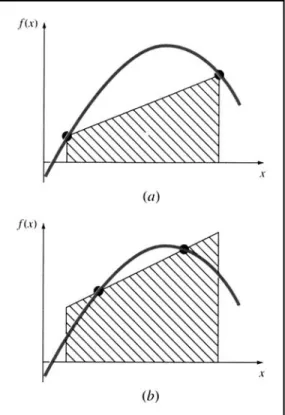
Gambar 2.6 (a) Penggambaran secara grafik dari

aturan trapesium sebagai daerah di bawah garis lurus yang menghubungkan titik-titik akhir. (b) Sebuah pendugaan integral yang lebih baik yang diperoleh dengan cara mengambil area di bawah garis lurus yang melewati dua titik yang ada di antaranya. Dengan memposisikan titik-titik tersebut dengan bijak, maka

error positif dan negatif menjadi berimbang, dan

sebuah pendugaan integral yang lebih baik akan dihasilkan.

Sekarang, seandainya halangan titik dasar yang tetap tersebut dihilangkan dan kita dengan bebas menempatkan titik-titik tersebut dengan bijak, maka kita dapat menghasilkan sebuah garis lurus yang akan menyimbangkan error positif dan negatif. Seperti gambar 2.6, kita akan melihat sebuah pendugaan integral yang telah diperbaiki.

Kuadratur Gauss adalah nama untuk sebuah teknik untuk mengimplementasikan strategi tersebut. Rumus kuadratur Gauss ini disebut rumus Gauss-Legendre. Rumus

Gauss-Legendre dikembangkan dengan menggunakan teknik yang dapat menurunkan rumus integrasi numerik seperti aturan trapesium yang menggunakan metode koefisien tak tertentu.

2.4.1. Metode Koefisien Tak Tertentu

Metode koefisien tak tertentu memberikan sebuah pendekatan yang memiliki perangkat untuk menurunkan teknik integrasi lainnya seperti kuadratur Gauss.

Gambar 2.7 Dua integral yang dievaluasi

dengan tepat oleh aturan trapesium: (a) sebuah konstan dan (b) sebuah garis lurus.

Sebagai contoh, pers. (2.20) dinyatakan sebagai

( )

a c f

( )

b

f c

I ≅ 0 + 1 Pers. (2.21)

di mana c adalah konstan. Ingat bahwa aturan trapesium akan menghasilkan hasil yang tepat ketika fungsi yang diintegrasikan adalah sebuah konstan atau garis lurus. Dua persamaan sederhana yang menggambarkan kasus tersebut adalah y =

berikut akan menjadi ( ) ( )

∫

−− = + /2 2 / 1 0 1 a b a b dx c c dan ( ) ( )

∫

−− = − + − − /2 2 / 1 0 2 2 a b a b xdx a b c a b c

atau, dengan mengevaluasikan integral,

a b c c0 + 1= − dan 0 2 2 1 0 = − + − −c b a c b a

Berikut adalah dua persamaan dengan dua variabel yang tidak diketahui yang dapat diselesaikan dengan

2 1 0 a b c c = = −

yang mana, ketika disubstitusikan kembali ke dalam pers. (2.21), sehingga memberikan

( )

a b a f

( )

b f a b I 2 2 − + − =

2.4.2. Penurunan Rumus Gauss-Legendre Dua Titik

Seperti halnya penurunan aturan trapesium di atas, tujuan kuadratur Gauss adalah untuk menentukan koefisien dari sebuah persamaan dari bentuk

( )

0 1

( )

1 0 f x c f x

c

I≅ + Pers. (2.22)

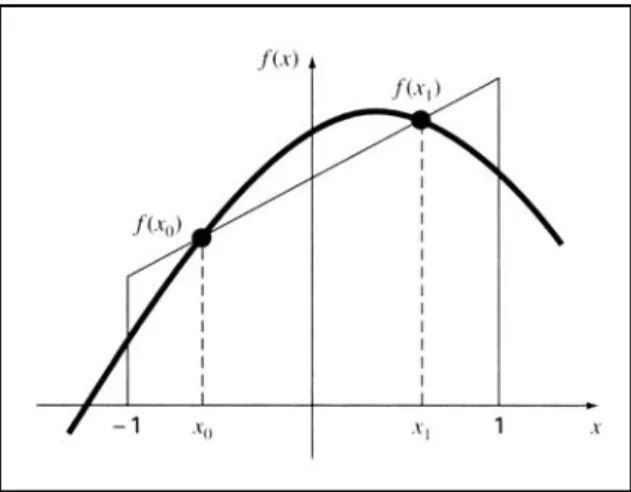
di mana c adalah koefisien yang tidak diketahui. Walau bagaimanapun, berlawanan dengan aturan trapesium yang menggunakan titik-titik akhir a dan b yang tetap, argumen fungsi x0 dan x1 yang tidak tetap pada titik akhir, namun

tidak diketahui (Gambar 2.8). Dengan demikian, kita sekarang memiliki empat variabel yang tidak diketahui yang harus dievaluasi, dan akibatnya, kita membutuhkan empat kondisi untuk menentukan variabel yang tidak diketahui tersebut secara tepat.

Gambar 2.8 Penggambaran secara grafik dari variabel x0 dan x1 untuk pengintegrasian dengan

menggunakan kuadratur Gauss

Seperti halnya aturan trapesium, kita dapat memperoleh dua dari kondisi tersebut dengan mengasumsikan bahwa pers. (2.22) cocok dengan integral dari sebuah konstan dan sebuah fungsi linier secara tepat. Kemudian, untuk sampai

pada kedua kondisi lainnya, kita hanya melanjutkan argumen ini dengan mengasumsikan bahwa kondisi ini juga cocok dengan integral dari sebuah fungsi parabolik (y = x2) dan fungsi kubik (y = x3). Dengan melakukan hal itu, kita menentukan keempat variabel yang tidak diketahui dan sebagai pertukarannya menurunkan sebuah rumus integrasi linier dua titik yang tepat untuk kubik-kubik. Keempat persamaan yang akan diselesaikan adalah

( )

( )

11 2 1 1 1 0 0f x +c f x =

∫

₋ dx= c Pers. (2.23)

( )

( )

1 0 1 1 1 0 0f x +c f x =

∫

₋ xdx= c Pers. (2.24)

( )

( )

3 2 1 1 2 1 1 0 0f x +c f x =

∫

₋ x dx= c Pers. (2.25)

( )

( )

1 0 1 3 1 1 0 0f x +c f x =

∫

₋ x dx= c Pers. (2.26)

Pers. (2.24) hingga pers. (2.26) dapat diselesaikan secara simultan dengan

1 1 0= c = c Pers. (2.27) ... 5773503 . 0 3 1 0=− =− x Pers. (2.28) ... 5773503 . 0 3 1 1= = x Pers. (2.29)

yang mana bisa disubstitusikan ke dalam pers. (2.22) untuk menghasilkan rumus Gauss-Legendre dua titik

⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ + ⎟⎟ ⎠ ⎞ ⎜⎜ ⎝ ⎛ − ≅ 3 1 3 1 f f I Pers. (2.30)

Dengan demikian, kita sampai pada hasil yang menarik bahwa penambahan yang sederhana nilai fungsi pada x=1/ 3 dan −1/ 3 menghasilkan sebuah pendugaan integral yang memiliki keakuratan ordo ketiga.

Ingat bahwa batas integrasi pada pers. (2.23) hingga (2.26) adalah dari -1 hingga 1. Hal ini dilakukan untuk menyederhanakan perhitungan dan untuk rumus tersebut seumum mungkin. Sebuah penggantian sederhana terhadap variabel dapat digunakan untuk menerjemahkan batas lainnya dari integrasi ke dalam bentuk ini. Hal ini dilakukan dengan mengasumsikan bahwa sebuah variabel baru xd dihubungkan dengan variabel asli x dengan cara yang linier,

sebagaimana dalam d x a a x= ₀+ ₁ Pers (2.31)

Jika batas bawah, x = a, sama dengan xd = -1, nilai ini dapat disubstitusikan ke

dalam pers. (2.31) untuk menghasilkan

( )

1

1 0+ − =a a

a Pers (2.32)

Dengan cara yang sama, batas atas, x = b, sama dengan xd = 1, untuk

memberikan

( )

1 1 0 a a b= + Pers (2.33)

2 0 a b a = + Pers (2.34) dan 2 1 a b a = − Pers (2.35)

yang dapat disubstitusikan ke dalam pers. (2.31) untuk menghasilkan

(

) (

)

2 d x a b a b x= + + − Pers. (2.36)

Persamaan ini dapat diturunkan untuk memberikan

d dx a b dx 2 − = Pers. (2.37)

Pers. (2.36) dan (2.37) dapat disubstitusikan untuk x dan dx, masing-masing, dalam persamaan yang akan diintegrasikan. Penyubstitusian ini secara efektif mengubah interval integrasi tanpa mengubah nilai dari integrasi tersebut.

2.4.3. Rumus dengan Jumlah Titik yang Lebih Banyak

Lebih jauh dibandingkan rumus dua titik dideskripsikan dalam subbab sebelumnya, versi jumlah titik yang lebih banyak dapat dikembangkan dalam bentuk umum

( )

_{0 1} ( ₁) ... ₁ ( ₁)

0 + + + − −

≅c f x c f x d_n f x_n

I Pers. (2.38)

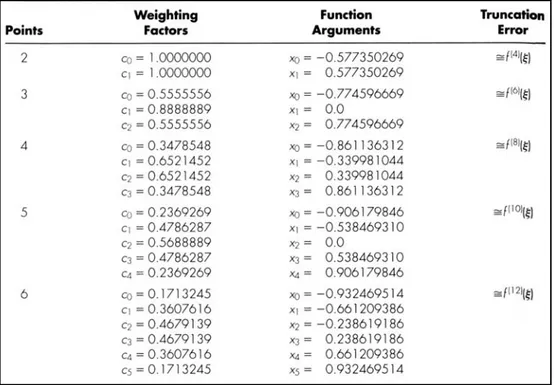
di mana n adalah jumlah dari titik. Nilai untuk c dan x untuk (≤) enam titik dirangkum dalam tabel 2.1.

Karena kuadratur Gauss memerlukan evaluasi fungsi pada titik dengan jarak yang tidak seragam pada interval integrasi, hal ini tidak ditujukan untuk kasus fungsi yang tidak diketahui. Oleh karena itu, metode ini tidak cocok untuk permasalahan teknik yang berhubungan dengan data berbentuk tabel. Bagaimanapun, ketika fungsinya diketahui, keefisienannya dapat menjadi sebuah keuntungan. Hal ini sangat benar ketika sejumlah besar evaluasi integral harus dilakukan.

Tabel 2.1 Faktor pembobot c dan argumen fungsi x yang digunakan dalam Gauss-Legendre

2.4.4. Analisis Error untuk Gauss-Legendre

Error dari rumus Gauss-Legendre dispesifikasikan secara umum oleh

(

)

[

]

(

) (

[

)

]

3 (2 2)

( )

ξ 4 3 2 ! 2 2 3 2 ! 1 2 + ₊ + + + = n n t f n n n E Pers. (2.39)

di mana n adalah jumlah titik dikurangi satu dan f(2n + 2)(ξ) adalah turunan ke (2n

+ 2) dari fungsi setelah perubahan terhadap variabel dengan ξ terletak di suatu

tempat pada interval -1 hingga 1. Perbandingan terhadap pers. (2.38) dengan tabel 2.1 menandakan kelebihan dari kuadratur Gauss dibandingkan dengan rumus Newton-Cotes, menyediakan turunan dengan ordo yang lebih tinggi yang tidak meningkat secara nyata dengan meningkatnya n.

2.5. Metode Simulasi Monte Carlo

Metode simulasi Monte Carlo merupakan sebuah kelas dari algoritma komputer untuk melakukan simulasi terhadap sifat-sifat dari sistem kefisikaan dan kematematikaan. Metode simulasi Monte Carlo sangat penting dalam perkomputasian fisika dan bidang terapan yang berhubungan. Metode ini sudah teruji dalam menyelesaikan persamaan integro-diferensial yang mendefinisikan bidang radiasi, dan metode ini telah digunakan dalam perhitungan global illumination yang menghasilkan citra yang terlihat nyata dari model buatan berdimensi tiga, untuk penerapan pada permainan video, arsitektur, desain, film yang dihasilkan dengan komputer, efek khusus dalam film, bidang bisnis, ekonomi, dan bidang lainnya. Metode ini terutama sangat berguna untuk sistem pembelajaran dengan sejumlah besar derajat bebas berpasangan, seperti cairan, material tidak teratur, dan benda padat yang berpasangan sangat kuat.

Lebih jauh, metode Monte Carlo berguna untuk memodelkan fenomena dengan ketidakpastian yang signifikan pada input, seperti penghitungan dari resiko pada bisnis.

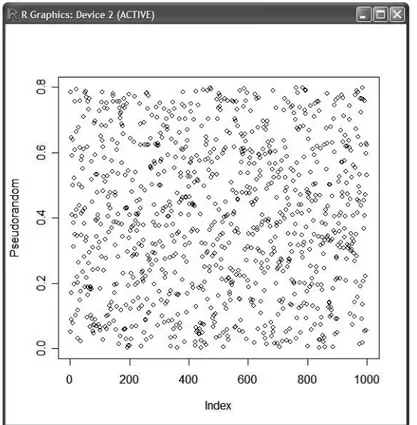
Yang menarik, metode Monte Carlo tidak memerlukan bilangan acak yang sejati agar berjalan dengan baik. Banyak dari teknik-teknik yang sangat berguna menggunakan barisan bilangan acak palsu (pseudo-random sequences) yang bersifat deterministik (tanpa keacakan), membuatnya mudah untuk diuji dan melakukan simulasi ulangan. Satu-satunya kualifikasi yang dibutuhkan untuk membuat simulasi yang baik adalah agar barisan bilangan pseudo-random itu terlihat “cukup acak” dalam beberapa hal.

Gambar 2.9 Hasil plotting menggunakan R Language terhadap 1000 bilangan pseudo-random

Proses membuat bilangan tersebut tampak acak disebut proses pseudo-random, sebuah proses yang terlihat acak tetapi tidak. Barisan pseudo-random secara khusus memperlihatkan keacakan secara statistik yang dihasilkan oleh sebuah proses komputasi yang seluruhnya bersifat deterministik/tanpa keacakan. Apa arti dari hal ini tergantung pada penerapannya, namun secara khusus hal tersebut harus melewati sebuah tes

statistik berseri. Menguji apakah bilangan-bilangan tersebut terdistribusi secara seragam atau mengikuti distribusi lainnya yang diinginkan ketika jumlah elemen yang cukup besar dari barisan tersebut dipertimbangkan, merupakan salah satu yang paling sederhana dan yang paling umum.

Sebuah algoritma Monte Carlo merupakan metode Monte Carlo yang digunakan untuk mencari solusi dari permasalahan matematik (yang mungkin memiliki banyak variabel) yang tidak mudah untuk dihitung dengan integral kalkulus atau metode numerik lainnya. Keefisienannya secara relatif meningkat dibandingkan dengan metode numerik lainnya bila dimensi dari permasalahan tersebut meningkat. Karena perulangan dari algoritma dan sejumlah besar perhitungan dilibatkan, Monte Carlo merupakan sebuah metode yang cocok untuk melakukan perhitungan dengan komputer, dengan menggunakan banyak teknik dari simulasi komputer.

Bagian ini akan menjelaskan tentang teori probabilitas di balik integrasi Monte Carlo. Oleh karena itu akan digunakan contoh hypercube C = [0,1)d dengan unit dimensi

d. Integrannya adalah sebuah fungsi f(xr ) yang diasumsikan real dan tidak negatif dan tentunya dapat diintegrasikan terhadap C. Dengan demikian akan didefinisikan sebagai berikut: ... , 3 , 2 , 1 ) ( = =

_∫

f x d x m I C d m m r r Pers (2.40)

sehingga I1 adalah integral yang dibutuhkan. Perlu diingat bahwa Im tidak selalu harus

tertentu (finite) untuk m ≥ 2. Dalam Monte Carlo, diasumsikan bahwa titik-titik integrasi sebanyak N dipilih secara bebas, dari distribusi peluang seragam terhadap C. Hal itu

berarti bahwa himpunan titik X = {xr₁,xr₂,...,xr_N} di mana integrasi didasarkan, diasumsikan menjadi sebuah anggota yang khas dari kelompok himpunan titik-titik tersebut, sedemikian rupa sehingga distribusi peluang N yang dikombinasikan menunjuk ke kelompok himpunan titik-titik tersebut bersifat seragam, bebas, dan bersitribusi identik. 1 ) , ..., , , ( _{1 2 N} = N x x x P Pers. (2.41)

Rata-rata dari kelompok himpunan di atas akan diambil, diasumsikan bahwa sebuah himpunan titik dari X telah dihasilkan, dan nilai-nilai dari integran f(xr) sudah dihitung. Hal ini dilambangkan dengan fj ≡ f(xrj), j = 1, 2 , ... , N. Dari sini kita dapat

menghitung analogi diskrit dari integral Im yang dapat dihitung dalam waktu linier:

∑

= = N j m j m f S 1 ) ( Pers. (2.42)

Penduga Monte Carlo dari integral tersebut menjadi

1 1 1 S

N

E = Pers. (2.43)

Nilai harapan E1 dari himpunan kelompok titik-titik di atas adalah

∫

∑

= = = d C d i i f x d x I f N E1 ( ) 1 1 _{r r} Pers. (2.44)

yang mana merupakan integral yang dibutuhkan. Ini adalah basis dari metode Monte Carlo. Kegunaannya terlihat jika kita menghitung ragam dari E1

) ( 1 ) ( 2 12 2 1 2 1 2 1 I I N E E E = − = − σ Pers. (2.45)

Karena nilai di atas menurun sejalan dengan N-1, metode Monte Carlo sebenarnya konvergen untuk N yang besar. Ingat bahwa O(N0), hubungan E , dan 12

2 1

E saling menghilangkan: hal ini merupakan sebuah fenomena biasa dalam pendugaan ragam jenis ini.1 Ragam σ(E₁)2 diduga dengan penduga error ordo pertama

2 1 3 2 2 2 1 1 S N S N E = − Pers. (2.46)

sehingga kita memiliki

( )

(

2

)

1 2 1 2 2 2 1 3 4 3 2 2 4 8 4 1 I I I I I I I N E = − − + − σ Pers. (2.47)

yang mana penduganya adalah

(

4

)

1 2 1 2 2 2 2 1 3 2 4 3 7 4 4 8 4 1 S S NS S N S S N S N N E = − − + − Pers. (2.48)

yang juga dapat dihitung dalam waktu linier; maka kita memiliki

( )

2

( )

4 2 4 − + = E O N E σ Pers. (2.49)

Galat dari metode Monte Carlo ini adalah

1

Perlu diketahui bahwa apa yang diduga adalah rata-rata dari squared error, bukan error itu sendiri, dan penguadratan dan perataan tidak menyebabkan perubahan. Karena itu, inilah alasan mengapa penduga berordo dua dikatakan relevan.

( )

∑

∫

− ₌ = N i i C n f x N dx x f d 1 1 ) ( ε Pers. (2.50)

Jika nilai N besar, maka

( )

( )

2 / 1 ⎥ ⎥ ⎦ ⎤ ⎢ ⎢ ⎣ ⎡ ⎟ ⎟ ⎠ ⎞ ⎜ ⎜ ⎝ ⎛ − =

_∫

f x

_∫

f x dx dx s d c C n ε Pers. (2.51)

2.6. Metode Simulasi Quasi-Monte Carlo

Dalam analisis numerik, sebuah metode quasi-Monte Carlo merupakan metode untuk perhitungan integral (atau permasalahan lainnya) yang didasarkan pada barisan bilangan dengan ketidakcocokan/ketidaksesuaian yang rendah (low-discrepancy

sequences). Hal inilah yang membedakan metode quasi-Monte Carlo dengan metode

Monte Carlo yang menggunakan barisan bilangan acak palsu (pseudo-random).

Gambar 2.10 Hasil plotting

menggunakan R Language terhadap 1000 bilangan

quasi-random menurut barisan Sobol

Monte Carlo dan quasi-Monte Carlo dinyatakan dengan cara yang sama. Masalahnya adalah untuk menduga fungsi f sebagai rataan dari fungsi yang dievaluasi pada sehimpunan titik-titik x1, ... , xN.

∫

∑

= ≈ d C N i x f N du u f 1 ) ( 1 ) ( Pers. (2.52)

di mana C adalah kubus dengan dimensi d, Cd = [0,1] x ... x [0,1]. Sehingga masing-masing xi adalah sebuah vektor dari elemen sebanyak d. Dalam metode Monte Carlo, xi

adalah bilangan-bilangan pseudo-random. Dalam metode quasi-Monte Carlo, himpunan tersebut adalah akibat dari sebuah barisan low-discrepancy atau disebut dengan bilangan

quasi-random.

Error pendugaan dari metode di atas dibatasi dengan sebuah syarat yang

proporsional terhadap ketidaksesuaian (discrepancy) dari himpunan x1, ... , xN, oleh

pertidaksamaan Koksma-Hlawka.

( )

( )

HK

( )

N

( )

N C N i N f x dx V f D x x f N d ∗ = • ≤ →

_∫

∑

1 1 Pers. (2.53)

di mana D_N∗

( )

x_N adalah discrepancy dan V_HK

( )

f adalah variasi (Hardy Krause).

Discrepancy adalah ukuran simpangan dari keseragaman suatu barisan titik-titik dalam

d

D=[0,1] . Discrepancy menyebabkan galat dalam metode quasi-Monte Carlo.

Discrepancy suatu barisan secara khusus yang digunakan untuk metode quasi-Monte

(

)

N N d

log

Pers. (2.54)

Sebagai perbandingan, dengan peluang bernilai satu, discrepancy yang diharapkan dari barisan acak seragam (seperti yang digunakan dalam metode Monte Carlo) memiliki ordo konvergensi N N 2 log log Pers. (2.55)

menurut hukum dari algoritma teriterasi.

Hal ini memperlihatkan bahwa keakuratan dari metode quasi-Monte Carlo meningkat lebih cepat dibandingkan dengan metode Monte Carlo. Walau bagaimanapun, menurut Morokoff and Caflisch (1995, p218-230), keuntungan dari quasi-Monte Carlo masih di bawah harapan dibandingkan dengan teorinya. Namun, masih menurut penelitian Morokoff and Caflisch, metode quasi-Monte Carlo dapat menghasilkan hasil yang lebih akurat dibandingkan dengan metode Monte Carlo dengan jumlah titik yang sama. Morokoff and Caflisch menambahkan bahwa keuntungan dari quasi-Monte Carlo jauh lebih baik jika integrannya halus (smooth) dan jumlah dimensi d dari integral adalah kecil.

Untuk memperjelas, katakanlah terdapat sebuah fungsi D(x) dari himpunan titik yang bertambah dengan ketidakseragamannya. D(x) = 0 terjadi jika himpunan titik tersebut seragam sempurna dalam semua pernyataan, situasi yang ideal yang tidak pernah dapat diperoleh untuk himpunan titik apapun. Metode quasi-Monte Carlo didasarkan pada penggunaan himpunan titik x yang mana D(x) memiliki beberapa nilai s

(sangat banyak) yang lebih kecil dari s , nilai yang mungkin diharapkan untuk titik yang bebas, terdistribusi identik, dan seragam yang sebenarnya.

Bagaimana menggunakan himpunan titik quasi-random setelah kita memperolehnya? Hal yang pasti adalah dengan terlebih dahulu menentukan di kelompok manakah himpunan quasi-random dari titik x menjadi anggota yang khas. Distribusi dengan banyak titik dari himpunan titik PN yang demikian tidak lagi merupakan

kesatuan yang sederhana, yang akan berarti kebebasan dari titik-titik tersebut di dalam himpunan titiknya. Karena itu, kita tulis distribusi dengan banyak titik sebagai

(

N

)

N

(

N

)

N F s x x x N x x x s P ;r₁,r₂,...,r =1− 1 ;r₁,r₂,...,r Pers. (2.56)

di mana kita telah mengantisipasi sebuah faktor 1/N sebelum korelasi dengan banyak titik FN. FN(s; ...) harus simetris total; selain itu kita harus memiliki

(

; 1, 2,...,

)

=

∫

+1

(

; 1, 2,..., , +1

)

k+1 d k k C k K k s x x x F s x x x x d x F r r r r r r r r Pers. (2.57)

Untuk memenuhi syarat minimum bahwa integral quasi-Monte Carlo haruslah tidak bias, kita harus memiliki

( )

; ₁ 1 1 s x = P r Pers. (2.58) sehingga

(

)

∫

= C d_x d x x s F₂ ;r₁,r₂ r₂ 0 Pers. (2.59)

seharusnya pendugaan yang dilakukan didasarkan. Kita akan mengindikasikan sifat alamiah quasi-Monte Carlo mengenai penduga dengan menggunakan (q). Berikut adalah penduga pertama dari integral

( )

_∑

= = N i j q _f N E 1 1 1 Pers. (2.60)

Penjumlahan akan berjalan dari 1 hingga N. Berdasarkan rataan (q) terhadap kelompok

quasi-random yang telah didiskusikan di atas, kita kemudian memiliki

( ) ( ) 1

( )

1 1 f(x)P s;x d x J E d C q q _{= =}

∫

r r r Pers. (2.61)

sebagaimana sebelumnya: berdasarkan fakta bahwa distribusi satu titik adalah seragam, pendugaan quasi-Monte Carlo memang tidak bias sebagaimana yang dimiliki oleh metode Monte Carlo. Perbedaan yang jelas antara kedua metode tersebut tampak pada pendugaan error ordo satu. Kita definisikan

(

xri,xrj

)

=1+F2

(

s;xri,xrj

)

α Pers. (2.62)

kemudian kita memiliki

( )

( )

_{( )}

(

)

⎟ ⎠ ⎞ ⎜ ⎝ ⎛ + − = ₂

_∫

_{1 2 12 2} 2 1 1 1 N O f f I N E q _{q α} σ Pers. (2.63) di mana

( ) ( ) (

)

∫

=

∫

C d d_{xd x} d x x x f x f f f1 2 12 1 2 1, 2 1 2 r r r r r r _α α Pers. (2.64) dan lainnya.

Keuntungan dari metode quasi-Monte Carlo sekarang menjadi jelas: jika kita dapat memastikan bahwa α₁₂> 1, yaitu saat xr₁ dan xr₂ “dekat” pada suatu pengertian, maka error quasi-Monte Carlo akan lebih kecil dibandingkan metode Monte Carlo. Sebuah himpunan titik quasi-Monte Carlo yang baik adalah himpunan titik yang mana setiap titiknya saling menolak untuk beberapa perluasan.

Pendugaan error ordo pertama secara sederhana

( )

_∑

_∑

= = − = N i i j ij N i i q _{f f} N f N E 1 3 1 2 2 2 1 1 _α Pers. (2.65)

Mudah untuk menunjukkan bahwa sesungguhnya

( ) ( ) ( )

( )

( ) ( 2) 2 1 2 − + = E O N E q _q q q _σ Pers. (2.66)

ragam dari penduga E2( )q dapat dievaluasi menjadi

( )

( )

q =

(

_∫

_fi −

_∫

_{fi fj ij}−

_∫

_{fi fj ij}+

_∫

_{fi fkfl ik kl} N E α α α α σ 4 3 2 2 2 3 2 2 4 4 1 +4

∫

f_i2f_kf_lα_ikα_il−4

∫

f_if_jf_kf_lα_ijα_jkα_kl

)

+O

( )

N−4 Pers. (2.67)

yang mana penduga yang bersesuaian adalah

( ) ⎜⎜ ⎝ ⎛ − − =

∑

∑

∑

= = = N i i j ij N i i j ij N i i q _{N f N f f N f f} N E 1 2 2 2 1 3 2 1 4 3 7 4 4 1 _{α α}

∑

∑

= = + + N i i k l ik il N i i k l ik kl f f f N f f f N 1 2 1 2 4 4 α α α α

_⎟⎟ ⎠ ⎞ −

∑

= N i kl jk l k j if f f f 1 4 α α Pers. (2.68)

2.6.1. Barisan Sobol (Sobol Sequence)

Barisan Sobol (Sobol sequence) dihasilkan dari sebuah himpunan bilangan pecahan biner khusus sepanjang w bit, v dengan i = 1, 2, ... , w dan j = _ij

1, 2, ... , d. Bilangan j i

v disebut direction numbers.

Untuk menghasilkan direction numbers untuk dimensi j, digunakan sebuah polinom primitif (tidak dapat disederhanakan lagi) terhadap bidang F2

dengan elemen {0, 1}. Polinom primitif tersebut dalam dimensi j akan menjadi

( )

x =x +a₁x −1+ +a ₋₁x+1

p q q _q

j K Pers. (2.69)

Direction numbers tersebut dalam dimensi j dihasilkan menggunakan

hubungan q berulang berikut

(

j q

)

q i j q i j q i q j i j i j i av a v a v v v v = _{1 −1}⊕ _{2 −2}⊕_K⊕ _{−1 − +1}⊕ ₋ ⊕ ₋ 2 Pers. (2.70)

di mana i > q. ⊕ menandakan operasi XOR. Bilangan v 2₁j⋅ w, v 2₂j⋅ w, ... , v 2_qj⋅ w masing-masing dapat berupa bilangan integer ganjil lebih kecil dari 2, 22, ... , dan

2q. Barisan Sobol x (_nj =

∑

w₌

i i i

b

n ₀ 2 , b_i∈{0, 1}) dalam dimensi j dihasilkan oleh

j w w j j j n bv b v b v x = _{1 1} ⊕ _{2 2} ⊕_K⊕ Pers. (2.71)