Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 1
DIBUAT OLEH : PAK SUKANI
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 2
Hak Cipta GO! MATEMATIKA JENIUS
Http://okemat.blogspot.com
Penulis, Pak Sukani dan Http://okemat.blogspot.com, telah mengeluarkan semua kemampuan terbaiknya untuk menciptakan produk informasi bermutu tinggi, informatif,
dan sangat membantu siswa/siswi SMA, SMK dan MA kelas X, XI IPA/IPS, dan XII IPA/IPS yang ingin sukses dan mendapatkan nilai tertinggi pada pelajaran Matematika di
Ulangan Harian, Ulangan Semesteran, Ujian Nasional (UN), SPMB dan Ujian Mandiri Universitas Negeri atau Swasta, atau bahkan guru mata pelajaran matematika yang ingin
lebih professional.
Ebooks ini di publikasikan secara resmi oleh Http://okemat.blogspot.com. Semua teks dan grafis yang ada di dalamnya merupakan hak cipta Http://okemat.blogspot.com. Ebook yang telah publikasikan ini boleh digandakan, disebarkan, atau direproduksi dengan cara apapun juga, termasuk mengcopy dan mencetaknya dengan ijin tertulis dari penulis.
GO! MATEMATIKA JENIUS
Http://okemat.blogspot.com
Hak Cipta Dilindungi Allah SWT
Ebooks ini GRATIS untuk Guru-Guru Indonesia..!!!
Saya Persembahkan Untuk GURARU
Salam Sukses,
Pak Sukani
Http://okemat.blogspot.com
Email : likeny_rbg@yahoo.com HP : 085695685815
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 3
”Terimakasih untuk istriku tercinta, Ela Lisnawati ... Karena doronganmu, karya besar ini bisa selesai tepat waktu”.
Pak Sukani
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 4
DAFTAR ISI
GO! MATEMATIKA JENIUS
1. Operasi Bilangan Real 2. Aproksimasi Kesalahan
3. Persamaan dan Pertidaksamaan Linear 4. Persamaan dan Pertidaksamaan Kuadrat 5. Matriks
6. Program Linear 7. Logika Matematika 8. Trigonometri 9. Relasi dan Fungsi
10. Sigma, Barisan dan Deret 11. Geometri Dimensi Dua 12. Geometri Dimensi Tiga 13. Vektor
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 5
OPERASI BILANGAN REAL
SIFAT-SIFAT OPERASI BILANGAN REAL
PERBANDINGAN
Ada dua jenis perbandingan, yaitu :
Untuk menyelesaikan permasalahan perbandingan caranya adalah :
d c b a
→ a =
d c . b
; b = c
d . a
; c = b
d . a
; d = a
c . b 1. Perbandingan senilai :
2 1
2 1
y y x x
2. Perbandingan berbalik :
1 2
2 1
y y x x
1. Komutatif
a + b = b + a (komutatif terhadap penjumlahan) a x b = b x a (komutatif terhadap perkalian) 2. Asosiatif
a + (b + c) = (a + b) + c (asosiatif terhadap penjumlahan) a x (b x c) = (a x b) x c (asosiatif terhadap perkalian) 3. Distributif
a x (b + c) = (a x b) + (a x c) (distributif terhadap penjumlahan) a x (b – c) = (a x b) – (a x c) (distributif terhadap pengurangan) 4. Identitas
a + 0 = 0 + a = a (0 = identitas penjumlahan) a x 1 = 1 x a = a (1 = identitas perkalian) 5. Invers
a + (–a) = –a + a = 0 (–a, invers penjumlahan dari a)
a x a 1
= a 1
x a = 1 (
a 1
, invers perkalian dari a)
6. Jika a > b, maka a + b > b + c
7. Jika c > 0 dan a > b, maka a x c > b x c 8. Jika c < 0 dan a > b, maka a x c < b x c
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 6 Laba = Harga Jual – Harga Beli
Rugi = Harga Beli – Harga Jual
Persentase keuntungan = x 100%
beli harga
beli harga -jual harga
Persentase kerugian = x 100%
beli harga
jual harga -beli harga
Harga beli Untung =
untung) %
1 (
untung jual
harga
Harga beli Rugi =
rugi) % 1 (
rugi jual harga
a
n. a
m= a
n + m , jika a 0 contoh : 52 . 56 = 58a
n: a
m= a
n – m , jika a 0 contoh : 37 : 32 = 35a
n. b
n= (a . b)
n contoh : 32 . 52 = (3 . 5)2 = 152
a
n: b
n= (a : b)
n contoh : 83 : 23 = (8 : 2)3 = 43
(a
m)
n= a
m . n contoh : (52)4 = 58n n
a
a 1
, jika a
0
contoh : 5-2 =25 1 5
1
2
SKALA
Sebenarnya Jarak
Gambar Pada
Jarak
Skala
Jarak pada gambar = skala x Jarak sebenarnya
Jarak sebenarnya =
Skala
Gambar Pada
Jarak
PERHITUNGAN UNTUNG RUGI
EKSPONEN (PANGKAT)
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 7
AKAR
LOGARITMA
Konsep dasar : ; dimana a > 0 ; y > 0 dan a ≠1
Contoh: 32= 9 ↔ 3log 9 = 2 Sifat-Sifat :
LOGARITMA BIASA
Logaritma biasa adalah logaritma yang bilangan pokoknya 10 dan biasanya tidak perlu ditulis. misalnya : 10log 5 ditulis log 5
Contoh : log 10 = 1
ab = c ↔ alog c = b
n
b
.
a
b
.
a
n
n
contoh :
2
.
8
16
4
n n n b a b :
a contoh :
27
:
3
9
3
n m
n m
a
a contoh : 3 2 3 2 5 5 a c b a c a
b
(
)
contoh :3
7
2
7
5
3
b b a b b a b b . b a b a
contoh : 5
5 3 5 5 3 5 5 . 5 3 5 3 b a b a = b a b a . b a b a = b a ab b a 2
1. alog a = 1 contoh : 2log 2 = 1
2. alog an = n contoh : 2log 16 = 2log 24 = 4 2log 2 = 4 3. alog 1 = 0 contoh : 7log 1 = 7log 50 = 0
4. log an = n log a contoh : log 8 = log 23 = 3 . log 2 5. alog n
a 1
= - n contoh : 3log 9 1
= 3log 2 3
1
= 3log 3-2 = -2
6. alogan
1
-n contoh : 1/3log 9 = 1/3log 3 = -2 2
7. alog b = a log
b log
contoh : 2 log
16 log
= 2log 16 = 2log 24 = 4
8. glog a + glog b = glog a x b contoh : 6log 4 + 6log 9 = 6log 36 = 6log 62 = 2 9. d c log d log - c
log g g
g
contoh : 3log 18 –3log 2 = 3log 2 18
= 3log 9 = 3 10. log a + log b = log(axb) contoh : log 2 + log 5 = log (2x5) = log 10 = 1 11. alog b . blog c . clog d = alog d contoh : 2log 7 . 7log 4 . 4log 8 = 2log 8 = 3 12. anlogbm =
n m
. alog b contoh : 9log 25 = 32
log
5
2 = 2 2Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 8
APROKSIMASI KESALAHAN
a. Kesalahan Pengukuran
Kesalahan pengukuran adalah merupakan penyimpangan pada hasil pengukuran. b. Satuan Pengukuran Terkecil (SPT)
Satuan pengukuran terkecil adalah tingkat ketelitian dalam pengukuran. c. Salah Mutlak (SM)
Salah mutlak dari suatu pengukuran adalah kesalahan terbesar yang mungkin timbul dalam pengukuran. Salah mutlak besarnya adalah setengah dari satuan pengukuran terkecil.
d. Salah Relatif (SR)
Salah relatif adalah perbandingan antara salah mutlak dengan hasil pengukuran.
e. Persentase Kesalahan
Persentase kesalahan adalah salah relatif yang dinyatakan dalam bentuk persen.
f. Toleransi
Toleransi adalah selisih antara ukuran terbesar dan ukuran terkecil yang masih dapat diterima.
g. Ukuran Maksimum
Ukuran maksimum adalah ukuran nominal hasil pengukuran ditambah salah mutlak. h. Ukuran Minimum
Ukuran minimum adalah ukuran nominal hasil pengukuran dikurangi salah mutlak. i. Selisih Maksimum
Selisih maksimum = ukuran maksimum – ukuran minimum j. Selisih Minimum
Selisih minimum = ukuran minimum – ukuran maksimum k. Hasil Kali Maksimum
Hasil kali maksimum dari dua hasil pengukuran adalah sama dengan perkalian ukuran maksimum dari masing-masing pengukuran
l. Hasil Kali Minimum
Hasil kali minimum dari dua hasil pengukuran adalah sama dengan perkalian ukuran minimum dari masing-masing pengukuran
SM =
2 1
SPT
SR =
(HP) pengukuran hasil
(SM) mutlak salah
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 9
PERSAMAAN DAN PERTIDAKSAMAAN
LINEAR
Persamaan linear adalah suatu kalimat terbuka yang variabelnya berderajat satu dengan menggunakan tanda penghubung "sama dengan" ( = ).
Pertidaksamaan linear adalah suatu kalimat terbuka yang variabelnya berderajat satu dengan
menggunakan tanda panghubung > (lebih besar), < (lebih kecil), ≥ (lebih besar sama dengan),
≤ (lebih kecil sama dengan).
a. Persamaan dan Pertidaksamaan linear dengan satu variabel
Contoh :
1. x + 2 = 10 6. -2x < 10
Maka x = 10 – 2 = 8 Maka x > 10 : -2 2. x – 2 = 10 x > -5 Maka x = 10 + 2 = 12 7. 8 + 2x ≤ 12 + 6x 3. 2x = 10 2x - 6x ≤ 12 - 8 Maka x = 10 : 2 = 5 -4x ≤ 4
4. 5x + 2 = 12 x ≥ 4 : -4
5x = 12 – 2 x ≥ -1 5x = 10
x = 10 : 5 = 2 5. 2x < 10
Maka x < 10 : 2 → x < 5
b. Menyelesaikan persamaan linear dengan dua variabel Bentuk umum :
Cara penyelesaian dengan 3 cara yaitu subsitusi, eliminasi, dan determinan. 1. Substitusi
Nyatakan salah satu variabel dalam variabel yang lain dari salah satu persamaan Substitusikan hasil dari langkah pertama ke persamaan yang lainnya.
2. Eliminasi
Jika yang ditanyakan x maka yang harus dihilangkan y. Jika yang ditanyakan y maka yang harus dihilangkan x 3. Determinan
ax + by + c = 0 px + qy + r = 0
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 10 Untuk menyelesaikan persamaan linear dengan determinan, persamaannya diubah dulu dalam bentuk matriks.
c. Menyelesaiakan persamaan linear dengan tiga variabel Ada dua cara, yaitu :
1. Gabungan Eliminasi dan Substitusi 2. Cara Determinan
3 3 3 3 2 2 2 2 1 1 1 1 d z c y b x a d z c y b x a d z c y b x a 3 3 3 2 2 2 1 1 1 b a b a b a c c c . z y x = 3 2 1 d d d
Selanjutnya diberi notasi : D, Dx, Dy, dan Dz
D = 3 3 3 2 2 2 1 1 1 b a b a b a c c c
; Dx =
3 3 3 2 2 2 1 1 1 b d b d b d c c c
; Dy =
3 3 3 2 2 2 1 1 1 d a d a d a c c c
; Dz =
3 3 3 2 2 2 1 1 1 d b a d b a d b a
Nilai x = D Dx
; y = D Dy
; dan z = D Dz
Cara untuk mencari determinan dengan menggunakan cara Sarrus, yaitu : - - - D = 3 3 2 2 1 1 3 3 3 2 2 2 1 1 1 b a b a b a c b a c b a c b a + + +
D = (a1 . b2 . c3 + b1 . c2 . a3 + c3 . a2 . b3) – (a3 . b2 . c1 + b3 . c2 . a1 + c3 . a2 . b1) q p y x . d c b a q dx cx p bx ax
Maka nilai x dan y didapat dari :
x = D Dx
dan y = D Dy
dimana : D = d c
b a
= a . d – c . b
Dx = d q
b p
= p . d – q . b
Dy = q c
p a
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 11
PERSAMAAN DAN PERTIDAKSAMAAN
KUADRAT
Bentuk umum persamaan kuadrat : ax2 + bx + c = 0 Menentukan akar-akar persamaan kuadrat
Sifat-sifat persamaan kuadrat Pada rumus abc : x1,2 =
2a ac 4 -b b
- 2
b2– 4ac disebut diskriminan dan disingkat D
Akar-akar persamaan kuadrat dapat ditentukan dari diskriminan :
* jika D > 0, maka persamaan kuadrat mempunyai akar-akar nyata dan beda (x1 x2) * jika D = 0, maka persamaan kuadrat mempunyai dua akar sama dan nyata (x1 = x2) * jika D < 0, maka persamaan kuadrat mempunyai akar yang kompleks (tidak nyata)
Sifat-sifat :
x1 + x2 = a b
dan x1 . x2 = a c
(x1 + x2)2 = ( a b
)2
x12 + x22 = ( a b
)2– 2
a c
1
x 1
+
2
x 1
= c b
x1 – x2 = a
D
D = b2 - 4.a.c 1. Memfaktorkan : (x – x1) . (x – x2) = 0 2. Melengkapi kuadrat
Bentuk : ax2 + bx + c = 0 diubah ke bentuk : (x + p)2 = q ; q > 0 Syarat : a = 1 dan p =
2 b
3. Rumus abc : x1,2 =
2a ac 4 -b b
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 12 Hubungan antara sifat akar dan koefisien persamaan :
Pertidaksamaan adalah kalimat terbuka dengan menggunakan penghubung < , > , ≤ , ≥. Cara menyelesaiakannya sama dengan persamaan kuadrat yaitu dengan memfaktorkan.
Untuk soal dengan < atau ≤, kata hubung "dan". HP : { x … ≤ x ≤ … } Untuk soal dengan > atau ≥, kata hubung "atau". HP : { x x ≤ … atau x ≥ … }
1. Menyusun persamaan kuadrat dengan akar-akar diketahui Jika akar-akar dari persamaan kuadrat adalah x1dan x2 , maka : Persamaan kuadrat = atau
Dimana : x1 + x2 = – a b
dan x1 . x2 = a c
2. Menyusun persamaan kuadrat berdasarkan akar-akar persamaan kuadrat lain Akar-akar dari persamaan kuadrat : ax2 + bx + c = 0 adalah x1 dan x2.
Persamaan kuadrat baru yang akar-akarnya : px1 dan px2 adalah :
Persamaan kuadrat baru yang akar-akarnya : px1– q dan px2– q adalah :
Persamaan kuadrat baru yang akar-akarnya :
1
x 1
dan
2
x 1
adalah :
(x – x1) . (x – x2) = 0 x2– (x1 + x2) x + x1 . x2 = 0
a ( p x
)2 + b ( p x
) + c = 0
a ( p
q x
)2 + b ( p
q x
) + c =
ax2 + bx + c = 0 cx2 + bx + a = 0 ax2– bx + c = 0 cx2– bx + a = 0 ax2– bx – c = 0 cx2 + bx – a = 0 ax2 + bx – c = 0 cx2– bx – a = 0
a. b = 0 kedua akarnya berlawanan (x1 = -x2) b. a = c kedua akarnya berkebalikan (x1 =
2
x 1
)
c. c = 0 sebuah akarnya (x1 = 0 dan x2 = a b
)
d. x1 = x2 = 2a
b
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 13
MATRIKS
A. Pengertian matriks
Matriks adalah kumpulan bilangan-bilangan yang disusun berdasarkan baris dan kolom sehingga berbentuk persegi panjang dan ditulis antara sepasang tanda kurung.
Contoh :
A = 4 3 2 1 2 ke baris 1 ke baris
kolom ke 2 kolom ke 1 Dan biasanya ditulis :
A =
22 21 12 11 a a a a 2 kolom 2 baris pada elemen a ; 1 kolom 2 baris pada elemen a 2 kolom 1 baris pada elemen a ; 1 kolom 1 baris pada elemen a 22 21 12 11
Untuk menyatakan banyaknya baris dan kolom disebut dengan ordo.
Jika matriks mempunyai baris 3 dan kolom 2, maka matriks tersebut berordo (3 x 2).
B. Macam-macam matriks
1. Matriks baris, yaitu matriks yang hanya mempunyai satu baris. Contoh : A = (1 2 3)
2. Matriks kolom, yaitu matriks yang hanya mempunyai satu kolom.
Contoh : A =
5 4 3
3. Matriks bujur sangkar, yaitu matriks yang mempunyai baris dan kolom sama
Contoh : A =
7 1 0 4 3 4 1 5 2
4. Matriks Identitas, yaitu matriks bujur sangkar yang semua elemen pada diagonal utamanya 1 sedangkan yang lainnya 0.
Contoh : I =
1 0 0 0 1 0 0 0 1
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 14 Contoh : A =
9 6 3 8 5 2 7 4 1 → 9 8 7 6 5 4 3 2 1 At
C. Kesamaan dua matriks
Apabila dua matriks mempunyai ordo sama dan elemen-elemen yang bersesuaian juga sama, maka kedua matriks tersebut dikatakan sama dan dinyatakan dengan A = B.
D. Penjumlahan dan pengurangan matriks.
Dua matriks atau lebih dapat dijumlahkan atau dikurangkan jika ordonya sama.
E. Perkalian Matriks
Sifat-sifat operasi perkalian matriks :
F. Perkalian Matriks dengan skalar
G. Perkalian Matriks dengan Matriks
Dua matriks dapat dikalikan jika jumlah kolom matriks pertama (depan) sama dengan jumlah baris matriks kedua (belakang).
Caranya : Baris kali kolom
Elemen-elemen hasil kali diperoleh dengan menjumlahkan hasil kali elemen pada baris matriks pertama (depan) dengan elemen pada kolom matriks kedua (belakang).
1. (A . B) . C = A . (B . C) → asosiatif 2. A . (B + C) = A . B + A . C → distributif
3. A . B ≠ B . A → tidak komunikatif
4. k . (A . B) = (k . A) . B = A . (k . B) → k = bilangan real 5. A . I = I . A = A → I = matriks identitas 6. A . A-1 = A-1 . A = I → A-1 = matriks invers
Jika matriks A =
22 21 12 11 a a a a
dan k adalah slakar, maka :
k . A = k .
22 21 12 11 a a a a = 22 21 12 11 a . k a . k a . k a . k A = 22 21 12 11 a a a a
; B =
22 21 12 11 b b b b
C = A + B =
22 21 12 11 a a a a + 22 21 12 11 b b b b = 22 22 21 21 12 12 11 11 b a b a b a b a
D = A – B = A + (-B) =
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 15 A(p x q) dan B(q x r) , maka A x B ordonya adalah (p x r)
Misal : matriks pertama berordo (3 x 2) dan matriks kedua berordo (2 x 4), maka jika dikalikan akan menghasilkan matriks baru yang berordo (3 x 4)
H. Determinan
Determinan adalah nilai dari suatu matriks, dan syaratnya harus matriks bujur sangkar. a. Ordo (2 x 2)
Contoh : A = 4 3 1 2
→ det A = 2 . 4 – 3 . (-1) = 8 + 3 = 11
b. Ordo (3 x 3)
Untuk matriks bujur sangkar berordo (3 x 3), determinan dapat dihitung dengan dua cara, yaitu :
1. Cara Kofaktor
Tanda untuk kofaktor :
A =
a11 (+) ; a12 (–) ; a13 (+) ; a21 (–) ; a22 (+) ; a23 (–) ; a31 (+) ; a32 (–) ; a33 (+) ;
2. Cara Sarrus
Kolom 1 dan 2 ditambahkan kebelakang menjadi kolom 4 dan 5, kemudian dikalikan secara diagonal dengan diagonal kebawah bertanda positif dan diagonal keatas bertanda negatif. A = 22 21 12 11 a a a a
maka det A = a11 . a22– a21 . a12
A = 33 32 31 23 22 21 13 12 11 a a a a a a a a a
= a11 (a22.a33– a32.a23) – a12 (a21.a33– a31.a23) + a13 (a21.a32– a31.a22) A = 22 21 12 11 a a a a
; B =
22 21 12 11 b b b b
; maka C = A x B =
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 16
I. Matriks Invers
Jika A dan B adalah matriks bujur sangkar yang ordonya sama sehingga A . B = B . A = I, maka B adalah invers A dan A adalah invers B.
Dalam hal ini yang akan dibahas adalah matriks yang ordonya (2 x 2)
A-1 = A det. A Adj A = 22 21 12 11 a a a a
Adj A =
11 21 12 22 a a -a -a
Invers matriks A adalah A-1 =
12 21 22
11. .
1 a a a
a
11 21 12 22 a a -a -a - - - A = 33 32 31 23 22 21 13 12 11 a a a a a a a a a
det A =
33 32 31 23 22 21 13 12 11 a a a a a a a a a 32 31 22 21 12 11 a a a a a a + + +
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 17
PROGRAM LINEAR
Program linear adalah suatu cara penyelesaian masalah dengan menggunakan konsep pertidaksamaan linier. Petidaksamaan linear adalah kalimat terbuka yang menggunakan tanda <, >, ≤, dan ≥.
Membuat grafik himpunan penyelesaian
Harus diperhatikan hal-hal adalah sebagai berikut :
Menentukan nilai optimum sistem pertidaksamaan linier
Menentukan nilai maksimum atau minimum dapat dilakukan dengan mencari dulu nilai x dan y sebagai variabel bebas dengan cara eliminasi atau substitusi. Kemudian nilai x dan y disubstitusikan ke fungsi objektif.
Bentuk umum fungsi obyektif : Contoh :
1)
Nilai maksimum fungsi obyektif k = 5x + 4y adalah….
Jawab :
Persamaan garis yang melewati (0,6) dan (6,0) yaitu 6x + 6y = 36 maka x + y = 6
Persamaan garis yang melewati (0,4) dan (8,0) yaitu 4x + 8y = 32 maka x + 2y = 8 Mencari titik perpotongan dengan cara Eliminasi kedua persamaan :
x + 2y = 8 x + y = 6 -
y = 2 maka x = 4
Titik perpotongannya adalah (4,2)
Maka nilai maksimum : (4,2)→ k = 5x + 4y = 5.4 + 4.2 = 28 k = ax + by
1. Untuk tanda pertidaksamaan (< atau ) arah arsirannya ke dalam dan daerah penyelesaiannya adalah daerah yang terarsir.
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 18
LOGIKA MATEMATIKA
1. Kalimat pernyataan
Kalimat pernyataan adalah kalimat yang hanya benar saja atau salah saja, akan tetapi tidak sekaligus benar dan salah.
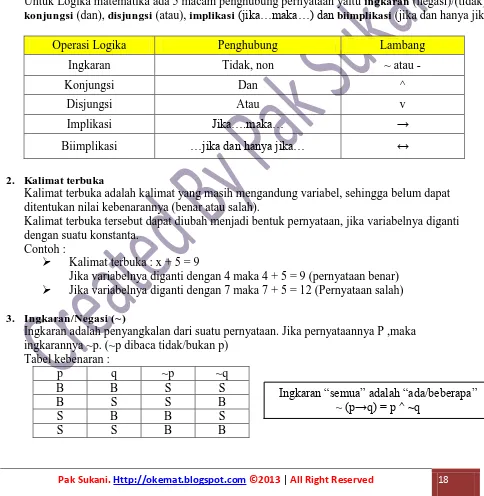
Untuk Logika matematika ada 5 macam penghubung pernyataan yaitu ingkaran (negasi)/(tidak), konjungsi(dan), disjungsi (atau), implikasi(jika…maka…) dan biimplikasi (jika dan hanya jika).
Operasi Logika Penghubung Lambang
Ingkaran Tidak, non ~ atau -
Konjungsi Dan ^
Disjungsi Atau v
Implikasi Jika….maka… →
Biimplikasi …jika dan hanya jika… ↔
2. Kalimat terbuka
Kalimat terbuka adalah kalimat yang masih mengandung variabel, sehingga belum dapat ditentukan nilai kebenarannya (benar atau salah).
Kalimat terbuka tersebut dapat diubah menjadi bentuk pernyataan, jika variabelnya diganti dengan suatu konstanta.
Contoh :
Kalimat terbuka : x + 5 = 9
Jika variabelnya diganti dengan 4 maka 4 + 5 = 9 (pernyataan benar)
Jika variabelnya diganti dengan 7 maka 7 + 5 = 12 (Pernyataan salah)
3. Ingkaran/Negasi (~)
Ingkaran adalah penyangkalan dari suatu pernyataan. Jika pernyataannya P ,maka ingkarannya ~p. (~p dibaca tidak/bukan p)
Tabel kebenaran :
p q ~p ~q
B B S S
B S S B
S B B S
S S B B
Ingkaran “semua” adalah “ada/beberapa”
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 19
4. Operasi pada logika matematika a. Konjungsi (p ^ q)
Operasi konjungsi merupakan operasi biner (operasi yang dikenakan pada dua
pernyataan) yang dilambangkan dengan tanda “ ^ ”.
Dengan operasi ini dua pernyataan dihubungkan dengan kata “ dan “.
Tabel kebenaran :
P Q p q
B B B
B S S
S B S
S S S
b. Disjungsi (p v q)
Operasi disjungsi merupakan operasi biner yang dilambangkan dengan tanda ” v ”. Operasi ini menggabungkan dua pernyataan menjadi satu dengan kata hubungan “atau”.
Tabel kebenaran :
P Q p q
B B B
B S B
S B B
S S S
c. Implikasi (p→q)
Operasi implikasi (kondisional) adalah operasi penggabungan dua pernyataan yang
menggunakan kata hubung “ jika …maka ….” Implikasi dilambangkan dengan “→“.
Syarat:
Tabel kebenaran :
P Q p q
B B B
B S S
S B B
S S B
d. Biimplikasi (p↔q)
Syarat : Kalau ada S → pasti SALAH!
Syarat : Kalau ada B → pasti BENAR!
Jika komponennya sama maka pasti BENAR!
Jika komponennya tidak sama maka lihat ujungnya: Jika ujungnya B, maka pasti BENAR!
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 20
Biimplikasi yaitu pernyataan majemuk yang menggunakan kata hubung “…jika dan
hanya jika ….” dinotasikan “↔” .
Syarat:
Tabel kebenaran :
P Q p q
B B B
B S S
S B S
S S B
5. Konvers, Invers,Kontraposisi
6. Negasi Pernyataan Majemuk
7. Penarikan Kesimpulan a. Modus Ponens :
Modus ponens dapat juga dirumuskan dengan : {(p q) p} q b. Modus Tallens :
Modus Tallens dapat juga dirumuskan dengan : {(p q) ~q} ~p
Jika komponennya sama maka pasti BENAR!
Jika komponennya tidak sama maka pasti SALAH!
Pernyataan : P Q (jika P maka Q) Konvers : Q P (jika Q maka P)
Invers : ~P ~Q (jika bukan P maka bukan Q) Kontraposisi : ~Q ~P (jika bukan Q maka bukan P) Ingkaran : P ~Q (P dan bukan Q)
Negasi dari Konjungsi : ~ (p q) = ~p ~q Negasi dari Disjungsi : ~ (p q) = ~p ~q Negasi dari Implikasi : ~ (p q) = = p ~q
Negasi Biimplikasi : ~ (p q) = ~p q = p ~q
Premis 1 : p q (dibaca jika p maka q) benar Premis 2 : p benar
Kesimpulan : q benar
Premis 1 : p q (dibaca jika p maka q) benar Premis 2 : q salah (~q)
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 21
c. Silogisme :
8. Kalimat berkuantor
Pernyataan atau kalimat yang menggunakan kata-kata kuantor dinamakan kalimat berkuantor.
Pernyataan berkuantor biasanya menggunakan : 1. " Semua " yang artinya setiap
2. " Beberapa " atau " ada " yang artinya sekurang-kurangnya 3. " Tidak ada " yang artinya semua tidak
Premis 1 : p p (dibaca jika p maka q) Premis 2 : q r (dibaca jika q maka r) Kesimpulan : p r (dibaca jika p maka r)
Ingkaran kalimat berkuantor :
Semua p adalah q ingkarannya : Beberapa p bukan q atau ada p yang bukan q Beberapa p adalah q ingkarannya : Semua p bukan q
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 22 a b c α
TRIGONOMETRI
1. Rumus Trigonometri untuk segitiga siku-siku sin = miring sisi depan sisi
sin = c a
; cosec =
depan sisi
miring sisi
cosec = a c cos = miring sisi dekat sisi
cos = c b
; sec =
dekat sisi
miring sisi
sec = b c tg = dekat sisi depan sisi
tg = b a
; cotg =
depan sisi
dekat sisi
cotg = a b
2. Tabel Trigonometri
00 15o 300 450 600 75o 900
Sinus 0 ( 6 2)
4 1 2 1 2 2 1 3 2 1 ) 2 6 ( 4 1 1
Cosinus 1 ( 6 2) 4 1 3 2 1 2 2 1 2 1 ) 2 6 ( 4 1 0
Tangens 0
2
3
33 1
1
3
2
3
∞Cotangens ∞
2
3
3
1 33 1
3
2
0Catatan : tabel diatas untuk sudut 0o s.d. 90o (kuadran I)
2. Rumus Perbandingan Trigonometri sudut berelasi a. Di Kuadran I (00 - 900)
Di kuadran I semua bernilai positif
sin α = cos (900
- α0) Contoh: sin 300 = cos (900 - 300) = cos 600 = 1/2
cos α = sin (900
- α 0) Contoh: cos 600 = sin (900 - 600) = sin 300 = 2 1
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 23
b. Di Kuadran II (900 - 1800)
Di kuadran II yang positif adalah sin
c. Di Kuadran III (1800 - 2700)
Di kuadran III yang positif adalah tan
d. Di Kuadran IV(2700 - 3600)
Di kuadran IV yang positif adalah cos
e. Relasi antara sudut dan (-)
3. Koordinat Kartesius dan Koordinat Kutub P (x , y) P (r , )
y P cos = r x
x = r . cos
r y sin = r y
y = r . sin
x r = x2
y2 dan tg = x yx
Hubungan Perbandingan Trigonometri suatu sudut
sin α = sin (1800
- α 0) Contoh: sin 1200 = sin (1800 - 120 0) = sin 600 = 3 2 1
cos α = -cos (1800 - α 0) Contoh: cos 1500 = -cos (1800 - 150 0) = -cos 300 = - 3 2 1
tan α = -tan (1800 - α 0) Contoh: tan 1350 = -tan (1800 - 1350) = -tan 450 = -1
sin α = -sin (1800+ α 0) Contoh: sin 2250 = -sin (1800 + 450) = -sin 450 = - 2 2 1
cos α = -cos (1800+ α 0) Contoh: cos 2400 = -cos (1800 + 600) = -cos 600 = -1/2
tan α = tan (1800+ α 0) Contoh: tan 2100 = tan (1800 + 300) = tan 300 = 3 3 1
sin α = -sin (3600 - α 0) Contoh: sin 3000 = -sin (3600 - 3000) = -sin 600 = - 3 2 1
cos α = cos (3600
- α 0) Contoh: cos 3300 = cos (3600 - 3300) = cos 300 = 3 2 1
tan α = -tan (3600 - α 0) Contoh: tan 3150 = -tan (3600 - 315 0) = -tan 450 = - 1
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 24 Menurut dalil Phytagoras : Kuadrat sisi miring sama dengan jumlah kuadrat sisi siku-sikunya.
y r2 = x2 + y2
r2 = (r . cos )2 + (r . sin )2 r2 = r2 . cos2θ + r2 . sin2θ r y r2 = r2 . (cos2θ + sin2θ)
θ cos2θ + sin2θ = 1
x Jadi : sin2θ + cos2θ = 1 x
Dari Koordinat Kartesius :
tg θ =
cos . r
sin . r x y
cotg θ =
tg 1
=
cos sin
1
Dari rumus dalil Phytagoras didapat perbandingan antara sisi siku-siku dan sisi miring. a. Aturan Sinus :
sinc sin
b sin
a
b a c
b. Aturan cosinus :
a2 = b2 + c2– 2bc cos atau cos =
bc 2
a c
b2 2 2
b a b2 = a2 + c2– 2ac cos atau cos =
ac 2
b c
a2 2 2
c c2 = a2 + b2– 2ab cos atau cos =
ab 2
c b
a2 2 2
Menentukan Luas Segitiga a. Segitiga siku-siku :
t
a
tg θ =
cos sin
cotg θ =
sin cos
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 25 b. Segitiga sama sisi :
t
a
c. Segitiga dengan sudut apit diketahui
b t c
a
Rumus Jumlah dan Selisih dua sudut
sin ( + ) = sin . cos + cos . sin sin ( - ) = sin . cos - cos . sin cos ( + ) = cos . cos - sin . sin cos ( - ) = cos . cos + sin . sin
tg ( + ) =
tan . tan 1
tan ta
tg ( - ) =
tg . tg 1
tg tg
Rumus sudut rangkap
Rumus jumlah dan selisih
Luas = ½ alas x tinngi L = ½ . a . t
t = a2 (21a)2
Luas = ½ alas x tinggi L = ½ . a . b . sin
1) sin 2 = 2 sin . cos
2) cos 2 = cos2 - sin2 3) cos 2 = 2 cos2 - 1 4) cos 2 = 1 – 2 sin2 5) tg 2 =
α
tg 1
α
tg 2
2
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 26 1. six x = a, ditulis dalam bentuk : sin x = sin
x = + k . 360o atau x = (180o–) + k . 360o 2. cos x = a, ditulis dalam bentuk : cos x = cos
x = + k . 360o atau x = – + k . 360o
3. tg x = a, ditulis dalam bentuk : tg x = tg → x = + k . 180o sin + sin = 2 . sin
2 1
( + ) . cos 2 1
( - )
sin - sin = 2 . cos 2 1
( + ) . sin 2 1
( - )
cos + cos = 2 . cos 2 1
( + ) . cos 2 1
( - )
cos - cos = - 2 . sin 2 1
( + ) . sin 2 1
( - )
Rumus Perkalian sin . sin =
2 1
{ cos ( - ) – cos ( + )
cos . cos = 2 1
{ cos ( + ) + cos ( - )
cos . sin = 2 1
{ sin ( + ) – sin ( - )
sin . cos = 2 1
{sin ( + ) + sin ( - )
Persamaan Trigonometri
a. Bentuk : sin x = a, cos x = a dan tg x = a pada (0o≤ x ≤ 360o)
b. Bentuk : a cos x + b sin x = c
Persamaan trigonometri bentuk a cos x + b sin x = c diubah menjadi :
r cos (x –) = c dengan r = a2 b2 dan tg = a b
c. Bentuk : sin (x + ) ± sin (x –) = c dan cos (x + ) ± cos (x –) = c Rumus yang digunakan :
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 27
RELASI DAN FUNGSI
1. Pengertian fungsi, daerah asal, daerah kawan dan daerah hasil
Fungsi atau pemetaan dari A ke B adalah suatu relasi khusus yang menghubungkan setiap anggota A dengan tepat satu anggota B.
A B
a 1
b 2 c 3 d 4
5
2. Menyatakan sebuah fungsi
Fungsi dapat dinyatakan dengan notasi, diagram panah, grafik Cartesius dan himpunan pasangan berurutan.
FUNGSI LINEAR
1. Grafik fungsi linear
Bentuk umum grafik fungsi linear adalah :
Gradien
Gradien adalah angka kemiringan dari grafik terhadap sumbu x positif. Notasi gradien adalah "m".
y
P (x1, y1)
x O
A = {a , b , c , d} disebut daerah asal atau domain
B = {1 , 2 , 3 , 4 , 5} disebut daerah kawan atau kodomain Semua anggota B yang mendapat kawan di A disebut daerah hasil atau range R = {1 , 2 , 3 , 4}
f (x) = ax + b atau y = ax + b, dimana a, b R.
Gradien garis OP
M =
1 1
x y
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 28
2. Persamaan garis melalui satu titik P (x1, y1) dengan gradien m Rumus :
3. Menentersamaan garis melalui dua titik P (x1, y1) dan Q (x2, y2) Rumus :
4. Sudut antara dua garis
Jika diketahui persamaan garis y = m1x + n1 dengan gradien m1 dan persamaan y = m2x + n2 , dengan gradien m2 seperti terlihat pada gambar
y y = m1x + n1 y = m2x + n2
0 x
5. Persamaan garis yang melalui titik P (x1, y1) dan sejajar garis y = ax + b
Sebuah garis dengan gradien m1 dikatakan sejajar dengan garis lain yang bergradien m2 jika m1 = m2
Rumus :
6. Persamaan garis yang melalui titik Q (x1, y1) dan tegak lurus garis y = ax + b Sebuah garis dengan gradien m2 akan tegak lurus dengan garis dengan gradien m1, jika m2 = –
1
m 1
.
Rumus :
y – y1 = m (x – x1)
1 2
1 1
2 1
x x
x x y y
y y
atau
y – y1 = m (x – x1) dengan m =
1 2
1 2
x x
y y
tg =
2 1
2 1
m . m 1
m m
y – y1 = m (x – x1) ; dengan syarat: m1 = m2
y – y1 =
m 1
(x – x1) ; dengan syarat : m2 = –
1
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 29
FUNGSI KUADRAT
Bentuk Umum : y = ax2 + bx + c
Untuk a > 0 (positif) kurva menghadap keatas dan mempunyai titik balik minimum.
x1 x2 x1 = x2
D > 0 D = 0 D < 0
(definet positif)
D = diskriminan D = b2– 4.a.c
Untuk a < 0 (negatif), kurva menghadap kebawah dan mempunyai titik balik maksimum. x1 x2 x1 = x2 (definet negatif)
D > 0 D = 0 D < 0 Untuk menggambar garfik fungsi kuadrat langkah-langkahnya sebagai berikut :
Menentukan persamaan funsi kuadrat
Beberapa hal yang perlu diingat dalam menentukan persamaan fungsi kuadrat adalah :
FUNGSI EKSPONEN
1. Tentukan sumbu simetrinya, yaitu dengan rumus : x = 2.a
b
2. Tentukan titik puncak (titik balik), yaitu P (x, y) dengan :
x = 2.a
b
dan y = 4a
-D
atau y =
4.a 4.a.c b2
3. Tentukan titik potong dengan sumbu y, untuk x = 0
4. Tentukan titik potong dengan sumbu x, dengan y = 0 → ax2 + bx + c = 0 Jika D > 0, grafik memotong sumbu x di dua titik (x1 dan x2)
Jika D = 0, grafik menyentuh sumbu x di titik x1 = x2
Jika D < 0, grafik tidak memotong sumbu x ( diatas atau dibawah sumbu x)
1. Jika diketahui titik balik (xp, yp), persamaan kuadrat : y = a (x – xp)2 + yp
2. Jika diketahui akar-akar kuadratnya (x1 dan x2), persamaan kuadrat : y = a (x – x1) . (x – x2)
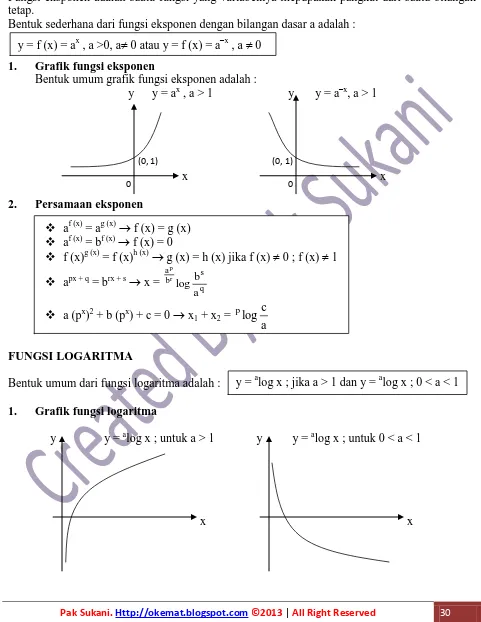
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 30 Fungsi eksponen adalah suatu fungsi yang variabelnya mepupakan pangkat dari suatu bilangan tetap.
Bentuk sederhana dari fungsi eksponen dengan bilangan dasar a adalah :
1. Grafik fungsi eksponen
Bentuk umum grafik fungsi eksponen adalah :
y y = ax , a > 1 y y = a–x, a > 1
x x
2. Persamaan eksponen
FUNGSI LOGARITMA
Bentuk umum dari fungsi logaritma adalah :
1. Grafik fungsi logaritma
y y = alog x ; untuk a > 1 y y = alog x ; untuk 0 < a < 1
x x
(0, 1) (0, 1)
0 0
y = f (x) = ax , a >0, a 0 atau y = f (x) = a–x , a 0
af (x) = ag (x) f (x) = g (x)
af (x) = bf (x) f (x) = 0
f (x)g (x) = f (x)h (x) g (x) = h (x) jika f (x) 0 ; f (x) 1
apx + q = brx + s x = q s b
a
a b log
r p
a (px)2 + b (px) + c = 0 x1 + x2 = a c log
p
[image:30.612.64.545.96.718.2]Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 31
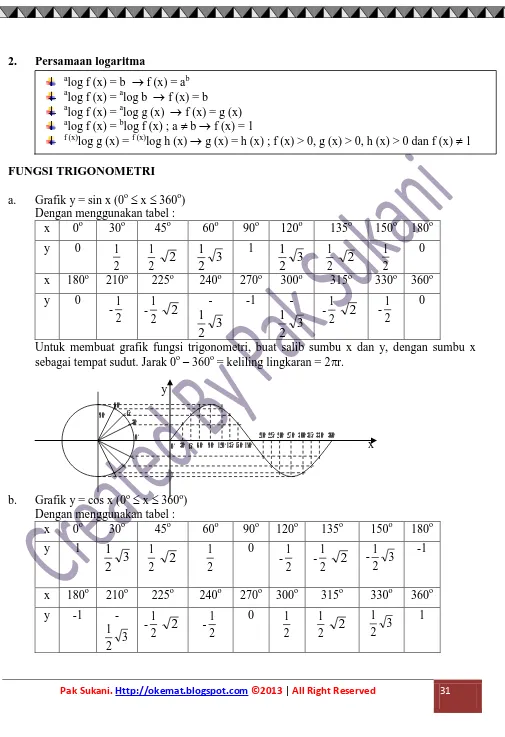
2. Persamaan logaritma
FUNGSI TRIGONOMETRI a. Grafik y = sin x (0o x 360o)
Dengan menggunakan tabel :
x 0o 30o 45o 60o 90o 120o 135o 150o 180o
y 0
2 1 2 1 2 3 2 1 1 3 2 1 2 1 2 2 1 0
x 180o 210o 225o 240o 270o 300o 315o 330o 360o y 0
-2 1 -2 1 2 -3 2 1
-1
-3 2
1 -2
1
2
-2
1 0
Untuk membuat grafik fungsi trigonometri, buat salib sumbu x dan y, dengan sumbu x sebagai tempat sudut. Jarak 0o– 360o = keliling lingkaran = 2r.
y
x
b. Grafik y = cos x (0o x 360o) Dengan menggunakan tabel :
x 0o 30o 45o 60o 90o 120o 135o 150o 180o
y 1
3 2 1 2 1 2 2 1 0 -2 1 -2 1
2 - 3
2
1 -1
x 180o 210o 225o 240o 270o 300o 315o 330o 360o
y -1
-3 2
1 -2
1 2 -2 1 0 2 1 2 1 2 3 2 1 1
0o 30o
45o 60o 90o 120o 135o 150o 180o
210o 225o 240o 270o 300o 315o 330o
360o 45o 30o 60o 90o 0o a
log f (x) = b f (x) = ab a
log f (x) = alog b f (x) = b a
log f (x) = alog g (x) f (x) = g (x) a
log f (x) = blog f (x) ; a b f (x) = 1 f (x)
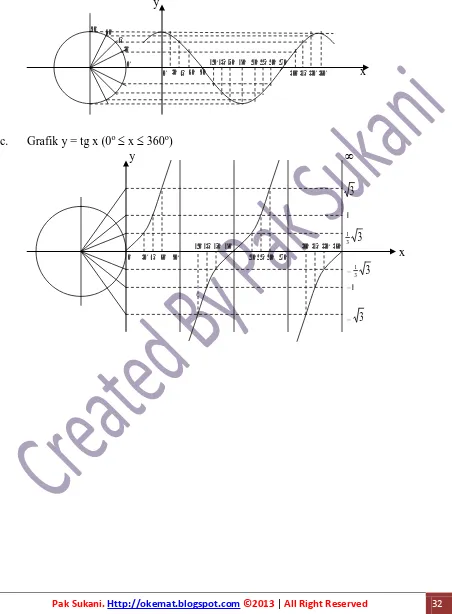
[image:31.612.64.569.18.755.2]Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 32 Untuk membuat grafik fungsi trigonometri, buat salib sumbu x dan y, dengan sumbu x sebagai tempat sudut. Jarak 0o– 360o = keliling lingkaran = 2r.
y
x
c. Grafik y = tg x (0o x 360o)
y
x
0o 30o 45o 60o 90o
120o 135o 150o 180o 210o 225o 240o 270o
300o 315o 330o 360o 45o
30o 60o 90o
0o
300o 315o 330o 360o 270o
240o 225o 210o 180o 150o 135o 120o 90o 60o 45o 30o 0o
3
3 1
3
1
–13 3
– 1
[image:32.612.72.524.105.719.2]Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 33
SIGMA, BARISAN DAN DERET
Misal : a1 + a2 + a3 + a4 + … + an, ditulis
n
1
i i
a dibaca sigma ai, i dari 1 sampai n.
Jika ditulis :
n
m k k
a
k = penunjuk yang berjalan dari m sampai n ; m = batas bawah ; n = batas atas.
Sifat-sifat notasi sigma
1. Barisan Aritmetika
Barisan Aritmetika adalah suatu barisan bilangan dengan beda antara dua suku yang berurutan tetap.
Bentuk umum barisan aritmetika :
U1, U2, U3, U4, … Un atau : a, (a + b), (a + 2b), (a + 3b), …, {a + (n – 1) b}
Rumus Suku ke n : Un = a + (n – 1) . b
dimana: a = U1 = suku pertama
b = beda = U2– U1 atau U3– U2 atau U4– U3atau … Un– Un - 1 Un = suku ke-n
n = banyaknya suku
1.
n
1 k
k
a = a1 + a2 + a3+ … + an
2.
n
m k
k n
m k
k c a
a c
3.
n
m k
k k b )
(a =
n
m k
k
a +
n
m k
k
b
4.
n
m k
k
a =
p n
p m k
k p)
(a
5.
n
m k
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 34
2. Deret Aritmetika
Deret Aritmetika adalah jumlah suku-suku barisan aritmetika. Bentuk umum Deret Aritmetika : U1 + U2 + U3 + U4 + … +Un = Sn Jumlah n suku pertama :
Sn =
(
a
Un
)
2
n
atau Sn =
.
{
2a
(
n
-
1
)
.
b
}
2
n
3. Barisan Geometri
Barisan geometri adalah barisan bilangan yang rasio antara dua bilangan yang berurutan tetap. Barisan Geometri : U1, U2, U3, U4, … Un
Suku ke n : Un = a . rn – 1
Dimana :
U1 = a = suku pertama Un = suku yang ke-n
r = rasio =
1 -n
n
3 4
2 3
1 2
U U ... U U U U U U
n 1 n
U U r
4. Deret Geometri
Deret geometri adalah jumlah suku-suku dari barisan geometri. Bentuk dari Deret Geometri : U1 + U2 + U3 + U4 + … +Un = Sn Jumlah n suku pertama :
Sn =
1
-r
)
1
-n
r
(
.
a
r 1 dan r > 1
Sn =
r
-1
)
n
r
-1
(
.
a
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 35
5. Deret Geometri tak terhingga
Deret geometri : a + a . r + a . r2 + a . r3 + … + a . rn – 1 disebut deret geometri tak terhingga jika r < 1 atau {-1 < r < 1}, r 0.
Jumlah deret geometri sampai suku tak terhinga :
S =
r
1
a
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 36
GEOMETRI DIMENSI DUA
1. Satuan Sudut
Satuan sudut ada 2 macam, yaitu derajat dan radian a. Derajat
b. Radian
2. Konversi Satuan Sudut
Tabel Konversi satuan sudut derajat dengan radian
Derajat 0 30 45 60 90 120 135 150 180
Radian 0
6
4
3
2
3 2
4 3
6
5
Sistem satuan derajat adalah sistem DMS (Derajat, Menit, Sekon) 1o = 60' (menit)
1' = 60" (detik) atau 1o = 3600" (detik)
2 rad = 360o atau rad = 180o 1 rad =
o
180
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 37
3. Rumus-rumus keliling dan luas bangun datar a. Segitiga (jumlah sudutnya 180o)
b c
a
b t c a
b t c
a
b c
a
Hukum Pythagoras untuk segitiga siku-siku :
" Kuadrat sisi miring sama dengan jumlah kuadrat sisi siku-sikunya "
Dari hukum Pythagoras tersebut ada beberapa perbandingan untuk segitiga siku-siku, yaitu (3 : 4 : 5) ; (5 : 12 : 13) ; (7 : 24 : 25) ; (8 : 15 : 17) atau kelipatannya.
b. Segiempat (jumlah sudutnya 360o)
Segitiga siku-siku L = ½ . alat . tinggi L = ½ . a . b
Kel. = a + b + c
Segitiga sama kaki L = ½ . alas . tinggi L = ½ . a . t
t =
2
2 a
2 1
(c)
; b = c
Segitiga sembarang dengan sudut diketahui L = ½ . a . t t = b . sin
L = ½ . a . b . sin
Segitiga sembarang dengan semua sisi diketahui
L = s .(sa) .(sb) .(sc) Keliling = a + b + c
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 38 1. Persegi panjang
L = panjang . lebar l L = p . l
Keliling = 2 . (p + l) p
2. Bujur sangkar
L = sisi . sisi L = a . a a Keliling = 4a
a
3. Jajaran genjang
L = panjang alas . tinggi b t L = a . t
θ L = a . b . sin θ
a Keliling = 2 . (a + b) 4. Belah ketupat
b L =
2 1
. diagonal . diagonal
a L = 2 1
a . b
5. Trapesium
b L = x tinggi
2
sejajar sisi jumlah
L =
2 1
(a + b) . t
a Keliling = a + b + c + d
6. Layang-layang
L =
2 1
. diagonal . diagonal
b L =
2 1
a . b a
c
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 39
c. Lingkaran
L = x jari-jari x jari-jari 7
22
O r L = .r2 7 22
Keliling lingkaran = x 2 x r 7
22
d. Ellips
L = . a . b
a a = ½ sumbu panjang
b b = ½ sumbu pendek
e. Segi n beraturan
L =
n 180 ctg . a . 4
n 2 o
atau L =
n 360 sin . r . 2
n 2 o
Untuk segi enam beraturan
r L = .a . 3 2
3 2
atau L = .r . 3 2
3 2
a a = r
4. Transformasi bangun datar
a. Translasi (Pergeseran)
Translasi adalah suatu transformasi yang memindahkan setiap titik pada bidang datar yang jarak
dan arahnya tertentu oleh translasi T = b a
.
y P' (x', y') P (x, y) → P' (x + a, y + b)
b
P (x, y) a
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 40
b. Refleksi (Pencerminan)
Refleksi adalah transformasi yang memetakan setiap titik pada bidang datar dengan pencerminan yang menggunakan sifat dari cermin datar.
1. Pencerminan terhadap sumbu x y Perhatikan gambar di samping
P' = 1 0 0 1 . P ' ' y x = 1 0 0 1 . y x x
atau P (x, y) P' (x, –y)
2. Pencerminan terhadap sumbu y y Perhatikan gambar di samping
P' = 1 0 0 1 . P ' ' y x = 1 0 0 1 . y x x
atau P (x, y) P' (–x, y)
3. Pencerminan terhadap garis y = x
P' = 0 1 1 0 . P ' ' y x = 0 1 1 0 . y x
atau : P (x, y) P' (y, x)
4. Pencerminan terhadap garis y = –x
P' = 0 1 1 0 . P ' ' y x = 0 1 1 0 . y x
atau : P (x, y) P' (–y, –x)
P (x, y)
P' (x, –y)
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 41 5. Pencerminan terhadap garis x = a
P (x, y) M . x = a P' (2a – x, y)
6. Pencerminan terhadap garis y = b
P (x, y) M . y = b P' (x, 2b – y)
c. Rotasi (Perputaran)
Rotasi adalah suatu tarnsformasi yang memindahkan setiap titik dengan cara memutar setiap ttiik tersebut denganm besar dan arah yang telah ditentukan.
y Pada rotasi terhadap titik O (0, 0) sebesar θ P' (x', y') dengan arah positif, maka titik P (x, y)
menjadi titik P' (x', y')
x' = x cos θ– y sin θ
y' = x sin θ + y cos θ
P (x, y)
x
1. Rotasi sejauh 90o, matriks transformasinya adalah : T =
0 1 1 0 ' ' y x = 0 1 1 0 . y x
2. Rotasi sejauh 180o, matriks transformasinya adalah : T =
1 0 0 1 ' ' y x = 1 0 0 1 . y x
3. Rotasi sejauh 270o, matriks transformasinya adalah ; T =
1 0
1 0 ' ' y x =
1 0
1 0 . y x
4. Rotasi sejauh derajat, matriks transformasinya adalah : T =
cos sin sin cos ' ' y x = cos sin sin cos . y x
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 42
d. Dilatasi (perkalian)
Dilatasi adalah transformasi yang mengubah ukuran (memperbesar atau memperkecil) dengan suatu faktor skala.
P (x, y) → P' (x', y') dengan x' = kx dan y' = ky
5. Komposisi Transformasi
a. Komposisi dua Translasi berurutan T1 =
1 1
b a
dan T2 =
2 2
b a
→ T2 o T1 =
1 1
b a
+
2 2
b a
(T2 o T1) A (x, y) → A" (x", y") dengan x" = x + (a1 + a2) dan y' = y + (b1 + b2) b. Komposisi dua Refleksi berurutan
1. Pencerminan terhadap garis x1 = k dan x2 = l
P (x, y)
l x , k x
x M o x M
2 1
1 2
P" (2 (l – k) + x , y)
2. Pencerminan terhadap garis y1 = m dan y2 = n
P (x, y)
n y , m y
y M o y M
2 1
1 2
P" (x, 2 (n – m) + y)
c. Komposisi dua Rotasi berurutan
Jika titik P (x, y) diputar sebesar θ1 dan diteruskan ke θ2 dengan arah positif sama dan titik pusat yang sama, maka bayangannya adalah : P" (x", y")
Dimana :
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 43
GEOMETRI DIMENSI TIGA
A. Luas Permukaan Bangun Ruang 1. Kubus
H G Jaring-jaring kubus
E F H G
D C D C G H D
A B
A B F E A
E F
Jika panjang sisi kubus adalah "a", maka : Panjang diagonal bidang = a 2
Luas bidang sisi L = a2 Luas bidang diagonal = a2 2 Luas permukaan kubus Lp = 6a2
2. Balok
H G Jaring-jaring balok G F
E F
D C C B F G C
A B
D A E H D
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 44 Lp = 2 {(p . l) + (p . t) + (l . t)}
Volume balok : V = p . l . t
3. Prisma
T Jaring-jaring prisma
R S T
Q T R S T
O P
Q O P Q
Q
Luas selimut prisma segi-n = keliling bidang alas segi-n x tinggi prisma Luas permukaan prisma segi-n = luas selimut + luas alas + luas atas
4. Limas
T Jaring-jaring limas T
D C
D C
A B T T
A B
T
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 45
5. Limas Terpancung
Jaring-jaring limas terpancung
Luas selimut = n . luas bidang trapesium n = jumlah segi bidang alas Luas permukaan = luas selimut + luas alas
6. Kerucut
T Jaring-jaring kerucut T
A
t s
s
A r B
r B
Luas selimut : Ls = x luaslingkaran bidang tegak tegak
bidang lingkaran
kel.
alas lingkaran kel.
= x s2 s 2
r
2
= r s
Luas permukaan : Lp = luas selimut + luas alas = r s + r2 = r (s + r)
A B
C D
E F G H
A B C D
E
E F
F G G
H
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 46
7. Kerucut terpotong
T Jaring-jaring kerucut terpotong T s1 s1 r r s
R s
R
Luas selimut = (R + r) s
Luas permukaan = luas selimut + luas alas + luas atas
8. Tabung
Jaring-jaring tabung
r
t
r 2 r t
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 47
9. Bola
Luas permukaan = 4 . r2 Volume : V = 4/3 . π . r3 r
B. Volum Bangun Ruang 1. Kubus
Volume kubus :
V = s . s . s
s = s3
2. Balok
Volume balok :
V = panjang x lebar x tinggi
t = p x l x t
l p
3. Prisma
Volume prisma :
V = luas alas x tinggi
4. Limas
T Volume limas :
V =
3 1
x luas alas x tinggi
D C
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 48
5. Limas Terpancung
6. Kerucut
Volume kerucut
V =
3 1
x luas alas x tinggi
=
3 1
. . r2 . t
7. Kerucut terpotong
Volume kerucut terpotong :
r V =
3 1
. . t . (R2 + R . r + r2)
t
R
8. Tabung
Volume tabung :
V = luas alas x tinggi
V = . r2 . t
A B
C D
E F G H
b
b t
a
a Volume limas terpancung :
V = 3 1
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 49
9. Bola
Volume bola :
V =
3 4
. r3 atau
V =
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 50
VEKTOR
A. Pengertian Vektor
1. Besaran Skalar, adalah besaran yang hanya mempunyai besar saja Misalnya : panjang, luas, volume, massa, suhu, waktu, laju.
2. Besaran vektor, adalah besaran yang mempunyai besar dan juga arah Misalnya : kecepatan, percepatan, gaya, momen.
B. Penyajian vektor
Vektor a dapat disajikan dalam bentuk :
C. Besar vector Vektor a =
2 1
a a
= a1i + a2 j , besarnya vektor atau panjang vektor a dinotasikan dengan
a , yang besarnya adalah : a = a12 a22
D. Vektor Satuan
Vektor satuan adalah suatu vektor yang panjangnya satu satuan. Vektor satuan dari
vektor
a
adalah : a a ea
matriks kolom a =
2 1
a a
matriks baris a = (a1, a2)
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 51
E. Operasi Vektor a. Penjumlahan vektor
Penjumlahan vektor dapat dilakukan dengan dua cara, yaitu cara segitiga dan cara jajaran genjang.
1. Cara segitiga
Vektor c = a + b adalah :
a
b
2. Cara jajaran genjang
a
bb. Pengurangan vektor
Pengurangan vektor merupakan penjumlahan dengan vektor inversnya (vektor negatif).
a – b = a + (–b)
b
a
–b
a – b
c. Perkalian skalar dengan vektor
Misalkan skalar m dikalikan dengan vektor
a
, maka hasilnya adalah suatu vektor yangpanjangnya merupakan k kali vektor
a
dan arahnya sama dengan arah vektora
.
a
2a
3a
a
b
c = a + b
a
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 52 R =
(
P1)
2
(
P2)
2
2
(
P1)(
P2).
cos
Sifat-sifat perkalian vektor dengan skalar :
1. m .
a
=a
. m2. m . (–
a
) = –m .a
3. m .a = m .a
4. m . (a + b) = m
a
+ mb 5. (m + n) .a
= ma
+ na
d. Resultan dua vektor
P1 R
P2 e. Perkalian skalar dua vektor
Perkalian skalar dua vektor adalah perkalian dua vektor dengan bentuk perkalian titik (dot product) dan hasilnya skalar.
Hasil kali vektor
a
dengan vektor b ditulisa
. b (dibaca a dot b) adalah :a
. b = a . b . cos 0o≤ ≤ 180oa = besar (panjang) vektor
a
a =(
a1)
2
(
a2)
2b = besar (panjang) vektor b b =
(
b1)
2
(
b2)
2 = sudut yang dibentuk oleh vektor
a
dan bf. Panjang vektor
Jika a = a1i + a2 j + a3k maka panjang vektor a adalah :
a = 3 2
2 2 2
1) ( ) ( )
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 53
g. Perbandingan vektor
Misalkan titik P membagi garis Ab dengan perbandingan AP : PB = m : n dengan a dan b vektor posisi titik A dan B. Vektor posisi titik P adalah :
A
m p =
n m
1
. (na + mb)
a P p n
O b B
Koordinat titik P adalah : xp =
n m
mx nx
2
1 ; y
p =
n m
my ny
2
1 ; z
p =
n m
mz nz
2
1
h. Perkalian skalar dua vektor
Jika a = a1i + a2 j + a3k dan b = b1i + b2 j + b3k
Hasil kali vektor
a
dengan vektor b ditulisa
. b (dibaca a dot b) adalah :a
. b = a . b . cos 0o≤ ≤ 180oa = besar (panjang) vektor
a
a = 3 2 22 2
1) ( ) ( )
(a a a
b = besar (panjang) vektor b b = (b1)2 (b2)2 (b3)2 = sudut yang dibentuk oleh vektor
a
dan bSifat-sifat perkalian skalar dua vektor :
a. Jika = 0o maka a dan bsejajar dan searah
a
. b = a . b b. Jika = 90o maka a dan b saling tegak lurus a
. b = 0c. Jika = 180o maka
a
dan b sejajar dan berlawanan arah a
. b = – a . b d.a
. b = b .a
sifat komutatifPak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 54 Perkalian skalar dua vektor dalam bentuk komponen adalah :
a
. b = (a1i + a2 j + a3k) . (b1i + b2 j + b3k)a
. b = a1.b1 + 0 + 0 + 0 + a2.b2 + 0 + 0 + 0 + a3.b3 = a1.b1 + a2.b2 + a3.b3Sudut antara dua vektor :
a
. b = a . b . cos cos = b . ab . a
i. Proyeksi skalar ortogonal
Gambar di samping adalah proyeksi dari
a
ke b diwakili oleh c, sehingga proyeksi skalar vektora
pada b adalah c .c =
b b . a
j. Proyeksi vektor ortogonal
Pada gambar di samping, proyeksi vektor
a
pada b adalah c.c = .b
b b . a
2
k. Perkalian vektor dua vektor
Perkalian vektor dua vektor
a
dan b ditulisa
x b (dibaca a cross b) atau disebut juga dengan perkalian silang (cross product). Hasil kalinya adalah :a
x b = a . b . sin a
x b =3 2 1
3 2 1
b b b
a a a
k j i
O C B
A
a
b
c
O C B
A
a
b
c
[image:54.612.65.548.69.724.2]Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 55
PELUANG
1. Pengisian tempat yang tersedia
Jika pada kegiatan pertama dilakukan dengan x cara berbeda, kegiatan kedua dengan y cara berbeda dan kegiatan ketiga dengan z cara berbeda, dan seterusnya, maka banyaknya cara untuk melakukan kegiatan tersebut berturut-turut adalah x . y . z cara.
2. Permutasi
Permutasi adalah susunan dari objek-objek atau unsur-unsur dengan memperhatikan urutannya. Ciri dari permutasi ini posisinya disebutkan sebagai apa.
a. Permutasi n unsur yang berbeda
b. Permutasi n unsur dengan unsur ada yang sama Pu =
! n . ... . ! n . ! n . ! n
! n
k 3 2 1
c. Permutasi r unsur dari n unsur yang berbeda nPr =
! r) -(n
! n
d. Permutasi melingkar
Ps (n) = (n – 1) ! atau Ps (n) = n
! n
2. Kombinasi
Kombinasi adalah susunan dari objek-objek atau unsur-unsur dengan tidak memperhatikan urutannya. (posisi tidak disebutkan sebagai apa)
Rumus Kombinasi :
nCr =
! r) -(n . r!
! n
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 56
a. Peluang dari suatu kejadian
Peluang dari suatu kejadian adalah perbandingan antara banyaknya titik sampel dan ruang sampel dari suatu kejadian dan dirumuskan dengan :
P = s n
n = titik sampel dan s = ruang sampel
misal : uang logam memiliki s = 2 ; dadu memiliki s = 6 ; kartu bridge s = 52 2 uang logam s = 22 = 4 ; 2 dadu memiliki s = 62 = 36
b. Frekuensi Harapan
Frekuensi Harapan adalah harapan munculnya kemungkinan dari suatu kejadian dan dirumuskan dengan :
Frekuensi Harapan = peluang kejadian x banyaknya percobaan :
FH = P (A) . N
c. Kejadian saling lepas ( kata penghubung "atau")
Jika P (A) adalah kejadian dari A dan P (B) adalah kejadian dari B, maka kejadian saling bebas antara A dan B adalah :
P ( A U B ) = P (A) + P (B)
d. Kejadian tidak saling lepas
Jika A adalah munculnya kejadian A dan B adalah munculnya kejadian B dimana A dan B tidak saling lepas karena ada anggota A yang juga anggota B, maka peluang A atau peluang B adalah :
P ( A U B ) = P (A) + P (B) –P ( A ∩ B )
e. Kejadian saling bebas (kata penghubung "dan")
Jika P (A) adalah kejadian dari A dan P (B) adalah kejadian dari B, maka kejadian saling lepas antara A dan B adalah :
Pak Sukani.Http://okemat.blogspot.com ©2013 | All Right Reserved 57
e. Kejadian tidak saling bebas (kata penghubung "dan")
Jika P (A) adalah kejadian dari A dan P (B) adalah kejadian dari B, dengan kejadian B sangat dipengaruhi oleh kejadian A maka kejadian tidak s